Nonclassical correlations in two-dimensional graphene lattices

Hao Wang

Shanghai Normal University Tianhua College,ShangHai 201815,China

Abstract We investigate nonclassical correlations via negativity,local quantum uncertainty (LQU) and local quantum Fisher information (LQFI) for two-dimensional graphene lattices.The explicitly analytical expressions for negativity,LQU and LQFI are given.The close forms of LQU and LQFI confirm the inequality between the quantum Fisher information and skew information,where the LQFI is always greater than or equal to the LQU,and both show very similar behavior with different amplitudes.Moreover,the effects of the different system parameters on the quantified quantum correlation are analyzed.The LQFI reveals more nonclassical correlations than LQU in a two-dimensional graphene lattice system.

Keywords: negativity,local quantum uncertainty (LQU),local quantum Fisher information(LQFI),graphene lattices,nonclassical correlations

1.Introduction

Quantum coherence and quantum correlation are two fundamental concepts of quantum computation and quantum communication theory [1].From the perspective of correlation,quantum and classical correlations manifest themselves in both bipartite and multipartite quantum systems,while quantum coherences can live in a single system.Various categories of quantum correlation have been put forward to date: quantum entanglement [2],Bell nonlocality (BN) [3],quantum discord (QD) [4] and Einstein–Podolski–Rosen(EPR) steering [5–7].

Quantum entanglement (non local quantum correlation),first recognized by EPR[8],is a burgeoning field in quantum mechanics and a key resource in applications related to quantum information processing.Some numerical measurements,such as concurrence[9,10],negativity and logarithmic negativity [11,12],global entanglement [13] and von Neumann entropy [14,15],have been introduced to quantify entanglement in bipartite as well as multipartite quantum systems.Bell nonlocality is the quantification of nonlocal correlations and is manifested unambiguously by the violation of different Bell-type inequalities;it plays a fundamental role in better understanding of quantum mechanics[16–18].Based on local measurements and optimization,the notion of QD goes beyond entanglement,which cannot be expressed by all correlations in a quantum system and captured by entanglement quantifiers.Up to now,a series of discord-like correlation measures have been proposed and studied from different aspects [19].The widely used measures of quantum correlations proposed in the past 10 years can be categorized roughly into four different families,namely,QD,quantum deficit,measurement-induced disturbance and relative entropy of discord [20].Recently,EPR steering has had important applications in quantum information processing.EPR steering corresponds to the quantum correlation measured by observable steering that is strong enough to demonstrate the EPR paradox [21],which generally lies between Bell non locality [22] and entanglement [23].

Two-dimensional(2D)layered materials such as tungsten diselenide (WSe2) [24],hexagonal boron nitride (hBN) [25],graphene [26],topological insulators [27],phosphorene[28,29] and transition-metal dichalcogenides [30,31],have become one of the most active areas of research and are believed to be promising candidates for future microelectronic devices thanks to their unique magnetic [32,33],electronic[34,35]and optoelectronic[36,37]properties.Stacking[38],twisting [39] and straining [40] 2D crystal layers alongside exploitable magnetic,electronic and optoelectronic properties have demonstrated 2D materials to be of paramount importance for classical and quantum device applications.

Single-layered graphene sheets,the first example of a truly 2D crystal observed in nature,have attracted enormous scientific interest due to their remarkable properties[41]such as optical response,mechanical strength,zero band-gap and large thermal conductivity.The reasons for this tremendous amount of interest are manifold.First,they represent one of the most promising materials for use in future technologies,such as ballistic field-effect transistors.The electric field applied to the graphene sheet (the electric field effect) can tune carrier densities by simple application of a gate voltage.This effect is a fundamental for the design of microelectronic devices.Furthermore,electrons show relativistic behavior in graphene and may be viewed as massless charged fermions.Therefore,this represents an exciting bridge between condensed-matter research and high-energy physics.The unusual quantum Hall effect in single layer graphene has propelled graphene research to new heights [42].Because of the lowenergy excitations and insensitivity to external electrostatic potentials due to the Klein paradox,significant progress has been made in the construction and experimental and theoretical understanding of graphene.Development of various fabrication methods allows for engineering of the electronic,optical and magnetic properties of graphene by controlling the size,shape,edge character,number of layers,impurities and screening [43,44].Remarkably,several schemes have been proposed for thermoelectric machines based on semiconductor quantum dots [45,46],monolayer graphene flakes[47,48] and twisted bilayer graphene [49].Significant attention has also been given to the study of possible applications in graphene-based entanglement [50],quantum memory [51,52] and quantum teleportation [53].Recently,many research works have studied the dynamics of entanglement in a graphene layer system [50,54–62].

Based on the notions of skew information and quantum Fisher information (QFI),Girolamiet al[63,64] proposed two computable measure of quantum correlation quantifiers.One is local quantum uncertainty(LQU)and the other is local quantum Fisher information (LQFI).These two computable measures behave similarly and satisfy the fundamental requirements of quantum correlations.LQU captures strictly non-classical correlations without computing their classical equivalent.LQFI can be used to characterize different parameters and their role in preservation of quantum correlation [65].

The growth of the technology has promulgated quantum correlation to revive a central problem.The problem of quantum inseparability of mixed states has attracted much attention recently and has been widely considered in different physical contexts.The first method to verify entanglement in mixed states was the partial transpose criterion.Negativity is chosen as the measure of entanglement because it can be calculated analytically in the multipartite mixed-state scenario.We use negativity to detect entanglement and LQU to measure discord-like correlations.To estimate quantum correlations,we plan to use negativity,LQU and LQFI,and a comparison of each measure to evaluate quantum correlations will also be drawn.Taken together,graphene systems offer a promising platform for seamlessly exchanging information and computing technologies.

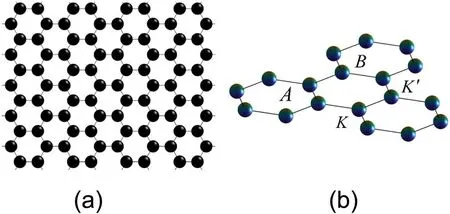
Figure 1. (a)Schematic diagram of the honeycomb lattice model.(b)The Dirac cones located at the K and K′ points.

2.Physical model

Isolated monolayer graphene sheets (MLGSs) consist of a number of carbon atoms which are inter-connected via covalent bonds in a honeycomb lattice.The hexagonal lattice of a graphene sheet is known to be bipartite,i.e.the primitive unit cell contains two carbon atoms,denoted by sublatticeAand sublatticeBas shown in figure 1.The Fermi surface of a half-filled honeycomb lattice consists of two points calledKandK′ at the boundary of the Brillouin zone.The electrons display contrasting properties in the two valleys,which dominate the conductivity.It is necessary to specify their valley indices,which introduces pseudospins associated with the electrons' valleys.

The Pauli matrices are introduced to the sublattice index asfor theA(B)site by up and down pseudospins,and for the valley index asfor theK(K′)points.The spinor basis is ψ(k)=[ψ↑(k),ψ↓(k)],with ψ(k)=[A1,σ(k),B1,σ(k),A2,σ(k),B2,σ(k)],whereA,Bare two sublattices,1,2 represent two inequivalent valleys of the single layer graphene lattice andσ=↑,↓are two projections of electronic spin.

Within the effective-mass approximation,the Hamiltonian around the Dirac points is given by [50,58,66]

whereγdenotes the band parameter,are wave number operators,ωrepresents the intervalley and intravalley scattering processes andis an identity matrix.Here we focus on the case where=(cosφ,sinφ,0)when the intravalley scattering process is accompanied by a phase shiftθ.The intravalley scattering process gives only the potential in the diagonal element in equation (1) and the non-diagonal element comes from the intervalley scattering process.

We consider the short-range impurity potential in the standard basis of the two pseudospin states ψ(k)=[A1,σ(k),B1,σ(k),A2,σ(k),B2,σ(k)].Hence,in the standard computational basis {∣00〉,∣01〉,∣10〉,∣11〉},the eigenvalues can be readily evaluated as

and the corresponding eigenvectors are given by

3.Thermal density and entanglement negativity

The thermal density matrix of the MLGSs at temperatureTis given by the Gibbs state

whereβ=andZis the partition function.The Boltzmann constantkBis set to1 in this work.The thermal density matrix?(T) can be analytically derived by using the spectral decomposition of the Hamiltonian (1).In the twoqubit computational basis,the bipartite density matrix takes the following form:

where the corresponding entries are provided by

The eigenvalues and eigenvectors associated with equation(5)are given by

where the asterisk denotes the complex conjugation.

Entanglement negativity leads to the characterization of entanglement for bipartite mixed states in quantum information theory.For the thermal state?(T) of the graphene sheets,which has two sublatticesAandB,negativity [11,12] is defined as

Using equations (5) and (10) in the negativity equation (9),we obtain the analytical expression for negativity which is given by

Negativity is presented as a function of temperature in figures 2(a) and (b).It is seen that negativity decreases to zero as the temperature increases.We observe that the threshold temperature can be manipulated by varying the scattering strength and wave number operators.It is interesting that the threshold temperature increases when the scattering parameterωincreases.The wave numberskxandkyalso affect the threshold temperature,but a higherkxresults in a slow decrease in negativity and a higherkyshows a rapid decrease in negativity at lower temperature for a given set of parameters.

It is quite obvious that negativity shows a monotonic behavior with the band parameterγand scattering strengthω.We observe that negativity is zero when the band parameterγis zero,and increases with increase in the band parameterγ(figure 2(c)).It is evident that the negativity was generated due to the increase in the band parameter.For higher values of the band parameterγ,the negativity reaches the maximum value.On the other hand,the variations of negativity show a very rapid increase for small values of the scattering strengthω,from zero to maximum values and decrease with increase of the scattering parameter,as shown in figure 2(d).

4.Quantum correlation quantifiers

LQU and LQFI are both tools used to capture purely quantum correlations in multipartite quantum systems.We introduce LQU and LQFI as quantum correlation quantifiers to examine their behaviors in 2D graphene lattices.

4.1.Local quantum uncertainty

The concept of LQU,the minimum skew information obtained via local measurement on a qubit part,is written as

In particular,for bipartite systems,the LQU with respect to subsystemAturns out to be

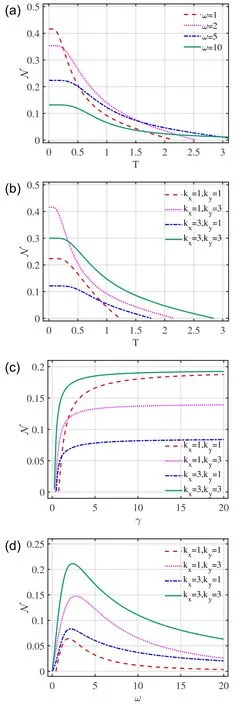
Figure 2. Negativity(N)as a function of(a)temperature T for fixed scattering coefficients ω with γ=1, kx=1 and ky=3,(b)temperature T for different values of wave numbers kx and ky with ω=1,γ=1,(c)the band parameter γ for different wave numbers kx and ky with T=1,ω=1 and (d) scattering strength ω for various wave numbers kx and ky with T=1,γ=1.The fixed parameter is μ=π/3.

where?11,?22and?33are the eigenvalues of the3 ×3 symmetric matrixWABwith the entries

Figure 3 depicts the values of LQU versus temperatureT,band parameterγand scattering strengthω,respectively.It is quite obvious that LQU shows a monotonic behavior with the band parameterγand scattering strengthω.We observe that LQU is zero when the band parameterγis zero,and LQU increases with increase inγ.It is evident that LQU between the lattice points reaches its maximum value for higher values ofγdue to the increase inγ.It is very interesting to observe that LQU first increases and then decreases with increase in the wave numberskxandky.Furthermore,LQU is maximum at the scattering strengthω=0 and decreases with increase in the scattering strength parameterω(shown in figure 3(d))for higher values of bothωand wave numberskxorky.

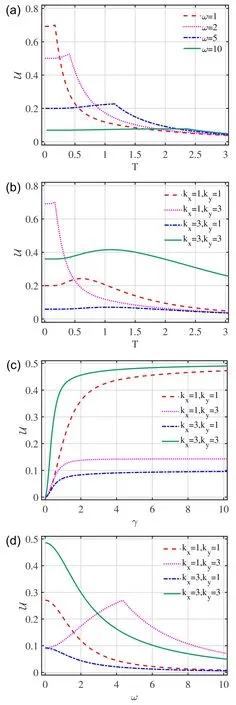
Figure 3. LQU (U) as a function of (a) temperature T for fixed scattering coefficients ω with γ=1,kx=1 and ky=3,(b)temperature T for different values of wave numbers kx and ky with ω=1,γ=1,(c) band parameter γ for different wave numbers kx and ky with T=1,ω=1 and (d) scattering strength ω for various wave numbers kx and ky with T=1,γ=1.The fixed parameter is θ=π/3.

4.2.Local quantum Fisher information

LQFI,introduced by Girolamiet al[63,64],is recognized as an important key computable measure of a discord-type quantum correlation quantifier in a bipartite quantum system [68].

The measure is defined as the worst-case QFI over all local Hamiltoniansaffecting the subspace of partyAin the bipartite system,as follows:

whereμ11,μ22andμ33are the eigenvalues of the3 × 3real symmetric matrix Mlkwith entries

According to equation (20),we find that the matrix Mlkis diagonal and its eigenvalues are calculated as

The behavior of LQFI in two-dimensional graphene is plotted in figure 4.Figures 4(a) and (b) show that LQFI is maximal for the temperatureT=0and is reduced by increasing the value ofT.In figures 4(c)and(d),we visualize LQFI as a function of the band parameterγand the scattering strengthωwithT=1andθ=.Figure 4(c) shows the LQFI versusγfor various values of the wave numberskxandky.The LQFI exhibits a sudden change in behavior withγ.Indeed,the quantifier of the LQFI displays an increasing behavior until a threshold valueγC.In addition,increasingγenhances the number of quantum correlations contained in the system until it reaches a maximum number of correlations.In particular,in figure 4(d) one can see that the LQFI shows an increase in quantum correlations to a maximum value with increasing scattering strengthωuntil a critical valueωC,which depends on the values ofkxandky.We notice that the value of the transition pointγC(ωC)increases with increase in the value ofkxandky.

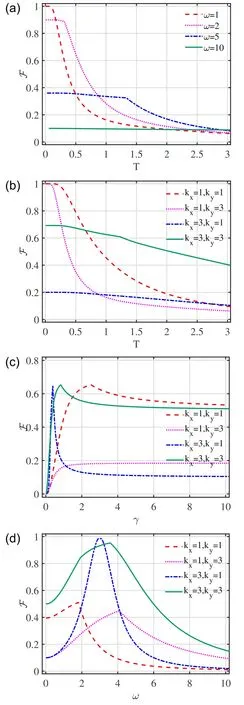
Figure 4. The LQFI (F) as a function of (a) temperature T for fixed scattering coefficients ω with γ=1,kx=1 and ky=3,(b)temperature T for different values of wave numbers kx and ky with ω=1,γ=1,(c)band parameter γ for various wave numbers kx and ky with T=1,ω=1 and (d)scattering strength ω for various wave numbers kx and ky with T=1,γ=1.The fixed parameter is θ=π/3.

5.Results and discussion

We observe that the negativity,LQU and LQFI show a similar behavior with respect to the three parameters temperatureT,band parameterγand scattering coefficientω,as shown in figures 2–4.

Negativity,LQU and LQFI are presented as a function of temperature in figures 2(a),3(a) and 4(a).It is clearly seen that negativity,LQU and LQFI decrease to zero as the temperature increases.Negativity diminishes more quickly than LQU and LQFI,and it vanishes suddenly.But LQU and LQFI tend to zero asymptotically for large values of temperature.Therefore,LQU and the LQFI appear more stable than negativity.We observe that the threshold temperature can be manipulated by varying the scattering strength and wave number operators.It is interesting that the threshold temperature increases when the scattering parameter increases.Figures 2(b),3(b) and 4(b) show that the wave numberskxandkyalso affect the threshold temperature,but a higherkxresults in a slow decrease in concurrence and a higherkyshows a rapid decrease in concurrence at a lower temperature for a given set of parameters.

The effect of the band parameterγon the behavior of correlation measures is illustrated in figures 2(c),3(c)and 4(c)forT=1,θ=.Apparently,not all correlations exist for a weak band parameter.They suddenly appear and increase until they obtain steady values and remain in this situation for strong band parameter values.It is clear that N ≤ U ≤F when they become fixed there are no correlations for weak band parametersγ,but with increasingγthey suddenly revive and obtain fixed values for strongγ.

Figures 2(d),3(d) and 4(d) display the correlations in terms for the scattering strengthωfor various wave numberskxandky.The negativity,LQU and LQFI increase and reach their own maximum values for some weak scattering strengthω.The negativity has a lower position than the LQU and LQFI.However,they disappear for strong values ofω.

Skew information (LQU) and LQFI are presented in figures 3 and 4,respectively.Both measures show the same behavior but with different upper bounds.It can be seen that increasingωandγhas a destructive effect on the non-classical correlations.As depicted in figures 3 and 4,it is obvious that LQU and LQFI exhibit similar variation versus temperatureT.Furthermore,it is clear to see from the above results that the amount of quantum correlation measured by LQFI is greater than by LQU.This result agrees with the inequality which states that LQFI is always greater than LQU

6.Conclusion

We employed the negativity,LQU and LQFI criteria for the measurement of quantum correlations in a graphene sheet system.The analytical expressions for negativity,LQU and LQFI were derived.Based on this,the impact of various parameters of the considered system,such as the scattering coefficients and band parameter,wave numbers and temperature on the dynamics of quantum correlations were studied.Our results confirmed that negativity,LQU and LQFI show a similar behavior with respect to the three parameters (temperature,band parameter and scattering coefficients).We observe that at low temperatures negativity remains robust.As the temperature becomes higher,LQFI and LQU remain non-zero,even if negativity vanishes completely.Additionally,we noticed that the degree of non-classical correlations shown by LQFI is always greater than or equal to the LQU.This reveals that the QFI is bounded by the skew information.As a consequence,we think that the presented analysis may offer interesting perspectives for actual and future models in quantum information processing.