Stability analysis of a time-delayed Van der Pol–Helmholtz–Duffing oscillator in fractal space with a non-perturbative approach

Yusry O El-Dib

Department of Mathematics,Faculty of Education,Ain Shams University,Roxy,Cairo,Egypt

Abstract The time-delayed fractal Van der Pol–Helmholtz–Duffing (VPHD) oscillator is the subject of this paper,which explores its mechanisms and highlights its stability analysis.While timedelayed technologies are currently garnering significant attention,the focus of this research remains crucially relevant.A non-perturbative approach is employed to refine and set the stage for the system under scrutiny.The innovative methodologies introduced yield an equivalent linear differential equation,mirroring the inherent nonlinearities of the system.Notably,the incorporation of quadratic nonlinearity into the frequency formula represents a cutting-edge advancement.The analytical solution’s validity is corroborated using a numerical approach.Stability conditions are ascertained through the residual Galerkin method.Intriguingly,it is observed that the delay parameter,in the context of the fractal system,reverses its stabilizing influence,impacting both the amplitude of delayed velocity and the position.The analytical solution’s precision is underscored by its close alignment with numerical results.Furthermore,the study reveals that fractal characteristics emulate damping behaviors.Given its applicability across diverse nonlinear dynamical systems,this non-perturbative approach emerges as a promising avenue for future research.

Keywords: Van der Pol–Helmholtz–Duffing oscillator,fractal space,time-delay,nonperturbative approach,stability analysis,El-Dib’s frequency formula

Introduction

Fractals,intricate structures that recur at every scale,play a pivotal role in a myriad of natural phenomena,capturing the attention of researchers across diverse scientific and engineering domains such as plasma physics,fluid mechanics,optical fiber technology,chemical engineering,and materials science.Concurrently,fractal theory has been instrumental in evaluating heat flux within network branches[1–3].In recent times,an inclination is growing towards fractal calculus as a tool to elucidate complex phenomena.Traditional integral calculus often falls short of providing comprehensive insights into these intricate systems,prompting researchers to turn to fractal calculus for a more nuanced understanding [4–8].

As essential components of micro-and nano-electromechanical systems (MEMS/NEMS),micro-and nanosensors have found a wide range of applications in cuttingedge engineering systems [9].The latest development in fractal MEMS theory incorporates fractal geometry into MEMS design to enhance performance,sensitivity,and efficiency.Fractal geometries,known for their recursive,selfsimilar patterns,offer a high surface area-to-volume ratio,beneficial for various MEMS applications,including sensors,actuators,and resonators.This advancement has led to MEMS with improved electrostatic forces,quality factors,and multi-functional capabilities.Advances in fabrication techniques have enabled the precise creation of these complex fractal structures at micro-and nano-scales,broadening the potential of MEMS in sectors such as biomedical engineering,environmental sensing,and telecommunications.As fabrication technology continues to evolve,fractal MEMS is expected to pave the way for devices that are more sensitive,energy efficient,and capable of performing more complex tasks,marking a significant shift in the capabilities of MEMS technologies [10].

The study of chaotic oscillators and their evolution has become a riveting area of research,garnering significant academic interest in recent times.This surge in investigations into chaotic synchronization is spurred by its myriad applications spanning fields such as network security,chaos-generating architectures,chemistry,lasers,biological systems,information technology,and neural networks,to name a few.These applications underscore the intricate and captivating nature of the real world.A notable study delved into the dynamical system of a periodically driven particle using a VPHD approach [11].The precision of this method is exemplified by the boundary of the fractal basin.Further research explored the potential for multi-parameter oscillators employing VPHD to achieve adaptive harmonization [12].Computational simulations substantiated the findings,revealing the fractal nature of the attraction basins.Feng[13]delved into the primary integrals of the Duffing–Van der Pol model,specifically under certain parameter constraints.By employing inverse transformations,initial integrals of the primary oscillator system were derived under the stipulated parameter conditions.Additionally,specific instances of these equations were presented.A novel and straightforward approximation technique was proposed for the nonlinear fractal Duffing–Van der Pol oscillator[14,15].The proposed method offered a unique perspective on addressing the VPHD oscillator [16],circumventing the challenge of accurately tracing the solution’s behavior and presuming a credible approximation of the solution over an extended duration.Regrettably,using the conventional technique,it was not feasible to negate these secular effects.Consequently,the non-perturbative approach yielded a constrained approximation solution.Recognizing the significance of the aforementioned factors,this study aims to derive an approximate solution for the VPHD.Delays are prevalent in numerous systems across engineering,physics,chemistry,biology,and economics.Factors such as sensor and actuator dynamics,signal transmission,and digital computations introduce time delays,which profoundly influence the stability and performance of control systems.The situation is further complicated when the time delay is indeterminate.Predicting temporal delays in a control system is a daunting task,and it becomes even more intricate when the nonlinear dynamical system is undefined.A nonparametric identification strategy was employed to pinpoint nonlinear dynamic systems and ascertain the time delay introduced by feedback control [17].The proposed method’s effectiveness and accuracy were showcased through the simulation of a nonlinear Duffing oscillator.The rationale for exploring time-delay systems was briefly touched upon,highlighting the observed alterations in models,stability,and structural dynamics due to the introduction of delays [18].Findings from numerical simulations,which utilized noisy datasets,as well as hands-on experiments on a process influenced by delays,were shared.Research has delved deep into the process of identifying and determining the discernibility of systems influenced by time delays [19].Initial results showcased the identification of linear delay systems,characterized by involvement equations.The robustness of the suggested approach was validated through real world experimental outcomes and simulations that incorporated noisy data.In the context of impulsive noise scenarios,a cutting-edge adaptive method for assessing time delays,which also factored in amplitude attenuation,was put forth [20].To bolster the proposed two-step algorithm,a recursive solution for the straightforward approach was articulated in a definitive closed form.This solution stands out as it does not rely on free parameters,setting it apart from the two-step process rooted in gradient-based techniques.The Jerk–Duffing oscillator’s nonlinearity was curtailed by introducing time-delayed position and velocity [21,22].The inclusion of this time delay acts as a protective barrier,ensuring the system in question does not undergo nonlinear vibrations [23].With advancements in artificial intelligence,computational methods were employed to scrutinize the behavior of multi-delay differential systems,emphasizing the significance of potential time [24].In addressing the challenges posed by nonlinear delays,an innovative approach was introduced,conceptualizing an intelligent computational model that leverages both the strengths and weaknesses of the established method through dual-layered network frameworks[25].For the computational analysis of the nonlinear delay system,particularly concerning the dynamics of plant virus propagation influenced by seasonality and delays,advanced stochastic models rooted in artificial intelligence were utilized [26].

Nonlinear oscillators are widely recognized for their potential in crafting solutions to an array of engineering challenges.While these oscillators present intricate complexities and boast only a handful of exact solutions,achieving comprehensive solutions for such categories often seems unattainable.This complexity has piqued the curiosity of researchers,leading them to explore asymptotic solutions for various nonlinear equations.Techniques like the small parameter method and the averaging method have been instrumental in addressing weak nonlinear scenarios[27,28].In recent times,iterative techniques,particularly those utilizing the HPM,have gained prominence.These methods have been pivotal in devising solutions for a broad spectrum of nonlinear challenges,yielding approximations that closely mirror their closed-form counterparts [29].The parameter expansion method is a mathematical approach utilized in solving nonlinear equations,particularly prevalent in perturbation theory.It entails expanding the solution in terms of a small parameter,yielding an approximate solution that becomes progressively more accurate as the parameter nears zero.This method simplifies complex nonlinear problems into a sequence of simpler problems,often resulting in a series of linear approximations that converge toward the nonlinear solution [30].The Li–He modified homotopy perturbation method (HPM) represents a notable advancement in analytical techniques for solving nonlinear differential equations.It is a refinement of the original homotopy perturbation method formulated by Ji-Huan He.The modification introduced by Li and He primarily aims to enhance the convergence rate and accuracy of the solution,thereby establishing it as an effective instrument for addressing highly nonlinear problems[31–33].These techniques often hinge on the initial approximation of the solution to the problem.Consequently,if this initial guess is inaccurate,the method might not converge,leading to unsatisfactory results.A significant challenge that has intrigued many researchers in the realm of nonlinear oscillators is the investigation of an expansive spectrum of vibrational frequencies [34–39].

The inherent complexity of nonlinearity has posed significant challenges for scholars and applied physicists in deriving precise or near-precise solutions for various nonlinear oscillations.El-Dib [40,41] pioneered the frequency formula,ingeniously converting a nonlinear problem into a linear one,yielding a remarkable solution.Since then,a plethora of frequency formula variants have been developed,aiming to swiftly and accurately decipher the vibrational characteristics of nonlinear oscillatory systems.

The fractal VPHD holds promise for a wide range of physical and practical applications,especially considering the aforementioned advantages.There remains significant scope for further research on the stability analysis of the delayed VPHD in both engineering and academic domains.This second-order equation,with its time delay,showcases cubic–quadratic nonlinearity.In this investigation,we employ a nonperturbative method to derive the most accurate approximate solution.In contrast to typical practices,this solution is not juxtaposed with a numerical approach [40,41].

The rest of the paper is organized as follows to outline the direction of our research.The investigated fractal oscillation is improved in the section ‘Methodology’ by incorporating quadratic nonlinearity into the stiffness function and applying the transformation formula of El-Dibet al.The homogeneous equivalent linearized oscillation is derived,considering the effects of delayed displacement and velocity on the equivalent frequency,in the section ‘Equivalent linearized problem’.El-Dib’s frequency formula is used in this section to estimate the equivalent damping coefficient and frequency.The frequency equation is evolved into a fourthorder polynomial in the ‘Stability investigation’ section,and the discernment is used to obtain the stability criterion.The‘Numerical validation’ section uses a variety of charts to display the results.The final section of the report,‘Conclusions,’ summarizes the main findings of the current investigation.

Methodology

The time-delayed Van der Pol–Helmholtz–Duffing oscillator is represented by the fractal derivative in the following way,where the variableu(tα) represents displacement:

whereμ,β,γ,η,λ,andω0are constants: the last one refers to the natural frequency,μ is the damping coefficient,βis the Helmholtz coefficient,γ is the Duffing coefficient,η is the coefficient of the delayed velocity,λis the coefficient of the delayed position variable,and τ is the time-delayed parameter.The initial conditions of equation (1) may be initiated as

Using a trial solution,one can obtain an approximation representation for the delayed velocity variable and the delayed displacement variable without resorting to the Taylor expansion.Typically,this would entail considering the unique dynamics of the system while examining a functional form that approximates the behavior of these variables.In the context of the nonlinear oscillator,the trial solution should ideally capture the key elements of the delayed variables.As a result,one might think about implementing the following trial solution:

This statement satisfies the first requirements stated in (2),hence the following statement is accurate:

It is simple to confirm that the delayed velocity function and delayed displacement function can be roughly obtained in the following way.

A simplified version of the nonlinear fractal equation(1)with the time-delayed parameter τ included is obtained by integrating (5) and (6).

wheref0(u2),f1(u2),andf2(u2) are quadratic nonlinear functions.The initial function pertains to the Van der Pol damping coefficient,the subsequent one denotes the Duffing contribution coefficient,and the final function signifies the Helmholtz contribution.These functions are delineated as follows:

Expanding upon El-Dib’s research [41],it is possible to enhance the Helmholtz functionf2(u2)to potentially aid in the formulation of the system’s frequency,manifesting as:

Concerning the improved form found in (11),the nonlinear oscillator (7) mentioned before becomes

where the new stiffness functionF(u2) is given by

The equivalent linearized fractal problem

Using the following steps,we can obtain the equivalent linearized form of equation (7):

Assume the following form for the linear equation we are searching for:

whereμeq(Ω) andare the equivalent damping coefficient and the equivalent natural frequency to be determined.When equation(7)is transformed into the linear form seen in(14) an error will occur.Minimizing this mistake is the goal.

The following mistakes result from comparing the nonlinear equation (7) with the linear equation (14) that contains unknowns:

This is when understanding mean square errors comes in handy.

whereTis the period corresponding to the system oscillation.It is observed that minimizing mistakes necessitates

Upon solving the aforementioned equations,

The equivalent damping coefficient and analogous natural frequency formulas can be obtained by applying the trial solution (3) to the aforementioned equations.

The formulas found here are identical to those found previously in[23,40,41].Completion of these integrations using(8)–(10) and (13) yields

When the initial conditions(2)are applied,the exact solution of the linear damping equation (14)can be found in the form

where Ω is given by

The aforementioned equation can be expressed in the frequency parameter Ω as a transcendental polynomial form.By incorporating (22) and (23) into (25) yields,we can achieve

where

Fractal problems in the traditional space

It is notably complex to find a representation of the fractal problem in the traditional derivative rather than a fractal derivative: an issue that frequently arises in real-world scientific and engineering applications [42].Since finding a precise solution to these nonlinear fractal models is inherently difficult,analytical and numerical approaches are the most effective ways to tackle the problem.The ability to convert a fractal space into its continuous counterpart is a distinctive advantage of a novel technique presented by El-Dibet al[2,15,42,43].

The fractal derivative that emerges in equation (14) is transformed into the traditional derivative in the continuous space using the formula of El-Dibet al[2].Note that this formula relies on He’s definition of the fractal derivative[7,44,45].

Consequently,we have

whereSis a real constant indicating a fractalness parameter of the medium,depending on the fractal dimension α to be determined later.

We present the subsequent notation:

Thus,the form of (27) and (28) is

By utilizing equations(31)and(32)within the context of the fractal equation (14),we may construct an alternate representation of the fractal time-delayed Van der Pol oscillator.This procedure successfully converts the equation into its equivalent in continuous space,yielding the following form:

It is noted that equation (33) is formulated in terms of the unknown fractal parameterSas well as the fractal dimension parameter α.To avoid the dependence on these parameters we proceed to find the parameters ξ and ζ in terms of the system’s coefficients.

Since equation (33) effectively converts equation (14)into a new space,a straightforward comparison of the two ought to make it easier to comprehend how the fractal oscillation behaves.We can obtain a set of equations by explicitly comparing the coefficient of the natural frequency in equation (33) with that of equation (14),and similarly comparing the coefficients related to the damping force.

These two coupled equations have the parametersξandζ.The following relation results from using (34) to solve (35):

This finding suggests the existence of a critical damping condition[46].In this special case,the system tries to restore to equilibrium as soon as feasible without fluctuating.A precise balance between the damping force and the oscillation propensity of the system is represented by critical damping.It should be highlighted that the study of the two scales provided by the solution (24) does not support this result.

The transformation (31) is applied to the initial conditions (2),resulting in the continuous space becoming

The trial solution in continuous space must be described by the following expression because of the disparate initial circumstances (37):

Through the process of integration of (38) into the linearized equation (33),the residual error function,which is represented asRE(Ω;t),can be obtained and expressed as follows:

We estimate the residual Galerkin technique,which is described as

By utilizing equation (25) to obtain the aforementioned integral,the two parameters,ξ and ζ,can be related as follows:

The notations(27)and(28)were reformulated as follows in terms of the damping coefficientμeqand the equivalent frequencyafter solving (35) with (41).

The comparison of equations(42)and(43)with the original definitions given in equations (27) and (28) reveals the values of the unknown parametersSandSα as follows:

Utilizing the values obtained from equations (42) and (43),equation (33) can be reformulated to reflect the coefficients specific to the system.This revised equation encapsulates the dynamics of the system more precisely,embedding the parameters derived from the comparative analysis of the original definitions,

where the damping coefficientσ(Ω) and the conservative frequency?2(Ω) in continuous space can be expressed as follows:

Concerning(47)and(48),the solution to equation(46)is as follows:

where the simplified version of the frequency Θ is provided by

In terms of the relation (25),this argument has the form

The damping linear harmonic equation arising from this argument is as follows:

Stability investigation

To assess the stability characteristics,the properties of the critical damping require that Ω2=,which leads to the following condition:

Regarding (50) the critical damping demands that,which necessitates the following condition:

The following transcendental quadratic equation is predetermined by removing the powers Ω3and Ω4between (53)and (54):

To assess the stability characteristics,it is possible to express the above equation as a perfect polynomial form in the frequency parameter Ω;it is convenient to normalize the delay parameter τ[47],which appears in(53)and(54),by the total frequency Ω such that τ→.This gives the error in the coefficientsb2,b1,andb0as

For stability to manifest,it is imperative that the frequency Ω possesses real values.To delineate the conditions for stability,one should identify the prerequisites that guarantee real values for Ω.

Given the quadratic frequency formula mentioned in(55),there is one associated discriminant.This discriminant must be positive to confirm the presence of real values for Ω.Hence,the condition for stability necessitates the subsequent relation:

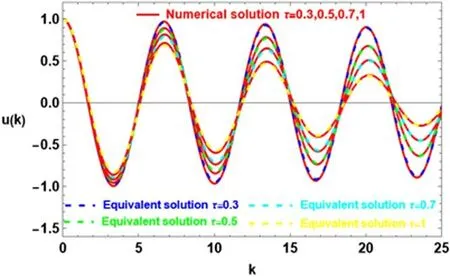
Figure 1. Comparison of the numerical solution of equation (1) and the analytical solution of (24) with the variation in τ for a system having μ=η=λ=0.1,γ=β=0.01,ω0=1 and A=1.

Numerical validation

This section is dedicated to verifying the approximate solution (24) obtained using the non-perturbative approach.By comparing it to the numerical solution of equation(1),where the variabletα is treated as a new variablek,this validation is accomplished.The parameters that are being examined have been determined to have the following values:μ=η=λ=0.1,γ=β=0.01,ω0=1,andA=1.Equation (26) provides a numerical determination of the frequency Ω,which makes the analytical solution (26) easier to compute.Upon examining the solutionu(k)waveform,one can observe a declining trend over the investigated time interval,indicating a tendency of the solution to approach stability.The influence of fractal properties can be used to explain this observation.More specifically,damping is acted upon by the fractal dimension α,as[2,15,42,43]emphasize.

Both solutions are shown simultaneously in figure 1,and a comparison shows that they are quite similar,particularly when delay parameter τ is considered.A detailed analysis of the delay parameter’s impact on the waveform reveals that a rise in τ is correlated with both a decrease in the waveform’s amplitude and an increase in the fractal system’s decay behavior.This indicates that in the context of a fractal system the delay parameter adds a degree of stability.Remarkably,this behavior aligns with findings found outside of fractal space,as reported in [23].

The waveform is imaged in figure 2 with three different values of the delayed velocity amplitude,η,while maintaining the same historical parameters as in figure 1.Notably,higher divergent behavior and increased waveform amplitude are caused by a small rise in η.This demonstrates how η maintains stability in the fractional system.[21]Documents results from non-fractal situations,which are reflected in this behavior.The reference’s analysis,which was based on homoscedasticity perturbation,concentrated on the lagged parameter τ‘s decaying effect.

Now let us look at figure 3 and examine the impact of the offset’s delayed amplitude,λ.Consecutive values of this variable were selected for analysis.The waveform’s amplitude gradually decreases and the decay behavior becomes more robust as λ values increase,according to observations.This suggests that this variable has a stabilizing effect.

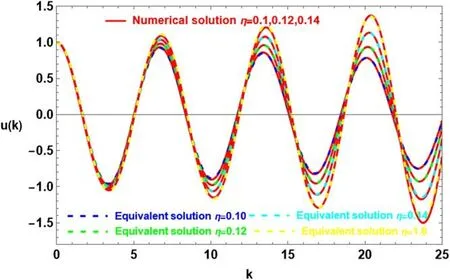
Figure 2. Comparison of the numerical solution of equation (1) and the analytical solution of (24) for the same system as given in figure 1 except that τ=0.4 with the variation in η.

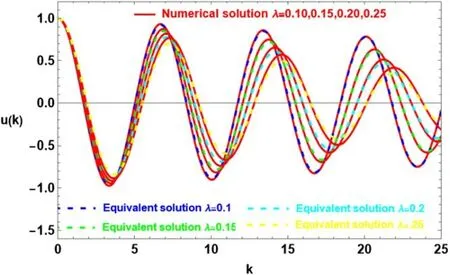
Figure 3. Comparison of the numerical solution of equation (1) and the analytical solution of (24) for the same system as given in figure 1 except that τ=0.4 with the variation in λ.

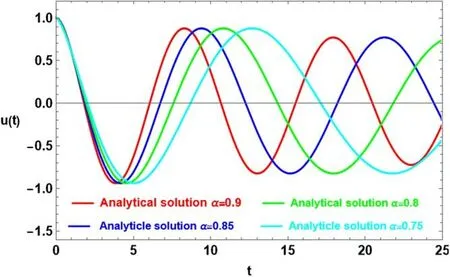
Figure 4. Temporal behavior for the solution of(24)with a variation of α for the same system as considered in figure 1 with =0.5.

The fractal solution as given by equation (24) is illustrated in figure 4,which highlights the effects of changes in the fractal parameter α.The graph shows that when α decreases the waveform’s cycle time lengthens.This behavior demonstrates how a decrease in α stabilizes the system within the framework of the delayed fractal.

Figure 5 plots the analytical solution of (49) that arises from the application of transformations (31) and(32),which,in traditional interpretations,convey the influence of the fractal system without the values of α directly appearing.Research revealed that a rise in oscillation amplitude,indicative of instability,is caused by the effect of a value for τ=0.1.The situation where the damping coefficient is negative is comparable to this role.The opposite behavior is seen when τ values rise,with a progressive amplitude decrease evident.This suggests the existence of a decaying state,which is indicative of stability.As a result,these τ values are consistent with the positive damping coefficient’s beneficial role.This conduct aligns with the patterns shown in figure 2.

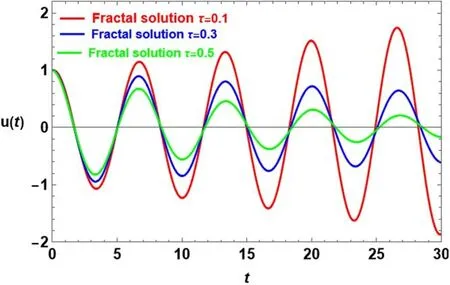
Figure 5. Temporal behavior for the solution of(49)with a variation of the delay parameter τ with arbitrary of the fractal parameter α.

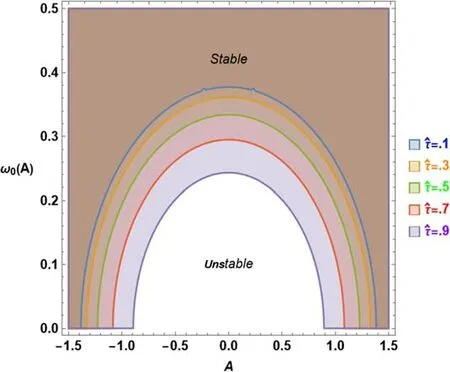
Figure 6. The stability plot for A–ω0 illustrates the stability conditions (56) in response to variations in the delayed parameter for a system characterized by μ =η=λ=γ=β=0.1.

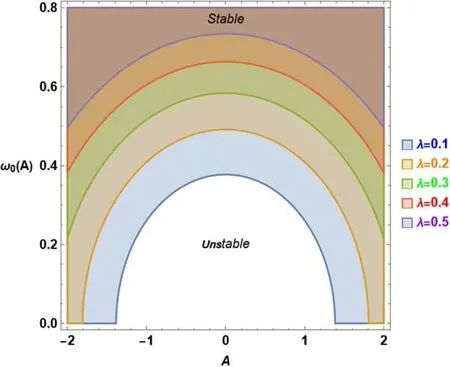
Figure 7. The stability plot for A–ω0 illustrates the stability conditions(56)in response to variations in the delayed displacement parameter λ for the same system as considered in figure 6 with =0.1.

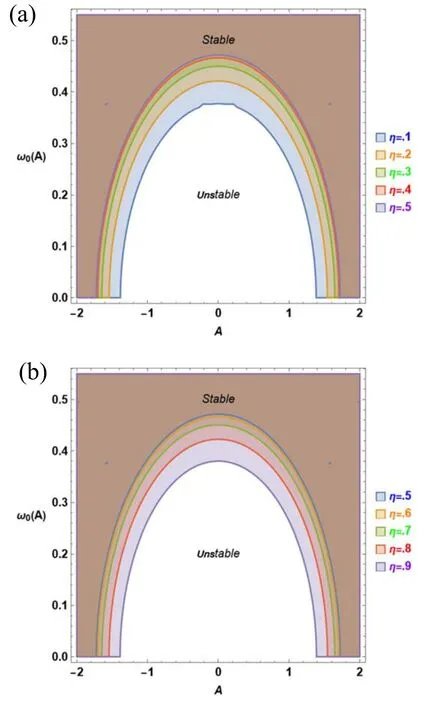
Figure 8. (a) The stability plot for A–ω0 illustrates the stability conditions (56) in response to variations in the delayed velocity coefficient η≤0.5 for the same system as considered in figure 7.(b)The stability plot for A–ω0 illustrates the stability conditions(56)in response to variations in the delayed velocity coefficient η >0.5 for the same system as considered in figure 7.

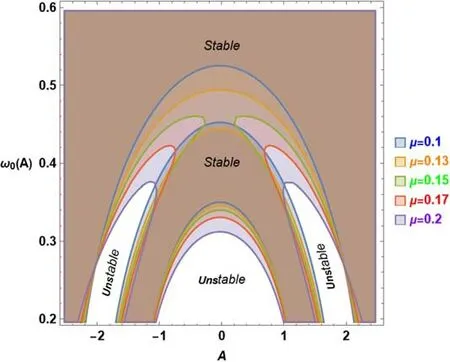
Figure 9. The stability plot for A–ω0 illustrates the stability conditions(56)in response to variations in the damping coefficient μ for the same system as considered in figure 7,except that η=1 and =0.6.

Figures 6 through 9 depict the stability behavior.A system with amplitudeAis displayed against the stability requirements (56) for ω0.The graph’s shaded region,represented by the term‘stability,’denotes the stability zone,while the unshaded portion,represented by the word ‘instability,’denotes instability.In this approach,the frequency parameter has been used to normalize the lagged parameter for simplicity of reading.The stabilizing impact of the delayed parameter is restored by such imaging.This observation validates the distinct patterns shown in figure 6.The graph demonstrates how the stable zone grows in size as the parameter is increased.

The examination of the series of values for the parameter λ is displayed in figure 7.The graph shows that the unstable zone grows with increasing absolute values of λ,as expected.This conduct aligns with the findings in figure 3,where the influence of λ seems to be erratic.

For the same system as in figure 6,figure 8(a) was plotted,but instead of allowing the amplitude η to change it had a fixed value.The parameter η in figure 8(a) changed from 0.1 to 0.5.The system has an unstable behavior as η increases,with the region of increasing instability gradually decreasing as η increases until it reaches the value η=0.5,as shown in figure 8(a).This behavior is consistent with the trends seen in figure 2.This illustrates the graph’s destabilizing effect of the η amplitude.The behavior appears to be inverted and the increase in η has a stabilizing behavior as the region of instability shrinks when it continues to exceed the value η=0.5,as seen in figure 8(b).Therefore,the change in η in the stability behavior has two distinct roles.

The mechanism depicted in figure 7 was used to construct figure 9 with η=1 fixed and the decay factor μ allowed to fluctuate somewhat.as depicted in figure 9.The numbers selected for this specific picture operate to produce two zones of instability: the first one corresponds to the oscillationA’s amplitude values,which vary from zero to±1.An additional unstable zone has emerged,roughly symmetrical toA=±2.It is seen that the stability feature holds for a small increase in μ.

Conclusion

This study delves into the time-delay Van der Pol–Helmholtz–Duffing oscillator within fractal space.It pioneers the exploration of delayed velocity and displacement within the fractal oscillator,a topic of increasing relevance given the burgeoning interest in time-delayed technologies.The analytical approach hinges on the conversion of the fractal derivative into its conventional counterpart in continuous space,notably without the explicit incorporation of the fractal parameter.A groundbreaking non-perturbative technique is employed to derive the damping term,the frequency,and the ultimate linear differential equation.The contributions of the Helmholtz and Duffing elements to the frequency are discerned,marking the inaugural formulation of frequency with the influence of quadratic nonlinearity.Notably,the resultant frequency/damping terms encapsulate all the intrinsic variables present in the foundational motion equation.

This investigation yields two potential profiles for the approximation solution.One showcases decaying behavior,offering an approximate periodic representation for a wave solution profile,while the other is realized through the simulation of the trial solution.Stability analysis is facilitated by relaxing the transcendental quadratic frequency formula.To corroborate the theoretical findings,a numerical methodology is proposed.The study’s hallmark is its application of an analytical approach to craft a practical approximation.This unique strategy,when juxtaposed with prior research,stands out for its efficacy,innovation,and simplicity.

Funding

The author received no financial support for this article,publication,or authorship of the current investigation.

Competing interests

The authors declare no competing interests.

ORCID iDs