一類Block型李代數(shù)的2-局部導(dǎo)子

肖明月,唐孝敏

(黑龍江大學(xué)數(shù)學(xué)科學(xué)學(xué)院,黑龍江 哈爾濱 150080)

0 引言

李代數(shù)及其相關(guān)課題已經(jīng)成為數(shù)學(xué)研究中的重要領(lǐng)域之一.李代數(shù)是一類非常重要的非結(jié)合代數(shù),源于對李群的研究,后經(jīng)相關(guān)學(xué)者對復(fù)數(shù)域上的有限維半單李代數(shù)有了更為深入且全面的研究,構(gòu)建了經(jīng)典的理論體系,奠定了理論基礎(chǔ).導(dǎo)子在研究李代數(shù)結(jié)構(gòu)理論體系中起著非常重要的作用,學(xué)者們在研究過程中進一步擴充了導(dǎo)子結(jié)構(gòu).1997年,emrl引入了2-局部導(dǎo)子[1]的概念,2-局部導(dǎo)子為導(dǎo)子概念的非線性推廣,此后學(xué)者們相繼對代數(shù)的2-局部導(dǎo)子進行了大量的研究.關(guān)于李代數(shù)的2-局部導(dǎo)子問題的研究主要是判斷其2-局部導(dǎo)子是否為導(dǎo)子[2-6].

Block型李代數(shù)[7]在1958年由Block引入,Block型李代數(shù)在數(shù)學(xué)及物理學(xué)科上有著廣泛的應(yīng)用,起著極其重要的作用,大量重要的無限維李代數(shù)都與其有著頗多相似之處,吸引了眾多研究者的關(guān)注.在Block型李代數(shù)的眾多研究成果主要集中在Block型李代數(shù)的結(jié)構(gòu)和表示理論[8-10]方面,但關(guān)于Block型李代數(shù)局部性質(zhì)的研究還很少.本文主要致力于研究一類Block型李代數(shù)的2-局部導(dǎo)子,確切地說,本文研究的Block型李代數(shù)如下:

Block型李代數(shù)B(q),q?,具有基{Lm,i|m,i∈},李括號如下:

[Lm,i,Ln,j]=(n(i+q)-m(j+q))Lm+n,i+j,?m,n,i,j∈.

1 預(yù)備知識

本文約定L是一個李代數(shù).給出一些基本的定義和一些引理.

定義1 設(shè)D為L上的線性變換,若D滿足

D([x,y])=[D(x),y]+[x,D(y)],?x,y∈L,

則稱D為導(dǎo)子.記所有L的導(dǎo)子構(gòu)成的集合為Der(L).對任意a∈L,映射

ad(a):L→L,x→[a,x],?x∈L

是導(dǎo)子,這種形式的導(dǎo)子稱為內(nèi)導(dǎo)子.記所有L的內(nèi)導(dǎo)子構(gòu)成的集合為Inn(L).

定義2 設(shè)Δ是L上的一個線性變換(不一定是線性的).若對任意的x,y∈L,都存在L的一個導(dǎo)子Dx,y,使得Δ(x)=Dx,y(x)且Δ(y)=Dx,y(y),那么稱Δ是L的一個2-局部導(dǎo)子.

引理1[11]Der(B(q))=Inn(B(q))??2,其中?2是B(q)的一個外導(dǎo)子且滿足:

?2：Lm,i→iLm,i,?m,i∈.

由引理1,易得如下引理:

引理2 設(shè)Δ是L上的一個2-局部導(dǎo)子.若任意x,y∈B(q),存在Dx,y使得Δ(x)=Dx,y(x),且Δ(y)=Dx,y(y),則Dx,y可寫成

其中:am,i(x,y),λ(x,y)∈;m,i∈.

2 Block型李代數(shù)2-局部導(dǎo)子

本節(jié)Δ是Block型李代數(shù)B(q)上的一個2-局部導(dǎo)子,?2是Block型李代數(shù)的一個外導(dǎo)子.給出關(guān)于Block型李代數(shù)2-局部導(dǎo)子的主要結(jié)果:

定理1 Block型李代數(shù)上的2-局部導(dǎo)子是導(dǎo)子.

為了證明這個定理,需要以下幾個引理.

引理3 設(shè)Δ是B(q)上的2-局部導(dǎo)子,則對任意y∈B(q),有:

(ⅰ) 對于n∈*,j∈,若Δ(Ln,j)=0,則

(1)

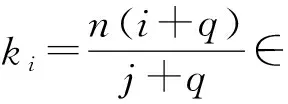
(ⅱ) 對于j∈,若Δ(L0,j)=0,則

(2)

其中:a0,i(L0,j,y),λ(L0,j,y)∈;

證明(ⅰ) 由引理2,設(shè)

其中am,i(Ln,j,y),λ(Ln,j,y)∈.

因為Δ(Ln,j)=0,則有

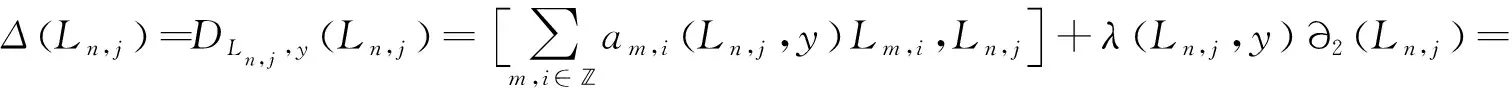
比較Ln,i+j,Ln,j,Lm+n,i+j的系數(shù),可得:

n(i+q)a0,i(Ln,j,y)=0,i∈*,n∈*,j∈;

nqa0,0(Ln,j,y)+jλ(Ln,j,y)=0,n∈*,j∈;

(n(i+q)-m(j+q))am,i(Ln,j,y)=0,m,i∈,n∈*,j∈.

綜上,

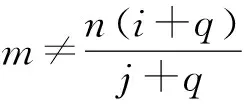
(ⅱ) 由引理2,設(shè)

其中am,i(L0,j,y),λ(L0,j,y)∈.

因為Δ(L0,j)=0,則有

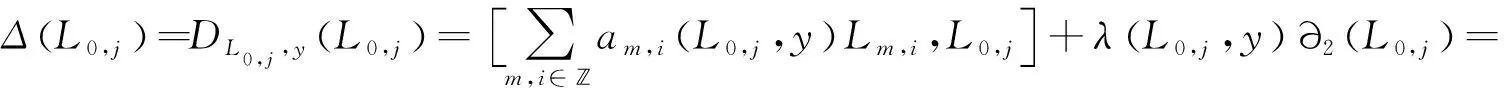
比較Lm,i+j,L0,j的系數(shù),則可得當m≠0時,am,i(L0,j,y)=0;當j≠0時,λ(L0,j,y)=0.結(jié)論得證.

引理4 設(shè)Δ是B(q)上的2-局部導(dǎo)子,使得Δ(L0,0)=Δ(L1,0)=0.則有Δ(Ln,j)=jξLn,jLn,j,?n,j∈,其中ξLn,j=λ(L1,0,Ln,j)∈.

證明易知

(3)

(4)

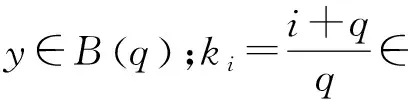
令y=Ln,j,則由(3)和(4)式可得

(5)

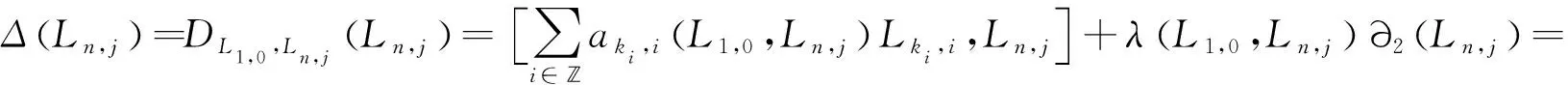
(6)

比較(5)和(6)式有

(n(i+q)-ki(j+q))aki,i(L1,0,Ln,j)=0.

從而Δ(Ln,j)=jλ(L1,0,Ln,j)Ln,j.令λ(L1,0,Ln,j)=ξLn,j,則結(jié)論得證.

證明因為Δ(L0,0)=Δ(L1,0)=0,由引理4可知Δ(Ln,0)=0,n∈*.再由引理3得

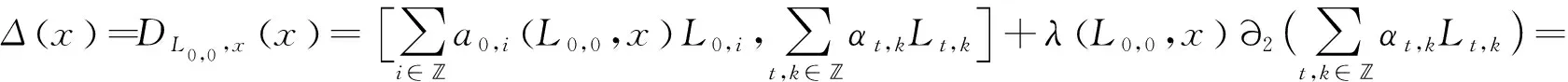
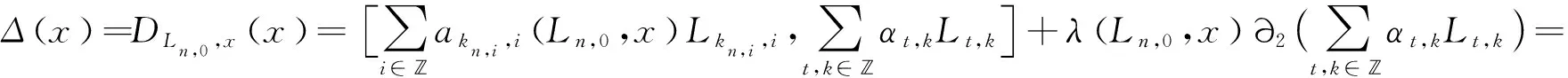
因為t是有限項的,所以可以找到足夠大的n∈*,使得αkn,i+t,i+k=0,t,i,k∈,其中*.比較Lkn,i+t,i+k的系數(shù),可得

(t(i+q)-kn,i(k+q))αt,kakn,i,i(Ln,0,x)=0,

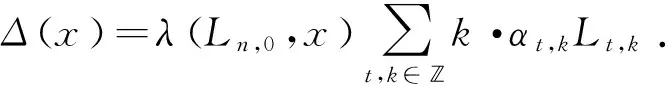
引理6 設(shè)Δ是B(q)上的2-局部導(dǎo)子,使得Δ(L1,0)=0.則對任意的p∈*,y∈B(q),都存在,使得

證明因為Δ(L1,0)=0,由引理3可得

其中a0,i(L0,1,y)∈.設(shè)tp=L0,P+L0,2P,并令y=tp,則有

因為Δ(tp)=0,由引理2可設(shè)

其中am,i(L0,p+L0,2p,y),λ(L0,p+L0,2p,y)∈.

由于Δ(tp)=0,則可得

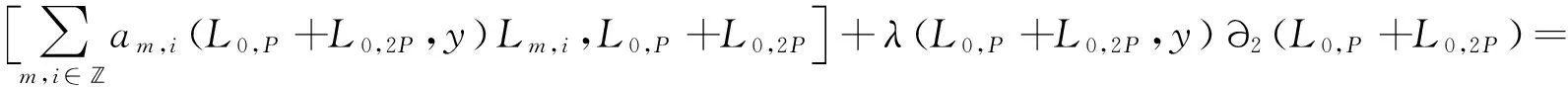
比較L0,p,L0,2p,Lm,i+p,Lm,i+2p的系數(shù),則可得λ(L0,p+L0,2p,y)=0.當m=0時,可得Δ(tp)=0.當m≠0時,有

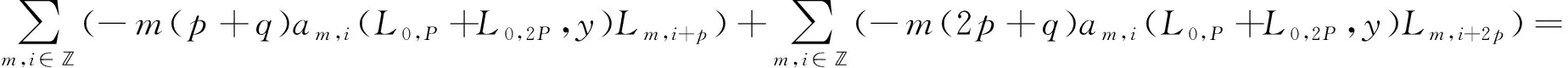
因為上式是有限項,又由上式可得

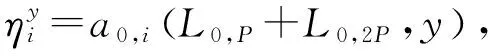
引理7 設(shè)Δ是B(q)上的2-局部導(dǎo)子,使得Δ(L0,0)=Δ(L1,0)=Δ(L0,1)=0.則?x∈B(q)有Δ(x)=0.

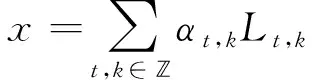
(7)

又因為Δ(L0,1)=0,則?p∈*,由引理6可知

從而

將之與(7)式做比較,可得

(8)

因為ξx的取值不同,分為2種情況進行討論.

情況1ξx=0.則由(7)式可知Δ(x)=0.

情況2ξx≠0.則需要證明{αt,k}=0,其中t,k∈且t=k時k≠0.

ξxkα0,k=0,

(9)

因為{αt,k}t,k∈是有限項,則存在b0∈,使得αt,k+b0i0=0.令k=k+bi0,其中b=1,2,…,b0-1,則有:

(10)

? ?

由(10)式可知當t≠0時,有{αt,k}t∈*,k∈=0.再由(9)式可知k≠0時,有{α0,k}k∈*=0.綜上可知{αt,k}=0,其中t,k∈且t=k時k≠0.又因為由(8)式可得Δ(α0,0L0,0)=0,則有Δ(x)=0.

定理1的證明Δ是B(q)上的2-局部導(dǎo)子,取導(dǎo)子DL0,0,L1,0,使得

Δ(L0,0)=DL0,0,L1,0(L0,0),Δ(L1,0)=DL0,0,L1,0(L1,0).

令Φ1=Δ-DL0,0,L1,0,則Φ1是2-局部導(dǎo)子,使得Φ1(L0,0)=Φ1(L1,0)=0.

由引理4可知Φ1(L0,1)=ξL0,1L0,1,其中ξL0,1∈.令Φ2=Φ1-ξL0,1?2,則Φ2是2-局部導(dǎo)子,使得

Φ2(L0,0)=Φ1(L0,0)-ξL0,1?2(L0,0)=0-0=0,

Φ2(L1,0)=Φ1(L1,0)-ξL0,1?2(L1,0)=0-0=0,

Φ2(L0,1)=Φ1(L0,1)-ξL0,1?2(L0,1)=ξL0,1L0,1-ξL0,1L0,1=0.

由引理7可知,Φ2=Δ-DL0,0,L1,0-ξL0,1?2≡0,則Δ=DL0,0,L1,0+ξL0,1?2是導(dǎo)子,結(jié)論得證.