Finite-time ?∞filtering for Markov jump systems with uniform quantization
Jingjing Dong(董敬敬), Xiaofeng Ma(馬曉峰), Xiaoqing Zhang(張曉慶),Jianping Zhou(周建平),?, and Zhen Wang(王震)
1School of Computer Science&Technology,Anhui University of Technology,Ma’anshan 243032,China.
2College of Mathematics&Systems Science,Shandong University of Science and Technology,Qingdao 266590,China
Keywords: Markov jump system,filter design,finite-time ?∞performance,uniform quantization
1.Introduction
A Markov jump system (MJS) is a distinctive type of hybrid system comprising a collection of continuous-time(or discrete-time) subsystems, which are mathematically described by differential (or difference) equations, as well as a Markov process that governs the transitions occurring between these subsystems.MJSs are particularly useful for analyzing complex dynamic systems that are susceptible to unpredictable changes in parameters or structures caused by component or link failures.[1]The origins of theoretical research on these systems can be found in the 1960s.In 1961,Krasovskii and Lidskii[2]presented an initial model of MJSs and provided the corresponding control design scheme.Subsequently,Rishel[3]applied the dynamic programming method to discuss the optimal control problem of MJSs.Costa and do Val[4]further studied some fundamental issues of MJSs, including observability and measurability.In recent years,more topics related to MJSs, ranging from almost sure stability,[5]state estimation,[6]fault detection,[7]and dissipativity-based stabilization,[8]to sampled-data synchronization,[9]have been extensively investigated in the automation community.
Disturbances are often unavoidable in dynamic systems.Filtering,a specific type of state estimation,provides a means to estimate unmeasurable state variables while mitigating the impact of external disturbances.Broadly speaking, there are two categories of filtering methods: infinite-horizon filtering and finite-time filtering(FTF).The former focuses on the asymptotic stability of the filtering error system(FES)over an infinite time horizon,while the latter emphasizes the boundedness within a fixed time interval.[10]When faced with application scenarios where excessively large values arise during the state evolution, the FTF becomes a more suitable choice.[11]For MJSs, the investigation of FTF has emerged as an attractive research subject.In Ref.[12], Wuet al.explored a stochastic MJS and proposed an optimization-based FTF method.Heet al.[13]established criteria to ensure the existence of finite-timel2-l∞filters for discrete-time MJSs.In Ref.[14], Saravananet al.examined the finite-time?∞filtering (FTHF) issue of delayed MJSs and presented a design methodology based on linear matrix inequalities(LMIs).It is noteworthy that the filter designs in these studies require the modes of the MJS and the filter to be fully matched, limiting their applicability to some degree.
The filtering strategies in the majority of existing studies are based on a traditional point-to-point architecture.With the rapid advancement of communication technology, signals between the sensor and the filter of a MJS can be transmitted through a wired or wireless network,forming a networked FES.The introduction of communication networks reduces wiring between the sensor and the filter, enabling data transmission across long distances.This results in cost savings and enhanced system flexibility.[15]Due to the limited communication bandwidth and network throughput, the measurement signals are often quantized to mitigate the communication load.[16]Two common types of quantization discussed in the literature on network-based filtering are logarithmic quantization and uniform quantization.In comparison to logarithmic quantization,uniform quantization,which utilizes fixed-point number representation, is considered easier to implement.[17]During the last few years, a number of attempts have been made on FTF for MJSs with logarithmic quantization.[18–20]However, to our knowledge, no research has been published on the FTF or FTHF for MJSs with uniform quantization effects.
Motivated by the above discussion,this paper revisits the FTHF issue for MJSs with signal quantization.The goal is to design quantized mode-dependent filters to ensure that the FES is not only mean-square finite-time bounded (MSFTB)but also has a prescribed finite-time?∞performance(FTHP)index.First,we consider the case where the switching modes of the filter align with those of the MJS.An LMIs-based filter design approach is put forward to achieve a predefined FTHP for the FES utilizing a mode-dependent Lyapunov function,Schur’s complement, and Dynkin’s formula.Then, we explore a more complex scenario where the switching modes of the filter are allowed to differ from those of the MJS.To address this, a mode-mismatched filter design method is developed by leveraging a hidden Markov model(HMM)to describe the asynchronous mode switching and the double expectation formula.Finally, we utilize a spring system model subject to a Markov chain to validate the quantized filter design approaches for the mode-matched and mode-mismatched cases,respectively.
The main contributions of this paper can be summarized as follows:
(i) Unlike previous studies on FTF for MJSs with signal quantization, the present work employs a uniform quantizer,designed as a piecewise function,to quantize the measurement output before transmission to the filter.
(ii) In contrast to the works of Refs.[12–14], which focused solely on the mode-matched filtering scenario, the present study encompasses both mode-matched and modemismatched filtering cases, and proposes the corresponding filter design approaches.
2.Preliminaries
In this section, we first describe the MJS model under consideration, explicitly formulate the FTHF issue, and then prepare some necessary lemmas.The notations involved throughout are standard unless explicitly stated otherwise.
2.1.Markov jump system model
We consider a continuous-time MJS described by
whereχ(t)∈Rnχ,ξ(t)∈Rnξ, andζ(t)∈Rnζrepresent the system state, performance output signal to be estimated, and measurement output, respectively;ω(t)∈Rnωis the external disturbance,which,as in Refs.[21,22],satisfies
within whichdis a given positive parameter and [0,Tf] is a fixed finite-time interval.In addition,Ams(t),Dχms(t),Cξms(t),Dξms(t),Cζms(t),andDζms(t)represent the given parameter matrices subject to a Markov chain{ms(t)}that takes values in set Sm={1,...,m}and is characterized by transition rate matrix?=(msr1r2)m×mwith
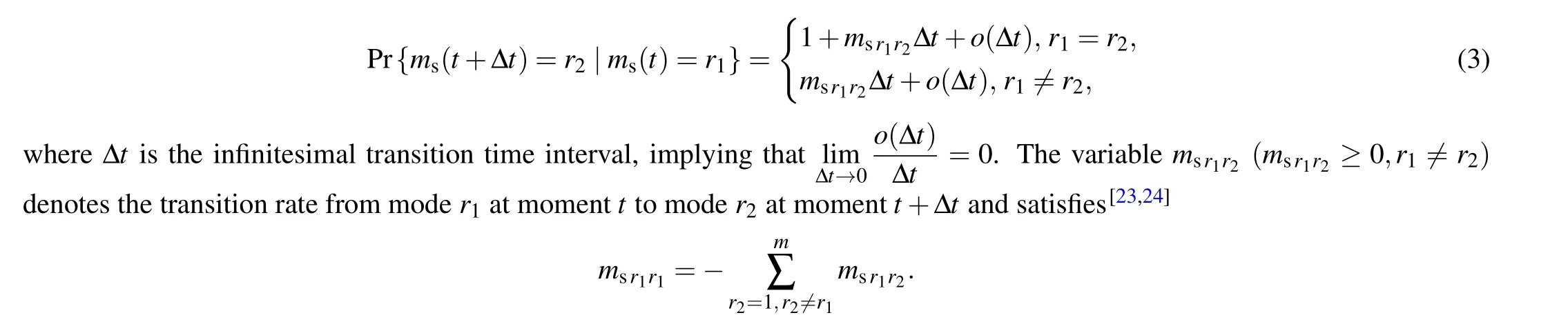
2.2.Uniform quantization
As shown in Fig.1,the measurement outputζ(t)is quantized using a uniform quantizer before being transmitted to the filter to reduce the communication load.The quantizerQ(·)is defined as
whereQv(ζv(t))(v ∈{1,...,nζ})are designed as the following piecewise function:
in which?·」is the round-down operation, andEb/2>0 andTs> 0 represent the error bound and saturation threshold level,respectively.Clearly,for anyv ∈{1,...,nζ},Qv(ζv(t))satisfies the following properties

holds when all quantizersQ1(ζ1(t)),...,Qnζ(ζnζ(t)) are not saturated.
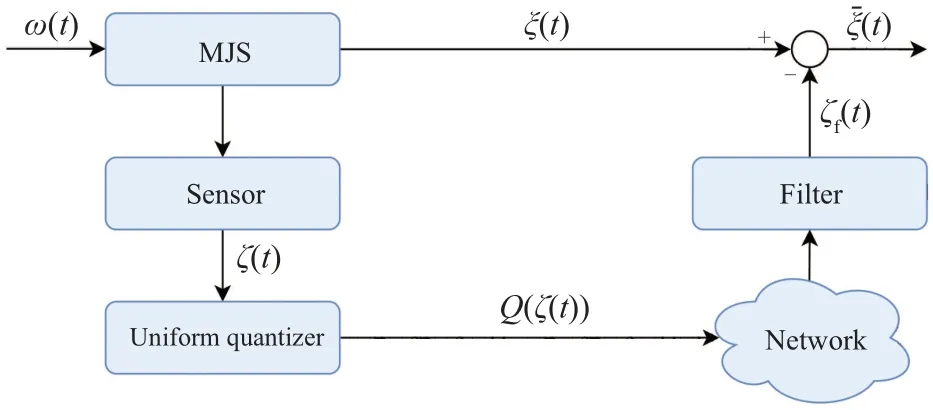
Fig.1.The framework of filter design for MJS with uniform quantization.
2.3.Mode-dependent filter
The form of the mode-dependent filter is presented as follows:
whereχf(t)∈Rnχis the filter state,ξf(t)∈Rnξis the filter output signal,{mf(t)}denotes the modes of the filter,andAfmf(t),Bfmf(t),Cfmf(t), andDfmf(t)represent the filter gains to be determined.
2.4.Filtering error system


We can further obtain from Eqs.(2)and(6)that

Remark 1In contrast to prior studies on FTF for MJSs with signal quantization, the present work employs the uniform quantizer, designed as a piecewise function, to quantize the measurement output before transmitting it to the filter.However, this will result in the estimation of a timeindependent upper bound for the quantization error, which poses challenges in handling.To tackle such an issue,inspired by Refs.[25,26],the quantization error is regarded as an additional disturbance term.
2.5.Problem statement
The definitions related to mean-square finite-time boundedness and FTHP are presented as follows.
Definition 1[27]Given scalarsη1,η2, andTfwith 0<η1<η2and a matrixH>0, the FES is said to be MSFTB with regard to(η1,η2,Tf,H)if
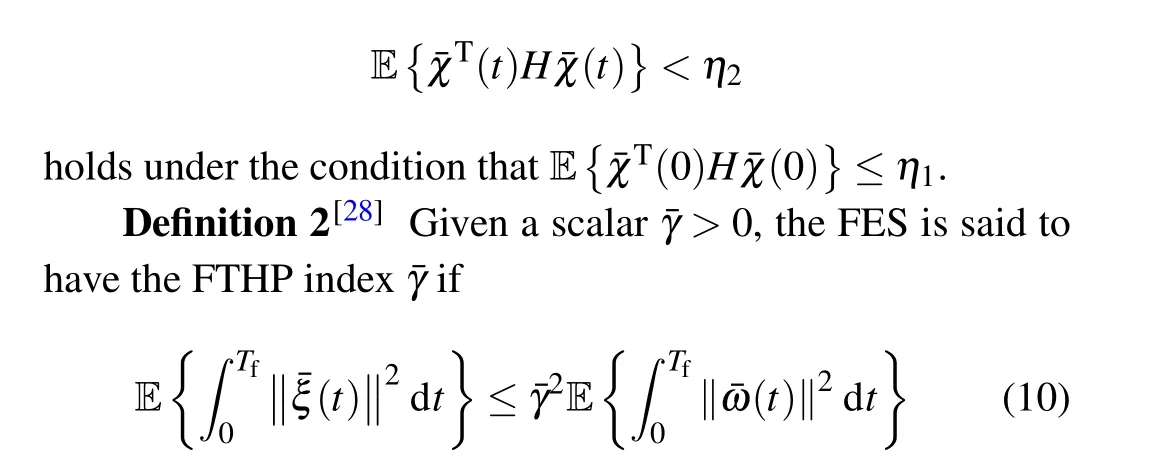
holds under the zero initial condition(i.e.,(0)=0).
Now, the objective of this paper can be explicitly expressed as follows: to design a quantized mode-dependent filter (7) for MJS (1) such that the FES in Eq.(8) is not only MSFTB but also has a prescribed FTHP index
2.6.Necessary lemmas
To facilitate the establishment of the subsequent results,we introduce two lemmas.
Lemma 1[29](Dynkin’s formula)For any stopping times 0≤t0≤t1,ifV(χ(t),ms(t))and?V(χ(t),ms(t))are bounded ont ∈[t0,t1],then we have
Lemma 2[30](Double expectation formula)For any random variables?andN,
holds, where E{?|N}is the conditional expectation givenN.
3.Mode-matched filter design
This section considers a simple mode-dependent filter referred to as the mode-matched filter, in which the switching modes of the filter are the same as those of MJS (1) (i.e.,mf(t)≡ms(t)).The mode-matched filter is described as follows:

A mode-matched filter design approach, which guarantees both mean-square finite-time boundedness and FTHP of FES(12),is provided in the following theorem.
Theorem 1 Given scalarsγ>0,α>0,β1,andβ2>0,suppose that,forr1∈Sm,there exist scalarsρ1>0 andρ2>0 and matricesP1r1> 0 andP2r1> 0 such that the following LMIs hold:

By means of Schur’s complement in Ref.[31],we deduce from inequality(17)that

Consider the following mode-dependent Lyapunov function
Define?by the weak infinitesimal generator.Then, we have the following expression:
It follows from Eqs.(3),(20),and(21)that




4.Mode-mismatched filter design
In networked systems, it is common for the modes of the filter and system not to fully match due to networkinduced constrains,such as data dropouts[32]and transmission delays.[33]Consequently,in this section we further explore the design of mode-mismatched filters.Specifically, the modemismatched filter model we consider is described by Eq.(7),where{mf(t)}is another stochastic process correlated with the Markov process{ms(t)}, which is characterized by a conditional probability matrix(CPM)Λ=(mfr1r3)m×nwith
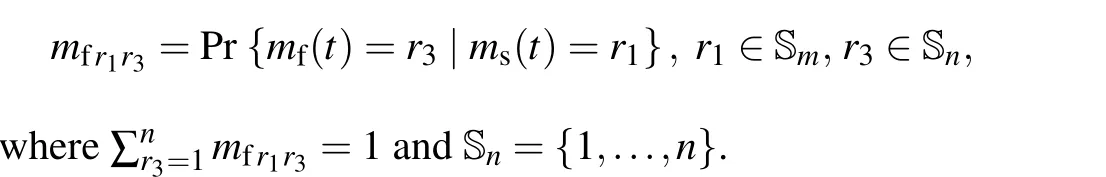
Remark 3 The switching modes of filter are represented by the stochastic process{mf(t)}, which is distinct from the Markov process{ms(t)}but hinges on it through the CPM.Motivated by Refs.[34–36], an HMM({ms(t)},{mf(t)},?,Λ) is employed to characterize the mode-mismatched behavior between MJS (1) and filter (7).Note that when CPMΛis an identity matrix, the switching modes of filter(7)align with those of MJS(1).
Theorem 2 Given scalarsγ>0,α>0,β1,andβ2>0,suppose that,forr1∈Smandr3∈Sn,there exist scalarsρ1>0 andρ2>0 and matricesP1r1>0,P2>0,Rr1r3,andGr1r3such that LMIs(14),(15),and

which, in conjunction withmfr1r3> 0 (r1∈Sm,r3∈Sn),yields that


Remark 4 Theorem 2 further proposes a modemismatched filter design approach to ensure that FES (8) is MSFTB and has the FTHP indexThis design approach allows the switching modes of the filter to differ from those of the system while depending on it through conditional probabilities.To tackle the mode-mismatched filter design issue,as in Ref.[36],we introduce two decision variablesRr1r3andGr1r3to separate inequality(40)from the conditional probabilitymfr1r3.However,this may bring some conservatism,which will be verified in Section 5.
5.Example
In this section, we utilize the spring system model in Ref.[37]to illustrate the effectiveness of the proposed modematched and mode-mismatched filter design approaches.In Fig.2,k1andk2denote the spring constants, andM1ms(t)andM2ms(t)represent the masses subject to a Markov chain{ms(t)},which can take values 1 or 2.
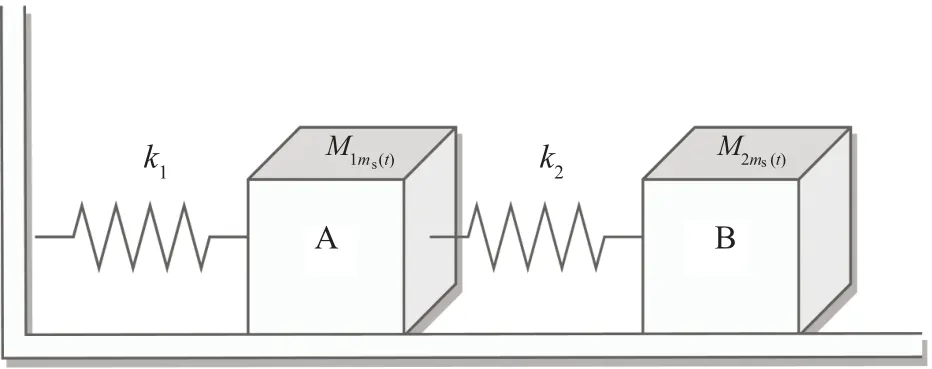
Fig.2.Spring system model.
Furthermore, the coefficient of friction between objects A, B, and the horizontal surface is denoted byc.The spring system model can be described by Eq.(1),and its system matrices are given by
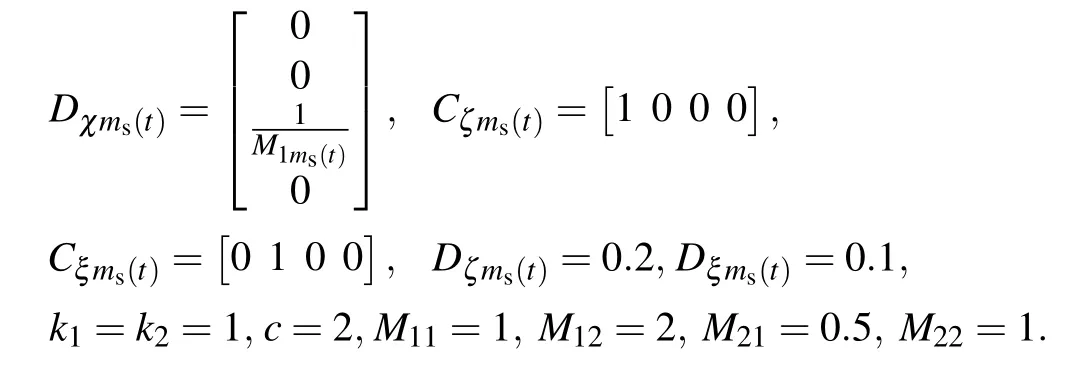
The uniform quantization and finite-time performance parameters are set asTs=10,Eb=0.05,η1=1,η2=36,d=8,Tf=20,andH=I,respectively.
We first consider the mode-matched scenario.In this case, the existing literature on filtering under uniform quantization (see,e.g., Refs.[38–40]) cannot be applied to find finite-time filters, while the design approaches proposed in Theorems 1 and 2 are applicable.In what follows, we take transition rate matrix as
and set the CPMΛto be an identity matrix.It should be noted that the smaller the FTHP indexthe better the performance of FES.Table 1 provides the minimum allowable FTHP indexfor different values ofβ1andβ2by solving the LMIs in Theorems 1 and 2, respectively.It can be observed from the table that adjusting the values ofβ1andβ2can influence the minimum allowable FTHP index significantly.Furthermore, in comparison with the quantized filter design approach presented in Theorem 2,the one in Theorem 1 always achieves a better minimum allowable FTHP indexThis outcome can be attributed to the introduction of additional variablesRr1r3andGr1r3in Theorem 2, which induce extra conservatism.
Table 1.Minimum allowable FTHP index for different values of β1 and β2.
ˉγmin β1=-0.05 β1=0.95 β1=1.95 β1=2.95 β1=3.95 β2=0.06 β2=1.06 β2=2.06 β2=3.06 β2=4.06 Theorem 1 0.9772 1.0745 1.2260 1.3240 1.3961 Theorem 2 0.9891 1.0949 1.2959 1.4708 1.6378
Next, we consider a mode-mismatched scenario where the CPM is set as
In this situation,the quantized filter design approach given in Theorem 1 is not applicable,while the approach presented in Theorem 2 can be utilized to ensure the mean-square finitetime boundedness and FTHP of the FES.In fact, if we setβ1=1.5 andβ2=2, then by using Theorem 2, we can obtain the minimum allowable FTHP index=0.9215 and the corresponding filter gains as follows:
In this simulation,the external disturbance is given by
and the initial values are set asχ(0)=[-0.4-0.2 0.4 0.1]Tandχf(0)=[-0.5-0.1 0.3 0.2]T.
Figures 3 and 4 show the switching modes of the Markov jump system and the filter, respectively, revealing the mode-mismatch behavior.Figure 5 shows the trajectories of the measurement output and the corresponding quantized measurement output.Figure 6 depicts the trajectory ofClearly,throughout the time interval[0,20],the value ofconsistently remains lower thanη2=36, which indicate that the FES is MSFTB.Lastly, we define the following equation
Then,figure 7 shows the trajectory ofγ(t)under the zero initial condition.We can find that the values ofγ(t)always stay below the minimum allowable FTHP index=0.9215.This shows the designed quantized mode-mismatched filter can ensure the FTHP of the FES.
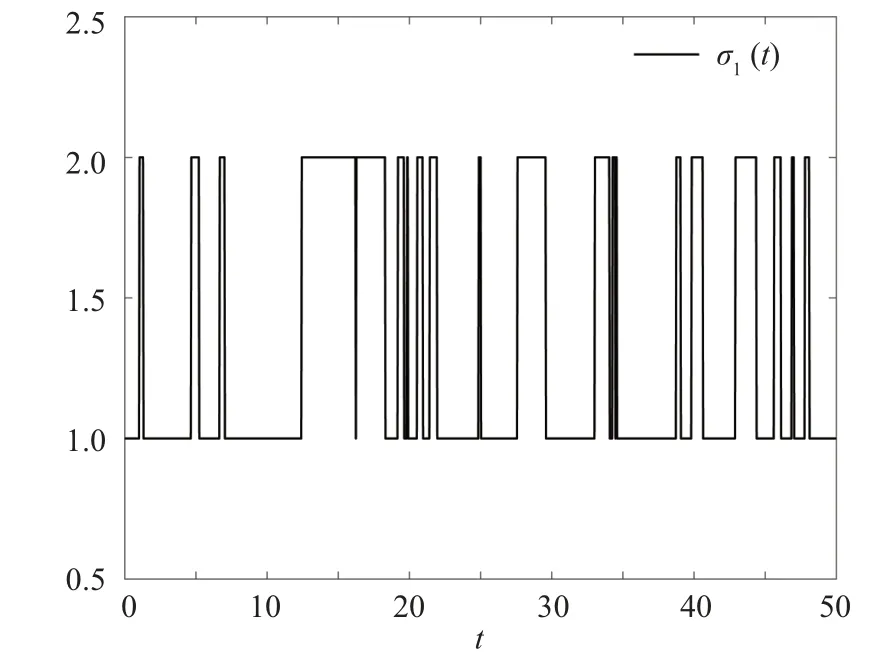
Fig.3.Switching modes of the system.

Fig.4.Switching modes of filter.
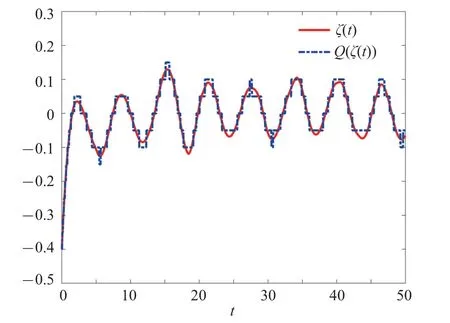
Fig.5.Trajectories of ζ(t)and Q(ζ(t)).
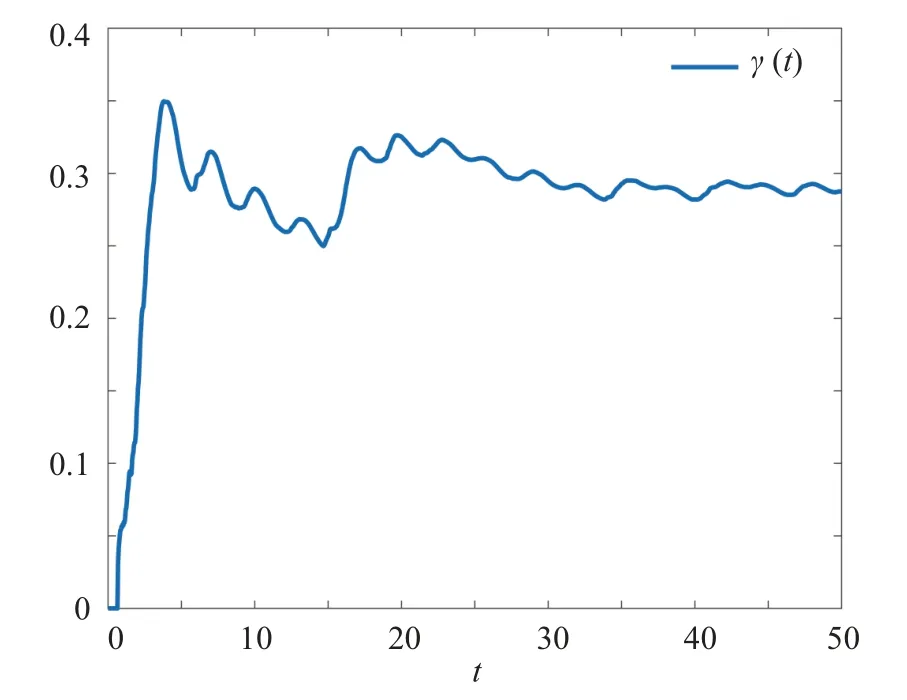
Fig.7.Trajectory of γ(t).
6.Conclusion
This work investigated the FTHF problem for MJSs with uniform quantization by considering two different modedependent filters.First, the case where the filter modes were the same as the system modes was considered.A modematched filter design method was given in Theorem 1 for MJS (1) to ensure that the FES is not only MSFTB but also satisfies a prescribed FTHP by employing a mode-dependent Lyapunov function, Schur’s complement, and Dynkin’s formula.Then, in order to solve the situation that the switching modes of the filter may differ from those of the MJS in practical systems, a mode-mismatched filter design approach was further proposed in Theorem 2 by leveraging an HMM to characterize the asynchronous mode switching between MJS (1)and filter (7) and the double expectation formula.Finally, a spring system model was utilized to validate the proposed filter design methods for the mode-matched and mode-mismatched cases,respectively.
Acknowledgement
Project supported by the Natural Science Foundation of the Anhui Higher Education Institutions (Grant Nos.KJ2020A0248 and 2022AH050310).
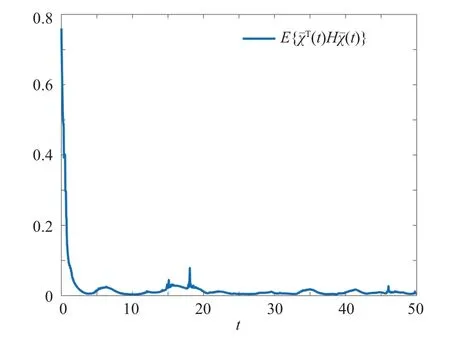
Fig.6.Trajectory of E(t)Ht).
- Chinese Physics B的其它文章
- The application of quantum coherence as a resource
- Special breathing structures induced by bright solitons collision in a binary dipolar Bose–Einstein condensates
- Effect of short-term plasticity on working memory
- Directional-to-random transition of cell cluster migration
- Effect of mono-/divalent metal ions on the conductivity characteristics of DNA solutions transferring through a microfluidic channel
- Off-diagonal approach to the exact solution of quantum integrable systems

