Synchronization transition of a modular neural network containing subnetworks of different scales*#

Weifang HUANG ,Lijian YANG ,Xuan ZHAN ,Ziying FU ,Ya JIA??

1College of Physics Science and Technology,Central China Normal University,Wuhan 430079,China

2School of Life Sciences,Central China Normal University,Wuhan 430079,China

Abstract: Time delay and coupling strength are important factors that affect the synchronization of neural networks.In this study,a modular neural network containing subnetworks of different scales was constructed using the Hodgkin-Huxley (HH)neural model;i.e.,a small-scale random network was unidirectionally connected to a large-scale small-world network through chemical synapses.Time delays were found to induce multiple synchronization transitions in the network.An increase in coupling strength also promoted synchronization of the network when the time delay was an integer multiple of the firing period of a single neuron.Considering that time delays at different locations in a modular network may have different effects,we explored the influence of time delays within each subnetwork and between two subnetworks on the synchronization of modular networks.We found that when the subnetworks were well synchronized internally,an increase in the time delay within both subnetworks induced multiple synchronization transitions of their own.In addition,the synchronization state of the small-scale network affected the synchronization of the large-scale network.It was surprising to find that an increase in the time delay between the two subnetworks caused the synchronization factor of the modular network to vary periodically,but it had essentially no effect on the synchronization within the receiving subnetwork.By analyzing the phase difference between the two subnetworks,we found that the mechanism of the periodic variation of the synchronization factor of the modular network was the periodic variation of the phase difference.Finally,the generality of the results was demonstrated by investigating modular networks at different scales.

Key words: Hodgkin-Huxley neuron;Modular neural network;Subnetwork;Synchronization;Transmission delay

1 Introduction

In the field of computational neuroscience,mathematical models that describe the dynamics of neurons are an important tool.The neural model proposed by Hodgkin-Huxley (HH),based on experimental data on the axons of giant squid,has great promise for research (Hodgkin and Huxley,1952;Yu D et al.,2023b).For example,He et al.(2021) studied the effect of temperature on signal transmission in a network using the HH model and found that signal propagation is significantly enhanced at intermediate temperatures.Xu Y et al.(2018) studied the effect of ion channel blockage on the neural spontaneous firing activity and network patterns by a modified HH model.Other mathematical models have also been widely used (Khoshkhou and Montakhab,2018;Liu Y et al.,2019),such as the Morris-Lecar (Morris and Lecar,1981),FitzHugh-Nagumo (FitzHugh,1961;Nagumo and Sato,1972),and Hindmarsh-Rose(Hindmarsh and Rose,1984) models.

The function of brain networks is closely related to the collective activity of neurons (Rodriguez et al.,1999;Ponce-Alvarez,2015).Many studies have indicated that the specific functions of the brain are achieved through the interaction of multiple functional subnetworks (Uhlhaas et al.,2009;Pisarchik et al.,2019).These subnetworks connect with each other to share and process information,although they are distributed in different areas of the brain and vary in size (van den Heuvel and Pol,2010).For example,the occipito-parietal and prefrontal regions of the brain are thought to be jointly involved in the processing of visual information when the information is of high complexity (Helfrich et al.,2017;Frolov et al.,2019).In cognitive activities,the default mode network,consisting mainly of the posterior cingulate cortex and the medial prefrontal cortex,is also thought to be involved in the integration of information (Greicius et al.,2003).

Complex network theory is widely used in the study of brain networks (Bullmore and Sporns,2009;Han XP et al.,2020).Many types,such as random,small-world,and scale-free networks,have been constructed to analyze the functions of the brain (Watts and Strogatz,1998;Barabási and Albert,1999;Wainrib and Touboul,2013).Experimental studies showed that the small-world topology is widespread in the nervous systems of living organisms,and the anatomical brain networks of many organisms reflect the properties of the small world (Eguíluz et al.,2005;van den Heuvel et al.,2008).In addition,its structural features of high clustering and small path length are closely related to the information-processing function of the brain (Bassett and Bullmore,2006;Andreev et al.,2019).Therefore,small-world networks(SWNs) can help improve our understanding of real brain network dynamics (Wang GP et al.,2015).For example,Yao et al.(2019) investigated the effect of autapses on signal transmission in small-world neural networks and found that an inhibitory autapse is more beneficial for signal transmission.Most of the complex networks in the brain are modular,with neurons connected to their own brain regions as well as to neurons in other brain regions (Hilgetag and Kaiser,2004;Meunier et al.,2010).Modular neural networks (MNNs) have been widely studied.Yu HT et al.(2011) studied pacemaker-driven stochastic resonance phenomena in an MNN.By studying two coupled small-world subnetworks,Andreev et al.(2021) found that the mechanism of synchronization between different brain regions is a reallocation of cognitive resources.

Synchronization is an important spatio-temporal pattern,and many experiments have demonstrated that the synchronization of neurons plays an important role in the functional realization of the brain(Singer,1993;Fries et al.,2002).For example,various physiological activities of organisms,such as visual cortical movements (Roelfsema et al.,1997),perceptual regulation (Gollo et al.,2014),and maintenance of memory and cognitive level (Fell and Axmacher,2011),and various diseases of organisms,such as parkinsonism (Galvan and Wichmann,2008),epilepsy (Mormann et al.,2000),and autism (Cheng et al.,2015),are thought to be importantly related to the synchronized activity of neurons.In addition,the effect of synchronization in real neural systems has been widely studied (Han F et al.,2018,2020;Liu ZL et al.,2022a),such as the relationship between rhythmic oscillations and synchronization of neural collectives(Gu et al.,2021a,2021b;Liu ZL et al.,2022b) and chimeric states in the neural system (Parastesh et al.,2021;Yuan et al.,2022a,2022b).Therefore,the study of synchronization phenomena in complex networks is of great importance (Majhi et al.,2022;Parastesh et al.,2022;Zhang et al.,2022).Many meaningful studies on synchronization have been conducted in modular networks (Sun et al.,2011;Yan et al.,2022).

The synchronization pattern of a neural network is affected by various factors,including noise(Wang GW et al.,2022).Gaussian white noise was used in this study.Information transfer delays are prevalent in neural networks as information is transferred through synapses (Gosak et al.,2012).Studies have shown that the delay time of chemical synapses can reach tens of milliseconds (Yu HT et al.,2013).The impact of time delays on network synchronization has been widely explored.Many studies have shown that time delays can both facilitate and disrupt the synchronization of neural networks (Dhamala et al.,2004;Guo et al.,2012;Wu et al.,2023).In addition,other factors,such as synaptic type and coupling strength,are considered important (Wang HT and Chen,2016;Lu et al.,2017;Xu YM et al.,2019).

Multiple synchronization transitions can occur in the networks under the influence of time delays.The time delays between neurons in a network were considered to be the same in many previous studies(Yu D et al.,2022,2023a).However,the time delays at different locations in an MNN may be different and may have different effects on the synchronization of the network (Sun and Li,2017).Furthermore,in the visual cortex of an organism,information is processed by passing through small-scale to largescale neural networks,with the accompanying synchronization of neurons (Yu S et al.,2008;Yang et al.,2019;Xie et al.,2022).However,there have been few studies on the synchronization of modular networks containing subnetworks at different scales.Therefore,whether small-scale networks affect the synchronization of large-scale networks or not and the effect of time delays on synchronization transitions in MNNs containing subnetworks of different scales are subjects worthy of study.In this study,an MNN containing two subnetworks of different scales was constructed and time delays were introduced to study the synchronization of the modular network.

2 Mathematical models and methods

2.1 Network architecture

The topology of neural networks has an important influence on the interactions between neurons.In this study,we considered a modular network that contained unidirectionally connected subnetworks of different scales.The small-scale subnetwork was a random network (RN) containing five neurons,and the neurons in the network were randomly connected by chemical synapses with a probability ofp1=0.3.The large-scale subnetwork was an SWN containing 50 neurons.We followed the standard algorithm proposed by Watts and Strogatz (1998) to build the network.First,we constructed a ring-like network with 50 nodes,each of which was connected tok=2 nodes to its left and right nearest neighbors.Then,each edge in the network was reconnected randomly with a probability ofp3=0.3;i.e.,one endpoint of each edge was unchanged and the other endpoint was disconnected and connected to a node in the network at random,where no heavy edges or self-loops were specified.The neurons in the network were connected by chemical synapses,and this construction method made the average degree of the SWN bek=Σiki/N=4.Based on the large-scale and small-scale networks we obtained,the network constituted an MNN.In this case,the small-scale subnetwork was connected to the large-scale subnetwork unidirectionally through chemical synapses with a random probability ofp2=0.4.Fig.1 shows the general structure of the modular network.

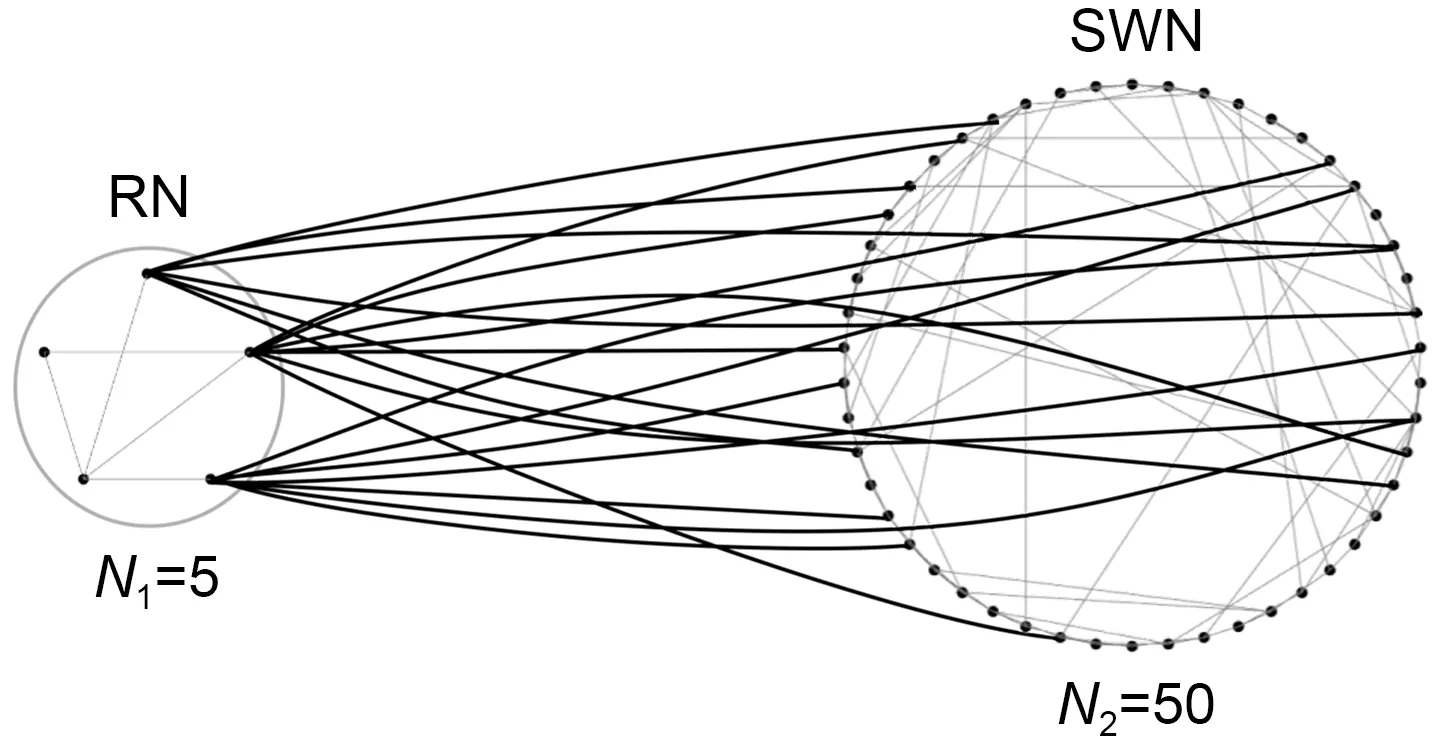
Fig.1 Schematic of the modular neural network (RN:random network;SWN: small-world network)

2.2 Neuron model

To investigate the effect of time delay on the dynamic firing of neurons in the network,the HH model was used to describe the change of membrane potential of each neuron with time.The mathematical model is as follows：

whereCm=1 μF/cm2represents the membrane capacitance per unit membrane area andVistands for the membrane potential of theithneuron in the network (i=1,2,…,N,Nis the number of all neuron nodes in the network).=120 mS/cm2,=36 mS/cm2,and=0.3 mS/cm2represent the maximum conductances of sodium,potassium,and leakage ions,respectively.VNa=50 mV,VK=-77 mV,andVL=-54.4 mV represent the reversal potentials of sodium,potassium,and leakage ions,respectively.is the external electrode current injected into the neuron,set to 20 mA.is all synaptic currents received by theithneuron.ξiis the Gaussian white noise,satisfying the following equation relationship：

where δ(t) is the Dirac function,andDrepresents the noise intensity,set to 0.1 in this study.,mi,andhirepresent the ion channel gating variables,n4andm3are the probabilities of opening the potassium and sodium ion channels respectively,and the dynamical equations satisfied by each gating variable are as follows：

where(Vi) and(Vi) are rate functions,defined as

We considered the connection between neurons as chemical coupling,and the chemical synapse is represented as

wheregis the coupling strength,representing the strength of the connections between neurons.For convenience,we considered the coupling strength between all neurons in the network to be the same value,g.εijis an element in the connection matrix,and if nodejinteracts with nodei,εij=1;otherwise,εij=0.τsis the time delay of information transmission in the synapse,wheres=1,2,and 3.τ1,τ2,andτ3represent the time delays between neurons within a small-scale subnetwork,between subnetwork connections,and within a large-scale subnetwork,respectively.tjrepresents the corresponding firing time of presynaptic neuronj.Erevis the synaptic reversal potential,set to 0 mV.α(t) is a function of time,reflecting the time-dependent decay of the effects of neurotransmitters released from presynaptic neurons on postsynaptic neurons (Bard Ermentrout and Terman,2010)：

The characteristic time constant for the interaction of neuronsτsynis fixed as 2 ms.Θ(t) is the Heaviside step function.

2.3 Measurements

To distinguish the observed spatio-temporal patterns of the network and to quantitatively characterize the synchronization of the network,we introduced a synchronization factorRbased on mean-field theory(Gonze et al.,2005)：

Here,Viis the transmembrane potential of theithneuron in the network,Fis the average membrane potential of the neurons in the network,andNis the total number of neurons in the network.〈〉 denotes the time average of this variable over time.The synchronization factorRtending to 1 and 0 indicates the complete synchronization and complete desynchronization of the network,respectively.

3 Results and discussions

In this study,the numerical simulation method of Euler’s algorithm was applied to integrate the nonlinear equations.The time step of the calculation was 0.01 ms and the time length of each simulation was 5000 ms.The average number of simulations for each result was about 20.In each calculation,the transient values caused by the initial values were removed.

3.1 Effect of time delay and coupling strength on the synchronization of networks

To investigate the effects of time delay and coupling strength on the firing of neurons in the MNN,it was first assumed that the time delays in chemical synapses between all neurons were the same,i.e.,τ1=τ2=τ3=τ,and then we proceeded with the following exploration.The five nodes on the left of each subfigure in Fig.2 represent neurons in the small-scale subnetwork,and the 50 nodes on the right represent neurons in the large-scale subnetwork;the dots are the moments of neuron firing.The spatial pattern was clearly chaotic whenτ=5 (Fig.2a),indicating that the firing of neurons in the network was not synchronized.However,whenτincreased to 10,the spatialtemporal pattern was orderly,indicating the emergence of synchronous patterns in the network (Fig.2b).Asτincreased further,the network appeared to have multiple synchronization transitions (Figs.2c-2f).The results showed that time delay has an important effect on the activity of the network neurons,and can either enhance or disrupt the synchronization of the neurons in the network.

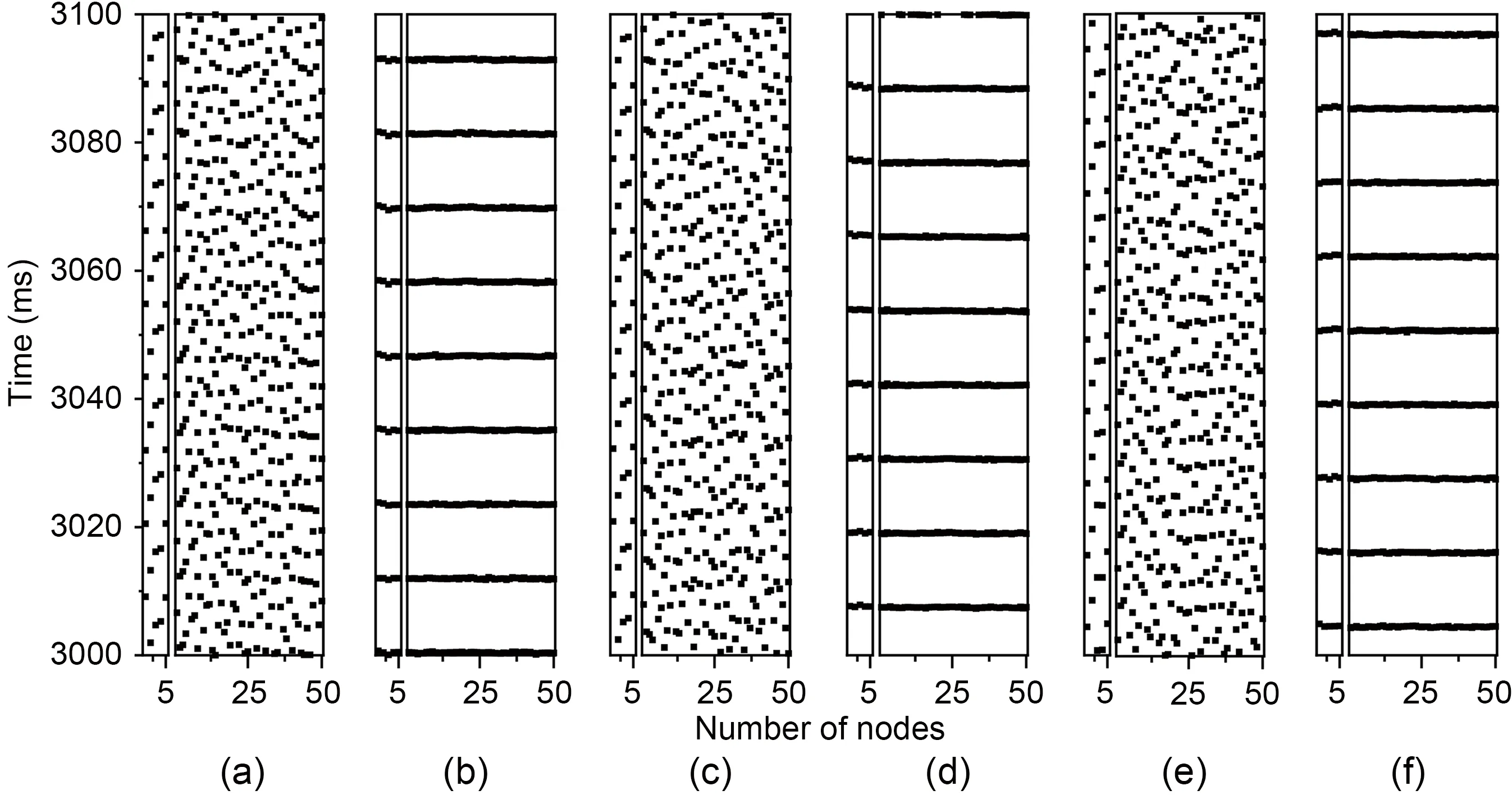
Fig.2 Spatial-temporal firing raster plots of neural membrane potentials of the modular neural network (MNN) with different time delays τ (ms): (a) τ=5;(b) τ=10;(c) τ=16;(d) τ=21.5;(e) τ=27;(f) τ=33 (g=0.1 and D=0.1)

The synchronization factor was used to quantify the synchronization phenomenon observed visually.The variation of the synchronization factor in RN,SWN,and MNN with increasing time delayτfor different coupling strengths is shown in Fig.3.The results showed that multiple synchronization transitions occurred in all three networks with increasing time delayτat different coupling strengths.Note that all synchronization transitions occurred roughly around an integer multiple of the firing period of a single neuron.Also,the coupling strength had an influence on the synchronization of the network.

Fig.3 Distribution of the synchronization factors of the networks with increasing time delay τ with different coupling strengths g (mS): (a) random network (RN);(b) small-world network (SWN);(c) modular neural network (MNN) (τ=10 and D=0.1)

The effect of coupling strength on the synchronization of the network is demonstrated in Fig.4.The results showed that the synchronization factors of the networks increased as the coupling strength increased when the time delayτwas near an integer multiple of the firing period of a single neuron (τ=10 and 21.5 ms).However,when the networks reached the synchronization mode,increasing coupling strength had almost no effect on the synchronization state of the network.In addition,when the time delay was near an odd integer multiple of the firing half-period of a single neuron (τ=5 and 16 ms),the synchronization factor was minimally influenced by the coupling strength.When there was no time delay in the network,the synchronization of the networks gradually became poor and then remained constant as the coupling strength increased.

To generalize the above findings,a two-parameter diagram of the synchronization factor with respect to coupling strengthgand time delayτwas plotted.Fig.5 indicates that the networks exhibited synchronization transitions with increasing time delays.Also,increasing the coupling strength enhanced the synchronization between neurons whenτwas near an integer multiple of the firing period of a single neuron,thus inducing the transition of the network from desynchronization to synchronization.In addition,the synchronization region with largerRvalues became wider with increasing coupling strength,which indicates that the synchronization transition of the network is more obvious at higher coupling strengths.

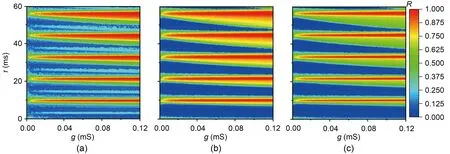
Fig.5 Two-parameter diagram of the synchronization factor with respect to the coupling strength g and time delay τ:(a) random network (RN);(b) small-world network (SWN);(c) modular neural network (MNN) (D=0.1)

3.2 Effect of time delay at different network locations on the synchronization of the networks

To clarify the effect of the time delays at different locations in a modular network on synchronization,we discuss the effect of time delay on network synchronization for the following three cases：the role of time delayτ3when the internal synchronization of the input network (RN) is good,the role of time delayτ1when the internal synchronization of the receiving network (SWN) is good,and the role of time delayτ2when the internal synchronization of both subnetworks is good.To keep the system in a stable state,the fixing synaptic coupling strengthg=0.1.

Fig.6a shows the change of the synchronization factor in RN,SWN,and MNN with increasing time delayτ3whenτ1=10 ms andτ2=5 ms.The results showed that multiple synchronous transitions were observed in SWN and MNN asτ3increased.The results in Figs.6b and 6c showed that for different values ofτ2,both SWN and MNN can exhibit synchronization transitions asτ3increased.The synchronization of SWN was hardly affected by the time delayτ2,butτ2affected the synchronization of MNN.The synchrony of MNN was enhanced with increasingτ2when the time delayτ3was near an integer multiple of the firing period of a single neuron.Next,the variation of the synchronization factor in MNN with increasing time delayτ2was studied when the neurons inside the two subnetworks were well synchronized.The results are shown in Fig.7.

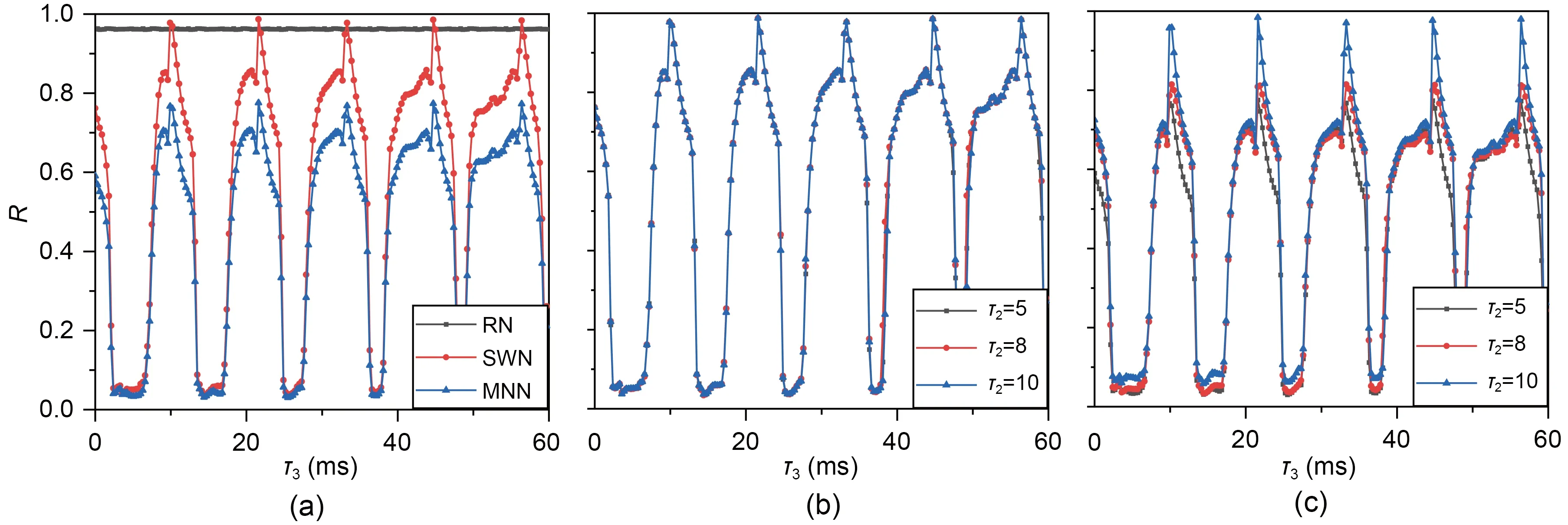
Fig.6 Distribution of the synchronization factor in the network with increasing time delay τ3: (a) variation of the synchronization factors of the three networks when τ2=5;(b) variation of the synchronization factors of small-world network(SWN) when τ2 is different;(c) variation of the synchronization factors of the modular neural network (MNN) when τ2 is different (τ1=10,g=0.1,and D=0.1)

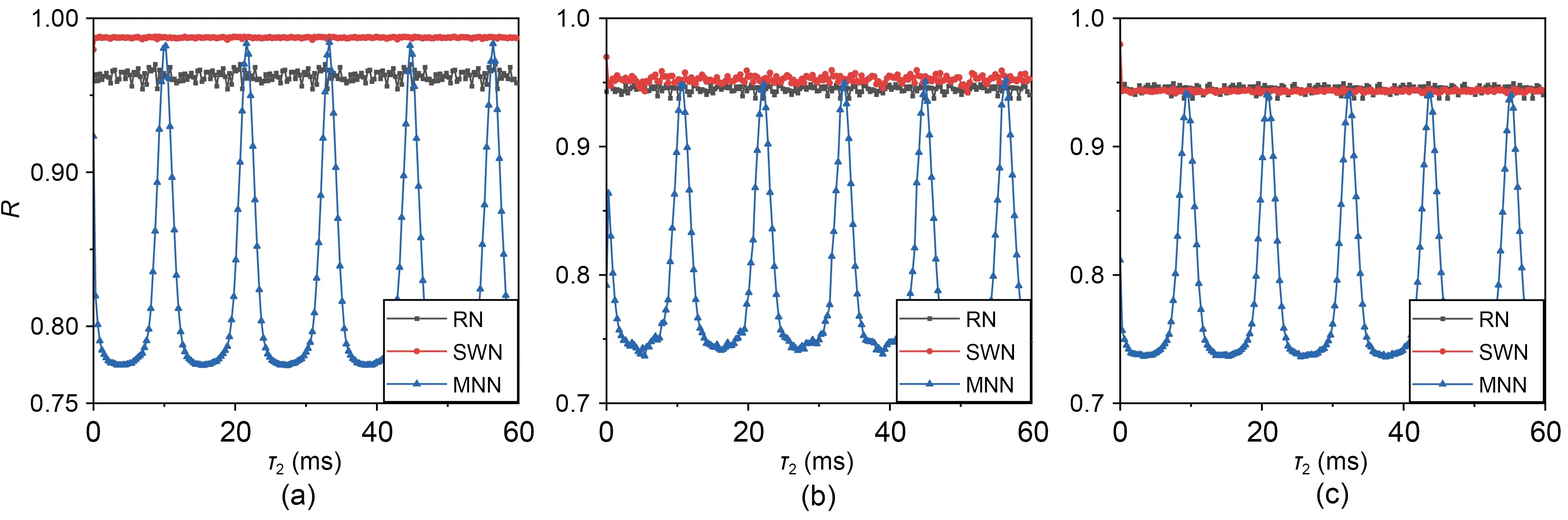
Fig.7 Distribution of the synchronization factor in the network with increasing time delay τ2: (a) τ1=10,τ3=10;(b) τ1=21,τ3=21;(c) τ1=21,τ3=10 (RN: random network;SWN: small-world network;MNN: modular neural network)

Fig.7 indicates that the synchronization factor exhibited an increasing and decreasing periodicity in MNN for all three cases,and that the period was about the same as that of the individual neuron firing period.Meanwhile,the synchronization factor in SWN changed significantly only when there was a time delayτ2.After that,there was almost no effect on the magnitude of the synchronization factor.

To further investigate the phenomenon that the synchronization of MNN becomes better and worse as described above,the phase difference statistic (Δt)was introduced.This measures the change of phase difference of neurons firing in the two networks,with the following expression：

The average membrane potential was used to represent the firing of neurons in each network.In the expression,tRandtSrepresent the spike time of the average membrane potential of neurons in RN and SWN respectively,andnis the number of spikes.The correspondence between the phase difference and the synchronization factor of the modular network is shown in Fig.8.The results showed that when the time delayτ2increased,the phase difference gradually decreased,making the synchronization factor larger.When the phase difference reached the minimum,the synchronization factor reached the maximum.At the same time,when the phase difference increased to the maximum,the synchronization factor value was minimized.The corresponding changes in the phase difference and synchronization factor indicated that the increase inτ2caused a change in the phase difference between the two subnetworks,which led to a periodic change in the synchronization factor of MNN.

To generalize the above results,a two-parameter diagram of the synchronization factor for ambient time delaysτ2andτ3is shown in Fig.9.The results showed that multiple synchronization transitions were observed in SWN and MNN asτ3increased,and the synchronization transition period was roughly the firing period of a single neuron,which was consistent with the pattern of Fig.6.Whenτ3was near an integer multiple of the firing period,the synchronization factor of MNN periodically had a maximum value asτ2increased.The time delayτ2affected the synchronization of MNN.

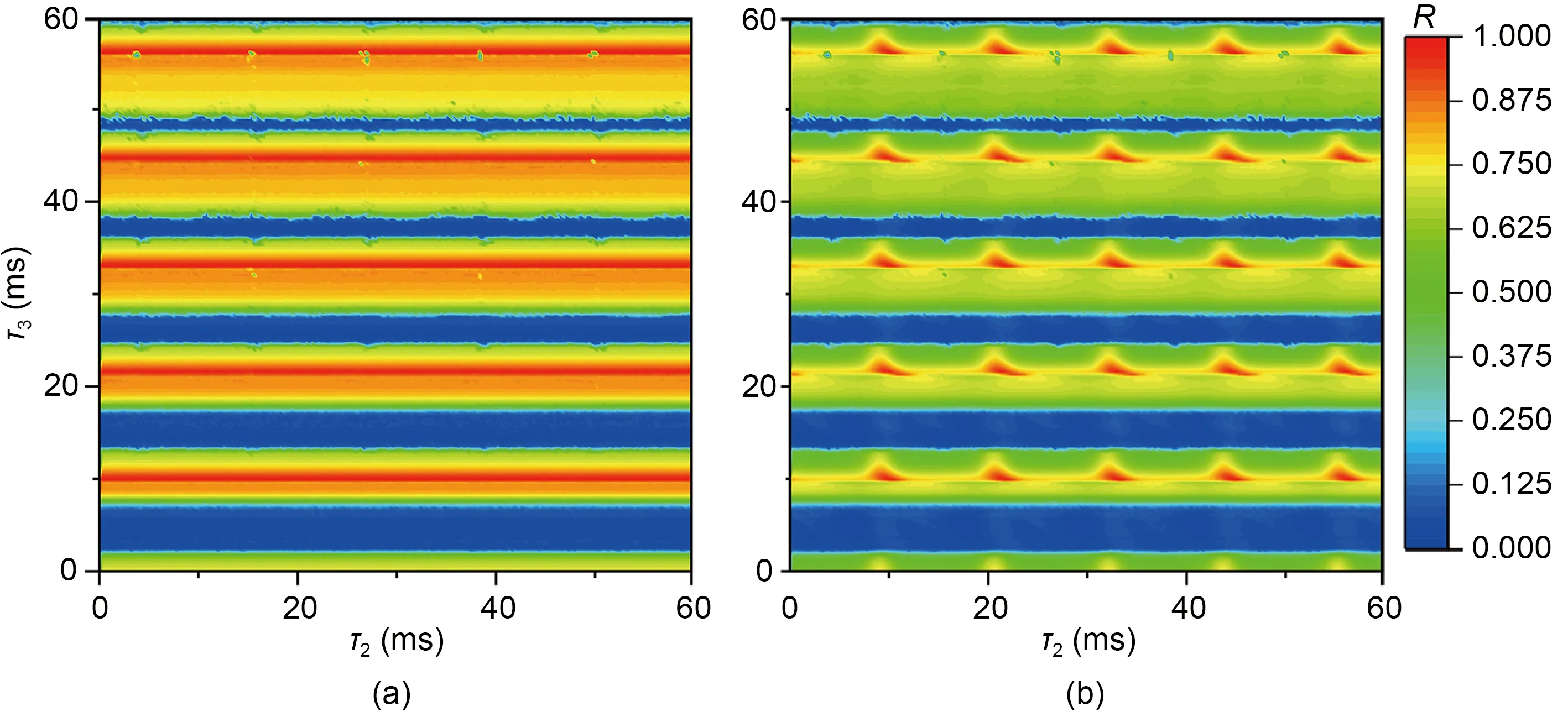
Fig.9 Two-parameter diagram of the synchronization factor with respect to time delays τ2 and τ3: (a) random network(RN);(b) small-world network (SWN) (τ1=10,g=0.1,and D=0.1)

Next,the effect of time delayτ1on network synchronization was investigated when the neurons within the receiving network (SWN) were well synchronized.Fig.10a shows that asτ1increased,multiple synchronization transitions occurred in all three networks.Although the scale of the input network was small,it still had an important impact on the synchronization pattern of the large-scale receiving network.When the time delayτ1induced a synchronous transition within the small-scale input network,the largescale receiving network experienced a similar synchronous transition under the influence of the smallscale input network.The results in Figs.10b and 10c showed that for different values ofτ2,the change of the synchronization factor in SWN was minimally affected byτ2.However,the synchronization of the MNN became better as the time delayτ2increased whenτ2was 5,8,and 10.

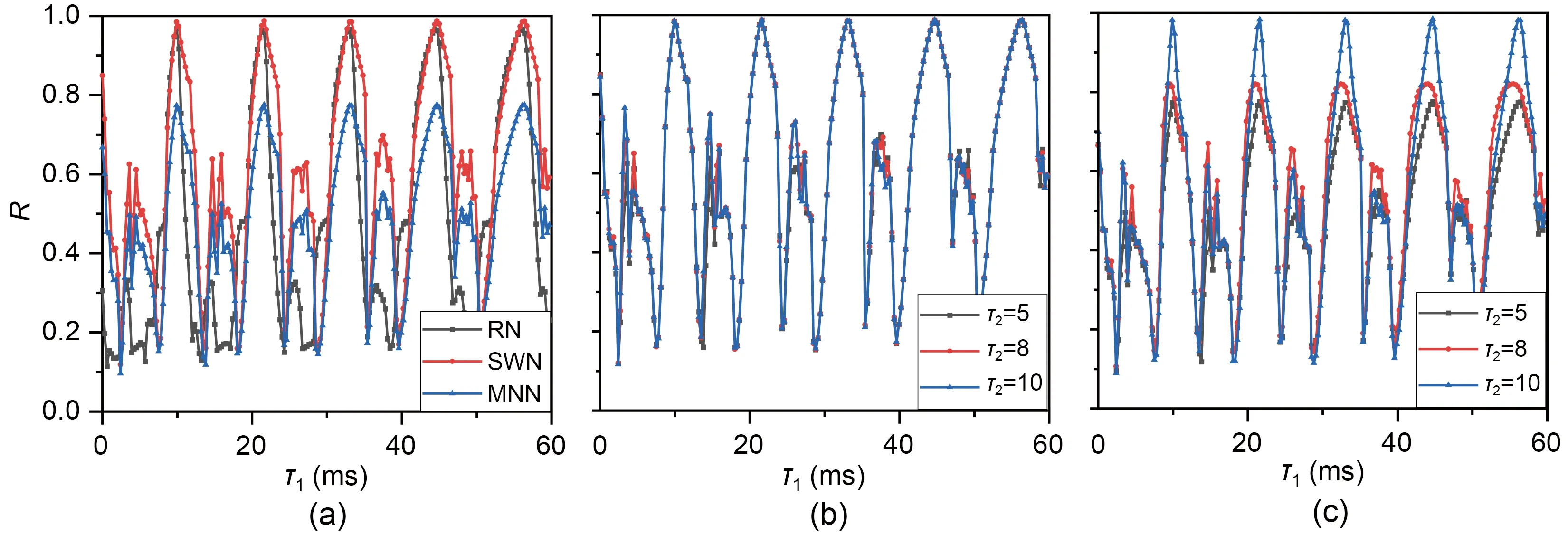
Fig.10 Distribution of the synchronization factors in networks with increasing time delay τ1: (a) distribution of the synchronization factors of the three networks when τ2=5;(b) variation of the synchronization factors of the small-world network (SWN) when τ2 is different;(c) variation of the synchronization factors of the modular neural network (MNN)when τ2 is different (τ3=10,g=0.1,and D=0.1)

The synchronization factors in RN,SWN,and MNN in the two-dimensional parameter space were affected byτ1andτ2(Fig.11).The results demonstrated that the three networks had synchronization transitions asτ1increased.Furthermore,the synchronization factor of MNN showed a periodic change with increasingτ2,with intermittent maxima whenτ3was near an integer multiple of the firing period of a single neuron.

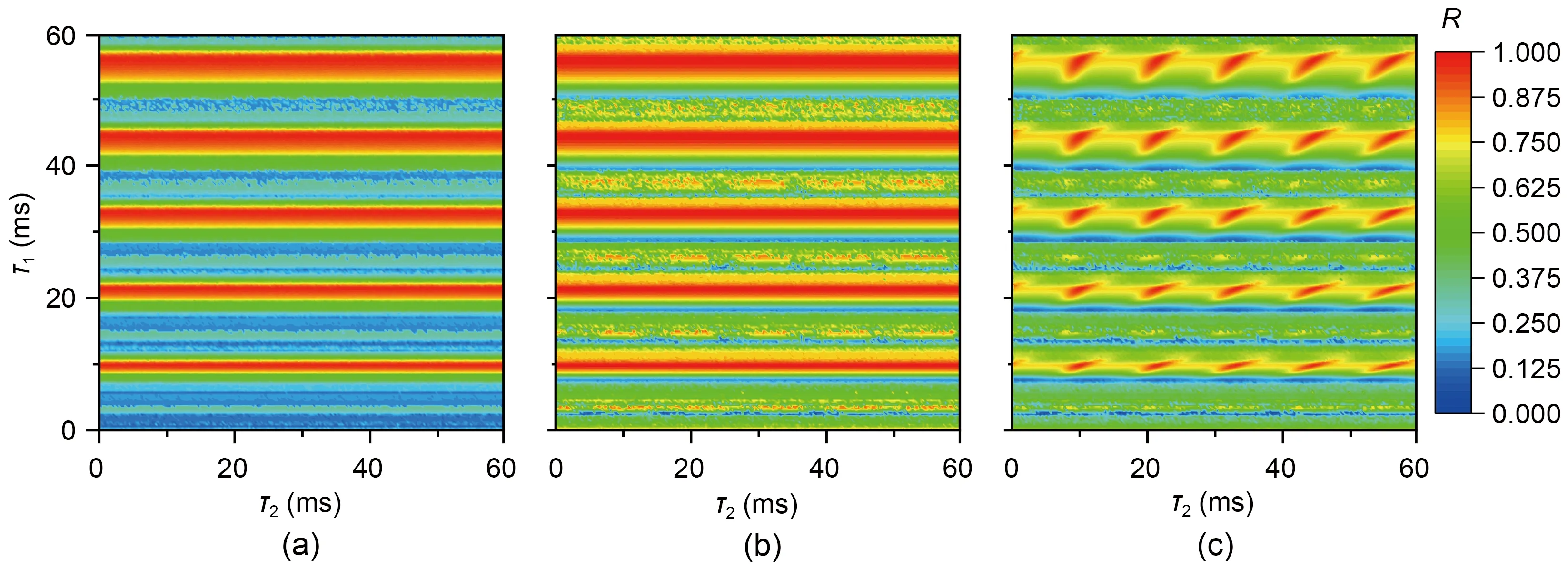
Fig.11 Two-parameter diagram of the synchronization factor with respect to time delays τ2 and τ1: (a) random network(RN);(b) small-world network (SWN);(c) modular neural network (MNN) (τ3=10,g=0.1,and D=0.1)

Fig.12 Distribution of synchronization factors of modular neural networks over different network parameters with increasing time delay

To further validate the generality of the study,we changed the parameters of MNN,i.e.,the connection probabilityp2between subnetworks and the number of nodesNwithin each subnetwork.Figs.12a and 12c show the effect of time delayτ3on the synchronization of the modular network;Figs.12b and 12d show the effect of time delayτ2on modular network synchronization.In this study,p2took values of 0.1,0.4,0.7,and 1.0,and the number of nodes in MNN was set toN1/N2=5/50,10/100,50/500,and 100/1000,separately.In particular,when changing the scale of the network,to ensure that the neurons in SWN receive the corresponding synaptic current magnitude,we adjusted the connection probability between the two subnetworks to 0.4,0.2,0.04,and 0.02.When one of the parameter values was investigated,the other parameter values of MNN remained unchanged.

The results showed that the synchronization factor of MNN has a periodic distribution with increasing time delay over a wide range of parameters of the network,which is consistent with our findings and shows stability.

4 Conclusions

In this paper,the synchronization of neuron firing in a modular neural network (MNN) was investigated at different time delays and coupling strengths.The considered MNN consisted of a small-scale input network (RN) and a large-scale receiving network(SWN).The results showed that time delays can enhance or disrupt the synchronization of neural activity in neural networks.In particular,the period of all these synchronization transitions was approximately an integer multiple of the firing period of a single neuron.In addition,the synchronization factor increased and then remained constant with increasing coupling strength when the time delay was near an integer multiple of the discharge period of a single neuron,and the network intermittent synchronization transition was more profound for largerg.The variation of synchronization with time delay for this MNN gave results similar to those of previous studies on other types of complex networks (Wang QY et al.,2010;Yu HT et al.,2015).

In this study,we explored the effect of time delay at different locations in an MNN on the synchronization of the networks.The results showed that when the neuron firing within the subnetwork was well synchronized,MNN showed synchronization transitions as the time delaysτ1andτ3increased.This indicates that a change of time delay within the subnetworks could induce synchronous transformations in the network.Also,the time delayτ2between two subnetworks had almost no effect on the internal synchronization of the receiving subnetwork,but affected the synchronization of MNN.Specifically,when the two subnetworks were well synchronized internally,the synchronization factor in MNN intermittently had a maximum value asτ2increased.This particular phenomenon was surprising and showed that changes of time delay at different locations in MNN had different effects on the synchronization of the network.By introducing the phase difference statistic,we found that the main reason was thatτ2affected the spike time of a neuron firing in the receiving network,thus making the phase difference of neurons between the two subnetworks vary periodically,which led to a periodic variation of the synchronization factor in MNN with increasingτ2.

Finally,to determine whether the phenomenon and mechanism studied in this paper are universal,the variation of the synchronization factor in MNN with increasing time delay was investigated for different parameters of the network.The results showed that our findings are robust.

Contributors

Weifang HUANG and Lijian YANG designed the research and processed the data.Weifang HUANG drafted the paper.Xuan ZHAN and Ziying FU helped organize the paper.Lijian YANG and Ya JIA revised and finalized the paper.

Compliance with ethics guidelines

Weifang HUANG,Lijian YANG,Xuan ZHAN,Ziying FU,and Ya JIA declare that they have no conflict of interest.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

List of supplementary materials

1 Results and discussions

Fig.S1 Spatio-temporal firing raster plots of neuronal membrane potentials of the modular neural network at different coupling strengthsg

Fig.S2 Spatio-temporal firing raster plots of neuronal membrane potentials of the modular neural network at different time delaysτ2

Fig.S3 Distribution of synchronization factors of modular neural networks over different network parameters with increasing time delay