Thermal Hall effect and the Wiedemann-Franz law in Chern insulator
Anxin Wang(王安新) and Tao Qin(秦濤)
School of Physics and Optoelectronics Engineering,Anhui University,Hefei 230601,China
Keywords: thermal Hall effect,quantum Hall effect,Chern insulator,Landauer-B¨uttike formula
1.Introduction
Topological properties of the quantum materials have been under extensive studies in the last decades.Thermal Hall effect is a versatile probe to investigate transport properties of quantum materials.The Wiedemann-Franz law states that in the low temperature limitκxy=L0σxyTwithL0=(π2/3)(kB/e)2the Lorentz number[1]andσxythe quantum Hall conductivity.Whether the Wiedemann-Franz law is valid in quantum materials is an interesting topic.Its validity has been verified theoretically,[2]where the key ingredient for the Wiedemann-Franz law to be valid is that there is a single non-interacting carrier for charge and thermal current,and experimentally[3]for anomalous Hall insulators.[4]Possible violations of the Wiedemann-Franz law has been explored in graphene,[5]where electrons and holes contribute differently to the quantum charge and thermal Hall transport due to special band structures of graphene in the magnetic field,and quasi-one dimensional conductor,[6]where an extra contribution of spinon to the thermal current has been identified.In high-temperature superconductors,huge thermal Hall conductivity and a violation of the Wiedemann-Franz law has been demonstrated[7]because of the contribution of chiral phonon to the thermal transport in the pseudogap phase of cuprates,[8]and opened a different avenue to rich physics.
Recent experimental progress has made it possible to investigate transport properties of topological materials under effectively very strong magnetic fields.The Haldane model[9]and the Harper-Hofstadter(HH)model,[10,11]as two paradigmatic models of Chern insulators to introduce magnetic fluxes,have served as playgrounds for seminal ideas.However,for a long time, the interesting properties of materials in this scenario is elusive to be observed in laboratories because of the requirement of hugely strong magnetic fields.Recently,great breakthroughs have been achieved.The Haldane model is realized with the ultracold atoms in the shaken honeycomb optical lattices,[12,13]and the HH model is realized with Raman laser assisted tunneling in the optical lattice[14,15]and in the Moir′e superlattice.[16,17]These achievements afford us the possibility to investigate Chern insulators with large fluxes.
In this work, we start with the HH model atφ=1/2,an interesting case with two Dirac cones in the first Brillouin zone, and with its generalization to introduce the complex next-nearest neighbor (NNN) hopping as the Harper-Hofstadter-Hatsugai (HHH) model.[18]For the HH model,the merging dynamics of Dirac cones resulting from uniaxial staggered potential in the first magnetic Brillouin zone (MBZ) has been investigated.[19]By combing the Bott index[20]and on-site disorders, the topological properties enhanced by onsite disorders and interactions has been detailed studied.[21,22]However,a detailed study of thermal Hall transport of the HHH model is still lacking.Using the Landauer-B¨uttiker formula,[5,23]we systematically investigate the quantum charge/thermal Hall transport in the HHH model with uniaxial staggered potentials presented,identify the validity of the Wiedemann-Franz law,and show that it is possible to characterize topological properties by the thermal Hall conductivity.Moreover, we introduce a small perturbation to the flux withφ=1/2+δφ,[19,24]equivalent to an effective magnetic field on top of the fluxφ=1/2,which brings about interesting transport physics.We need to point out that the defining property for the Chern insulator is the non-zero Chern invariant related to occupied Bloch bands, quite extensively discussed in the Haldane model,[25]and that the HHH model with a perturbation in the flux is still a Chern insulator because of non-trivial topological properties for occupied Bloch bands.Our work offers a different point of view to reveal topological properties of quantum materials.
The remainder of the paper is organized as follows.In Section 2,we presented our model and methods.In Section 3,we show our results on the quantum charge/thermal Hall conductivity for three typical cases, and its possibility to be realized in experiments is also discussed.In Section 4, a short summary and outlook is given.Because of a pedagogical purpose,we present some technique details in the Appendix A.
2.Model and methods
Firstly,we introduce the HHH model with uni-axial staggered potential on a two-dimensional square lattice,
wherem,nlabelsxandycoordinates of the sites.We consider a commensurate fluxφ=1/2.Δis the strength for the uniaxial staggered potential.Different from the usual HH model,the HHH model is featured in the NNN hopping with a complex phase.The staggered potentialΔbreaks the inversion symmetry, but keeps the reflection symmetry in thexdirection,therefore, a moderate strength ofΔshift positions of degenerate points,and strong enough one would open a gap.Whentc/=t'c, it breaks all symmetry operations in symmetry groupC4, so a non-zerotcort'cwould open a gap immediately.In this work,we focus on how to tune the topological properties with changes in parameters such astc,t'c,φ,andΔ.
Following the method in Refs.[18,19], we briefly outline how to obtain the quantum Hall conductivity of the HHH model atφ=1/2 with the uniaxial staggered potentials.Settingn=ql+jwithlthe cell index,q=2,andj=1,2,...,q,and using the Fourier transformation
we have
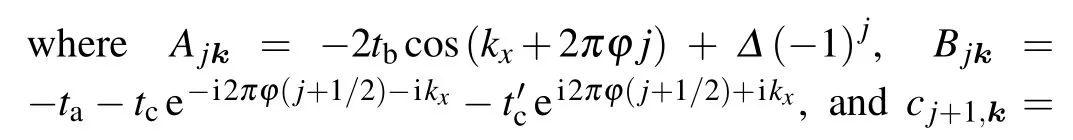


We then have a brief review of methods to calculate the quantum Hall conductivity and thermal Hall conductivity.Following the method of Ref.[18]Appendix A1,we have shown that the quantum Hall conductivity of the electron for the halffilling case is
with the condition thattb>0,ta/=0,tc+t'c/=0,and|Δ|<2tb.Electrons, as charge carriers, can transport energy simultaneously, and lead to the thermal Hall effect.One can show that for this model the Wiedemann-Franz law is valid at the low temperature limit.[2,26]All these derivations are based on bulk formulas.
In this work we focus on the quantum charge and thermal Hall transport in a nano-structure based on the Landauer-B¨uttiker formula,[5,23,27,28]explore the validity of the Wiedemann-Franz law, and demonstrate that the nontrivial topological properties can be revealed by the thermal Hall conductivity.As shown in Fig.1, the nano-structure consists of a central system described by the Hamiltonian in Eq.(1)and six simple leads.The charge current flowing to the terminalncan be described by the Landauer-B¨uttiker formula as


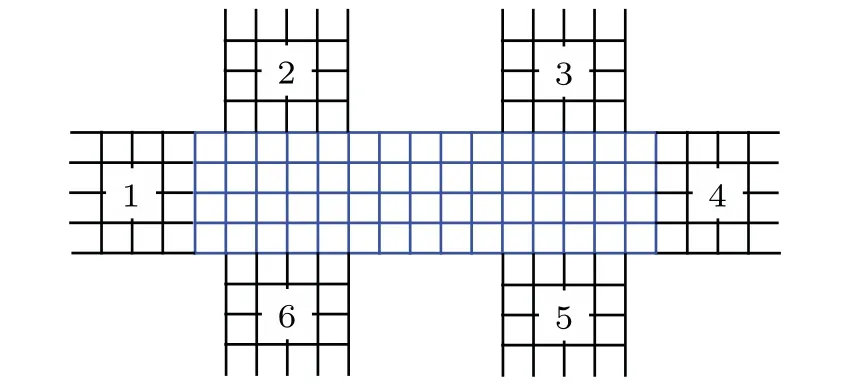
Fig.1.A typical set-up for quantum thermal Hall and charge Hall conductivity measurement: six-terminal nano-structure consisting of system and six leads.The central region has N+2+2L columns of lattice sites with L=5 and N=4.
3.Results and discussion
In this section, we presented our results for three different typical cases in the low temperatureT= 0.001.Case(i):φ= 1/2 andtc=t'c= 0.3.As shown in Fig.2, we find quantum Hall plateau for different stagger potentials in Figs.2(a) and 2(c) in the low temperature limit.The width of the plateaus is consistent with the bulk gaps in Figs.2(b)and 2(d),indicating that the charge transport is carried by the chiral edge states, which is a manifestation of the bulk-edge correspondence.[29,30]WhenΔ ≥2,the gap is closed and the plateau would disappear (Figs.2(e) and 2(f)).In Figs.2(a)and 2(b)one can determine the quantum Hall conductivity by counting how many edge states have been cut by the Fermi energy in Fig.2(b), where the band structure on a cylinder periodic in thexdirection is shown.The real-space distribution of different states in theydirection is encoded by color in Figs.2(b)and 2(d),where the color value 0,and 1 indicate two ends of the cylinder.Therefore, the edge states can be clearly identified.The numerical results for the quantum Hall conductivity is also the same as predicted by the analytical formula in Eq.(5),and the consistence benchmarked our working codes.We recall that the Harper-Hofstadter model atφ=1/2 withΔ=0 is semi-metallic.[19]It demonstrates that the topological properties of this model can be tuned by introduction of the complex next-nearest neighbor hopping.The quantum thermal Hall conductivityκxynormalized byπ2k2BT/3his nearly in coincident withσxyasκxy=L0σxy,indicating that the Wiedemann-Franz law is valid in the low temperature limit.Moreover,it means that one can reveal topological properties of a system by exploring the thermal Hall effect.
We need to point out the a couple of issues in the numerical results.(i) It is about the numerical stability beyond the plateau in Figs.2(a), 2(c), and 2(e), where very steep lines show up.In this energy region, the bulk is metallic.The apparent imperfect agreement between the two quantities in the metallic phase results from two main factors.Firstly,it is the physics reason.We carried our calculations atT=0.001 with the NN hopping as the energy unit,and the Wiedemann-Franz law is valid in the low temperature limit.While the finite temperature effect can be forbidden by large energy gap in the Chern insulator phase, it shows up when the system is in the metallic phase.We next turn to the technical reasons.The key part of our numerical calculations is to solve inhomogeneous linear equations.Indeed, in metallic phase the numerical stability is not perfect for some parameters, as introduces relatively large deviations between charge and thermal Hall conductivities.We tried different ways to solve linear equations and the method of least squares,which we implemented in the codes, turned out to be a better one.(ii)In Fig.2(d), there is clearly discontinuity in the color of the bands aroundkx=2,and it is a reflection of the fixed boundary condition in theydirection of the cylinder.
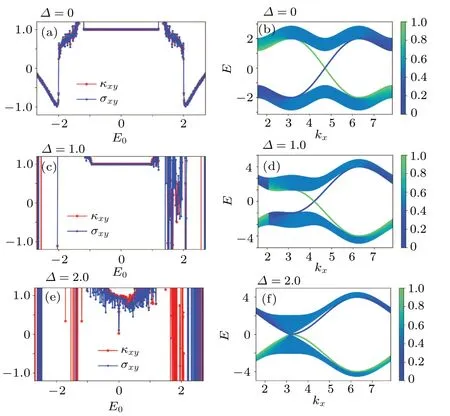
Fig.2.Panels (a), (c), and (e) are the quantum thermal Hall conductivity κxy (normalized by π2k2BT/3h) and charge Hall conductivity σxy (normalized by e2/h)versus the Fermi energy E for different staggered potential Δ,and their corresponding band structure with color encoded y position versus kx on a cylinder structure with periodic boundary condition in the x direction and open boundary condition in the y direction with a width of 400 in panels(b), (d), and(f).Other parameters are ta =tb =1,tc =t'c =0.3, and φ=1/2.The temperature T =0.001,which is very low compared with typical gaps around E =0.The size of the six-terminal structure in numerical calculations is N=L=80.
We go beyond the canonical case ofφ=1/2 and introduce a small perturbation to the integer flux.[19,24]It is equivalent to a small effective magnetic fluxδφ=0.05 on top ofφ=1/2.Similar to results for case(i)in Fig.2,we find the same coincidence between the quantum Hall conductivityσxyand thermal Hall conductivityκxyin Fig.3, indicating the validity of the Wiedemann-Franz law.Furthermore, we would like to point out that the picture of chiral edge states still works for this case.
One new feature for case (ii) is the steep change of the charge/thermal Hall conductivity around the Fermi energyE0=0 (Figs.3(a) and 3(c)).It is due to the change in the direction of the chiral edge states.We take Fig.3(b)as an example.The edge state with positive velocity (green lines) in the gap just belowE0=0,change its direction in the gap just aboveE0=0.It is this motion direction reversal which brings about the sign change in the charge/thermal Hall conductivity aroundE0=0, because carriers tansport both charge and energy.Therefore,as we have claimed,the Wiedemann-Franz is still valid for this case.Furthermore, we need to point out that one can generally characterize the topological properties of a system with thermal Hall conductivity.
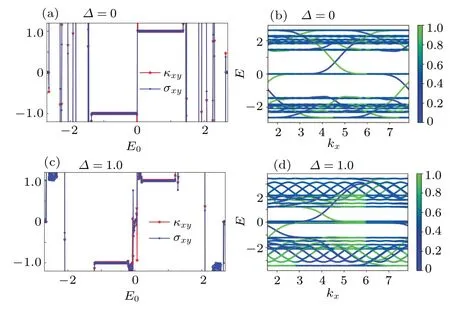
Fig.3.The physical quantities shown are the same as those in Fig.2.Different parameters are tc==0,φ =1/2+δφ,and δφ =0.05.
For case (ii),φ=11/20, so we find there are 20 energy bands in Fig.3(b)and 3(d),where some bands are nearly flat,a reflection of the Landau level.A zoom-in shown in Figs.4(a)and 4(b), corresponding to Figs.3(b) and 3(d) respectively,preseents the fine structures of the nearly flat bands.Moreover,we show the density of states(DOS)of the bulk bands in Fig.4,where we find that peaks show up for every bulk bands.
Case(iii):φ=1/2+δφ,δφ=0.05, andtc=t'c=0.3.In Figs.5(a) and 5(c), we find the same steep change in the charge/thermal Hall conductivity, which can be explained by the direction change in the edge states.In this case we have introduced the NNN hopping, and it indicates that this kind of steep changes in conductivity are rather universal.Even though there is anisotropy brought about by the NNN hopping,the Wiedemann-Franz law is still valid.
We finally discuss the possible experimental realization.In a real material,the NNN hopping amplitudestc,andcan be tuned by strain[31]and laser irradiation.[32]Onsite staggered potentialΔis usually induced by substrates.The fluxφcan certainly be adjusted by strength of external magnetic fields.
Our numerical simulation involves an extremely strong magnetic field.We have an estimate of the strength of magnetic fields required to realize the 1/2 flux byBl2=(p/q)(h/e) where the lattice constantlis approximately 1 °A andp/q=1/2.It follows thatB ≈4×104T,far beyond the reach in the laboratory, where the world record for strongest steady magnetic field is as high as approximately 45.22 T achieved on August 12 2023, in Hefei China, which cannot be directly achieved in the laboratory.However, indirectly,one can realize it with the help of the moir′e superlattice,[16,17]topolectrical circuits,[33]or Raman laser assisted tunneling of ultracold atoms in the optical lattice.[14,15]So far all the three techniques are rather sophisticated.We also need to point out that the HHH model has been realized in the metamaterial of topoelectrical circuits.[34]The possible proposal for experiment realizations in real materials will be explored in the near future.
4.Summary and outlook
To sum up, we have investigated the quantum charge/thermal Hall effect in the HH model and its generalization.We have numerically studied the quantum charge/thermal Hall conductivity in a six-terminal nanostructure and understood it from the point of view of the bulkedge correspondence.We demonstrate that the Wiedemann-Franz law is valid in the Chern insulator,even though there is a steep change of the Hall conductivity aroundE0=0.Our calculations show that the non-trivial topological properties can be revealed by both the charge Hall conductivity and the thermal Hall conductivity.
Appendix A: Energy spectrum of a cylinder structure
To make the results in this work self-contained, we present some details in this section following the methods outlined in Refs.[5,18,23].
Appendix A1: Quantum Hall conductivity of the HHH model with staggered potential
Following the method in Ref.[18], we presented the derivation of the quantum Hall conductivity of the HHH model atφ=1/2 with a staggered potential.We choose the first MBZ askx ∈[-π,π] andky ∈[0,π].The Hamiltonian in Eq.(4)reads
The eigenvector for the lower band is
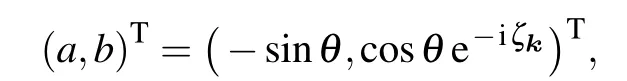
where we have chosen a gauge with the componentaas real and setb= ?be-iζk.The quantum Hall conductivity for the lower band can be calculated as[18,35]
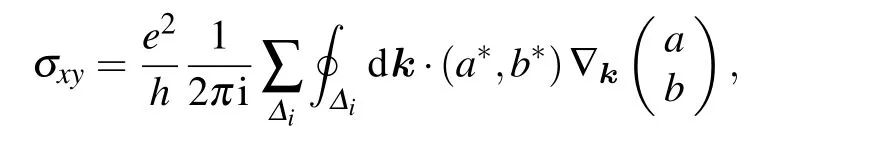
whereΔirefers to different parts for the first MBZ.Becauseais real,
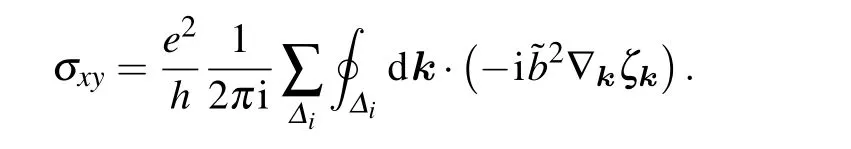

Appendix A2: Thermal Hall conductivity calculation based on the Landauer-B¨uttiker formula
We adopt the method in Refs.[5,23,27,28] to calculate the thermal Hall conductivity.We firstly expand respectively the charge current
and energy currentto the first order of voltageVnand temperatureTn(n=1,2,...,6)as follows:
where we have definedPnm=dETnm(E)?E f0,Qnm=dETnm(E)?T f0, Rnm =dEETnm(E)?E f0, and Snm =∫dEETnm(E)?T f0.For all these newly defined quantities,n/=m.We have a short comment on the integration.Since the temperature is rather low,the integral interval can be limited to a fewkBTaround the Fermi energy.To obtain the thermal Hall effect,a temperature gradient is applied across terminal 1 and 4,and we setJn=0(n=2,3,5,6)andIn=0,(n=1,2,...,6).Due to thermal current conservation,J1=-J4.Therefore,we obtain a group of linear inhomogeneous equations for unknown quantitiesTn,(n=2,3,5,6)andVn=0,(n=1,2,...,6)as follows:
wheren=2,3,5,6,andn'=1,2,...,6.Note in Eqs.(A4)and(A5), we have redefinedP11=-∑n/=1P1n, and similarly forQ11,R11,andS11.To solve the linear equations,a method of least square solutions is important to obtain a stable solution.The thermal Hall resistance and longitudinal resistance can be calculated as ?Rxy=(J2-J6)/T1and ?Rxx=(J2-J3)/T1, respectively.Finally, the quantum thermal Hall conductivity is defined asκxy= ?Rxy/(?R2xy+ ?R2xx).
Acknowledgements
Project supported by the National Natural Science Foundation of China(Grant Nos.U2032164 and 12174394)and the Start-up Fund from Anhui University in China.
——王安幫教授
- Chinese Physics B的其它文章
- Corrigendum to“Reactive oxygen species in plasma against E.coli cells survival rate”
- Dynamic decision and its complex dynamics analysis of low-carbon supply chain considering risk-aversion under carbon tax policy
- Fully relativistic many-body perturbation energies,transition properties,and lifetimes of lithium-like iron Fe XXIV
- Measurement of the relative neutron sensitivity curve of a LaBr3(Ce)scintillator based on the CSNS Back-n white neutron source
- Kinesin-microtubule interaction reveals the mechanism of kinesin-1 for discriminating the binding site on microtubule
- Multilevel optoelectronic hybrid memory based on N-doped Ge2Sb2Te5 film with low resistance drift and ultrafast speed

