Self-similarity of complex networks under centrality-based node removal strategy
Dan Chen(陳單), Defu Cai(蔡德福), and Housheng Su(蘇厚勝),?
1School of Artificial Intelligence and Automation,Huazhong University of Science and Technology,Wuhan 430074,China
2Institute of Artificial Intelligence,Huazhong University of Science and Technology,Wuhan 430074,China
3State Grid Hubei Electric Power Research Institute,Wuhan 430077,China
Keywords: complex networks,subgraph extraction,self-similarity,scale invariance
1.Introduction
A complex network is composed of a large number of nodes and edges,in which interactions between nodes are very complicated,[1–5]which makes it difficult for us to directly explore and analyze the key attributes from the large network.Therefore,how to“reduce”a large-scale network to a smaller one while preserving the global structure of the network is a common concern of network science researchers.[6–19]A new door is opened to solve this problem by borrowing the concepts and techniques related to renormalization groups in statistical physics.[20,21]Renormalization is essentially a technique based on repeated coarse-graining processes, often used to study scale invariance and criticality in statistical physics,[17]which can also simplify the analytical process and reduce computational complexity.
In network science,the basic idea of renormalization is to transform an original network into a smaller one by gradually merging some nodes and links.Related studies[6–10,16,18,19]have shown that some synthetic networks and real-world networks exhibit self-similarity and scale invariance in renormalization flows.For instance, Kim[6]studied coarse-graining processes in geographically embedded complex networks.Their results show that the process does not change the qualitative properties of the original scale-free network, which opens the possibility of subtracting smaller networks from the original network without destroying important structural features.Songet al.[7]found that real-world networks, including web pages, social networks, protein interaction networks, and cell networks, have self-similarity through the box-covering program, thus defining the fractal dimension of networks.Gfelleret al.[8]introduced a random walk-based coarse-graining method for complex networks, this approach can approximate a large network to a smaller one while preserving its important spectral properties.Serranoet al.[9]proved that some real scale-free networks are self-similar under a simple degree-thresholding renormalization procedure,finding a natural explanation for the assumption that network nodes exist in hidden metric spaces.They showed that a class of geometric models with hidden metric spaces can accurately reproduce the self-similar properties we measured in real networks.Garc′?a-Pérezet al.[10]proposed a geometric renormalization group for complex networks based on a hidden metric space.By embedding the network in the underlying metric space and using geometric similarity to unfold the network at different scales, it reveals the self-similar properties of real networks.In addition, this technique can also be used to construct high-fidelity small-scale replicas and multiscale navigation protocols, and provides a theoretical basis for exploring critical phenomena and universality in complex networks.Then, Zhenget al.[13]showed that multiscale human connectome networks exhibit self-similarity,the geometric renormalization model can well explain this self-similarity behavior, and revealed that the self-similarity of the human connectome network is closely related to efficient information navigation.After that, they presented a geometric branching growth model,[14]which can be regarded as a statistical inverse of geometric renormalization.This model provides empirical evidence for the self-similar growth of network structures during the evolution of two real systems, the journalcitation network and the world trade web.Recently, Villegaset al.[18]proposed a new Laplacian renormalization group diffusion method capable of identifying appropriate spatiotemporal scales in heterogeneous networks.Using several real networks, they demonstrated that the framework can perform network reduction while preserving important properties of the system.They also showed that not all network structures have this property and that artificial networks such as random graphs and random block models fail the scale invariance test.
All these works reported in Refs.[6–8,10,18]reduce the network size by coarse-graining multiple nodes into a supernode.In contrast, in Ref.[9] Serranoet al.proposed a procedure that removes nodes whose degree value is less than a given threshold from the initial network to produce a smaller subgraph.Therefore, the former is a virtual network abstracted from the initial network, while the latter is essentially a subgraph extraction technique, the resulting subgraph is a part of the initial network.There is no doubt that degreethresholding renormalization is easier to perform than coarsegraining renormalization.It should be noted that Ref.[9]mainly considers scale-free networks, and the degree values of such networks are usually distributed over a relatively wide interval.However,for other non-scale-free networks,such as homogeneous networks represented by Erd¨os–Rényi(ER)random networks,[22]national highway networks with homogeneous topology, or European power grids that approximately follow the exponential degree distribution,[23]their degree values are usually distributed in a relatively narrow range.This means that when selecting the degree threshold,scale-free networks have a larger selection interval than random networks.Therefore,a small degree threshold may induce a small-scale subnetwork for homogeneous networks,resulting in excessive reduction.In addition,considering that the node degree is a local feature of the network,the information it provides is often limited or incomplete to some extent.Therefore, it is worth exploring other characteristics besides degree as a basis for node removal,such as betweenness,closeness,or eigenvector centrality.
In this paper, we propose removal strategies based on node degree centrality (DC), betweenness centrality(BC),[24,25]closeness centrality(CC),[26]and eigenvector centrality (EC),[27]respectively, to achieve the reduction of network topology size, where the removal order of nodes is inversely proportional to the size of the centrality value, i.e.,the smaller the centrality value is, the earlier the node will be removed.Unlike degree-thresholding renormalization,[9]in our scheme the number of nodes in the subgraph is controllable and depends on a preset ratio of nodes to be removed,which facilitates the comparison between different node removal strategies.Simulation experiments on some synthetic and real-world networks show that some crucial attributes of the initial networks exhibit self-similarity behavior in the reduction process.Of course, there are also some structural properties that do not have self-similarity.
The paper is organized as follows: Section 2 first reviews the four centrality measures and then presents the node removal strategy of this study.In Subsection 3.2, subgraph extraction experiments are conducted on ten real-world networks and five types of synthetic networks.Then, the complementary cumulative degree distribution,degree-dependent clustering coefficient, and degree-degree correlation of the original networks and their subgraphs are investigated to test the performance of the reduction scheme.The dependence of the average degree, the average local clustering coefficient, and the modularity on the proportion of removed nodes of the network are further investigated in Subsection 3.3.Finally, a conclusion is given in Section 4.
2.Preliminaries and proposed method
2.1.Preliminaries
Give an undirected and unweighted networkG(N,E),withNandErepresenting the number of nodes and the number of edges,respectively.Next,we briefly introduce the DC,BC, CC, and EC of the network.For DC, it depends on the degree of the node, take nodeias an example, and its degree valuekiis defined as the number of neighbors of the node,then the DC of the nodeiis defined as
whereN-1 is the largest degree value the node may take.
In complex networks, the degree value of nodes can be used as an indicator to measure the importance of nodes.However,it also has some defects,for example,in social networks,some nodes with low degree values (similar to bridge nodes)may also have a critical position.For such nodes, relevant studies define another index to measure the importance of nodes,namely,the betweenness of nodes,[25]which is defined as follows:
whereNjlrepresents the number of shortest paths between nodesjandl, andNjl(i) represents the number of shortest paths between nodejandlthrough nodei.The BCiof nodeiis obtained by normalizing the node’s betweenness
where the factor (N-1)(N-2)/2 is the maximum possible number of shortest paths through a node.
For a connected graph,the CC of a node is a measure of network centrality.For nodei, Bavelas[26]defined closeness as the reciprocal of the sum of the shortest path lengths from the nodeito all other nodes in the graph,which multiplied byN-1 is usually defined as the CC of the node,i.e.,
wheredi jdenotes the shortest path length between nodesiandj.
EC depends on the adjacency matrixAof the network.Specifically, it is defined as the eigenvectorxcorresponding to the largest eigenvalueλmaxofA,
wherexiis theith component of thex, which represents the importance of nodeifrom another perspective.
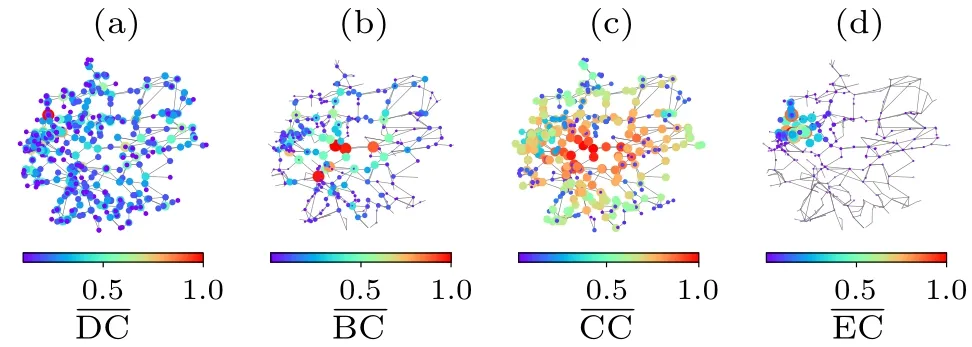
Fig.1.The four centrality values of the German network.


2.2.Proposed method
We employ the centrality measure DC as an example to illustrate the node removal strategy in this paper.Given the initial networkG0,the DC values of all nodes in this network are obtained and stored in the sequenceSDC.Then,the DC values of the nodes are sorted in ascending order, and the sorted sequence is noted asS′DC.Next,the nodes with the smallest DC values inS′DCare removed from the initial networkG0,and the removal ratio of the nodes is set toq,thus realizing the initial network topology size reduction.For other centrality measures,the node removal process is similar.Figure 2 shows the node removal process of the German network [see Fig.2(a)]under the two measures DC and BC,respectively.The results show some differences in the structure of the subgraphs generated by these two removal methods.For example,when the ratio of removed nodes is set toq=0.5,the DC-based reduction approach yields disconnected components in the subgraph[top of Fig.2(b)], while the subgraph obtained under the BC measure remains a connected network[bottom of Fig.2(b)].In Section 3,our experiments on synthetic and real networks will show that different subgraph extraction methods have different performances in preserving critical attributes of the original network.

Fig.2.Starting with (a) the original German network G0, the same proportion of nodes are removed under two measures DC(top)and BC(bottom): (b)q=0.5,(c)q=0.7,(d)q=0.9.
3.Simulation and analysis
In this section, we investigate the performance of the reduction scheme by conducting subgraph extraction experiments on ten real networks and five types of synthetic networks, and then compare the similarity between the statistical properties of the reduced subnetwork and the original network, which include the complementary cumulative degree distributionPc(k),the degree-dependent clustering coefficientˉc(k), and the degree-degree correlations ˉknn(k).In network science, the degree distribution is a crucial metric for characterizing the fundamental structural properties of a network.Specifically,the degree distribution can be used to distinguish between homogeneous and heterogeneous networks, where a network with a Poisson distribution of degrees is considered to be homogeneous, and one with a power-law distribution is considered to be heterogeneous.It should be noted that the degree of a node does not provide any information about the relationship between the node’s neighbors.To assess this,the clustering coefficient is used to measure the degree of closeness in connections between neighboring nodes.Thus, the clustering coefficient provides valuable insights into the relationships between nodes in a network.The degree-degree correlations are a measure of the correlation between degrees in a network system.Empirical studies have shown that the degree-degree correlations of networks has a significant impact on their structural and dynamic properties.For instance,in social networks, high-degree nodes tend to be connected to other high-degree nodes, while in protein interaction networks,high-degree nodes tend to be connected to low-degree nodes.Based on these motivations,we select these three representative network structural attributes as the main research objects of this paper.Furthermore,we also further investigate the variation of three single measures during the network reduction process, including the average edge density〈k〉, the average local clustering coefficient〈C〉,and the modularityQ.
3.1.Real-world network datasets
We employ ten real-world networks as the main object of study, including six categories: power grid (German[28]and Entsoe),[29,30]biology (Metabolic, Drosophila, and Proteome), languages (Music and Words), transportation (Airports), technology (Internet), and social (Enron).[10]The basic topological information of these networks is presented in Table 1, including the number of nodes, category, number of edges, and average edge density.All these networks are considered to be unweighted and undirected in our study.

Table 1.Basic network topology information of real-world networks.
3.2.Structural behavior under network reduction
Now, we investigate the structural behavior of each realworld network during the reduction process.In fact, the ten networks in Table 1 can be roughly divided into two categories structurally: one is the homogeneous network represented by Entsoe (containing German and Entsoe networks),whose degree distribution obeys an exponential distribution and is approximately a straight line under the semilogarithmic coordinate axis,as shown in Fig.3(a).The other category is the heterogeneous network represented by the Internet(the remaining eight networks),whose degree distribution obeys a power-law distribution and is approximately a straight line under the double-logarithmic axis,as shown in Fig.4(a).For this reason,we take the Entsoe and Internet networks as examples here to analyze their structural behavior under the four reduction schemes(see Figs.3 and 4).The results for the remaining eight networks are presented in the supplemental material.
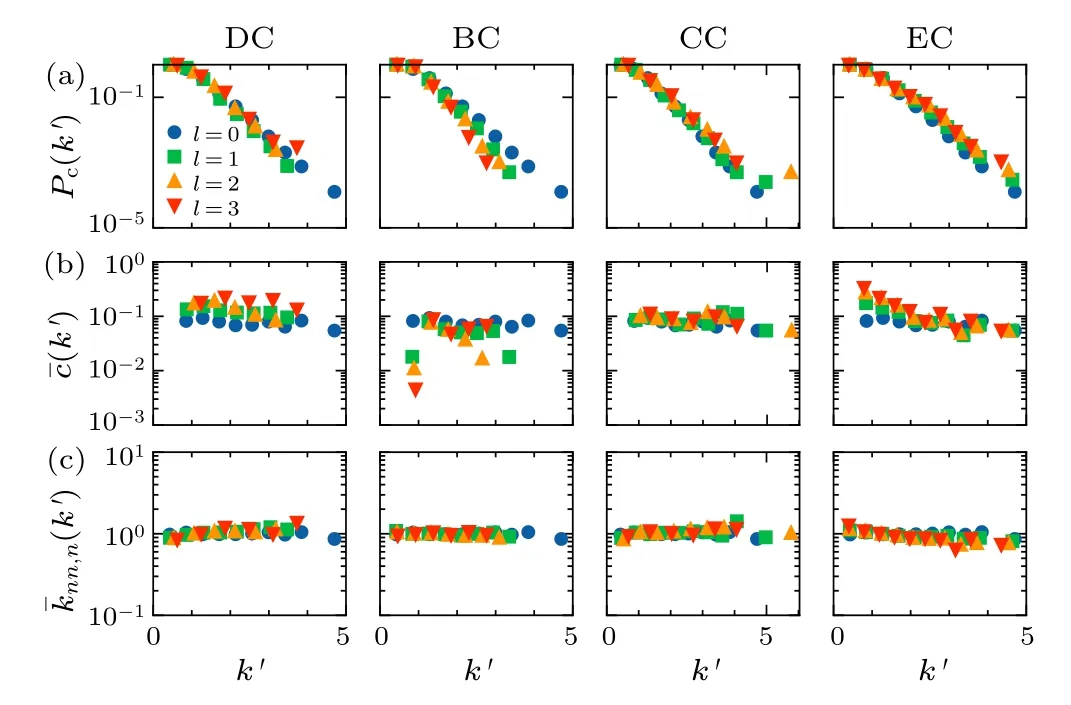
Fig.3.Structural characteristics of the Entsoe network and its subnetworks.
Figure 3 shows the dependence ofPc(k), ˉc(k), andˉknn,n(k) on the node degreekof the Entsoe network and its three subnetworks.The ˉc(k)is defined as the average of the local clustering coefficients of all nodes whose degrees arek.As we know,ˉknn,n(k)=knn(k)〈k〉/〈k2〉,whereknn(k)is defined as the average of the average nearest neighbor degree of all nodes whose degrees arek,〈k〉and〈k2〉are the average degree and the second moment of the degree distribution,respectively.We have shown the horizontal coordinate here as a rescaled degree,following the practice of Ref.[10],k′=k/〈k〉.Each row in Fig.3 shows the reduction results from left to right based on the four centrality measures, DC, BC, CC, and EC.For simplicity,we set the ratio of removal nodes here toq=1-1/2l,l=0,1,2,...,which can reduce the network to 1/2ltimes the original size,wherel=0 represents the original network.Depending on the usage scenario,we can also setqto other values between 0 and 1.The results show that the complementary cumulative degree distribution of the initial Entsoe network is approximately preserved under all four reduction schemes within a limited number of reduction steps,where the self-similarity of the complementary cumulative degree distribution is highest in the EC scheme and weakest in the BC scheme.Here,ˉc(k) shows strong self-similarity under the DC, CC, and EC methods but lacks self-similarity under the BC scheme.In addition, the four subgraph extraction strategies almost always preserve the degree-degree correlation of the original network well.This result implies that different node removal strategies have different effects on the structural behavior of the network.For Entsoe and German networks (see Fig.S1 in the supplemental material), the CC- and EC-based subgraph extraction strategies seem better to preserve the original network’s three critical structural properties.

Fig.4.Structural characteristics of the Internet network and its subnetworks.
Figure 4 shows the structural behavior of the Internet network and its subnetworks under reduction.The results show that the three structural properties of the initial Internet network are self-similar under the four reduction schemes.In terms of degree-degree correlation,although the CC-and ECbased subgraph extraction schemes cause the curve to shift to the left [see Fig.4(c)], it can be seen from the curve’s trend that these two reduction techniques do not destroy the degree-degree correlation of the original network.The results of the remaining seven real scale-free networks are shown in Figs.S2–S8 of the supplemental material.In summary, our results show that the complementary cumulative degree distribution,degree-dependent clustering coefficient,and degreedegree correlation of eight real scale-free networks remain approximately unchanged during the reduction process, which confirms the capability of our method to perform network reduction on real scale-free networks.
We have also performed further experiments on some synthetic networks(see Figs.S9–S13 in the supplemental material), such as ER random networks[22]with Poisson degree distribution and random growth(RG)networks[31]with exponential degree distribution,which are homogeneous networks.In addition,Barab′asi–Albert(BA)[32]scale-free networks,uncorrelated scale-free networks,[33]and S1geometric networks based on hidden metric spaces,[9]which are heterogeneous networks,have also been studied.
For ER random networks, our results show that within a small number of reduction steps (e.g.,l ≤2), the subgraph can approximately preserve the structural properties of the initial network (see Fig.S9).Whenl= 3, the degree distribution of the subgraph deviates significantly from the initial network, with most nodes having zero clustering coefficients[for the DC scheme not shown in the figure, see Fig.S9(b)].For RG networks, our results show that DC- and BC-based subgraph extraction strategies can well preserve the original network’s complementary cumulative degree distribution and degree-degree correlation, while the degree distribution and degree-degree correlation have weak self-similarity under the CC- and EC-based subgraph extraction strategies.In addition, the degree-dependent clustering coefficient lacks selfsimilarity under all four subgraph extraction strategies,and the curve gradually shifts upward aslincreases(see Fig.S10).For BA scale-free networks,the results are similar to the RG network(see Fig.S11).For all three types of networks mentioned above,the initial network size isN=104,and the average degree is〈k〉=10.Similar results can be obtained by changing the initial network sizeNand the average degree〈k〉.
Since BA networks are a special class of scale-free networks, we also performed further experiments on two other types of static scale-free networks:uncorrelated scale-free networks (USF) and S1geometric models.For USF, here withN=104and degree distribution exponentγ=2.5,the complementary cumulative degree distribution is self-similar under all four reduction schemes, while the degree-dependent clustering coefficient has weak self-similarity.Its degree-degree correlation is approximately self-similar under the DC and BC reduction schemes,while it shows weaker similarity under the CC and EC schemes(see Fig.S12).For the S1model,the initial network size isN=104,the degree distribution exponentγ=2.5, andβ=1.5, where the parameterβis used to control the average clustering coefficient of the initial network.[10]The results show that the complementary cumulative degree distribution and the clustering-degree correlation of this network are self-similar under all four reduction schemes.Similarly,its degree-degree correlation is self-similar under the DC and BC reduction schemes, while it shows weaker similarity under the CC and EC schemes(see Fig.S13).The results for all five types of synthetic networks mentioned above are averaged over 10 independent realizations.
Our results indicate that four node removal strategies have similar effects on preserving the structural properties of real scale-free networks (see Fig.4 and Figs.S2–S8), but they have some differences in homogeneous networks (see Fig.3 and Fig.S1).Therefore,for heterogeneous networks,it is currently impossible to distinguish the advantages and disadvantages of four strategies.However,compared to the other three strategies,the DC-based strategy has low computational complexity and is more easily scalable to large networks.In future research,we will further investigate how to select the appropriate subgraph extraction strategy based on the usage scenario,and further explore the underlying mechanisms.
3.3.Discussion
Finally,we investigate the variation of the average degree〈k〉, the average local clustering coefficient〈C〉, and the network’s modularityQwith the proportion of removed nodesq,where the modularity is obtained based on the Louvain[34]detection algorithm.Here, the Entsoe network, the Metabolic network, and the Drosophila network are taken as examples(see Figs.S14–S20 in the supplemental material for the other networks).For the Entsoe and Metabolic networks(see Figs.5 and 6), our results show that these properties of the subgraph always fluctuate around the initial values within a limited number of reduction steps, implying that the subgraph largely retains the structural properties of the initial network.For the Drosophila network (see Fig.7), the average degree is an increasing function ofq,and the average local clustering coefficient and modularity are approximately constant.
It is important to note that although the average degree of the initial network changes during the reduction process, this does not mean the network lacks self-similarity.We can see similar results under previous renormalization schemes, such as degree-thresholding[9]and geometric renormalization[10]schemes, which lead to an increase in the average degree of the network.However,these renormalization frameworks can still preserve some crucial properties of the initial network.Our recent study[19]shows that for scale-free networks,under finite-size scaling analysis, some basic observables including the average degree follow the scaling behavior during the reduction process,which reveals the existence of self-similarity of networks from another perspective.The same is true for the four node removal strategies we considered in this paper.The difference is that they have certain differences in the performance of preserving some key attributes of the initial network.

Fig.5.Dependence of the 〈k〉, 〈C〉, and Qlouvain on the proportion of removed nodes q for the Entsoe network.
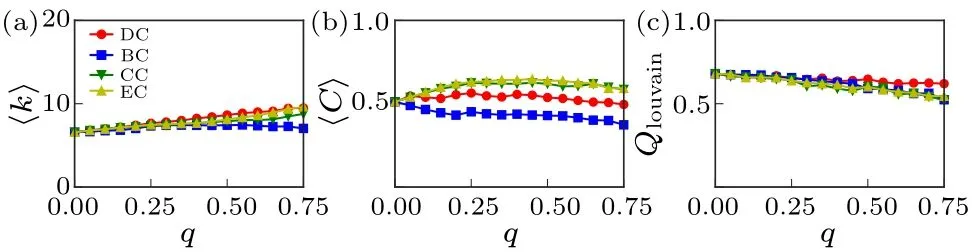
Fig.6.Dependence of the 〈k〉, 〈C〉, and Qlouvain on the proportion of removed nodes q for the Metabolic network.

Fig.7.Dependence of the 〈k〉, 〈C〉, and Qlouvain on the proportion of removed nodes q for the Drosophila network.
Taking the results of the three networks shown in Figs.5–7 as an example, the evolution behaviors of the average degree and the modularity degree under the four node removal strategies are almost consistent, while the average clustering coefficient shows some differences.For other networks, the supplementary results also give consistent conclusions (see Figs.S14–S20).These results show that different subgraph extraction techniques have different effects on the network clustering coefficient.For instance, in the German network,node removal strategies based on CC and EC can better maintain the clustering coefficient of the original network.For the Metabolic network, the DC-based node removal strategy is more effective in maintaining the clustering coefficient of the original network.Therefore, we need to choose appropriate subgraph extraction strategies according to different types of network topologies.For homogeneous networks, our results indicate that the node removal strategies based on CC and EC can better preserve the clustering coefficient of the initial network under the premise of preserving the average degree,degree distribution,degree-degree correlation,and modularity of the original network.However, for heterogeneous networks,these basic properties of networks exhibit some differences in behavior under the four node removal schemes.Specifically,the evolving behaviors of average degree and modularity are almost identical under the four strategies, while the average clustering coefficient shows significant differences.
Combining the results of real-world and synthetic networks,the four subgraph extraction schemes considered in this paper have approximate performance in preserving the crucial properties of real scale-free networks, and it seems to be the most reasonable to consider this scheme on large scalefree networks considering the low computational complexity of the DC-based node removal scheme.For real power grids and ER random networks, the CC- and EC-based reduction schemes are superior to the first two; for other synthetic networks considered in this paper,the DC-and BC-based reduction schemes are superior to the latter two.
4.Conclusion
Node centrality is usually used to measure the importance of network nodes.In this paper, we achieve network size reduction by preferentially removing nodes with small centrality values(those are not important nodes)from the network based on four common node centrality metrics.Our results show that some real networks,including power grids,technology,transportation,biology,social,and language,exhibit self-similarity behavior in their degree distribution, degree-dependent clustering coefficient, and degree-degree correlation in the reduction process.The network reduction scheme proposed in this paper is a further extension of degree-thresholding renormalization,[9]which is essentially different from other coarse-graining techniques,[6–8,10,18]and compared with the latter,the former is technically more straightforward and more efficient in execution.On the other hand,we control the number of nodes in the remaining subgraphs by introducing the node removal ratio, thus solving the uncontrollable problem of subgraph size in degree-thresholding renormalization.Our results reveal the self-similarity and scale invariance of realworld networks from a different perspective,providing an effective guide for simplifying the topology of large-scale networks and useful information for predicting the structural and functional behavior of networks.
Acknowledgment
Project supported by the Science and Technology Project of State Grid Corporation of China (Grant No.5100-202199557A-0-5-ZN).
- Chinese Physics B的其它文章
- Robustness of community networks against cascading failures with heterogeneous redistribution strategies
- Identifying multiple influential spreaders in complex networks based on spectral graph theory
- Percolation transitions in edge-coupled interdependent networks with directed dependency links
- Important edge identification in complex networks based on local and global features
- Free running period affected by network structures of suprachiasmatic nucleus neurons exposed to constant light
- High performance solar-blind deep ultraviolet photodetectors via β-phase(In0.09Ga0.91)2O3 single crystalline film

