A New Inertial Tseng’s Extragradient Method for Solving Split Variational Inclusion Problems and Fixed Point Problems

PEI Yonggang(裴永剛),GUO Jingyi(郭靜邑),SHAO Shuai(邵帥)

(College of Mathematics and Information Science, Henan Normal University,Xinxiang 453007, China)

Abstract: In this paper,we focus on solving split variational inclusion problems and fixed point problems for demimetric mappings.A new inertial Tseng’s extragradient method with non-increasing step size technique is proposed,which is inspired by Tseng’s extragradient method and the viscosity method.Strong convergence is analyzed under some mild conditions.Numerical results are also reported to show the performance of the proposed method.

Key words: Hilbert space;Strong convergence;Demimetric mapping;Split variational inclusion problem;Tseng’s extragradient method

1.Introduction

Assume thatH1andH2are two real Hilbert spaces,A:H12is a bounded linear mapping,B1:H12H1,andB2:H22H2are multi-valued maximal monotone mappings.Split variational inclusion problems (SVIP) are to findx?H1such that

whose solutions set is denoted by SVIP(B1,B2).SVIP (1.1) include split common fixed point problems,convex minimization,split variational inequality problems,and equilibrium problems,etc.[1,3-4,6-8,12,20-21,24]

Recently,for solving SVIP,Byrne et al.[6]introduced the following iterative method(IPPA) in Hilbert spaces: For a givenx11,let{xn}be generated by the following manner:

Alvarez and Attouch[2]considered the heavy ball method that was presented in [14-15]for maximal monotone operators on the proximal point algorithm.The algorithm is called to be the inertial proximal poin{t algorithm as follows.

The weak convergence of the sequence{xn}constructed by (1.3) to a zero point ofTwas also proved.

Employing the idea of Alvarez and Attouch[2],CHUANG[9]constructed a hybrid inertial proximal algorithm for solving SVIP in Hilbert spaces.

Assume thatS:H11is ak-demicontractive mapping,A:H12is a bounded linear operator with adjointA ?:H21,B1:H1andB2:H2are multi-valued maximal monotone mappings.Under certain appropriate assumptions,they have proved that the sequence generated by Algorithm 1 converges strongly to the unique element.Stepsizes play an important role in the convergence properties of iterative methods like Algorithm 1.Armijo line search procedure is one of the effective methods which can avoid the requirement to know the Lipschitz constant or some estimation of it.It is known that the Armijo-like searches adopted can be viewed as a local approximation of the Lipschitz constant ofA.However,such method with a line search may be time-consuming because it requires many extra-computations.

YANG et al.[23]introduced a new self-adaptive subgradient extragradient method for solving the VIPs.

In Algorithm 2,the mappingfis a contraction onH.It should be noted that Algorithms 2 has strong convergence in real Hilbert spaces.

Stimulated by Byrne et al.[6],Alvarez and Attouch[2],CHUANG[9]and YANG et al.[23],we propose a new hybrid inertial accelerated method for finding a common solution of split variational inclusion problems and fixed point problems to a demimetric mapping in a real Hilbert space.This method benefits from the idea of Tseng’s extragradient method and is combined with non-increasing step size technique.Strong convergence of the proposed method is shown under some mild conditions.Furthermore,we also present numerical experiments to demonstrate the efficiency of the proposed method and the comparison results with some other methods.

2.Preliminaries

Throughout this paper,denote byB-1(0):0,D(T) the domain ofTandFix(T) the fixed point set ofT,that is,Fix(T):xT x}.

Lemma 2.1[18]In a real Hilbert spaceH,we have the following results.

1)∥ku+(1?k)v∥2k∥u∥2+(1?k)∥v∥2?k(1?k)∥u ?v∥2,?u,and[0,1];

2)∥u±v∥2∥u∥2±2〈u,v〉+∥v∥2,u,;

3)∥u+v∥2≤∥u∥2+2〈v,u+v〉,u,.

Lemma 2.2[11]LetCbe a nonempty closed convex subset of a real Hilbert spaceH.Forand,thenvPCuif and only if〈u ?v,w ?v〉≤0,,wherePCis the metric projection fromHontoC.

Definition 2.1A mappingS:is called to be:

1) nonexpansive,if

2)γ-contractive,if there exists[0,1) such that

3) quasi-nonexpansive,if Fix(S)? and

4)α-strongly pseudo-contractive,if there exists a constant[0,1),such that

5) pseudo-monotone,if

6)k-demicontractive,if Fix(S)?and there exists[0,1),such that

7)k-demimetric,if Fix(S)?and there exists(?∞,1),such that

To obtain the main results,we give the following lemmas first.

Lemma 2.3[5]LetCbe a nonempty closed convex subset of a real Hilbert spaceH,andT:be nonexpansive.Then,the mappingI ?Tis demiclosed at zero,i.e.,if{xn}converges weakly to a pointand{I ?T)xn}converges to zero,thenxT x.

Lemma 2.4[16,19]SupposeCis a nonempty close convex subset of a real Hilbert spaceH.AssumeS:isk-demimetric such that Fix(S) is nonempty.Letκbe a real number with(0,∞) and defineT(1?κ)I+κS.Then it holds that

1) Fix(T)Fix(S) ifκ0;

2)Tis a quasi-nonexpansive mapping for(0,1?k];

3) Fix(S) is a closed convex subset ofH.

Lemma 2.6[22]Assume{an}is a sequence of nonnegative numbers satisfying the following inequality:an+1≤(1?βn)an+γn+βnδn,N,where{βn},{γn},{δn}satisfy the restrictions:

Lemma 2.7[16]LetHbe a real Hilbert space,B:2Hbe a set-valued maximal monotone mapping.Then,

Lemma 2.9[16]Assume thatH1andH2are real Hilbert spaces,andA:H12is a linear and bounded operator with its adjointA ?.LetB1:H11andB2:H22be a set-valued maximal monotone mappings,and letr,λ>0.Then,the following statements hold:

3.Main Results

LetCandQbe nonempty convex closed subsets of real Hilbert spacesH1andH2,respectively,andA:H12be a bounded linear operator with adjointA ?:H21.LetB1:H11andB2:H22be a set-valued maximal monotone mappings.Assume thatS:H11isk-demimetric andI ?Sis demiclosed at zero.LetG:H11be contractive with constant(0,1).Assume that Sol :SVIP(B1,B2)∩Fix(S)?and the following conditions are satisfied:

Lemma 3.1[23]The sequence{λn}generated by(3.2)is well defined and limn→∞λnλand

Lemma 3.2Suppose that(C1)-(C3)hold.Let{un},{yn}and{zn}be three sequences created by Algorithm 3.Then,forSVIP(B1,B2),

From Lemma 2.7,we can obtain that

NoticingA qwe obtain from Lemma 2.7(2) that

It follows from (3.2),(3.3),(3.4) and (3.5) that

Then,the proof is completed.

Lemma 3.3Suppose that the sequences{un}and{yn}are created by Algorithm 3.If?z?and limn→∞∥un ?yn∥0,thenz?SVIP(B1,B2).

This together with (3.4) and Lemma 2.8 1) and 2) yield that

This indicates that

Again using Lemma 2.7 and the definition ofyn,we derive

which together with (3.6) gives that

From limn→∞∥yn ?un∥0,one obtains that

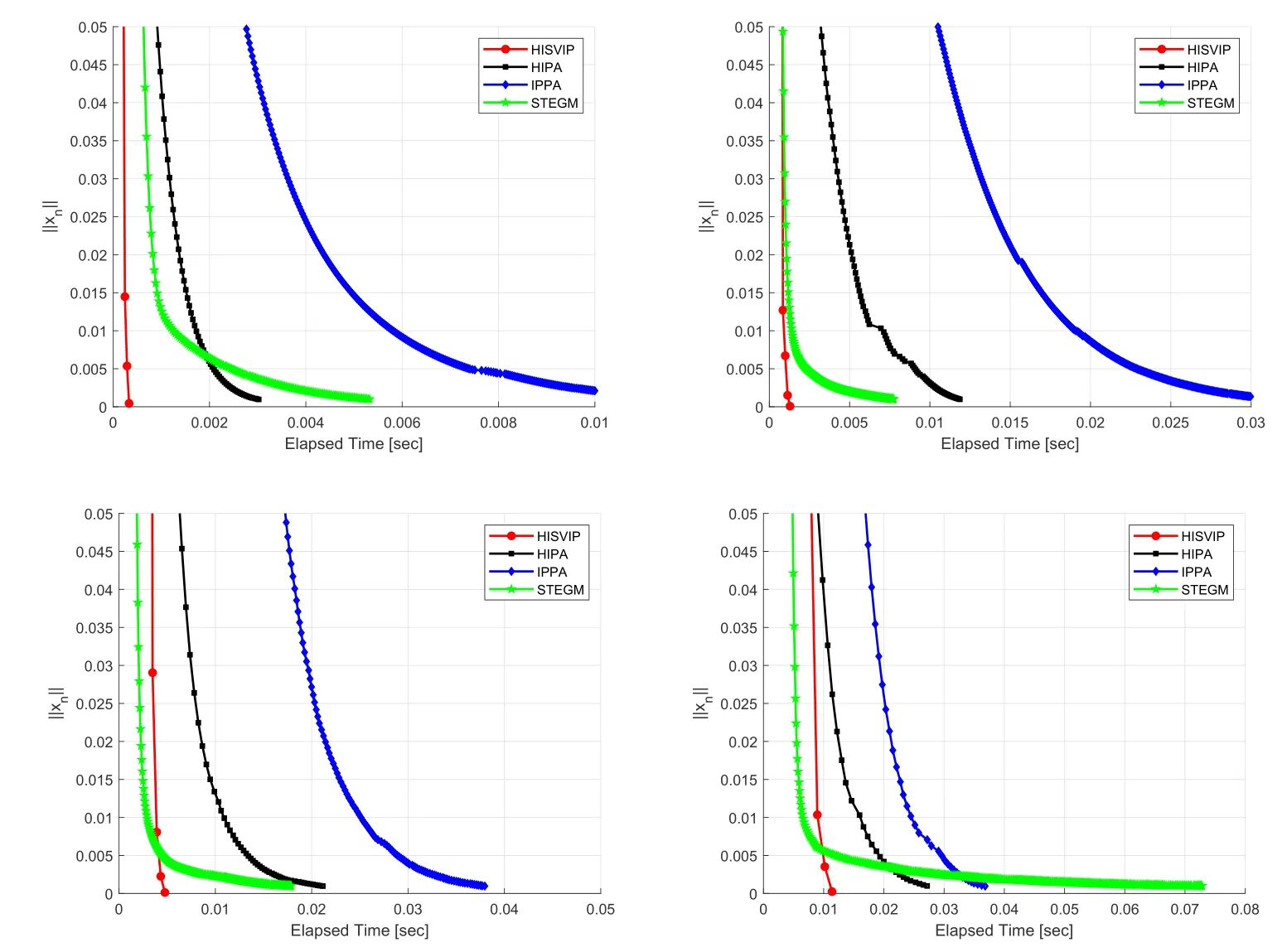
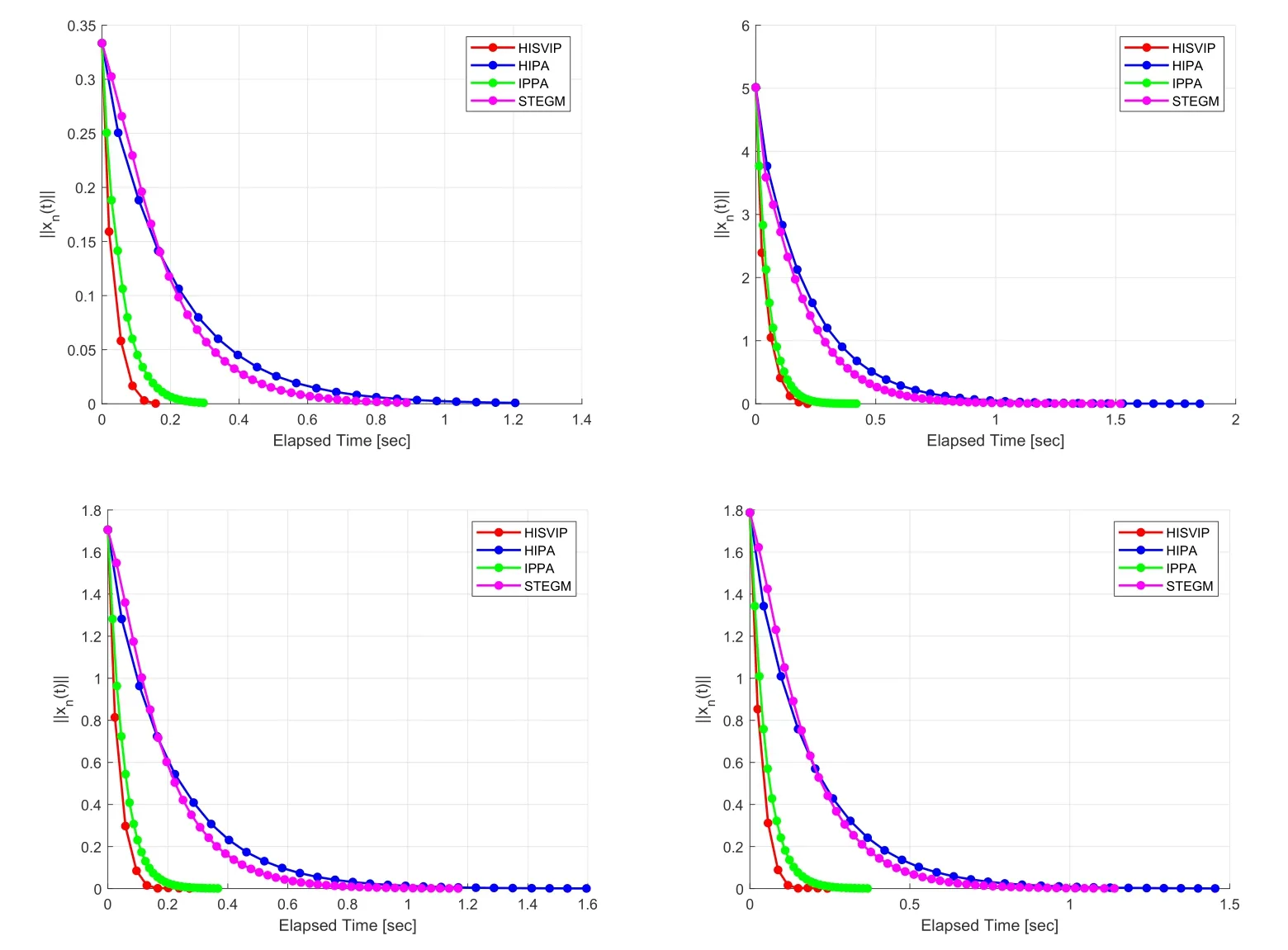
According to (C4),there exist a positive numberrand some positive integerN0such that 0

Using (3.6) and Lemma 2.7 3),we obtain

Theorem 3.1Assume that conditions(C1)-(C3)are satisfied.Then the sequence{xn}generated by Algorithm 3 converges toqin norm,whereqPSolgq.

ProofFirstly,we prove that the sequence{xn}is bounded.Taking anySol,we can conclude from Lemma 3.2,Lemma 3.3 and assumptions(0,1) that there existsn0≥1 such that 1?>0 for alln ≥n0.Hence,we have,for alln ≥n0,

In view of the definition ofun,one can deduce that

Invoking (C3),there exists a positive constantM1<∞such that

From (3.9),(3.10) and Lemma 2.4,we can obtain that

which yields that{xn}is bounded.Using (3.9),(3.10) and the definition of{yn},we get that{zn},{yn}and{un}are bounded.According to Lemma 2.1 3),we obtain that

whereM2supn≥0{2∥un ?q∥}<∞.

Then,it follows from Lemma 2.4,Lemma 3.2 and (3.11) that

SettinggnαnG xn+(1?αn)znand using (3.9),(3.11) and Lemma 2.1 1),we infer that

Next,we shall prove that the sequence{∥xn ?q∥}converges to zero for the following two cases.

Case 1 Suppose that there existsN0N such that the sequence{∥xn ?q∥}n≥N0is monotone decreasing.Then,limn→∞∥xn ?q∥exists.From(C1)and taking the limit of both sides in (3.13) (),we have that

It follows from (C1),(C3) and the definitions ofunthat

By (C1),(C2),(C3) and (3.14),we obtain that

Due to the fact thatgnαnG xn+(1?αn)zn,we infer that

Noting min{ζ,δl ∥A ∥-2}≤λn ≤ζand the definition ofzn,Lemma 2.7 1)and(3.15),we can deduce that

Using (3.15),(3.16) and (3.19),we have that

Taking into account that

we deduce from (3.17) and (3.18) that

Noticing∥xn+1?xn∥≤∥xn+1?zn∥+∥zn ?xn∥,this together with(3.20)and(3.21)implies

Since{xn}is bounded,it follows that there exists a subsequence{xnk}of{xn}that converges weakly to some1and

From(3.15),(3.16)and Lemma 3.3,we obtain thatSVIP(B1,B2).From the assumption thatI ?Sis demiclosed and using (3.17),(3.18) and (3.20),we haveFix(S).Therefor,Sol.Obviously,PSolgis a contractive mapping.Banach’s Contraction Mapping Principle yields thatPSolghas a unique fixed pointqPSolgq.It follows from Lemma 2.2 that

Therefore,we have that

This together with (3.22) implies that

It follows from (3.9),(3.11),Lemma 2.1 3) and Lemma 2.4 that

Then,from (3.23),(C1),(C3) and Lemma 2.6,we obtain thatxnq.

Case 2 Assume that{∥xn ?q∥}is not monotone decreasing.Then there exists a subsequence{∥xni ?q∥}of{∥xn ?q∥}such that

From Lemma 2.5,there exists a nondecreasing sequence{mk}?N such that

Similar to the argument in Case 1,we can obtain that

As in Case 1,we can also obtainSol.Thus,we have by Lemma 2.2 that

This together with (3.26) implies that

Due to (3.9),(3.11),Lemma 2.1 and Lemma 2.4,we can deduce that

which yields that

Noticing (3.24),we obtain that

By applying (C1),(C3) and (3.27),we get

It thus follows from (3.25) that

Based on the above results,we can conclude that the sequences generated by Algorithm 3 converges strongly toSol,which is the unique fixed point of the contractive mappingPSolg.Then,the proof is completed.

Letg:(?∞,+∞] be a proper convex lower semi-continuous function.Then,the subdierential?gofgis defined as follows:

From [13],we know that?gis maximal monotone.It is easy to verify that 0(x) if and only ifg(x)miny∈H g(y).LetICbe the indicator function ofC,i.e.,

Then,ICis a proper lower semi-continuous convex function onH,and the subdierential?ICofICis a maximal monotone operator.Furthermore,supposeCis a nonempty closed convex subset.Then,

For more details,one can refer to [17].

The following algorithm is a special case of Algorithm 3 with a specifical projection in Step 2.

The convergence of Algorithm 4 can be obtained from Theorem 3.1.

Corollary 3.1Assume that Conditions (C1)-(C4) are satisfied.Then the sequence{xn}constructed by Algorithm 4 converges strongly to a pointq,whereqPSVIP(C,Q)fq.

4.Numerical Results

In this section,we present the numerical performance of the proposed method Algorithm 3 (HISVIP) in comparison with related methods,Algorithm (1.2) (IPPA in [6]),Algorithm 1 (HIPA in [9]),and Algorithm 2 (STEGM in [23]) .Numerical testing is implemented as a MATLAB code and run under MATLAB version 9.4.0.813654 (R2018a).

The initial valuesx0are randomly generated in(0,1)and the stopping criterion is∥xn∥<10-3.We test Algorithm (1.2) (IPPA),Algorithm 1 (HIPA),and Algorithm 3 (STEGM) and Algorithm 4 (HISVIP) forx0x1and different valuesm: Case I:m10;Case II:m50;Case III:m100;Case IV:m200.The numerical results are shown in Fig.1.

Fig.1 Example 4.1,top left: Case I;top right: Case II,bottom left: Case III,bottom right:Case IV

Algorithm(1.2)(IPPA),Algorithm 1(HIPA),and Algorithm 2(STEGM)and Algorithm 3 (HISVIP) are compared for different values ofx0andx1as follows:

Case Ix0t4andx1t+1;

Case IIx03t4+t ?6 andx15t;

Case IIIx02cos(t) andx1sin(t);

Case IVx0etandx13et.

The comparison results are presented in Fig.2.

Fig.2 Example 4.2,top left: Case I;top right: Case II,bottom left: Case III,bottom right:Case IV

From the numerical results,it can be seen that the efficiency of Algorithm 3 is able to be comparable with Algorithm (1.2) (IPPA),Algorithm 1 (HIPA),and Algorithm 2 (STEGM),at least for these examples.