Anomalous non-Hermitian dynamical phenomenon on the quantum circuit

Chenxiao Dong(董陳瀟), Zhesen Yang(楊哲森), Jinfeng Zeng(曾進(jìn)峰), and Jiangping Hu(胡江平),3,?

1Beijing National Laboratory for Condensed Matter Physics,and Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2Kavli Institute for Theoretical Sciences,University of Chinese Academy of Sciences,Beijing 100190,China

3South Bay Interdisciplinary Science Center,Dongguan 523808,China

4Beijing Academy of Quantum Information Sciences,Beijing 100193,China

Keywords: spectral degeneracy splitting, discrete-time quantum walk, quantum circuit, non-Hermitian skin effect

1.Introduction

The non-Hermitian skin effect (NHSE), which refers to the phenomenon that the extensive number of eigenstates are localized on the boundary in the non-Hermitian openboundary system,[1]is systematically studied in theory[1–13]and widely realized in the experiment.[14–25]It is regarded as the non-perturbative breakdown of Bloch theorem,[26]which leads to new physical phenomena.Recently, people theoretically predicted some anomalous non-Hermitian dynamical phenomena in the NHSE system,[27–35]for example, the edge burst phenomenon in a lossy quantum walk,[28]the invisibility phenomenon in tight-binding lattices.[30]In experiment, people implement part of non-Hermitian dynamical phenomena,[14,18,36]for example, the funneling phenomenon in the optic system.[36]Generally, those NHSE experiments are constructed in the topolectrical circuits,[15,16,22]the photonic system[14,36]and the acoustics system,[24,25]which mostly are the classical system.It is challenging to develop an easy-to-control and scalable quantum experiment platform to study new non-Hermitian dynamical phenomena.

The quantum circuit is a quantum computation model based on a sequence of quantum gates and quantum measurement.[37]Theoretically,an ideal quantum circuit with enough qubits and enough circuit depth can simulate the evolution under any Hamiltonian.[38]The digital gate-base quantum simulators,such as superconducting quantum devices,[39]can directly implement the quantum circuit models.Therefore, it is a selective experiment platform to implement the non-Hermitian dynamical phenomenon.

Due to the experimental advancement of the quantum technology,[40,41]we are entering the so-called noisyintermediate-scale quantum (NISQ) machines era[42]with hundreds of noisy qubits.A challenge is to develop applications by harnessing the computational power of these nearterm quantum devices.[43]Recently, Google[44]and Wuet al.[45]perform random quantum circuits sampling on superconducting quantum processors to show a quantum advantage.Although these specifically designed tasks may seem useless,these quantum advantage experiments motivate efforts to search practical real-world applications on near-term quantum devices.One of the active research hotspots is solving scientific problems which are not tractable on a classical quantum computer.Many quantum algorithms based on quantum circuits are developed for quantum chemistry,[46,47]combinatorial optimization problems,[48]and machine learning.[49]Another notable direction for harnessing the NISQ devices is regarding the near-term programmable quantum computer as a new experimental platform for the simulation of quantummechanical systems,[41]which takes advantage of the extensive control and measurement capabilities in programmable quantum simulators.Two recent works simulate the discretetime crystals[50]and many-body localization[51]on near-term superconducting quantum circuits.The simulation of the NHSE system can be a promising application of the NISQ devices.[52]

In this paper,we propose quantum circuits as the new experiment platform to study the non-Hermitian dynamical phenomenon based on a new type of discrete-time quantum walk(DTQW).We construct a new non-unitary DTQW model by introducing the non-unitary evolution to the one-dimensional standard DTQW.We study the physics of this non-unitary DTQW and design its quantum circuit implementation.Besides, based on this non-unitary DTQW, we construct the domain wall experiment and the phase impurity experiment,which break the global space-translational-symmetry to exhibit more anomalous non-Hermitian dynamical phenomena.At last,we numerically simulate all these quantum circuit experiments with quantum noises to verify the robustness of the non-Hermitian dynamical phenomenon on the NISQ devices.

2.Theoretical definitions and models

In this section,we introduce the common physical origin of the NHSE and some non-Hermitian dynamical phenomena,the degeneracy splitting of the periodic-boundary spectrum,which directs the design of our model.Then we construct our non-unitary DTQW model and analyze its physics, including the spectrum,the eigenstate,and the dynamic.

2.1.Non-Hermitian skin effect and non-Hermitian dynamical phenomenon

Firstly, we discuss the relation between the non-Hermitian skin effect and the non-Hermitian dynamical phenomenon.

The non-Hermitian skin effect is defined as the phenomenon that an extensive number of skin modes appear in the open boundary non-Hermitian system.In the onedimensional non-Hermitian tight-binding system, the nonzero winding number of the periodic-boundary spectrum leads to the presence of skin modes with the open boundary condition (OBC).[3,6]Recently, people proposed a new criterion of the NHSE,the degeneracy splitting of the periodic boundary spectrum,defined as that a point on the periodic-boundary spectrum only corresponds to a momentum.[32]Besides, different from the winding number,the degeneracy splitting criterion is applicable for the higher-dimensional non-Hermitian tight-binding system.[13]Here, we take the Hatano–Nelson model[53]for example,whose Hamiltonian follows

Here,tLandtRrepresent the nearest-hopping strength.WhentL=tR, due to the time-reversal symmetry, the momentumkand?kshare the same energy.Therefore, its spectrum is degenerate.WhentL／=tR, due to the imaginary part of the energy,the degeneracy of the periodic-boundary spectrum breaks, and the system exhibits the NHSE with the OBC, as shown in Figs.2(a)–2(c).

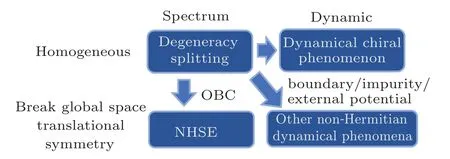
Fig.1.The degeneracy splitting.This figure shows that the NHSE,[1] the dynamical chiral phenomenon[27]and other non-Hermitian dynamical phenomena with the global space-transitional-symmetry break[28,30–32,36]originate from the(periodic-boundary spectral)degeneracy splitting.[32]

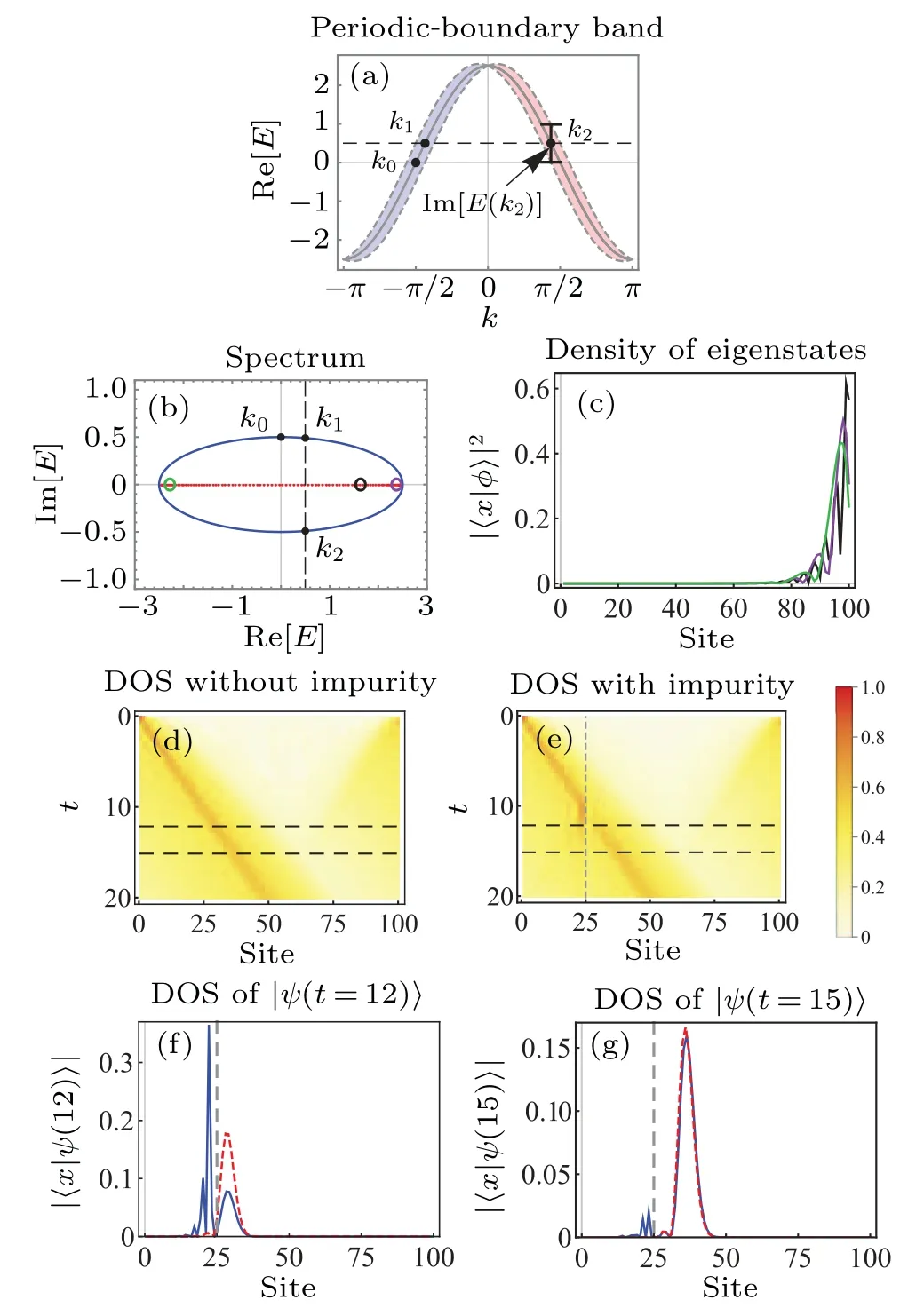
Fig.2.The Hatano–Nelson model.(a) The periodic-boundary band of the Hatano–Nelson model.(b)The spectrum of the Hatano–Nelson model, where the red line marks the open-boundary spectrum, and the blue line marks the periodic-boundary spectrum.(c) The density distribution of the right eigenstates corresponding to the open-boundary eigenvalues circled in (b).(d) and (e) The density distribution of the evolving state with and without the on-site impurity for the initial state|ψ(t=0)〉=|x=1〉.(f) and (g) The density distribution of the state when t =12 and 15 (labeled by the black dashed line in (d) and (e))with the initial state |ψ(t=0)〉=|x=1〉, where the red dashed line marks the evolution in the homogenous system,and the blue line marks the evolution with the on-site impurity on x=25.The parameter of the Hatano–Nelson model in this figure is(tL,tR)=(1.5,1).

On the other hand, the degeneracy splitting of the periodic-boundary spectrum can be regarded as the physical origin of many non-Hermitian dynamical phenomena.Here,we take the evolution under the Hatano–Nelson model as an example.The evolution equation follows

Here,HH?Nis the Hamiltonian of the Hatano–Nelson model in Eq.(1).We set(tL,tR)=(1.5,1).In this model,the evolving state trend to form the wavepacket moving toward the right, defined as the dynamical chiral phenomenon.Generally,the state can be regarded as the composition of the plane wave of different momentum.In a homogenous evolution,the plane wave component which has the largest imaginary part of energy in the open boundary spectrum grows the fastest and gradually becomes dominant.Due to the degeneracy splitting of the periodic-boundary spectrum, the dominant plane wave component corresponds to only a certain momentum.In this model, this momentum isk0=?π/2.Therefore, the state forms a wavepacket with the center momentumk0=?π/2 moving towards the right.

Then we introduce the on-site impurityμ=10 on the sitex=25 to the Hatano–Nelson model.When the wavepacket hits the on-site impurity, part of the wavepacket is reflected.The reflected wavepacket gradually decreases and eventually disappears.The reflection on the impurity changes the momentum component of the reflected wavepacket.By contrast, the wavepacket across the impurity remains approximately unchanged.Based on the above discussion, the wavepacket across the impurity remains the dominant plane wave component withk0=?π/2, whose increasing rate is larger than other plane wave components.Therefore, the reflected wavepacket exponentially decreases compared to the wavepacket across the impurity.Our discussion also applies to the reflection on the boundary or the trapping potential.Further quantitative discussion of the reflection and the scattering will be in our following articles.

In summary, the non-Hermitian skin effect and some non-Hermitian dynamical phenomena originate from the same physics, the degeneracy splitting of the periodic boundary spectrum, which also is the key physics of our non-unitary DTQW model.

2.2.Standard DTQW and non-unitary DTQW

The Hatano–Nelson model is simple but it is difficult to simulate its evolution directly and accurately on the quantum circuit.Here, we select the non-unitary DTQW system as our experimental model.The DTQW is the quantum extension of the random walk[37,54]and the component of many quantum algorithms,[54–58]which is easy to implement in quantum circuits.In other experiment platforms, the non-unitary DTQW system also serves as the non-Hermitian simulation.[14–16,18,59,60]

The standard DTQW[54,61]describes the quantummechanical discrete-time evolution of particles(called“quantum walkers”).It is defined on the Hibert space spanned by the coin space{|↑〉,|↓〉}and the position space{|x〉}.In the standard DTQW, we select an initial state|ψ0〉, for example,|↑,0〉=|↑〉?|x=0〉, then apply the unitary evolution operatorUin series, and approach the final state|ψn〉=Un|ψ0〉afternsteps evolution.The single-step evolution operator of the one-dimensional standard DTQW,Us,is combined by the coin rotation operatorCand the position shift operatorS:

The position shift operatorSmoves the walker on the position space depending on their coin state.In this paper,the position space of the quantum walk is a one-dimensional loop.Therefore,the shift operatorSsets as

The coin rotation operatorConly rotates the coin state and keeps the position states invariant.It follows

where?posis the identity operator on the position space.

Here, we introduce the non-unitary evolution to the discrete-time quantum walk by inserting a new operatorMbetween the coin operatorCand the shift operatorSin the evolution operatorU.The operatorMonly acts on the coin space,which decreases the particle number of the coin state|↑〉,and keeps the coin state|↓〉invariant.It follows

Here,αis a real number and 0<α<1.

In summary, the non-unitary DTQW follows the same process as the standard DTQW, besides the difference in the single-step evolution operator.This operator in the nonunitary DTQW,Un,follows

2.3.The effective Hamiltonian and the dynamical chiral moving

Generally,we can define the effective Hamiltonian of the DTQW

Here,Uis the single-step evolution operator.If we take the coin space as the spin-1/2 space, the DTQW process is regarded as the evolution of the state under the spinful Hamiltonian.We can calculate the spectrum and the eigenstates of the effective Hamiltonian for the standard DTQW and the nonunitary DTQW,which determine their dynamics,as shown in Fig.3(numerical detail in supplemental material I).

For the standard DTQW,its effective Hamiltonian is Hermitian.It indicates that the spectrum of its effective Hamiltonian is a real number with the periodic boundary condition(PBC) and keeps invariant with the open boundary condition(OBC), as shown in Fig.3(b1).Correspondingly, its eigenstates are composed of the plane wave both with OBC and with PBC,as shown in Fig.3(c1).For the dynamic feature,the evolution process in the standard DTQW is a quantum spread behavior and depends on the initial states,as shown in Fig.3(d1)and 3(e1).

For the non-unitary DTQW, its effective Hamiltonian is non-Hermitian.And it shows the degeneracy splitting of the periodic-boundary spectrum,as shown in Fig.3(b2).According to the previous discussion, the degenerate splitting leads to the NHSE with the OBC,where most eigenstates are localized on the left boundary, as shown in Fig.3(c2).It also induces the dynamical chiral phenomenon in the homogeneous system, where the walker forms the wavepacket moving toward the left,as shown in Figs.3(d2)and 3(e2).Further,this dynamic phenomenon is independent of any localized initial state for the long-time evolution.

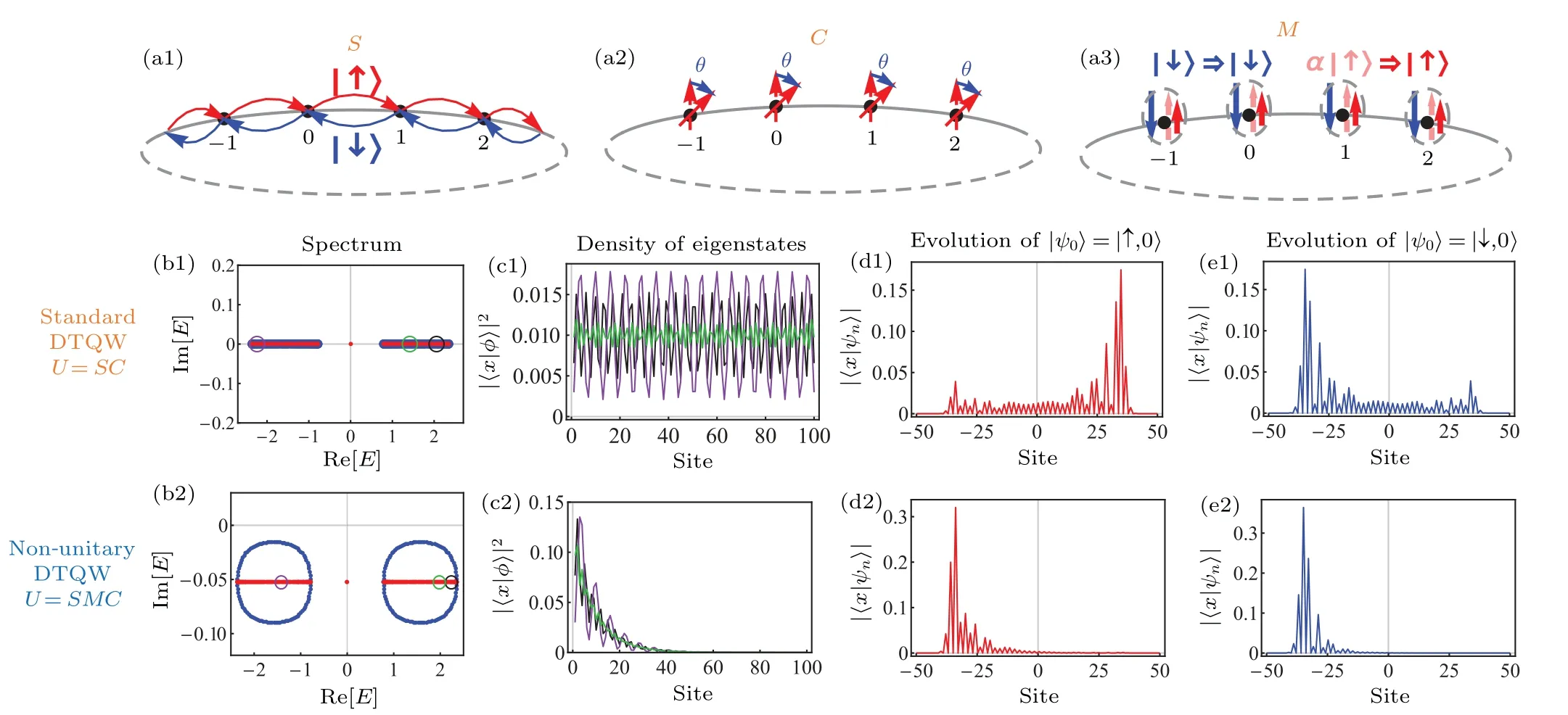
Fig.3.The standard DTQW,the non-unitary DTQW,and their effective Hamiltonian.(a1)–(a3)The operator components in the single-step evolution operator of the standard DTQW and the non-unitary DTQW:the shift operator S,the coin operator C,the additional non-unitary operator M.(b1)and(b2) The spectrum of effective Hamiltonian in the standard DTQW and in the non-unitary DTQW, where the red line represents the spectrum with the open boundary condition (OBC), and the blue line marks the spectrum with the periodic boundary condition (PBC).(c1) and (c2) The density distribution of the right eigenstates corresponding to the eigenvalues circled in (b1) and (b2).(d1) and (d2) The density distribution of the final state after 50-step evolution with the initial state|ψ0〉=|↑,0〉in the standard DTQW and the non-unitary DTQW.(e1)and(e2)The density distribution with the initial state|ψ0〉=|↓,0〉in the standard DTQW and in the non-unitary DTQW.The parameter of the DTQW in this figure is(θ,α)=(π/4,0.9).

3.The general quantum circuit implementation

In this section,we discuss the quantum circuit implementation of the non-unitary DTQW in the qubit system.

As discussed in Subsection 2.2, the standard DTQW and the non-unitary DTQW follow the same physical process despite the difference in the single-step evolution operator.Their evolution operator shares the same component,the coin operatorCand the shift operatorS.For the standard DTQW, people have developed many different quantum circuit implementations.[61,62]Here we follow a simple and fundamental implementation in Ref.[62] and design the implementation of the non-unitary DTQW based on it.

In this implementation of the standard DTQW,Nqubits construct the position space with the size 2Nnamed position qubits, and a qubit constructs the coin space named the coin qubit.Specially, we separately set the state of the coin qubit|1〉 and|0〉 as the coin states|↑〉 and|↓〉.The coin operatorCis implemented as a single-qubit quantum gate, RX,on the coin qubit.And we encode the position of a loop with the natural order.In this paper,we follow the order shown in Fig.4(b).The shift operatorScan be constructed by the generalized CNOT gates and two single-bit quantum gatesXshown in Fig.4(a).

Besides,the preparation of the initial state depends on the physical implementation of the quantum circuit.In this paper,we only choose the states|↑,0〉 and|↓,0〉 as the initial state.If we suppose the initial state of the whole quantum circuit is|000···〉as the state|↑,0〉, we can approach another initial state|↓,0〉only by the single-qubit gate X on the coin qubit.In the last of the quantum circuit,the distribution of the final state in the position space can be directly measured on the position qubits.

Next, we discuss the implementation of the non-unitary operatorM.Generally,the ideal quantum gate only carries the unitary evolution.By introducing quantum measurement, we can implement the non-unitary evolution.[63]Here, we need an additional ancilla qubit.As shown in Fig.4, we need a two-qubit gate,RY on the ancilla qubit controlled by the coin qubit, and a measurement on the ancilla qubit.If the initial ancilla qubit is|0anc〉and the ancilla qubit stays in|0anc〉after the measurement, the non-unitary operation on the coin state is

Hereais the rotation degree of the RY gate and the parameter of the operatorM,α=cosa.

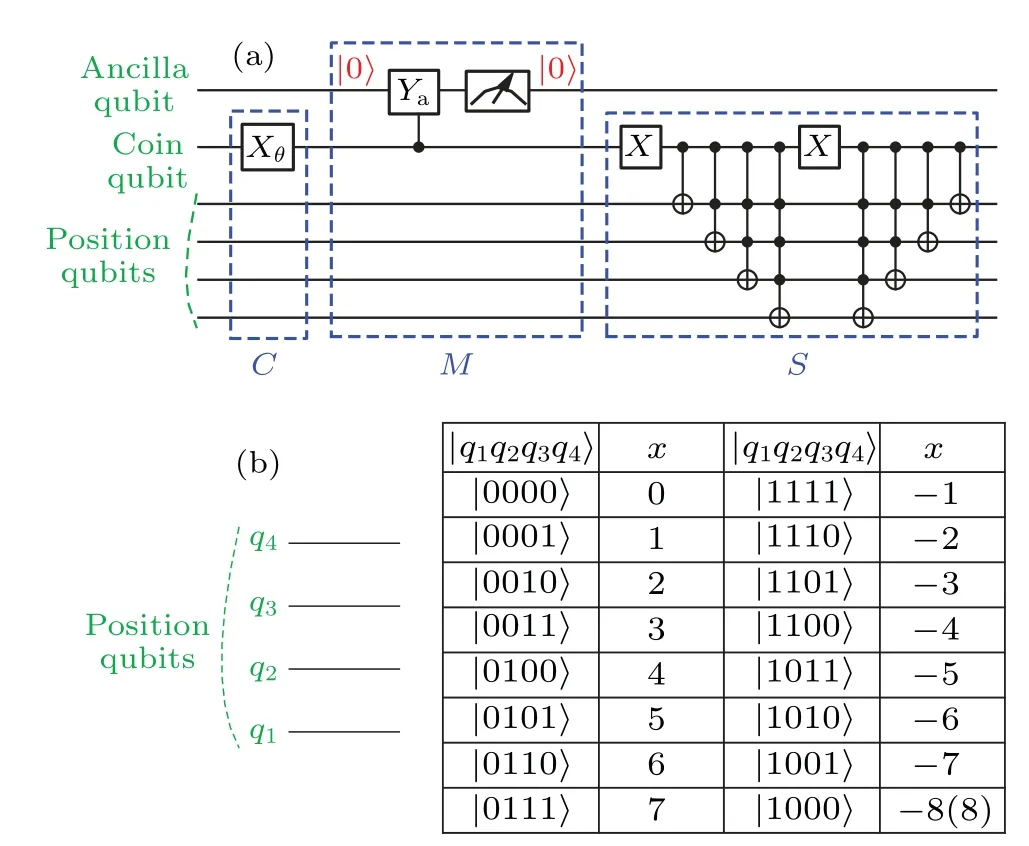
Fig.4.The quantum circuit implementation of the non-unitary DTQW.(a) The quantum circuit implementation of the non-unitary DTQW.(b)The encoding of the position state on the position qubits.

In summary, the quantum circuit implementation of our non-unitary DTQW with the system size 2Ncontains at leastN+2 qubits in whichNqubits construct the position space,one qubit constructs the coin space,another qubit serves as an ancilla qubit.

4.Experimental design

In this section,we design three different experiments,including the chiral moving experiment,the domain wall experiment,and the phase impurity experiment.We simulate them in the ideal quantum circuit and discuss their dynamic phenomenon.

4.1.Chiral moving experiment

Firstly, we implement the dynamical chiral phenomenon of the homogenous system in the quantum circuit.The nonunitary DTQW model defined in Subsection 2.2 acts as the experimental model of this phenomenon.Its single-step evolution operator follows

Its quantum circuit implementation is detailedly discussed in Section 3.We simulate it in the ideal quantum circuit and show the position distribution of the walker after 5-step evolution,where the wavepacket of different initial states always moves towards the left.For comparison,we also simulate the evolution of the standard DTQW in the ideal quantum circuit,as shown in Fig.6.The physics of the dynamical chiral phenomenon has been discussed in Subsection 2.3.

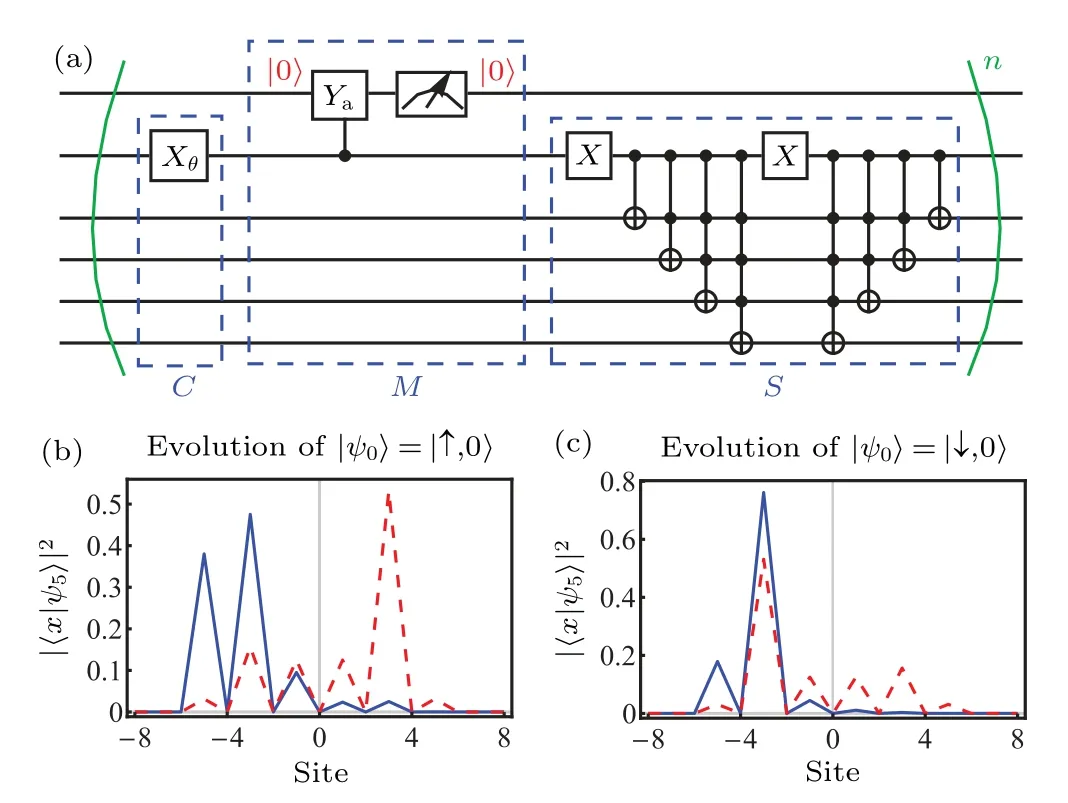
Fig.5.The quantum circuit implementation of the chiral moving experiment.(a)The quantum circuit implementation of the chiral moving experiment.Here we ignore the initialization of the initial state and the final measurement on the position qubits.(b)and(c)The density distribution of the final state after 5 steps with the initial state |ψ0〉=|↑,0〉and|ψ0〉=|↓,0〉.The red dashed line represents the result of the standard DTQW, and the blue line represents the result of the non-unitary DTQW.The parameter of the standard DTQW and the non-unitary DTQW in this figure is(θ,α)=(π/4,0.5).

4.2.Domain wall experiment

In Subsection 2.3,we indicate that the right eigenstate of our non-unitary DTQW is localized on the left boundary with OBC.If we replace the operatorMwith its dual operatorM′in the single-step evolution operator

The right eigenstate of this new non-unitary DTQW will be localized on the right boundary (detail in supplemental material II).As discussed in Subsection 2.1, the wavepacket’s moving direction depends on the eigenstates’ skin direction with OBC.The moving direction of the wavepacket on this new non-unitary DTQW is opposite to one on the non-unitary DTQW in Subsection 2.2.

Here, we can design a hybrid non-unitary DTQW which is divided into two domains.The skin direction of the left domain is right,while the one in the right domain is left.Correspondingly,the wavepacket in the left domain moves to the right, while the one in the left domain moves in the opposite direction.Finally, the wavepacket in this hybrid non-unitary DTQW funnels on the center domain wall, which is defined as the funneling phenomenon on the domain wall.This hybrid non-unitary DTQW can be implemented by constructing a new non-unitary operator,MDW, which is equal toMwhenx ≥0,and equal toM′whenx<0.It follows

The single-step evolution operator of this hybrid nonunitary DTQW set as

This hybrid non-unitary DTQW acts as the domain wall experiment exhibiting the funneling phenomenon.Similar configurations and the funneling phenomenon have been proposed and successfully realized in the optic experiment.[14,36]

In quantum circuit implementation, the new non-unitary operator,MDW,can be constructed as two RY gates on the ancilla qubit controlled by the coin qubit and the position qubitq1, as shown in Fig.6(a).In our implementation, the center domain wall locates between positions 0 and 1.To decrease the steps that the walkers approach the localized states, we keep the initial states as|ψ0〉=|↑,0〉and|ψ0〉=|↓,0〉.

In our simulation,different from the standard DTQW,the walker after 8-step evolution of the hybrid non-unitary DTQW remains localized around 0 to 1, as shown in Figs.6(b) and 6(c).

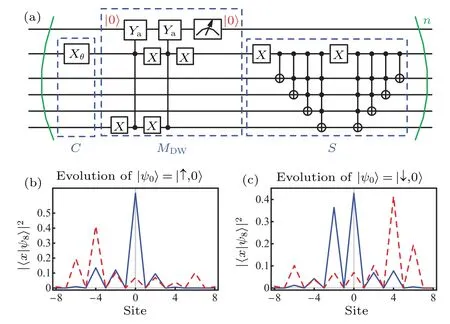
Fig.6.The quantum circuit implementation of the domain wall experiment.(a) The quantum circuit implementation of the domain wall experiment(we ignore the initialization of the initial state and the final measurement on the position qubits).(b) The density distribution of the final state after 8-step evolution with the initial state |ψ0〉=|↑,0〉.(c)The density distribution of the final state after 8-step evolution with the initial state|ψ0〉=|↓,0〉.The red dashed line represents the result of the standard DTQW,and the blue line represents the result of the nonunitary DTQW.The parameter of the standard DTQW and the hybrid non-unitary DTQW in this figure is(θ,α)=(π/4,0.5).

4.3.Phase impurity experiment

In Section 3, we discuss the reflection behavior on the onsite impurity in the Hatano–Nelson model.However, it is difficult to introduce the onsite impurity, the trapping potential or the open-boundary condition to our non-unitary DTQW by adding the simple operator into the single-step evolution.Fortunately, we can set the phase impurity.It adds the additional phase on a position in the single-step evolution by the simple impurity operatorPimp,which follows

Hereδ(x) is the Dirac delta function,θpis the additional phase,andx0is the position of the impurity.

Now,the single-step evolution operator of the non-unitary DTQW with the phase impurity sets as

In quantum circuit implementation,the operatorPimpcan be implemented by the multi-controlled RZ gate on the position qubits.In our simulation,we setθp=πandx0=?7.The correspondent implementation of the impurity operatorPimpis theZgate on the position qubitq4controlled by the other position qubits,as shown in Fig.7(a).

Then we simulate the evolution behavior of the nonunitary DTQW with the phase impurity in the ideal quantum circuit.Before the walker moves across the impurity,the evolution in the non-unitary DTQW with and without the phase impurity is the same, as shown in Fig.7(b).When the wavepacket hits the impurity, we find that a part of the wavepacket is reflected and gradually decreases in Figs.7(c)and 7(d).Finally, the reflected part of the wavepacket disappears, and the wavepacket moves through the impurity in Fig.7(e).

We find that the reflection behavior on the phase impurity in the non-unitary DTQW is similar to the one on the on-site impurity in the Hatano–Nelson model.Their physics is also similar.In DTQW,the wavepacket of the walker is regarded as the composition of the plane wave with different momentum.For the effective Hamiltonian with OBC, due to the degeneracy splitting, different momentum corresponds to different energy.The imaginary part of energy represents the decay ratio of the plane wave.In a homogeneous system, the plane wave component with the largest imaginary part of the energy in the spectrum grows the fastest and gradually becomes dominant.The reflection on the impurity or the boundary changes the momentum composition of the wavepacket.By contrast,the wavepacket across the impurity remains approximately unchanged.Therefore,the decay ratio of the reflected part is less than the other.The reflected wavepacket relatively decreases and even disappears.We provide the numerical detail in the momentum space in supplemental material III.

Here, we provide an observable to verify our argument.We define the discrete related decay ratio (DRDR) of the walker population

Here,Nnis the population of the walker inn-th step.In the quantum circuit experiment,we can measure the walker population for each step by the quantum measurement on the implementation of the operatorM.The DRDR of the phase impurity experiment rapidly decreases when the wavepacket moves across the impurity and recovers after the reflected part disappears, as shown in Fig.7(e).It is in line with our physical analysis.

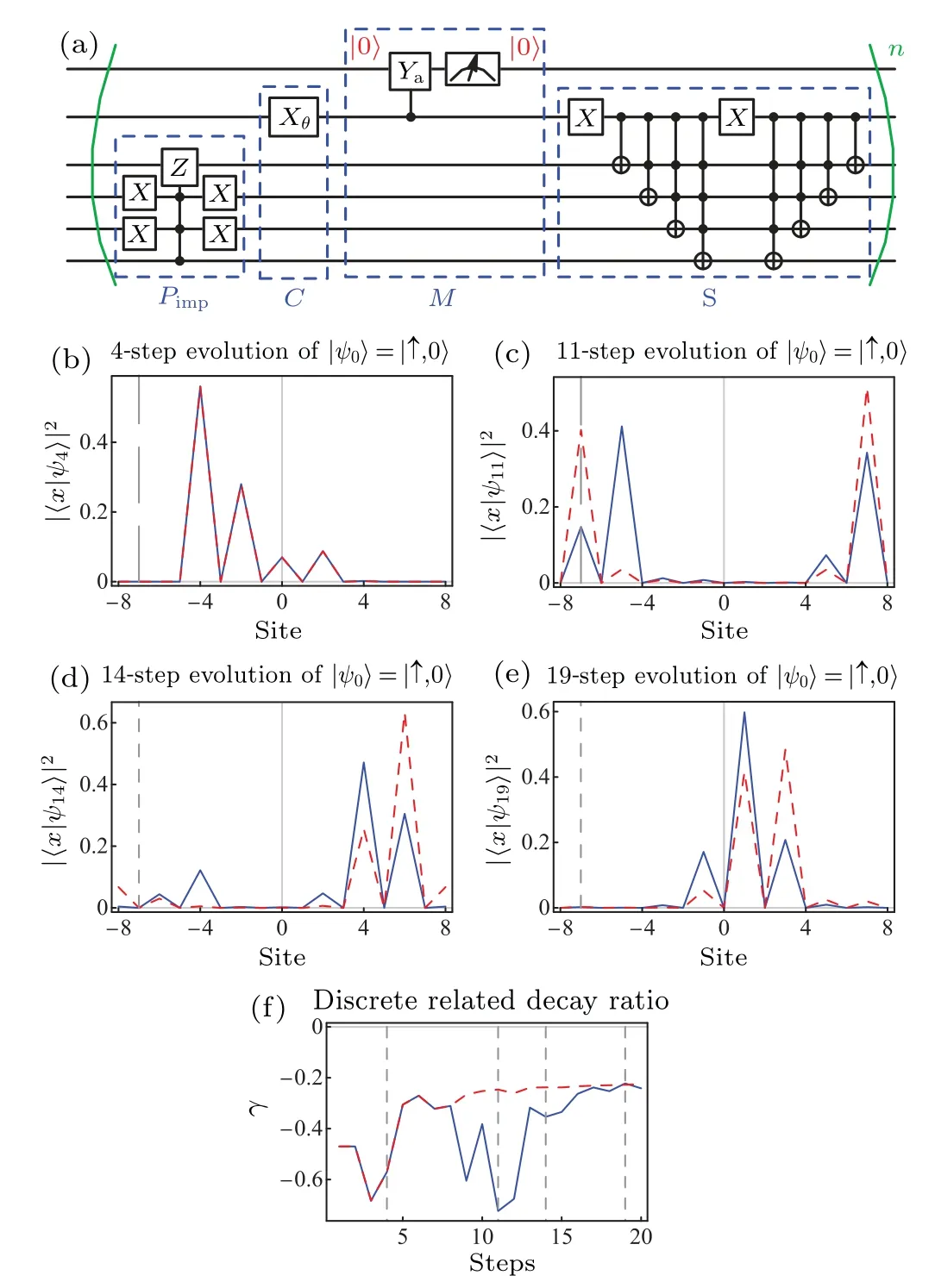
Fig.7.The quantum circuit implementation of the phase impurity experiment.(a) The quantum circuit implementation of the phase impurity experiment (we ignore the initialization of the initial state and the final measurement on the position qubits).(b)–(e) The density distribution of the final state after 4, 11, 14 and 19 steps of evolution with the initial state |ψ0〉=|↑,0〉.(f) The discrete related decay ratio for the first 20-step evolution in the non-unitary DTQW with and without phase impurity.The red dashed line represents the result without the phase impurity, and the blue line represents the result with the phase impurity.The parameter of the non-unitary DTQW in this figure is(θ,α,θp,x0)=(π/4,0.5,π,?7).

5.Simulation with quantum noises

In Section 4,we simulate the ideal quantum circuit implementations for different dynamical phenomena without noise.However, noise is inevitable in the NISQ devices.Generally,the type and the strength of the quantum noise depend on the physics implementation of the quantum circuit.In this section, we focus on quantum noise and consider two types of common quantum noise,measurement error,and environmental decoherence.Besides the quantum error, we also discuss two types of random perturbations in our experiment in supplemental material V.

5.1.Measurement error

Firstly,we consider the measurement error on the implementation of operatorM.We model this noise as the stochastic flipped on the ancilla qubit measurement with probabilitypm.The effective evolution ofMwith the measurement error on the coin qubit follows

It indicates that the measurement error renormalizes the parameterαas

To quantify the influence of the measurement error in our experiment,we induce two observers,the average position and the DRDR.

The average position is defined for a state of the DTQW,which follows

where|〈ψn|x〉|2is the density of the state|ψn〉on the positionx.We calculate the average position of the final state to quantify the result in the chiral moving experiment and the domain wall experiment.The relation of the parameterαand the average position is shown in these experiments in Figs.8(a)and 8(b).We can observe the qualitative phenomenon in these experiments under the measurement errorpm～0.2, which is much larger in the general experimentpm～0.05.It indicates that the experiments are robust under measurement noises on the NISQ device.

In the phase impurity experiment, we can measure the walker population to calculate the DRDR.The difference is that the walker population measured in the noisy experiment is the result of the effective evolution with the non-unitary operatorMerr.When the measurement errorpmincreases, the DRDR of the non-unitary DTQW with the phase impurity decreases and is close to one without the phase impurity, as shown in Fig.8(c).We calculate the difference of the DRDR in the non-unitary DTQW with and without the phase impurity ?γnand show the relation of the phase impuritypmand the maximum DRDR’s difference Max?γfor the first 20-step evolution in Fig.8(d).It is proved that we can approach the anomalous decay phenomenon in the phase impurity under the large measurement errorpm～0.2.

In summary,these non-Hermitian dynamical phenomena are stable under the measurement errorpm.Their robustness depends on the robustness of NHSE under the parameterα.With the measurement errorpmincreasing, the effective parameterαincreases,but the effective system still exhibits the NHSE(detail in supplemental material I).

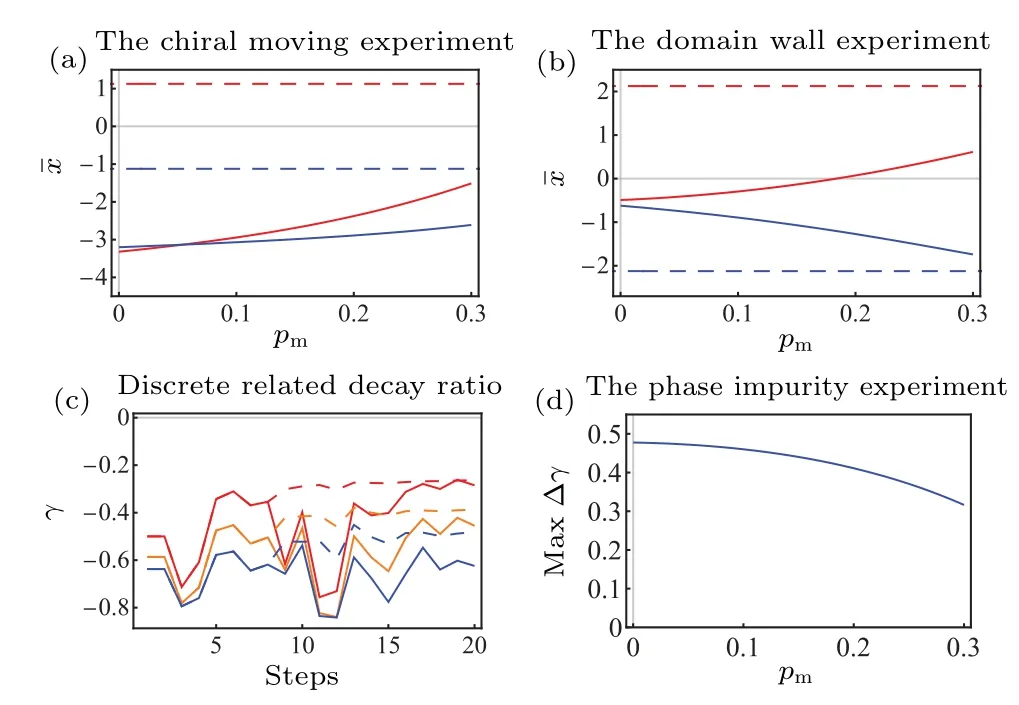
Fig.8.The influence of the measurement error.(a) The average position of the walker after 5-step evolution under different measurement error pm in the chiral moving experiment.The red line marks the result with the initial state |ψ0〉=|↑,0〉 while the blue line marks the result with the initial state |ψ0〉 = |↓,0〉.The dashed line represents the result of the standard DTQW while the solid line represents the result of the non-unitary DTQW.(b) The average position of the walker after 8-step evolution under different measurement error pm in the domain wall experiment.The marks in (b) are the same as those in (a).(c) The measuring DRDR for the first 20 steps in the phase impurity experiment for pm=0.05(red), pm=0.2(orange)and pm=0.3(blue).The dashed line represents the result of the non-unitary DTQW with the phase impurity while the solid line represents the results without the phase impurity.(d) The relation between the measurement error pm and the maximum measuring DRDR’s difference Max?γ in the phase impurity experiment.The parameter in this figure is(θ,α,θp,x0)=(π/4,0.5,π,?7).

5.2.Environmental decoherence

Next, we consider environmental decoherence, which comes from the interaction between the system and the environment.Here, we model it by considering one-qubit and two-qubit depolarizing error models,[37]acting on the system’s density matrixρa(bǔ)s

Here,σα,iis the Pauli operator on thei-th qubit, and the primed sum denotes (α,β)／=(0,0).In our simulation, we compile our experiment design with the CNOT gate and the single qubit gate (detail in supplemental material IV), apply the channelΦto the single qubit gate,and apply the channelΦto the CNOT gate.Here,we setpd=p2=10p1as the decoherence rate which qualifies the strength of the environmental decoherence.

In the chiral moving experiment and the domain wall experiment, with the decoherence ratepdincreasing, the position distribution trends to the uniform distribution, as shown in Figs.9(a1) and 9(a2).In view of the quantum information, the information of the system leaks to the environment,and the state turns towards the homogeneous mixed state due to the environmental decoherence.Correspondingly, the average position in the experiment rapidly decreases to 0 with the decoherence ratepdincreasing,as shown in Figs.9(b)and 9(c).The non-Hermitian dynamical phenomena in these experiments cannot be observed whilepd>0.01.

Fig.9.The influence of the environmental decoherence.(a1) The position distribution of the walker after 5-step evolution in the standard DTQW under different decoherence rate pd.(a2)The position distribution of the walker after 8-step evolution in the domain wall experiment under different decoherence rate pd.(b)The average position of the walker after 5-step evolution under different decoherence rate pd in the chiral moving experiment.The red line marks the result with the initial state|ψ0〉=|↑,0〉while the blue line marks the result with the initial state|ψ0〉=|↓,0〉.The dashed line represents the result of the standard DTQW while the solid line represents the result of the non-unitary DTQW.(c)The average position of the walker after 8-step evolution under different decoherence rate pd in the domain wall experiment.The marks in (c) are the same as those in (b).(d1)–(d3)The measuring DRDR for the first 20-step evolution in the phase impurity experiment.The gray line is the result of the ideal experiment.(e) The relation of the decoherence rate pd and the maximum DRDR’s difference Max?γ in the phase impurity experiment.The parameter in this figure is(θ,α,θp,x0)=(π/4,0.5,π,?7).

In the phase impurity experiment, with the decoherence ratepdincreasing, the difference between the non-unitary DTQW with and without the impurity decreases,as shown in Figs.9(d1)–9(d3).The maximum DRDR difference in this experiment rapidly decreases to 0 with the decoherence ratepincreasing topd～10?3, as shown in Fig.9(e).It indicates that a tiny decoherence ratepd(pd<0.002) is necessary for our phase impurity experiment.

In summary,the environmental decoherence weakens the stability of the non-Hermitian dynamical phenomenon in the experiment.Generally, the influence of environmental decoherence is exponentially related to the depth of the quantum circuit or the number of quantum gates and quantum measurement.In the next section, we discuss the possible improvement to reduce the depth of the quantum circuit in our experiments.

6.Discussion and conclusions

In conclusion, we propose a quantum circuit as the new experiment platform to study the non-Hermitian dynamical phenomenon based on a new type of non-unitary DTQW.We study the effective Hamiltonian of non-unitary DTQW to analyze its dynamic.Based on this non-unitary DTQW,we then construct three quantum circuit experiments, including chiral moving, domain wall, and phase impurity experiments, to exhibit the non-Hermitian dynamical phenomenon.Further,we discuss the robustness of those phenomena under different noises.Our proposed quantum circuits can be implemented on near-term superconducting quantum devices and on future fault-tolerant digital quantum computers.

The previous papers study many non-Hermitian tightbinding systems whose hopping range is finite.However,the hopping range of the effective Hamiltonian for our non-unitary DTQW is infinite.In this paper, we numerically study the spectrum and the dynamic of the non-unitary DTQW and find that the degeneracy splitting criterion for the NHSE and some non-Hermitian dynamical phenomena keeps valid in our system.The generalization of the non-Hermitian theory to more systems is meaningful work.

In this paper, we design three experiments based on the non-unitary DTQW model in the quantum circuit.In fact,the other physical systems also can implement the non-unitary DTQW model, for example, the topolectrical circuits[15,16]and the optic system.[14,18,59,60]Our work also inspires the implementation of the non-Hermitian dynamical phenomenon in the other experiment platform.Besides, we also provide the remaining probability of states on all our designs for experimenters in supplemental material VI.

At last,we consider the possible improvement of our experiment implementation.In Subsection 4.2,we indicate that the reduction of the quantum circuit depth can strengthen the robustness under the environmental decoherence in the NISQ device.In our design, the realization of the operatorSdenotes lots of quantum gates(more detail in supplemental material IV).A selective method is changing the position encoding to reduce the number of quantum gates.[61]

Noted addedAfter this work was submitted toChinese Physics B,a relevant paper appeared on arXiv,[64]implementing the edge-burst phenomenon with the same operator design in the photonic platform.

Acknowledgements

Project supported by the National Key R&D Program of China (Grant No.2022YFA1403901), the National Natural Science Foundation of China (Grant No.NSFC-11888101),the Strategic Priority Research Program of Chinese Academy of Sciences(Grant No.XDB28000000),and New Cornerstone Investigator Program.Z.Y.was also supported by the fellowship of China National Postdoctoral Program for Innovative Talents(Grant No.BX2021300).