Turing/Turing-like patterns: Products of random aggregation of spatial components

Jian Gao(高見), Xin Wang(王欣), Xinshuang Liu(劉心爽), and Chuansheng Shen(申傳勝)

1International Joint Research Center of Simulation and Control for Population Ecology of Yangtze River in Anhui,Anqing Normal University,Anqing 246011,China

2School of Mathematics and Physics,Anqing Normal University,Anqing 246011,China

Keywords: Turing-like pattern,collective behavior,random aggregation,pattern formation,multi-particle system

1.Introduction

Ordered spatiotemporal patterns arising out of randomness are typical and interesting phenomena during morphogenesis.[1]Turing,[2],in his groundbreaking work,has put forward a type of explanation for a variety of patterns observed in nature.[3–6]He believes that emergences of these spatially periodical patterns are induced by interaction between a long-range inhibitor and a short-range activator.Turing’s theory of reaction diffusion (RD) has been proved to be greatly influential across many research fields.[7]For instance, patterns in chlorite iodide malonic acid chemical reactions,[8–12]stripes on tropical fishes,[3,13]and pigment patterns on sea shells[14,15]have been investigated as Turing patterns via the RD theory.Moreover, Turing patterns have the property of cross scale.The typical length scale of Turing patterns on the surface of animals ranges from millimetres to centimetres,and that in chemical reactions is about sub-millimetres.Recent studies[16–18]have found that the scale of Turing patterns can be observed at the nanoscale.

In addition to RD systems, Turing/Turing-like patterns can also be observed in fluid systems,[1,19–23]gas discharges,[24–26]spatial distribution of bacterial population,[27,28]and even distribution of human settlements.[29]In this article, we call the patterns, which are similar to Turing patterns but have different or ambiguous generation mechanisms, the Turing-like patterns.Generally,Turing/Turing-like patterns are studied in systems driven far from thermodynamic equilibrium.[1]Turing’s RD mechanism containing a long-range inhibiting agent and a local catalytic agent only appears in this type of nonequilibrium systems.Specifically, most of the experimental studies of Turing/Turing-like pattern are devoted to finding the two elements supporting the Turing mechanism, i.e., a long-range inhibition and a short-range self-activation, which exist in systems driven far from thermodynamic equilibrium.[3,5,30,31]

In fact, a large number of studies[3,8–29]based on different systems show that, the formation mechanism of Turing/Turing-like patterns across different systems should be of a spatial problem, not of local dynamics.Therefore, Turing/Turing-like patterns could exist in systems near thermodynamic equilibrium.The conjecture is encouraging.Studying Turing/Turing-like patterns in near-equilibrium thermodynamic systems can avoid complex dynamics problems in dissipative systems far from thermodynamic equilibrium,thus greatly simplifying the related problems of the mechanism for Turing/Turing-like patterns.Consequently,it is more meaningful and important to study Turing/Turing-like patterns in near-equilibrium systems for understanding the formation mechanism of Turing/Turing-like patterns.

We accidentally observed a type of Turing-like pattern with a‘labyrinthine’stripe structure in a system near thermodynamic equilibrium, which can hardly be explained by the classical Turing mechanism(see Fig.1).This pattern appears during the slow cooling process of the starch solution.In particular,the pattern still exists when the system finally reaches thermodynamic equilibrium,which is quite different from the Turing/Turing-like patterns in dissipative systems.For instance,Turing/Turing-like patterns in chemical reactions,[8–12]thermal convection[1,19–23]and gas discharges[24–26]can only appear in the process of violent reactions,and disappear when the systems reach thermodynamic equilibrium.

In this article, by investigating this phenomenon, we put forward new ideas on the formation mechanism of Turing-like patterns.We find that the random aggregation of spatial components leads to the formation of Turing-like patterns,and the proportion of spatial components determines the pattern structures.The rest of the article is organized as follows: Section 2 introduces the materials and methods.Section 3 shows the results, including the experimental results and numerical results.Finally, conclusions and discussions are presented in Section 4.

Fig.1.(a)A Turing-like pattern with a‘labyrinthine’stripe structure observed in a rice porridge(the area in the white circle).Structure description: Bulges and depressions appear on the original flat surface,namely peaks and valleys.The peaks and valleys are long strips, which appear alternately in space to form a ‘labyrinthine’ stripe structure.The white lumps in the figure are expanded rice grains,e.g.,the one indicated by the white arrow.(b)Schematic diagram of the longitudinal section along the white dotted line of the Turinglike pattern in panel (a).The distance between adjacent stripes λ is about 0.27 cm.

2.Materials and methods

2.1.Experiment 1

We believe that the Turing-like pattern in Fig.1 is a selforganized structure formed by the starch solution in rice porridge with a certain concentration.To reproduce the Turinglike pattern in Fig.1,we designed a group of experiments with starch solution, and took the concentration of starch solutionρ ≡ms/Vas the control parameter,withmsandVindicating the quality of starch and the volume of starch solution,respectively.

Materials:Starch(rice powder)and water.

Experimental procedure:

Step 1: Dissolvemsg of starch in water.

Step 2: Keep the starch solution at 90?C for three hours.

Step 3: Place the starch solution in a horizontal container keeping a 3 mm thin layer.For easy observation, we use a black container to hold the starch solution.

Step 4: Cool naturally at 10?C.

2.2.Experiment 2

Studies have shown that thermal convection can lead to the appearance of Turing-like patterns.[1,21–23]A natural conjecture is that,during the cooling process of the starch solution in Experiment 1,thermal convection was generated due to the lower temperature of the upper surface,resulting in the Turinglike patterns in Experiment 1.To examine whether the Turinglike patterns obtained in Fig.1 and Experiment 1 are caused by thermal convection, we designed Experiment 2.Figure 2 shows the experimental design of Experiment 2.This design would reverse the direction of the temperature gradient and eliminate thermal convection.In this group of experiments,we also took the concentration of starch solution as the control parameter.

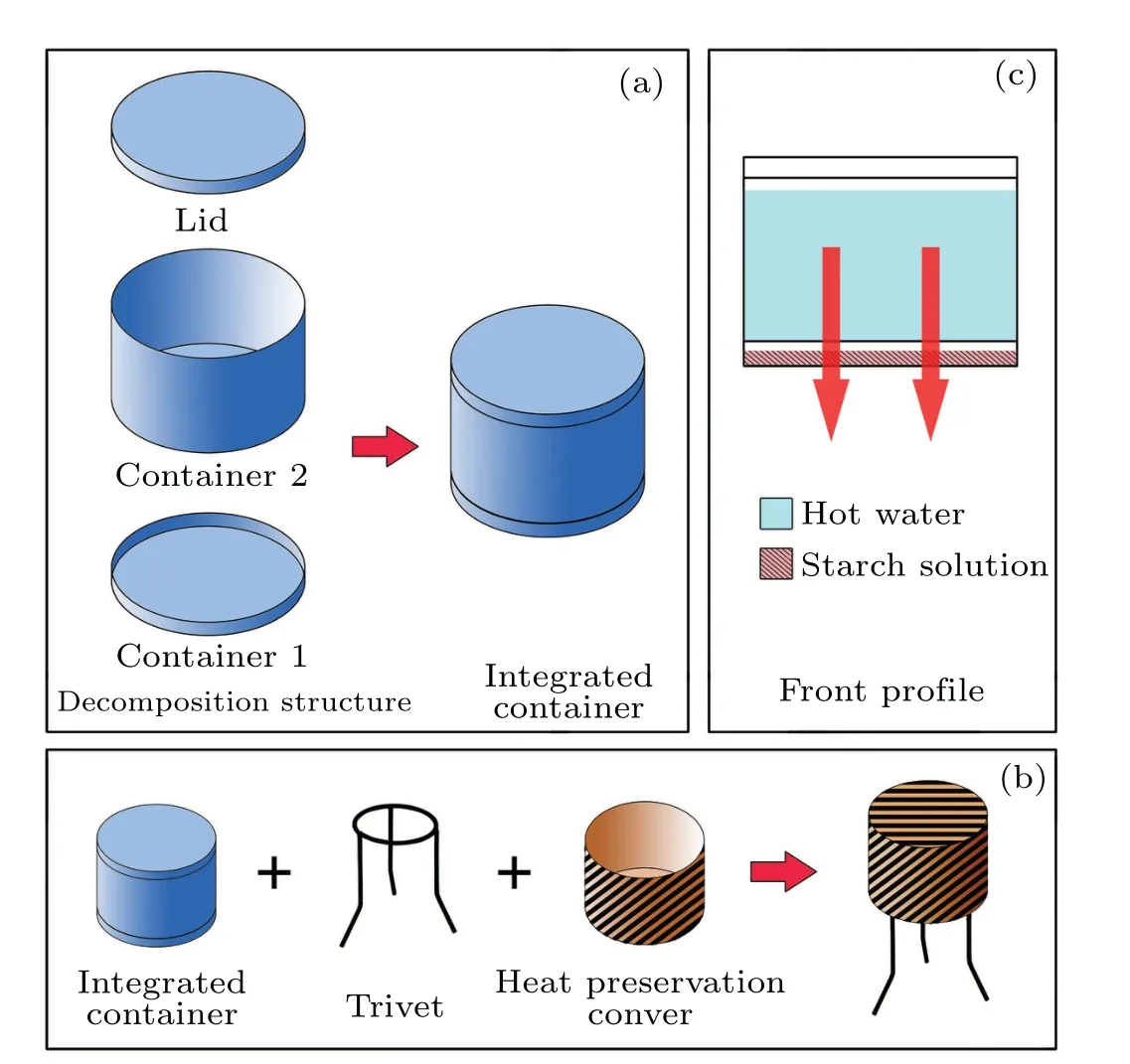
Fig.2.Design for Experiment 2.(a)Container structure.Containers 1 and 2 are used to hold starch solution and hot water, respectively.In order to obtain a high rate heat transfer, the containers are made of metal(stainless steel).(b) Placement of equipments.Place the integrated container on a trivet so that no objects prevent heat from escaping from the bottom of the container into air.Then cover the side and top of the container with a heat preservation cover.(c)Front profile of the integrated container.The red arrows in panel(c)indicate the direction of heat flow.The heat flow direction is downward,thus avoiding the occurrence of thermal convection.

Materials:Starch(rice powder)and water.

Experimental procedure:

Step 1: Dissolvemsg of starch inmwg of water.

Step 2: Keep the starch solution at 90?C for three hours.

Step 3: As shown in Fig.2,place the starch solution and hot water (90?C) in Containers 1 and 2, respectively.Keep the starch solution in a 3-mm-thick layer.Then place the integrated container containing starch solution and hot water on a trivet and keep it warm with a heat preservation cover.

Step 4: Cool naturally at 10?C.

2.3.Model 1

Starch is a polymer compound with molecular formula(C6H10O5)x(xis an uncertain positive integer).The results of Experiment 2 proved that the patterns observed in experiments are not products of thermal convection.Accordingly,we believe that the Turing-like patterns in experiments are induced by random aggregation of starch macromolecules, and the random aggregation is attributed to the interactions between starch macromolecules.Here, we propose a model to verify the conjecture.

We regard the thin liquid layer in the experiment as anL×Ltwo-dimensional (2D) system filled with a large number of particles(starch macromolecules),which are evenly and randomly distributed in the system.(There is no interaction between the system boundary and particles.)The position vector of the particlei(i=1,2,3,...,N)can be expressed aspi.Consider repulsive,attractive,and viscous forces between particles, denoted asfr,fa, andfv, respectively.Generally, the magnitude of force between the particlesiandjis negatively correlated with the distancerbetween them,i.e.,

wherenis a positive integer.In addition, when the distance is less than the equilibrium distance, the repulsive force increases faster with the decreasing distance.When the distance is greater than the equilibrium distance (within the action range), the repulsive force decreases faster with the increasing distance.This feature of the forces prevents the particles from being infinitely close or being isolated from each other.Therefore, the parameterncorresponding to the repulsive force should be greater than that corresponding to attractive force,i.e.,nr>na.Specifically,the forces applied by the particlejto the particleican be expressed as

with

We presume that particleimoves along the direction of the resultant forceFiat a constant velocityυ, ifFiis greater than the thresholdFthr,i.e.,

whereFirepresents the resultant force on the particlei;αrepresents a unit vector with a random direction,WGrepresents a Gaussian white noise with with a mean of 0 and a variance of 1,andσis a parameter that controls the degree of noise.The parameters are fixed:L=50,nr=3,na=2,kr=1,ka=1,kv=5,zr=1,za=3,zv1=1,zv2=1.2,Fthr=0.05,υ=1,andσ=0.2.The spatial density of the particlesρ ≡N/L2has similar physical meaning to the concentration of starch solutionρin the experiments, and is set as the control parameter.The system was carried out by the Euler method with time steps of?t=0.02.Note that, the same results can be obtained when the parametersnrandnaare equal to 2 and 1,respectively(see Fig.A1 in Appendix A).We also got the same results when considering the interaction between the system boundary and particles(see Fig.A2).MATLAB codes to calculate the system are available from the authors on request.

2.4.Model 2

Model 1 is based on the specific system of starch solution, so this model has no generalisability.In order to verify our general conclusion (Turing-like patterns are induced by the random aggregation of spatial components),we propose a general model in the following.

N(N=1,2,3,...,n2)small balls are randomly dispersed in ann×ngrids (each grid can hold only one small ball and the side length of each grid ish=1).Select one small ball randomly and let it walk randomly(in the continuous 2D space)until it meets another small ball(the selected small ball can only walk in the empty grid and cannot cross other small balls).The random walk follows the equations

whereptrepresents the position vector of the selected small ball at timet;vtis the change of the position vectorpt+1;θtindicates the direction angle ofvt;andrepresents a Gaussian white noise with a mean of 0 and a variance of 0.15.This process is recorded as one operation.Then repeat the above operation.The total number of steps taken by all selected balls is recorded asT.The parameters are fixed:n=300,υ=1,andσ=π/4.The initial valuesp0andθ0are taken randomly in their ranges.The fill ratio of the gridsR ≡N/n2,which has similar physical meaning toρa(bǔ)ndρ, is set as the control parameter.Codes for this model are available from the authors on request.

3.Results

3.1.Results of experiment 1

We examined the effects ofρon the structure of patterns.The results show that Turing-like patterns would not appear on the surface when the concentration of starch solution is too small or too large.Turing-like patterns can appear only when the concentrationρis in a certain range from 0.04 g/cm3to 0.10 g/cm3, and the structural characteristic of the patterns changes with the change of the concentrationρ.The bulges(peaks) in the pattern show circular spots or strips whenρis 0.06 g/cm3[see Fig.3(a)].The peaks(or valleys)in the pattern show a ‘labyrinthine’ stripe structure whenρis 0.07 g/cm3[see Fig.3(b)].The peaks are intertwined to form a network structure,and the valleys in the pattern are scattered spots(inverse spot structure),whenρis 0.08 g/cm3[see Fig.3(c)].

Fig.3.Two-dimensional patterns observed in Experiment 1 with different values of ρ: (a)ρ =0.06 g/cm3,(b)ρ =0.07 g/cm3,(c)ρ =0.08 g/cm3.

3.2.Results of experiment 2

The results of Experiment 2 are consistent with those of Experiment 1.As shown in Fig.4, the same patterns as those in Fig.3 can be obtained in the concentration interval [0.04 g/cm3, 0.10 g/cm3].Specifically, with the increase of the concentrationρ, the structure of the pattern changes from spots to inverse spots (reticular structure)through‘labyrinthine’stripe.

Fig.4.Two-dimensional patterns observed in Experiment 2 with different values of ρ: (a)ρ =0.06 g/cm3,(b)ρ =0.07 g/cm3,(c)ρ =0.08 g/cm3.

Findings from Experiment 2 suggest that the Turing-like patterns observed in the experiments in this article are not caused by thermal convection,but may be caused by an undiscovered mechanism.The results also indicate directions for the establishment of models.

3.3.Numerical results of model 1

To reproduce the results in our experiments,we examined the effects ofρon the patterns’structure.By the gradual modulation of the parameterρin the system, various 2D patterns can be produced,including spot patterns,‘labyrinthine’stripe patterns and inverse spot patterns(see Fig.5).

When the particle density is small, the particles can self organize into spots[see Fig.5(a)].With the increase of the particle density, spots closed together can form long strip structures[see Figs.5(b)–5(d)].When the particle density reaches a certain degree,the particles may organize into‘labyrinthine’stripe structures[Figs.5(e)and 5(f)].When the particle density is larger, the white regions will dominate and black strip structures will appear [see Figs.5(g)–5(i)].As the particle density continues to increase, black spots will appear [see Fig.5(j)].

We also found that the ‘labyrinthine’ stripe patterns appear during the evolution of the spot structure [see Fig.6(b)and 6(c)].However,the temporary‘labyrinthine’stripe structures eventually evolve into spot patterns because of the instability.The result shows that the random aggregation of particles always tends to generate the‘labyrinthine’stripe structure, but the final pattern structure is determined by specific conditions(particle density)of the system.

Fig.5.Two-dimensional patterns generated by numerical simulations.Gradual modulation of the value the parameter ρ (from 1 to 10 indicated below each figure)can induce pattern changes from spots to inverse spots.Intermediate values appear as labyrinthine stripe patterns.In each figure,the white areas are formed by the accumulation of particles in a stationary distribution.

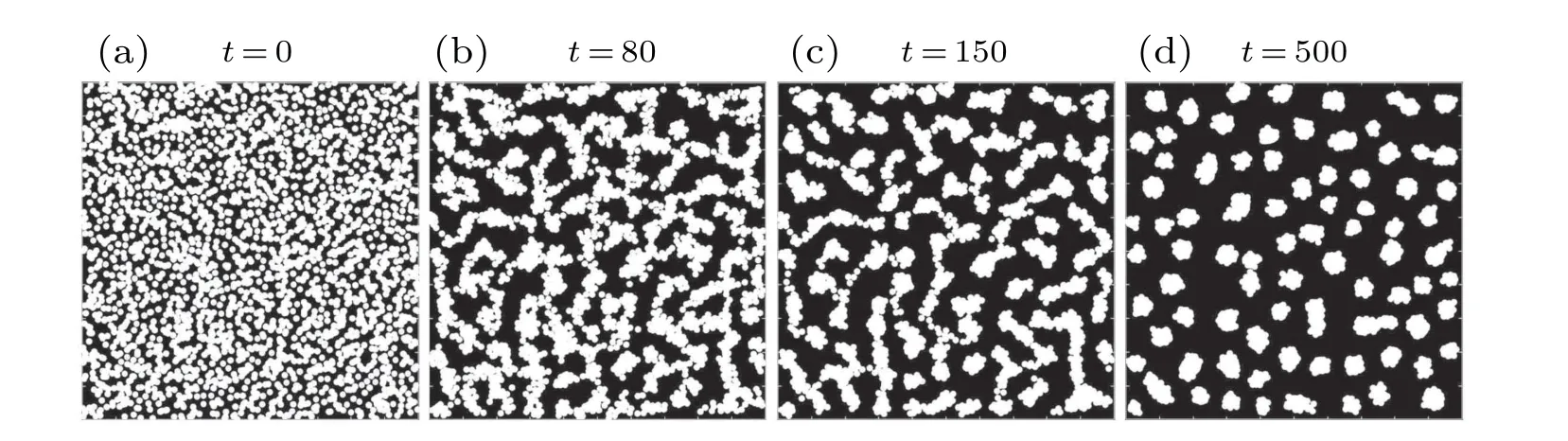
Fig.6.The evolution process of the pattern for parameter ρ =1 at different times [(a)–(d)].The ‘labyrinthine’ stripe patterns can appear during the evolution process[(b),(c)].(d)The pattern reached a stationary stable.See Movie 1 in the supplementary materials for the evolution process.

3.4.Numerical results of model 2

The results show that the random aggregation of spatial components can generate Turing-like patterns,and the proportion of spatial components can control the specific structures.

Specifically,we examined the effects of the fill ratioRon the structure of patterns.By the gradual modulation of the fill ratioR,various 2D patterns can be reproduced,including spot patterns, ‘labyrinthine’ stripe patterns, and inverse spot patterns,as shown in Fig.7.When the fill ratio is small,the small balls can self organize into spots[see Fig.7(a)].With the increase of the fill ratio,spots closed together can form long strip structures[see Fig.7(b)].When the fill ratio reaches a certain degree,the small balls may organize into‘labyrinthine’stripe structures[Fig.7(c)].When the fill ratio is larger,the white regions will dominate and black strip structures will appear[see Fig.7(d)].As the fill ratio continues to increase, white spots(inverse spots)will appear[see Fig.7(e)].

Generally, the spatial scale of Turing-like patterns is related to the effective action distance of the force in the system.Since there is no specific force in Model 2,the generated Turing-like patterns have no fixed spatial scale.Taking the pattern withR=50% as an example, we studied the effect of the time length of random aggregation on the pattern.We found that the spatial scale of the pattern(e.g.,the width of the stripes in patterns)increases with the evolution of the pattern,however, the structural characteristic of the pattern does not change(see Fig.8).This result shows that the process of random aggregation can continuously increase the spatial scale of the Turing-like patterns.One can obtain the same conclusion when the parameterRis equal to other values.

Fig.7.Two-dimensional patterns generated by numerical simulations at T =1×106.Gradual modulation of the value the parameter R(from 15%to 85%)can induce pattern changes from spots to inverse spots.Intermediate values appear as labyrinthine stripe patterns.In each figure,the white areas are formed by the accumulation of small balls.

Fig.8.Two-dimensional patterns generated by numerical simulations with R=50%at different T.In each figure,the white areas are formed by the accumulation of small balls.See Movie 2 in the supplementary materials for the evolution process.

3.5.Quantification of patterns

It is necessary to quantitatively describe the different structures of Turing/Turing-like patterns.Here, we propose a quantitative method.The spots and inverse spots in Turing/Turing-like patterns are relative and can be considered to have the same structure.We introduce the parameter

where ?Srepresents the area difference of two spatial components, andSis the total area.WhenΦis in the intervals [0,0.1), [0.1,0.6] and (0.6,1), the pattern is labyrinthine stripes[see Figs.5(a)and 5(j)],irregular strips[see Figs.5(d)and 5(g)[and spots[see Fig.5(e)].

4.Discussion and conclusion

We have observed Turing-like patterns in starch solution and suggest that they are caused by random aggregation of starch macromolecules.Through Experiment 1,we study the effect of concentration of starch solution on the patterns, and obtain the corresponding structures of Turing-like patterns,namely,spots,labyrinthine stripes,and inverse spots.To prove that these patterns are not caused by thermal convection, we design and carry out Experiment 2, and obtain the same results.Based on this assumption, we establish Model 1 and reproduce the experimental results perfectly.The mechanism can be generalized:If there are two components in a 2D space,and one of them has the ability to aggregate, the random aggregation of spatial components can generate Turing-like patterns,and the proportion of components determines the structure.To validate this mechanism,we propose Model 2 and obtain the expected results.Our mathematical analysis explains the formation of such Turing-like patterns and the choice of specific structures (see Appendix B).In summary, we have studied the formation of Turing-like patterns in a system near thermodynamic equilibrium experimentally and theoretically,and put forward new ideas on the formation mechanism of Turing-like patterns.

The experiments and models in this paper belong to nearequilibrium thermodynamic systems.Non-equilibrium systems can be divided into two types according to the degree of leaving the thermodynamic equilibrium,i.e.,near-equilibrium and far-from-equilibrium thermodynamic systems.Nearequilibrium thermodynamic systems, described in an earlier paper,[32]are not far from the thermodynamic equilibrium.They follow the Onsager reciprocal relations and the principle of minimum entropy production.Near-equilibrium thermodynamics is a branch of classical equilibrium thermodynamics which has been used to evaluate many central reactions in intermediary metabolism.It involves the study of systems that are not in their own state of equilibrium,instead have changes in variables that are not infinitely slow.[33]This includes studies on thermodynamics and kinetics near equilibrium,as well as those beyond local equilibrium.Far-from-equilibrium thermodynamic systems are such that they are not in or near a state of thermodynamic equilibrium.Thermodynamics far from equilibrium can be studied using the principles of maximum entropy production[34]and global validity for effectively onevariable, irreversible chemical systems with multiple steady states.[35]For example, the Bernard convection,[1]when the temperature difference between the upper and lower parts is 0,the system is in thermodynamic equilibrium.When the temperature difference is small, the system is near equilibrium and is still laminar flow.As the temperature difference increases,the degree of the system leaving the equilibrium state increases.When the temperature difference exceeds a certain critical value, non-equilibrium phase transition will occur.The original laminar flow loses its stability and forms the Bernard convection, which is a dissipative structure.The slowly cooled, uniform liquid without chemical reaction follows the Onsager reciprocal relations and the principle of minimum entropy production,which is a near-equilibrium thermodynamic system.[1,32]Therefore, the experiments in this paper are near-equilibrium thermodynamic systems.The uniformly distributed particles in Model 1 are only affected by the thermal noise,and there is no self-driving force and quantity change of particles, so the particle system is in a nearequilibrium state.Model 2 is a simplification of Model 1,which is to gradually apply the thermal noise to a single particle.

The findings of this paper are of great significance to pattern formation.In the 1970s, the dissipative structure theory proposed by Prigogine was widely accepted.[36]According to this theory, dissipative systems can generally self-organize into spatiotemporal patterns.Therefore, patterns have been studied in dissipative systems,for example, Bernard hexagon patterns in thermal convection, distribution patterns of bacterial populations and Turing patterns in chemical reactions.These systems are far from thermodynamic equilibrium and have very complex dynamic behavior.Such complex dynamic behavior may mask the real mechanism of dissipative structure.The generation of ordered structures is a matter of space,so the spatial problem should not depend on the complex dynamic behavior of dissipative systems.We believe that complex dynamic behavior in dissipative systems produces different spatial components, and the spatial components produce Turing/Turing-like patterns due to random aggregation.For example, the ascending heat flow and descending cold flow in the Bernard hexagon pattern correspond to different spatial components, and the viscosity of fluid corresponds to the ability of aggregation.The area of ascending heat flow is consistent with the spot structure of Turing patterns,and the edge of the spots shows hexagonal structures.Also,the long-range inhibitor in the Turing mechanism corresponds to the low concentration spatial component with the ability of aggregation.Specifically, the inhibitor corresponds to the spatial component with low concentration,and the long-range property corresponds to the ability of aggregation.Therefore,our mechanism includes the Turing mechanism.The mechanism of pattern formation across different systems can only be grasped by leaving aside dynamic behavior of specific systems.Consequently, our results provide a new perspective for pattern formation,which may explain the formation of Turing/Turinglike patterns in various systems (including systems far from thermodynamic equilibrium and near-equilibrium systems),and provide a unified mechanism for generation of patterns in different systems.

Miyazawaet al.[31]pointed out that crossing between animals having inverted spot patterns(for example,light spots on a dark background and dark spots on a light background)will necessarily result in hybrid offspring that have camouflaged labyrinthine patterns as ‘blended’ intermediate phenotypes.For instance, as shown in Fig.7, the ‘blending’ of the spot patterns in (a) and (e) will produce the ‘labyrinthine’ stripe structures in (c).In addition, when Turing patterns exist in a system, the transition from spot patterns to inverse spot patterns can generally be observed,during which the labyrinthine stripes are experienced.[31,37,38]

In previous studies,the description of different structures of Turing/Turing-like patterns is only qualitative, lacking objective quantitative criteria.Representative examples are spots and labyrinthine stripes.Here,based on our spatial component mechanism,we propose a quantitative description method for Turing/Turing-like patterns.

Appendix A: Supplementary numerical results of model 1

We studied the patterns that appeared in the system when the parametersnrandnatake as 1 and 2, respectively.The results show that the pattern structure appearing in the system does not depend on the values ofnrandna(see Fig.A1).

Fig.A1.Two-dimensional patterns generated by numerical simulations with different ρ: (a)ρ=2,(b)ρ=4,(c)ρ=6,(d)ρ=8,(e)ρ=10.In gradual modulation of the value the parameter ρ can induce pattern changes from spots to inverse spots.Intermediate values appear as labyrinthine stripe patterns.In each figure,the white areas are formed by the accumulation of particles reaching a stationary distribution.

In other words,each set ofnrandnavalues can describe the general characteristics of attraction and repulsion between particles.

We examined the influence of the interaction between particles and system boundary on the pattern structure.The results show that the boundary conditions of the system do not change the pattern structure(see Fig.A2).

Appendix B:Supplementary analytical results

Based on our spatial component mechanism, we explained the formation of different structures in Turing/Turinglike patterns by a simple plane geometry method.

The 2D plane was discretized into regular hexagonal meshes of uniform size to meet the particle aggregation towards the center of each regular hexagon.The spot pattern is a common structure in Turing/Turing-like patterns(see Fig.B1).We took two adjacent hexagons as an example to explain the choice of pattern structure.As shown in Fig.B1,his the characteristic scale.The characteristic scalehis divided into entity-scalehfand empty-scalehe.Because the space filled by particles is completely equivalent to the space not filled,hfcannot be greater thanhewhen the particle fill ratio is less than 50%.We considered the case wherehfequalshe,and the minimum fill ratio of particles is

whereScandSare the areas of circular spots and hexagon,respectively.

Fig.B1.Discretization of 2D plane.The red and blue circles represent the aggregated particles,and only 7 circles within the hexagon are drawn in the figure.

Since the space filled by particles is completely equivalent to the space not filled, it is necessary only to analyze the case that the fill ratio is less than or equal to 50%.When the fill ratio of particles is less than 23%,the pattern in the system shows a spot structure,and the diameter of spot increases with the increase of the fill ratio.When the filling rate of particles is greater than 23%and less than 50%, in order to preventhffrom being greater thanhe,the diameter of spot will no longer increase.Instead, some adjacent spots will be connected to each other [as shown in Fig.2(b)].With the increase of fill ratio,the number of particles connected increases.

When the fill ratio of particles is about 50%,the circular spots no longer exist.The filling of discrete spatial elements(regular hexagon)can be divided into six types(see Fig.B2).

The random combination of the six types of filling elements on the 2D plane can form patterns similar to the‘labyrinthine’stripe patterns(see Fig.B3).

We smoothed the pattern in Fig.B3 to eliminate sharp corners.(Codes are available from the authors on request.)The final pattern is the ‘labyrinthine’ stripe pattern (see Fig.B4).

In summary,we have explained the choice of the structure for Turing-like patterns through the method of plane geometry.That is,we explained how the fill ratio of particles determines the structure of Turing-like pattern.

Fig.B2.Six types of filling elements.

Fig.B3.A‘labyrinthine’stripe pattern formed by random combination of the six filling elements.

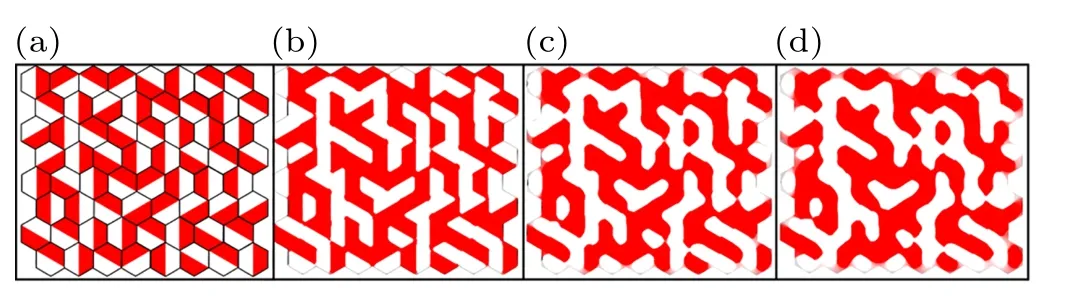
Fig.B4.The smoothing process of the ‘labyrinthine’ stripe pattern in Fig.B3.Also see Movie 3 in the supplementary materials for the evolution process.

Appendix C:Supplementary material

See the supplementary materials for Movies 1, 2, and 3.Movie 1 shows the evolution process of the pattern when the parameterρis equal to 1.Movie 2 shows the evolution process of the pattern when the parameterRis equal to 50%.Movie 3 shows the smoothing process of the ‘labyrinthine’ stripe pattern in Fig.B4.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant Nos.12205006 and 11975025),the Excellent Youth Scientific Research Project of Anhui Province(Grant No.2022AH030107), the Natural Science Foundation of Anhui Higher Education Institutions of China (Grant No.KJ2020A0504),and the International Joint Research Center of Simulation and Control for Population Ecology of Yangtze River in Anhui(Grant No.12011530158).