A novel algorithm to analyze the dynamics of digital chaotic maps in finite-precision domain
Chunlei Fan(范春雷) and Qun Ding(丁群)
Electrical Engineering College,Heilongjiang University,Harbin 150080,China
Keywords: digital chaos,dynamic degradation,state-mapping graph,periodicity analysis
1. Introduction
As we all know, Lorenz’s outstanding contribution opened the way for the study of chaos theory in 1963.[1]After more than half a century,scholars from various countries have also made many distinguished achievements in chaos theory and applied research,[2,3]which undoubtedly deepened people’s understanding of chaotic systems. Some basic characteristics of chaos are also revealed, such as long-term unpredictability,positive Lyapunov exponent,intrinsic randomness,topological transfer, high sensitivity to initial conditions, and boundedness. These good characteristics of chaotic systems are highly consistent with the basic principles of confusion and diffusion in cryptography, which makes chaotic systems widely used in chaotic secure communication.
In recent years, scientific research achievements of chaos in engineering applications emerge one after another,such as a true random sequence generator,[4–6]multimedia data encryption,[7,8]digital watermarking,[9,10]a chaotic pseudo-random sequence generator and chaos-based masking technology.[11,12]However,while chaotic systems play an active role in secure communication and cryptography, the dynamic degradation of digital chaos has also become prominent.According to the mathematical definition of chaos such as Li–Yorke or Devaney,the classical chaos theory is defined in the continuous domain.[13]Nevertheless,when the chaotic system is implemented in a hardware processor (e.g., FPGA, DSP)with limited computational accuracy, it is not chaos in the strict mathematical sense. Due to the influence of truncation error and rounding error,the dynamic characteristics of digital chaos will undergo a series of degradation phenomena.[14,15]For example, the original non-periodic chaotic sequence will have a short-period phenomenon, and its high sensitivity to initial conditions, intrinsic randomness and ergodicity will also be greatly reduced or even disappear.[16]These dynamic degradation phenomena of digital chaos will undoubtedly have a negative impact on the security of chaotic secure communication and chaotic cryptography. Therefore, it is very crucial to analyze the dynamic degradation of digital chaos,especially to estimate the number of fixed points and periodic limit cycles accurately.
Actually, as early as 1988, Grebogiet al. found that a chaotic system that was numerically simulated on a computer would be affected by the rounding error of hardware equipment, and its chaotic orbit would become periodic.[17]In 2003, Liet al. analyzed the degree of dynamic degradation of the digital one-dimensional piecewise linear chaotic map(PWLCM)in fixed-point arithmetic domain.[18]They designed a set of dynamic indicators, which can quantitatively describe the dynamic degradation of the PWLCM to a certain extent. This method can promote the designs of chaotic pseudo-random generators with good performance and reduce the difficulty of cryptanalysis of chaotic encryption systems based on PWLCMs. In 2011, Miyazakiet al. found that different rounding methods have different effects on the transient branch length and cycle length of the digital logistic map.[19]The properties of discrete sequences generated by the digital logistic map depend heavily on the rounding method. In Ref. [20], based on strict statistical tests, a new algorithm is designed to analyze the weak keys of digital chaos. When analyzing the security of chaotic ciphers, it is found that the short periodicity of the digital chaotic orbit is the essential factor that causes many weak keys in chaotic ciphers. In addition, compared to floating-point operations, chaotic systems implemented by fixed-point operations have a longer average period of chaotic sequences. In 2016, Yoshioka and Kawano analyzed the periodic properties of Chebyshev polynomial sequences over the residue ringZ/2kZ.[21]The analysis results show that a recently proposed public-key algorithm based on the polynomial is insecure. In Ref. [22], for different finite calculation precisions, Persohn and Povinelli conducted a detailed analysis of the periodicity of logistic chaotic sequences generated by floating-point operations. Due to the low efficiency of the calculation method,they used the Condor cluster supercomputer to perform large-scale parallel calculations,and statistically analyzed the transient length and period length of these sequences. The results show that the performance of the logistic sequence generator is not ideal. In 2018,when Frahmet al. analyzed the dynamic characteristics of the Chirikov standard map and the Arnold map, they found that there is a certain internal relationship between the dynamic system and the complex network.[23]In recent years,scholars at home and abroad have made outstanding contributions to the study of the dynamic characteristics of digital chaos.[24–27]Nevertheless,these algorithms have several limitations. First,most conventional methods have high time complexity.Therefore, it is bound to use high-performance supercomputers or graphics processing unit(GPU)for parallel computing to improve the execution speed of programs,which undoubtedly increases the consumption of hardware resources and the cost of experiments. Second, some proposed schemes lack a certain degree of versatility,that is,these methods are only suitable for analyzing the dynamic characteristics of one or several digital chaotic systems. Third,most schemes only calculate a general performance index, and cannot accurately locate all periodic cycles and fixed points contained in a digital chaotic map.
In this work, aiming at the limitations of the current schemes, we design a periodic cycle location algorithm(PCLA)from a new perspective to analyze the dynamic degradation of digital chaos. The PCLA can divide the statemapping graph of digital chaos into several connected subgraphs with the purpose of locating all fixed points and periodic limit cycles contained in a digital chaotic map. In addition, this algorithm can also used to calculate the total number of state variables contained in each connected subgraph.Furthermore,in order to test the versatility and performability of our proposed algorithm,the periodic distribution and security of several typical digital chaotic maps (i.e., logistic map and Baker map) are analyzed in detail. Numerical simulation results show that these digital chaotic maps have obvious short period and multi period phenomena. This algorithm can clearly describe the internal mapping structure of the digital chaotic system under different calculation accuracies,thereby promoting the effective resistance and accurate evaluation of dynamic degradation of digital chaotic maps. In addition, a full understanding of the periodic distribution of digital Baker map is also helpful to design more excellent digital watermarking and image encryption schemes.
The rest of this paper is organized as follows: Section 2 describes digitization of chaotic maps in finite-precision domain. Section 3 puts forward a periodic cycle location algorithm. The performance of two chaotic maps,i.e.,logistic and Baker, in finite-precision domains is analyzed in Section 4,and Section 5 concludes the paper.
2. Digitization of chaotic maps in finite-precision domain
In the classical chaos theory, all chaotic maps are defined in the continuous domain, and their dynamic characteristics are meaningful only in the continuous space with positive Lebesgue measure. However,when chaotic maps are implemented on hardware devices (e.g., FPGA and DSP) with limited computational accuracy, these chaotic maps will go through the process of digitization. In this section, let us assume that the iterative formula of a chaotic map can be defined as
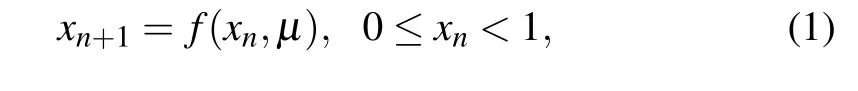
whereμdenotes the control parameter. In binary representation,xncan be written as

where (·)2means the contained digits in binary format. Assuming thatmdenotes limited computational accuracy,the binary representation ofxncan be approximated as
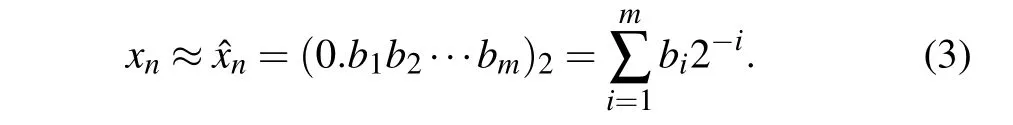
In order to convert decimal fractions to integer representation,we introduce a new variable,i.e.,yn,which is defined as

Based on Eq.(4),the binary representation ofyncan be given by

whereyndenotes the bits stored in the memory of hardware devices with the limited computational accuracym. Substitutingyninto Eq.(1),we obtain
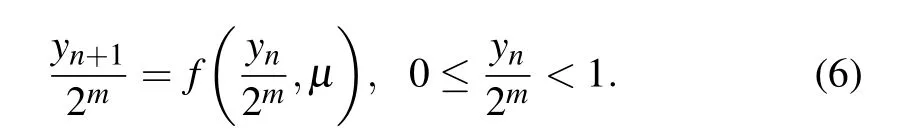
Multiplying both sides of Eq.(6)by 2m,we obtain

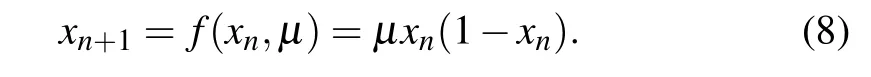
Furthermore, Eq. (8) can be re-expressed by substituting for the functionf(·)from Eq.(8)into Eq.(7)to obtain
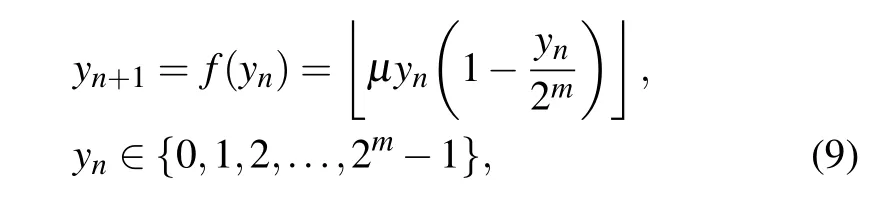
whereμis generally set as 4. Based on Eq. (9), we can analyze the dynamic characteristics of the digital logistic map under different limited calculation accuracy.
3. Periodic cycle location algorithm for digital chaotic maps
In this section, in order to effectively analyze the dynamic degradation and internal structure of digital chaotic maps under different finite calculation precision, we develop a periodic cycle location algorithm (PCLA) that is based on a state-mapping graph. This algorithm has strong universality and can accurately calculate all periodic cycles and fixed points contained in a digital chaotic map. Due to the finite calculation accuracy of microprocessors, the value range of the digital logistic map will be limited to a finite state setΩm={0,1,...,2m-1}. Based on Eq.(9), we plot the statemapping graph of the digital logistic map with limited calculation accuracym=4, as shown in Fig. 1. It is obvious that the state-mapping graph is composed of three connected subgraphs, among which the connection subgraph 1 containing the most state variables is called the maximal connection subgraph. Undoubtedly, if any two state variables are in the same connected subgraph, the two state variables must converge to the same fixed point or periodic cycle after several iterations. The core idea of the periodic cycle location algorithm is to divide the state-mapping graphs of digital chaotic maps with different calculation accuracies into multiple connected subgraphs and extract the unique periodic cycle or fixed point contained in each connected subgraph. In addition,this algorithm can also be used to calculate the number of state variables contained in each connected subgraph.
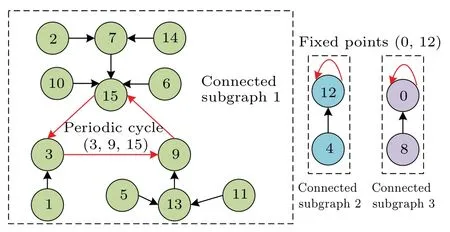
Fig.1. State-mapping graph of the digital logistic map with limited calculation accuracy m=4.
Specifically, the periodic cycle location algorithm(PCLA)is proposed as follows:
Step 1Define an array of 1-D variablesε={ε0,ε1,...,εi,...,εL}, whereL=2md-1 andddenotes the dimension of digital chaos in finite-precision domains.Please note that if the dimension of a digital chaotic map exceeds 1,dimensionality reduction is required before executing this algorithm. Then,the 1-D arrayεcan be initialized as


Step 2We can define a 2×2LmatrixA,which is given by
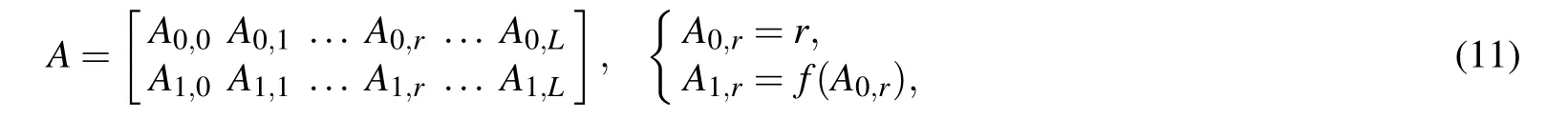
wherer ∈{0,1,2,...,L}, and the functionf(·) denotes the iterative equation of digital chaos. Subsequently, variables[A0,r,A1,r]Tin each column are separately used as a formal parameter of the state variable union algorithm (SVUA). Then,the SVUA with different formal parameters is executed one by one from variable [A0,0,A1,0]Tto [A0,L,A1,L]T. Furthermore,the state variable union algorithm is presented in algorithm 1 as a pseudocode. This algorithm can filter out state variables that are connected to each other, that is, it can split the state-mapping graph of digital chaos into several connected subgraphs.
Step 3After Step 2 is carried out,the corresponding elements in the 1-D arrayεare also updated.Moreover,we define a 1×Larrayγ,which can be initialized as
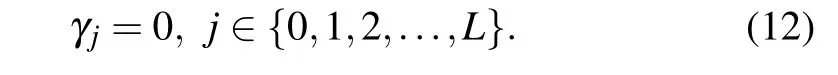
Then, the elementγεiin the arrayγis incremented by 1 and letirange from 0 toL. Based on the above operation,the updated arrayγcontains the structural information of the digital chaotic map. Here, we can search for all non-zero elements in the arrayγand defineCas the set of all non-zero elements.The sum of all elements in setCis equal to 2m. Ifγj >0,the state variablejwill be a fixed point or a node in a periodic cycle for digital chaos. In addition,the total number of nodes in the connected subgraph containing the state variablejis equal toγj. Moreover,ifj >0 andj=f(j),the state variablejwill be a fixed point of digital chaos in finite-precision domains.Ifj >0 andj/=f(j),the state variablejwill be a node in a limit cycle. The core idea of this algorithm is to assume that each node (i.e., state variable) of the digital chaotic map is isolated. Then, SVUA is used to determine which nodes are connected by the state-mapping relationship of the digital chaotic system. Those interconnected nodes are constructed into a connected subgraph. The above-mentioned periodic cycle location algorithm can precisely locate the fixed point and periodic distribution of digital chaos, which is of great significance for analyzing the degree of dynamic degradation of digital chaotic systems. It is worth noting that this algorithm is limited by storage bottlenecks when the computational accuracymis greater than 32. This can make the program difficult to run. Therefore,when the finite calculation accuracy is relatively high,we can use Floyd’s cycle-finding algorithm to calculate the cycle length of a single chaotic orbit,which occupies almost no memory(only a few variables’storage space).Furthermore, in order to speed up the running efficiency of the program, the CUDA platform can be used for large-scale parallel computing.
Furthermore, to assess the effectiveness and practicality of the PCLA, we take the case of the digitized logistic map with finite calculation accuracym=3 as an example. Based on the execution steps of the PCLA,we first define an array of 1-D variablesε={ε0,ε1,...,εi,...,εL}. Because the dimension of the digital logistic map is 1 and the calculation accuracymis 3,the variableLis equal to 7. Therefore,the arrayεcan be initialized asε={0,1,2,...,7}. Next,according to the iterative formula of the digitized chaotic map,the matrixAis given by

According to the column order of matrixA,the periodic cycle location algorithm is performed from element[0,0]Tto[7,3]T.The update process of each elementεiin the arrayεis shown in Fig. 2. First, we can regard all state variables as multiple sets (i.e., connected subgraphs), and the nodes in each connected subgraph are connected. As shown in Fig.2,based on the iterative relationship of the digital logistic map,these isolated state variables are continuously connected and eventually construct multiple connected subgraphs.
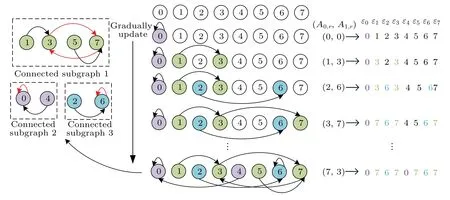
Fig.2. Update process of each element εi in the array ε.
Moreover,the general structure diagram of the connected subgraph is illustrated in Fig.3,which is composed of branch nodes and cyclic nodes.All branch nodes will eventually point to a cyclic node and fall into a limit cycle. Specifically,if the lengthpof a limit cycle is equal to 1, the cyclic node in the limit cycle will be a fixed point. Based on the above analysis,we find that if the subscriptiofεiis equal to a branch node of the connected subgraph, the final value of the updatedεiwill equal the value of a cyclic node. As an example,the variableε1is continuously updated from initial value 1 to 7. Note that,for the state-mapping graph of the digital logistic map with the precisionm=3,all branch nodes(1,5)and partial cyclic nodes 3 of the connected subgraph 1 will eventually point to a cyclic node 7 in the limit cycle(3,7).
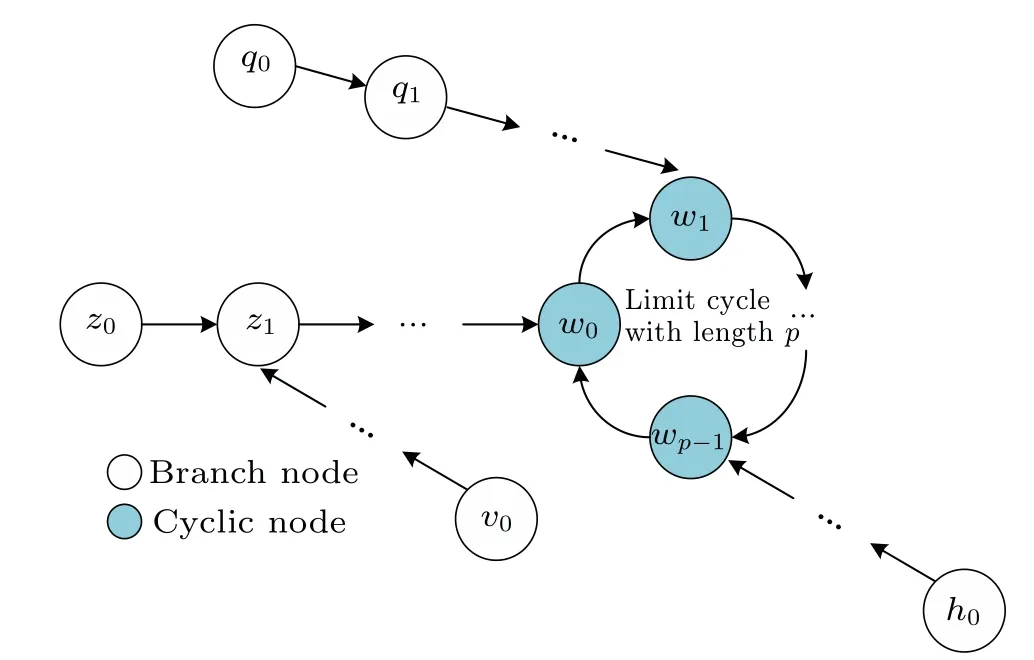
Fig.3. General structure diagram of the connected subgraph.
Next, after the arrayεis updated, we can calculate the 1×Larrayγ={2,0,0,0,0,0,2,4}. Sequentially, we can search for all non-zero elements(i.e.,γ0,γ6andγ7)in the arrayγ, the setCof all non-zero elements is{2,2,4}. Since 0=f(0), 6=f(6) and 7/=f(7)=3, we can conclude that the digitized logistic map with the precisionm=3 contains two fixed points(0,6)and one limit cycle(3,7).
4. Performance analysis of chaotic maps in finite-precision domains
4.1. Analyzing the dynamic degradation of the digital logistic map
4.1.1. Short-period and multi-period phenomena
In cryptography, the confidentiality of sequence ciphers depends on the performance of key stream generator. For chaotic cryptography, the key stream is usually generated by chaotic pseudo-random sequence generators. In order to improve the security of the encryption algorithm as much as possible, the generated key stream needs to have certain characteristics of a random sequence. An extremely large period can effectively increase the anti-attack ability of the cryptographic algorithm. Generally speaking, since the data rate of modern cipher machines is as high as 108b/s,the period length of the key stream should not be less than 3×1016. Chaotic time series in the continuous domain have the characteristics of nonperiodicity and good randomness. Nevertheless, due to the limited calculation accuracy of hardware equipment, chaotic maps in finite-precision domains emerge many short-period and multi-period phenomena. In this section, for the digital logistic map,we perform the periodic cycle location algorithm for different calculation accuracym,and the experimental results are listed in Table 1. Here,NcsandNsvrepresent the number of connected subgraphs and the total number of state variables contained in each connected subgraph. The variable nodecndenotes the cyclic node located by the PCLA,andpis the period length of the limit cycle contained in a certain connected subgraph. Note that ifp=1, the variable nodecnwill be a fixed point.
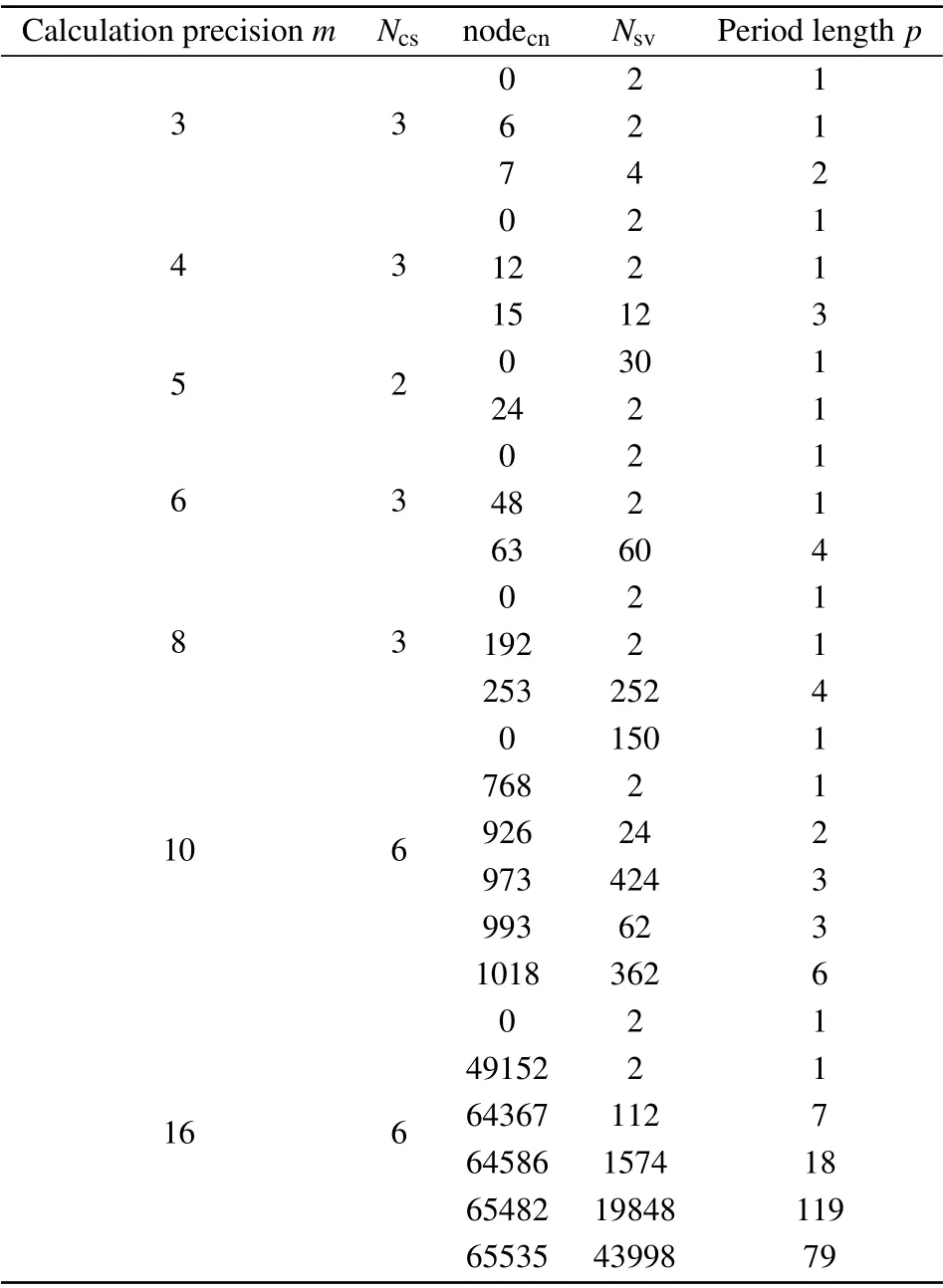
Table 1. Periodicities of the digital logistic map with various calculation precisions.
As an example,the state-mapping graph of the digital logistic map with limited calculation accuracym=6 is divided into three connected subgraphs,as shown in Fig.4. The variables nodecn=0,48,63 are located as the cyclic nodes. Based on the corresponding period lengthp, we can draw conclusions that the digital logistic map has two fixed point (0, 48)and one limit cycle (63, 3, 11, 36). Since the largestNsvis equal to 60, the maximal connection subgraph has sixty state variables. Undoubtedly, if the sixty state variables are used as initial values of the digital logistic map,all discrete chaotic sequences generated by them will eventually fall into the periodic limit cycle(63, 3, 11, 36). From the table, as the calculation accuracymincreases,the maximum value of the period lengthpalso becomes longer. However, the period length is far less than 3×1016. The experimental results show that the digital chaotic map has obvious short-period and multi-period phenomena, which cannot guarantee the security of chaotic sequence ciphers.

Fig.4. State-mapping graph of the digital logistic map with limited calculation accuracy m=6.
4.1.2. Cross-correlation of discrete chaotic sequences
Chaotic systems have strong initial value sensitivity.When the initial conditions change slightly,the difference between the two chaotic trajectories is not obvious in a short time. However, as time goes on, the chaotic trajectories under different initial conditions will occur huge deviation. The initial value sensitivity of chaos reduces the correlation between different discrete chaotic sequences. This characteristic makes the chaotic encryption algorithm have a large key space.However,for digital chaotic maps,the initial sensitivity is severely degraded due to the negative influence of limited calculation accuracy. As an example, we set the calculation accuracym=7 and generate three discrete logistic sequences with initial values 7,23 and 39. Furthermore,we analyze the cross correlation between different discrete logistic sequences,as given in Fig.5. The result of cross-correlation operation reflects the measure of similarity between two signals. Here,we assume that{x(n)}and{y(n)}denote two different logistic sequences. The cross-correlation function is defined as
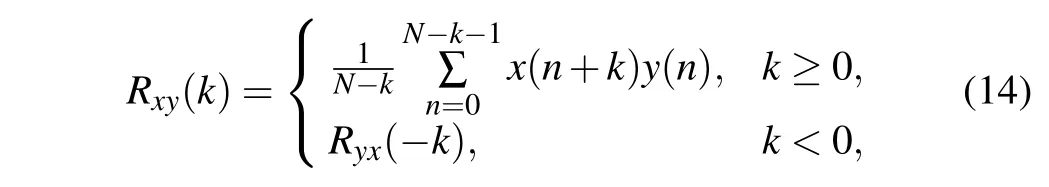
whereRxy(k) andNrepresent the cross-correlation function and the length of digital logistic sequence. As shown in Fig.5(a),the cross correlation of two logistic sequences with the initial values 7 and 39 shows dense peak lines,which implies strong correlation. When the initial values are equal to 7 and 23,it can be seen from Fig.5(b)that the cross correlation of the two sequences is significantly reduced.
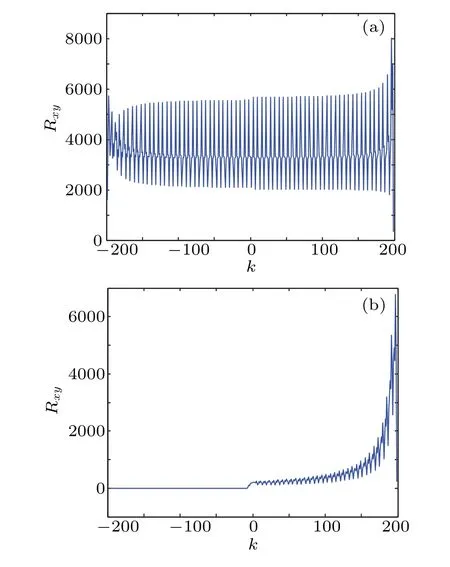
Fig.5. Cross correlation of discrete logistic sequences with different initial values of(a)7,39 and(b)7,23.
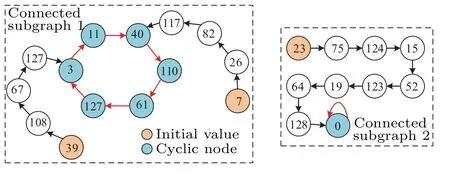
Fig.6. Partial state-mapping graph of the digital logistic map with calculation accuracy m=7.
Moreover,the reason for this phenomenon is that the three initial values are in different connected subgraphs. Partial state-mapping graph of the digital logistic map with calculation accuracym=7 is shown in Fig. 6. According to the figure, the initial values 7 and 39 are in the same connected subgraph,and the initial values 7 and 23 are in different connected subgraphs. This phenomenon implies that the discrete chaotic sequences generated by these initial values in the same connected subgraph are approximately equal to each other and differ only in the transient state. Based on the PCLA,we can obtain that the digital logistic map with the precisionm=7 has two fixed point (0, 96) and one limit cycle (11, 40, 110,61,127,3). This phenomenon is common for the digital logistic map, which will reduce the effective key space of chaotic ciphers. From the above analysis, it can be concluded that the sensitivity of initial value and long-term unpredictability of digital chaotic maps are degraded due to the influence of calculation accuracy,and this undesirable phenomenon has caused a non-negligible effect on the security of the chaotic pseudorandom sequence generator.
4.1.3. Ergodic property of the digital logistic map
In the classical chaos theory,the chaotic system has good ergodicity in its attraction domain. However,the digitized logistic map is affected by limited calculation accuracy, and its dynamic characteristics are severely degraded. It is difficult to achieve complete coverage of state variables in the range of state space. Therefore,in order to evaluate the degradation degree of ergodicity of the digital logistic map, under the same calculation accuracy,2mdiscrete logistic sequences are generated with different initial values.Furthermore,a set of discrete data can be obtained by calculating the state-space utilization of each logistic sequence. Based on the box-whisker plot,these data are statistically analyzed. The simulation results can be shown in Fig. 7. The box-whisker plot can describe the distribution of data in a relatively stable manner without being affected by outliers. As presented in Fig.7,with the calculation accuracy increases, the state-space utilization of the digital logistic map gradually tends to 0.
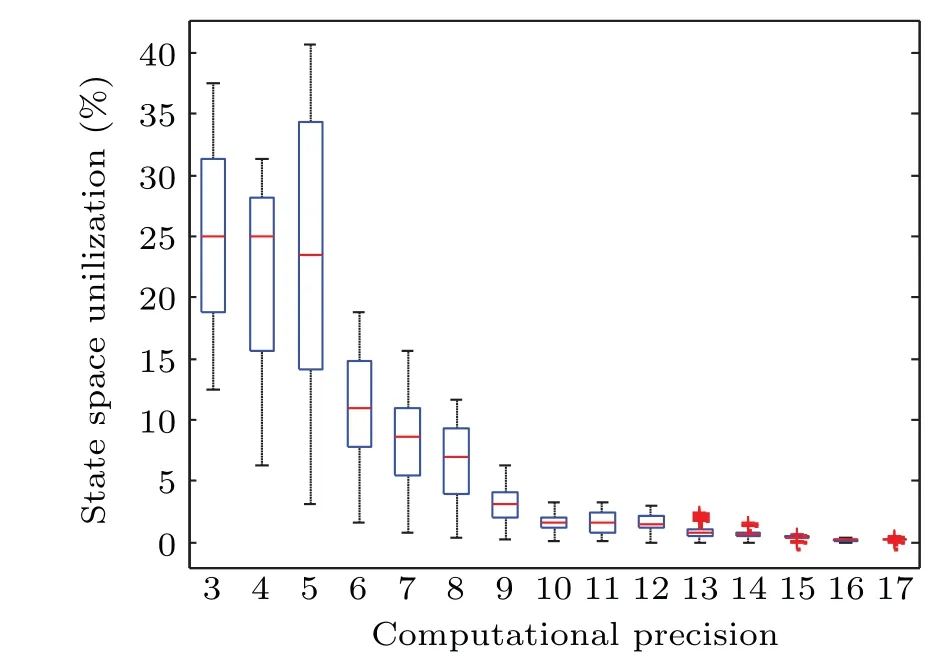
Fig.7. State-space utilizations of the digital logistic map with various computational precisions.
4.1.4. Low permutation entropy
In 2002, Bandtet al. proposed a mensuration to analyze the complexity of discrete-time sequences, that is, permutation entropy(PE).[28]This method has many advantages,such as its robustness,fast-computing speed,and invariance to nonlinear monotonic transformations. The range of permutation entropy is between 0 and 1. The larger the PE value,the better the randomness and the higher the complexity of the discretetime sequence. In this section, we calculate the permutation entropy of digital logistic sequences with various limited calculation precisions. The parameters of PE include embedding dimensionθand time delayτ,which are set as 6 and 1,respectively. For different digital logistic sequences, the results are listed in Table 2. From the table,as the calculation accuracymincreases, the PE value of the discrete logistic sequence also increases. However, when the calculation accuracy reaches 20, the PE value is only 0.62507, which cannot still meet the requirements of chaotic ciphers.
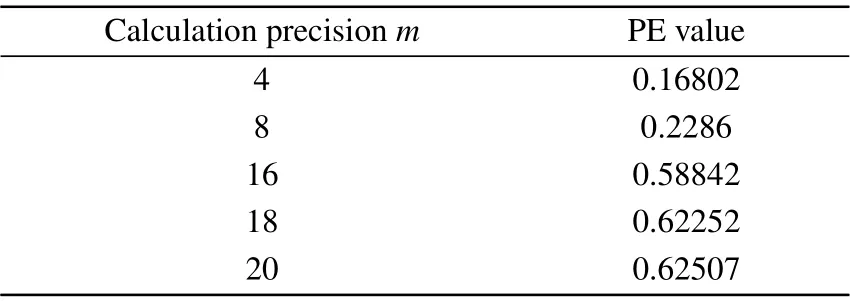
Table 2. PEs of digital logistic sequences with various calculation precisions.
4.2. Analyzing the periodicity of the 2-D digital Baker map
Baker map is widely used in the field of multimedia data encryption, which is often responsible for scrambling digital images.It is called Baker map because the folding and stretching effect of this chaotic map is like that of a baker kneading dough. In this section,we briefly introduce the digitization of the 2-D Baker map. First, we assume thatTcis the iterative equation of the Baker map,which is based on the mapping relationship from a unit square to itself. Furthermore, the unit square is divided intokvertical bars (i.e., [Ni-1,Ni]×[0,1])along thex-axis,wherei ∈{1,2,...,k}andNiis defined by

wherePirepresents the width of the above vertical bar andP1+P2+···+Pi=1. Each vertical bar is stretched along thex-axis direction and then compressed along they-axis direction,and the schematic diagram of the Baker map is shown in Fig.8. This process can also be expressed by a mathematical formula as

where(x,y)∈[Ni-1,Ni-1+Pi]×[0,1]andi ∈{1,2,...,k}. In this section,we consider the case ofk=2,and the mathematical equation of the digital 2-D Baker map can be given by

wheremdenotes the limited computational precision, andxn,yn ∈{0,1,2,...,2m-1}. Furthermore, we reduce the dimension of the 2-D digital Baker map,which is define as
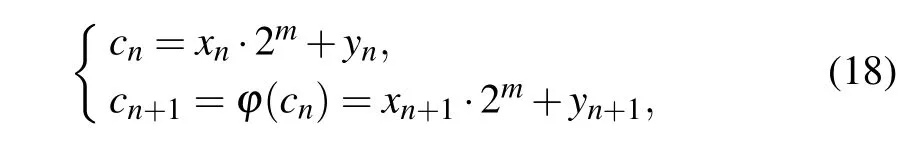
wherecnis an integer,andcn ∈{0,1,...,22m-1}. Based on Eq.(18),numerical conversion can be realized betweencnand(xn,yn).
Furthermore, based on the periodic cycle location algorithm, the period distribution of the digital Baker map under different calculation accuracies is analyzed in detail, and the experimental results are listed in Table 3. From the table, we can see that the digital Baker map has two fixed points and many short periodic limit cycles. When the calculation accuracym=8,it has 4116 connected subgraphs.
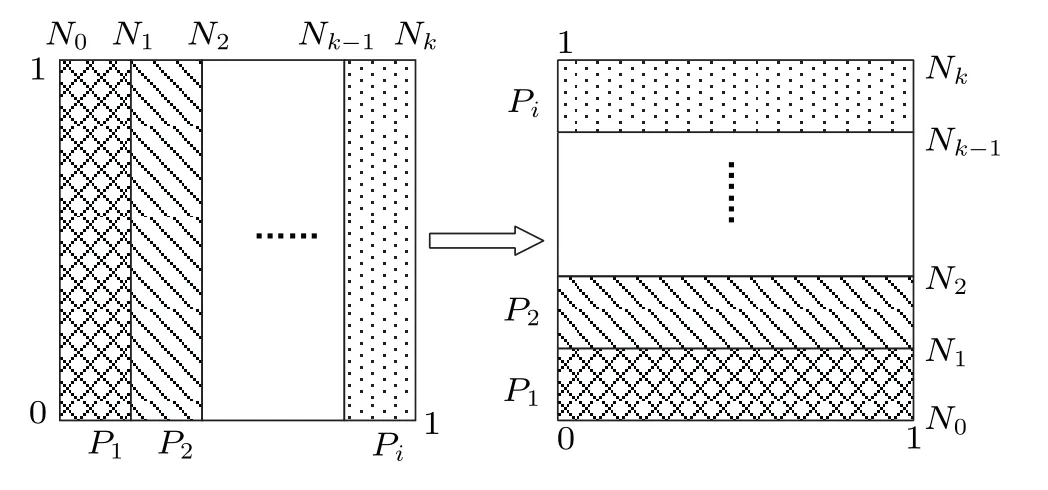
Fig.8. Schematic diagram of the Baker map.
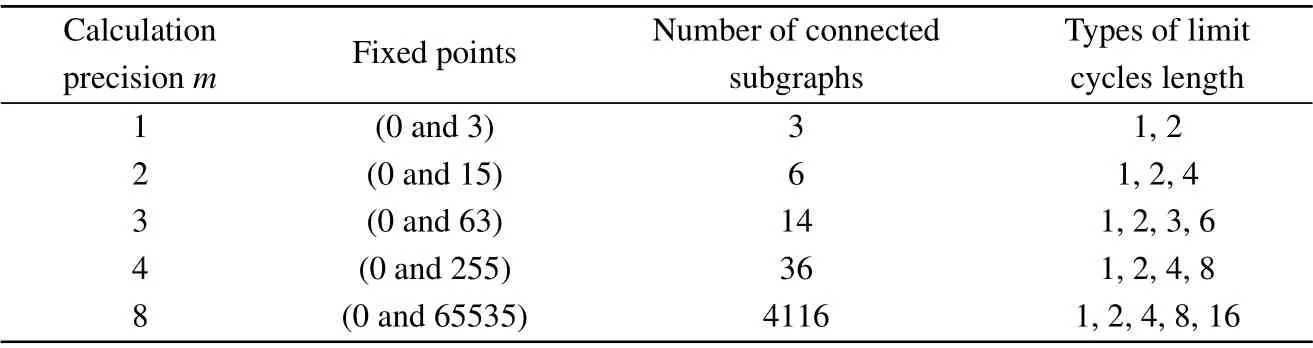
Table 3. Periodicities of the digital Baker map with various calculation precisions.
In order to reflect the internal mapping structure of the digital Baker map more intuitively, state-mapping graphs of the digital Baker map with calculation precisionsm=2,3 are shown in Fig.9. From the figure,regardless of the calculation accuracym,all connected subgraphs of the digital 2-D Baker map have only cyclic nodes and no branch nodes. Compared with the digital logistic map,the digital Baker map has a large number of short limit cycles and no transient state. For the calculation accuracym,the length of the limit cycle contained in the maximal connected subgraph is equal to 2m.
When using the 2-D digital Baker map to scramble the pixels of a digital image, an important issue is to select the number of iterations. In this section, we consider how to choose an appropriate number of scrambling from the aspect of the period distribution of the Baker map. When the Baker map is used to scramble an image, (xn,yn) in Eq. (17) represents the position of the pixel of the digital image,and 2m×2mdenotes the size of the digital image. Furthermore, we adopt the Fruits image with a size of 256×256 as the experimental data. Based on the PCLA,we can calculate the period distribution of the digital Baker map with the calculation accuracym=8, and the results are listed in Table 4. As can be seen from Table 4, there are five types of periodic cycles (i.e., 1,2, 4, 8, and 16) for the Baker map. Among these limit cycles, there are 4080 periodic cycles with a length of 16, and the proportion of nodes is as high as 99.61%.

Fig.9. State-mapping graph of the digital Baker map with different calculation precisions: (a)m=2,and(b)m=3.
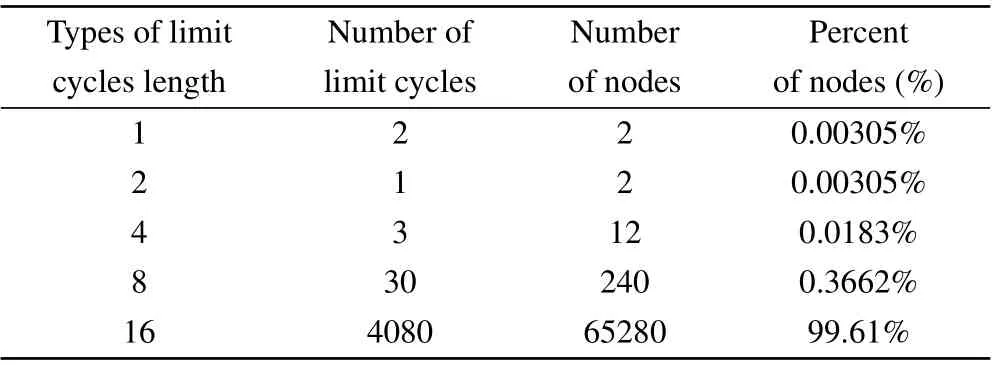
Table 4. Period distribution of the digital Baker map in the precision m=8.
It is not difficult to find that when the numberNbof iterations of the digital Baker map is an integer multiple of the length of any limit cycle, there must be corresponding pixels that are not scrambled in the digital image. The Fruits image with different scrambling times are shown in Fig.10. A subjective evaluation method can be used to obtain that the three sub-graphs in Figs.10(h)–10(j)have better scrambling effects.However,according to the above analysis of the periodicity of the digital Baker map, there are still 256 pixels that are not scrambled in Fig. 10(i). Therefore, based on the periodicity of the digital Baker map and the subjective evaluation method,we believe that the scrambling effect of digital image is the best when the scrambling numberNbis equal to 7 or 9.

Fig.10. Fruits image after being scrambled by the digital Baker map with various numbers of scrambling iterations Nb: (a)original image,(b)Nb=1,(c)Nb=2,(d)Nb=3,(e)Nb=4,(f)Nb=5,(g)Nb=6,(h)Nb=7,(i)Nb=8,(g)Nb=9,(k)Nb=10,(l)Nb=11,(m)Nb=12,(n)Nb=13,(o)Nb=14,(p)Nb=15,and(q)Nb=16.
5. Conclusion
In order to facilitate the application of chaos in engineering practice,it is very crucial to effectively evaluate the characteristic degeneration of digital chaotic maps. In this paper,we employ a periodic cycle location algorithm (PCLA) that is based on state-mapping graph of digital chaos. This algorithm can precisely locate all fixed points and limit cycles contained in a digital chaotic map from a new perspective.Related experiments have been performed to verify the versatility and availability of the PCLA in terms of cross correlation of discrete chaotic sequences,period distribution,sequence complexity and state-space utilization.This algorithm can not only analyze the degree of dynamic degeneration of digital chaotic systems,but also effectively improve the security of the multimedia data encryption algorithm and help to understand the internal mapping law of the digital chaos.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant No. 62101178) and the Fundamental Research Funds for the Higher Institutions in Heilongjiang Province,China(Grant No.2020-KYYWF-1033).
- Chinese Physics B的其它文章
- LAMOST medium-resolution spectroscopic survey of binarity and exotic star(LAMOST-MRS-B):Observation strategy and target selection
- Vertex centrality of complex networks based on joint nonnegative matrix factorization and graph embedding
- A novel lattice model integrating the cooperative deviation of density and optimal flux under V2X environment
- Effect of a static pedestrian as an exit obstacle on evacuation
- Chiral lateral optical force near plasmonic ring induced by Laguerre–Gaussian beam
- Adsorption dynamics of double-stranded DNA on a graphene oxide surface with both large unoxidized and oxidized regions

