Diffusion dynamics in branched spherical structure
Kheder Suleiman Xue-Lan Zhang(張雪嵐) Sheng-Na Liu(劉圣娜) and Lian-Cun Zheng(鄭連存)
1School of Energy and Environmental Engineering,University of Science and Technology Beijing,Beijing 100083,China
2School of Mathematics and Physics,University of Science and Technology Beijing,Beijing 100083,China
Diffusion on a spherical surface with trapping is a common phenomenon in cell biology and porous systems. In this paper,we study the diffusion dynamics in a branched spherical structure and explore the influence of the geometry of the structure on the diffusion process.The process is a spherical movement that occurs only for a fixed radius and is interspersed with a radial motion inward and outward the sphere.Two scenarios govern the transport process in the spherical cavity:free diffusion and diffusion under external velocity. The diffusion dynamics is described by using the concepts of probability density function(PDF)and mean square displacement(MSD)by Fokker–Planck equation in a spherical coordinate system.The effects of dead ends, sphere curvature, and velocity on PDF and MSD are analyzed numerically in detail. We find a transient non-Gaussian distribution and sub-diffusion regime governing the angular dynamics. The results show that the diffusion dynamics strengthens as the curvature of the spherical surface increases and an external force is exerted in the same direction of the motion.
Keywords: anomalous diffusion,Fokker–Planck equation,branched spherical structure
1. Introduction
Diffusion is a process in which particles move randomly from an area of high concentration to another area of low concentration,[1–4]and it is also essential for other processes to attain their functions,for example,but not limited to,cellular processes,metabolism,carburization,and conduction.[5–7]Given the importance of diffusion in controlling these processes, not to mention other potential applications in nanomedicine and nanotechnology, it has become a hot interdisciplinary research field among physics, chemistry, and biology. Realizing the characteristics of the diffusion process and understanding its mechanism, which is affected by its microscopic dynamics and environmental space occurs in,is the cornerstone.This can be achieved by conducting experiments and introducing physical–mathematical models. Recently, it has been established that diffusion in heterogeneous media, such as the cytoplasm of biological cells and porous mediums, is anomalous.[8]Namely,the mean square displacement(MSD)of the particle position is nonlinear with time,in contrast to the theory of Brownian motion in homogeneous media, in which the probability distribution is Gaussian and MSD grows linearly with time.
In 1975 Pierre-Gilles de Gennes suggested modeling the transport in heterogeneous media through performing random walks on percolation clusters, and he coined the term “ant in the labyrinth”.[9]Later, this problem was extended to fractal,as it is recognized a good model for disordered systems.[10]At the percolation threshold, a percolation structure can be idealized as a single infinite cluster consisting of a conducting
path,which corresponds to a backbone,and side branches,or fingers with dangling bonds.[11,12]This structure corresponds to a comb. A simple comb-like structure is a two-dimensional structure in which the particle moves along thexdirection only aty=0 (backbone), while the motion along theydirection(fingers)is not restricted. The diffusion dynamics in the comb can be described as follows: while the particle moving randomly along the backbone it may be trapped inside the deadends(fingers). It has been found that the sub-diffusion regime dominates the process along the backbone with〈x2(t)〉~■t,if the particle performs a Brownian motion in the fingers,until it returns by chance to the backbone.[9]In this context, a comb-like structure has been used to understand the underlying mechanism of anomalous diffusion in low-dimensional percolation clusters.[13,14]
To describe the diffusion process in comb-like structure,different approaches have been proposed, such as a mesoscopic approach used by Weiss and Havlin,[14]a macroscopic approach used by Arkhincheev and Baskin,[15]and a microscopic approach used by M′endezet al.[16]Arkhincheev and Baskin in Ref. [15] have expressed the diffusion process in the comb by using the following Fokker–Planck equation:?P/?t=δ(y) ?D?2P/?x2+D?2P/?y2. Here,Dx=δ(y) ?DandDy=Dare the diffusion coefficient in thexandydirections, respectively, and theδ-function in the Fokker–Planck operatorLFP=δ(y) ?D?2x+D?2ymeans that the diffusion along thexdirection (the so-called backbone) is allowed only aty=0.
Recently,the comb-like model has been used to describe anomalous diffusion in spiny dendrites,[17]the mechanism of super-diffusion of ultracold atoms in a one-dimensional (1D)as a phenomenology of experimental study,[18]as well as anomalous diffusion in porous materials.[19]Diffusion along the backbone in two and three-dimensional (3D) comb-like structure with finite finger are the sub-diffusion for short times and the normal diffusion at long times, the same results are obtained as those in Ref. [20] by using the trap model of energetic nature. Whereas, the diffusion along the backbone in a 3D comb-like structure with infinite two-dimensional(2D)branch is an ultra-slow diffusion/enhanced sub-diffusion if normal/sub-diffusion occurs inside branches.[21,22]In addition, recent theoretical studies have demonstrated that performing different microscopic dynamics in comb-like model leads to different types of anomalous diffusions.[23–27]
In the recent decades,there has been a notable interest in studying the properties of transport on a curved surface,where the particle motion is limited by this surface.[28–30]Diffusion on a curved surfaces is inherently complex compared with diffusion on a planer surface[31,32]due to its distinct geometric and topological properties. This process has emerged in biology,such as diffusion on the surface of a spherical porous particle in a porous medium,[33]the free diffusion of biological molecules across the cell membrane,[34,35]transport of protein in DNA,[36]and diffusion of drug particles within the vascular network found in solid tumors.[37,38]However, most of these systems are crowded and diffusion is anomalous.[35]
The diffusion of particles on a 2D spherical surface has been used as a model for describing a variety of processes in nature, for example lateral diffusion in biological membranes.[39–41]Jianget al.[42]studied the 3D diffusion of quantum dots (QDs) in adherent A549 (human lung carcinoma) cells using 3D single particle tracking (SPT) microscopy. They found that the QDs prefer to diffuse laterally in quasi-2D space rather than isotropically in the 3D space.Besides, the axial diffusion rate is five times lower than that for the lateral diffusion. They concluded that the quasi-2D diffusion in the lateral direction is likely to be an intrinsic feature of adherent cells, based on demonstrating the fact that disrupting the cytoskeleton component or endoplasmic reticulum (ER) does not change the quasi-2D diffusion pattern,although ER reduces the diffusion rates and slightly relieves the constraint in the axial diffusion. In Ref. [43], Jianget al.studied the transport dynamics of endocytic cargos using the 3D single particle tracking. With the timescale varied,the intracellular transport changes from the thermal-dominated 3Dconstrained motion into the active-dominated quasi-2D motion. Spatially, the lateral motion is heterogeneous, with it being faster in the peripheral region than in the perinuclear regions,while the axial motion is homogeneous across the cells.In this paper,we study the dynamic behaviors of random motion on a branched spherical surface (see Fig. 1). In the proposed structure, the particles move randomly on the surface of the sphere and then enter into the branches heading inward or outward. Our motivation also comes from the diffusion of calcium across hippocampal neurons, in which its cell body corresponds to the sphere and dendritic trees correspond to branched fingers.[44]This problem also related to restricted diffusion of spin-bearing particles in spherical layers in inhomogeneous magnetic fields,[40]and the nuclear magnetic resonance diffusion(dNMR)measurements of water molecules in heterogeneous systems.[45]
The rest of the paper is organized as follows. We first formulate the mathematical description of the problem in Section 2.The numerical method,and example on the verification of the numerical algorithm are collected in Sections 3. Then results and discussion are presented in Section 4. Some conclusions are drawn from the present researches in Section 5.
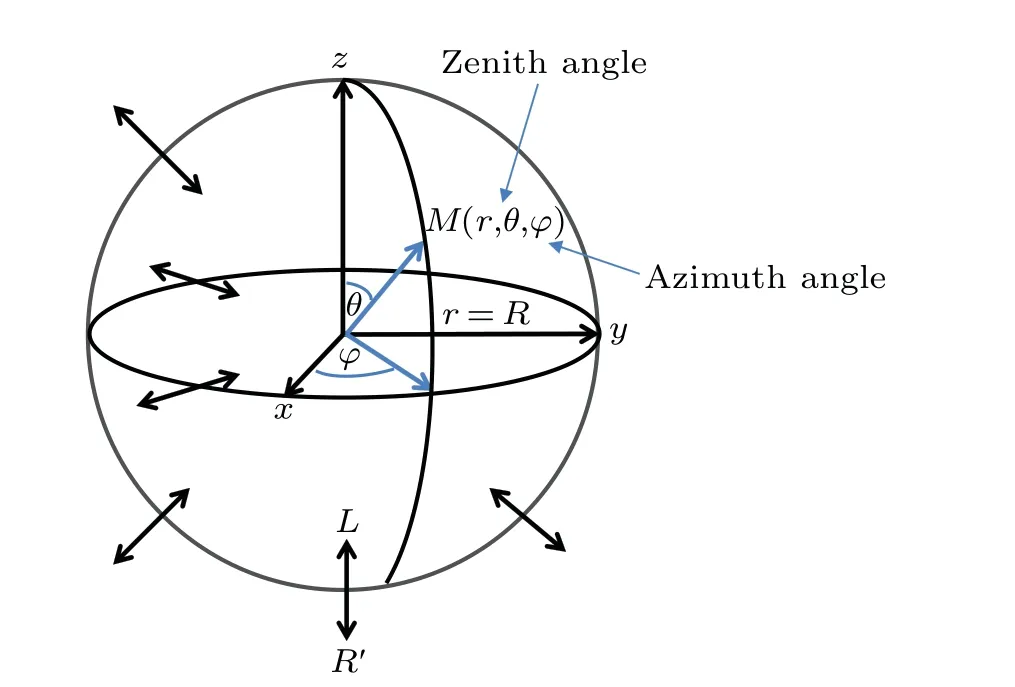
Fig.1. Schematic diagram of spherical comb-like structure,where the radii are continuously distributed over the surface of a sphere of radius R,θ zenith angle,and φ azimuth angle. The characteristic of the diffusion in the spherical comb-like structure is that the particle performs a spherical movement only at r =R, interspersed with a radial motion inward and outward the spherical surface.
2. Mathematical formulation
The structure we consider here consists of a narrow spherical annular cavity,with radii’s dead ends pointing inside and outside as shown Fig.1. During particle movement in the cavity, it may be trapped in the dead ends, exhibiting diffusion inside the cavity for a period until returning to the cavity by chance,thus the particle can escape from the lateral branches.Related to spherical diffusion, two mechanisms are considered:the first mechanism the diffusion is free,while in the second mechanism the diffusion is subjected to external velocity fieldV. Mathematically,suppose a sphereSto have a radiusLin the Cartesian spaceXYZ,then for any point(x,y,z)∈Swe have
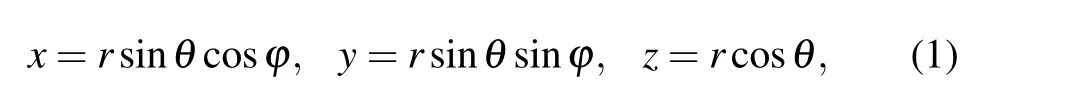
wherer ∈[0,L],θ ∈[0,π],andφ ∈[0,2π]. The characteristic of the diffusion in the spherical comb-like structure is that the particle performs a spherical movement only atr=R, whereR ∈[L,R′], interspersed with a radial motion inward and outward the spherical surface.Therefore,the diffusion coefficient is highly inhomogeneous in the angular direction.Namely,the diffusion coefficients are expressed asDφ= ?Dδ(r-R) andDθ= ?Dδ(r-R), while the diffusion coefficient in the radial direction along the teeth is a constantDr=D. The dynamic behavior of particles on the structure can be described by the probability density functionP(r,θ,φ,t). In what follows, we derive the diffusion equation with drift in a spherical coordinate system, then find the differential equation that expresses the diffusion process in our structure.
2.1. Derivation of diffusion–advection equation in spherical coordinate system

2.2. Diffusion–advection equation in spherical comb-like structure
The movement of the particles in the structure is a spherical diffusion in a homogeneous velocity field,vθ=v1δ(r-R)andvφ=v2δ(r-R),occurs only whenr=Rin whichDφ=?Dδ(r-R)andDθ= ?Dδ(r-R)with unbiased diffusion in the lateral branches whereDr=Dandvr=0. The free surface diffusion corresponds tov1=0 andv2=0. Now,according to Eq.(4),the diffusion process in the structure can be described through the following equation:
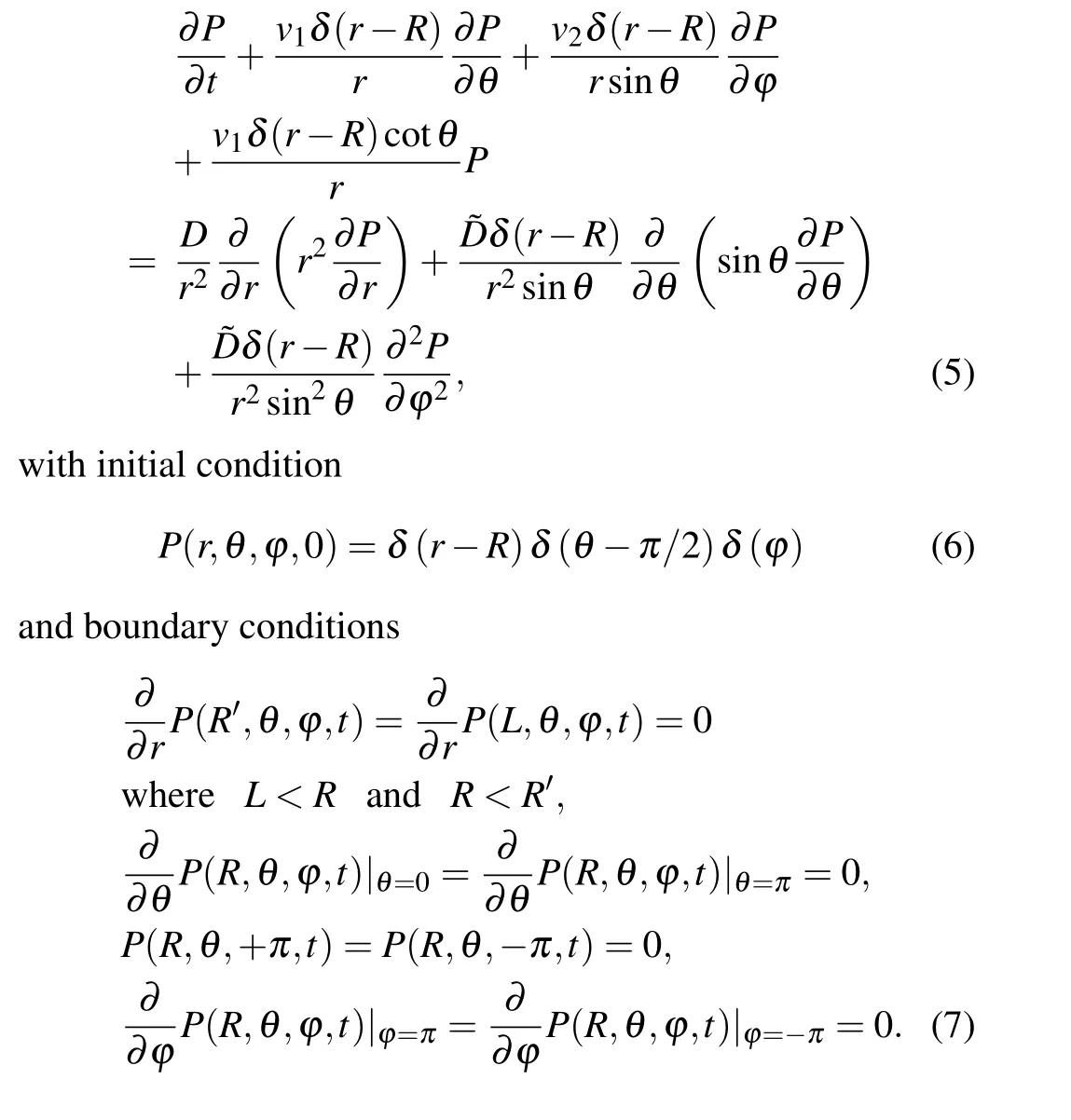
3. Numerical procedure
3.1. Numerical algorithm

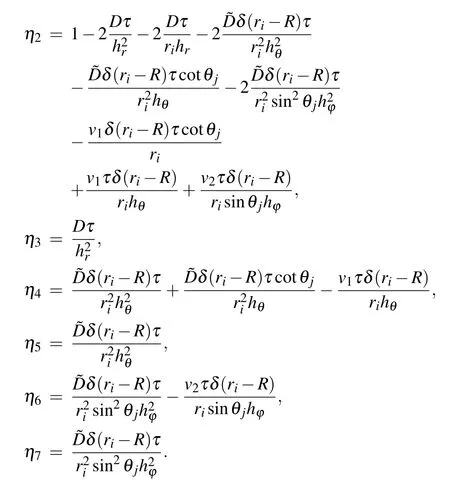
3.2. Verification of validity of numerical solution


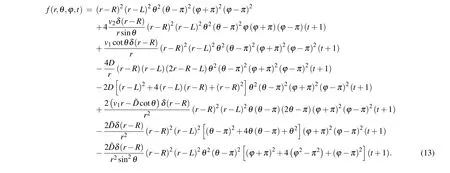
The solution of the previous initial-boundary problems (10)–(12)is given as follows:
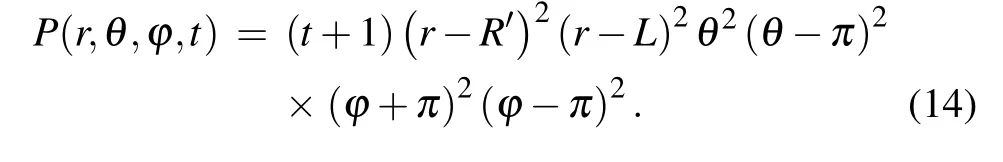
We have applied the proposed numerical scheme to the Eqs. (10)–(12). The comparison between the numerical solution with the analytical solution, Eq. (14) forv1=v2=0,R=3,θ=π/2,D= ?D=1,τ=10-4,hr=0.6, andhθ=hφ=π/20 att=1 is plotted in Fig. 2. We can see that the numerical solution is in good agreement with the analytical solution.
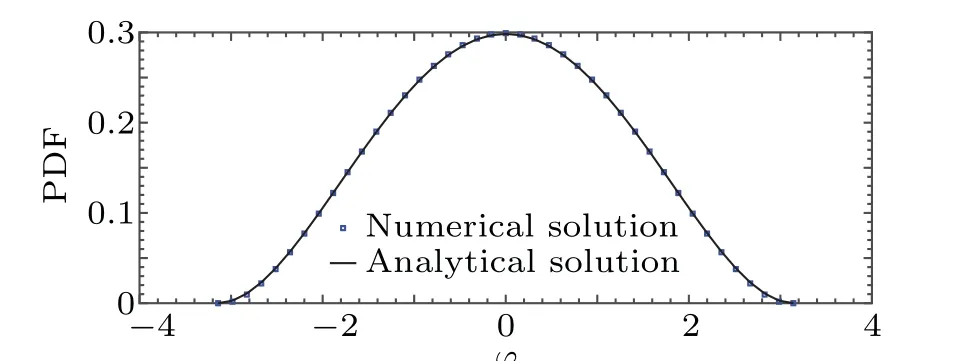
Fig. 2. Comparison of the exact solution with numerical solution for v1 =v2=0,R=3,θ=π/2,D= ?D=1,τ=10-4,hr=0.6,and hθ =hφ =π/20 at t=1.
4. Results and discussion
In this section, we outline the influence of geometric properties of the branched spherical structure,namely,the lateral fingers and sphere curvature, on stochastic dynamics of the sphere surface. As indicated above,two processes are considered to be free surface diffusion and surface diffusion with constant drift. In this context, we analyze the underlying dynamics by using the statistical concept,i.e., marginal probability density function(PDF) ?P(x,t)and the mean square displacement(MSD),i.e.,〈(x(t)-x(t0))2〉,where
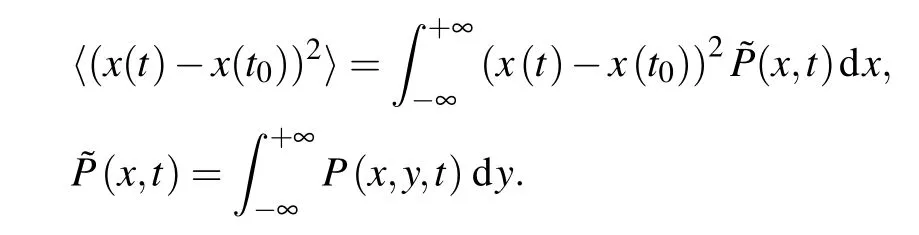
4.1. Free surface diffusion
The PDF is one of the most popular tools to describe stochastic processes. Figures 3(a)–3(c) show the effects of the lengthRof the sphere radius on the time evolution of the azimuth angular marginal PDF ?P(φ,t)of particle diffusion in the branched spherical structure.In each of Figs.3(a)–3(c),we observed a transient non-Gaussian curve with a cusp peak followed by Gaussian curve with smooth one. This phenomenon can be attributed to heterogeneity of the considered structure.
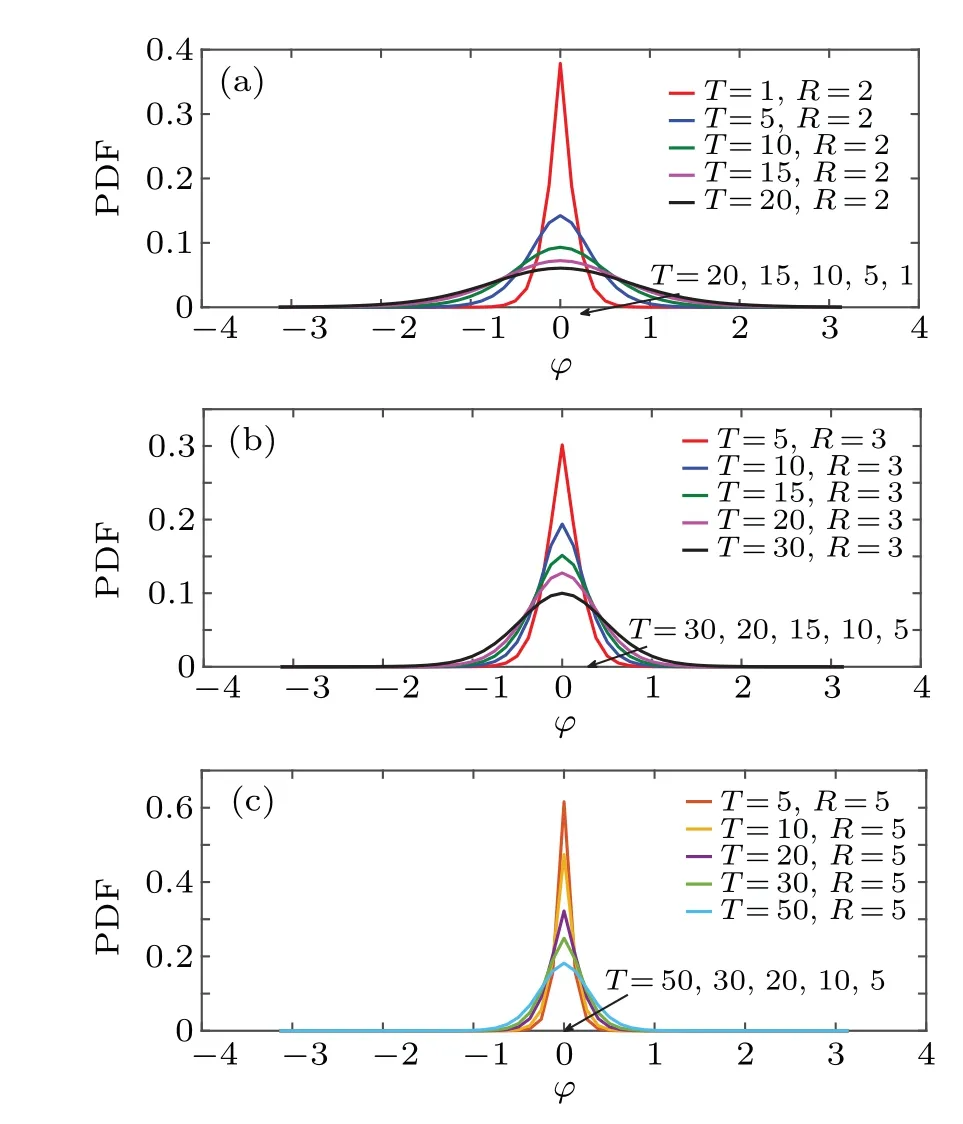
Fig. 3. Time evolution of azimuth angular marginal PDF for D= ?D=0,v1=v2=0,and R=2,3,5.
Moreover, the transient period is noticeably affected by the length of the radiusRof the sphere, in which the peak of the curve declines slowly as the length of the radius increases.Since the Gaussian curvature of the sphere equals the inverse of its radius length 1/R,we may conclude that the decrease of the Gaussian curvature of the sphere,which is proportional to the increase in the radius of the sphere,will result in increasing the hindrance of the particle’s motion in the branched spherical structure. In addition, figure 3 shows that there is also a saturation state that the particles reach after a time due to the limitation of the structure, in which reaching this state takes more time as the spherical radius gets longer.
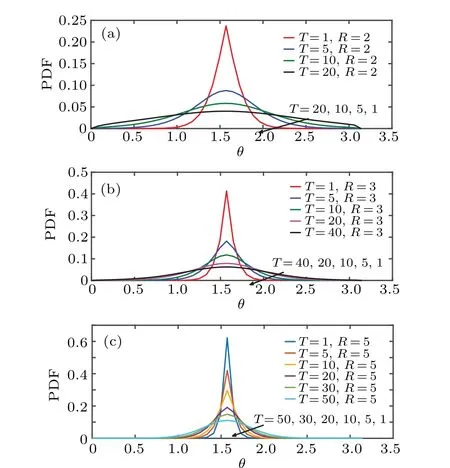
Fig. 4. Time evolution of zenith angular marginal PDF for D = ?D = 0,v1=v2=0,and R=2,3,5.
Figures 4(a)–4(c)show the influences of length of sphere radiusRon the time evolution of the zenith angular marginal PDF ?P(θ,t) of free surface diffusion in the branched spherical structure. We can observe that the curve is unimodal and symmetric with respect to its maximum, besides the fact that the peak has a cusp shape,the peak changes into a smooth one over time. However, the rate of the peak drop decreases with the radius length increasing. Besides, it is obvious that the peak of azimuth PDF ?P(θ,t)slopes slowly compared with the dynamics of the peak for zenith PDF ?P(φ,t),which is due to the density of the fingers in which the particle is trapped during the latitudinal movement compared with its density during the longitudinal movement. We may conclude that the diffusion dynamics in the branched spherical structure is enhanced as the curvature of the structure increases, and the longitudinal diffusion is symmetric yet not normal, namely, the particles slow down before reaching a saturation state, and the reaching time is inversely proportional to the Gaussian curvature of the surface of the sphere. Once again it appears that twodimensional diffusion cannot well characterize the diffusion in three-dimensional structures. Recently,Jianget al.[42]studied the 3D diffusion of quantum dots(QDs)in adherent A549(human lung carcinoma)cells by using 3D single-particle tracking(SPT)microscopy. They found that the QDs prefer to diffuse laterally in quasi-2D space rather than isotropically in the 3D space. Besides,the axial diffusion rate is five times lower than that of the lateral diffusion.
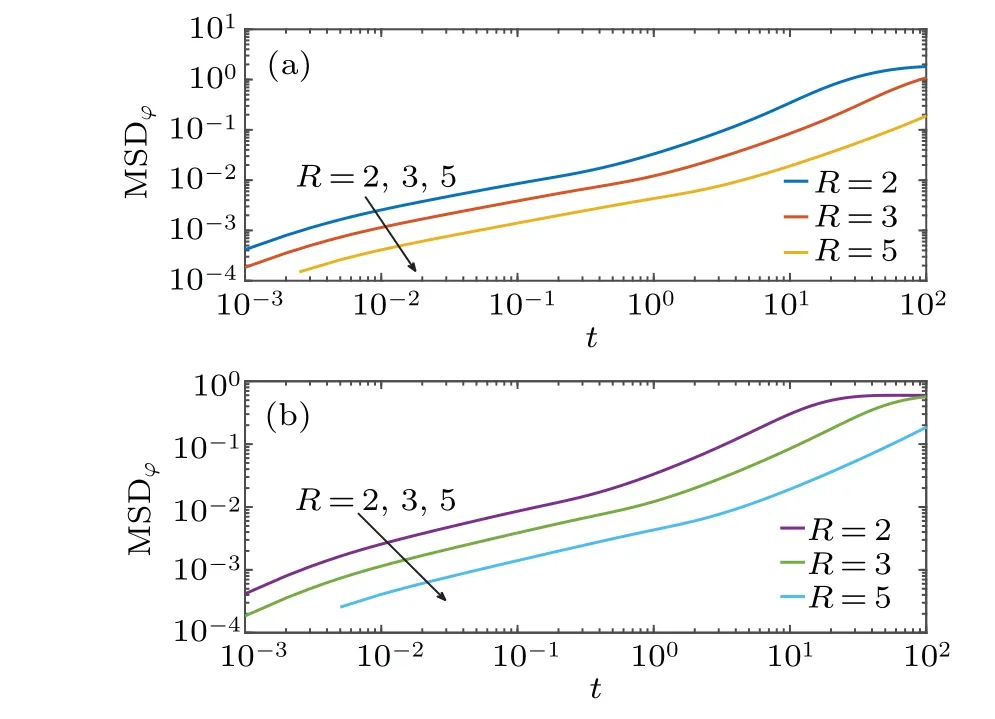
Fig.5. Temporal evolution of angular MSD of particle position for D= ?D=0,v1=v2=0,and R=2,3,5,for(a)azimuth angular MSD,and(b)zenith angular MSD.
The MSD is another important tool to describe diffusion dynamics. The effects of the length of radiusRof the sphere radius on the time evolution of both the zenith angular MSD and azimuth angular MSD are depicted in Figs.5(a)and 5(b),respectively. The MSD in Figs.5(a)and 5(b)show a transient non-linear behavior, which may be scaled as MSD~tαwith 0<α <1, and converges to a constant value. We observe from these panels that in a short time the MSD magnitude increases with the decrease of parameterR. The MSD converges to plateau over time due to confinement,and the speed of convergence to the plateau decreases as the length of radiusRincreases. Namely,a transient sub-diffusion regime governs the angular dynamics,however,the transport is enhanced with the increase of the Gaussian curvature of the sphere surface.Then,we may conclude that the increase of the curvature can facilitate particle diffusion. Moreover,there is a slowdown in the longitudinal surface diffusion,which may be attributed to a higher rate of hindering particle diffusion due to trapping during longitudinal motion.
4.2. Surface diffusion with constant drift
In this subsection, we examine the properties of the diffusion dynamics subjected to the external velocity field in a branched spherical structure. The effects of drift force in lateral direction or longitudinal direction or both directions are analyzed. Figures 6 and 7 show the effects of velocity parameter on temporal evolution of azimuthal and zenith angular marginal PDF,respectively. As in the case of free surface diffusion,the curves of PDF are unimodal and symmetric with respect to their maximum values,besides the fact that the peak has a transient cusp shape. However, the magnitude of the velocity parameter significantly affects the diffusion dynamics. Comparing Fig.6 with Fig.3(b),we observe that the peak of the PDF comes down as the velocity gets larger. Moreover,when the drift is applied to the azimuthal coordinate,the distribution drifts toward the applied force over time,while it remains symmetric under the drift applied to the zenith coordinate. The same phenomenon can be observed in Fig.7,in the context of the longitudinal diffusion, however, the diffusion dynamics becomes slower over time.
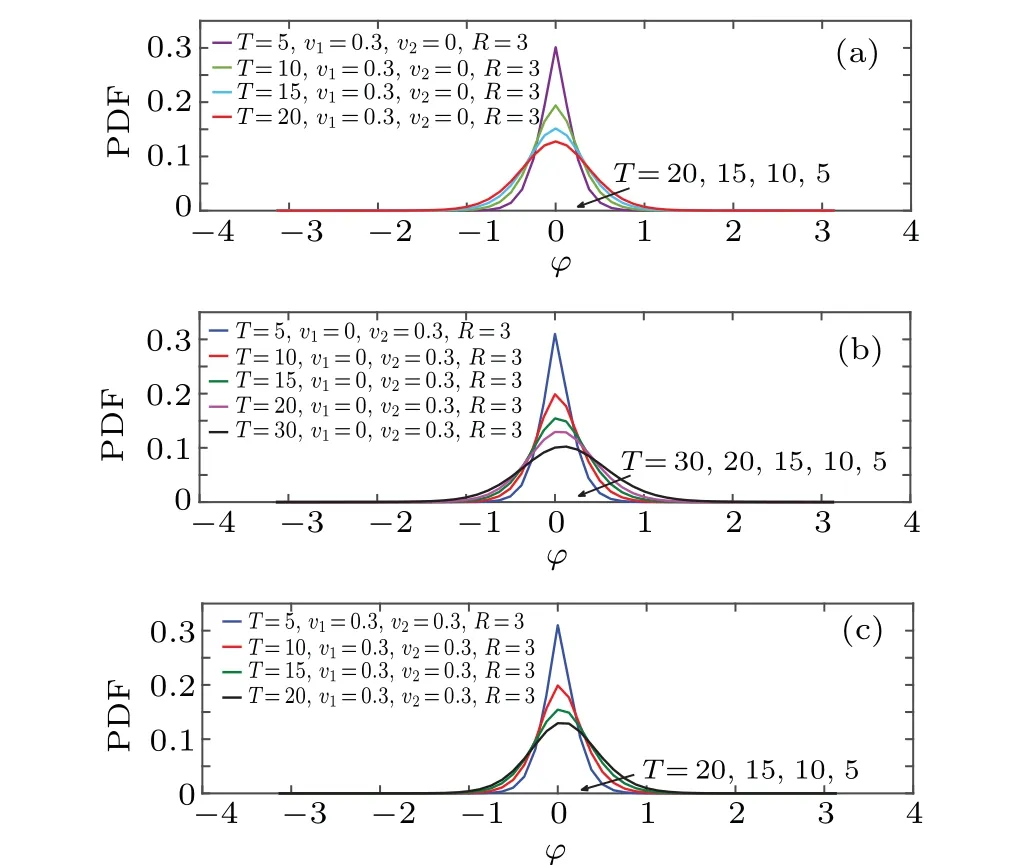
Fig. 6. Time evolution of azimuth angular marginal PDF for D= ?D=0,R=3, where (a) v1 =0.3 and v2 =0, (b) v1 =0 and v2 =0.3, and (c)v1=0.3 and v2=0.3.
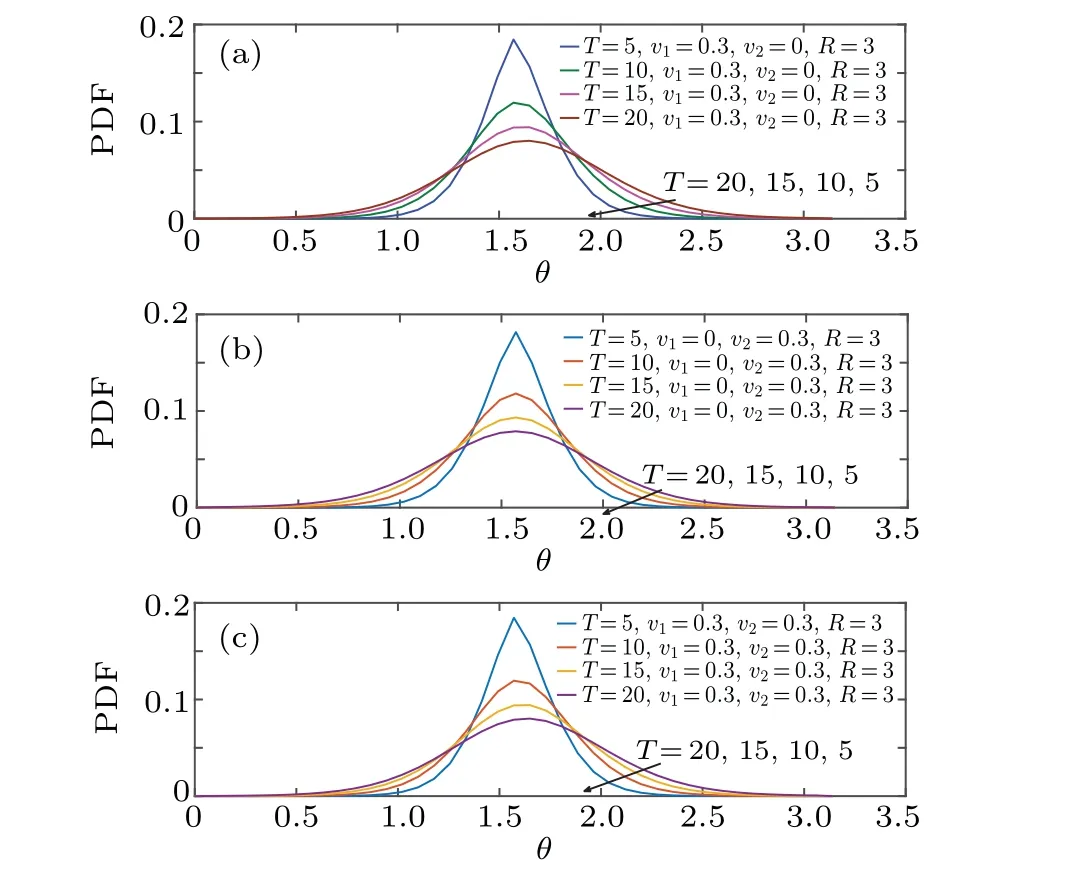
Fig. 7. Time evolution of zenith angular marginal PDF for D= ?D=0 ,R=3, where (a) v1 =0.3 and v2 =0, (b) v1 =0, and v2 =0.3, and (c)v1=0.3 and v2=0.3.
The influence of the velocity parameter on the MSD are shown in Fig.8. It dramatically affects the growth of MSD in a long time, in which the magnitude of MSD increases with the increase of the velocity. Namely,there is an enhancement in the diffusion process along the direction corresponding to the direction of the applied force. This improvement is noticeable if the surface curvature is greater, namely, the radius of the sphere is smaller. Like free diffusion, the MSD converges to plateau over time due to confinement. We conclude that the diffusion on a spherical surface with lateral dead ends is enhanced as the curvature increases and an external force is applied in the same direction as that of the motion.

Fig. 8. Temporal evolution of MSD of particle position for D= ?D=0,v1 =0.3,v2 =0;v1 =0,v2 =0.3;v1 =0.3,v2 =0.3 and R=2,3,for(a)azimuth angular MSD and(b)zenith angular MSD.
5. Conclusions
In this paper, we have examined the properties of diffusion dynamics in narrow spherical annular cavity with radii’s dead ends pointing inside and outside. Here,two scenarios are taken into account,i.e., free diffusion and diffusion with external velocity. The diffusion dynamics is described by using the concepts of probability density function (PDF) and mean square displacement (MSD) by Fokker–Planck equation in a spherical coordinate system. The model is solved numerically and the correctness of the numerical algorithm is verified by comparing it with the analytical solution in a specific case.The effects of dead ends,sphere curvature,and velocity on probability density function,and mean square displacement are analyzed numerically in detail. We find that for free surface a transient sub-diffusion regime governs the angular dynamics,however, the transport is enhanced with the increase of the Gaussian curvature of the sphere surface. Besides, the longitudinal diffusion is symmetric but not normal,namely,it slows down before reaching a saturation state,and the reaching time is inversely proportional to the Gaussian curvature of the surface of the sphere. For diffusion under external velocity, the magnitude of the velocity parameter significantly affects the diffusion dynamics. The results show that there is an enhancement in the diffusion process in the direction corresponding to the direction of the applied force.
Acknowledgement
Project supported by the National Natural Science Foundation of China(Grant Nos.11772046 and 81870345).
- Chinese Physics B的其它文章
- Microwave absorption properties regulation and bandwidth formula of oriented Y2Fe17N3-δ@SiO2/PU composite synthesized by reduction–diffusion method
- Amplitude modulation excitation for cancellous bone evaluation using a portable ultrasonic backscatter instrumentation
- Laser-modified luminescence for optical data storage
- Electron delocalization enhances the thermoelectric performance of misfit layer compound(Sn1-xBixS)1.2(TiS2)2
- TiO2/SnO2 electron transport double layers with ultrathin SnO2 for efficient planar perovskite solar cells
- Sputtered SnO2 as an interlayer for efficient semitransparent perovskite solar cells

