Dynamical behavior and optimal impulse control analysis of a stochastic rumor spreading model

Liang’an Huo(霍良安) and Xiaomin Chen(陳曉敏)

Business School,University of Shanghai for Science and Technology,Shanghai 200093,China

The Internet era has brought great convenience to our life and communication. Meanwhile, it also makes a bunch of rumors propagate faster and causes even more harm to human life. Therefore, it is necessary to perform effective control mechanisms to minimize the negative social impact from rumors. Thereout,firstly,we formulate a rumor spreading model considering psychological factors and thinking time,then,we add white noise(i.e.,stochastic interference)and two pulse control strategies which denote education mechanism and refutation mechanism into the model. Secondly,we obtain the global positive solutions and demonstrate the global exponential stability of the unique positive periodic rumor-free solution. Thirdly,we discuss the extinction and persistence of rumor. Moreover,we use Pontriagin’s minimum principle to explore the optimal impulse control. Finally, several numerical simulations are carried out to verify the effectiveness and availability of the theoretical analysis. We conclude that the pulse control strategies have a great influence on controlling rumor spreading,and different control strategies should be adopted under different transmission scenarios.

Keywords: rumor spreading, stochastic process, optimal impulse control, education mechanism, refutation mechanism

1. Introduction

As a vital form of social communication,the spread of rumors has had a great impact on human society. At present,the progressively expanding social networking platforms have facilitated the dissemination of information,thus providing more diversified channels for rumor spreading. Generally, these widespread rumors not only cause individual panic, but also endanger social stability. For example, in the recent time of COVID-19, several negative rumors were constantly emerging and spreading widely,which undoubtedly brought psychological, reputational, economic, and even social damage.[1,2]Therefore,how to grasp the overall dynamics of rumor spreading and thus effectively curb the spread of rumors is an urgent issue to be addressed. Meanwhile,minimizing the social negative impact caused by rumor spreading and control the cost brought by control strategies is our ultimate research goal.

There has been an increasing interest of rumor spreading models over the past several decades. Initially, Daleyet al.put forward a classical DK model in order to describe dynamic process of rumor spreading,[3]providing some new ideas for later studies. Since then,Maki and Thompson made improvements according to the DK model and then formulated the MT model.[4]These models both provided effective theoretical guidance for scholars to explore the properties of rumor spreading models. Subsequently, the topological characteristics of social networks are started to be considered in some models.[5,6]In subsequent studies, some scholars introduced various microscopic mechanisms to rumor spreading models and revealed these mechanisms’relationship with rumor spreading.[7,8]Recently,based on these pioneering works,some scholars also devoted themselves to studying the dynamics and control strategies of controlling rumor spreading.[9–12]

It is well known that rumor spreading is more than a simple social behavior, and it also involves the psychological aspects of social groups. Especially, whether the susceptible individuals accept rumors and turn into spreaders is affected by personal psychological quality. For example, when a susceptible individual is surrounded by a large number of rumor spreaders, the susceptible individual will be more inclined to spread rumors. In the existing rumor spreading models, the rate of interaction between the two groups is mostly measured with either a constant or a bi-linear incidence rate. However,considering the susceptible individuals’ crowd psychological factor,it is obvious that nonlinear incidence rate is more practical than a constant or a bi-linear incidence rate.[13]Especially,the Holling II functional response function may demonstrate interactive relationship between two groups well by saturation incidence.[14]Moreover, through the introduction of psychological factors in the process of rumor spreading, we can specifically depict the behavior change and aggregation effect of individuals to rumors.

In addition, time delay is a universal phenomenon in a system. As is known to all, it takes time to react to an action from start to finish. In particular, a statement that is not verified casts doubt on individuals, so they cannot respond to a rumor immediately and it takes time for them to think whether to spread. Hence, when susceptible individuals contacted spreaders, the time delay needs to be imported. In regard of it, Laarabi established a rumor spreading model containing latent period,[15]and Zhu investigated the dynamical behaviors of a delayed rumor spreading model.[16,17]However,they donot seem to have considered the influence of external disturbance on rumor spreading.

Actually, real life is full of randomness, the external environmental factor can also interfere with rumors.[18–20]Here,when a rumor is disturbed by external circumstances or when the events that trigger it may constantly evolve or change, its spread will be influenced by stochastic factors. Since people’s attitude towards rumors changes accordingly as events evolve continuously and external environment changes at random in these cases,which exerted corresponding effects on stochastic rumor spreading. Hence,it is essential to study stochastic rumor spreading, which may contribute to more novel research results.

To sum up,factors affecting rumors are complicated and varied,which reminds us to take positive control measures to suppress the negative impact of rumors. A number of control strategies have now been proposed to address the problem of controlling the spread of rumors,[21–23]and these control strategies in previous studies were mostly considered to be continuous functions in time. In addition, there have been intensive researches about optimal continuous control strategies,[24–28]the most typical of which are science education and rumor refutation. As a matter of fact, whether it is science education or rumor refutation,they are discrete and spaced in time, rather than continuous. Moreover, pulse, the repeated application within a specified time frame,[29–31]is a discrete way of describing these controls well. Therefore,we may consider two pulse control strategies: pulse education mechanism to strengthen the susceptible individuals’comprehensive quality periodically and pulse refutation mechanism to help rumor spreaders identify rumors as true or false termly.Among them,education mechanism denotes scientific knowledge propagation by various channels such as books,and internet,and refutation mechanism means refuting rumors and pronouncing the truth by official platforms such as government,and media.

In general,there are a couple of innovations in this work.Firstly, on the base of a rumor spreading model that has already contained psychological factors and thinking time, we introduce stochastic interference and two pulse control strategies simultaneously. Besides, we explore optimal impulse control strategies, which can minimize the control cost and negative impact caused by rumor spreading. The following sections are mainly composed of modeling, theoretical analysis, and numerical simulation. We build a stochastic rumor spreading model and consider two pulse control strategies in Section 2. Moreover, Section 3 gets the existence of global positive solutions, and the uniqueness and global exponential stability of a rumor-free periodic solution. We analyze extinction and persistent of the rumor in Section 4. The optimal impulse control strategies are explored under a pulse version of Pontryagin’s minimum principle in Section 5. Several numerical results are given in Section 6. The last section gives a conclusion.

2. Modeling

Assuming that the above parameters are positive,and we generalize them in Table 1.

However,in addition to internal psychological factors and personal reaction time,rumor spreading is undoubtedly influenced by external environment disturbance caused by development of events. As the changes of external environment and the evolution of the event that sparked rumor,individuals’attitude and response could be changed accordingly. Thus, it is necessary to take stochastic disturbance into consideration,which makes model more in accordance with the fact. As we all know, the white noise is helpful to model a phenomenon prone to fluctuation and the primary source of white noise is various uncertainties. So,we consider using the white noise to represent the uncertainties such as evolution of events,which makes the model more realistic.

And from what has been presented above,rumor spreading is subject to various complex and changeable factors,which may bring uncontrollable social harm. In terms of this,we put forward several control strategies to reduce rumors’negative impact. On the one side,considering that the susceptible individuals have a poor cultural quality and knowledge base,we introduce the education mechanism aimed at the susceptible individuals to improve their comprehensive quality,which may let the susceptible individuals not spread rumors and then convert them directly to stiflers. On the other side,given that spreaders are the main force of rumor spreading,we bring in the refutation mechanism aimed at spreaders to refute certain rumors,which may make the number of spreaders reduce directly and sharply. However,since the education mechanism and refutation mechanism are often neither carried out continuously, using pulse controls seems more appropriate. Furthermore, for the sake of minimizing the social harm and control cost,we try to find the optimal impulse control.

Here,in order to be more in line with the facts and demonstrate this process more accurately, on the base of model (1),we add white noise and two pulse control strategies:

where all parameters involved are summarized in Table 1.Moreover, set (Ω,F,{Ft}t≥0,P) as a complete probability space with a filtration{Ft}t≥0, which meets the usual conditions.

Table 1. Parameter description.

3. Global positive solution and rumor-free periodic solution

Here, we will focus on the mechanism of rumor spreading. Firstly, our first concern is whether there is a global and positive solution.Then,we study whether there exists a rumorfree periodic solution and whether it is globally stable.

The following lemma provides a lot of support for the theorem we want to prove.

Lemma 1[32]Consider the following stochastic pulse system:

where 0＜t ＜T, andu0=u(0). Besides, combining it with the last equation of system(3),we get the unique periodic solution of system(3)given by

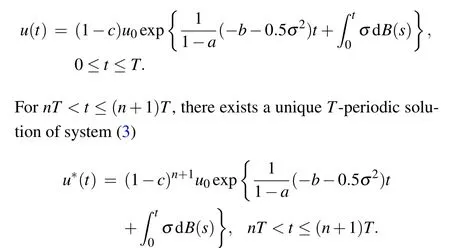
It is well known that the coefficients of the stochastic differential equation need to meet both the linear growth condition and local Lipschitz condition, which ensures that its solution is positive and global. Nevertheless,it is obvious that the coefficients of system (2) do not satisfy the former, that is, the solution is likely to explode in finite time. Thus, using Lyapunov analysis method, we shall demonstrate the solution of system(2)is positive and global.

Theorem 1 For any given initial value (S0,I0,R0) =(S(θ),I(θ),R(θ))∈R+3,θ ∈[-τ,0], there is a unique solution (S(t),I(t),R(t))Tof system (2) fort ≥0, and it would absolutely remain in R+3, that is, (S(t),I(t),R(t))Texists for allt ≥0 almost surely(a.s.).

Proof First, for any initial value (S(θ),I(θ),R(θ))∈R+3,θ ∈[-τ,0](i.e.,(S0,I0,R0)),we prove that system(2)has a unique global solution on intervalt ∈[0,nT].

Firstly,we consider the first three equations of system(2)fort/=nT. In regard of it,we formulate a function

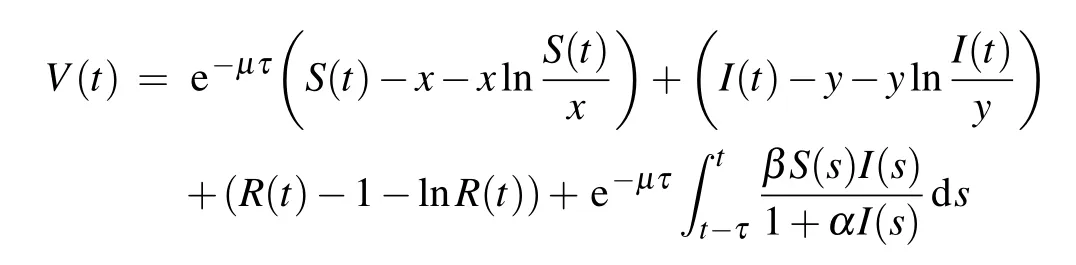
and then get that none ofS(t),I(t) andR(t) will explode in finite time,which is presented in Ref.[20]in detail.

Att=nT,n ∈N, with 0＜ω1,ω2＜1, there is a pulse which transfers solution(S(T),I(T),R(T))T∈R+3into((1-ω1)S(T),(1-ω2)I(T),R(T)+ω1S(T)+ω2I(T))T∈R+3.

Similarly, we can derive there exists a unique global solution defined on [T+,2T] and ((1-ω1)S(2T),(1-ω2)I(2T),R(2T)+ω1S(2T)+ω2I(2T))T∈R+3,which is obvious to be carried out infinitely. This completes the proof.

Then, we prove the existence and global stability of a rumor-free periodic solution,where dI(t)=0.Under this condition,we get the following system

Theorem 2 If 2μ ＞max(σ21,σ23), then system (6) has a unique positiveT-periodic solution (S*(t),R*(t)), which is globally exponentially stable.

Proof On the basis of Lemma 1,it is obvious that if 2μ ＞σ21,then system(6)has a unique positiveT-periodic solutionS*(t),which is globally exponentially stable.Then we analyzeR(t)in system(6). Suppose thatR(t,ξ)is an optional solution of system(6),and we defineR(t,ξ)=?,thenR(t,?)is another solution of system(6).DefineV2(t)=(R(t,ζ)-R(t,?))2,and it is continuous and positive fort ∈[0,+∞), whereV2(0)=(ζ-?)2.

Applying It?o’s formula, integrating and then taking the mathematical expectation toV2(t),we can get

whereλ ＞1 is a positive constant.

Using the same method in Refs.[32–34],we getEV2(t)≤ρEV2(0)e-δtfort ≥0,whereδ=2μ-σ23-2lnλ/T ＞0 andρ ＞1 are two positive constants,and then 2μ ＞σ23.

Then,we can use the same method to get if 2μ ＞σ23,the positiveT-periodic solutionR*(t) is unique and at the same time all solutions converge toR*(t)ast →∞.

Above all,if 2μ ＞max(σ21,σ23),system(6)has a unique positiveT-periodic solution(S*(t),R*(t)) and all solutions converge exponentially to (S*(t),R*(t)) ast →∞. The proof is completed.

In addition, according to Lemma 1, we can get the specific form of theT-periodic solution

4. Extinction and permanence

In this section, we always suppose that 2μ ＞max(σ21,σ23), and then come to study the extinction and permanence of system(2).

Before starting the theorem,let us define these notations as follows:

(i)Iff(t)is integrable fort ≥0,define

It is easy to see that dS(t)≤[(1-p)b-μS(t)]dt+σ1S(t)dB1(t) from the first equation of system (2), then takey1as a variable and formulate a pulse comparison system as follows:

In addition, for convenience, we setS*(t)=y*1(t). Then according to comparison theorem, we can getS(t)≤y*1(t) =S*(t),in other words,

Combine the above inequality (14) and the fifth equation of system(2),we have

Here, we takey2as a variable and formulate pulse comparison system as follows:

5. Optimal impulse control

Here, we will study optimal impulse control of the system(2).As mentioned above,the pulse control is a proper way to demonstrate the control strategies in discrete time. Besides,the intensity of each pulse control strategy has a prominent influence on controlling rumor spreading.As is known to all,the purpose of control rumor spreading is to minimize the negative social impact from rumors. Hence, we consider two aspects:(i) minimize the number of spreaders, when the number of spreaders becomes smaller,the intensity and scope of rumors will become smaller, so the negative social impact will become smaller;(ii)minimize the cost of education mechanism and refutation mechanism during the whole rumor spreading period. Therefore, the objective function that we consider is given by

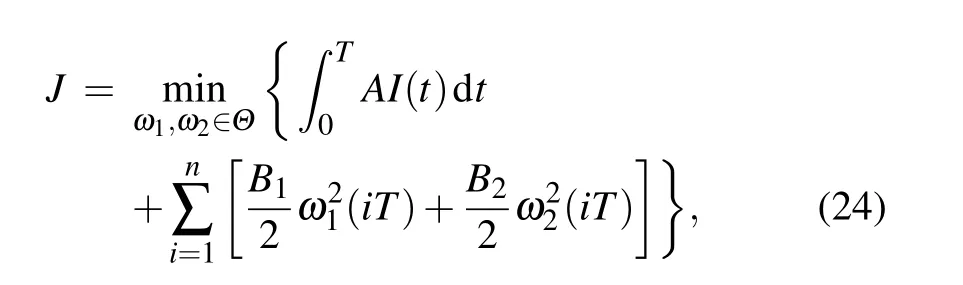
subject to system(2),whereA,B1andB2are all positive constants,Arepresents the weight coefficient ofI(t),B1andB2denote the control cost of one unit control variable. Moreover,suppose that 0≤ω1(t),ω2(t)≤1, whereω1(t)=1 denotes maximizing the degree of education mechanism andω2(t)=1 represents maximizing the intensity of refutation mechanism.

To resolve the optimal problem(24), the following steps are taken.

Firstly,we formulate the HamiltonianHwithout control,defined as

Then the pulse minimum principle can be declared as follows.

Theorem 5 Consider optimal impulse controlω1(iT),ω2(iT),i=1,...,n, which minimizes (24) with the optimal trajectoriesS*(t),I*(t),R*(t)related to system(2),then there are adjoint variablespk(t),k=1,2,3, which conform to the following adjoint system fort/=iT

6. Numerical simulations

In this section, some numerical results are presented in two parts for supporting the analytic results obtained above.On one side, we will study the influence of the strength of pulse controlsω1andω2on systems(2)and(6)by numerical analysis, which will demonstrate the effectiveness of Theorems 2–4. On the other side,we will find the optimal strength of the pulse controlsω1andω2to minimize Eq. (26) by numerical analysis,which will visualize the result of Theorem 5.We set the pulse periodTas 5 in all simulations.

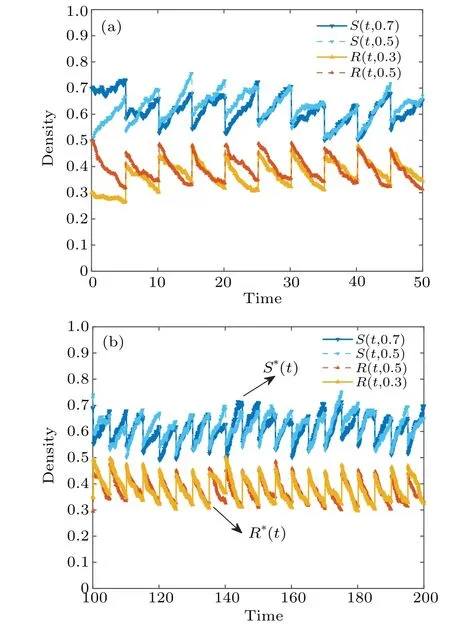
Fig.1.Trajectories and the periodic solution(S*(t),R*(t))of system(7)with ω1=ω2=0.2.

Fig. 2. The periodic solution(S*(t),R*(t)) of system (6) with ω1 =ω2=0.05 and ω1=ω2=0.95.

In the first part, firstly, to explore the existence and globally exponentially stability of the periodic solution According to Theorem 1, the susceptible individuals and stiflers will persist and the spreaders will go to extinction. As is clearly illustrated in Fig.3(a),the susceptible and spreaders decrease and the stiflers increase during initial period,then the susceptible and stiflers are in a globally asymptotically stable state and spreaders go to extinction, which supports this analytical result.

Furthermore, other conditions being the same, we adopt different pulse proportionω1=ω2=0.05 to explore the persistence of the spreaders of system (2). As clearly shown in the Fig.2,we satisfy the condition

Then comparing Figs. 3(a) and 4(a) yields that strengthening scientific knowledge propagation and intensifying rumor refutation are both effective mechanisms to control the rumor, which can reduce the number of the susceptible and spreaders,and even can suppress spreading of the rumor. Taking an example during COVID-19, there is a rumor that setting off firecrackers can prevent the novel coronavirus going around, which comes from old people who claim that ‘when firecrackers sound, sulfur spews out, it’s disinfection’. It is obvious that the rumor exploited a loophole of ignorance. If individuals knew the scientific knowledge that the smoke produced by firecrackers is mainly composed of sulfur dioxide,which forms a dilute sulfuric acid gas solvent with water in the air, they would realize it is not only unable to cure diseases,but also causes diseases,so they would not believe and spread the rumor. And if the official platforms refute this rumor timely and repeatedly, those spreaders would learn the truth and stopped spreading. Therefore, on the one side, we need to strengthen education learning by various approaches in order to widen the scope of the scientific knowledge,so that we do not easily believe and spread rumors;on the other side,the official platforms should make the truth public to dispel the rumor timely,which may suppress rumor spreading.

In the second part, we aim to illustrate the optimal impulse control by numerical method which is applicable to the discover of Theorem 5. By algorithm 1 in Ref.[35], we take four numerical calculation steps to address the optimal impulse control problem.

Firstly, we take the initial valueS0=0.7,I0=0.2, andR0=0.1 with following parametersp=0.3,b=0.1,μ=0.08,β=0.7,α=0.1,η=0.1,τ=3,σ1=σ2=σ3=0.1,A=0.1,B1=1, andB2=1. In this case, we get the Figs.5 and 6, which depicts the dynamical paths with and without optimal control and the recommended pulses.

Fig.3. The rumor will be extinct. (a)Dynamics of solutions of system(2). (b)Phase portrait of(S(t),I(t),R(t)). (c)Phase portrait of(S(t),I(t)).

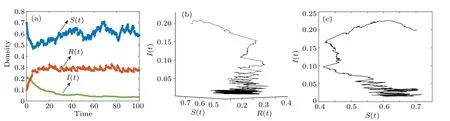
Fig.4. The rumor is persistent. (a)Dynamics of solutions of system(2). (b)Phase portrait of(S(t),I(t),R(t)). (c)Phase portrait of(S(t),I(t)).

Fig.5. Paths simulations of(S(t),I(t),R(t))with and without optimal control(ω*1(t),ω*2(t)).

Fig.6. Values of the optimal controls(ω*1(t),ω*2(t))at every period.

From Fig. 5(a), we can observe that if without control,the proportion of susceptible individuals fluctuate around 0.25 after the first control period; if not, the susceptible proportion does a slight jump again and again,and there is a temporary reduction after each control cycle. As is obviously shown in Fig. 5(b), the proportion of spreaders with optimal control dropped sharply after each pulse control period and is always less than the one without control. Once control is stopped,it continues the previous trend. Simultaneously,with optimal impulse control,the proportion of stiflers in Fig.5(c)oscillates periodically and is always larger than the one without control.Just as in real life,when rumors appear and start to spread,if we can regularly promote science to improve the quality of the population and hold regular press conferences to dispel them,each time we took the control measure, the rumor mill was suppressed to a certain extent and the strength of the impact of the rumor spreading will be greatly reduced in the end.

Then from Fig. 6, we can get the optimal pulse valuesω*1of education mechanism take the values between 0.05 and 0.3 in all periods; meanwhile the optimal pulse valuesω*2of refutation mechanism take values between 0.05 to 0.4 in various periods. Moreover, combined with Fig. 5, we can find that the optimal control values are related to the proportion of susceptible individuals and spreaders, in other words, as the proportion of susceptible individuals and spreaders varies,the optimal control values are adjusted accordingly.

Above all,the main result we can summarize from Figs.5 and 6 is when there exist control strategies,all the proportion of susceptible individuals,spreaders and stiflers oscillate in all times of pulsed controls,and once the control is stopped,they will continue the previous trend.Meanwhile,the optimal pulse values are connected with the proportion of individuals in the population. Moreover,by optimal control strategies,the number of spreaders will reduced greatly and the rumor will get suppressed.

Besides what’s mentioned above, we explore under different transmission ratesβ, what control strategies should be taken. Therefore,all other conditions being the same,we use different transmission ratesβ=0.3,0.5,and 0.7.From Fig.7,we can clearly see howω*1education mechanism andω*2refutation mechanism should be set up at different transmission rates. By comparing the data in the figure on the left, we can find that when the transmission rate decreases, the focus should be on the education mechanism. Similarly,comparing the data in the right figure, we find that when the transmission rate increases, the strength of the refutation mechanism should be strengthened. Hence, we infer that the higher the transmission rate, the less the strength of education mechanism and the more the strength of refutation mechanism are required to introduce, which is in accordance with the fact.For example,there was a rumor recently that said vaccination with the COVID-19 vaccine can alter the genetic information of humans and make them infertile. When the transmission rate of this rumor increased, that is, more susceptible individuals turn into spreaders, so more efforts should be put on refutation mechanism,i.e clarifying the truth and refuting the rumor. Otherwise,we should pay more attention to education mechanism.

The validity of our theoretical results is then demonstrated by way of a practical example and the actual data is provided by Yuet al.in Ref.[38]. In Fig.8, we take the initial valueS0=0.9,I0=0.05, andR0=0.05 with following parametersp=0.1,b=0.01,μ=0.015,β=0.4,α=0.001,η=0.25,τ=3,andσ1=σ2=σ3=0.1. In terms of this,we study the fits of the simulation data and actual data in Fig.8(a)and compare the different control strategies in Fig.8(b).In real situation,the official platform refuted this rumor att=23,so we set the impulsive control strategy att=23. From Fig.8(a),it is clearly that the trajectory closely corresponds to the actual data.Tmeans control period as in Table 1, and it compares the effect of periodic impulse control strategies (T=5) with the actual control strategy(t=23)in Fig.8(b), which shows the periodic impulse control strategies can suppress the spread of rumor faster and reduce the negative impact of rumor. In this way, we believe that the impulse control strategy has its validity.

Fig.7. Values of the optimal controls(ω*1(t),ω*2(t))for different values of β.

Fig.8. Model comparison chart and control comparison chart. (a)The comparison of model simulation and actual data. (b)The dynamics of I(t)in different control contexts.

7. Conclusions

To conclude, this paper is principally respecting with the dynamic behaviors and the optimal impulse controls of a stochastic rumor spreading model. Firstly, we introduced stochastic disturbance and two pulse control strategies simultaneously to a novel rumor spreading model, where stochastic disturbance considers complex and changing environment and two pulse control strategies denote education mechanism and refutation mechanism, respectively. Besides, we studied the spreading mechanisms of stochastic rumors and got the existence of global positive solutions and the global exponential stability of the unique positive periodic rumor-free solution. Moreover, we explored the extinction and persistence by means of two threshold parametersR1andR2. WhenR1＜1,the susceptible individuals and stiflers will persist and the spreaders will go to extinction, in other words, the rumor will be controlled. And whenR2＞1, the spreaders will persist,that is,the rumor will be likewise persistent. In addition,we explored optimal impulse controls by Pontryagin’s minimum principle, which minimizes the population density and control cost of the spreader, and then minimizes the negative social impact. Finally, by several graphical representation of the numerical simulation,the correctness of the theoretical results was confirmed. We proved the effectiveness of education and refutation mechanisms, and simultaneously, we find out in different transmission scenarios,different control strategies should be emphasized.

Acknowledgements

This work was partially supported by the Project for the National Natural Science Foundation of China (Grant Nos. 72174121 and 71774111), and the Program for Professor of Special Appointment(Eastern Scholar)at Shanghai Institutions of Higher Learning, and the Project for the Natural Science Foundation of Shanghai (Grant No. 21ZR1444100),and Project Soft Science Research of Shanghai (Grant No.22692112600).