一類含絕對值函數(shù)問題的求導策略
2022-10-26 09:42:34蔡建華
高中數(shù)學教與學 2022年17期
蔡建華
(江蘇省常州市第三中學, 213000)
高中階段含絕對值的函數(shù)問題試卷中屢見不鮮,常考查恒成立(能成立)以及取值范圍等問題.學生遇到此類問題往往感到比較棘手.其原因之一是含絕對值問題一般需要分類討論去掉絕對值符號,二是含參數(shù)問題一般需要結(jié)合參數(shù)取值范圍分類討論,而這恰恰是學生的能力薄弱之處.那么如何避免此類痛點?這是一個值得思考的問題.
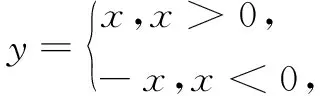
例1已知f(x)=ex|x-a|在(-1,2) 單調(diào)遞增,則實數(shù)a的取值范圍是______.
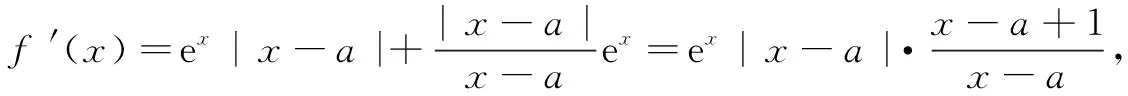
評注本題用常規(guī)解法比較繁瑣,而采用上述方法能避免分類討論,方便了對導函數(shù)的符號判別,起到化繁為簡的效果.
例2對于任意x∈[1,3],不等式x|x-a|+2≥a(a≥1)恒成立,求a的取值范圍.
解問題等價于(x|x-a|)min≥a-2,x∈[1,3].令g(x)=x|x-a|,則
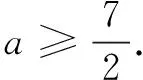
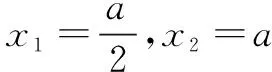
例3設函數(shù)f(x)=(x-a)|x-a|-x|x|+2a+1(a<0),若存在x0∈[-1,1],使f(x0)≤0,則a的取值范圍是______.
解本題是存在性問題,依題意,僅需f(x)min≤0,x∈[-1,1].由絕對值函數(shù)求導策略,f′(x)=2(|x-a|-|x|),即
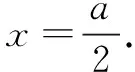
評注該題對原函數(shù)求導后,要確定導函數(shù)f′(x)=2(|x-a|-|x|)的符號,仍需要通過絕對值函數(shù)常規(guī)處理方法,利用分類討論得出導函數(shù)圖象,確定原函數(shù)在[-1,1]的單調(diào)性.
猜你喜歡
初中生學習指導·中考版(2023年9期)2023-09-30 15:22:41
新世紀智能(數(shù)學備考)(2021年11期)2021-03-08 01:08:12
卷宗(2020年34期)2021-01-29 05:36:24
新世紀智能(數(shù)學備考)(2020年11期)2021-01-04 00:38:24
中學生數(shù)理化·高一版(2019年9期)2019-10-12 07:25:44
中學生數(shù)理化·高一版(2019年4期)2019-01-11 19:26:25
新高考·高二數(shù)學(2017年9期)2018-03-16 18:02:26
中央民族大學學報(自然科學版)(2017年2期)2017-06-11 07:14:46
西安工程大學學報(2016年6期)2017-01-15 14:09:32
幼兒智力世界(2016年1期)2016-05-30 10:48:04

