Advances and challenges in DFT-based energy materials design

Jun Kang(康俊), Xie Zhang(張燮), and Su-Huai Wei(魏蘇淮)

Beijing Computational Science Research Center,Beijing 100193,China

Keywords: density functional theory,materials design,energy applications

1. Introduction

To sustain the growing worldwide energy needs, there are strong demands for developing novel materials for energy applications, such as photovoltaics, photocatalysts, thermoelectrics, and battery materials. Such developments require explorations beyond known materials and deep into the chemical space. Since first formulated in 1964–1965,[1,2]density functional theory (DFT) calculations have had an increasing important impact on materials design.[3,4]Material-specific studies during the 1970s and 1980s demonstrated the feasibility to predict material properties withab initioDFT calculations at the atomic scale.[5–8]In the late 1980s,the developments in exchange–correlation functionals greatly improved the accuracy of DFT, and many DFT calculation packages appeared, such as FLAPW[9,10]and CASTEP.[11]Since then,DFT became widely accepted and was applied to a broad range of materials from molecules to solids.

Historically, materials design is usually carried out in a “trial-and-error” manner, inspired by empirical intuitions and rules obtained from known materials. In this paradigm,computations provide retrospective insights into experiments.Experimental groups synthesize and characterize a material and computations help to understand the experimental observations. Theorists take a given material to study its properties and then inform experimentalists if they find a suitable material with good properties for potential applications.With rapid developments over the past six decades, the continuously improving predictive power of DFT is now leading to a paradigm change in collaborations between computation and experiment in modern materials science, towards“materials-by-design”.[12,13]In this new paradigm, the desired functionality is specified first, and DFT calculations are then employed to construct structure-property relationship and to predict completely new and synthesizable materials with the target properties, followed by an experimental validation.Through iterative design and data-exchange cycles between computation and experiment, the accuracy of the prediction model improves,greatly accelerating materials design.

The change of the role of DFT calculations in materials design is,of course,facilitated by the growing computing power,which follows the Moore’s law;but more importantly,it should be attributed to the advances in DFT methodologies that greatly increase the accuracy and enhance the capability of DFT simulations through removal of long-standing approximations and/or extending the simulation scale.For energy materials design, the key physical quantities of concern include stability, band gap, density of states, optical absorption, carrier mobility, thermal conductivity, defect concentration, and ionization, excited-state dynamics, carrier relaxation, and recombination,etc.The construction of reliable prediction models relies on accurate DFT calculations of these key quantities,without which the“materials-by-design”approach is impossible.

The objectives of this perspective are to introduce the methodological advances in the predictive capabilities of DFT for energy materials design, to show examples of how these advances accelerate the discovery of new energy materials,and to discuss challenges and future research directions in computational design of energy materials. We will present state-of-the-art DFT methods for accurate simulation of various key properties of energy materials,including total energyrelated properties, band structure, optical and excited-state properties, transport properties, as well as defect and alloy properties. Then we will provide examples to show how the advances of the DFT-based computational techniques have helped the discovery of novel photovoltaic, photocatalytic,thermoelectric, and battery materials. Finally, we conclude with an outlook on the remaining challenges in DFT methods for energy materials design.

Fig.1. The Jacob’s ladder of DFT.

2. DFT methods for accurate property prediction

The main idea of DFT can be summarized as follows:[1](i)every observable(including energy)of a quantum mechanical system can be written as a unique functional of electron density; and (ii) the ground-state electron density minimizes the total energy functional. The most popular implementation of DFT is the Kohn–Sham (KS) scheme.[2]It assumes that the ground-state electron density of any interacting system can be reproduced by a non-interacting system, and all of the complexities of the electron–electron interaction effects are attributed to the exchange–correlation(xc)energyExc,resulting in the well-known single-particle KS equation.In principle,the KS-DFT is exact. However,the exact form ofExcis unknown yet,and it has to be calculated with approximations.The predictive power of a KS DFT calculation largely depends on the approximations adopted. Development of reliable xc functionals is one of the major issues of DFT research. So far,there have been a huge number of approximated functionals proposed. The levels of sophistication and complexity for different approximations are often represented by the rungs of a ladder,namely,Jacob’s Ladder of DFT[14]as schematically shown in Fig. 1. The three lower rungs are local or semilocal functionals. The local density approximation (LDA)[2,15]employs only the local value of electron density(ρ),while the generalized gradient approximation(GGA)[16]adds the gradient ofρ,and meta-GGA[17,18]further adds the kinetic energy density. The hybrid functionals[19,20]on the fourth rung include a portion of exact exchange energy. On the top rung of the ladder,namely,the random phase approximation(RPA)functionals,information of the unoccupied KS orbitals is also taken into consideration.

In the remaining part of this section,we discuss how the advances in methodology developments eventually improve the predictive power of DFT calculations for the key properties of energy materials,such as total energy related properties,band structure, optical and excited-state properties, transport properties,and defect and alloy properties.

2.1. Total energy related properties

The ground-state total energy is a key quantity that can be directly computed from DFT calculations. The accuracy of the calculated total energy is,to a large extent,a reflection of the predictive power of DFT methods. Extensive tests have been carried out on the performance of various xc functionals in predicting the total energy and related properties such as lattice constant, cohesive energy, and bulk moduli across a broad range of materials.[21–23]A general trend is that the error of the calculated total energy significantly reduces over time, with 3.7 times reduction from 1980s to 2010s,[23]reflecting the advances in the xc functionals(it is also noted recently that, in addition to energy, accurate prediction of electron density should also play an important role in xc functional development[24]). Although the functionals on higher rungs of Jacob’s Ladder are in principle more accurate,this is not guaranteed, and in practice the performance can be casedependent.

In Fig.2 the errors of different xc functionals in the predicted lattice constants, bulk moduli, and cohesive energies for 64 strongly bound solids were plotted(the data were taken from Ref. [21]). It is seen that even the rung 1 LDA can already give reasonable lattice constants, typically with an underestimation of 1%–2%. However, LDA tends to over-bind atoms,resulting in severely overestimated cohesive energy by～20%. The GGA functionals such as the one formulated by Perdew, Burke, and Ernzerhof (PBE)[16]reduce the overbinding of LDA, mostly by more accurate prediction of total energy of isolated atoms and molecules,but with a slight overcorrection.In general,to compare the relative structural stability of a compound,GGA prefers the structure with larger volume, whereas LDA favors the structure with smaller volume.The GGA-predicted lattice constants are typically～1%–2%larger than experimental values, and the cohesive energy is underestimated by～5%. GGA is also found to be more realistic for magnetic solids compared to LDA.[25]Overall, the total energy related properties predicted at the GGA level are fairly good, although higher-rung functionals may have further improvements. In addition, there could be error cancellation when comparing energy differences between different materials. Thus, for strongly bound solids, considering the balance between accuracy and efficiency,the GGA-level functional is often a reasonable starting point. For instance,it has been shown that the phase diagrams for the Cs–Pb–Cl system calculated with GGA and the hybrid functional are quite similar.[26]

Nevertheless, meta-GGA or hybrid functionals may be necessary for specific cases. For example,no GGA can be excellent for both solids and molecules at the same time,[22]and meta-GGA like SCAN[18]should be more suitable for systems involving both finite and infinite systems.The hybrid functionals partially remove the self-interaction error in LDA/GGA and tend to localize electrons, leading to better descriptions of materials with highly localized and strongly correlated d or f electrons. For example, compared to LDA/GGA, hybrid functionals significantly improve the predicted magnetic ground state and magnetic coupling constants of transitionmetal monoxides.[27,28]They can also correctly describe the formation of intrinsic polaronic defects in strongly correlated systems like TiO2.[29]Moreover,hybrid functionals are superior in predicting the band gap,as will be discussed later.

Despite their successes,a major shortcoming of the commonly used functionals at rungs 1–4 is that the long-range van der Waals (vdW) dispersion interactions are formally not included. As a result, for weakly bound systems where dispersion interactions are significant,none of these non-dispersion corrected functionals is able to give qualitatively correct total energies in most cases.[22]There have been many approaches proposed to include the long-range dispersion interaction.One way is adding a posteriori correction, similar to an atomic force field, on top of standard functionals. Examples are the DFT-D[30]and DFT-TS[31]methods. An alternative approach is treating the long-range interaction as explicit nonlocal correlation functionals of the density, such as the vdW-DF[32,33]and rVV10[34]methods. It is also possible to fully account for the dispersion interaction with high-level methods like quantum Monte Carlo (QMC)[35]and RPA to the correlation energy,[36,37]but the applications are currently limited by their high computational costs. With these approaches, the dispersion interactions in weakly bound materials can be described quite well.For instance,the typical error in binding energies of layered materials predicted by the SCAN+rVV10 method is～2%.[38]The accuracy of various posteriori vdW corrections and nonlocal vdW functionals was systematically examined in Ref. [39], with test sets including rare gases, layered solids,and molecular solids. It is concluded that the rev-vdW-DF2 functional leads overall to the best performance.

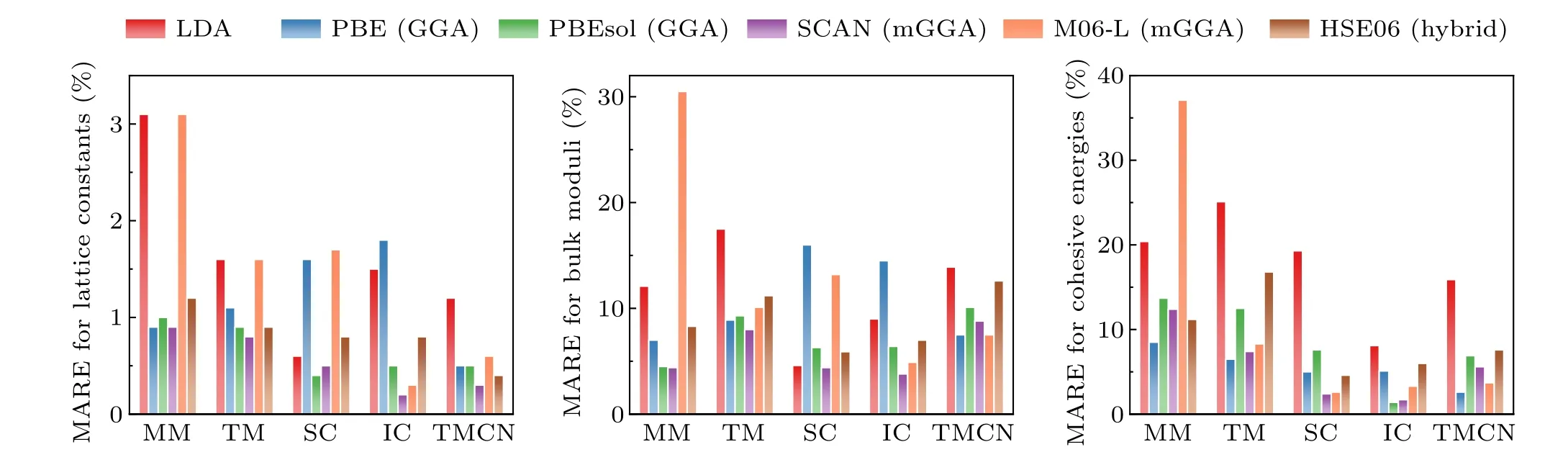
Fig. 2. The mean absolute errors (MARE) in calculated lattice constants, bulk moduli, and cohesive energies using different xc functionals for 64 solids including main-group metals (MM), transition metals (TM), semiconductors (SC), ionic crystals (IC), and transition metal carbides and nitrides (TMCN).Plotted with the data taken from Ref.[21].

When accurate total energy is available, the force and stress can be computed from its derivatives according to the Hellmann–Feynman theorem,[40,41]with a proper treatment of the Pulay force/stress in case the basis is atomic-position dependent. With the total energy, force, and stress, a vast number of materials properties could be evaluated. Structural optimizations can be performed by minimizing the energy or force/stress. The force constant matrix can be obtained by the finite-displacement method[42]or perturbation theory,[43]and used to compute phonon spectrum and vibrational properties.By a careful search of the potential energy surface with methods like nudged elastic band[44]or dimer,[45]one can obtain the minimum energy path and energy barrier for a chemical reaction. Taking all these total energy related properties into account,it is possible to evaluate the stability and efficiency of materials for energy applications.[46,47]

2.2. Band structure

2.2.1. Band gap

In practice, the lower-rung semilocal xc functionals like LDA and GGA are often adopted for a broad range of materials, due to the balance of accuracy and computational efficiency. In many cases they yield reasonable band structures(thus density of states). However,the fundamental band gaps predicted by these functionals, which are usually determined by the eigen-energy difference between the highestoccupied and the lowest-unoccupied KS orbitals, suffer from severe underestimation (see Fig. 3). The typical error is 30%–100%, and sometimes a metallic band structure is predicted for a semiconductor. Correspondingly, the predicted conduction-band minimum (CBM) and valence-band maximum (VBM) positions are incorrect. This band-gap problem of the semilocal functionals is attributed to the lack of derivative continuity[48]and the delocalization error[49]in the xc functionals, which are different for different atomic orbitals.Therefore, the band-gap problem is most severe if the VBM and CBM have very different atomic orbital characters.

One of the solutions to the DFT band-gap problem is hybrid functionals [such as the one developed by Heyd, Scuseria,and Ernzerhof(HSE)[20]],which mix the LDA/GGA functional with exact (and possibly screened) Hatree–Fock (HF)exchange energy. The localization error of the HF exchange largely compensates the delocalization error of LDA/GGA,[49]therefore resulting in much improved band gap. The typical value of the mixing ratio of the HF exchange in the HSE hybrid functional is 0.25, and it can be further tuned to better reproduce experimental band gaps,e.g., using smaller mixing ratio for more covalent materials and larger ratio for more ionic materials.

A more rigorous method is the many-body perturbation theory under theGWapproximation,[50,51]which goes beyond the single-particle DFT framework. In this method the xc functional in DFT is effectively replaced by a nonlocal,energy-dependent self-energyΣ, which is given by integrating over the product of the electronic Green’s functionGand the screened interactionW. In principle, theGW-calculation should be performed self-consistently, and the final result is independent of the starting point, which is often provided by a DFT calculation. However, due to numerical cost and algorithmic difficulties, practical calculations are often carried out with the partially self-consistentGW0scheme where only theGis evaluated iteratively, or with the one-shot, non-selfconsistentG0W0scheme. In these schemes, the results could be dependent on the starting point. In general, theG0W0method works quite well. It has been shown that hybridfunctional calculations could be a good starting point,[52]resulting in a typical error of 2.3% for band gap. While different levels of self-consistency may sometimes lead to better results thanG0W0,systematic improvements over a broad range of materials are not guaranteed. For example, for extended solids,fully self-consistentGWtends to overestimate the band gap due to an underestimation of the dielectric screening,thus the vertex correction inWis important.[53–55]

In Fig. 3 we plotted the calculated band gaps for the SC40 solid test set[20]using PBE,HSE,andG0W0,as well as the experimental values. The data are collected from various literatures.[56–61]It can be clearly seen that the performance of PBE is poor. The slope of the corresponding linear fitting between theoretical and experimental results is only 0.68, far away from the ideal value of 1. HSE andG0W0show significant improvements, with the slopes close to 1, andG0W0performs slightly better.

While providing quite accurate band structures, a major disadvantage of the hybrid functional andGWmethods is their high computational costs. Compared to an LDA/GGA calculation, the required computation time is one to two and two to three orders of magnitude longer for hybridfunctional andGWcalculations, respectively. Many methods have been developed to correct the band-gap problem at a moderate computational cost, such as the DFT+Umethod,[62]meta-GGA-type TB-mBJ potentials,[63]the generalized Delta self-consistent-field method,[64]modification of pseudopotentials,[65]the DFT-1/2 method,[66]and the Wannier–Koopman method.[67]These methods have shown great successes in predicting the band gaps,but may also suffer from certain disadvantages like the lack of self-consistency,the absence of a total-energy formalism,and the ad hoc nature.Careful tests are always recommended when they are applied to a particular material of interest.

Fig.3. Calculated and experimental band gaps for the SC40 solid test set.[20]The data were taken from Refs. [56–61] . Solid lines are linear fits. The dashed line corresponds to =

2.2.2. Deformation potential and band alignment

Once correct band gap and eigenvalues of band edges are available, it is possible to compute other important bandrelated properties such as deformation potentials and band alignment between materials. The deformation potentials reflect the strength of electron–phonon coupling and determine the eigen-energy shift due to volume change. The band alignment between materials affects the carrier distribution and transport across the interface,as well as the dopability of semiconductors. A critical issue in computing these properties is finding a common energy reference,since the DFT-calculated eigenvalues for different material systems cannot be compared directly due to the periodic boundary conditions used in these calculations.

For low-dimensional materials,the vacuum level is a natural choice for the energy reference,[68]but it is absent in bulkmaterial calculations. For bulk materials, a widely adopted method is carrying out an explicit calculation for a heterostructure supercell constructed by the two materials of interest.[69]The atomic core-level or the averaged electrostatic potential at the two sides of the heterostructure can serve as the common energy reference to determine the relative position of the band edges of the two materials. Because of the periodic boundary condition,lattice-match is required at the heterostructure interface when constructing the supercell. If the volume deformation effect is not considered,then this method is only applicable to materials with negligible lattice mismatches. A correction taking into account the absolute deformation potential was later proposed,[70]resulting in improved band offset for materials with small lattice mismatches. Based on the transitivity rule, a three-step approach[71]and its modification[72]were developed to deal with materials with large lattice mismatches and low symmetries. For materials with dissimilar structures,the direct construction of a heterostructure supercell is difficult. In this case, one can construct an intermediate structure that well interfaces with both materials,and a searching algorithm for such structures was reported in Ref.[73]. With these advanced methods, the band offset between materials can be accurately predicted,in good agreement with experiments.

2.3. Optical and excited state properties

2.3.1. Optical properties

The optical property of a material is basically the response of its electron to the light-induced, time-dependent electromagnetic perturbation. The linear optical properties,such as absorption spectrum, reflectivity, and loss function,can all be deduced from the frequency-dependent complex dielectric function.[74]Under the RPA of polarization,which assumes independent particle transitions, one can directly use the DFT-calculated wavefunctions and eigenvalues to compute the matrix elements for optical transitions and then evaluate the dielectric function.[75,76]With LDA/GGA, the static macroscopic dielectric constant is often quite reasonable, but the absorption spectrum is not satisfactory. This can be attributed to the poor description of electron–electron interaction by LDA/GGA and the lack of electron–hole interaction in RPA. The inaccuracy in the electron–electron interaction results in incorrect band gap and eigenvalues as discussed above.This can be greatly improved through the hybrid-functional orGWmethods. The lack of electron–hole interaction can lead to large errors for materials with significant exciton effects,especially for low-dimensional materials where the Coulomb screening is weak.[77]This effect can be included from full solution of the Bethe–Salpeter equation(BSE)[78]built on top of theGWapproximation.[51,79,80]For example, theGW+BSE approach well reproduces the first peak of the imaginary part of the dielectric function of bulk BN, which is not well captured withGW+RPA,as shown in Fig.4(a).[81]

Another class of methods which can be used to calculate the optical properties is based on the time-dependent density functional theory (TDDFT),[82,83]which extends DFT to the time domain. For the time-dependent case, Runge and Gross proved that the one-to-one correspondence between external potential and charge density remains hold, establishing the foundation of TDDFT.[84]According to the linearresponse formalism of TDDFT (LR-TDDFT), the inverse dielectric function for a periodic solid can be obtained from the full response function,[51,85,86]with the latter expressed by the KS response function and a proper xc kernel. The xc kernel is defined as the functional derivative of the timedependent xc potential with respect to the time-dependent density. A correct long-range behavior of the xc kernel is critical for periodic systems.[87,88]Alternatively, within LRTDDFT the optical spectrum can be computed by solving the so-called Casida equation,[82]which treats electric excitations as the eigenmodes of the system.[89]This approach usually works quite well for finite systems like molecules. Beyond the linear response regime, real-time TDDFT (RT-TDDFT)directly propagates the time-dependent KS equation.[90]With RT-TDDFT, the optical spectrum can be computed with the Fourier transform of the time-dependent dipole moment (for isolated systems) or current (for periodic systems) under an external field.[91,92]

Fig. 4. (a) Imaginary part of the macroscopic dielectric function for bulk hexagonal BN calculated with GW+RPA and GW+BSE. Reproduced with permission from Ref.[81]. Copyright 2018 American Physical Society. (b)RT-TDDFT study of plasmon in an Ag55 nanocluster. Reproduced from Ref.[93]in accordance with the Creative Commons Attribution(CC BY)license. Copyright 2015 Springer Nature. (c)NAMD simulation of hot carrier cooling in an Si quantum dot. Reproduced with permission from Ref.[94]. Copyright 2020 American Physical Society.

2.3.2. Excited-state properties

RT-TDDFT provides time-domain evolutions of electronic wavefunctions together with ionic motions, thus it is a powerful tool to study the dynamics of various photoexcited processes [Fig. 4(b)], for example, ultrafast dynamics of photo-excited carriers,[95]optically excited structural transitions,[96]photochemical reaction,[97]light-induced demagnetization,[98]and plasmonic processes.[93]Strategies have also been developed to include critical features like decoherence, detailed balance and trajectory branching properties into the RT-TDDFT Ehrenfest dynamics.[99]For accurate evolution of wavefunctions, RT-TDDFT usually requires a quite small simulation time step at the attosecond scale,which limits the simulation time scale. A great acceleration can be achieved with a recently developed Hamiltonian interpolation technique,which increases the time step to 0.1 fs–0.5 fs.[100]

To further extend the simulation size and time scales of excited carrier dynamics, nonadiabatic molecular dynamics(NAMD)methods are widely adopted,with either the Ehrenfest dynamics[101]or the surface hopping formalism.[102]For condensed matter systems, NAMD is often combined with the neglect of the back-reaction approximation (also called classic path approximation), in which the effect of the wavefunction evolution on the nuclear movement is explicitly ignored, and the nuclear trajectory is generated from the conventional ground-state Born–Oppenheimer molecular dynamics.[103]This leads to considerable computational saving and makes the simulation of systems with several hundred atoms feasible. Many DFT-based NAMD methods with detailed balance and decoherence effect have been proposed,such as DISH[103]andP-Matrix,[94]with successful applications in studying hot carrier dynamics like relaxation[104,105]and transfer,[106,107]as shown in Fig.4(c). NAMD simulation with electron–hole interactions for exciton dynamics has also been realized recently.[108]

2.4. Transport properties

The performance of energy materials strongly depends on their carrier and phonon transport properties. For example,the challenge in improving the figure of merit of thermoelectric materials is how to increase the carrier conductivity and reduce the thermal conductivity at the same time.[109]The design of efficient energy materials thus calls for accurate prediction of transport properties.

2.4.1. Carrier transport

For perfect crystals,the diffusive carrier transport is limited by phonon scattering. In case diffusive transport is dominant,the phonon-limited mobility can be calculated by solving the Boltzmann transport equation(BTE)for the electronic distribution function.[110]Due to its complex integro-differential nature, direct solution of BTE is difficult, thus various approximations are often used to simplify the BTE.One approximation is using a constant relaxation time, either taken as an empirical parameter,[111]or estimated through the effective mass approximation combined with the deformation potential theory,[112,113]but the results are merely qualitative rather than quantitative due to the neglect of detailed scattering events.

A more accurate approach is computing the scattering rate and state-dependent relaxation time fromab initioelectron–phonon coupling(EPC)matrix elements.[110,114]This is quite challenging,especially for semiconductors,since a very denseqgrid in the reciprocal space is required to obtain converged scattering rates. For instance,～106q-points in the first Brillouin zone are needed for Si.[115]The difficulty is overcome by two technical advances. One is the density functional perturbation theory (DFPT), which allows efficient calculations of electron–phonon coupling matrix elements at arbitraryqvectors using a primitive unit cell.[43]The other one is the Wannier interpolation method,with which one can interpolate the matrix elements from more coarse grids.[116]

The approach that evaluates the mobility with EPC from full DFT calculations was first reported for bulk silicon in 2009,[117]and has been successfully extended to other materials in recent years.[118,119]A direct solution of the BTE beyond the relaxation time approximation has also been demonstrated with iterative algorithms.[115,120]Besides phonon scattering, another factor limiting the carrier mobility in realistic materials is the Coulomb scattering due to ionized impurities.This effect can also be included in the BTE,with the impurity scattering potential either described by analytical models,[120]or computed self-consistently with DFT.[117]Considering both phonon and impurity scatterings,the mobility and conductivity can be well described by DFT calculations, as shown in Fig.5(a).

When the size of materials goes down to the nanoscale,the dominant transport mechanism is not carrier diffusion but quantum tunneling. Nanoscale devices are often modeled by a central scattering region connected to left and right electrodes,and the carrier transport is described as a one-dimensional coherent scattering process for the incoming electrons from the electrodes. The problem can be solved by either combining DFT calculations with the non-equilibrium Green’s function method using localized basis sets,[121–123]or by direct calculation of the scattering states using planewave basis sets under auxiliary periodic boundary conditions.[124,125]The latter method,together with a linear scaling algorithm,[126]has been applied to large-scale systems with 4000 atoms.[127]

Carrier transport can also occur between highly localized states,such as the cases of many organic semiconductors and disordered/defective structures. This process can be described by a hopping model using the Marcus theory.[128–130]The required electronic coupling strength and reorganization energy can be obtained from DFT calculations. For disordered/defective structures where a very large supercell is needed,ab initiomultiscale simulations in combination with the Marcus theory have been demonstrated, as illustrated in Fig.5(b).[131,132]

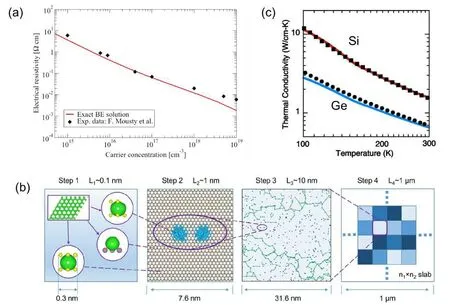
Fig.5. (a)The calculated electrical resistivity of Si at 300 K as a function of carrier concentration from exact solution of BTE.Reproduced with permission from Ref. [120]. Copyright 2016 American Physical Society. (b) A multiscale model used to study the hopping transport in defective 2D material combining DFT calculations with the Marcus theory. Reproduced with permission from Ref. [132]. Copyright 2020 American Chemical Society. (c) Lattice thermal conductivities of Si and Ge calculated by solving phonon Boltzmann equation. Blue and red lines are calculated values, and squares and dots are experimentally measured values. Reproduced with permission from Ref.[133]. Copyright 2007 AIP Publishing.

2.4.2. Thermal conductivity

Thermal conductivity is an important fundamental property of materials. For semiconductors, lattice thermal conductivity dominates,and now it can be theoretically predicted by advanced DFT methods. For perfect crystals at low temperatures, thermal conductivity can be accurately calculated by solving the BTE for phonon transport with phonon spectrum and anharmonic interactions from DFT, as shown in Fig.5(c).[133–135]The size effect in this method is minor thus one can use a small unit cell. However, it is not suitable for cases where anharmonicity is rather complex, such as amorphous materials and liquid which are highly disordered, or high-temperature conditions under which higher-order anharmonicity becomes important.

Another class of methods is based onab initiomolecular dynamics(MD),in either a nonequilibrium or an equilibrium manner.[136]In principleab initioMD simulation contains full anharmonic interactions and can be applied to arbitrary temperatures. Disorder can also be included with reasonable construction of supercells. In the nonequilibrium MD approach one simulates the heat flux directly using a sustained temperature gradient, and then obtains the thermal conductivity by applying Fourier’s law.[137,138]However, it suffers from huge size effects since a rather large supercell is needed to get a reasonably small temperature gradient. Therefore, extrapolation to infinite supercell length is usually required.[139]

In contrast,the equilibrium MD-based Green–Kubo(GK)method has a weak system-size dependence.[140,141]It relates the thermal conductivity with the heat current autocorrelation function (HC-ACF) through the dissipation-fluctuation theorem. Due to the ill-definition of heat current in DFT calculations of periodic systems, for a long time, the applications of the GK method were limited to force-field Hamiltonians. This ill-definition problem has been overcome recently by several works.One approach is evaluating atom-decomposed DFT energy and then using a two-step integration method in MD.[142]Other solutions include converting the position operator into the well-defined commutator between the position operator and the Hamiltonian,[143]and quantum-mechanically defining a stress tensor for each atom.[144]

2.5. Defect and alloy properties

2.5.1. Defect properties

Defect control is one of the most important issues for energy materials. In the past few decades,the basic formalisms of point-defect modeling through DFT calculations have been established with great successes. The formation energy ΔHfof a defect characterizes how easily it can be formed. Under thermodynamic equilibrium conditions,the defect concentrationnDat temperatureTfollows the Boltzmann relation,nD=Nexp(-ΔHf/kBT),whereNis the available lattice sites in the host per volume. As illustrated in Fig.6,the formation energy ΔHf(α,q)for a particular defectαwith charge stateqis calculated by[145,146]

whereE(α,q)andE(host)are the total energies of the defective and pristine materials in a supercell,respectively.EVBMis the host VBM energy, andEFis the Fermi energy referenced to VBM.niis the number of atomiexchanged with the reservoirs to create the defect in the host.The chemical potentialμiinvolves the effects of growth environments. Thermodynamic equilibrium growth requires that the host material is stable,and there is no elemental precipitates or secondary phases,thusμiis confined in a finite range by these conditions. By considering surfaces and edges also as“defects”,the formula of defect formation energy can be further extended to calculate surface/edge energy.[147]It should be noted that when determining the available range of the chemical potentials, it is critical to consider all possible competing phases and dissociation paths,otherwise the stability of the host material would be overestimated,[148,149]and the trends of the defect formation energy might be qualitatively wrong. The defect charge transition energy level is defined as theEFat which the formation energies of a defect in two charge statesqandq′are equal,namely,ε(q/q′)=[E(α,q)-E(α,q′)+(q-q′)EVBM]/(q′-q). With ΔHfandε, the equilibrium Fermi level and carrier density can be self-consistently evaluated by considering charge neutrality condition.[150]Computational frameworks to automate the calculations of these defect properties have been developed recently.[151–153]

A major impact of defect is that it can capture carriers and cause nonradiative carrier recombination. The carrier capture is a multi-phonon assisted electronic transition process.[154–156]The capture rate can be computed from DFT calculations,[157]and used to identify detrimental defects.[158,159]The key issue here is the calculation of electron–phonon coupling matrix for a large supercell containing defects. A direct calculation using the finite displacement method or DFPT is expensive. Efficient calculations can be realized by a variational approach[160]or using a onedimensional effective phonon mode.[161]There have also been applications of NAMD to the calculations of carrier capture rates,but a proper rescaling of the carrier and/or defect densities to realistic values is critical.[162]

Fig.6. A schematic illustration of defect formation energy calculation.

To achieve high accuracy in practical defect simulations,it is important to adopt a proper level of DFT methods[bare-DFT, hybrid,GW, spin–orbit coupling (SOC),etc.] that can correctly describe the structural and electronic properties of the material of interest. For example, to accurately calculate the structure and transition levels of certain intrinsic defects in halide perovskites,one has to use high-level xc functionals together with the SOC effect to obtain proper band-edge positions,otherwise there could be qualitative errors.[26,163–166]

Another important issue is how to appropriately take into account the finite-size effect for charged defects. This effect originates from the unphysical electrostatic interaction among the defect, its periodic images, and the compensating background jellium charge.The resulting error can be huge for systems with weak dielectric screening,and sometimes may even lead to divergence in the calculated formation energy (such as the case of 2D materials.[167]) For bulk materials, widely used corrections include the Makov–Payne scheme(MP),[168]the Lany–Zunger scheme (LZ),[169]and the Freysoldt–Neugebauer–Van de Walle scheme (FNV).[170]Their performances have been systematically investigated.[171]The MP correction works well for defects with point-like charge density, but leads to overcorrections for defects with more extended charge density. The LZ approach undercorrects the formation energy for point-like defect states,but improves the results for defects with less localization. The FNV scheme leads to overall meaningful formation energies, and it is also extended to low-dimensional systems.[172]However,all these three methods adopt a macroscopic dielectric constant/profile,which is adjustable and does not give information of microscope screening effects. There have been efforts to avoid the use of such parameters by using a rigorous defect screening model,[173]or self-consistent potential correction.[174]Especially,by replacing the virtual jellium state with realistic host band-edge states,a physical,straightforward,and dimensionindependent universal model to calculate the formation energy of charged defects was recently demonstrated.[175]

2.5.2. Alloy properties

Most of the calculation methods described above are for materials with periodic boundaries. For the simulation of random or disordered alloys without a periodic boundary,a key issue is how to construct a proper supercell to describe the chemical disorder so that standard DFT calculation methods can be applied. The simple approaches are the virtual crystal approximation (VCA),[176]which describes the alloys using single type of hybrid atoms that are composition-averaged mixture of atoms in the parent compounds,and coherent-potential approximation(CPA),[177]where all atoms with the same chemical types are assumed to be equivalent and each is embedded in a structureless averaged uniform medium.The VCA or CPA is computationally efficient since one can use a parent primitive cell for the calculation, but at the price of ignoring any possible short-range order and local atomic distortion, which could be critical in determining alloys properties.[178]These effects can be captured by the special quasi-random structures(SQS).[179,180]The SQS are periodic finite-size supercells, in which the atomic correlations between neighboring sites best match those of the fully random structures,and have been successfully applied to predict various alloy properties, such as elastic constants,[164]band bowing,[181]and doping.[182]Similar approaches can also be used for partially disordered alloys with short-range order.[183]

3. DFT-guided design of energy materials

The above DFT-based approaches,with increasing accuracy and predictive power, allow efficient design and exploration of novel energy materials. Very often this process is combined with high-throughput screening towards target properties and/or predictive models constructed via machine learning. In this section we first briefly discuss the typical routes for computational materials design and then present representative examples of energy materials design guided by advanced DFT calculations.

3.1. Routes for computational materials design

There are three typical routes for computational materials design: (i) knowledge-based materials design, (ii) highthroughput materials design,and(iii)genetic algorithm-based materials design. We illustrate the three routes in more detail in the following.

3.1.1. Knowledge-based materials design

This is a conventional approach to materials design. In order to design novel materials for a specific application, we focus on one or few of the prototypical materials that have been identified and demonstrated for the application in earlier experiments. Then,we thoroughly compute and analyze their basic properties with the aim to establish the correlations between structure,composition,and properties. Using the identified correlations,we could then design new structures and/or new compositions that yield certain properties required by the application of interest.

3.1.2. High-throughput materials design

With the rapid developments in DFT calculations and computer power, the basic materials properties become more easily accessible,leading to the construction of numerous materials databases,e.g., the Materials Project.[184]Very often,it is already clear that for a specific application what the requirements for the basic properties are. Hence,we could build up a series of selection/filtering criteria,and then use them to screen a large materials database,which would likely lead to a small set of materials candidates for the target application.For these newly identified materials,we can perform more refined calculations and narrow down to a few of the most promising candidates, which can be transferred to experimentalists for verification and demonstration.

3.1.3. Genetic algorithm-based materials design

High-throughput materials screening relies largely on the availability of materials databases. Even if one could compute such a database of their own, one needs input structural and compositional information from established structural databases,e.g.,the Inorganic Crystal Structure Database(ICSD). However, when these databases are not available,there is also an alternative approach that one can use for the design of novel materials,which is based on the genetic algorithm (GA). Inspired by Darwin’s idea of evolution, we may think of the design of novel materials for a target application as finding the ideal solutions to a difficult optimization problem(that is defined by an optimizable objective function).[185]Starting from a population of materials candidates (if unknown,they could also be random structures or compositions),selection, crossover, and mutation operations can be applied to generate a new generation of materials. Keep repeating this procedure,the objective function gets optimized,which yields promising material candidates after many generations.

Although we discussed the three routes separately, we note that the three routes are not mutually exclusive. In fact,they can be well combined to accelerate materials design.For instance, the construction of selection criteria relies on knowledge extracted from extensively studied known materials. Very often,even before the high-throughput screening,it might be already clear that some material compositions can be simply excluded based on common sense or established knowledge. In this case, it is unnecessary to perform firstprinciples calculations, which might save lots of time and effort. The identified materials from high-throughput screening may also require detailed computations and investigations,which may serve as a feedback loop that allows to optimize the screening process. For the GA-based route,the initial population may also come from the candidates identified from the first two routes.

Another issue worth noting is that it could be beneficial to introduce certain degree of flexibility to the criteria of material screening in high-throughput calculations. For example,a material is typically considered to be unstable if the formation energy is calculated to be positive. However,there could be inaccuracy in DFT calculations,leading to an overall shift of the computed formation energy. In this case the calculated trend in the formation energy is more informative,rather than the absolute value. In addition, for materials with positive but small formation energies, experimental synthesis remains possible.[186,187]Thus, a reasonable choice of the screening criteria based on common sense or established knowledge of systematic calculation errors is important for efficient materials design.

3.2. Examples for DFT-guided design of energy materials

In this section, we present selected examples for DFTguided design of various types of energy materials,including photovoltaic,photocatalytic,thermoelectric,and battery applications.

3.2.1. Photovoltaic materials

Solar absorber plays a vital role for the efficiency of a photovoltaic device. The design of stable and efficient solar absorbing materials is key in realizing high-performance solar cells. We first present an example to illustrate how we can make use of established knowledge to design novel efficient solar absorbers.

Yuet al.[188]tackled this challenge by analyzing a key metric — the spectroscopic limited maximum efficiency(SLME)[189]for various I–III–VI materials. One interesting finding was that comparing to the case of Tl occupying the III sites and Cu occupying the I sites in I–III–VI compounds,the SLME increases when Tl changes from high-valence Tl3+to low-valence Tl+by occupying some of the I sites. Careful investigations revealed that the origin of this enhancement is because for the materials with low-valence Tl,there is a considerable contribution of Tl s orbital hybridization in the VBM,and the CBM is characterized by Tl p orbitals. As the major character of the VBM is still Cu d states,both d→p and s→p transitions are possible,which enhances solar absorption.

Tl is rare and toxic, but the knowledge established here inspired to design Cu–V–VI materials,in which group-V elements could have both +5 and +3 oxidation states, mimicking the effect of Tl. Hence,Yuet al.investigated the SLMEs for different Cu–V–VI compounds,through which they found seven compounds that have comparable or higher SLMEs than CuInSe2[Fig.7(a)].

To further validate the theoretical predictions, they compared the theoretically computed band gaps[Fig.7(b)]and absorption spectra [Fig. 7(c)] against experimental results. The band gaps exhibited only an average of 0.15-eV deviation from the experimental gaps. The absorption profiles were also similar between theory and experiment, which further demonstrated that Sb in the low-valence state leads to a strong absorption.

The above example nicely illustrates how to employ knowledge derived from careful investigations of known materials to design novel high-absorption compounds. However,in this example we have not taken into account another two requirements for a high-performance solar absorber: stability and tolerance to defects. We use another two examples to demonstrate these two aspects.

Lead-halide perovskites are known for their highly efficient solar absorption. However,they suffer from severe instabilities and toxicity due to the presence of Pb. To overcome these issues,Zhaoet al.[190]proposed to search for stable and non-toxic halide perovskites through cation transmutation. As shown in Fig.8(a),one can double the formula of a cubic perovskite APbX3and then replace the two Pb2+cations with one metallic cation in the 1+oxidation state and another in the 3+oxidation state,forming the so-called double perovskite. Such atomic transmutation can greatly enhance the Coulomb energy of the system,thus making the materials more stable.

To have optimal absorption efficiencies, Zhaoet al.focused on materials with band gaps in the range of 0.8 eV–2.0 eV [Fig. 8(b)]. For good thermodynamic stabilities, they excluded materials with negative decomposition enthalpies.In addition, they took into account electron and hole effective masses, both of which should be smaller than 1.0m0. The small carrier effective masses are beneficial for ambipolar carrier conduction and carrier extraction. Exciton binding energies were limited to be lower than 100 meV in order to avoid the formation of excitons. Using these criteria, they identified 14 candidate materials. Excluding three compounds that contain toxic element Tl,11 optimal compounds were found.

The absorption spectra of the 11 compounds were calculated and depicted in Fig.8(c). Despite the differences in the absorption onset, all of these materials exhibit strong absorption profiles that compare well with that of the prototypical Pbbased hybrid perovskite CH3NH3PbI3(or MAPbI3). Among the 11 compounds, there are two materials with ideal direct band gaps: Cs2InSbCl6(1.02 eV)and Cs2InBiCl6(0.91 eV),for which they further computed the SLMEs as shown in Fig.8(d). Clearly,the SLMEs of these two materials are similar to that of MAPbI3, demonstrating their promise in being highly efficient solar absorbers.

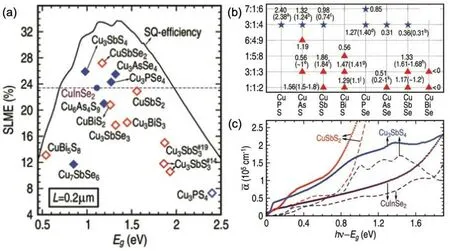
Fig.7. (a)Theoretically computed SLMEs for Cu–V–VI compounds. (b)Accurate band gaps for Cu–V3+–VI (red triangles)and Cu–V5+–VI (blue stars)compounds with V =P, As, Sb, Bi, and VI =S, Se, computed using G0W0, which are compared with available experimental data in parenthesis. (c)Theoretically computed(dashed lines)and experimental(open circles)absorption spectra for CuSbS2,Cu3SbS4,and CuInSe2. Reproduced with permission from Ref.[188]. Copyright 2013 Wiley.

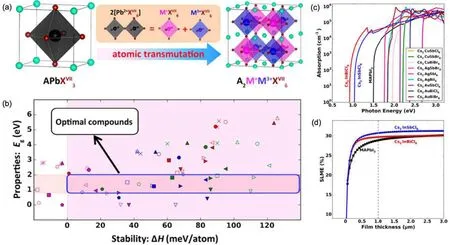
Fig. 8. (a) Candidate double-perovskite materials obtained through atomic transmutation. (b) Identification of optimal compounds based on band gap and stability. (c)Computed absorption spectra of the optimal compounds obtained from the screening. (d)Simulated SLMEs of Cs2InSbCl6 and Cs2InBiCl6 in comparison with CH3NH3PbI3. Reproduced with permission from Ref.[190]. Copyright 2017 American Chemical Society.

Fig.9. (a)Workflow for the materials search. (b)Information for the candidate materials identified from the high-throughput screening. (c)Crystal structure of the most stable compound MnAg(SeO3)2. Reproduced with permission from Ref.[183]. Copyright 2019 American Chemical Society.

Maximally absorbing sunlight is necessary, but does not guarantee excellent solar conversion efficiency, for which we also need to consider the loss mechanisms during energy conversion. For solar cells, one major energy loss is due to the presence of deep-level defects that induce carrier recombination,leading to energy dissipation in the form of phonons,i.e.,heat.[191]By compiling various experimental data from the literature, Dahliahet al.[192]showed that for the same material composition the experimental solar conversion efficiency can be quite different from the theoretical ones, which, to a large extent,is due to the ignored impacts of defects in the material.

Hence, to design solar absorbers that will more likely to enable high power conversion efficiencies, Dahliahet al.[192]further included defect-assisted nonradiative recombination in their high-throughput screening process. They employed the configuration coordinate diagram to study the charge-state transitions of point defects, which allows to analyze and compute the electron and hole capture barriers and coefficients.[161]The capture coefficients can be further employed to estimate the theoretical efficiency with the impacts of defects considered.

Using this improved screening scheme for more than 7000 Cu-based materials in the Materials Project database,Dahliahet al.identified handful defect-tolerant solar absorbers. Most notably, K3Cu3P2and Na2CuP exhibit not only high theoretical efficiencies,but they are also earth abundant as indicated by their low Herfindahl–Hirschman index(HHI),[193]making them very strong candidates for potential high-performance solar absorbers.

High-throughput screening relies critically on the availability of accurate materials properties computed using DFT.DFT calculations are overall expensive.For commonly known materials, one can make use of publicly available databases such as the Materials Project. However, for many new materials,one would have to compute the required materials properties by themselves. This can be very expensive if one aims for a large number of structures and chemical compositions.To address this challenge,one can combine machine learning with high-throughput screening.

As shown in Fig. 9(a), Davieset al.[194]built a statistical model to predict the band gap from chemical compositions based on supervised machine learning. By making use of the machine-learning model,Davieset al.could efficiently screen more than one million quaternary oxides,through which they have successfully identified four materials(two of them have the same chemical composition,but are different polymorphs)as shown in Fig.9(b).These four materials are thermodynamically stable or metastable,and have direct band gaps in the visible range of the solar spectrum. Figure 9(c)shows the crystal structure of one of the candidate materials MnAg(SeO2)2.One can see that the chemical composition and the corresponding crystal structure are relatively complicated; without efficient machine-learning algorithm to accelerate the high-throughput workflow,it is very challenging to identify promising yet complex materials like the ones found here.

3.2.2. Photocatalytic materials

In addition to solar cells which covert solar energy to electrical energy, photo-induced water splitting is another way to utilize the sunlight by converting solar energy to chemical energy. However, to achieve high conversion efficiency, photoelectrocatalysts for the oxygen evolution reaction(OER)in water splitting are critical.[195]Through experimental efforts of multiple decades, only 16 metal-oxide photoanodes were found, which have band gaps in the desired range of 1.2 eV–2.8 eV. Apparently, this is a challenging and costly task. By combining theory and experiment in a high-throughput fashion, Yanet al.[196]developed a very efficient computational approach to the design of novel photocatalysts,which successfully yielded 12 new photocatalysts for the OER in water splitting.

They approached this challenge by first carefully analyzing known photoanode materials such as monoclinic BiVO4[197]andβ-Mn2V2O7[198](even thoughβ-Mn2V2O7is not photoactive for the OER, it has a suitable band gap of 1.8 eV).One feature in common between the two materials is the existence of a VO4structural motif,in which hybridization between V 3d orbitals and O 2p orbitals leads to a desired band gap and a suitable VBM energy level(EVBM). This inspires a hypothesis that the presence of VO4motif is a common feature in ternary vanadates that are potentially suitable for being photoanode materials in water splitting.

Motivated by this hypothesis, Yanet al.[196]designed a high-throughput screening scheme. Starting from more than 6.6×104ternary vanadates with VO4motif in the Materials Project, they first used DFT calculations to search for the compounds with suitable band gaps, stabilities, andEVBM,which resulted in 34 candidate materials. Further, they carried out experimental characterizations of these materials to verify their applicability to photocatalysts for the OER in water splitting. In the end, 15 materials passed through the screening, which also triggered lots of follow-up experimental studies.[199–205]For instance,the photoelectrocatalytic performance ofβ-Cu2V2O7was experimentally evaluated by Songet al.;[206]a solar-to-hydrogen efficiency of 16% was demonstrated.

They also analyzed the relation between the VBM position and the O 2p band character at the VBM for the newly identified materials. They found that both the band gap andEVBMcan be tuned in a broad range through changing the VO4band-edge character. This demonstrates flexible and tunable properties of these materials,making them very promising materials for photoelectrocatalysts in water splitting.

This example here again nicely shows how to combine knowledge extracted from known materials and highthroughput screening to achieve successful materials design.In this case,the authors identified the structural motif by their physical intuition and careful analyses of the existing materials. However,this process is non-trivial and very often rather challenging. However, one can actually more systematically search for “descriptors” that could well characterize the photocatalytic(or other applications related)performance.

For instance, employing symbolic regression Wenget al.[207]systematically derived a simple descriptor for the OER performance of various perovskite oxides. As shown in Fig.10(a),they first synthesized a number of oxide perovskite catalysts and characterized their OER activities. Based on the obtained activity data and selected materials features,they performed symbolic regression for the datasets using different descriptors; the descriptors were generated by combining materials parameters in different mathematical forms, as implemented in the genetic programming code gplearn.[208]

Figure 10(b) shows the mean absolute errors (MAE) of the descriptors at different levels of complexities. One can see that descriptorC(μ/t)can best balance between simplicity and accuracy, whereμandtare the octahedral and tolerance factors,respectively. Using this new descriptor,one can nicely capture the chemical trend of the potentials of the oxide perovskite catalysts(VRHE)using a linear correlation with the descriptor,even for materials beyond the ones synthesized by the authors(i.e.,the ones used for the symbolic regression)[see Fig.10(c)].This demonstrates the predictive capability of the descriptor and the reliability of its linear correlation withVRHE.

With the newly derived descriptor, Wenget al.further screened a large compositional space for oxide perovskite catalysts as shown in Fig. 10(a). By doing so, they identified 13 potential candidates for enhanced OER activity, and managed to successfully synthesize and characterize five of them. Impressively, four out of the five new materials (including Cs0.4La0.6Mn0.25Co0.75O3, Cs0.3La0.7NiO3,SrNi0.75Co0.25O3, and Sr0.25Ba0.75NiO3) exhibited the highest intrinsic activities among oxide perovskite catalysts. This example again nicely shows the powerfulness of machinelearning techniques in accelerating the DFT-guided materials design.

Fig.10. (a)Workflow for the identification of OER descriptors. (b)The mean absolute errors(MAE)versus complexity for 8640 mathematical formulas,and the well-performing ones at different levels of complexities. (c)Performance of the descriptor μ/t in determining the potential relative to reversible hydrogen electrode(RHE).Reproduced from Ref.[207]in accordance with the Creative Commons Attribution(CC BY)license. Copyright 2020 Springer Nature.

3.2.3. Thermoelectric materials

Thermoelectric materials can make use of temperature gradient and convert it into electricity, and thus they are also promising energy materials for applications such as power generation and refrigeration.

The efficiency of a thermoelectric material is determined by a number of materials properties,including electrical conductivity (σ), thermal conductivity (κ), and Seebeck coefficient (S). The efficiency is also temperature (T)-dependent.Hence,a figure of meritzTis defined to characterize the maximum energy conversion efficiency of a thermoelectric material,namely,[209,210]

To design efficient thermoelectric materials, there are multiple target properties required,and there often exists a trade-off between some properties.For instance,high electrical conductivity and low thermal conductivity cannot be easily achieved simultaneously. These complications make the computational design of novel efficient thermoelectric materials difficult.

Recently,Zhanget al.[211]systematically implemented a package for inverse design of materials by multi-objective differential evolution(IM2ODE),which is based on the GA algorithm and supports both single-objective and multi-objective optimizations[see Figs.11(a)and 11(b)]. Each candidate solution to the objective function is considered as a vector in the multidimensional space. As discussed above, three types of operations on the vectors(mutation,crossover,and selection)are involved during the evolution process.

By using the GA algorithm as implemented in the IM2ODE package, Yanget al.[212,213]successfully identified two new thermoelectric materials: SiS and SiSe monolayers with the Pmma symmetry [see Fig. 11(c)]. These two materials are comprised of earth-abundant and non-toxic elements,and exhibit attractive thermoelectric performance because of intrinsically low thermal conductivities and high power factors(σS2). The low thermal conductivity is due to low electron–phonon scattering, and the high power factor is primarily a result of the high density of states in the vicinity of the band edges[see Fig.11(d)]. Combining these advantages,the finalzTvalues are greater than 1 over a wide range of temperatures,and may even exceed 2.

Fig.11. Two differential evolution processes in the IM2ODE package: (a)single-objective optimization and(b)multi-objective optimization. Reproduced with permission from Ref.[211]. Copyright 2015 Elsevier. (c)Crystal structure of Pmma SiS(or SiSe). (d)Thermoelectric performance of Pmma SiS and SiSe at different temperatures. Reproduced with permission from Ref.[213]. Copyright 2017 American Chemical Society.

3.2.4. Battery-cathode materials

After energy conversion have been successfully realized,we still need materials for energy storage,for which batteries are a key technology. Currently, Li-ion batteries have been successfully commercialized and used in various electronic devices and electrical vehicles. However,the abundance of Li on earth is relatively limited. In particular, with the rapid development of electrical vehicles in recent years,the Li demand and consumption have dramatically increased. The search for alternative battery cathode materials is extremely important and useful.

Zhanget al.[214]developed an effective scheme to screen cathode materials for Na-based batteries. Among the known Na-based cathode materials,Na-bearing layered materials are of particular interest, since they allow fast and reversible intercalation of Na ions without pronounced lattice distortions.As shown in Fig.12(a), Zhanget al.formulated a simple but effective algorithm to extract Na-containing layered materials from the Materials Project database. By doing this, they obtained more than 150 candidate materials,which cover a variety of space groups(38 in total)[Fig.12(b)].

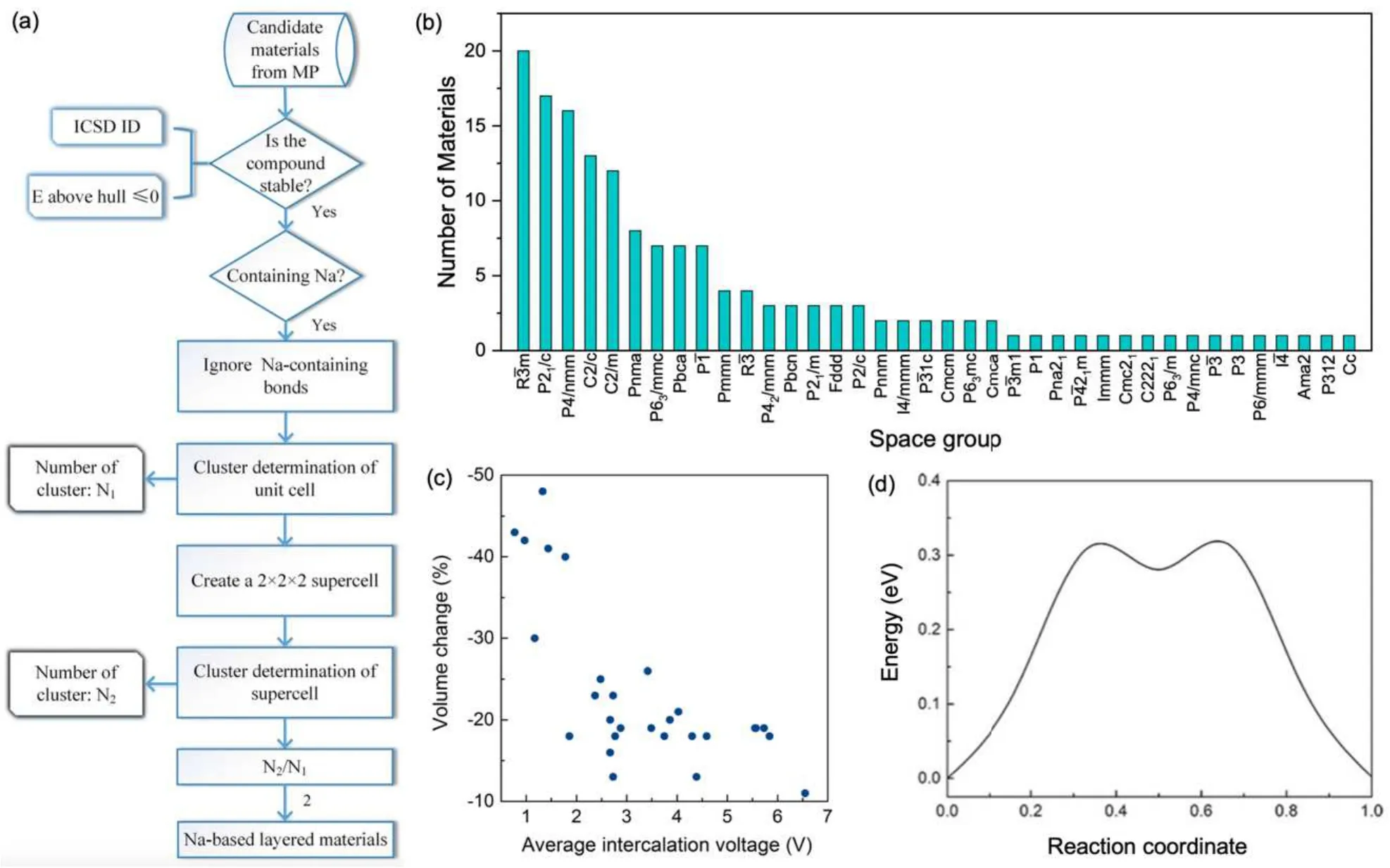
Fig.12. (a)Workflow for the high-throughput search of Na-battery cathode materials. (b)Distribution of the materials space groups. (c)Correlation between the volume change due to Na de-intercalation and the average intercalation voltage. (d) Na interlayer migration barrier in NaCoO2. Reproduced from Ref.[214]in accordance with the Creative Commons Attribution(CC BY)license. Copyright 2018 Springer Nature.

In addition to basic thermodynamic consideration, there are more factors that need to be taken into account, such as volume change due to Na de-intercalation, average intercalation voltage, and Na ion migration barriers. As shown in Figs. 12(c) and 12(d), Zhanget al.further filtered the candidate materials based on the three additional properties. In the end, they identified a number of promising cathode materials for Na–ion batteries,including Na(CuO)2,NaTiF4,Na2Zr(CuS2)2, Na3Co2SbO6, and Na2Cu(CO3)2. These materials have suitable voltages, high capacities, low volume changes during Na intercalation/de-intercalation, as well as small Na diffusion barriers. This finding could then serve as a guide for experimentalists to synthesize these materials of great promise,boosting the development of Na-ion battery technology.

4. Summary and outlook

In summary, we show that the rapid developments in computational methodologies and computer power greatly enhance the predictive power of DFT calculations for various key properties of energy materials, and result in the discovery of many novel materials for potential energy applications.There is no doubt that the robustness and accuracy of DFT prediction will continuously improve in the future,e.g., with the development of better DFT functionals that are accurate for both molecules and solids and betterGWapproaches that have less dependence on the DFT calculated input parameters. We expect a growing number of successful applications of DFT calculations to practical developments of energy materials will emerge. Nevertheless,there remain challenges regarding how to make DFT simulations closer to real materials and conditions, in terms of length- and time-scales, material complexities, and temperature. Here we discuss a few topics of potential interest for future studies.

(i) How to extend the length- and time-scales of DFT simulations towards realistic experimental conditions? Due to the O(N3) scaling, the system size of conventional DFT calculations is usually limited to＜103atoms, and the timescale is typically on the order of picoseconds. However, energy conversion involves many physical processes with different length- and time-scales, which can go beyond the capacity of conventional DFT calculations. To extend the length-and time-scales,it is desirable to develop linear-scaling DFT methods.[215]A few examples of such methods are the charge patching method[216]and the linear scaling 3D fragment method,[126]which can deal with structures containing over 104atoms at moderate computational costs.[217,218]Another promising approach is combining machine learning techniques with DFT inputs. MD simulation of 100 million atoms with machine learning force fields has been demonstrated,at a speed of one nanosecond per day.[219]In low-dimensional materials with inhomogeneous deformation such as torsion and bending,translational symmetry is missing,thus an extremely large supercell is required for direct DFT calculations. In this case, the generalized Bloch method could be a good choice,which considers the helical symmetry and rotational symmetry to deal with torsion and bending, allowing the simulations of deformed structures with a relatively small repeating cell.[220,221]

(ii)How to take into account different types of disorder or partial order/disorder in complex materials? The flexibility in materials design and emerging new properties of structurally and compositionally complex materials facilitate their applications in energy conversion.The increased complexity often results in structural and chemical disorder. It is important to develop algorithms to efficiently generate accurate models to describe the disorder,e.g.,the SQS for multicomponent systems,and amorphous structures. To investigate partial short-range or long-range disorder,the concept of SQS can be extended to special quasi-disordered structure(SQDS),whose correlation functions best match those of the target structure with partial order/disorder. There are also conceptual challenges in defect simulations of disordered or partially disordered materials,such as the definition of defects in this case,[222]and how to conduct the statistical averages over site-dependent defect properties.

(iii) How to properly include temperature effects during property prediction? Standard DFT ground-state calculations only yield properties at 0 K. Temperature is a key factor affecting the performance of energy materials. Some materials that are unstable at 0 K can be stabilized by vibrational or configurational entropies.[223]Entropy also plays important roles in chemical reactions. In addition, lattice anharmonicity could be greatly enhanced by temperature.[224,225]Developments of methods considering these temperature effects are highly desirable.[226,227]

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant Nos.12088101,11991060,12074029,52172136,and U1930402).