Quantum simulation of τ-anti-pseudo-Hermitian two-level systems
Chao Zheng(鄭超)
Department of Physics,College of Science,North China University of Technology,Beijing 100144,China
Keywords: quantum simulation,linear combination of unitaries,non-Hermitian,anti-pseudo-Hermitian
1. Introduction
Non-Hermitian (NH) systems, closely relating to open and dissipative quantum systems,[1–9]are more common in real physical world than closed Hermitian systems, and are attracting increased research interest in recent decades. The featured properties of NH systems enlighten various investigations both in fundamental researches and in applications.[10–33]parity-time-reversal (PT) symmetric systems and the antisymmetric counterparts can be investigated experimentally in different physical systems by different methods, such as NMR,[34]optical micro-cavities,[35]photons–magnons coupled optical systems,[36]quantum photonics,[37]metalsemiconductor complex systems,[38]other optical systems,[39]etc.
Besides thePTsymmetric systems,[11–17]pseudo-Hermitian (PH) systems,[10,18–22,40–46]and their antisymmetric counterparts,[31,47–58]a class of NH systems ofτ-anti-pseudo-Hermitian (τ-APH) Hamiltonian was defined and investigated in 2002.[21]Both theτ-APH and its antilinear operatorτrelevant to the symmetry are important to thoroughly investigate the sufficient and necessary conditions of an NH Hamiltonian having real spectrums.[21]
Obeying Feynman’s thinking that nature should be simulated by itself,[59]quantum simulation has become an efficient way to investigate various phenomena and properties by controllable quantum systems. Besides Hermitian systems,[60–71]NH systems can be investigated effectively and efficiently in the way of quantum simulation, such asPT-symmetric andP-pseudo-Hermitian systems,[34,37,72–76]their anti-symmetric counterparts,[40,57,58]and other novel systems.[77–79]
In this work, we investigate quantum simulation ofτanti-pseudo-Hermitian two-level systems, proposing in detail both for a general case and for special cases that theτbeingTandPT. We use linear combination of unitaries (LCU) in the scheme of duality quantum computing[80]and the unitaryexpansion(UE)technique[6,7]to achieve the quantum simulation in an indeterministic way, optimize the quantum circuit,and calculate the success probability. At last,we discuss how to generalize our method to simulate a generalτ-APH highlevel system,and suggest experimental systems for implementation in the near future.
2. The τ-anti-pseudo-Hermitian symmetry
Aτ-APH HamiltonianHτ, defined by Mostafazadeh,[21]satisfies

?ξandζ ∈?.τcan be the time-reversal (T) operator,parity-time-reversal (PT) operator, etc. Notice that the antisymmetry of the PH Hamiltonian introduced in Ref. [40] is relevant to a linear Hermitian automorphism(such as the parity operatorP),so it is completely different from theτ-anti-PH Hamiltonian that relevant to an antilinear anti-Hermitian automorphismτ[21]we investigate in this work.
3. The τ-APH two-level systems
SinceP,Tand their combinations are basic symmetries attracting increased research interest,[81–85]we illustrate the NH systems by specifyingτas operatorsTandPTin twodimensional cases. Notice thatPT-anti-pseudo-Hermiticity andPT-symmetry are two distinguishable symmetries, of which Hamiltonians can be classified by the relevant mathematical relations of symmetries, i.e.,PTH(PT)-1=HandPTH?(PT)-1=H,respectively.
3.1. τ =T
In the two-dimensional case,the general form ofT-APH HamiltonianHTcan be decided by settingτ=Tand the symmetry in Eq.(1)
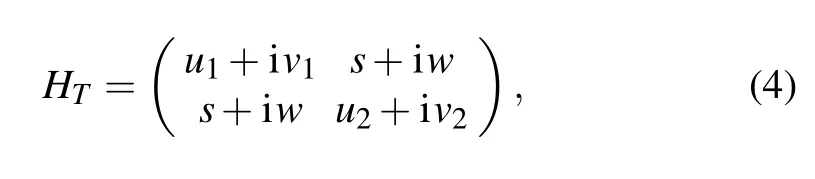
wheres,w,ukandvk(k=1,2) are real parameters, and the time-reversal operatorThas an effect as the complex conjugate operating on its right operators and state-vectors.
3.2. τ =PT
In the two-dimensional case,the general form ofPT-APH HamiltonianHTcan be decided by settingτ=PTand the symmetry in Eq.(1)


Fig.1. Subsets of the τ-anti-pseudo-Hermitian systems. The intersection of the T-anti-pseudo-Hermitian and the PT-symmetric systems are P-pseudo Hermitian, while that of the PT-anti-pseudo-Hermitian and PT-symmetric systems are Hermitian.
We show the relations between typical NH two-level sets in Fig. 1:τ-APH (τ=TorPT),PT-symmetric,P-pseudo-Hermitian systems,and Hermitian cases. In special cases,theτ-APH systems becomeP-pseudo-Hermitian or trivial Hermitian systems.
4. Quantum simulation of T- and PT-antipseudo-Hermitian two-level systems
It is the Hermiticity that guarantees the unitarity of the time-evolution of a Hermitian system,which can be simulated in the Hilbert space of the same dimensions. However, the two-dimensional time-evolutionary operator,

that we will simulate, is not unitary. Thus, one qubit cannot achieve the simulation. Aτ-APH subsystem will be constructed in a larger Hilbert space and simulated by qubits using LCU and duality quantum algorithm.
The exceptional points (EPs),[86,87]consist of the points in the parametric space,lead the eigenvalues ofHτto be zero.Except the EPs, our quantum simulation is applicable to the whole parametric space(including the neighborhoods of EPs).Because the NH systems are simulated in a Hermitian system,the conventional Hilbert–Schmidt inner product will be used.
4.1. LCU and duality quantum algorithm
We now propose the quantum simulation of the timeevolution in Eq. (6) based on LCU and duality quantum algorithm[80]in a Hermitian quantum device.
LCU and duality quantum algorithm were proposed in 2002,[80]and they were developed fast,[88–93]becoming one of the strongest tools in designing quantum algorithms.[94]Besides to accelerate and optimize Hermitian quantum simulation, we developed LCU to simulate NH systems,[34,37,40,57,58,72–76]other novel systems,[77,78]and time-dependent non-unitary operators.[6]Our unitary expansion(UE)technique is used to realize the LCU in the detailed cases.
4.2. UE of the time-evolutionary operator
In two-dimensional cases,[6]the maximum of the number of UE-terms is four in general, and it can be reduced to two in some special cases when the parameters meet the phase matching conditions. We now applied the UE techniques to the non-unitary time-evolutionary operator. In detail,

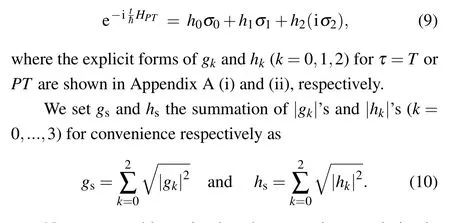
Now,we are able to simulate the non-unitary evolution in Eq. (6) using LCU. A qudit or a qudit-qubit-hybrid device is able to achieve the simulation,and qudits take advantages over qubits in some quantum algorithm,[95]e.g.,it reaches a higher accuracy to solve the eigenvalue problem using quantum phase estimation algorithm by qudits[96]than by qubits.[97]However,we focus on quantum simulations using qubits here,since qubit-quantum computers are available technologies.
4.3. Qubits simulation of T-APH two-level systems
We first take aT-anti-pseudo-Hermitian system as an example for illustration. One evolutionary qubiteand two ancillary qubitsaare able to simulate the time-evolution of a generalT-APH system by our theory. The evolutionary qubit will evolve as Eq.(8)with the assistance of the ancillary qubits in a probabilistic way. We will use a six-dimensional Hilbert subspace extended by|l j〉a|k〉e’s(l j=00,01,10 andk=0,1)to achieve the simulation,and the rest two dimensions are spared.Notice that the success probability using six dimensions is larger than that using the full eight dimensions,[6]while the later one can also achieve the simulation.
The quantum circuit to simulate aT-APH two-level system is shown in Fig.2. At the beginning,the whole system is initialized to a pure state|00〉a|0〉e,and the evolutionary qubitewill be prepared in an arbitrary state|ψ〉eas need by a singlequbit rotationRψ. The two ancillary qubits will assist the evolutionary qubit to evolve governed by theT-APH Hamiltonian. In the first block,we will spare the two dimensions relevant to|11〉a|k〉e(k=0,1)to prepare the six-dimensional subspace,and assign the three UE-parametersgk’s(k=0,1,2)to|l j〉a|k〉e’s(l j=00,01,10 andk=0,1). During this process,the first and second ancillary qubits are swapped,and then two single-qubit operatorsG1and-σ3rotate them. A controlled-NOT gate follows,of which the first and the second qubits are the target and control qubits, respectively. After operated byG2, the first qubit is swapped again with the other ancillary qubit. The explicit forms of the two single-qubit operators are
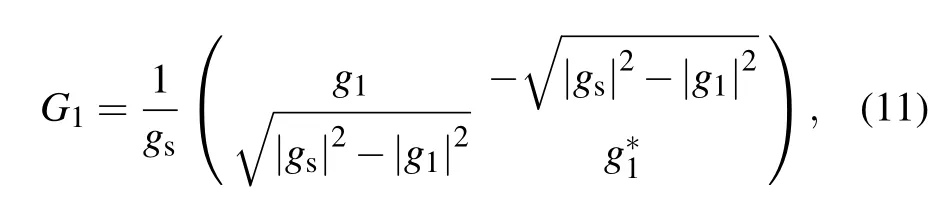
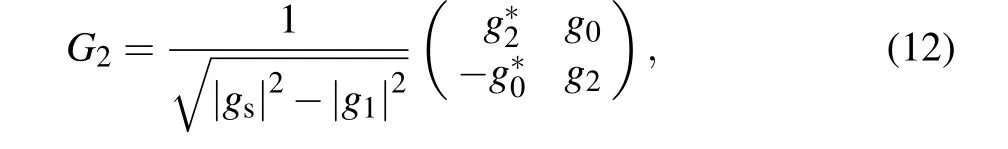
whereg0,g1,g2andgsare those in Eqs.(8)and(10).
In the second block of Fig. 2, the three UE-terms in Eq. (8) will be generated. Notice that the unit-matrixC00-σ0has theoretical meaning to show our method clearly, while no operation is needed in practice. The other two jointlycontrolled gates are necessary,and their explicit forms are
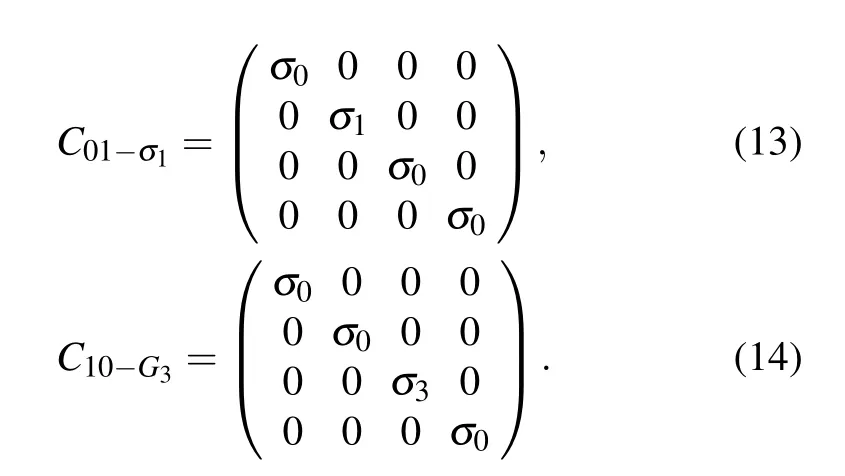
Now the three UE terms are generated, and we will combine them together in the next step.
The third block aims at combining the three UE-terms.Five operators will be applied in series, i.e., a first swapping gate, a Hadamard gateH2, a second swapping gate, a singlequbit rotationG3, and a third swapping gate, as shown in Fig.2,where


If one of the rest two results of|01〉aor|01〉ais measured,the simulation will be terminated. The whole process will then be started over until|00〉ais obtained. Therefore, it is an probabilistic protocol to simulate the time-evolution ofT-APH twolevel systems.

Fig.2. Three-qubit quantum circuit. The system is prepared to|00〉a|ψ〉e. The six-dimensional subspace is constructed in the first block. At the meantime,the three UE-parameters are assigned.Then,the UE-terms generation is realized by three controlled-controlled operators(the first dashed one is a trivial unit matrix)in the second block. UE-terms superposition in Eq.(8)is achieved in the third block. Finally,quantum measurements are performed on the ancillary system to evolve the qubit e as the T-APH system in a probabilistic way if|00〉a is obtained.
4.4. Qubits simulation of PT-APH two-level systems
The simulation of a generalPT-anti-pseudo-Hermitian system(Fig.3)is similar to that of aT-APH system,in which three qubits are essential for a general case. The operatorsGk(k=1,2) and the controlled-σ3in Fig. 2 should be replaced byRk(k=1,2)and a controlled-iσ2as show in Fig.3,respectively. Their explicit forms are

Before quantum measurements,the whole system evolves to a superposition

Otherwise, the simulation will be restarted until|00〉ais output.
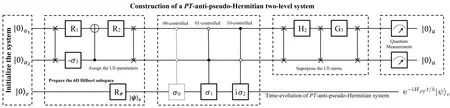
Fig. 3. Three-qubit quantum circuit. Detailed operations will be replaced, while the whole process is similar to that in Fig. 2. Finally, quantum measurements are performed on the ancillary subsystem to evolve the qubit e as the PT-APH system in a probabilistic way when the output is|00〉a.
4.5. Special cases
In special cases, when the Hamiltonians satisfy phase matching conditions,[6]the four UE-terms in Eq. (7) can be merged to two,and two qubits are enough to simulate the timeevolution. We take
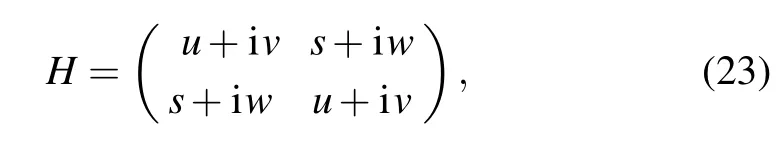
as an example, which is bothT- andPT-APH. The timeevolution operator can be expanded to
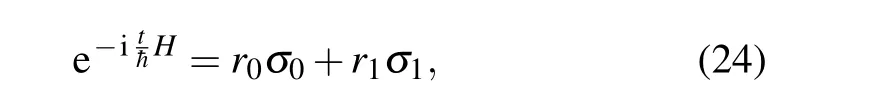
where the explicit forms ofr0andr1are given in Appendix A(iii).


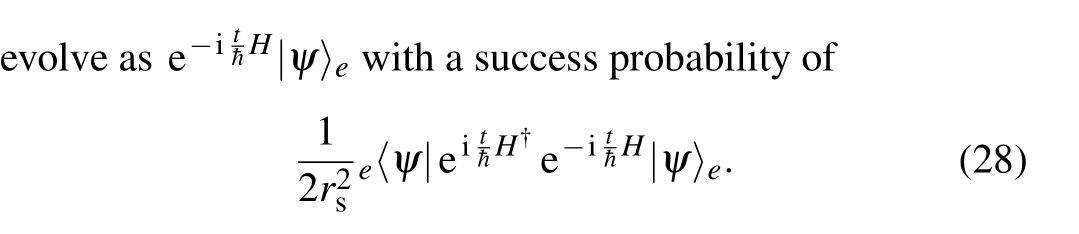
In this case, the time-evolution can be simulated by two qubits as the quantum circuit shown in Fig.4. After prepared Otherwise, if the ancillary qubit is observed in state|1〉a, the process will be terminated and the result will be discarded.We will start over the quantum simulation until|0〉ais measured at last.
Notice that the evolution ofHcan be simulated by both the three-qubit in the previous two subsections and this twoqubit protocol here. However, from Eqs. (17), (22) and (28),the success probability using two qubits is larger than that using three qubits (noticers,gsandhsare the same for a fixedH). Therefore, it is meaningful to reduce UE-terms before quantum simulation,decreasing the complexities of the quantum circuit but increasing the success probability.
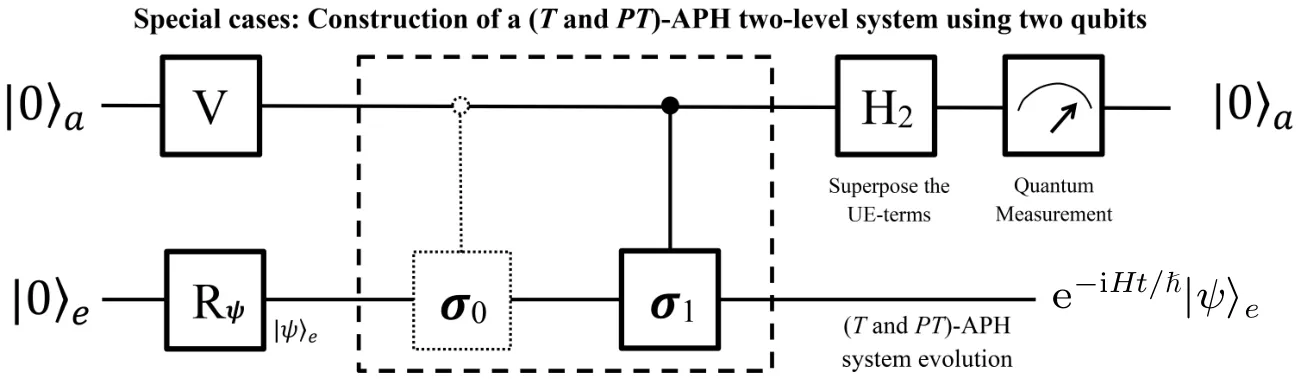
Fig.4. Two-qubit quantum circuit. The system includes an ancillary qubit a and an evolutionary qubit e. After initialized to|0〉a|ψ〉e, operators areapplied in series,i.e., asingle-qubit rotationV, twocontrolledoperators (the frist one is a trivial unit-matrix), and a Hadamard. Finally, the evolutionary qubit e will evolveas e-i htˉ H|ψ〉e if|0〉a ismeasured.
4.6. High-dimensional cases
For a high-dimensional case,assume that the dimensions of theτ-APH system areDand the evolutionary operator can be expanded toNUE-terms. The qubit numbers of the ancillary and the evolutionary subsystems,N1andN2, should not less than log2Nand log2D,respectively.
At the beginning, the whole system is initialized to state|0〉a|ψ〉e. Designing the quantum circuit by LCU and duality quantum algorithm, a series of operators will be applied on the system to assign the UE-parameters, generate and superpose the UE-terms to constructing theτ-APH subsystem. At last, quantum measurements will be performed on the ancillary subsystem to complete the time-evolution in a probabilistic way if the ancillary qubits are measured in state|0〉a.In this situation, the subsystemewill evolve as governed by the the high-dimensionalτ-APH system. Otherwise, this simulation will be terminated and started over.
5. Discussion and conclusion
Investigations of novel phenomena by controllable and available quantum devices are one of the main tasks of quantum simulation. We discuss experimental implementations of quantum simulation of theτ-APH here. Our proposals can be implemented in small quantum devices that are available technologies, such as nuclear-magnetic-resonance (NMR) quantum simulator,quantum optics systems,superconductor quantum systems,ultracold atoms,trapped ions,etc. Our proposals can also be realized on the IBM QE 5-qubit quantum processor as that in Ref.[98].

In conclusion, we mainly investigate quantum simulation of theτ-anti-pseudo-Hermitian systems using LCU in the scheme of duality quantum computing. In detail,we propose how to simulate theT-APH andPT-APH two-level system both in general cases using three qubits and in a special case using two qubits. In general cases, a minimum sixdimensional Hilbert space is essential to simulate the timeevolution by our unitary expansion technique. The simulation is achieved in a probabilistic way. Although the special cases can be simulated by both the two proposals, the twoqubits one has a higher success probability, deciding by the initial state, the Hamiltonian and the dimensions of the used Hilbert space. Therefore, it is meaningful to merge the UEterms based on our UE technique and phase matching conditions to reduce the needed dimensions before quantum simulation, saving qubit source and increasing the success probability. Furthermore, we discuss schematically for general high-dimensional cases and experimental implementation of the two-dimensional cases,expecting experimental implementation in various small quantum devices.

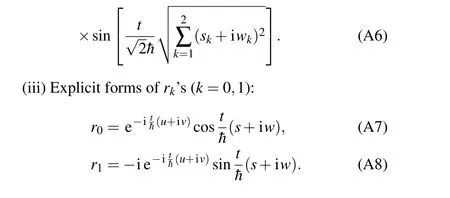
Acknowledgments
This work was funded by the National Natural Science Foundation of China (Grant No. 12175002), Beijing Natural Science Foundation(Grant No.1222020),and NCUT Talents Project and Special Fund for C.Z.
- Chinese Physics B的其它文章
- Design of vertical diamond Schottky barrier diode with junction terminal extension structure by using the n-Ga2O3/p-diamond heterojunction
- Multiple modes of perpendicular magnetization switching scheme in single spin–orbit torque device
- Evolution of the high-field-side radiation belts during the neon seeding plasma discharge in EAST tokamak
- Phase-matched second-harmonic generation in hybrid polymer-LN waveguides
- Circular dichroism spectra of α-lactose molecular measured by terahertz time-domain spectroscopy
- Recombination-induced voltage-dependent photocurrent collection loss in CdTe thin film solar cell

