Modified spin wave theory applied to the low-temperature properties of ferromagnetic long-range interacting spin chain with the antiferromagnetic nearest-neighbor interaction
-,
(School of Physics and Materials Science, Guangzhou University, Guangzhou 510006, China)
Abstract: In this paper, the modified spin-wave theory is applied to the Heisenberg ferromagnetic chain with the ferromagnetic long-range interaction J0/rp and antiferromagnetic nearest-neighbor interaction J. The spin-wave thermodynamics of the system are obtained within the self-consistent method by constraining the total magnetization to be zero. It is shown that the ferromagnetic long-range and antiferromagnetic nearest-neighbor interactions have great influence on the low-temperature properties of the system. At low temperatures, it is found that the specific heat C exhibits the temperature-dependent peak behavior which is induced by p and J, along with the specific heat coefficient C/T1/(p-1); while the susceptibility coefficient T2 shows the low-temperature behavior with a minimum induced by p and J. For J=0 and in the large-p limit, our results agree well with the exact Bethe ansatz results and the quantum Monte Carlo data.
Key words: modified spin wave theory; Heisenberg ferromagnetic chain; long-range interaction; nearest-neighbor interaction
0 Introduction
The standard spin-wave theory[1-3]is known as a powerful method in the study of the low-temperature thermodynamics of magnetic systems which can be described by the Heisenberg model. It still gives a boost to further theoretical and experimental explorations[4-8]of Heisenberg magnets. However, when the space dimension is lower than three, the traditional spin-wave theory can’t work well, and gives no quantitative information on the thermodynamic physical properties in the paramagnetic phase. This is because there has no long-range order in the paramagnetic phase in low-dimensional isotropic magnetic systems[9]. The spin-wave theory can’t cure the thermodynamic divergences which come from the absence of long-range order in the paramagnetic phase.
Fortunately, these thermodynamic divergences can be suppressed by use of Takahashi’s idea[10], which is to modify the traditional ferromagnetic spin-wave theory by constraining the total magnetization be zero. As a consequence, Takahashi[10]succeeded in deriving the correct low-temperature properties which are in excellent agreement with Bethe ansatz (BA) results in one dimension. His idea had been extended to many different kinds of low-dimensional magnets, such as the antiferromagnets[11-14], ferrimagnets[15-18], frustrated magnets[19-23], planar magnets[24-26], and spin-phonon coupling systems[27-29]. Based on Takahashi’s idea, the modified spin-wave theory gives the good description for inelastic-neutron-scattering measurements of the high-temperature-superconductor-parent antiferromagnet La2CuO4[14], and the existence of magnetically ordered phases of magnetic organic salts[30], and the quantum spin-liquid behavior of ultracold bosons on an inhomogeneous triangular lattice[31]. The nuclear spin-lattice relaxation time for the molecular cluster Mn12O12acetate[32]and the ferrimagnetic chain compound NiCu(C7H6N2O6)(H2O)3·2H2O[33]is explained well in terms of the modified spin-wave theory. Modified spin-wave analysis of the delta chain with competing ferro- and antiferromagnetic interactions[34]is in agreement with the experimental results of the synthesized cyclic compound Fe10Gd10.
In this paper, along the same lines, we formulate a theory for the one-dimensional ferromagnetic long-range interacting Heisenberg model with the antiferromagnetic nearest-neighbor interaction (ANNI). The ferromagnetic long-range interaction (FLRI) considered in this paper decays asJ0/rpwithrbeing the distance between lattice sites. For the case without the ANNI, the FLRI effect was investigated for the low-temperature and critical properties of the one- and two-dimensional quantum Heisenberg ferromagnets by using modified spin-wave theory[35]and Green’s function method[36]. Quantum criticality induced by the transverse magnetic field was obtained in the competition between the anisotropic FLRI (in which its isotropic part decays asr-3) and nearest-neighbor ferromagnetic exchange interactions in the ferromagnetic chain within the traditional spin-wave theory and renormalization group method[37]. Exploiting the renormalization group theory and numerical density matrix renormalization group analysis, continuous symmetry breaking in the Heisenberg chain was shown[38]to take place in the presence of the FLRI without the ANNI. For the ferromagnetic chain in coexistence of the FLRI and ANNI, however, little is known about the thermodynamic properties and critical phenomena. Its corresponding one-dimensional antiferromagnetic cases had been studied for the ground-state properties affected by both the ANNI and antiferromagnetic long-range interactions within Lanczos exact diagonalization[39]and density matrix renormalization group[40]. The recent experimental studies of the perovskites suggested that Pr0.5Sr0.5MnO3[41]and Pr0.5Sr0.5CoO3-x[42]as well as Y2CoMnO6[43]can be described by the Heisenberg models with both the FLRI (decays asr-3.252in two dimensions[41]andr-4.5in three dimensions[42-43]) and the ANNI. Those theoretical and experimental studies show that the FLRI can lead to the novel magnetic properties. Motivated by the experimental studies, we will consider the magnetic properties which are induced by the competition between the FLRI and ANNI in the ferromagnetic chain. Unlike in the ground state of the one-dimensional ferromagnetic long-range systems without the ANNI[35-38], the ANNI tends to flip the spins and destroys the stability of the ferromagnetic ground state which is kept by the FLRI. In this paper, the scheme to realize Takahashi’s idea is a self-consistent method, which can cure the usual thermal divergences by introducing a Lagrangian multiplier in the Hamiltonian to keep zero magnetization. In the frame of spin-wave theory within Takahashi’s idea, how the FLRI and the ANNI affect the low-temperature behaviors of the thermodynamic properties is the aim in our paper.
This paper is organized in the following manner. In Section 1, we rewrite the Hamiltonian by using the modified spin-wave theory within the self-consistent method. Then we obtain the analytical expression of the thermodynamic properties (such as the critical temperature, internal energy, specific heat, and susceptibility) as a function of the temperature, the FLRI and the ANNI. Numerical results and some discussions are displayed in Section 2. A brief conclusion is exhibited in Section 3.
1 Model
In this section, the modified spin-wave method will be used to study the thermodynamic properties of the quantum Heisenberg chain with the FLRI and ANNI. The Hamiltonian of the system can be described by
(1)
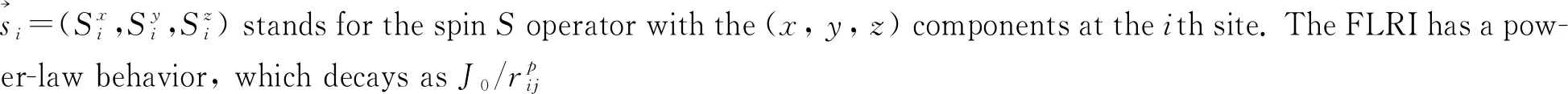
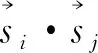
Two- and three-dimensional versions of the Hamiltonian (1) with the coexistence of the FLRI and ANNI have been experimentally shown to be realized in the perovskites Pr0.5Sr0.5MnO3[41], Pr0.5Sr0.5CoO3-x[42]and Y2CoMnO6[43]. As pointed out in Ref.[41] in the experimental study on the perovskites, the change in shape and size of the ferromagnetic clusters with temperature around the critical temperature can lead to quasi-one-dimensional perovskites, which may realize the chain Hamiltonian in Eq.(1). The perovskite is an example of the ABX3compounds, where A is an alkaline metal ion, B is a magnetic ion, and X is a halogen. These materials are particularly interesting because the ANNI is of the same order of magnitude as the FLRI. In these systems, due to the polarization of the itinerant electrons by interaction with the localized spins at a distancer[44], results in the FLRI between the localized spins of the magnetic ions. The Hamiltonian in Eq.(1) can also be realized in the experimental manipulation of quantum long-range interacting spin chains, which are designed by optical-dipole-force-induced spin-spin interactions in a trapped-ion ferromagnetic Heisenberg chain[45-47]. When the Coulomb interaction is considered as a perturbation to the trapping potential, the FLRI is approximated as a power-law-decayr-pwithin the frame of the quantum perturbation theory[45-47]. The exponentpof the FLRI corresponds physically to the Coulomb-like interaction forp=1, the monopole-dipole interaction forp=2, the dipole-dipole interaction forp=3, and van de Waals interactions forp=6.
As mentioned above, the divergences of the occupation number per site are encountered in the usual spin-wave theory in the disorder phase in one dimension. In order to overcome these divergences, we use Takahashi’s idea[10]which constrains the total magnetization to be zero:
(2)
To enhance the Constraint (2), we introduce a Lagrange multiplierλin the Hamiltonian, then the effective Hamiltonian is given by
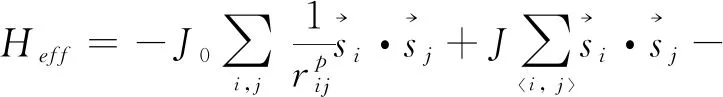
(3)
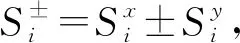
(4)
the Hamiltonian is rewritten as
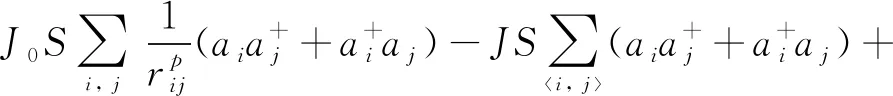
(5)
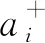
After making the Fourier transformations
(6)
the effective Hamiltonian is computed to be
(7)
where
E0=-λNS-(J0(0)-JZ)NS2
(8)
and
ωk=S[J0(0)-J0(k)]-S[ZJ-J(k)]+λ
(9)
HereJ0(k)/J0(0) andJ(k)/(JZ) are the structure factors for the long-range and nearest-neighbor interactions, respectively. They are given by
(10)
In one-dimensional case,J(k)=2 coskwithZ=2; andJ0(k) can be expanded in smallk[35-36, 49], i.e.,
(11)
with
(12)
in the thermodynamic limitN→∞.HereΓ(p) andξ(p) denote the gamma function and Riemann’s zeta function, respectively.
Taking account of the Bose-Einstein distribution function
(13)
and inserting it into the thermal average of the Eq.(2), we can get the consistent equation
(14)
HereTstands for the temperature. In the largeNthermodynamic limit, the summation in Eq.(14) is replaced by the integral in the first Brillouin zone. The Lagrange multiplierλis self-consistently determined by Eq.(14).λgiven by Eq.(14) is a kind of nonzero chemical potential. Thus, ifλis known, we can obtain the solutions for the thermodynamic properties of the system.
2 Results and discussions
In this section, we will discuss how the FLRI and the ANNI affect the thermodynamic properties (such as the critical temperature, internal energy, specific heat, and susceptibility) of one-dimensional ferromagnetic Heisenberg model. For convenience, the interactionJ0and the spinSare all set to beJ0=1 andS=1/2, respectively. The coordination number takesZ=2.
2.1 Lagrange multiplier
In order to obtain the thermodynamic properties, it is important to know the temperature-dependent behavior of the Lagrange multiplierλ. Note thatλcan be computed from Eq.(14) which is obtained under the constraint condition of zero magnetization. As pointed out in Ref.[10], the Lagrange multiplierλhas the physical meaning of being treated as the nonzero chemical potential.
Using the consistent Eq.(14),λis plotted as a function of the temperatureTin Fig.1 forp=2.2, 2.5, 3.0, 3.5 atJ=0.1 in Fig.1 (a), and forJ=0.1, 0.5, 0.9 whenp=2.2 in Fig.1 (b), respectively. If the ANNIJand the interaction rangepare given, it is easily found thatλincreases as the temperatureTincreases. WhenTandpare given,λincreases with the increasingJ. ForTfixed, the biggerporJ, the largerλ. The calculation of Eq.(14) at smallJshows thatλhas the low-temperature behavior of being proportion toT(p-1)/(p-2)for 2
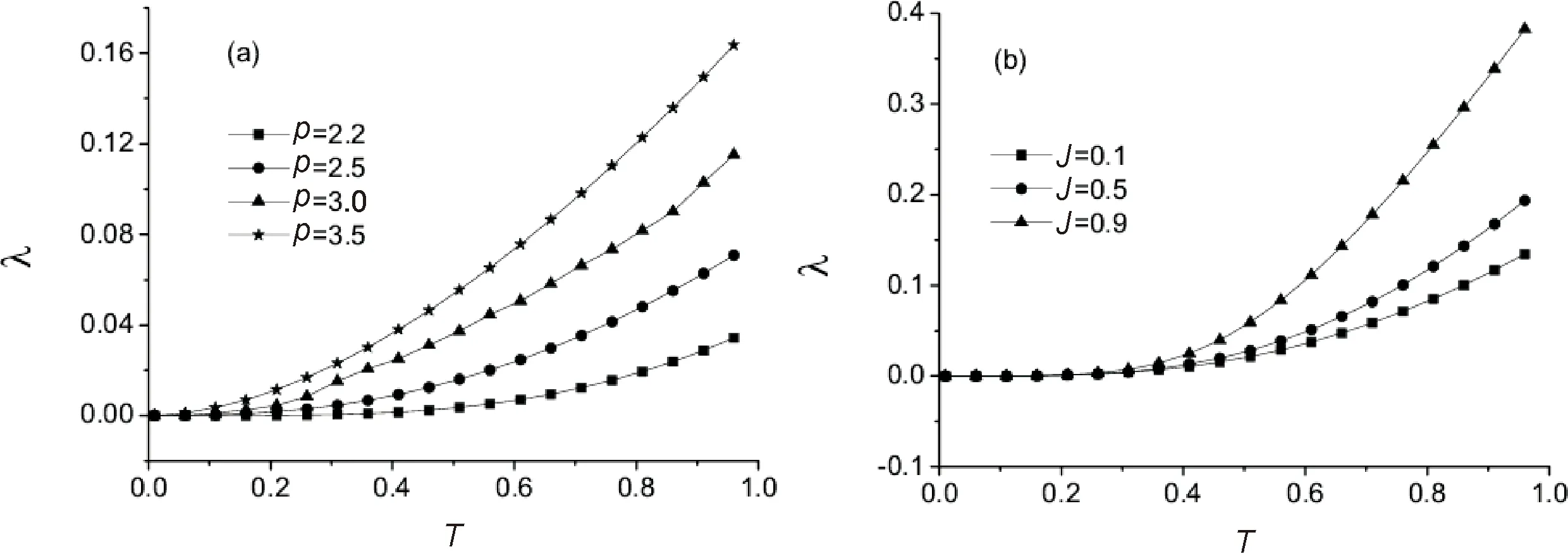
Fig.1 Temperature dependence of the Lagrange multiplier λ (a) for p=2.2, 2.5, 3.0, 3.5 at J=0.1, and (b) for J=0.1, 0.5, 0.9 when p=2.2, respectively
As seen in Fig.1 (a),λobtained at the smallerpdecreases more slowly than one obtained at the largerp. It is found in Fig.1 (b) that at a givenp, no matter what the valueJtakes,λhas the similar decaying behavior when the chain is in the low-temperature region ofT<0.2.
2.2 Critical temperature
In the former section, we have discussed the low-temperature behavior of the nonzeroλ. It is interesting that what happens whenλbecomes zero at the finite temperature.
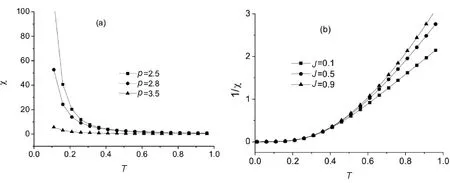
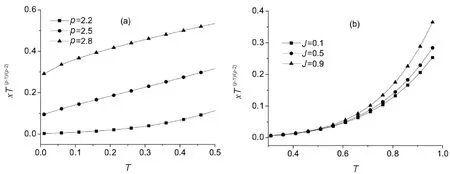
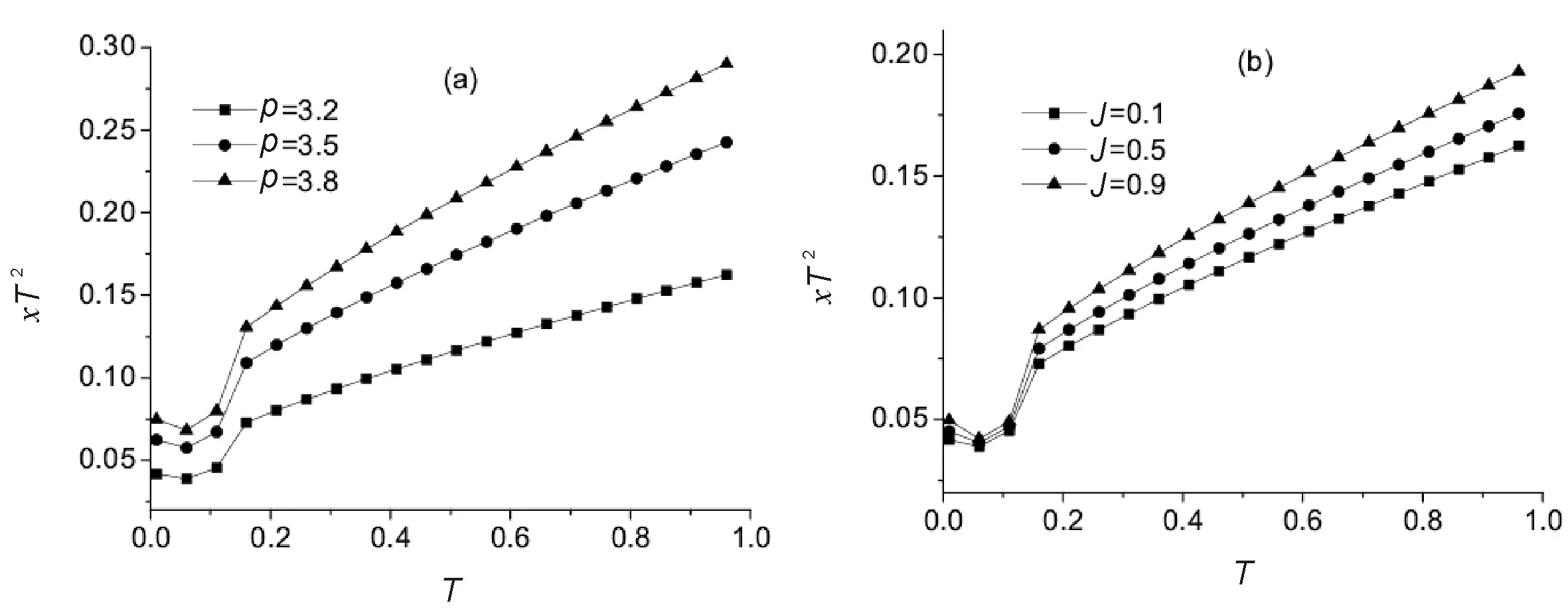
Seen from Eqs.(3) and (14),λ=0 shows that the systems can keep the zero-magnetization condition without needing to introduce the Lagrange multiplierλin the Hamiltonian (1). This means that the system has a ferromagnetic-paramagnetic phase transition at some finite temperatureTc, which is the critical temperature of the system. BelowT (15) with (16) In the largeNthermodynamic limit, Eq.(15) becomes the integral: (17) where 1BZdenotes the first Brillouin zone in one dimension. The calculations of Eq.(17) display that the finite-temperature phase transition exists atT=Tc≠0 when 1 To obtain the influence of the interaction rangepand the ANNIJin the behavior of the critical temperatureTc, Eq.(17) is used to plot the critical temperatureTcas a function ofpandJin Fig.2. Fig.2 The critical temperature Tc plotted as a function (a) of the interaction range p for J=0.1, 0.6, 0.8, and (b) of the ANNI J for p=1.2, 1.4, 1.6, respectively For 1 It is interesting that what happens for the critical temperatureTcwhen the ANNIJis changed to the ferromagnetic next-neighbor interaction -J. In this situation, in the region 1 It is shown in Ref.[38] that the continuousU(1) symmetry in the ferromagnetic chain is spontaneously broken for the FLRI in the regionp Now, let us consider the behavior of the internal energyU, which is defined byU=〈Heff〉/N.From Eq.(7),Uis computed to be (18) in one dimension. In Fig.3, the temperature dependence of the internal energyUis presented for theS=1/2 chain atJ=0.1 forp=2.2, 2.5, 2.8, andp=3.2, 3.5, 3.8, respectively. Fig.3 Temperature dependence of internal energy U at J=0.1 for (a) p=2.2, 2.5, 2.8, and (b) p=3.2, 3.5, 3.8, respectively From the figures, forp>2 in the disorder phase, we can see thatUis the increasing function of bothTandpforJgiven. The main reason for this phenomenon ofUincreasing with the temperature is that aspincreases, the FLRI becomes weak, but the thermal fluctuations get stronger. It is noticed that the effect of the interaction rangepon the temperature dependence ofUfor 2 Fig.4 illustrates that the temperature-dependent behavior of the internal energyUaffected by the ANNIJ. Fig.4 Temperature dependence of internal energy U for J=0.1, 0.5, 0.9 when p=2.2 When both the temperature and the interaction range are given, the internal energyUis on the increase as the ANNIJgoes up. This behavior induced by the ANNI causing harm to the stability of the long-range ferromagnetic ordering at the finite temperatures. In this section, we will study how the FLRI and ANNI affect the temperature-dependent behavior of the specific heatC=?U/?T.By mean of Eq.(18), one has (19) (20) In the low-temperature region, we employ Eqs.(19) and (20) to obtain the temperature dependence of the specific heatC, as shown in Fig.5. The specific heatCexhibits the peak phenomenon which is characteristic of the interaction rangepand the ANNIJin the low-temperature region. Fig.5(a) shows that the specific heatCstarts from zero, and increases with the temperature, arrives at its maximum in the low-temperature region. Aspdecreases, the maximum height of the specific heat increases, and its maximum width is widening, and the corresponding maximum position moves to the higher temperature. Ifpis fixed, the largeJhelps the increase of the specific heat and its maximum height. Fig.5 Temperature dependence of the specific heat capacity C for (a) p=2.2, 2.5, 2.8, 3.5 at J=0.1, and (b) J=0.1, 0.5, 0.9 at p=2.2, respectively. At low temperatures and the small ANNI, the spin-wave calculations give the specific heatCto be in the form ofT1/(p-1)for 2 Fig.6 Temperature dependence of C/T1/(p-1) for (a) p=2.2, 2.5, 2.8 at J=0.1, and (b) J=0.1, 0.5, 0.9 at p=2.2, respectively. Fig.7 Temperature dependence of C/T1/2 for (a) p=3.2, 3.5, 3.8 at J=0.1, and (b) J=0.1, 0.5, 0.9 at p=3.2, respectively Whenpis not far away fromp=2 in the region ofp>2, the coefficientC/T1/(p-1)displays the maximum behavior at low temperatures. Its maximum becomes larger and more widens with increasingJ, and shifts to the higher temperature. However, if the largepis far fromp=2, this kind of the maximum behavior disappears, andC/T1/(p-1)decreases as the temperature increases. Unlike the behavior ofC/T1/(p-1)for 2 In the zero-temperature limit, the values ofC/T1/(p-1)is the decreasing (or increasing) function ofp(orJ). For example, the zero-temperature values ofC/T1/(p-1)are computed to be 0.168 313, 0.169 393, 0.170 503 forJ=0.1, 0.5, 0.9 atp=2.2, respectively. ForJ=0 andp=2.2, limT→0C/T1/(p-1)=0.166 91 which agrees with the result obtained in Ref.[35]. As shown in Fig.7, the zero-temperature values ofC/T1/2are the increasing function of bothpandJ. In the nearest-neighbor limitp→∞, the FLRI is reduced to the ferromagnetic nearest-neighbor interaction, and then the model discussed in this paper becomes the Heisenberg chain with the ferromagnetic and antiferromagnetic nearest-neighbor interactions. In this case, forJ=0 andS=1/2, the analytical calculation within the modified spin wave theory gives the zero-temperature value of the specific heat coefficient to be limT→0C/T1/2=0.781 64, which recovers the result obtained by the Takahashi’s scheme[10], and agrees very well with the BA value 0.781 5[51]. In the following, we turn to consider the behavior of the magnetic susceptibility, which is defined by (21) Due to the absence of the applied magnetic field in Eq.(1), the system has the spin-rotational symmetry, which results in the spin-correlation functions (22) With the help of Holstein-Primakoff and Fourier transformations, the susceptibilityis computed to be (23) In the regime of the very low temperature, the susceptibilitycan be solved from Eq.(23) at the small ANNIJ. The susceptibilitybehaves asT-(p-1)/(p-2)for 2 Temperature dependence of the susceptibility and its coefficients are plotted in Figs.8~Figs.10 for some selected values ofpandJ, respectively. Fig.8 shows that the susceptibilityis a decreasing function of the temperature. However, the susceptibility coefficientT(p-1)/(p-2)is the increasing function of the temperature for both 2 The interaction rangepaffects the temperature-dependent behaviors of the susceptibility and its coefficients in a similar way to the ANNIJ. If the temperatureTis fixed, the largeJand the largepboth impede the increase of the susceptibility, while the susceptibility coefficientsT(p-1)/(p-2)andT2both increase asporJincreases. Fig.8(a) shows that the interaction range causes the stronger suppression of the susceptibility forp>3 than for 2 Fig.8 Temperature dependence of susceptibility for (a) p=2.5, 2.8, 3.5 at J=0.1, and (b) J=0.1, 0.5, 0.9 at p=2.2, respectively Fig.9 Temperature dependence of T(p-1)/(p-2) for (a) p=2.2, 2.5, 2.8 at J=0.1, and (b) J=0.1, 0.5, 0.9 at p=2.2, respectively Fig.10 Temperature dependence of T2 for p=3.2, 3.5, 3.8 at J=0.1, and (b) J=0.1, 0.5, 0.9 at p=3.2, respectively Note that in the zero-temperature limit, the values of the susceptibility coefficients limT→0T(p-1)/(p-2)and limT→0T2all increase with the increase inporJ, as shown in Fig.9 and Fig.10. Atp=2.2, limT→0T(p-1)/(p-2)=0.000 153, 0.002 977 forJ=0, 0.1, respectively. This value 0.000 153 is just the result in the case without the ANNI[35]. ForJ=0 andp→∞, our limT→0T2=1/24, which is obtained by the self-consistent method, reproduces the result obtained by Takahashi’s scheme[10]. It is also in good agreement with the BA value 0.041 675[51], and with 0.041 667 obtained by Green’s function method[52-53]and the quantum Monte Carlo[53]. In this paper, with the help of Takahashi’s idea constraining the total magnetization to be zero, the modified spin-wave theory has been applied to the ferromagnetic Heinsenberg chain with the FLRI and the ANNI. It is found that the FLRI rangepand the ANNIJhave great influence on the low-temperature properties of the system. ForJ=0, our results agree well with the exact BA results and the quantum Monte Carlo data. The internal energyUas well as the chemical potentialλis the increasing functions of bothpandJ. But the magnetic susceptibilityand the temperatureTcdecreases with the increase inporJ. At the very low temperatures and the smallJ, the specific heatCand susceptibilitydisplay the power laws in temperatureT:C~T1/(p-1)and~T(p-1)/(p-2)for 2 At low temperatures, it is found that the specific heatCexhibits the temperature-dependent peak behavior, along with the specific heat coefficientC/T1/(p-1); while the susceptibility coefficientT2shows a minimum. Aspincreases, the maximum ofCshortens and narrows, and its position shifts to the lower temperature. Note thatJpromotes the growth ofC. Whenpis close top=2, the coefficientC/T1/(p-1)has the maximum which grows up and widens with increasingJ, and shifts to the higher temperature. However, for the largepthe maximum behavior ofC/T1/(p-1)can’t survive. Forp>3, as the temperature increases, the susceptibility coefficientT2firstly decreases, and then increases after passing through the minimum whose height increases with the increase of bothpandJ.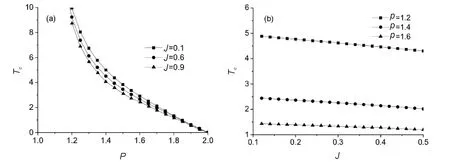
2.3 Internal energy
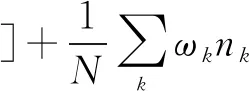

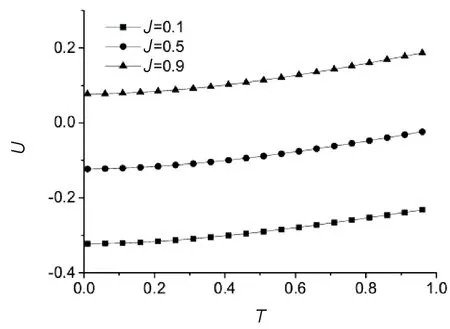
2.4 Heat capacity
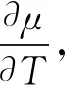


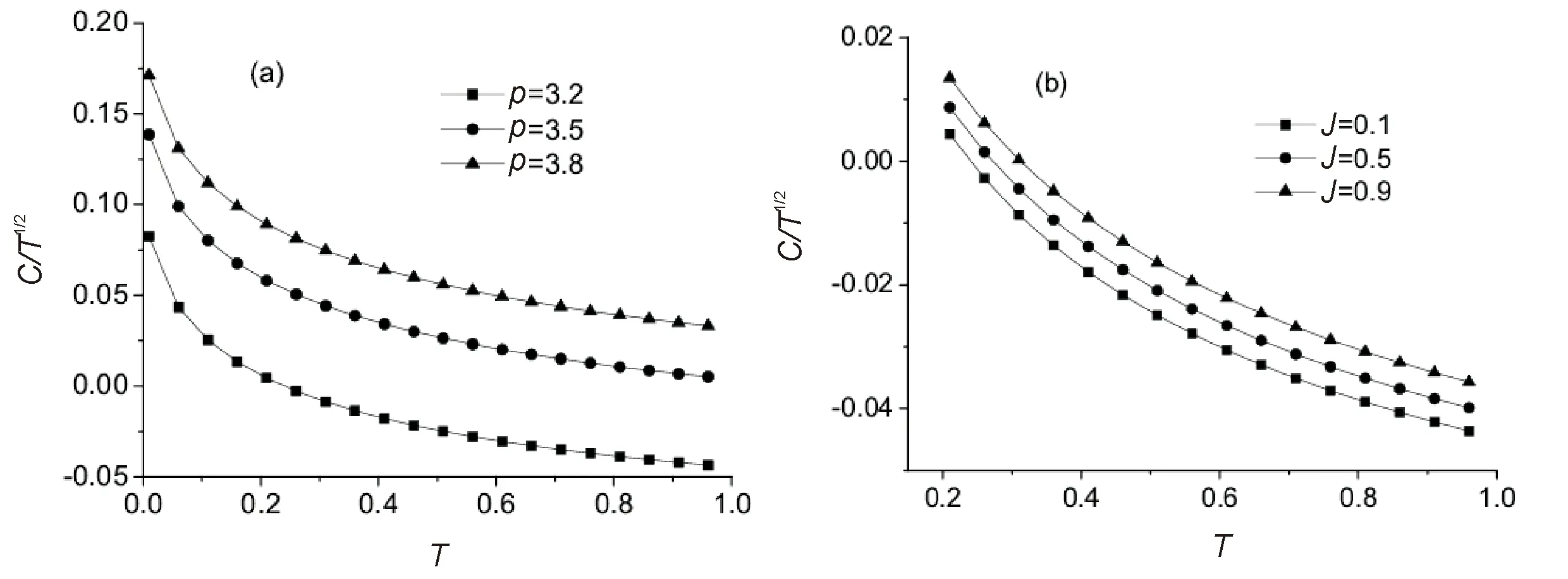
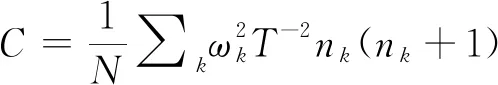
2.5 Magnetic susceptibility
3 Conclusion

