Effects of the mixing degree upstream of the diverging area on the pollutant allocation characteristics of a braided river

Jun ZOU, Jian-min ZHANG, Chang-yuan LI

Research Article

Effects of the mixing degree upstream of the diverging area on the pollutant allocation characteristics of a braided river

Jun ZOU1,2, Jian-min ZHANG, Chang-yuan LI2

1College of Water Resource & Hydropower, Sichuan University, Chengdu 610065, China2Jiangxi Provincial Institute of Water Sciences, Nanchang 330029, China

The mixing degree upstream of the diverging area is one of the important factors influencing the pollutant allocation characteristics of braided rivers, but the effect remains unclear at present. In this paper, physical model tests were designed to study the effect on the pollutant flux ratio with six branching forms and a series of longitudinal discharge distances. The results indicated that the mixing degree upstream of the diverging area, which is closely related to the longitudinal discharge distance, notably affected the pollutant flux ratio. The lower the mixing degree, the larger was the deviation of the pollutant flux ratio from the discharge ratio. Moreover, a linear relationship was attained between the dimensionless mixing degree and the dimensionless deviation of the pollutant flux ratio from the discharge ratio. Consideration of different branching angles or different water layers or different branches did not affect this trend. The experimental results further demonstrated that the intercept and slope of the aforementioned linear relationship depended on the branching angle and exhibited an opposite monotonicity with a symmetric branch angle as the dividing point. These results help towards a better understanding of the mechanism of the factors influencing pollutant transport in complicated braided rivers, and provide a new approach to predicting the pollutant flux ratio of braided rivers.

Mixing degree upstream; Diverging area; Longitudinal distance; Deviation of pollutant flux ratio; Standard deviation; Linear relationship

1 Introduction

River pattern includes meandering, braiding, and relatively straight rivers (Leopold and Wolman, 1957). In the classification proposed by Leopold and Wolman (1957), rivers with branching structures are included in braided rivers. Braided rivers are widely distributed on the earth. For example, in Northern Eurasia up to 35% of total river length is characterized by this pattern (Alexeevsky et al., 2013). Compared to a single river, the spatial complexity of a braided river is higher (Chalov and Alexeevsky, 2015).

A river with branching structure is composed of an upstream mainstream and at least two downstream branches, and the upstream flow is divided in the diverging area, as shown in Fig. 1. When water flows into the diverging area, it can be diverted and the flow direction can be altered. The process exhibits notable 3D turbulence characteristics.

In braided rivers, the pollutant diffusion and allocation are of great significance, and usually are a difficult problem. The concentration distribution and pollutant flux ratio are influenced by many factors, such as branching angle, pollutant discharge distance, anabranch width ratio, slope, upstream flow rate, and so on. These conditions can become increasingly complex, especially when pollutants in the upstream stream are still in the first or second stage of diffusion. These influencing factors are the research focus of scholars. Much valuable research has been carried in the field of transport and diffusion characterization in braided rivers.

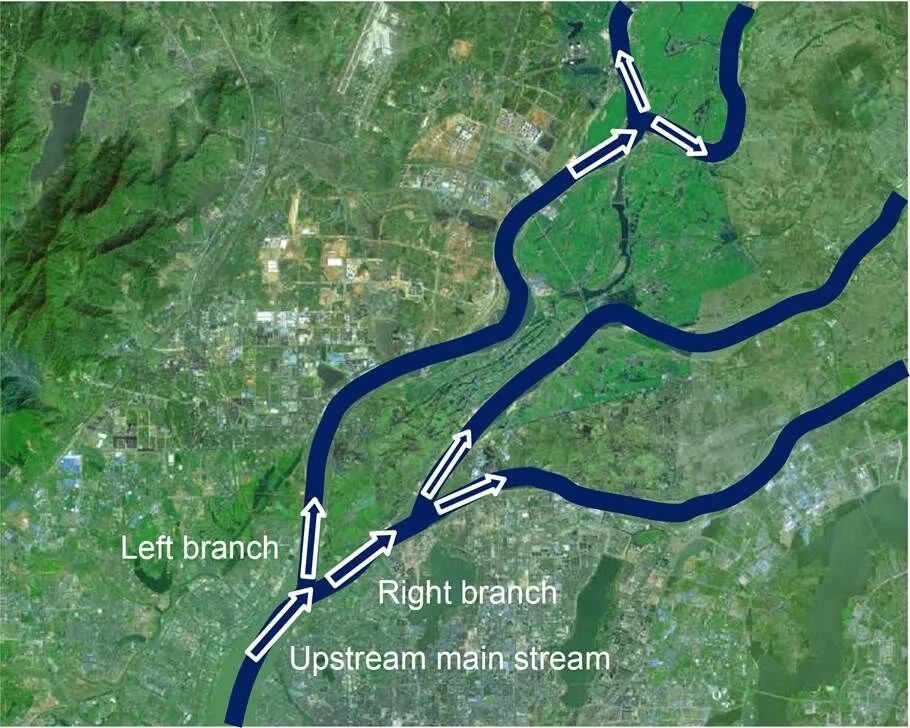
Fig. 1 River with branching structure: map from the SIWEI Earth

Li and Zhao (1994) studied diffusion and mixing patterns in braided rivers under the effect of the discharge position and incidence momentum. However, they did not consider the relationship between discharge ratio and pollutant flux ratio, nor was the relationship between the mixing degree and pollutant flux ratio accounted for. Hua and Gu (2008) ex amined the effect of the upstream flow rate and ana branch width ratio on the concentration distribution in each branch. Their findings revealed that the pollutant flux ratio increased with increasing discharge ratio. Hua et al. (2013a) further studied the pollutant transport and mixing characteristics of a braided river with three branches. They found that the pollutant discharge position (the transverse distance) was the main factor influencing the pollutant transport process. In addition, Hua et al. (2013b) investigated pollutant transport in a braided river and evaluated the effect of the upstream flow rate and discharge location on the pollutant concentration distribution. Gu et al. (2011a) investigated the effects of the upstream flow rate, anabranch width ratio, and discharge location (the transverse distance) on the pollutant concentration distribution in downstream branches. They reported that the pollutant flux ratio increased with increasing discharge ratio under central discharging. Gu et al. (2011b) studied the effects of the discharge location (transverse distance), upstream velocity, and anabranch width ratio on the pollutant mixing characteristics of braided rivers. Similar studies have also been performed by Ji et al. (2012). Yang et al. (2015) simulated the evolution process of a braided river dominated by suspended load transport and concluded that there was a close relationship with the periodical erosion and deposition cycles of braiding. Chalov and Alexeevsky (2015) believed that due to water partitioning along channels, sediment transport was affected significantly and that flow pattern alterations along a braided reach induced changes in the amount and types of mobilizing sediments. Redolfi (2015) investigated the effect of the flow unsteadiness on the sediment transport in a braided river. Okuyade and Abbey (2016) proposed a hydrodynamic model for pollutant diffusion in braided rivers for studying the role of river dynamics in the pollutant diffusion process. The results demonstrated that the branching angle, Reynolds number, and temperature difference could increase the flow velocity, which affected pollutant diffusion in the River Niger. Hunyun et al. (2019) used a transient storage model to analyse the behavior of contaminants entering a braided river. Similar studies have also been performed by Lee and Seo (2007) and Jiang et al. (2006). Khan and Sharma (2018, 2019) analyzed the turbulence characteristics of flow around the island in a braided river model. Chalov et al. (2020) discussed the downstream effects of pollutants spreading due to hydromorphological gradients and associated changes in sediment transport conditions along the braided-meandering and deltaic distributary reach of the downstream section of a large river and found quantitative relationships between the ratio of particulate metals sorting throughout depth in a single river channel and the hydrodynamic conditions of sediment transport. Das et al. (2022) described the sediment distribution of different sediment sizes for a branching angle of 37° and used three different sizes of sediment to investigate the influence of sediment distribution over the branches. Lu et al. (2022) set up a morphodynamic numerical model in the local braided channel of the Tuotuo River. Their results suggested that an increasing discharge significantly altered the characteristics of water and sediment movement.

There are many studies on transport of pollutants and sediment in braided rivers. Some scholars (Chalov and Alexeevsky, 2015; Redolfi, 2015; Chalov et al., 2020) have focused, based on abundant regional studies, on long-term sediment transport changes. In addition, certain factors, such as the upstream flow rate (Hua and Gu, 2008; Gu et al., 2011a, 2011b; Hua et al., 2013a), anabranch width ratio (Hua and Gu, 2008; Gu et al., 2011a, 2011b), branching angle (Okuyade and Abbey, 2016), discharge position (Li and Zhao, 1994; Gu et al., 2011a, 2011b; Hua et al., 2013a, 2013b), have been examined from different aspects and perspectives. However, at present, research on the characteristics of transport and diffusion in braided rivers is still insufficient. The relationship between the pollu tant flux ratio and the discharge ratio requires further study. Previously, researchers have considered the effect of the discharge position, but in-depth research on the impact of the longitudinal distance is lacking, and the effect mechanism of the mixing degree upstream of the diverging area has not been directly studied. The mixing degree upstream of the diverging area is closely related to the longitudinal discharge distance. One way to resolve this problem is to conduct a systematic experimental study on the longitudinal discharge distance and the mixing degree upstream of the diverging area. Pollutant diffusion in water can be studied by numerical simulation, and there are many related studies (Peng et al., 2021). However, considering the strong 3D turbulence characteristics of braided rivers, the physical model is more direct. This paper focuses on the mixing degree upstream of the diverging area, which is closely related to the longitudinal discharge distance of the point source. A physical model is employed as the main means of studying the relationship between the pollutant flux ratio and corresponding discharge ratio under the effect of the mixing degree upstream of the diverging area. This study helps towards a better understanding of the mechanism of the factors influencing pollutant transport in braided rivers.

2 Experimental setup

2.1 Model construction

The physical model comprised a water supply system, branch flume, backwater system, tracer liquid addition system, and measurement system. The branch flume was made from perspex, and comprised an upstream mainstream and left and right branches. The flume simulated a braided river with a width ratio of 1.0. The branching form with two branches is a common form in braided rivers. The anabranch width ratio was 1.0, which meant that the influence of that ratio was excluded in the tests. The upstream mainstream flume section had a length of 9.6 m, and all corresponding cross-sections were rectangular, with a width of 0.30 m and a height of 0.25 m. The mainstream of the flume needs sufficient length to arrange a series of measuring points in order to form a differentiated diffusion process. The left branch flume was 4.8 m long, all cross-sections of which were rectangular, with a width of 0.30 m and a height of 0.25 m. The left branch exhibited a fixed branching angle1, i.e., 45°. The branch also needs enough length to adjust the flow to a gradual flow so that the measurement can be carried out in a relatively stable flow. The right branch flume was 4.8 m long (length of the right bank), and all corresponding cross-sections were rectangular, with a width of 0.30 m and a height of 0.25 m. The right branch2had a variable branching angle ranging from 15° to 90°. The overall slope of the branch flume was zero, as shown in Figs. 2 and 3. The water fell into the backwater system. The longitudinal discharge distancefis the distance from the discharge point to the branching vertex.

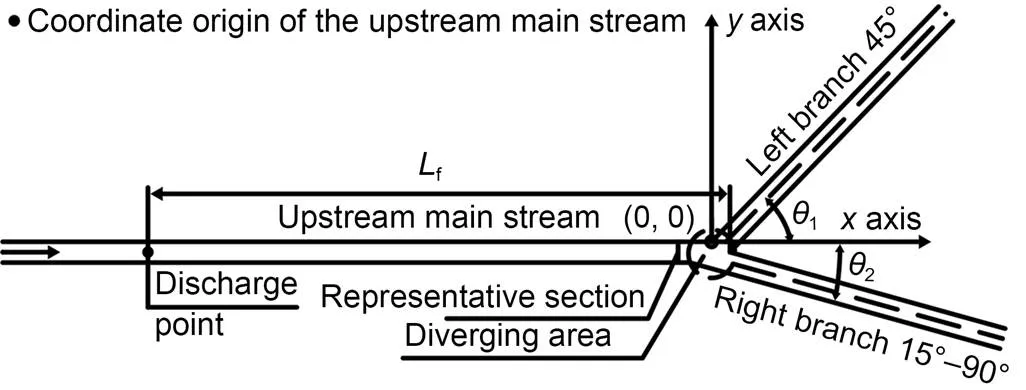
Fig. 2 Sketch of the braided river model

Fig. 3 Model photo

The coordinate system was set as follows:thecoordinate axis was set along the flow mainstream direction, and the-coordinate axis was set transversely in the plane. The-coordinate axis was established along the water depth direction. The zero point of theaxis was set at the bottom plate of the flume and the upward direction was considered positive.

The representative section upstream of the diverging area was selected based on the following principles: the section should occur close enough to the diverging area and should be less affected by the diverging area and basically maintain the flow structure characteristics of a single channel, as shown in Fig. 2.

Six groups of plane branching angles were established. The branching angle ranged from 15° to 90°, as indicated in Table 1 and Fig. 4.

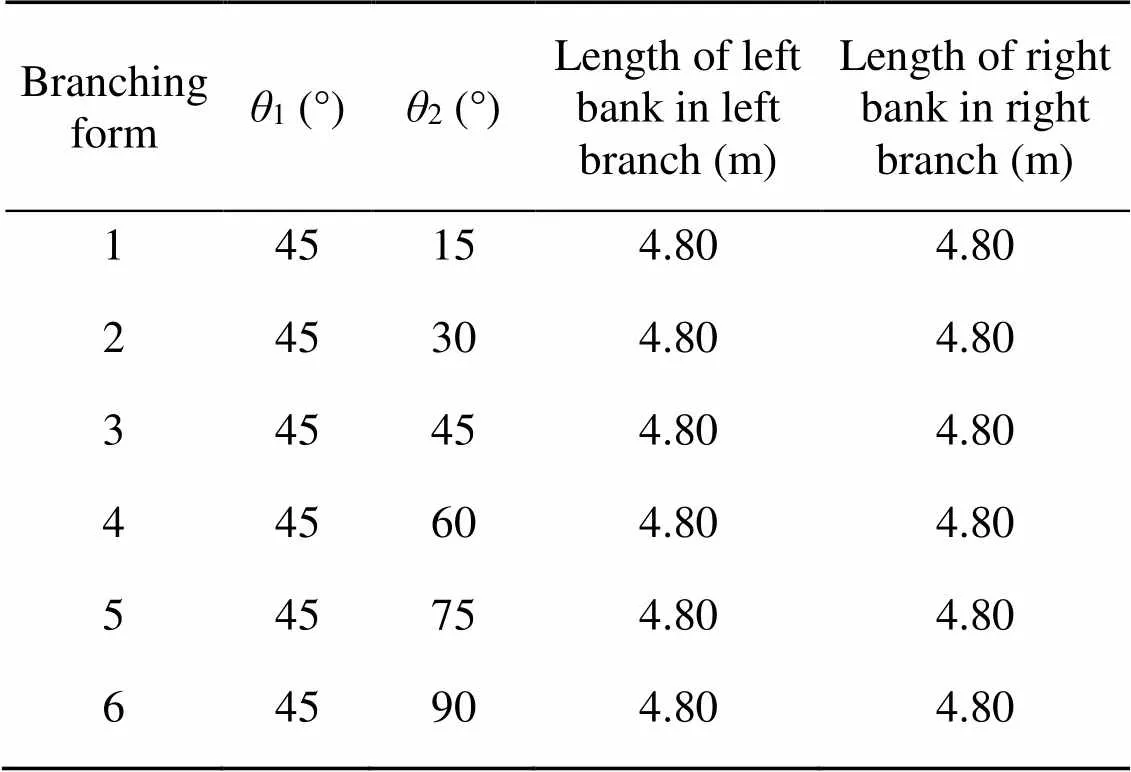
Table 1 Parameters of the branching forms

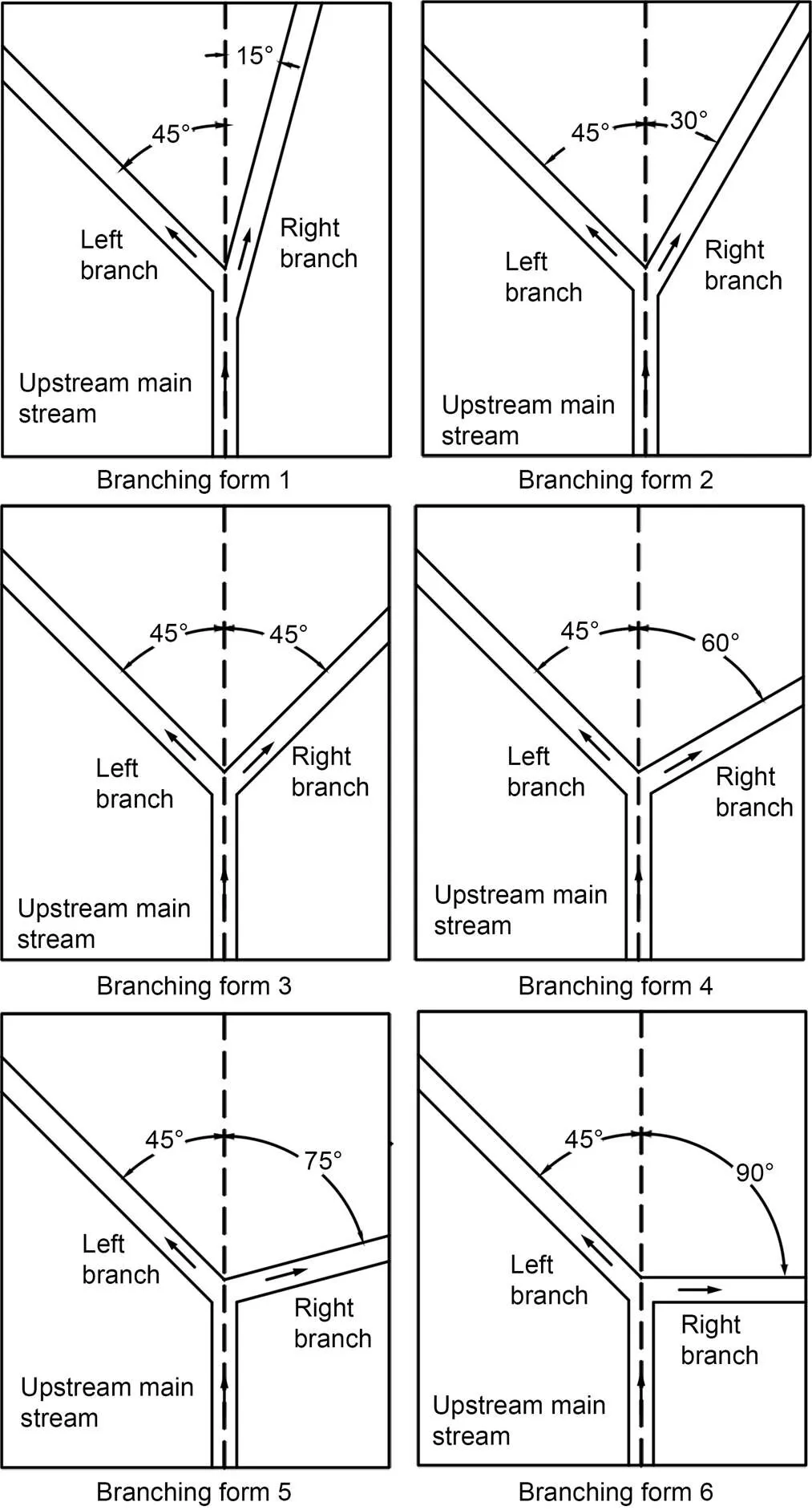
Fig. 4 Diagram of the six branching forms

2.2 Simulation of pollutant discharge

A sodium fluorescein solution, a dynamic inert conservative tracer, was adopted to simulate water pollu tants. The tracer solution concentration was 20.0 mg/L, and the discharge amount reached 1.70 mL/s. The-coordinate of the discharge point was determined by the test conditions. The-coordinate was -?15 cm (central discharge). The height of the discharge point occurred close to the free surface. The sodium fluorescein solution was discharged at the discharge point at a constant flow rate through the pump, and the discharge outlet was vertical to the liquid level. The concentration was measured at positions downstream of the discharge point, such as the representative section upstream of the diverging area and the ends of the left and right branches, as indicated in Figs. 5 and 6. In order to obtain sufficient concentration information, there were two measuring positions in the water depth direction. One was the surface layer, which was 10.0 mm below the water surface, and the other was the bottom layer, which was 11.5 mm above the bottom plate. Based on the principle of monochromatic light-induced fluorescence detection concentration (LIF), the concentration could be measured by detecting the fluorescence intensity. Under the excitation of a laser, the fluorescent substances produced fluorescent light intensity reflecting their concentration, as indicated in Fig. 7.

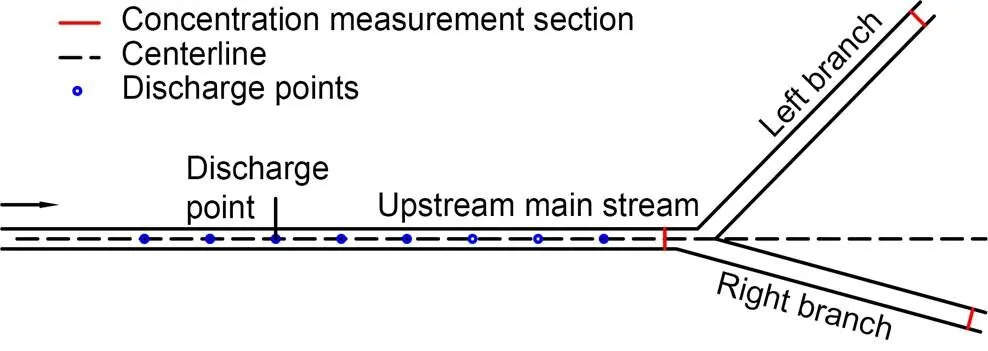
Fig. 5 Sketch of the discharge points and measurement sections

Fig. 6 Fluorescent solution discharge device

Fig. 7 Fluorescent solution measuring device

A series of longitudinal discharge distances was determined for each branching form, which ensured that the tracer experienced the first or second diffusion stage before entering the diverging area. The first or the second stage of diffusion indicated that the upstream pollutants do not diffuse uniformly in the cross-section when entering the diverging area. The first diffusion stage suggests that pollutants are non-uniformly mixed along the transverse and vertical directions, while the second diffusion stage indicates that pollutants are basically uniformly mixed along the vertical direction but non-uniformly mixed along the transverse direction. At the third diffusion stage, water pollutants are basically uniformly mixed in the cross-section.

The mainstream section with=?-?50 cm was selected as the representative section upstream of the diverging area for studying the role of the longitudinal distance in pollutant allocation.

2.3 Basic parameters

Table 2 shows the representative hydraulic para meters during the tests.

The discharge ratiofwas calculated according to Eqs. (1)?–?(3), and the pollutant flux ratiopwas calculated according to Eqs. (4)–(6). The subscript 1 represents the left branch, and the subscript 2 represents the right branch.

(1)

(2)

(3)

wheredenotes the total flow rate, and1and2are the flow rates in the left and right branches, respectively.

Table 2 Hydraulic parameters

The representative section was located in the mainstream=-50 cm

(4)

(5)

(6)

wheredenotes the total tracer discharge amount, and1and2denote the tracer amounts in the left and right branches, respectively.

3 Results and discussion

3.1 Pollutant flux ratio

The tests were based on a symmetrical branching form (branching form 3), including five asymmetric branching forms, covering a variety of size relationships between the left and right branching angles. The test results for six branching forms and the corresponding series of longitudinal distance are shown in Figs. 8–13.

The test results indicated that the longitudinal discharge distancefand pollutant flux ratiopof each branch generally attained a monotonic relationship. Moreover, the pollutant flux ratiopexhibited a trend indicating deviation from the corresponding discharge ratiof, resulting in the deviation of the pollu tant flux ratio from the discharge ratio Δp(Δp=p-f). The pollutant flux ratio of the branch with high discharge ratio was higher than the corresponding discharge ratio. In contrast, taking the branch with a low discharge ratio, the pollutant flux ratio was lower than the corresponding discharge ratio. This is consistent with previous research results (Hua and Gu, 2008; Gu et al., 2011a).

Further analysis revealed that |Δp| had a negative correlation withf. The value of |Δp| varied greatly, which reflected the complexity of diffusion in braided rivers, especially when the diffusion process has occurred at the first or second stage.

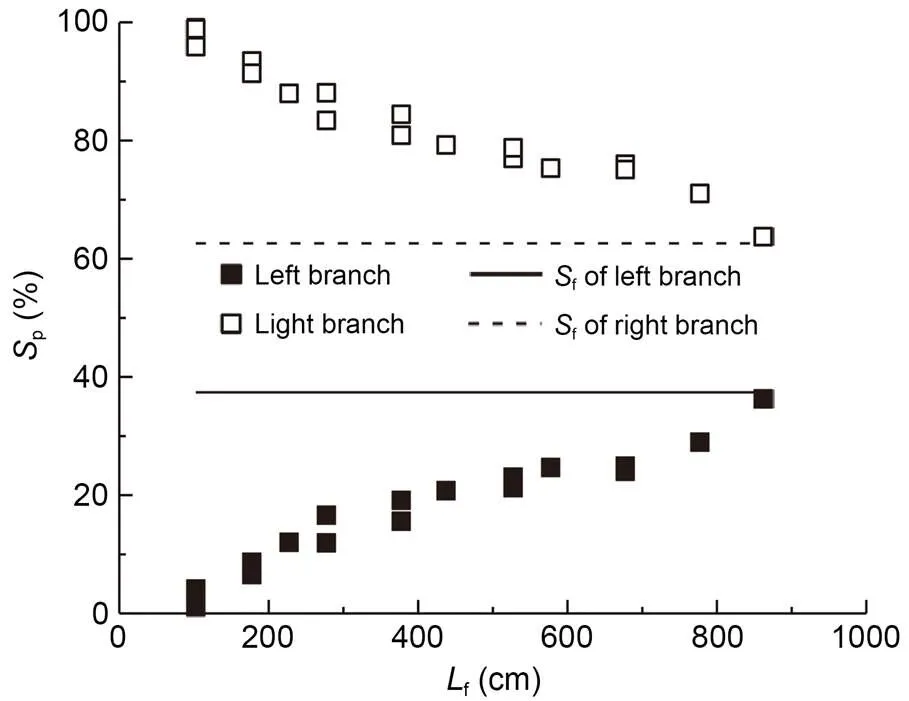
Fig. 8 Results for the pollutant flux ratio: branching form 1, θ2=15°

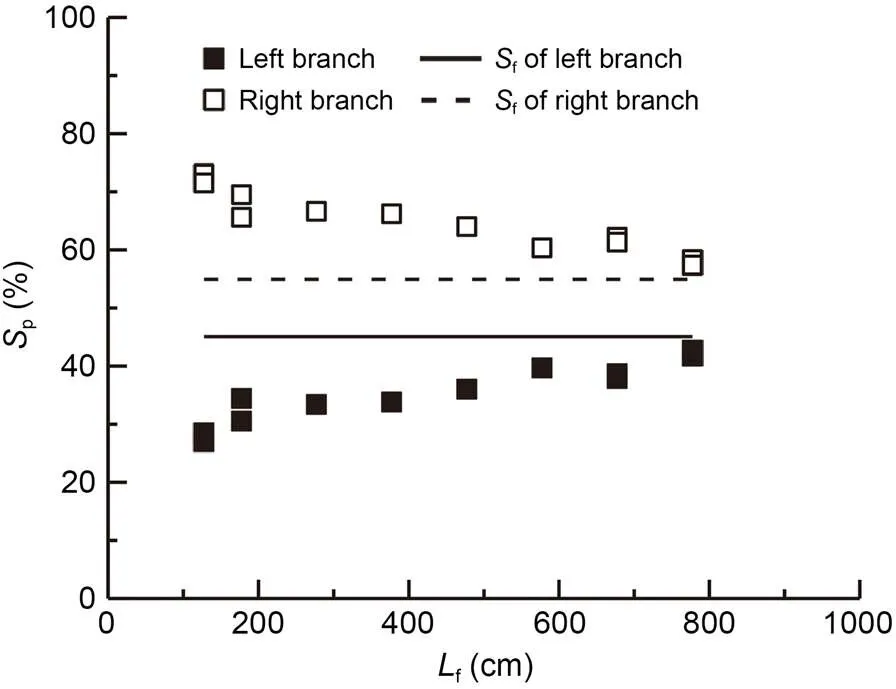
Fig. 9 Results for the pollutant flux ratio: branching form 2, θ2=30°

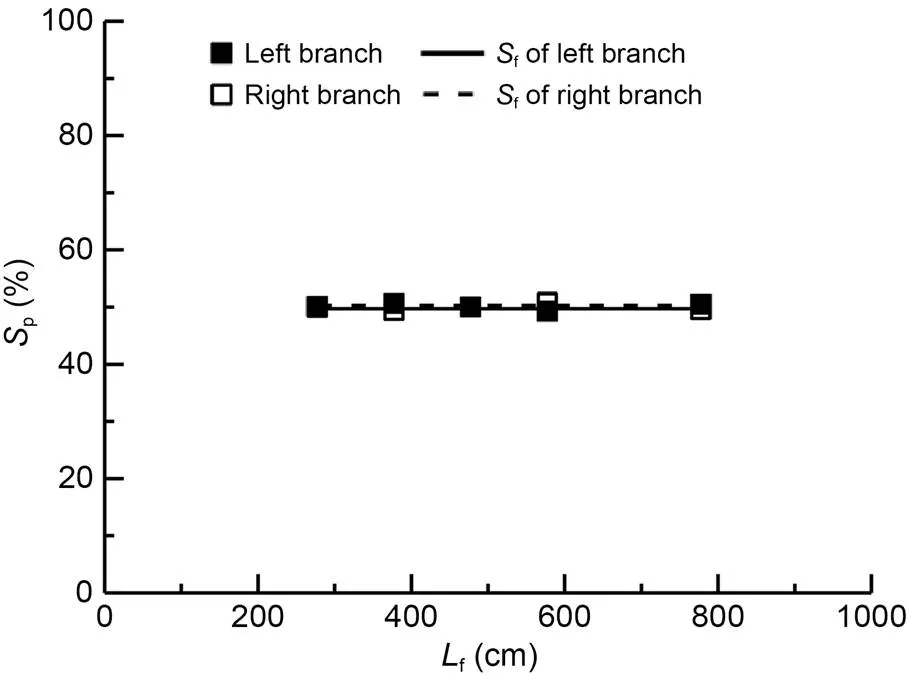
Fig. 10 Results for the pollutant flux ratio: branching form 3, θ2=45°

3.2 Degree of mixing upstream of the diverging area

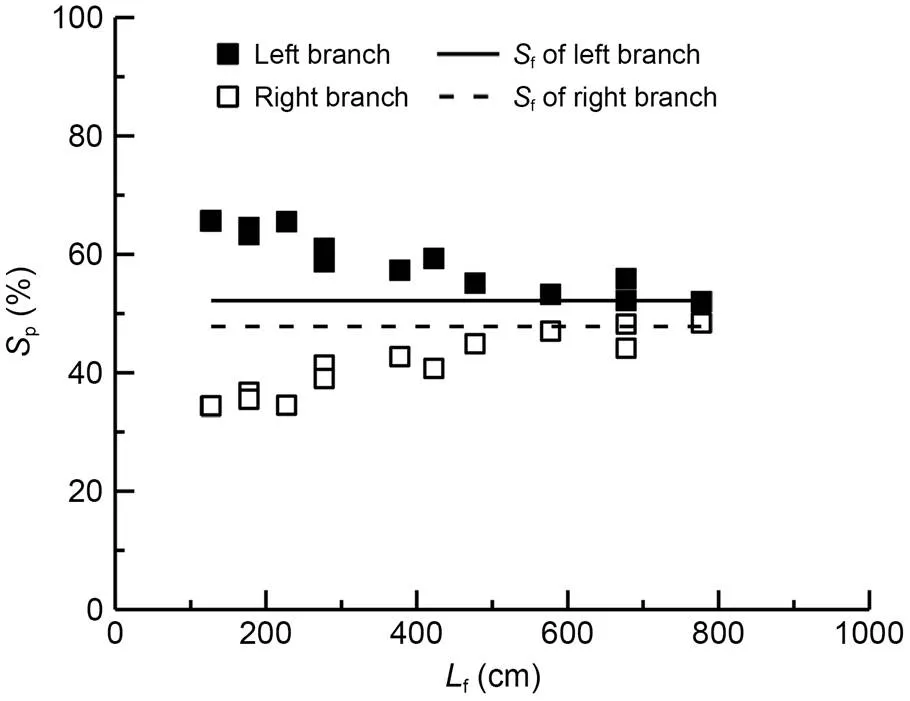
Fig. 11 Results for the pollutant flux ratio: branching form 4, θ2=60°

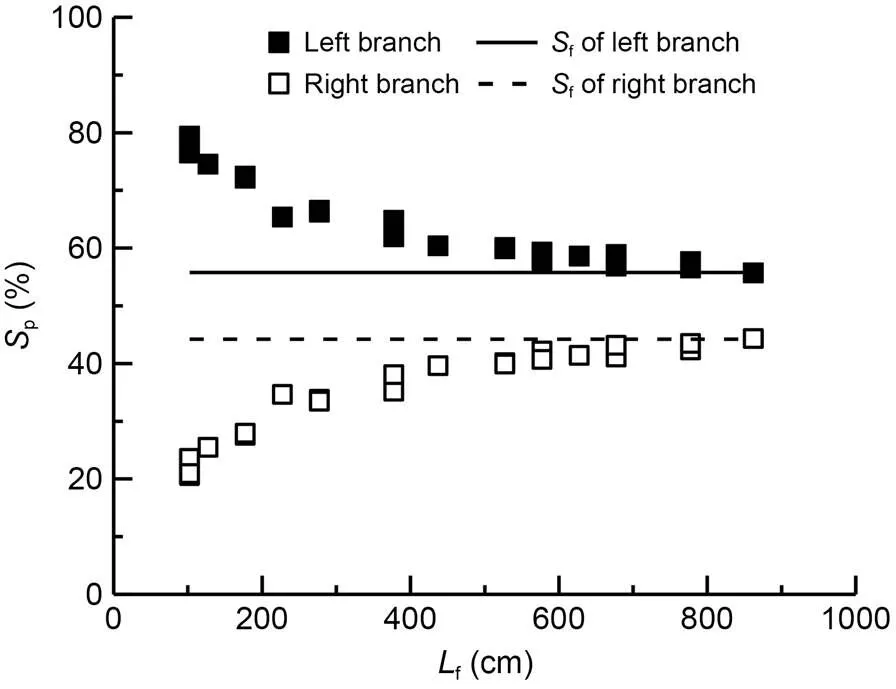
Fig. 12 Results for the pollutant flux ratio: branching form 5, θ2=75°

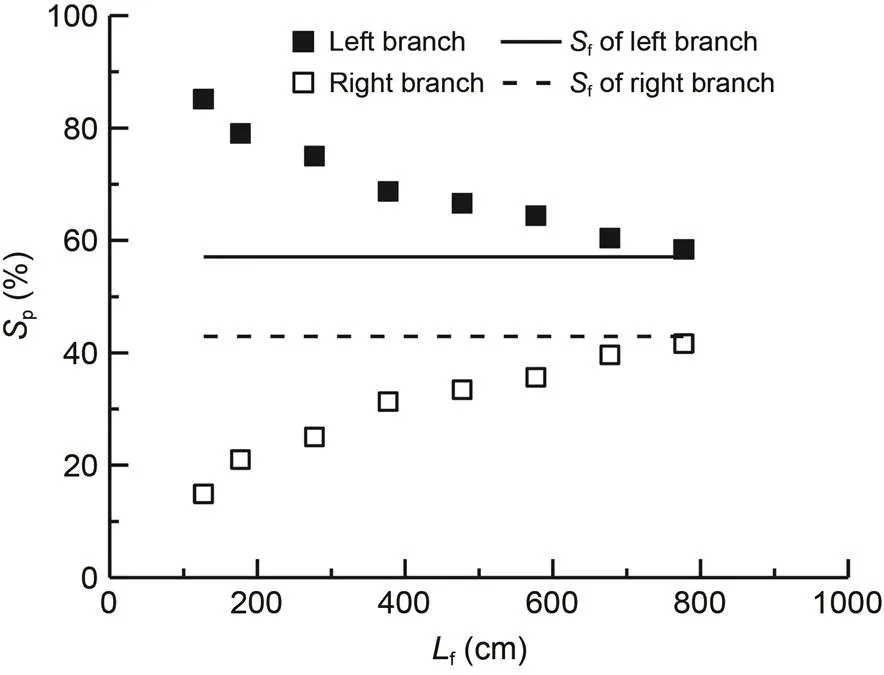
Fig. 13 Results for the pollutant flux ratio: branching form 6, θ2=90°

The above tests were carried out in the first or second stage of diffusion. The first or second diffusion stage means that the upstream pollutants are non-uniformly diffused in the cross-section before entry into the diverging area. In the absence of other factors, different longitudinal distances led to varying cross-sectional concentration distribution upstream of the diverging area.

Adopting branching form 1 as an example, the concentration distributions in the representative section upstream of the diverging area under different longitudinal discharge distances are shown in Fig. 14.is the concentration, andis the coordinate value along thedirection. The closer the discharge point to the diverging area, the more uneven was the concentration distribution, and the lower the mixing degree. Therefore, at the first or second diffusion stage,, a parameter capturing the mixing degree upstream of the diverging area, could be considered in addition to the longitudinal discharge distancefand the pollutant flux ratiop. Their relationship is thatfaffected, andinfluencedp. Compared to the longitudinal discharge distancef, the mixing degree upstream of the diverging areawas a more important influencing factor on the pollutant flux ratiop.

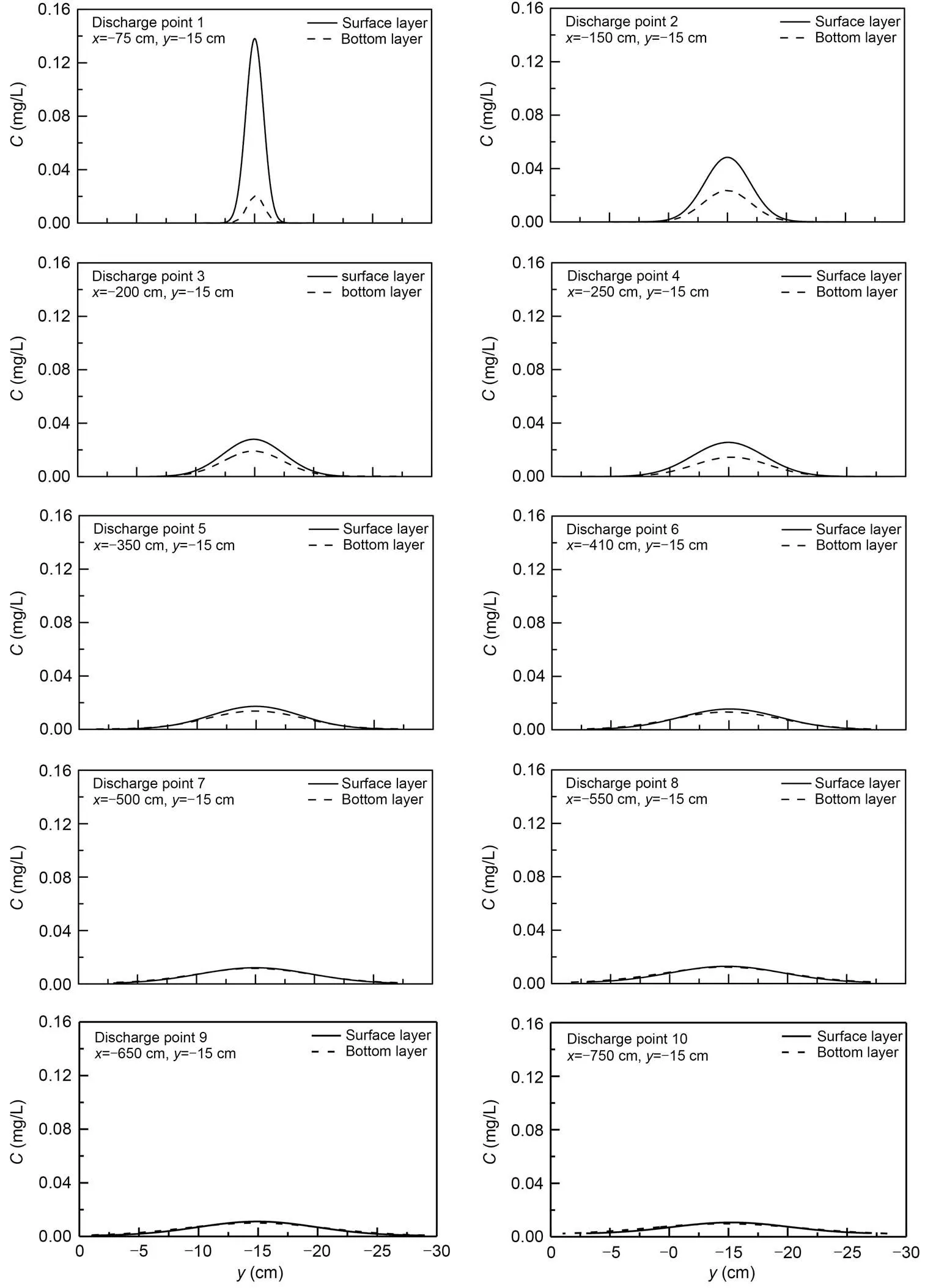
Fig. 14 Concentration distributions in the representative section: branching form 1

The following quantitative methods were proposed regarding the mixing degree upstream of the diverging area: Gaussian distribution fitting was carried out to determine the concentration distribution in the representative section upstream of the diverging area. A width of one standard deviation of the fitting curve was obtained for, which represented the mixing degree of the concentration and exhibited a length dimension. The lower the value of, the more focused is the concentration distribution in the cross section and the lower the mixing degree. Under central discharge, the difference of the mixing degree can be displayed intuitively, as shown in Fig. 15. It is obvious that the mixing degree of the discharge point 1 is lower than that of the discharge point 2, and1is less than2.

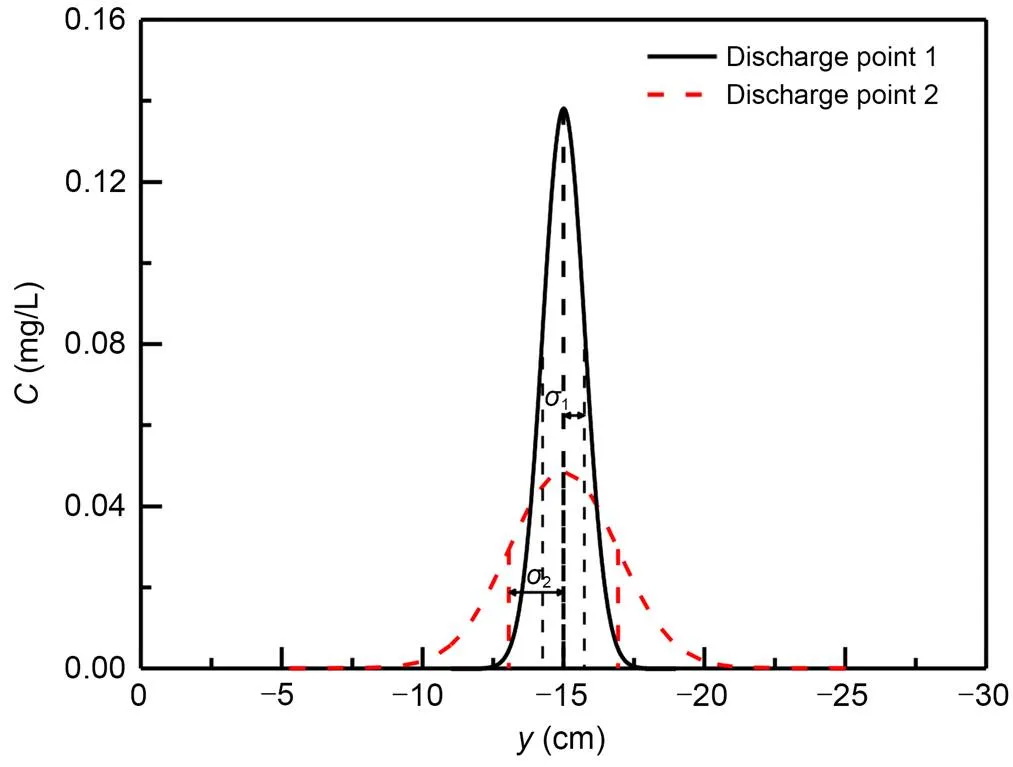
Fig. 15 Sketch of the mixing degree σ

Eq. (7) is the basic Gaussian distribution function, whereis the position parameter. Based on this function, Eq. (8) was applied to obtain the concentration spatial curve by fitting, where0,, and PP are fitting parameters.

(7)

(8)

Hua et al. (2013b) proposed that the standard deviation of concentration data represents the mixing degree in the downstream branch, and the mixing degree has been calculated with the basic standard deviation equation. In this study, the concept of the mixing degree was proposed, considering the section upstream of the diverging area rather than the downstream branch. The Gaussian distribution function was applied rather than the basic standard deviation equation.

3.3 Relationship between the mixing degree upstream of the diverging area and the pollutant flux ratio

According to the above definition, combined with the measured data obtained in the tests, a series of, coefficient of determination2, and peak position PP values were obtained via Gaussian distribution fitting, adopting branching form 1 as an example (please refer to Table S1 in the electronic supplementary materials (ESM)). It can be seen thatincreased with increasingf, but was negatively correlated with |Δp|, as shown in Fig. 16. The lower the mixing degree, the larger was the deviation of the pollutant flux ratio from the discharge ratio.

Fig. 16 Relationship between ΔSp and σ : branching form 1

To further study the regularity relationship between Δpand, Δpandwere nondimensionalized. The dimensionless parameters of |Δp|/fand/(/2) were adopted for analysis. |Δp|/fis the ratio of the absolute value of the deviation of the pollutant flux ratio from the discharge ratio to the discharge ratio, and/(/2) is the ratio of the mixing degree to the half-width of the flume cross section, whereis the flume width.

Adopting branching form 5 as an example, the relationship between |Δp|/fand/(/2) is shown in Figs. 17 and 18 (results of other branching forms are given in Figs. S2?–?S11 in the ESM). Under asymmetric branching, when the pollutant diffusion process upstream of the diverging area occurred at the first or second stage, the results of dimensionless treatment revealed that, regardless of the branch considered (either the left or right branch), there existed an app roximately linear relationship between |Δp|/fand/(/2).

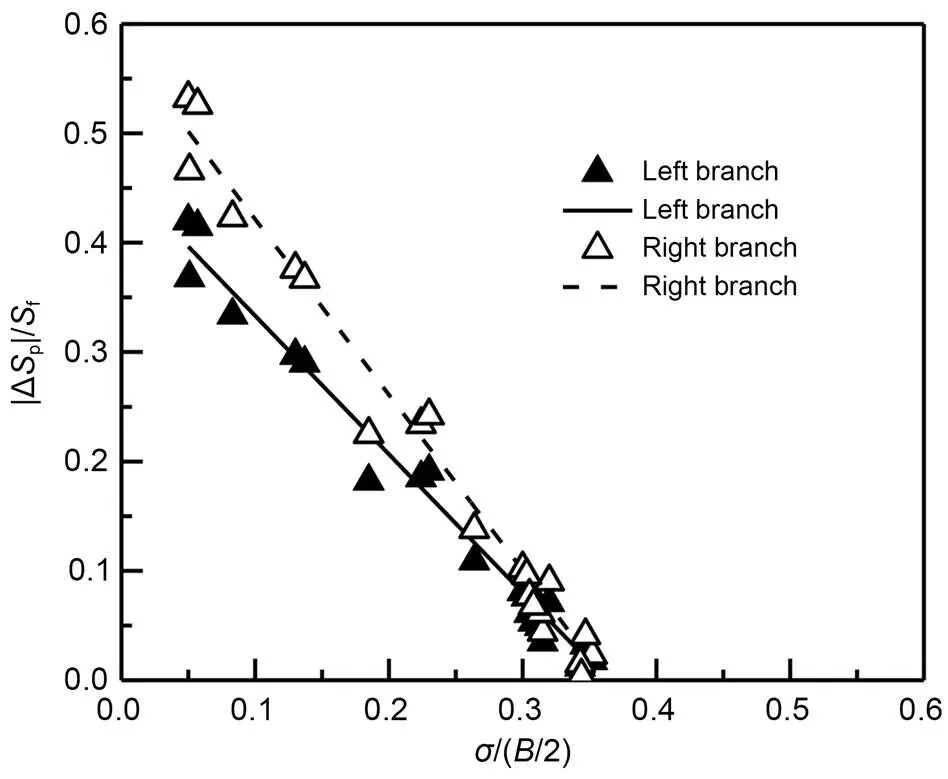
Fig. 17 Relationship between |ΔSp|/Sf and σ/(B/2): surface layer under branching form 5

Fig. 18 Relationship between |ΔSp|/Sf and σ/(B/2): bottom layer under branching form 5

Regardless of the chosen layer (surface or bottom layer), there occurred an approximately linear relationship between |Δp|/fand/(/2).

Both under the branching forms in which the left branching angle was larger than the right branching angle and the branching forms in which the left branching angle was smaller than the right branching angle, an approximately linear relationship was observed between |Δp|/fand/(/2).

Based on the above analysis, |Δp|/fand/(/2) attained the relationship as shown in Eq. (9).

(9)

wheredenotes the intercept anddenotes the slope. According to the selected water layers, this relationship generated surface and bottom curves. According to the considered branches, the data were divided into left and right branch pollutant flux ratio curves. The linear fitting results are summarized (please refer to Table S12 in the ESM).

The pollutant flux ratio can be calculated by the following equations, as shown in Eqs. (10) and (11). For a specific braided river, the pollutant flux ratiopwas only related toandfand did not depend on the distance information and downstream pollutant data.

(10)

(11)

Sediment is one of the important river characteristics. Sediment was not added in this test. It is necessary to consider the distribution, sorption, and release capacity of sediment while considering the distribution of pollutants. If the phenomenon of the sorption, storage, and release of pollutants by sediments is located upstream of the diverging area, the concentration distribution upstream of the diverging area will be affected. The sorption of pollutants by sediment leads to the decrease of pollutant concentration in the whole or part of the section, and the release of pollu tants by sediments leads to the increase of pollutant concentration in the whole or part of the section. The mixing degree by Gaussian fitting method will no longer accurately reflect the degree of pollutant diffusion. However, one of the keys mentioned in this study is that the mixing degree upstream of the diverging area is the joint action of many factors, including the sorption, storage, and release of pollutants by sediments. The role of various factors is a process, and the concentration distribution upstream of the diverging area is the result. Therefore, for the pollutants existing in water rather than sorbed by sediment, only the distribution characteristics upstream of the diverging area need to be considered. Of course, the phenomenon of the sorption, storage, and release of pollutants by sediments will distort the existing linear relationship to some extent and the influence of the release of pollutants by sediments is similar.

The pollutants simulated in this test were conservative substances. If non-conservative pollutants degrade after entering the water, it can be understood as the continuous reduction of pollutants, which is similar to the sorption of pollutants by sediments. The focus of the problem is still the pollutant concentration distribution upstream of the diverging area. Relatively speaking, the complexity brought by sediment factor is higher than that of non-conservative substances, because the former needs to consider the spatial relationship between the distribution of the pollutants and the sediment, as well as the relative relationship between the sorption or release capacity of pollu tants by sediment and the quantity of pollutants.

3.4 Relationship between the linear coefficients and the branching angle

According to Eq. (9),denotes the intercept anddenotes the slope in the linear relationship. Further ana lysis reveals thatandchanged with the branching form (branching angle2), as shown in Figs. 19 and 20.

The regularity relationship betweenand2is as follows: When2<45°, the value ofdecreased with increasing2, and the value ofof the left-branch curve was larger than that of the right-branch curve. When2>45°, the value ofincreased with increasing2, and thevalue of the left-branch curve was smaller than that of the right-branch curve. With the symmetrical branching angle (2=45°) as the dividing point,and2exhibited an approximate linear relationship on both sides of the dividing point.

The regularity relationship betweenand2was as follows: When2<45°, the value ofincreased with increasing2, and thevalue of the left-branch curve was smaller than that of the right-branch curve. When2>45°, the value ofdecreased with increasing2, and thevalue of the left-branch curve was larger than that of the right-branch curve. With the symmetrical branching angle (2=45°) as the dividing point,and2attained an approximate exponential type relationship on both sides of the dividing point.

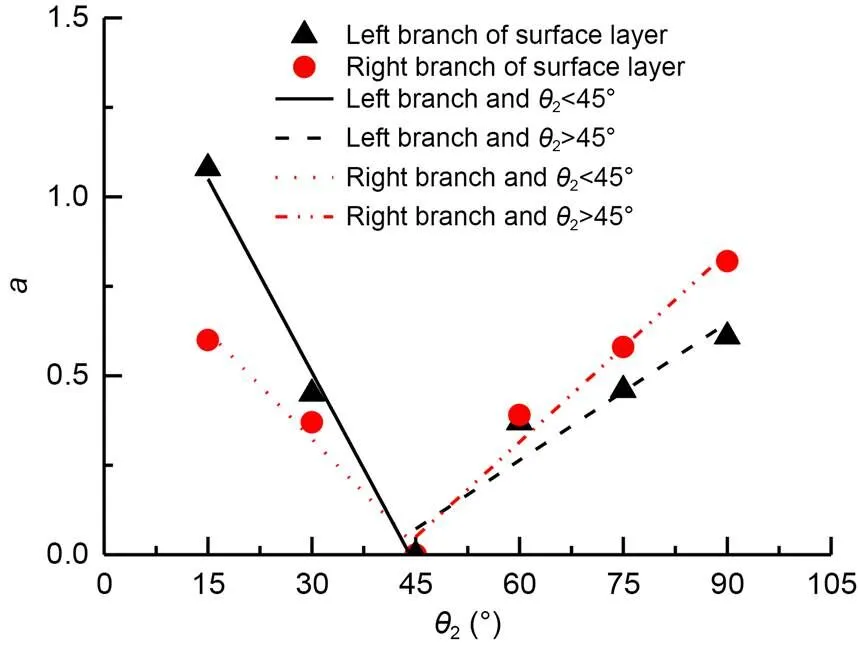
Fig. 19 Relation curve of a and θ2: surface layer

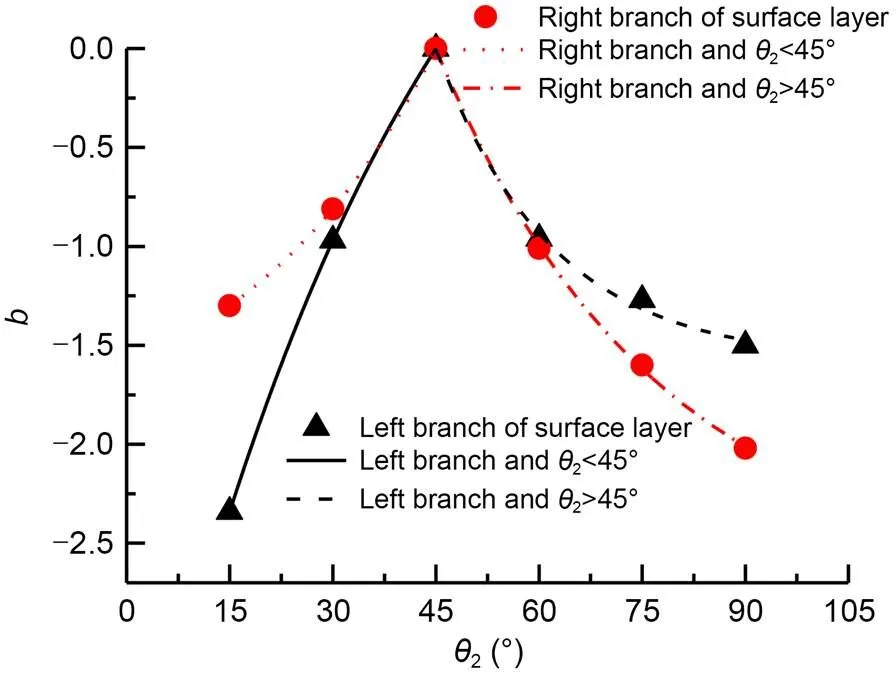
Fig. 20 Relation curve of b and θ2: surface layer

The linear relationship coefficients and the bran ching angle indicated an opposite monotonicity with the symmetric branch angle as the dividing point. Consideration of different water layers or branches did not affect this trend (please refer to Tables S13 and S14 and Figs. S15 and S16 in the ESM).

4 Conclusions

The aim of the present research was to determine the effects of the mixing degree upstream of the diverging area on the allocation characteristics of braided rivers. The conclusions are as follows:

1. Under asymmetric branching, when the pollu tant diffusion process upstream of the diverging area occurred at the first or second stage, the pollutant flux ratio exhibited a trend of deviating from the corresponding discharge ratio. The mixing degree upstream of the diverging area, which was closely related to the longitudinal discharge distance, notably affected the pollutant flux ratio. The lower the mixing degree, the larger was the deviation of the pollutant flux ratio from the discharge ratio. A linear relationship was attained between the dimensionless mixing degree/(/2) and the dimensionless deviation of the pollutant flux ratio from the discharge ratio |Δp|/f. Consideration of different branching angles or different water layers or different branches did not affect this trend.

2. The interceptand slopeof the linear relationship between |Δp|/fand/(/2) varied with the branching angle2. Coefficientsand2attained an approximately linear relationship. Coefficientsand2exhibited an approximately exponential type relationship. The linear relationship coefficients and the branching angle indicated an opposite monotonicity with the symmetric branch angle as the dividing point.

3. In this study, the concept of the mixing degree upstream of the diverging area helps to explain that other factors in the section from the discharge point to the diverging area, which can alter the mixing degree upstream of the diverging area (such as incident angle and incident momentum), can also affect pollutant allocation downstream by influencing the mixing degree. Their comprehensive effect is finally reflected in the mixing degree. This research is helpful in better understanding the mechanism of the factors influencing pollutant transport in complicated braided rivers.

4. This study provided a new approach for predicting the pollutant flux ratio of a braided river, namely, the pollutant flux ratio can be indirectly determined by the concentration distribution in a representative section upstream of the diverging area. The current limitation of this method is that it is only applicable to central discharge conditions, and the calculation accuracy of the linear relationship has not been verified in practice. Although the above results are preliminary results and suffer limitations, this study revealed the regularity relationship between the mixing degree upstream of the diverging area and the pollutant flux ratio. In future work, data from actual rivers should be obtained in comparative research as far as possible, and the comprehensive effect of transverse and longitudinal positions on the pollution allocation characteristics should be considered.

This work is supported by the National Natural Science Foundation of China (No. 51879176) and the Jiangxi Provincial Water Conservancy Science and Technology Project (No. 202022YBKT09), China.

Jun ZOU designed the research. Jun ZOU and Chang-yuan LI processed the corresponding data. Jian-min ZHANG provided the test scheme reference. Jun ZOU wrote the first draft of the manuscript, and revised and edited the final version.

Jun ZOU, Jian-min ZHANG, and Chang-yuan LI declare that they have no conflict of interest.

Alexeevsky NI, Chalov RS, Berkovich KM, et al., 2013. Channel changes in largest Russian rivers: natural and anthropogenic effects., 11(2):175-191. https://doi.org/10.1080/15715124.2013.814660

Chalov S, Moreido V, Sharapova E, et al., 2020. Hydrodynamic controls of particulate metals partitioning along the Lower Selenga river—main tributary of the Lake Baikal., 12(5):1345. https://doi.org/10.3390/w12051345

Chalov SR, Alexeevsky NI, 2015. Braided rivers: structure, types and hydrological effects., 46(2):258-275. https://doi.org/10.2166/nh.2013.023

Das A, Barman BC, Nandi N, 2022. On some aspects of flow characteristics of the bifurcated channel?–?an experimental approach., in press. https://doi.org/10.1080/09715010.2022.2042862

Gu L, Hua ZL, Chu KJ, et al., 2011a. Experimental study on transport characteristics of pollutants with different density in braided river., 30(6):242-250 (in Chinese).

Gu L, Hua ZL, Zhang CK, et al., 2011b. Mixing characteristics and transport flux ratio of pollutants in braided rivers., 20(9):2315-2325.

Hua ZL, Gu L, 2008. Experiments on pollutant transport of centerline discharge into the braided river. Proceedings of the 16th IAHR-APD Congress and the 3rd Symposium of IAHR-ISHS. https://doi.org/10.1007/978-3-540-89465-0_96

Hua ZL, Peng J, Ji W, et al., 2013a. Modeling experiment on characteristics of pollutant transport and mixing in waterway with multi-anabranch and Five Islets., 36(8):6-10 (in Chinese).

Hua ZL, Ji W, Shan NN, et al., 2013b. Pollutant mixing and transport process via diverse transverse release positions in a multi-anabranch river with three braid bars., 6(3):250-261. https://doi.org/10.3882/j.issn.1674-2370.2013.03.002

Ji W, Hua ZL, Wu W, et al., 2012. Transport and mixing characteristics of pollutants by continuous point source discharge in the multi-anabranch river with Three Braid Bars. Proceedings of the International Conference on Biomedical Engineering and Biotechnology. https://doi.org/10.1109/iCBEB.2012.454

Jiang F, Chen WP, Chen M, et al., 2006. Primary study on diffusion of contaminants in meandering furcated rivers., 22(4):30-32 (in Chinese). https://doi.org/10.3969/j.issn.1004-6933.2006.04.008

Lee ME, Seo IW, 2007. Analysis of pollutant transport in the Han River with tidal current using a 2D finite element model., 1(1): 30-42. https://doi.org/10.1016/j.jher.2007.04.006

Leopold LB, Wolman MG, 1957. River Channel Patterns: Braided, Meandering, and Straight. USGS Numbered Series, U.S. Government Printing Office, Washington, USA. https://doi.org/10.3133/pp282B

Li KF, Zhao WQ, 1994. Study on diffusion and mixing law of pollutants in braided river., (1):8-12 (in Chinese).

Lu HY, Li ZW, Hu XY, et al., 2022. Morphodynamic processes in a large gravel-bed braided channel in response to runoff change: a case study in the source region of Yangtze River., 15(5):377. https://doi.org/10.1007/s12517-022-09641-y

Okuyade WIA, Abbey TM, 2016. Pollutants spread in a bifurcating river: the River Nun, Bayelsa, Nigeria., 12(6):1-19. https://doi.org/10.9734/JSRR/2016/26722

Peng FJ, Li KF, Liang RF, et al., 2021. Shallow lake water exchange process before and after water diversion pro jects as affected by wind field., 592:125785. https://doi.org/10.1016/j.jhydrol.2020.125785

Redolfi M, 2015. Sediment Transport and Morphology of Braided Rivers: Steady and Unsteady Regime. PhD Thesis, Queen Mary University of London, London, UK.

Yang HY, Lin BL, Zhou JJ, 2015. Physics-based numerical modelling of large braided rivers dominated by suspended sediment., 29(8):1925-1941. https://doi.org/10.1002/hyp.10314

Yun SH, Seo IW, Kwon SY, 2019. Analysis of analysis of behavior of contaminants at the braided river using the transient storage model. Proceedings of the 38th IAHR World Congress. https://doi.org/10.3850/38WC092019-1174

Figs. S1–S16 and Tables S1–S4

Oct. 26, 2021;

Revision accepted May 23, 2022;

Crosschecked Aug. 12, 2022

? Zhejiang University Press 2021