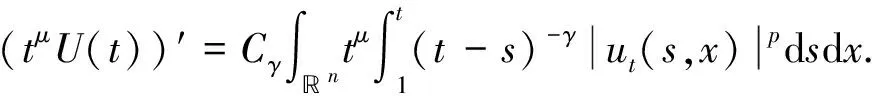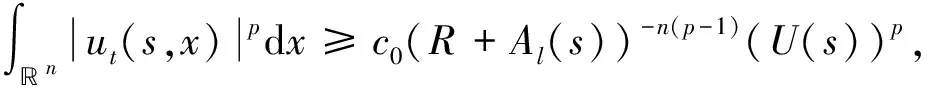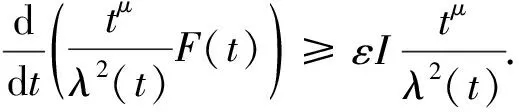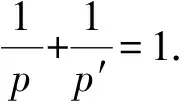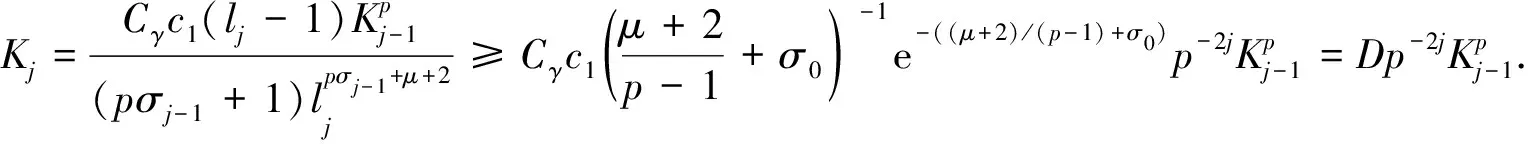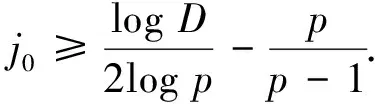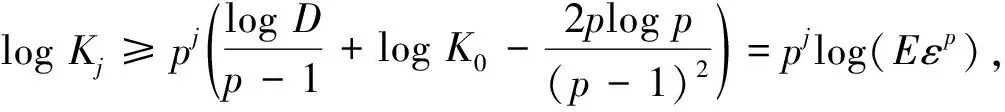一類具有導(dǎo)數(shù)型非線性記憶項(xiàng)和變系數(shù)耗散的廣義Tricomi方程全局解的非存在性
歐陽(yáng)柏平
(廣州華商學(xué)院 數(shù)據(jù)科學(xué)學(xué)院, 廣州 511300)
0 引 言
考慮如下導(dǎo)數(shù)型非線性記憶項(xiàng)和變系數(shù)耗散的廣義Tricomi方程全局解的非存在性問(wèn)題:

(1)
其中

Γ為第二類Euler積分,p>1,ε>0,l≥0, Δ是Laplace算子,μ為非負(fù)實(shí)數(shù).目前具有如下形式的Tricomi方程解的爆破等性態(tài)研究受到廣泛關(guān)注[1-5]:

(2)
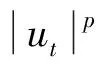



當(dāng)1

(4)
證明了當(dāng)
時(shí)其Cauchy問(wèn)題解的爆破, 并得到了生命跨度估計(jì):
其中k∈[0,1),μ為非負(fù)數(shù).文獻(xiàn)[13]研究了更一般的Euler-Poisson-Darboux-Tricomi方程解的爆破問(wèn)題:

(5)
給出了問(wèn)題(5)中具有衰減性的阻尼項(xiàng)和質(zhì)量項(xiàng)對(duì)解爆破的影響, 同時(shí)得到了其Cauchy問(wèn)題解的生命跨度估計(jì), 其中p>1,ε>0,l>-1, Δ是Laplace算子,μ,ν2均為非負(fù)實(shí)數(shù).
本文采用基于Bessel方程和迭代方法以及相關(guān)的泛函分析方法, 首先考慮問(wèn)題(5)中當(dāng)ν=0、 右邊項(xiàng)為導(dǎo)數(shù)型非線性記憶項(xiàng)時(shí)解的爆破問(wèn)題, 主要研究導(dǎo)數(shù)型非線性記憶項(xiàng)對(duì)其Cauchy問(wèn)題爆破解的非局部影響以及變系數(shù)對(duì)其爆破解的影響.根據(jù)實(shí)際應(yīng)用, 在非局部影響中, 本文側(cè)重于越近的信息影響越大, 故其影響因子取為(t-s)-γ.其次, 由于問(wèn)題(4)中t-2k(k∈[0,1)), 故文獻(xiàn)[12]研究了衰減情形下其Cauchy問(wèn)題解的爆破問(wèn)題.本文考慮t2l(l≥0), 即增長(zhǎng)情形下問(wèn)題(1)解的爆破問(wèn)題.并考慮對(duì)解的非局部影響.即通過(guò)構(gòu)造若干泛函, 用基本的泛函分析技巧, 先給出該泛函需要滿足的基本不等式框架, 再利用迭代方法得到其解的爆破及其生命跨度估計(jì).記
1 主要結(jié)果
定義1假設(shè)(u0,u1)∈H1(n)×L2(n).若對(duì)于u∈C([1,T),H1(n))∩C1([1,T),L2(n))并且n), 有

應(yīng)用分部積分, 進(jìn)一步化簡(jiǎn)式(6)為
本文主要結(jié)果如下:
定理1設(shè)(u0,u1)∈H1(n)×L2(n)為非負(fù)緊致函數(shù), 支集包含于半徑為R(R>0)的球BR上, 1 p2((l+1)(n-1)+μ-l)-p(2(1-γ)+μ+3+(l+1)(n-4))-2(l+1)=0. 本文主要采用迭代的思路完成定理1的證明.為此需先構(gòu)造若干能量泛函U(t),F(t),G(t), 然后利用這些能量泛函得到問(wèn)題(1)的迭代框架和第一下界, 進(jìn)而得到本文結(jié)果.設(shè) 其中Φ=Φ(s,x)是下列方程的正解: Φss+μs-2Φ=s2lΔΦ+μs-1Φs. (11) 式(7)中, 取φ=φ(s,x)=1, 其中(s,x)∈[1,t]×n且|x|≤R+Al(s), 可推出 由式(8)和式(12), 有 (13) 對(duì)式(13)關(guān)于t求導(dǎo)數(shù), 進(jìn)一步化簡(jiǎn)得 (14) 積分式(14), 有 借助已知條件和H?lder不等式, 可得 (16) 其中c0=c0(n,p,l)>0.結(jié)合式(15),(16), 得到U(t)的迭代框架.即 其中c1>0. 下面研究U(t)的第一下界.為此, 首先給出正光滑函數(shù)[14]: Ψ(x)有下列性質(zhì): 取Φ=Φ(s,x)=λ(s)Ψ(x), 結(jié)合式(11), 易得 λ″+μs-2λ=s2lλ+μs-1λ′. (18) 做變換η=wl(s), 化簡(jiǎn)式(18)有 (19) 再做變換 化簡(jiǎn)整理得 (20) λ(s)=s(μ+1)/2Km(wl(s)). (21) 由此得方程(11)的正解為 Φ(s,x)=λ(s)Ψ(x)=s(μ+1)/2Km(wl(s))Ψ(x). (22) 由波方程的有限傳播速度可知,u具有緊支集, 因此Φ的支集條件可以去掉.將式(7)中Φ替換φ, 并注意到式(9), 可得 記 下面證明I>0. 由式(21), 有 λ′(t)=μt(μ-1)/2Km(wl(t))-t(1+μ)/2+lKm+1(wl(t)). (24) 由第二類Bessel函數(shù)關(guān)系式 得 λ′(1)=μKm(wl(1))-Km+1(wl(1)), μλ(1)-λ′(1)=Km+1(wl(1))>0, λ(1)=Km(wl(1))>0. 故I>0. 重寫式(23), 得 (25) (26) 對(duì)式(26)積分, 并化簡(jiǎn)可得 (27) (28) 因此, 存在t0>1,m1,m2>0,t≥t0, 使得 m1e-2wl(t)tμ-l≤λ2(s)≤m2e-2wl(t)tμ-l. (29) 由式(27),(29), 得 其中c1為正數(shù),t≥2t0. 由Φ(s,x),F(t),G(t)的定義, 有 (31) 結(jié)合式(23),(31), 得 (32) 對(duì)式(32)關(guān)于t求導(dǎo)數(shù), 得 利用式(18), 進(jìn)一步化簡(jiǎn)式(33)得 (34) (35) 對(duì)式(35)進(jìn)行積分, 有 結(jié)合式(29),(36), 當(dāng)t≥2t0時(shí), 有 其中c2,c3>0. 對(duì)式(10)泛函G(t), 并應(yīng)用H?lder不等式, 有 (38) (39) 又由Φ的漸近性[14], 可得 其中C0,C1,C2>0. 將式(40)代入式(39), 并化簡(jiǎn)整理得 其中C3>0,t≥2t0.聯(lián)立式(15),(41), 對(duì)于t≥t1,t1=2t0, 可推出U(t)的第一下界, 即 取 重寫式(42), 得 U(t)≥K0t-α0(t-t1)σ0. (43) 下面由式(17)的迭代框架及式(43)的第一下界, 再利用對(duì)U(t)進(jìn)行迭代完成定理1的證明.令 U(t)≥Kjt-αj(t-Ljt1)σj, (44) 其中{Kj}j∈′,{αj}j∈′,{σj}j∈為非負(fù)實(shí)序列,t≥Ljt1.序列{Lj}j∈定義為 聯(lián)立式(17),(44), 有 其中t≥Lj+1t1.式(45)表明式(44)對(duì)j+1成立.同時(shí), 由式(45)得 由式(47),(48)可推出αj,σj的表達(dá)式, 即 (50) 由式(50), 易知 (51) 又 (52) 下面結(jié)合式(50)~(52)及式(46)估計(jì)Kj, 即 (53) 對(duì)式(53)兩邊取對(duì)數(shù), 并結(jié)合遞推關(guān)系, 可得 取j0∈, 使得 于是, 當(dāng)j≥j0時(shí), 由式(54)可推出 (55) 其中E=E(u0,u1,n,p,l,μ,γ)>0. 由對(duì)數(shù)的性質(zhì)和式(55), 易得 Kj≥exp{pjlog(Eεp)}. (56) 由Lj和L定義, 當(dāng)j→∞時(shí)有Lj→L.從而下式成立: U(t)≥Kjt-αj(t-Lt1)σj. (57) 聯(lián)立式(49),(50)及(56),(57), 對(duì)于j≥j0,t≥t1, 有 式(59)對(duì)數(shù)函數(shù)中t的指數(shù)為 取1 令ε0=ε0(u0,u1,n,p,l,μ,γ)>0, 使得 于是當(dāng)j→∞時(shí), 可推出式(59)中U(t)的下界爆破.從而可得問(wèn)題(1)不存在全局解.同時(shí), 可得問(wèn)題(1)的另一個(gè)結(jié)果, 即u的生命跨度估計(jì)為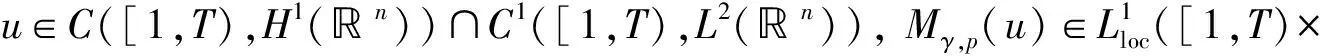
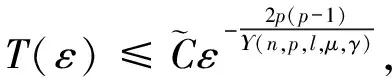

2 定理1的證明