Substitutions of vertex configuration of Ammann–Beenker tiling in framework of Ammann lines

Jia-Rong Ye(葉家容), Wei-Shen Huang(黃偉深), and Xiu-Jun Fu(傅秀軍)

School of Physics and Optoelectronics,South China University of Technology,Guangzhou 510640,China

Keywords: quasicrystals,Ammann–Beenker tiling,Ammann lines,substitution rules

1. Introduction

A variety of quasicrystals have been fabricated in experiment and widely investigated in theory since the pioneer work by Shechtmanet al.[1]Because of their nontrivial properties,quasicrystals have been of growing interest for the past decades. Quasiperiodic structures have been employed in many fields,which leads to abundant new features. Recently,researchers have studied many physical properties based on different theoretical models ranging from one-dimensional(1D)to three-dimensional(3D)quasicrystals. The high-order harmonic generation in a Fibonacci quasicrystal was simulated and the electron dynamics on the attosecond time scale was investigated.[2]A tenfold symmetric photonic quasicrystal was proposed and linear propagation of light wave was studied.[3]A two-dimensional(2D)octagonal quasicrystal was modeled and the plane elasticity problems were studied by the symplectic approach.[4]A 3D multilayered quasicrystal was constructed and the static response and free vibration analysis was presented.[5]

2D quasicrystals are materials in which atoms are arranged quasiperiodically on a plane and are repeated periodically along the perpendicular direction of the plane. Even though many rotational symmetries are permitted in mathematics, only fivefold, eightfold, tenfold and twelvefold symmetric structures have been observed in real quasicrystals. As a prototype model, the Penrose tiling, which possesses fivefold symmetry, has been extensively studied in the past and many meaningful results have been presented. However,other quasiperiodic models have received relatively little attention.This paper is devoted to studying the structural properties of an eightfold symmetric quasiperiodic lattice, the Ammann–Beenker tiling.

The construction methods of the Ammann–Beenker tiling(AB tiling)were proposed and its fundamental characteristics were presented in the early literature.[6–8]Because of the complexity and rich content of the quasilattice,the structural properties of the AB tiling have aroused continuous interest of scientists in recent years. For instance, by analyzing the coordination numbers of the vertex of the AB tiling, it is proved that there exists a limit growth form for the vertex graph of the tiling.[9]Based on the square and rhombus inflationdeflation,the self-similar transformation of the vertex configuration of the AB tiling was obtained.[10]Guided by the local matching rules and configuration selection,an improved algorithm for aggregation of square and rhombus tiles to generate an octagonal quasilattice was proposed.[11]

The novel physical properties in the AB tiling structure have also been discovered recently. For example,the disorderinduced chiral Majorana edge mode and helical Majorana edge mode in a quasicrystal of the AB tiling type were revealed and it was demonstrated that the edge modes are robust against weak disorder in the quasicrystalline lattice.[12]For the case of AB tiling, the level-spacing statistics for noninteracting Hamiltonians were studied, showing that the spectral properties can be well described by the universal Gaussian orthogonal random matrix ensemble.[13]A vertex tight-binding model on the AB lattice was investigated,and strictly localized states in the center of the spectrum were found.[14]A tight-binding model for superconductor on the AB tiling was constructed and topological phases protected by quasicrystalline symmetries were established.[15]Significant progress of topological states in AB tiling quasicrystals has been made.[16–19]

2. AB tiling and Ammann lines

An intuitive method to produce the AB tiling is the socalled self-similar transformation of squares and 45?rhombuses. As shown in Fig. 1(a), an original square is divided into nine parts consisting of one small square, four small rhombuses and four halves of small square. One half small square will combine the adjacent half square resulting from the transformation outside the original square,and thus forming a full square. Counting for the number of tiles enclosed by the original square, we note that a square will produce three small squares and four small rhombuses after one transformation. Similarly,a rhombus will produce two small squares and three small rhombuses after one transformation as shown in Fig.1(b). Successive use of the self-similar transformation results in a finite AB tiling.

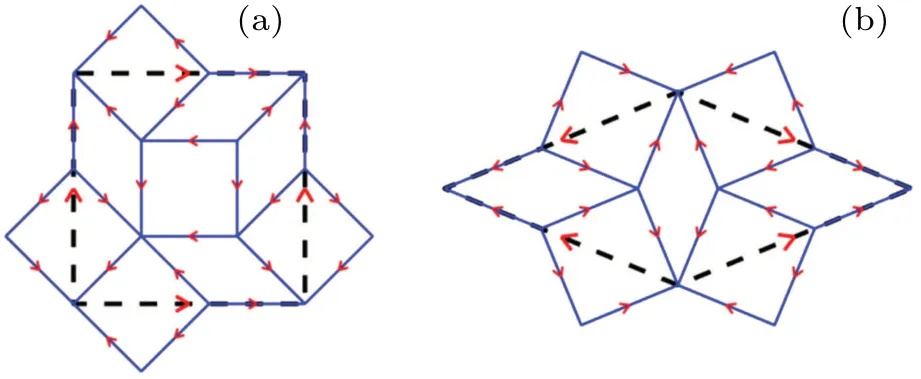
Fig.1. Self-similar transformation for(a)a square and(b)a 45?rhombus,with thick line and thin line representing tiles before and after the transformation,respectively.

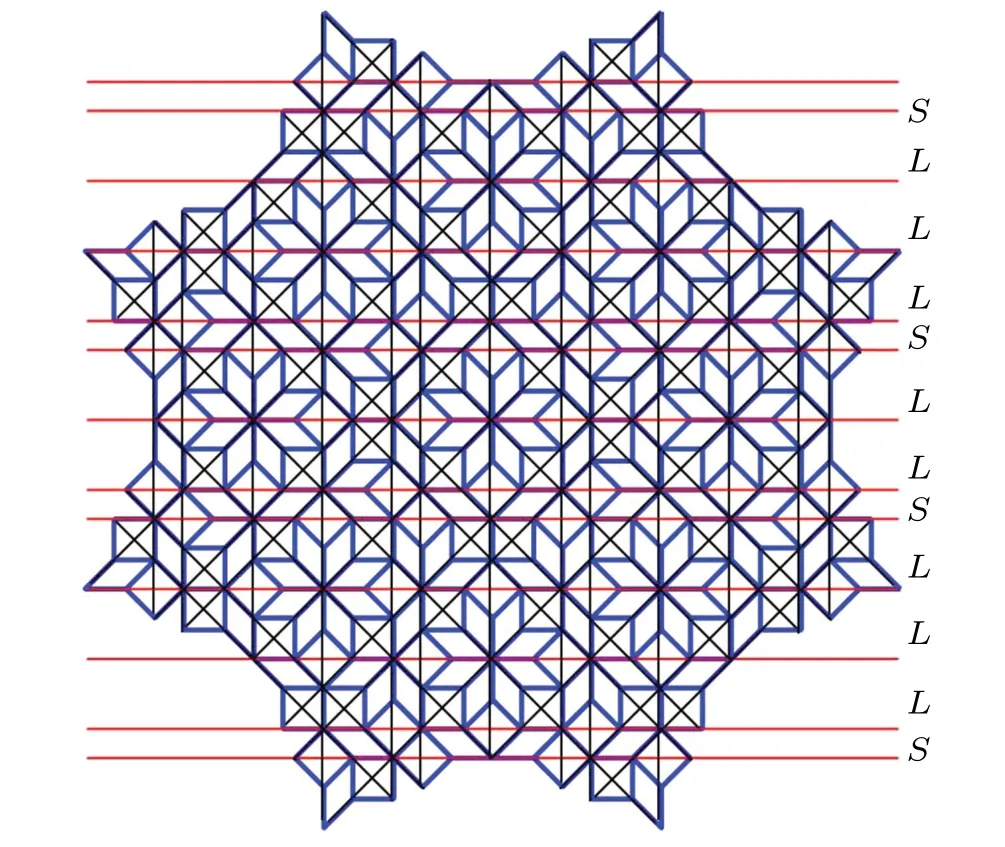
Fig.2. Four sets of Ammann lines formed by connecting diagonals of each square, with red lines denoting one of the grids consisting of parallel lines with two spacings L and S between adjacent lines.

3. Vertex types and orientations along Ammann lines

The distribution of sites in a quasilattice never simply repeat themselves as that in a crystalline lattice but rather in a quasiperiodic way. In order to reveal the structural properties,vertex configuration analysis is often used,which reflects the local order. A vertex configuration refers to a cluster of nearest-neighbor tiles that share a common vertex. The angle of the vertex of a single tile can beπ/4 or 3π/4 for a rhombus andπ/2 for a square,and the sum of the angles around a vertex must be 2π. Considering only the local combination of the tiles, there would be 19 types of different configurations.However, some of them do not exist in a perfect AB tiling.If the arrows on the sides of tiles are also taken into account,there are seven vertex types in the AB tiling named A,B,C,D,E,F,and G,which correspond respectively to Figs.3(a)–3(g).The vertices C and D have the same tiles and arrangement,but the three arrows on the horizontal sides of two squares are in the opposite directions.

In the following, we are going to study the vertex distribution along the Ammann lines including their orientations,so we define the direction from the left to the right horizontally as the direction of a vertex configuration, by choosing a reference line labeled by 0 on each vertex as shown in Fig.3.The possible values of the angle between an Ammann line and the reference line of a vertex can benπ/4 withn=0, 1, 2,3, 4, 5, 6, and 7. Thus, a vertex, including both its type and the orientation on a designated Ammann line can be specified by a letter and an integer, in which the former represents its type and the latter denotes its orientation. For vertex of type A,only one Ammann line passes through it and there are two relative directions between the Amman line and the reference line. So A0 and A4 are used to distinguish these two scenarios in Fig.3(a). For the vertex of type B,two Ammann lines including their directions make four angles with the reference line, so B0, B1, B4, and B5 are used in Fig. 3(b). The other four vertices of type C-F and their orientations relative to different Ammann lines are shown in Figs.3(c)–3(f). The vertex configuration of type G is special in that it has eightfold symmetry,so there is no need to label its direction by an additional integer.

Fig.3.Seven types of vertex configurations and their orientations relative to a specific Ammann line.The numbers represent the angles between the horizontal reference line and an Ammann line,which are integer multiples of π/4.

4. Self-similar transformation of vertices

The self-similar transformations shown in Fig. 1 display the new tiles developed from a single square or rhombus.When the transformations are applied to all the tiles around a vertex, the resulting tiles form new vertices and their distribution correlations can be obtained from the process. The transformation rules guarantee that the new tiles occupying original two neighboring tiles overlap each other without mismatching. The number and concentration of the seven types of vertex configurations after a transformation were studied in previous work and analytical expressions was derived.[11]However, the orientations of the vertex distribution have not been considered. In a quasilattice,both the long-range translational order and the orientational order are of significance. In the framework of the Ammann lines,it is convenient to study the correlations of vertex distribution and orientation.

Figure 4 shows the patterns before and after the transformation. In Fig.4(a),four new vertices along the horizontal direction(Ammann line)are generated after the transformation from a vertex of type A.They are labeled as A0,D4,C0,and A4,respectively,observed from left to right. This means that the reference lines defined in Fig. 3 for each individual vertex make angles of 0,π,0,andπwith the horizontal Ammann line,respectively.In Fig.4(b),four new vertices along the horizontal direction are of types A,E,B,and B,respectively,and the angles between the reference line and the Ammann line are respectively,π/4,5π/4,andπ,so they are labeled as A0,E1,B5,and B4,respectively.Only the new vertices along the horizontal Ammann lines are shown. There are new vertices along other Ammann lines which are not drawn in the figure. By a series of investigations and calculations,all the vertices developed after a self-similar transformation into the seven types of vertex are obtained and listed in Table 1.

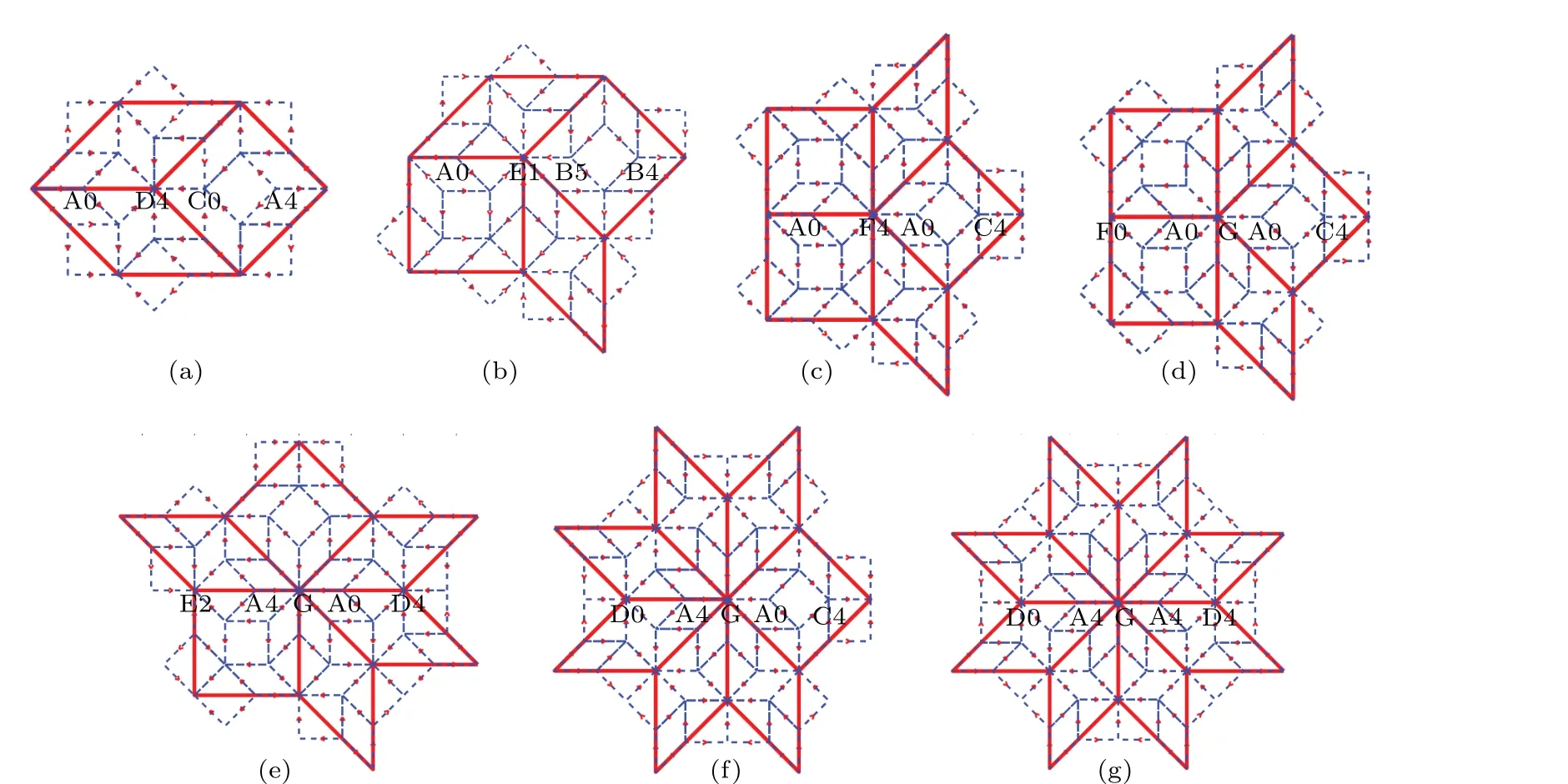
Fig. 4. Self-similar transformation of seven types of vertex. There are more than one Ammann line in each pattern, and only the vertices along the horizontal Ammann line are shown.

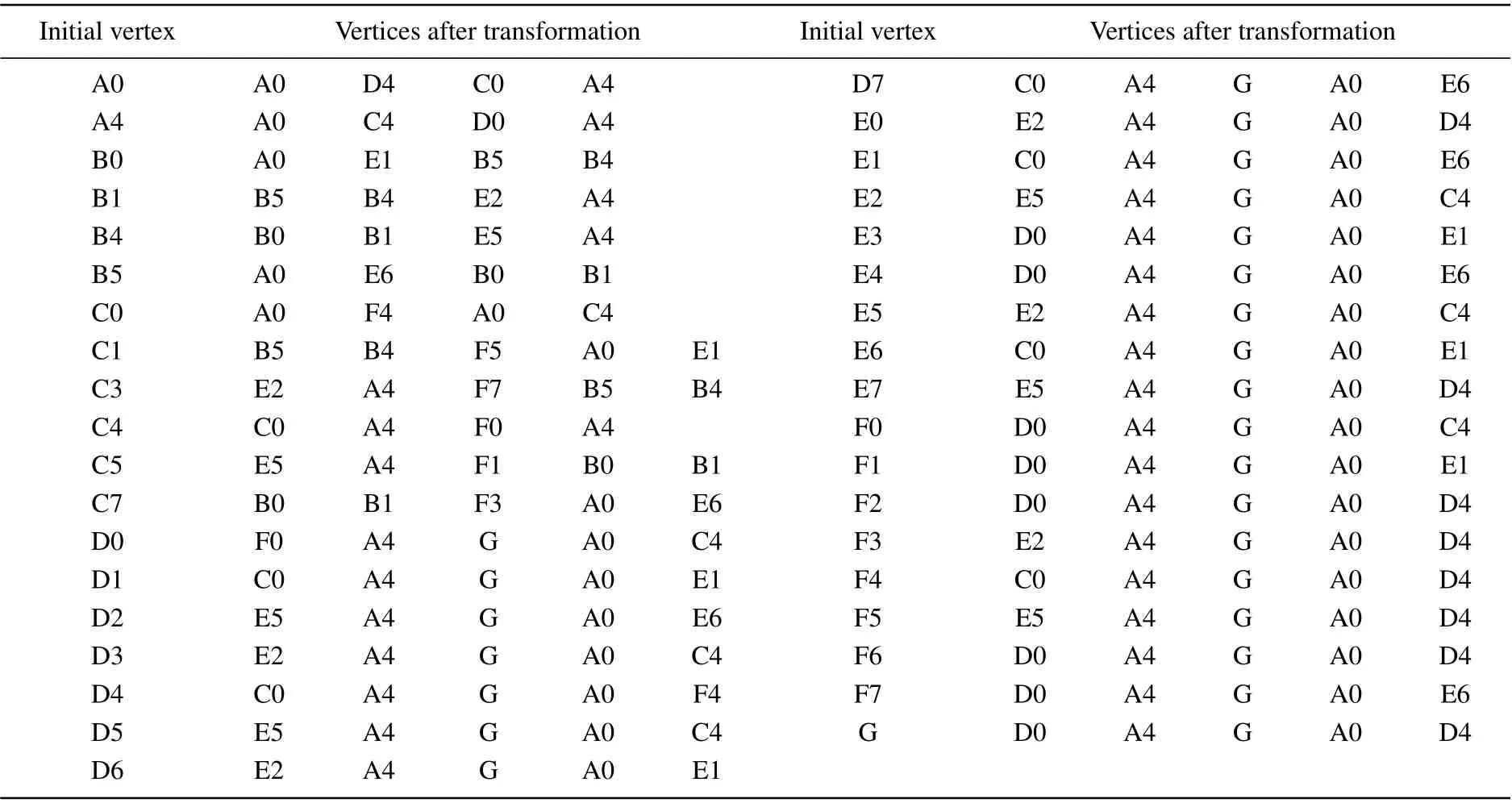
Table 1. Distribution of vertices after self-similar transformation. Each row lists a vertex before transformation (initial vertex) and vertices along one of Ammann lines after e transformation.

5. Vertex substitution along Ammann lines

In the 1D case, a quasiperiodic sequence can be generated by successive substitutions according to certain rules.For example,the rules A→AB and B→A produce a Fibonacci sequence ABAABAABAABB···. In the 2D AB tiling, the sequence of spacingsLandSbetween adjacent parallel Ammann lines follow the substitution rulesL →LLSandS →L, but it does not include the information of vertex configurations.Here we investigate the substitutions of vertices along an Ammann line. A self-similar transformation on an AB tiling produces not only new tiles of square and rhombus but also new Ammann lines. The Ammann lines cross the center of the squares. According to the self-similar transformation shown in Fig.1(a),a new square appears after the transformation,so the original Ammann lines keep invariant during the transformation.If we observe the vertices along such an Ammann line,after the self-similar transformation,one of the new Ammann lines coincides with the original Ammann line. The new vertices along this Ammann line follow certain substitution rules.

The self-similar transformation shown in Fig.4 and listed in Table 1 can be used to construct the substitution rules. We start from B0 which is a type B vertex and the Ammann line gets through it in the same direction as its reference line. The first transformation produces four vertices associated with orientations,A0,E1,B5,and B4,as shown in Fig.5. The second transformation for these four vertices will be A0→(A0, D4,C0, A4), E1→(C0, A4, G, A0, E6), B5→(A0, E6, B0, B1),and B4→(B0,B1,E5,A4),with 17 vertices in total. However,two vertices (C0, A4) resulting from original A0 overlap the adjacent vertices(C0,A4)from E1,and so is the case for the other neighboring vertices. So the vertices in the next generation are(A0,D4,C0,A4,G,A0,E6,B0,B1,E5,A4)and the total number is 17?2×3=11 as shown in Fig.5.

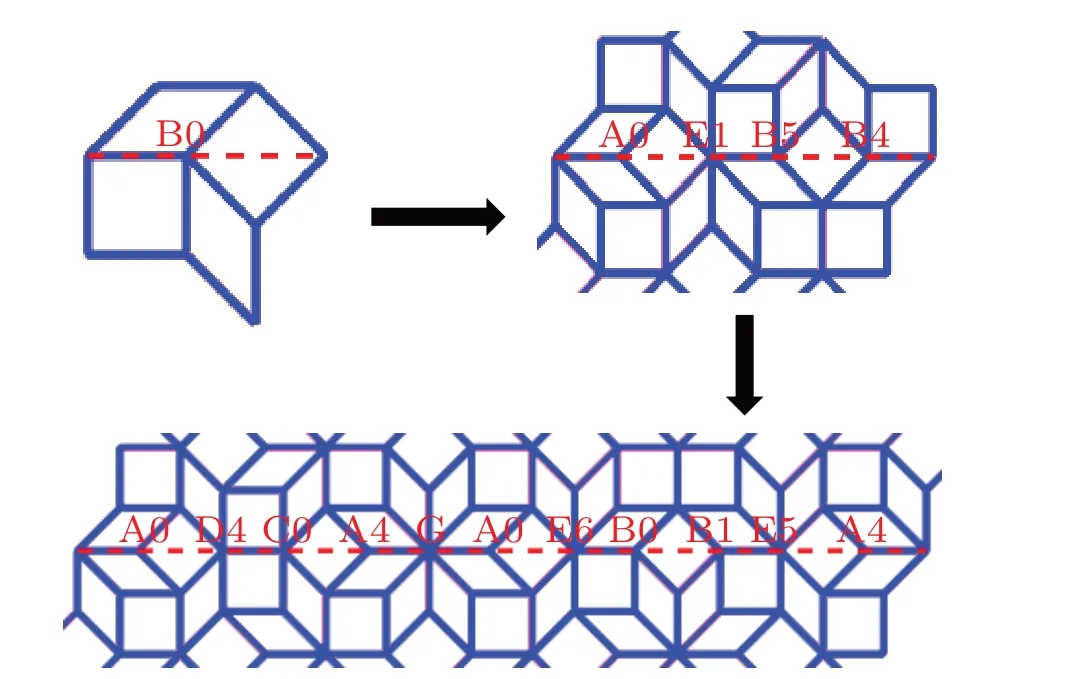
Fig.5.Arrangement of vertices when substitutions are applied to B0 vertices twice. Resulting configurations are of the first-and the second-generation.

Now the substitution rules of vertices along an Ammann line are described as follows. Starting from any initial vertex listed in the first(third)column of Table 1,the substitution is implemented according to the second(fourth)column,generating 4 or 5 new vertices. In the next step of substitution, all the new vertices resulting from the first vertex are kept, and the leading two vertices resulting from the other initial vertices are neglected. Taking the above B0 vertex for example,the first-generation vertices are(A0,E1,B5,B4),the secondgeneration vertices are (A0, D4, C0, A4, G, A0, E6, B0, B1,E5,A4),the third-generation vertices are(A0,D4,C0,A4,G,A0,F4,A0,C4,D0,A4,G,A0,D4,C0,A4,G,A0,E1,B5,B4, E2, A4, G, A0, C4, D0, A4), and the fourth-generation vertices are(A0,D4,C0,A4,G,A0,F4,A0,C4,D0,A4,G,A0,D4,C0,A4,G,A0,D4,C0,A4,F0,A4,G,A0,C4,D0,A4, G, A0, D4, C0, A4, G, A0, F4, A0, C4, D0, A4, G, A0,D4,C0,A4,G,A0,E6,B0,B1,E5,A4,G,A0,C4,D0,A4,G,A0,D4,C0,A4,F0,A4,G,A0,C4,D0,A4).

The vertex distribution in a large patch of the AB tiling is shown in Fig. 6. This pattern is generated by two times of self-similar transformation starting from a vertex of type G,which has eightfold rotational symmetry. Only the vertices and their orientations along a set of parallel Ammann lines are indicated.

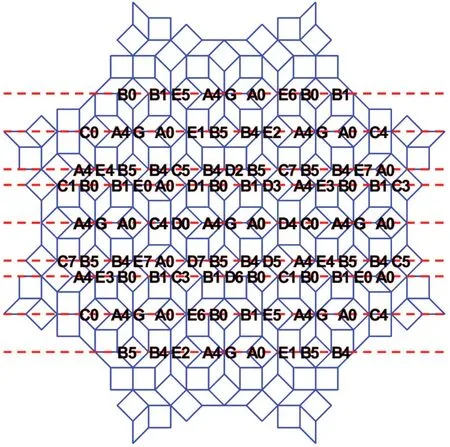
Fig. 6. Vertex distributions of AB tiling for a finite pattern with eightfold symmetry, with vertex types and orientations relative to a set of parallel Ammann lines indicated.

6. Discussion

The above results reveal the vertex correlations by considering both the local configurations and the orientations relative to the Ammann lines. They display an intuitive understanding of the eightfold quasiperiodic structure and also provide implications for growing a quasiperiodic tiling according to the local rules. One of the fundamental concerns of the quasicrystal models is how the quasiperiodic structures are formed. As is well known, there are different methods to construct a quasiperiodic lattice, including the deflationinflation, the higher-dimensional projection, and the general dual method. However,the formation of a real quasicrystal is not so easy and the growth mechanisms of quasicrystals have not been fully understood. In previous studies, growth algorithms of the Penrose tiling based on the local configurations were developed[21]which can produce an ideal quasiperiodic tiling with fivefold symmetry. As for the AB tiling, a growth algorithm based on three growth rules were proposed and perfect tiling has been obtained.[10]However, this algorithm is applicable only to an eightfold symmetric seed cluster. The present work reveals strong correlations among vertices along Ammann line, which may serve as an arrangement confinement of tiles and improve the growth rule for a perfect AB tiling.

Acknowledgement

Project supported by the National Natural Science Foundation of China(Grant No.11674102).