Topological and dynamical phase transitions in the Su–Schrieffer–Heeger model with quasiperiodic and long-range hoppings

Wei-Jie Zhang, Yi-Piao Wu, Ling-Zhi Tang and Guo-Qing Zhang,2

1 Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials, School of Physics and Telecommunication Engineering,South China Normal University,Guangzhou 510006,China

2 Guangdong-Hong Kong Joint Laboratory of Quantum Matter, Frontier Research Institute for Physics,South China Normal University, Guangzhou 510006, China

Abstract Disorders and long-range hoppings can induce exotic phenomena in condensed matter and artificial systems.We study the topological and dynamical properties of the quasiperiodic Su–Schrier–Heeger model with long-range hoppings.It is found that the interplay of quasiperiodic disorder and long-range hopping can induce topological Anderson insulator phases with nonzero winding numbers ω = 1, 2,and the phase boundaries can be consistently revealed by the divergence of zero-energy mode localization length.We also investigate the nonequilibrium dynamics by ramping the long-range hopping along two different paths.The critical exponents extracted from the dynamical behavior agree with the Kibble–Zurek mechanic prediction for the path withW =0.90.In particular, the dynamical exponent of the path crossing the multicritical point is numerical obtained as 1 /6 ～ 0.167,which agrees with the unconventional finding in the previously studied XY spin model.Besides,we discuss the anomalous and non-universal scaling of the defect density dynamics of topological edge states in this disordered system under open boundary condictions.

Keywords: topological Anderson insulator, higher winding number, Kibble–Zurek machanic

1.Introduction

Topological insulators, characterized by topological invariants and non-trivial surface states, have witnessed fast development in condensed-matter [1, 2] and tunable artificial systems [3–14].In general, topological insulators are robust against certain types of weak disorder due to symmetric protection.However, in the presence of strong disorder, the system usually becomes trivial insulators due to the Anderson localization [15].The nontrivial interplay between topology and localization leads to a surprising phenomenon of topological Anderson insulators (TAIs), which is an exotic topological phase induced by moderate disorders [16].The disorder-induced topological phase transitions and TAIs have been widely studied [16–41] and experimental evidenced in various systems [37, 42–46] such as ultracold atom [44] and photonic waveguide array [46].Notably, random disorders attached to on-site potentials or hopping terms are mainly considered in most of these works.It has been shown that quasiperiodic disorder can lead to unique localization behaviors,such as localization transition[47,48]and intermediate or critical phases [49–55].In addition, the presence of longrange hopping in disordered systems can give rise to the power-law localization [56–59], and the topological phases are studied in extended Su–Schrieffer–Heeger (SSH) model with long-range hoppings [60–63].However, the topological phase transition due to the interplay of quasiperiodic disorder and long-range hopping remains largely unexplored.

On the other hand, non-equilibrium dynamics hold a complementary and important way to explore the phase transitions.In particular,the Kibble–Zurek mechanics(KZM)[64,65]have been proposed to study the universal dynamical properties of second-order phase transitions with parameter ramping.According to KZM [64–67], the non-equilibrium dynamics react to the phase transition near the critical point and is immune to the detail setting.The excitation production obeys the power-law scaling with respect to the quench velocity.This can be vividly understood that the slower system moves,the less excitation comes into forge due to the loss of adiabaticity when crossing the critical point.The power-law exponent can be determined by the universal exponents,such as correlation length exponent and dynamical exponent.In experiments, the KZM of dynamical phase transitions has been observed in superfluid [68], Bose–Einstein condensation [69–71], trapped ions [72–75], and superconducting circuits [76, 77].Recently, considerable effort is devoted to studying the dynamical phase transitions in topological systems[78–87].For the dynamical topological phase transition, the edge states may exhibit anomalous scaling [78–80] and the local Berry curvature [86] and topological marker[86]can be connected to the characteristic correlation length in the context of the KZM.In addition,the characteristic correlation length is also verified in the localization transition in the presence of disorders [88, 89].However, the dynamical phase transition with the KZM in disordered topological systems is still less understood [86].

In this work, we study the topology, localization, and dynamics of the quasiperiodic SSH model with next-nextnearest-neighbor (NNNN) long-range hoppings.Firstly, we numerically compute the topological phase diagram by the real-space winding number to characterize the effects of disorder and long-range hopping.We find a higher winding number TAI phase together with other two different phases which consist a multicritical point.The topological phase boundaries are also characterized by the divergence of the zero-energy mode localization length.We then investigate the localization property by using the inverse partition ratio of eigenstates.The disorder induced extend to localization transition and non-trivial to trivial transition as well as a fully localized TAI region are observed.Furthermore, we extend our study to the nonequilibrium dynamics and study the KZM with topological phase transitions by ramping the long-range hopping strength along two representative paths in the topological phase diagram.The critical exponents numerical calculated from the dynamical behavior is consistent with the KZM power-law scaling prediction for one path withW=0.90,and the dynamical exponent for the path crossing the multicritical point is the same as the previously studied XY model.In addition, we discuss the defect density dynamics of the topological edge states and show their anomalous and non-universal scaling in this disordered system.

The rest of this paper is organized as follows.The extended SSH model with quasiperiodic disordered and longrange hoppings is proposed in section 2.Section 3 is devoted to studying the topological phase transitions and TAIs.In section 4,we explore the dynamical phase transition with the KZM in this disordered topological system.A brief conclusion is given in section 5.

2.Model

We consider the extended SSH model consisting of two sublattices A and B in a unit cell with an additional NNNN hopping, as shown in figure 1.The corresponding tightbinding Hamiltonian reads

Figure 1.The sketch of the extended SSH model with the incommensurate intracell hopping (tn), the intercell hopping (J) and the long-range NNNN hopping (J′).Blue and red balls indicate sublattices A and B in a unit cell circled by the dashed square.

whereandcA(B),ndenote the creation and annihilation operators on sublattice A(B) in thenth unit cell,Jis the nearest-neighbor intercell hopping, andJ′ is the NNNN hopping between different sublattices.We further consider the quasiperiodic disordered intracell hoppingtnwith the incommensurate modulation form [90, 91]

whereαis an irrational number,φis a random phase for sampling,mis the overall hopping strength, andWis the quasiperiodic disorder strength.We consider the model ofNunit cells with a total number of2Nsublattice sites.This model with the disordered and long-range hoppings still satisfies the chiral symmetry [92] Γ-1HΓ = -Has only hoppings between different sublattices are contained, where Γ =IN?σzbeing the chiral operator,INis the identity operator, andzσthe Pauli matrix.For simplicity and without the loss of generality, we setJ=1 as the energy unit andα=as the golden ratio.

In the clean limit,the topology of the SSH model can be characterized by the winding number of Bloch vectors in the momentum space.However, the translational symmetry is broken in the presence of disorders.We can use the real-space winding number in a spectral projection method [21, 93] to characterize the bulk topology.The real-space winding number is given by [21, 93]

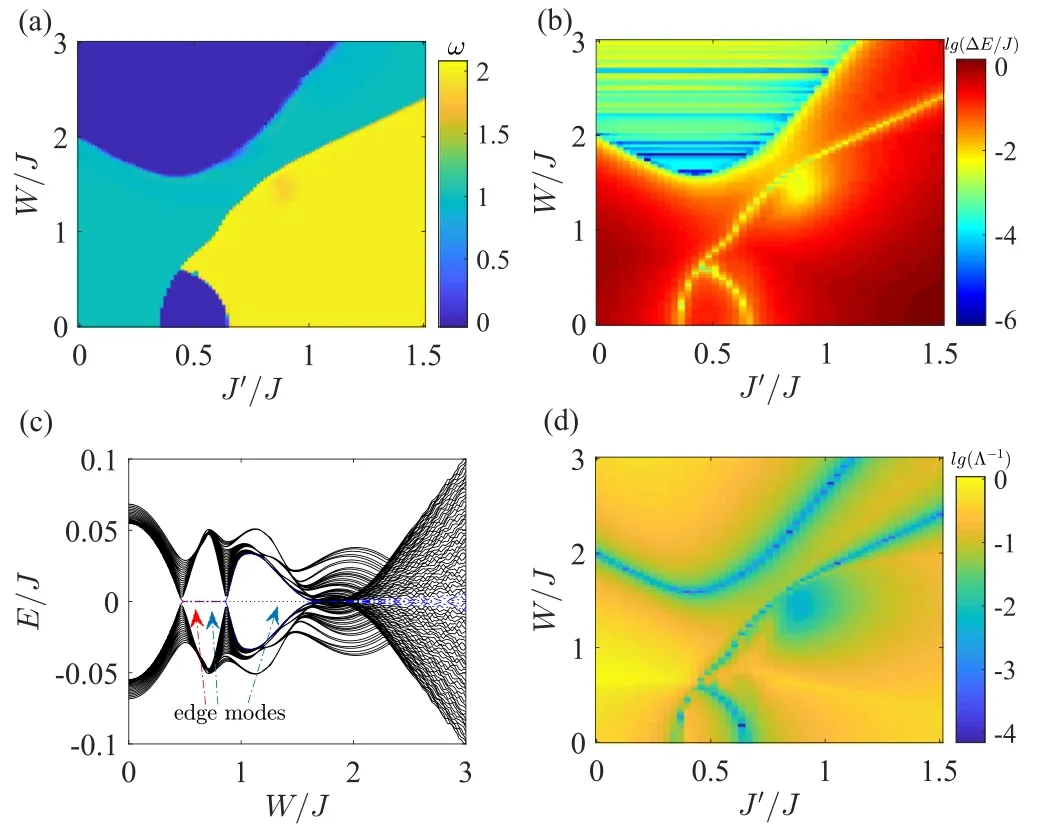
Figure 2.(a) Topological phase diagram in the J′–W plane.(b)Logarithm plot of the bulk energy band gap ΔE under PBCs.(c)Eigenenergies at the middle of the energy spectrum plotted as a function of W for J′=0.55under OBCs, where the red arrow indicates the second centered pair of edge modes (red dotted lines)and the blue arrows mark the most centered pair of edge modes(blue solid lines).(d)Logarithm plot of the inverse localization length Λ-1 computed by the transfer matrix method.Other parameters are N =987,m =0.65,φ =0.

3.Topological phase transitions

We now study the topological properties of the system in the static case.In figure 2(a), we present the topological phase diagram revealed by the real-space winding number in the W-J′plane forφ = 0and m =0.65.As shown in figure 2(a),when W =0,the topological phase transition for ω = 1 → ω= 0happens at J ′ = J - m = 0.35,and the topological phase transition for ω = 0 → ω= 2occurs at J ′ = m = 0.65.Thus, the long-range NNNN hopping can induce the topological phase with a high winding number(ω = 2) and related topological transitions even in the clean limit [60, 63, 94].When the quasiperiodic disorder is considered, there are more topological phase transitions induced by the interplay between the disorder strengthW and longrange hopping strength J ′.For instance,the topological phase transitions ω = 1 → ω= 2,ω= 1 → ω= 0 → ω= 2,and ω= 1 → ω= 0 → ω= 1 → ω= 2can be induced by increasing J′ for different fixed values ofW.In addition, the topological phase transitions ω= 0 → ω= 1 → ω= 0and ω= 0 → ω= 2 → ω= 1 → ω= 0can be induced by increasingW for 0.35 ? J′? 0.65.This indicates the disorder-induced TAI from the trivial phase, which becomes trivial insulators under strong disorder.We can also find that the long-range NNNN hopping significantly enlarges the topological region when J′ ＞m.

To reveal the behavior of the bulk gap with respect to the topological phase transitions, we calculate the gap ΔE given by the difference of the most centered two eigenenergies:

under the PBC.In figure 2(b), we plot ΔE in the log scale.The bulk gap closes and reopens when crossing the topological phase boundaries, which are consistent with the topological phase diagram shown in figure 2(a).Note that the bulk gaps in two trivial regions are significantly different.For large W, the bulk gap tends to close and the system is a trivial gapless Anderson insulator, while the bulk gap is not closed and the system is a band insulator for smallW and moderate J ′.We further show the bulk-boundary correspondence which relates the winding number with the edge states under OBC.In figure 2(c),we plot the most centered energy spectrum as a function ofW under OBC with fixed J ′ = 0.55.There is an energy gap forW ?0.48,where the system is in the band insulator region.When 0.48 ? W ? 0.86,two pairs of zeroenergy edge modes(blue solid lines and red dot lines)exhibit,corresponding to the TAI phase withω =2.When 0.86 ? W ? 1.64,one of the two pairs of edge modes disappears and the system becomes another TAI phase with ω = 1.WhenW ?1.64,the upper and lower bands are mixed due to strong disorder and the system is in the trivial gapless phase.

The zero-energy eigenstates related to the topological phase transitions are exponentially localized and their localization length Λ will be divergent at the transition points[21, 63].To further reveal the topological transitions, we numerically calculate the localization length by using the transfer matrix method [95].Expanding the Schr?dinger equation H ∣ φ〉 = E ∣φ〉 in matrix element in the basis of φ=[φ1,A, φ1,B…φN,A, φN,B]T,we can readily obtain the following iteration relation

where the transfer matrix for then-unit cell is written as [63]

which takes J =1 and depends on the quasiperiodic disorder strength tn(see equation (2)).The localization length Λ of zero-energy eigenstate with E =0 can be iteratively calculated based on the following matrix

with the smallest positive eigenvalue being denoted by γmin.The inverse of the localization length of the zero-energy mode Λ-1is then obtained as

In figure 2(d),we show the numerical results of Λ-1in the log scale.One can find the vanishing of Λ-1for the divergence of localization length (Λ →∞) accurately characterizes the boundaries of different topological phases.The results not only show the trivial-nontrivial phase transitions but also reveal that transition between two different topological phases withω =1 andω =2 in this disordered long-ranged SSH model.

To study the localization effect of the quasiperiodic disorder on the bulk state, we numerically compute the inverse partition ratio (IPR) for each eigenstatein real space as

where {∣n 〉} is the complete set of the real space basis and∣β〉is the β-th eigenstate.An eigenstate is extended whenThe overall localization of the bulk states can be characterized by the eigenstate-averaged IPR:

In figure 3(a),we showas functions ofW and J.′ One can see that the disorderW drives the bulk states more localized while the NNNN hopping J′ tends to make them delocalized.This can be intuitively understood that the long-range hopping serves as another channel for a particle to move between sites and thus enhances the possibility of particle delocalization.In figure 3(b),we plot the real-space IPR of each eigenstateas a function of W for J ′ = 0.55.For smallW,the bulk states are fully extended with a vanishingThere is a transition from the extended phase to localized phase atW ≈1.06before the system turns into a trivial Anderson insulator atW ≈1.64.

4.Dynamical phase transitions

In this section,we study the nonequilibrium dynamical phase transitions in this model based on the KZM with the critical exponents.It has been known that the KZM predicts the defect density based on the analysis of critical slowing down phenomenon and the static critical exponents [66, 96–98].Here we focus on the quantum quench [88, 89, 99] of the long-range hopping J′ for two fixed typical disorder strengths.The first quench is from the topological phase with ω = 1to the one withω = 2forW =0.90.Another quench path crosses the multicritical point atW =0.61.To this end,we first calculate the correlation length exponentν via

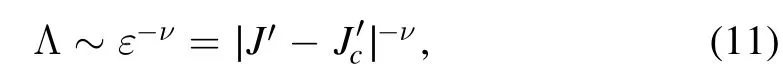
where the localization length Λ (see equation (8)) is taken as the correlation length for the topological phases here,is the critical point of the respective phase transition, andε the distance from current quenching J′to the critical pointBy numerically computing Λ from the transfer matrix method,we can determine the correlation length exponent ν.We plot the numerical data as well as a log–log linear fit to those data in figure 4(a), and all points are disorder averaged from 100 random configurations byφ s.For the first quench path with W =0.90and0.5632,we obtain the correlation length exponent ν ≈ 0.983 ± 0.005.For the second quench path crossing the multicritical point atW =0.61with≈0.4391,we obtain ν ≈ 0.480 ±0.005.

The dynamical exponent z can be extracted from the finite-size scaling of the relevant gaprΔ as

We proceed to relate the obtained correlation-length and dynamical exponents to the scaling of the defect density after the quench dynamics,as predicted by the KZM.At the initial time t0, the system is prepared far away from the topological phase transition point,and the initial state which occupies half the lowest single-particle energy levels(up to a normalization constant) reads

where ∣ βinstan(t0)〉is the instantaneous eigenstate of the Hamiltonian at t0.We consider the quench parameter in a linear form

wheres the initial hopping parameter at the beginningt0andτis the quench time controlling the evolution velocity.As the system timetevolves and crosses the topological phase transition point, the time-evolution state∣ψ(t) 〉undergoes an adiabatic–diabatic–adiabatic process, which can be numerically obtain by solving the time-dependent Schr?dinger equation.The state can be excited to the upper band in the diabatic regime and then the defect densitynexproducts after the quench.As a consequence of disorder effects, the dynamic behavior can no longer be separated into independent series of subspaces like the Landau–Zener tunneling[100, 101].When the population transition happens, the evolved state interferes with all energy levels and one can define the defect density as [78]

where the defect density is counted by the probability occupying the upper half bands at the final timetf,i.e.the states with energiesEβhigher than the Fermi energyEF=0.

as the Kibble–Zurek scaling law of the defect production after the dynamical phase transition.

In figure 5, we show our numerical results of the defect densitynexas functions ofτin log–log scale, obtained from real-time dynamics for three system sizesN=377, 610, 987.Data points are averaged over 80 random configurations and the linear fittings are conducted to extract the power-law exponents of the Kibble–Zurek scalings, which converge for the three system sizes investigated.As shown in figure 5(a)for the dynamical topological phase transition forW=0.9,the power-law exponents extracted from dynamics are respectivelyα≈ 0.508, 0.503, 0.505forN=377, 610,987, which are consisting with the theoretical prediction of KZMnex～τ-0.501,via combining critical exponentszandνin equation (16) withd=1.However, figure 5(b) shows the obtained power-law exponentsα≈ 0.169, 0.158, 0.167forN=377, 610, 987,respectively.The exponents violate the conventional KZM prediction withnex～τ-0.242as the evolution path crosses the multicritical point in this case.However,quenching through the multicritical point in the XY spin model takes the modified Kibble–Zurek scaling of the defect densitynex～τ-1/6as their critical exponents should beν=0.5andz=2,which belongs to Lifshitz universal class [102].Thus, our numerical results ofν≈ 0.480 ± 0.005,z≈2.053 ±0.021andα≈0.169,0.158, 0.167 agree with the theoretical predictions for multicritical point cases withα= 1 /6 ～ 0.167[102].Note that the calculation of the effective critical exponents for the multicritical point in the XY model [102] cannot be directly used in our model since the quasiperiodic disorder breaks the translation invariance.A natural conjecture is to adapt the recently proposed self-consistent Born approximation method[17, 29] to smooth disorders into an effective momentum space Hamiltonian, and then figure out the effective critical exponents.We leave the deduction of the effective critical exponents at the multicritical point in disordered systems for further studies.

As revealed in [78, 80], the topological edge states can cause the anomalous and non-universal scaling of defect dynamics in clean systems under the open boundary condiction.To reveal this scaling behavior in our disordered system,we simulate the dynamics of the topological edge states under the parameter quench fromω=1 toω=2 in the topological phase diagram under the open boundary condiction.As shown in figure 6, we plot typical results of the scaling between the defect densitynexand the quench timeτ.We can find the topological edge states result in the anomalous scaling, which cannot be predicted by the static critical exponents based on the Kibble–Zurek mechanism.The scaling exponents are bigger than the Kibble–Zurek exponents resulting from bulk states, indicating that topological edge states may be more stable in the quench process.The scaling of topological edge states dynamics is also not universal and depends on the disorder strength.

5.Conclusion

In summary, we have investigated topological phases, localization transition, and KZM critical exponents of the extended SSH model with quasiperiodic disordered and long-range hopping.The phase diagram revealed by the real-space winding number shows a higher winding numberω=2 region, and boundaries of different topological phases characterized by bulk gap closing under PBCs are consistent with those indicated by the winding number.Moreover, the zeroenergy modes under OBCs indicate the number of pairs of edge modes in the TAI region.The divergence of zero modes localization length can also mark the topological phase transition and reveal the? classification of the topological index.We have calculated the eigenstate-averaged real-space IPR and IPR of each eigenstate to reveal the localization properties.DisorderWcan drive the system from extend to localized and from topological non-trivial to trivial regions,and a fully localized TAI occurs before the system is driven into a trivial Anderson insulator.We have also investigated the nonequilibrium dynamical behavior in terms of the KZM with a topological phase transition or crossing the multicritical point.We have calculated the critical exponentsνandzby numerical scalings of physical quantities.The dynamically extracted exponent is consistent with the theoretical prediction of KZM forW=0.90,while dynamical and static exponents of the other ramping path crossing the multicritical point agree with the previously studied XY model.Finally,we have shown that the topological edge states result in anomalous scaling, which is non-universal and depends on the disorder strength.

Acknowledgments

The authors thank D-W Zhang for helpful discussions.This work was supported by the National Natural Science Foundation of China (Grant No.12104166), the Key-Area Research and Development Program of Guangdong Province(Grant No.2019B030330001), the Science and Technology of Guangzhou (Grant No.2019050001), and the Guangdong Basic and Applied Basic Research Foundation (Grant No.2020A1515110290).

ORCID iDs