Aggregation Operators for Interval-Valued Pythagorean Fuzzy SoftSet with Their Application to Solve Multi-Attribute Group Decision Making Problem

Rana Muhammad Zulqarnain,Imran Siddique,Aiyared Iampan and Dumitru Baleanu

1Department of Mathematics,University of Management and Technology,Sialkot Campus,Lahore,54770,Pakistan

2Department of Mathematics,University of Management and Technology,Lahore,54000,Pakistan

3Department of Mathematics,School of Science,University of Phayao,Mae Ka,Mueang,Phayao,56000,Thailand

4Department of Mathematics,Cankaya University,Balgat Ankara,06530,Turkey

5Institute of Space Sciences,Magurele-Bucharest,077125,Romania

6Department of Medical Research,China Medical University Hospital,China Medical University,Taichung,40447,Taiwan

ABSTRACT Interval-valued Pythagorean fuzzy softset(IVPFSS)is a generalization of the interval-valued intuitionistic fuzzy softset (IVIFSS) and interval-valued Pythagorean fuzzy set (IVPFS).The IVPFSS handled more uncertainty comparative to IVIFSS;it is the most significant technique for explaining fuzzy information in the decision-making process.In this work,some novel operational laws for IVPFSS have been proposed.Based on presented operational laws,two innovative aggregation operators(AOs)have been developed such as interval-valued Pythagorean fuzzy softweighted average (IVPFSWA) and interval-valued Pythagorean fuzzy softweighted geometric (IVPFSWG)operators with their fundamental properties.A multi-attribute group decision-making(MAGDM)approach has been established utilizing our developed operators.A numerical example has been presented to ensure the validity of the proposed MAGDM technique.Finally,comparative studies have been given between the proposed approach and some existing studies.The obtained results through comparative studies show that the proposed technique is more credible and reliable than existing approaches.

KEYWORDS Interval-valued Pythagorean fuzzy softset;IVPFSWA operator;IVPFSWG operator;MAGDM

1 Introduction

MAGDM is considered as the most appropriate technique to find the finest alternative from all possible alternatives,following criteria or attributes.Conventionally,it is supposed that all information that accesses the alternative in terms of attributes and their corresponding weights are articulated in the form of crisp numbers.On the other hand,in real-life circumstances,most of the decisions are taken in situations where the objectives and limitations are usually indefinite or ambiguous.To overcome such ambiguities and anxieties,Zadeh offered the notion of the fuzzy set (FS) [1],a prevailing tool to handle the obscurities and uncertainties in decision making (DM).Such a set allocates to all objects a membership value ranging from 0 to 1.Mostly,experts consider membership and a non-membership value in the DM process which cannot be handled by FS.Atanassov [2] introduced the idea of the intuitionistic fuzzy set (IFS) to overcome the aforementioned limitation.In 2011,Wang et al.[3] presented numerous operations on IFS,such as Einstein product,Einstein sum,etc.,and constructed some novel AOs.They also discussed some important properties of these operators and utilized their proposed operators to resolve multi-attribute decision making (MADM).Atanassov [4] presented a generalized form of IFS in the light of ordinary interval values,called interval-valued intuitionistic fuzzy set (IVIFS).Garg et al.[5] extended the concept of IFS and presented a novel concept of the cubic intuitionistic fuzzy set (CIFS) which is a successful tool to represent vague data by embedding both IFS and IVIFS directly.They also discussed several desirable properties of CIFS.

The above-mentioned models have been well-recognized by the specialists but the existing IFS is unable to handle the inappropriate and vague data because it is considered to envision the linear inequality between the membership and non-membership grades.For example,if decision-makers choose membership and non-membership values 0.9 and 0.6 respectively,then the above-mentioned IFS theory is unable to deal with it because 0.9 + 0.6≥1.To resolve the aforesaid limitation,Yager [6] presented the idea of the Pythagorean fuzzy set (PFS) by amending the basic conditionκ+δ≤1 toκ2+δ2≤1 and developed some results associated with score function and accuracy function.Rahman et al.[7] developed the Pythagorean fuzzy Einstein weighted geometric operator and presented a MAGDM methodology utilizing their proposed operator.Zang et al.[8] developed some basic operational laws and prolonged the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method to resolve multi-criteria decision-making (MCDM) complications for PFS information.Wei et al.[9] offered the Pythagorean fuzzy power AOs along with basic characteristics,they also established a DM technique to resolve MADM difficulties based on presented operators.Wang et al.[10] offered the interaction operational laws for Pythagorean fuzzy numbers (PFNs) and developed power Bonferroni mean operators.To assess the professional health risk,IIbahar et al.[11] offered the Pythagorean fuzzy proportional risk assessment technique.Zhang [12] proposed a novel DM approach based on similarity measures to resolve multi-criteria group decision making (MCGDM)difficulties for the PFS.

All of the aforementioned techniques have a wide range of applications,but owing to their ineffectiveness,they have several restrictions with the parameterization tool.Presenting a solution to this type of uncertainty and obfuscation Molodtsov [13] established the idea of soft sets (SS)and described some basic operations with their characteristics to handle the above-mentioned confusion and ambiguity.Maji et al.[14] expanded the concept of SS and developed many basic and binary operations for it.Maji et al.[15] developed the fuzzy soft set with some desirable properties by merging two existing notions FS and SS.Maji et al.[16] developed the notion of the intuitionistic fuzzy soft set (IFSS) and some fundamental operations with their necessary properties.Garg et al.[5] presented the cubic IFSS and established some AOs for cubic IFSS.They also planned a DM technique based on their developed operators.Zulqarnain et al.[17]planned the TOPSIS method based on the correlation coefficient for interval-valued IFSS to solve MADM problems.Jiang et al.[18] introduced the notion of the interval-valued intuitionistic fuzzy soft set (IVIFSS) and discussed some of their basic properties.Narayanamoorthy et al.[19]proposed the score function for a normal wiggly hesitant fuzzy set and utilized it to expose the deepest ideas hidden in the thought-level of the decision-makers.Narayanamoorthy et al.[20]introduced the hesitant fuzzy subjective and objective weight integrated method to find weights under hesitant fuzzy information.They also presented a novel ranking methodology for hesitant fuzzy sets.Ramya et al.[21] developed the interval-valued hesitant Pythagorean fuzzy set under the normal wiggly mathematical methodology and used it to solve the MCDM problem.Peng et al.[22] merged two well-known theories PFS and SS and offered the concept of Pythagorean fuzzy soft set (PFSS).Zulqarnain et al.[23] developed the AOs for PFSS with their application for the green supplier chain management.Zulqarnain et al.[24] introduced an advanced form of AOs considering the interaction and construct a DM approach based on their developed interactive AOs.Smarandache [25] prolonged the idea of SS to hypersoft sets (HSS) by substituting the single-parameter functionfwith a multi-parameter (sub-attribute) function.He privileges that HSS proficiently contracts with inexact data comparative to SS.

MAGDM is a very effective and well-known tool to examine fuzzy data more effectively.Therefore,it is obvious from the published literature that the interval-valued structures are more general and increase more consideration in decision-making difficulties.The choice of vehicle is a key part of real-life and will advise on complications of MAGDM.Lack of thinking about the ambiguity of alternative associations will be the core motivation for some MAGDM concerns about the undesirable consequences.By using a wealth of existing content,it contains previous criticisms and suppressed sensitivities.Many logical and scientific tools/procedures are offended in the literature for choosing the most suitable vehicle.As far as we know,there is currently no work on the AOs of IVPFSS.Therefore,this article proposes some operational laws for interval-valued Pythagorean fuzzy soft numbers (IVPFSN).The presented IVPFSN is well worth observing the inaccurate information that occurs in the complications of daily life.Therefore,the main purpose of this work is to propose new IVPFSWA and IVPFSWG operators based on the established operational laws.An algorithm based on the proposed operators to solve the decision-making problem is proposed.To prove the effectiveness of the proposed decision-making method,we use a numerical example to illustrate it.The main benefit of the proposed operator is that the proposed operator can reduce to IVIFSS and IVFSS operators under some specific conditions of unconfidence.The organization of this paper is given as follows: Section 2 of this paper consists of some basic concepts which help us to develop the structure of the following research.In Section 3,some novel operational laws for IVPFSN have been proposed.Also,in the same section,IVPFSWA and IVPFSWG operators have been introduced based on our developed operators with their basic properties.In Section 4,a MAGDM approach has been constructed based on the proposed AOs.To ensure the practicality of the developed approach a numerical example has been presented for the selection of the best vehicle in Section 5.

2 Preliminaries

This section consists of some basic definitions which will provide a structure to form the following work.

Definition 2.1[1]

LetUbe a collection of objects then a fuzzy set (FS)AoverUis defined as

A={(t,κ(t))|t∈U}

where,κA(t):X→[0,1] is a membership grade function.

Definition 2.2[26]

LetUbe a collection of objects then an interval-valued fuzzy set (IVFS)AoverUis defined as

where,κl(t),κu(t)∈[0,1] and represents the lower and upper bounds of the membership value.

Definition 2.3[4]

LetUbe a collection of objects then an interval-valued intuitionistic fuzzy set (IVIFS)AoverUis defined as

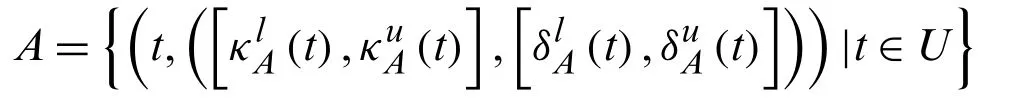
Definition 2.4[27]

LetUbe a collection of objects then an interval-valued Pythagorean fuzzy set (IVPFS)AoverUis defined as

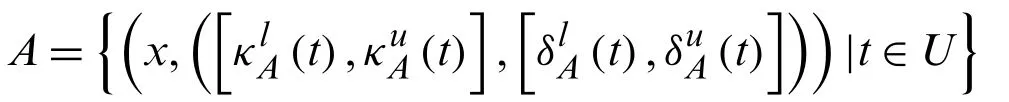
Definition 2.5[13]

LetUbe a universal set and N={t1,t2,t3,...,tm} be set of attributes then a pair (F,N)is called a soft set (SS) overUwhereF: N→KUis a mapping andKUis known as a collection of all subsets of universal setU.

Definition 2.6[19]

LetUbe a universal set and N be a set of attributes then a pair (Ω,N)is called an intervalvalued intuitionistic fuzzy soft set (IVIFSS) overU.WhereΩ: N→IKUis a mapping andIKUis known as a collection of all interval-valued intuitionistic fuzzy subsets of universal setUandA?N.

Definition 2.7

LetUbe a universal set and N be set of attributes then a pair ((Ω,N)is called an intervalvalued Pythagorean fuzzy soft set (IVPFSS) overUwhereΩ: N→?KUis a mapping and?KUis known as the collection of all interval-valued Pythagorean fuzzy subsets of universal setU.

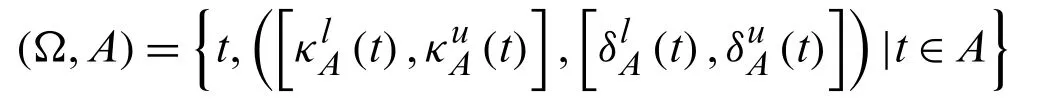
Definition 2.8

Definition 2.9

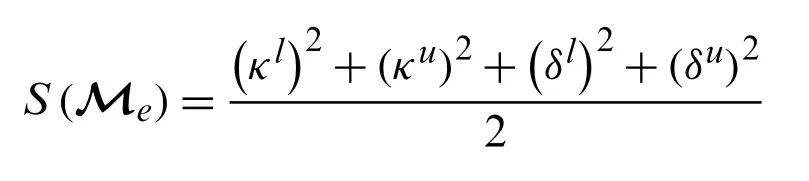
3 Aggregation Operators for Interval Valued Pythagorean Fuzzy Soft Sets

In this section,we are going to define operational laws under IVPFSNs.Based on these operational laws,we shall also present interval-valued Pythagorean fuzzy soft weighted average(IVPFSWA) and interval-valued Pythagorean fuzzy soft geometric (IVPFSWG) operators.

3.1 Operational Laws for Interval Valued Pythagorean Fuzzy Soft Numbers

3.2 Interval Valued Pythagorean Fuzzy Soft Weighted Average Operator

Theorem 3.1

where ωiandνjare weight vector for expert’s and attributes respectively with given conditions

Proof.We shall prove the IVPFSWA operator by utilizing the principle of mathematical induction:

Forn=1,we getω1=1.Then,we have

Form=1,we getν1=1.Then,we have

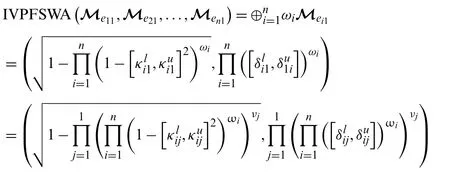
This shows that the above theorem holds forn=1 andm=1.Now,consider the above theorem also holds form=α1+1,n=α2andm=α1,n=α2+1,such as

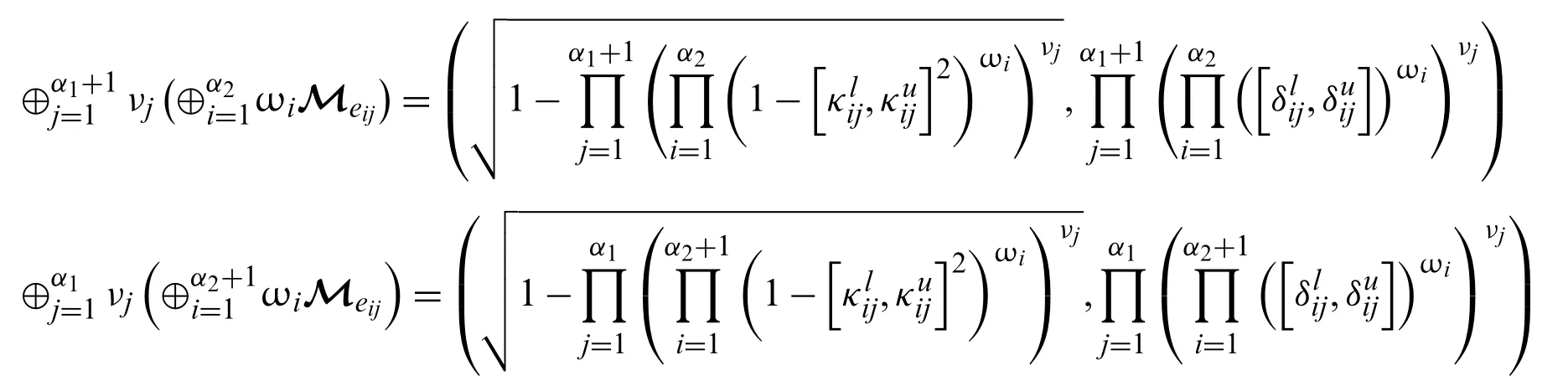
Form=α1+1 andn=α2+1,we have

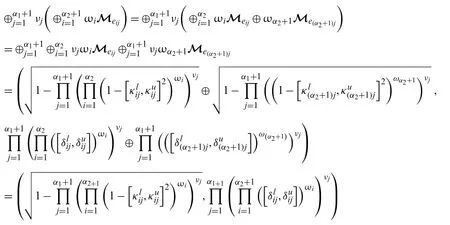
Therefore,it holds form=α1+1 andn=α2+1.So,we can judge that the above theorem also holds for all values ofmandn.

Example 3.1

Letχ={x1,x2,x3} be the set of specialists with weightsωi=(0.38,0.45,0.17)Twho wants to choose a bike under some defined set of propertiesφ={e1=Resale Value,e2=Mileage,e3=Cost of bike} with weightsνj=(0.25,0.45,0.3)T.We suppose the rating values of the specialists for each property in the form of IVPFSNsis given as

By using the above theorem,we have

3.3 Properties of PFSWA Operator

3.3.1 Idempotency

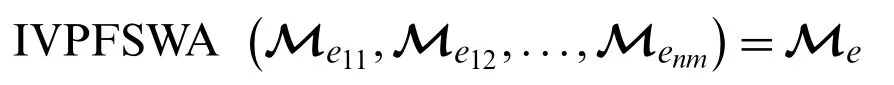
Proof: As we know that allthen,we have

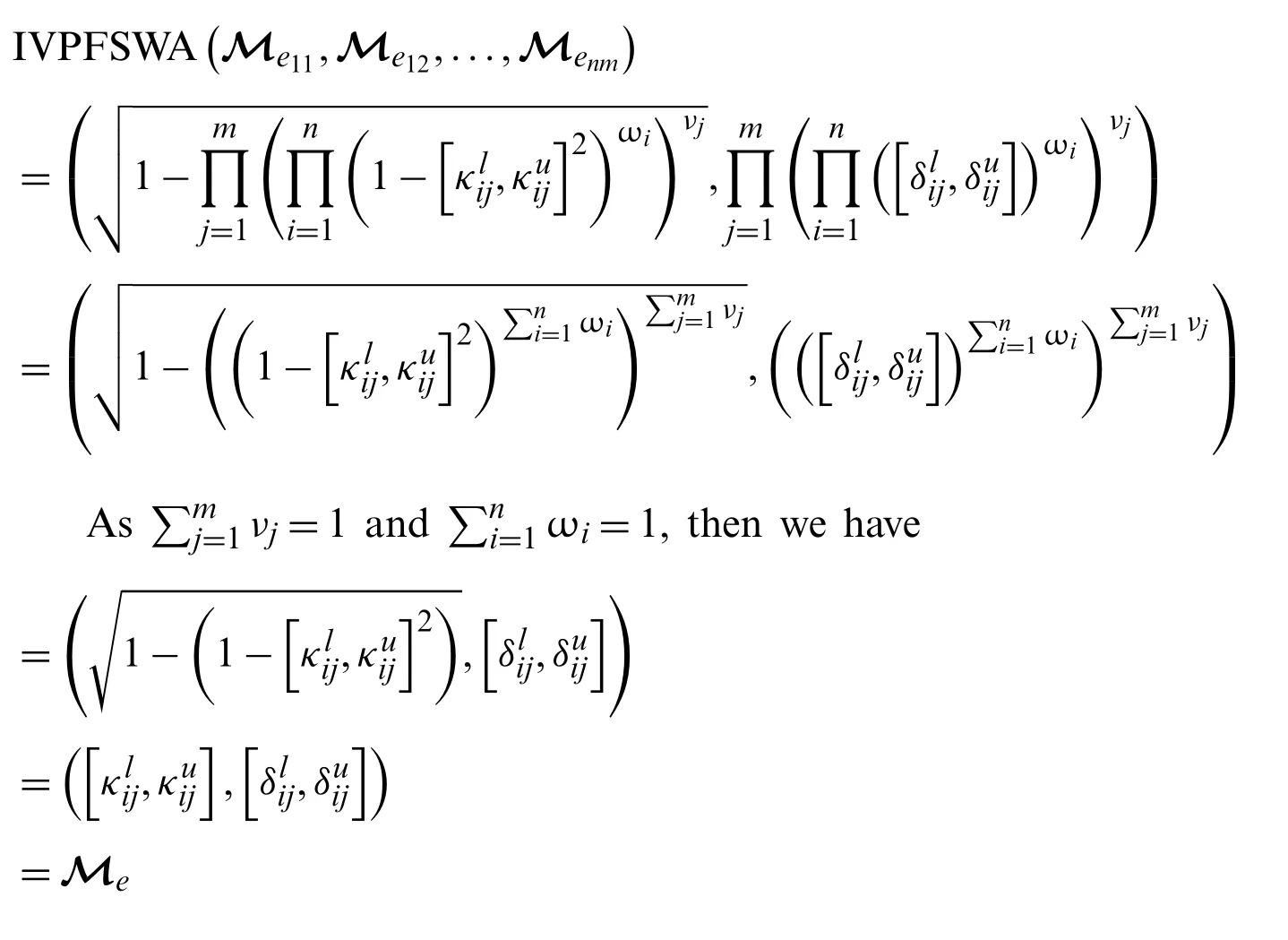
Hence proved.

3.3.2 Boundedness

LetMeijbe a collection of PFSNs whereandthen

Proof.As we know thatbe an IVPFSN,then

Similarly,we can prove that

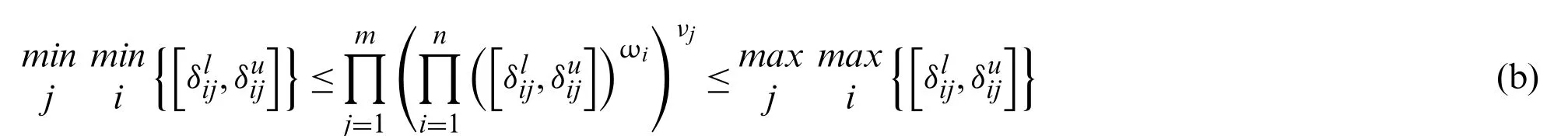
Let IVPFSWA (Me11,Me12,...,Menm)=then inequalities (a) and(b) can be transferred into the form:andrespectively.

So,by using the score function,we have

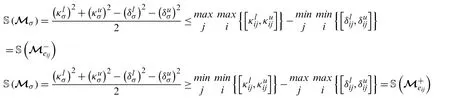
Then,by order relation between two IVPFSNs,we have

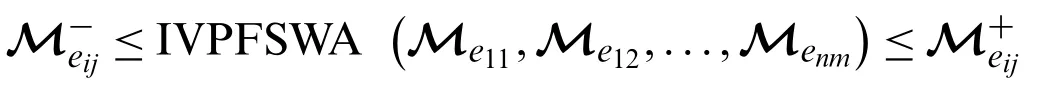
Hence proved.

3.3.3 Shift Invariance

IVPFSWA(Me11⊕Me,Me12⊕Me,...,Menm⊕Me)=IVPFSWA(Me11,Me12,...,Menm)⊕Me

Proof.ConsiderMeandMeijbe two IVPFSNs.Then,by operational laws defined under IVPFSNs defined above,we have

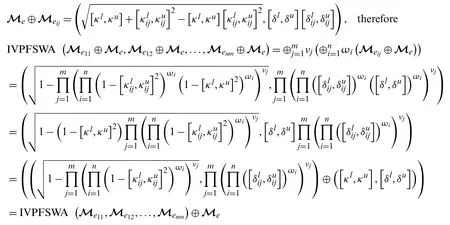
Hence proved.

3.3.4 Homogeneity

Prove that IVPFSWA(βMe11,βMe12,...,βMenm)=βIVPFSWA(Me11,Me12,...,Menm)for any positive real numberβ.

Proof.LetMeijbe an IVPFSN andβ＞0,then by using the operational laws mentioned above,we have

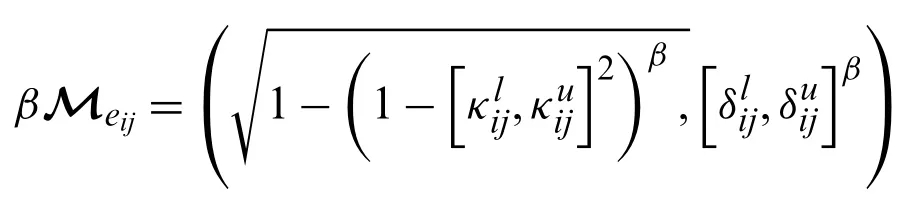
So,

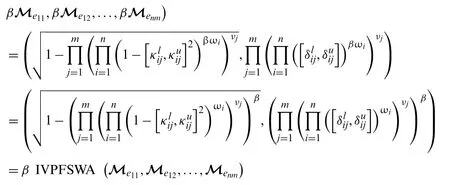
which completes the proof.

3.4 Interval Valued Pythagorean Fuzzy Soft Weighted Geometric Operator

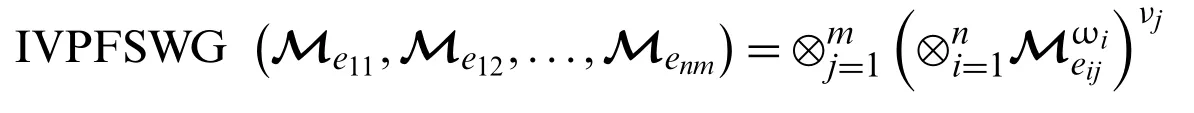
Theorem 3.2

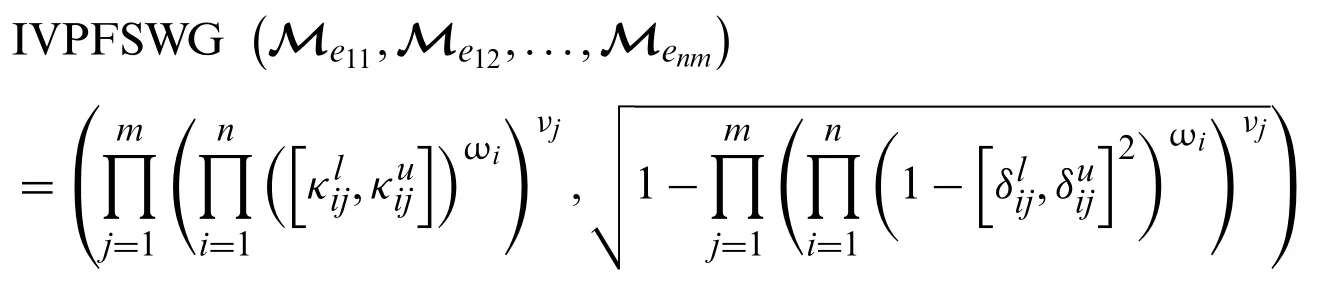
where ωiandνjare weight vector for expert’s and attributes respectively with given conditions

Proof.We can prove the IVPFSWG operator by using the principle of mathematical induction as follows:

Forn=1,we getω1=1.Then,we have

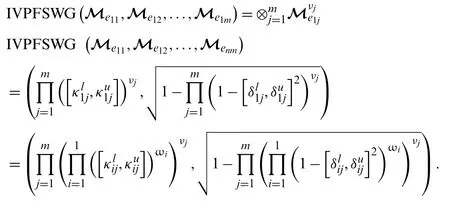
Form=1,we getν1=1.Then,we have

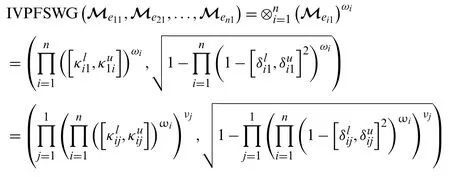
This shows that the above theorem holds forn=1 andm=1.Now,consider the above theorem also holds form=α1+1,n=α2andm=α1,n=α2+1,such as

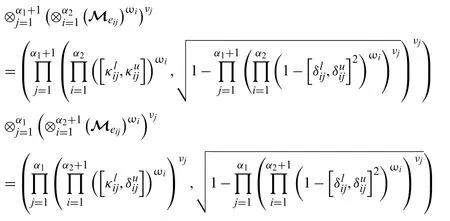
Form=α1+1 andn=α2+1,we have

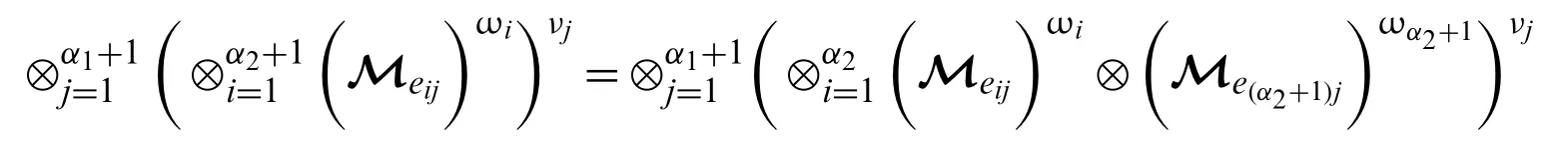
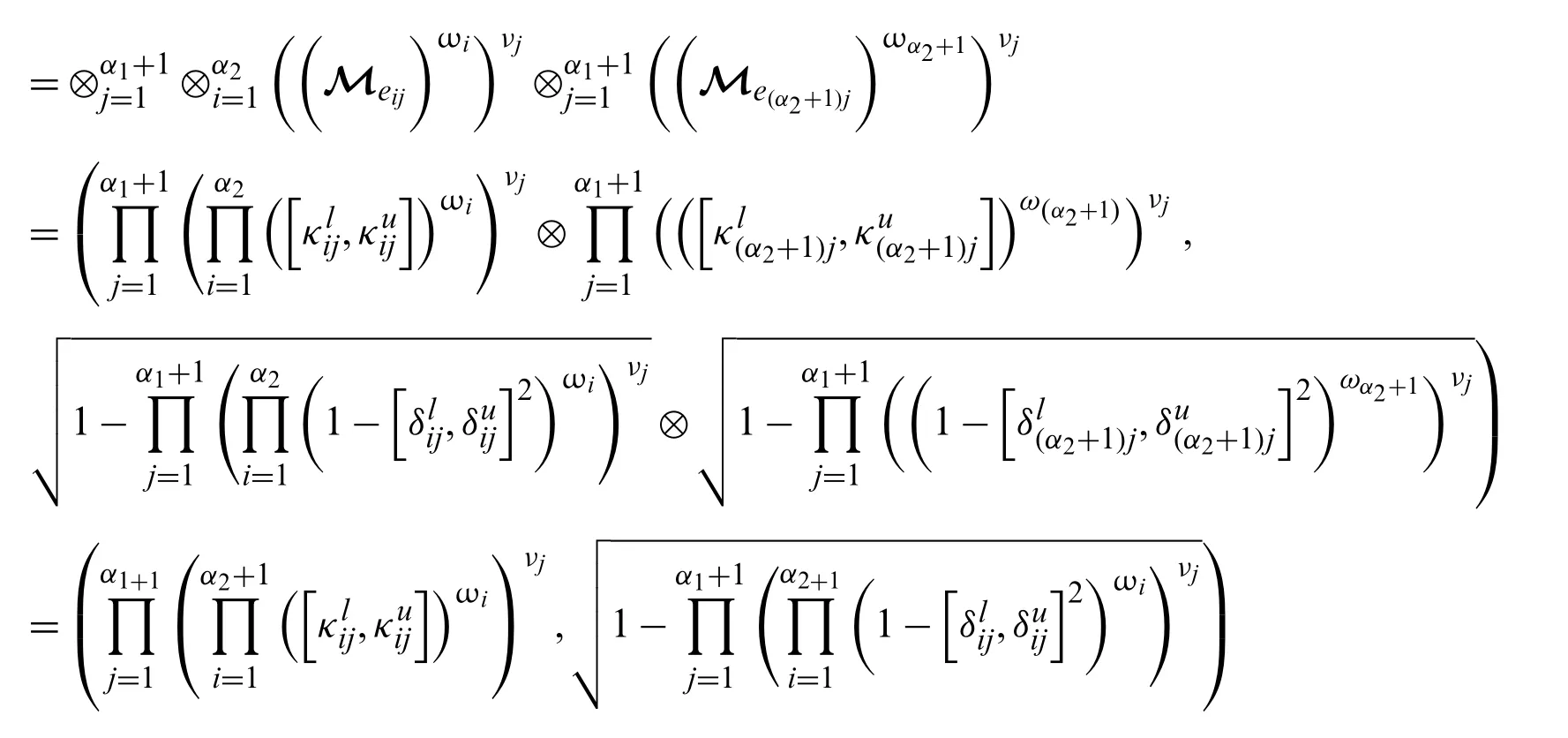
It is clarified from the above equation that the theorem holds form=α1+1 andn=α2+1.So,we can say that the theorem holds for all values ofmandn.

Example 3.2

Again,consider Example 3.1 with rating values of the specialists for each property in the form of IVPFSNsis given as

By using the above theorem,we have

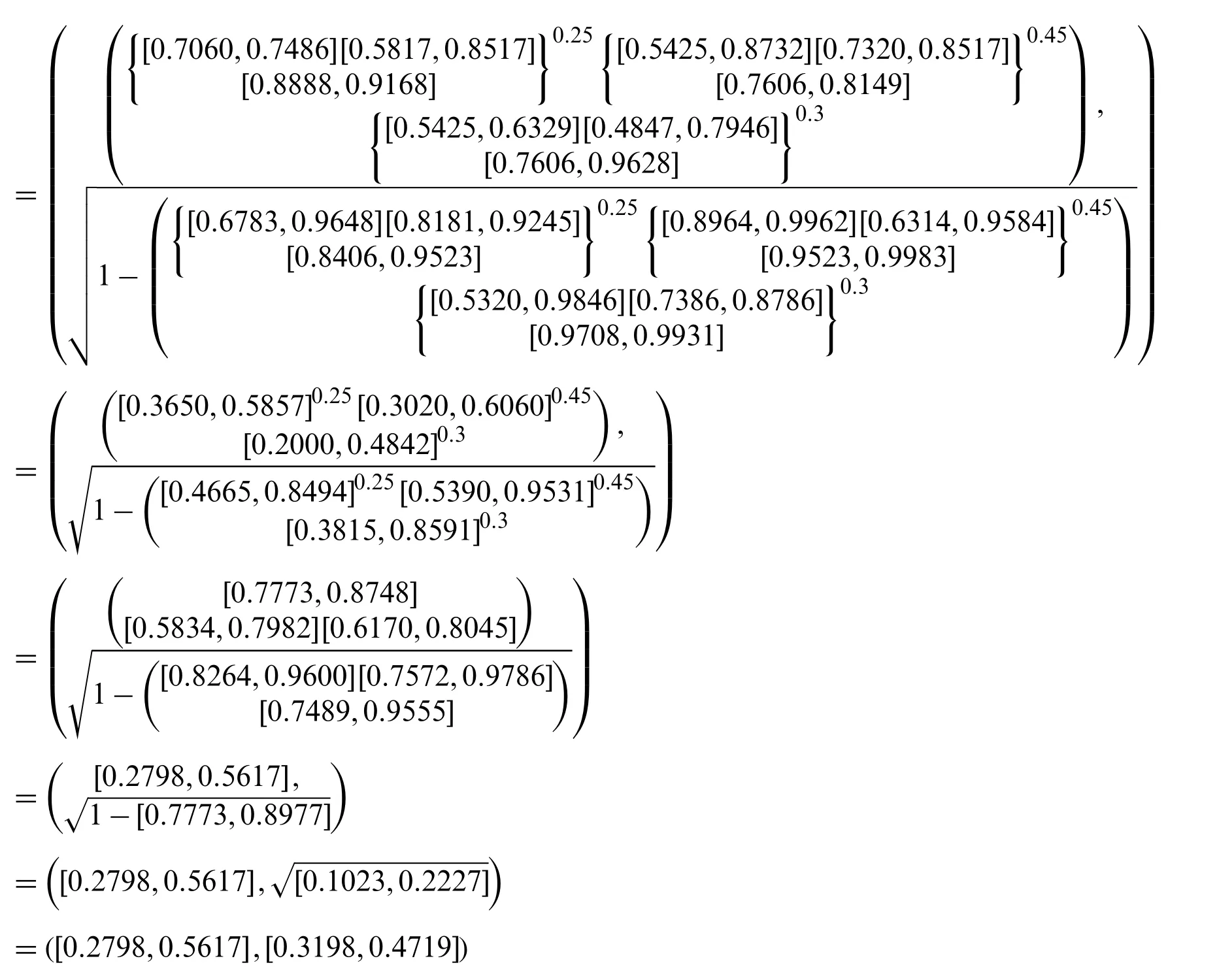
3.5 Properties of IVPFSWG

3.5.1 Idempotency

Proof.As we know that allthen,we have

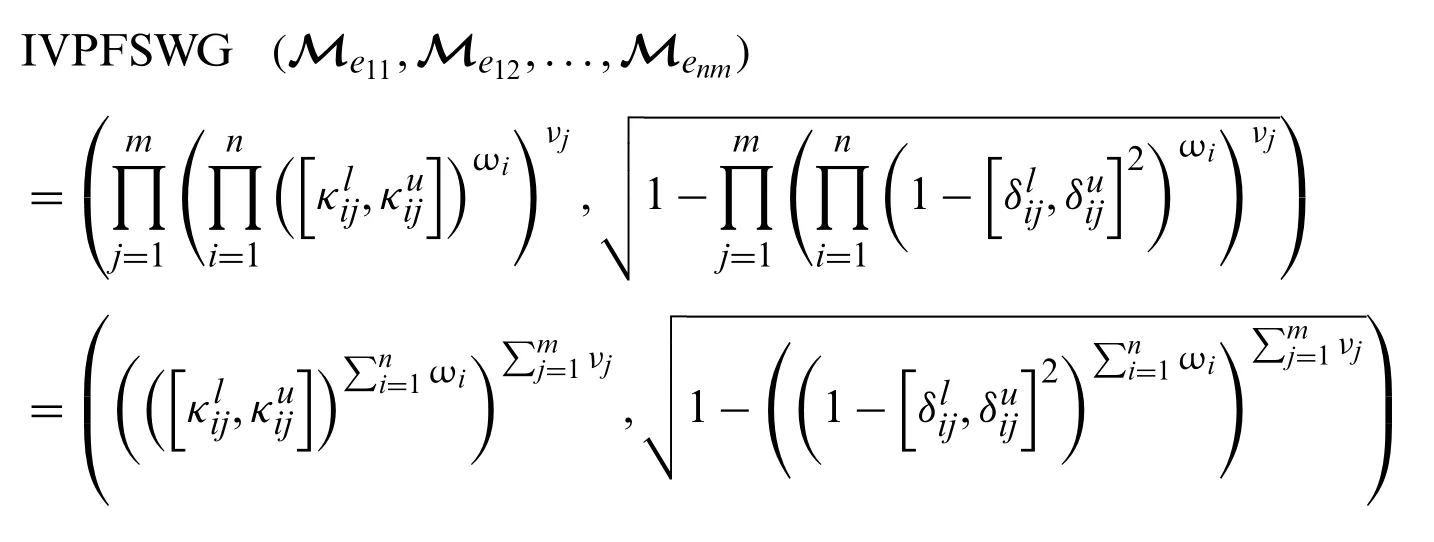
Hence proved.

3.5.2 Boundedness

LetMeijbe a collection of PFSNs whereandthen

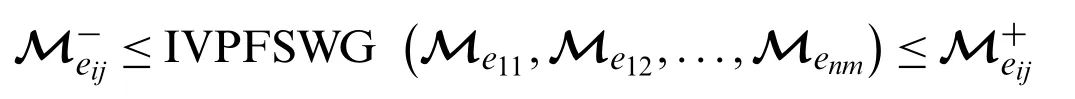
Proof.As we know thatbe an IVPFSN,then

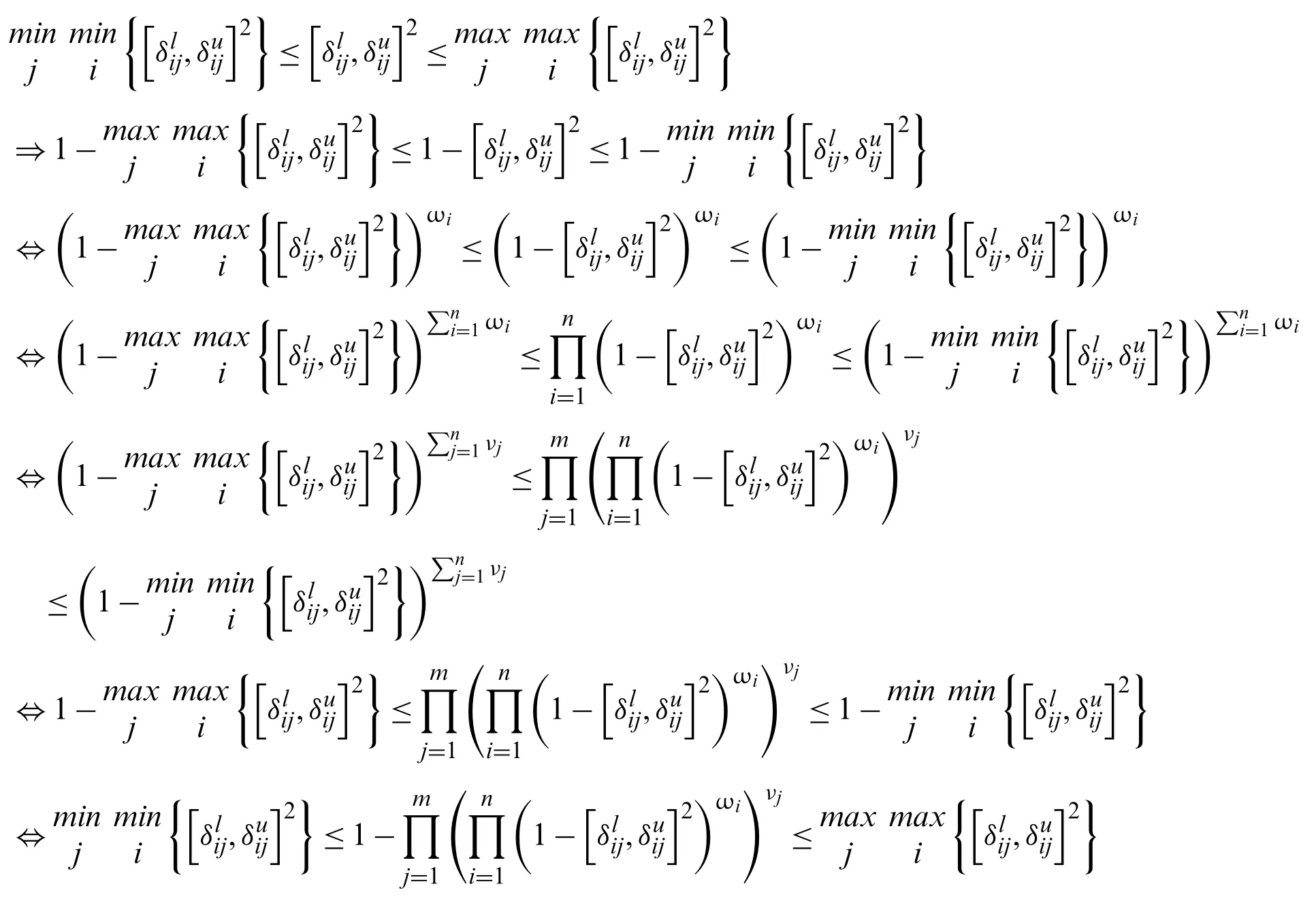
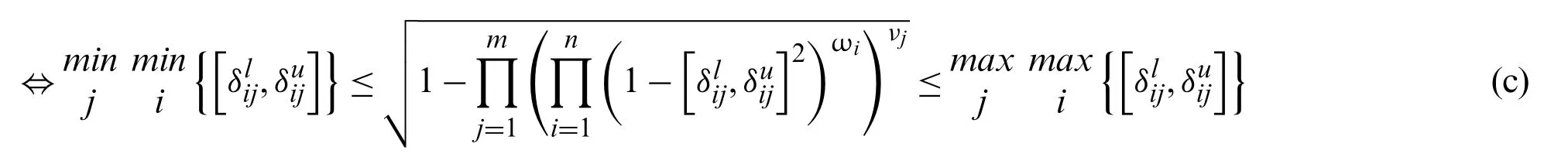
Similarly,we can prove that

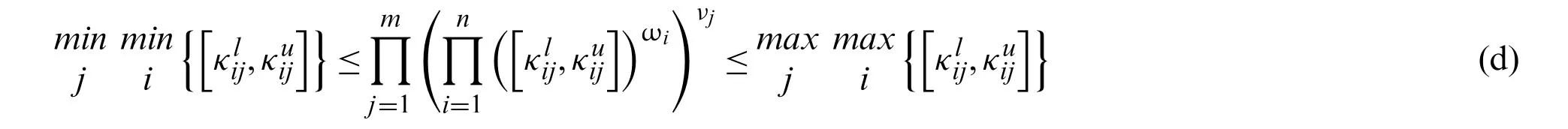
Let IVPFSWG(Me11,Me12,...,Menm)=then inequalities (c) and(d) can be transferred into the form:

respectively.

So,by using the score function,we have

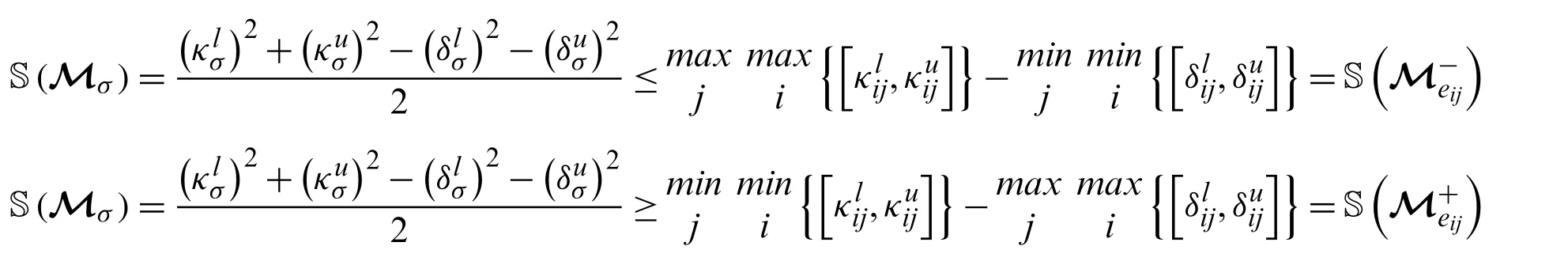
Then,by order relation between two IVPFSNs,we have

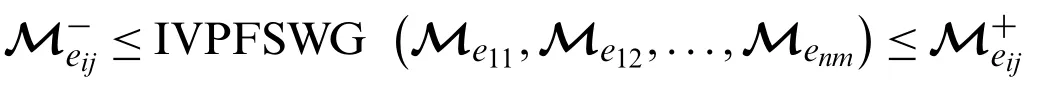
Hence proved.

3.5.3 Shift Invariance

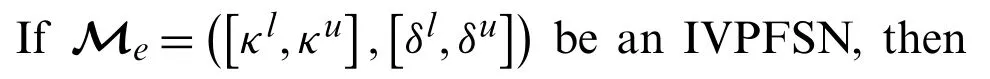
IVPFSWG (Me11⊕Me,Me12⊕Me,...,Menm⊕Me)=IVPFSW(Me11,Me12,...,Menm)⊕Me

Proof.ConsiderMeandMeijbe two IVPFSNs.Then,by operational laws defined under IVPFSNs defined above,we have

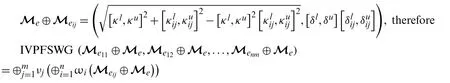
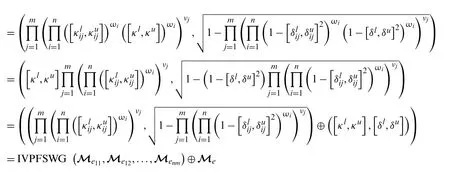
Hence proved.

3.5.4 Homogeneity

Prove that IVPFSWG(βMe11,βMe12,...,βMenm)=βIVPFSWA(Me11,Me12,...,Menm)for any positive real numberβ.

Proof: LetMeijbe an IVPFSN andβ＞0,then by using the operational laws mentioned above,we have

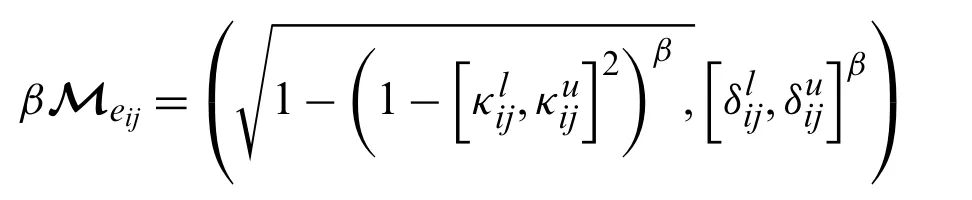
So,

which completes the proof.

4 Multi-Attribute Group Decision-Making Approach Based on Proposed Operators

In this section,a decision-making (DM) approach for solving multi-attribute group decisionmaking (MAGDM) problems based on proposed IVPFSWA and IVPFSWG operators has been developed along with numerical examples.

4.1 Proposed Approach

The procedure to apply proposed IVPFSWG and IVPFSWA operators for solving the MAGDM problem is summarized in the following steps:

Step-1: Obtain a decision matrix in the form of PFSNs for alternatives relative to experts.

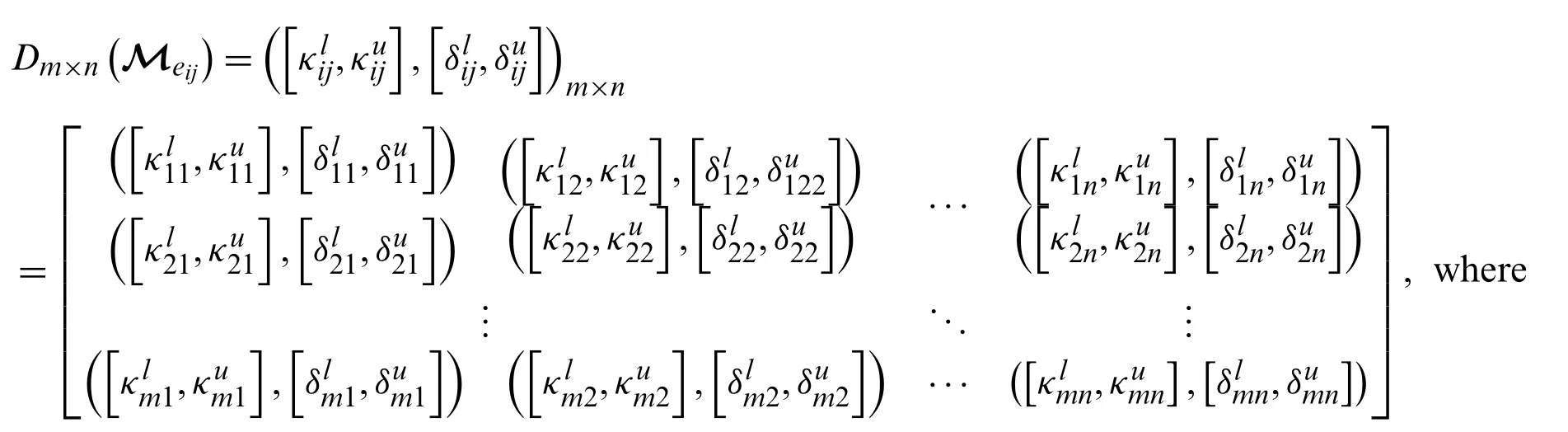
Step-2: By using the normalization formula,normalize the decision matrix to convert the rating value of cost type parameters into benefit type parameters.

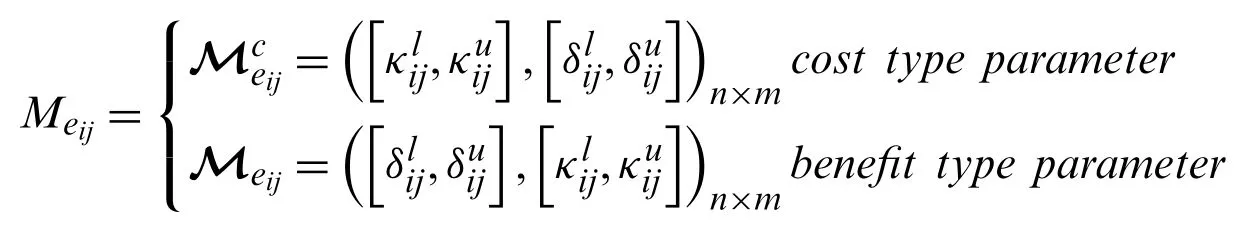
Step-3: Use the developed IVPFSWG and IVPFSWA operators to aggregate the IVPFSNsMeijfor each alternativeinto the decision matrixMij.

Step-4: Calculate the score values ofMfor all alternatives.

Step-5: Select the alternative having maximum score value and examine the ranking.

4.2 Numerical Example

Suppose a person wants to buy a car and he has four alternatives such as I1,I2,I3and I4.There are four considered attributes according to which the person has to take the decision such ase1;price of the car,e2;comfortability,e3;resale value,and,e4;growth rate with the weighted vectorν=(0.3,0.1,0.2,0.4)T.Heree1,e3are cost type parameters ande2,e4are benefit type parameters.The person hires a team of four expertsXr(r=1,2,3,4)for decision making with the weighted vectorω=(0.1,0.2,0.4,0.3)T.

4.2.1 By IVPFSWA Operator

Step-1: Obtain Pythagorean fuzzy soft decision matrices (Tables 1–4).

Table 1:IVPFS decision matrix for I1

Table 2:IVPFS decision matrix for I2

Table 3:IVPFS decision matrix for I3

Table 4:IVPFS decision matrix for I4

Step-2: Becausee1,e3are cost type parameters,so utilized the normalization formula to obtain normalized Pythagorean fuzzy soft decision matrices are given in the following Tables 5–8.

Table 5:Normalized IVPFS decision matrix for I1

Table 6:Normalized IVPFS decision matrix for I2

Table 7:Normalized IVPFS decision matrix for I3

Table 8:Normalized IVPFS decision matrix for I4

Step-3: Apply the proposed IVPFSWA operator on the acquired data,we will obtain an opinion of the decision-makers.

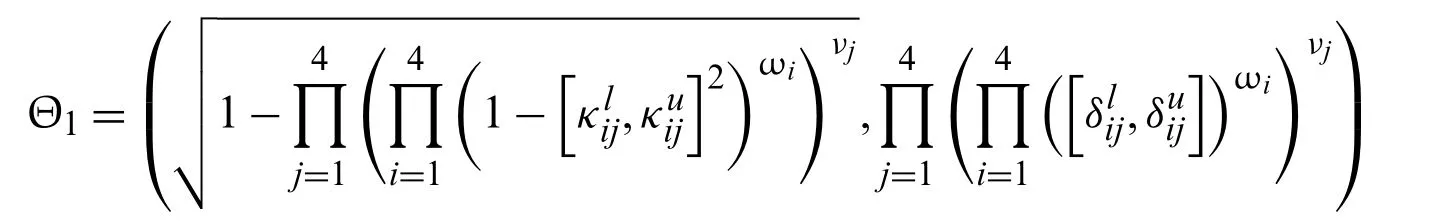
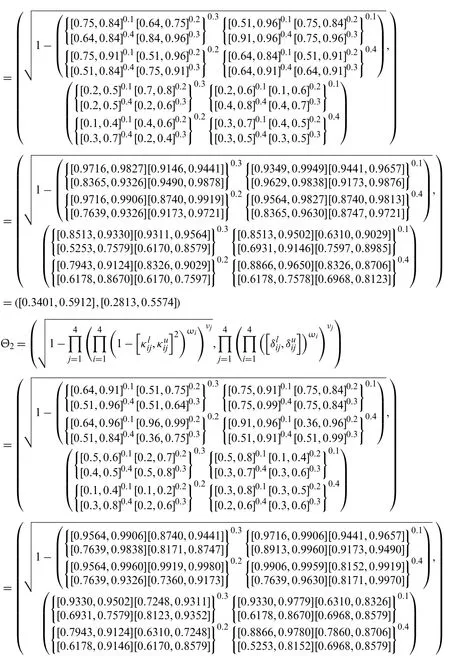
Step-4: Use the score functionS=for the interval-valued Pythagorean fuzzy soft set to calculate the score values for all alternatives.S(Θ1)=0.0377,S(Θ2)=0.0834,S(Θ3)=0.0113,andS(Θ4)=0.0141.

Step-5: From the above calculation,we getS(Θ2)＞S(Θ1)＞S(Θ4)＞S(Θ3),which shows that I2is the best alternative.So,I2＞I1＞I4＞I3.

4.2.2 By IVPFSWG Operator

Step-1: Obtain PFS decision matrices (Tables 1–4).

Step-2: Use the normalization formula to normalize the obtained PFS decision matrices(Tables 5–8).

Step-3: Apply the proposed IVPFSWG operator on the acquired data,we will obtain an opinion of the decision-makers

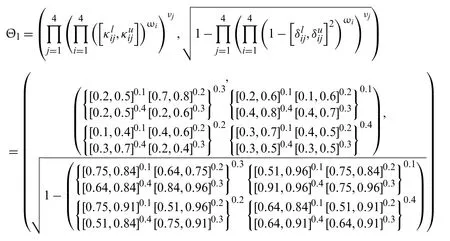
Step-4: Use the score functionS=interval-valued for the Pythagorean fuzzy soft set to calculate the score values for all alternatives such asS(Θ1)=0.0524,S(Θ2)=0.0754,S(Θ3)=0.0241,andS(Θ4)=0.0114.

Step-5: From the above calculation,we get the ranking of alternativesS(Θ2)＞S(Θ1)＞S(Θ3)＞S(Θ4),which shows that I2is the best alternative.So,I2＞I1＞I3＞I4.

5 Comparative Studies

To highlight the effectiveness of the presented method,a comparison between the proposed model and prevailing methods is proposed in the following section.

5.1 Comparative Analysis with Interval-Valued Pythagorean Fuzzy Weighted Average Operator[28]

Step-1: Obtain an IVPF decision matrices (Tables 1–4).

Step-2: Use normalization formula to normalize the obtained IVPF decision matrices(Tables 5–8).

Step-3: Apply the IVPFWA operator on the acquired data,then we get the opinion of decision-makers.

As we have

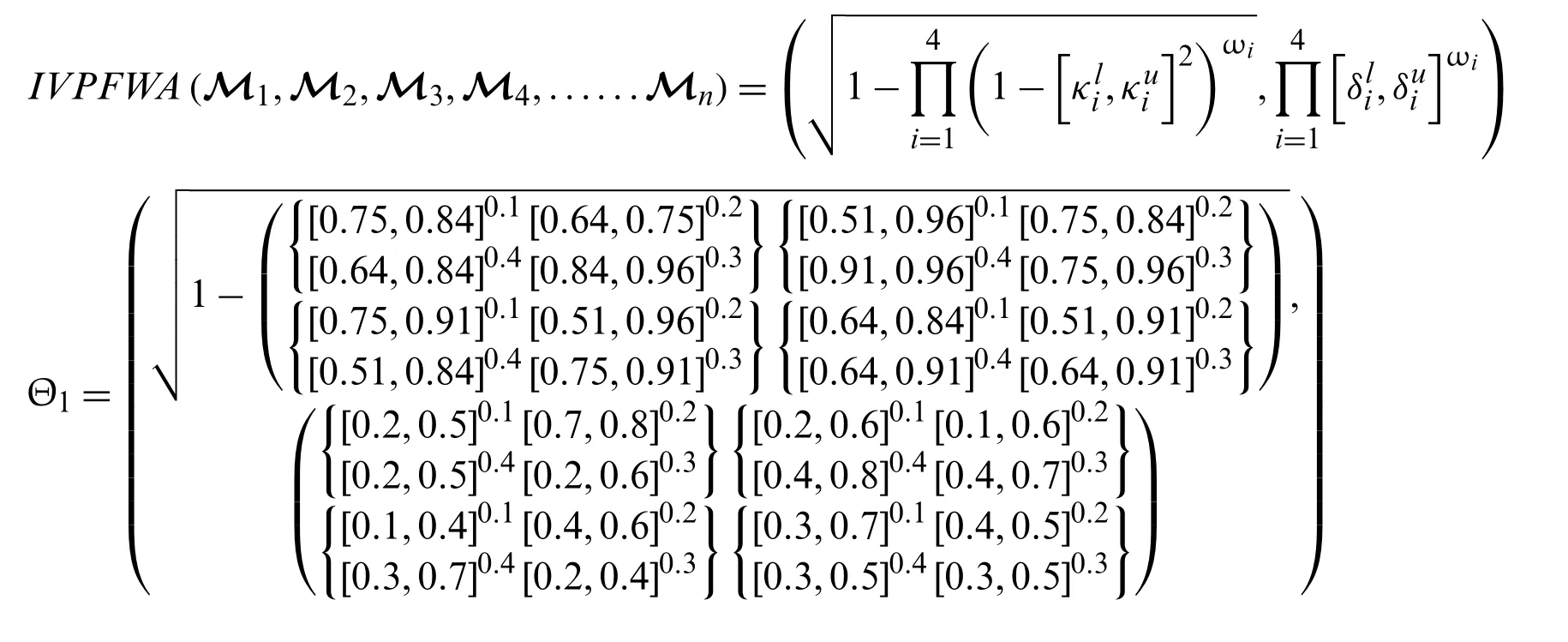
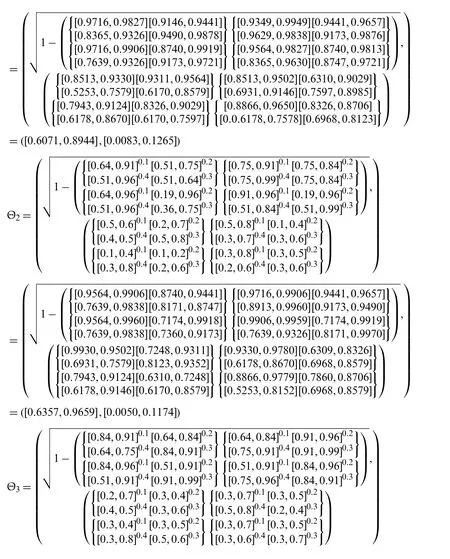
Step-4: Use the score functionfor IVPFS to calculate the score values for all alternatives.

Step-5: Ranking of alternativesS(Θ2)＞S(Θ4)＞S(Θ3)＞S(Θ1).So,I2＞I4＞I3＞I1.Hence,the best alternative is I2.

5.2 Comparison with Interval-Valued Pythagorean Fuzzy Weighted Geometric Operator[28]

Step-1: Obtain an IVPF decision matrices (Tables 1–4).

Step-2: Use normalization formula to normalize the obtained IVPF decision matrices(Tables 5–8).

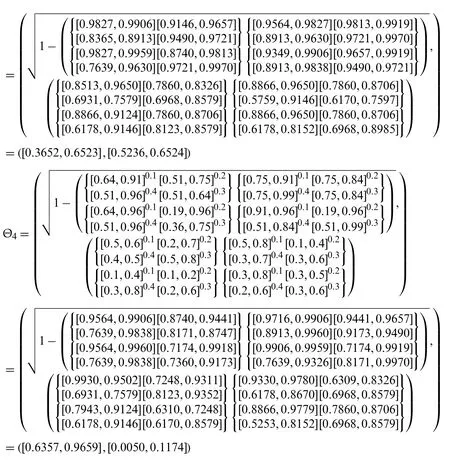
Step-3: Apply the IVPFWG operator on the acquired data,then we get the opinion of decision-makers.

As we have

Step-4: Use the score functionfor IVPFS to calculate the score values for all alternatives.

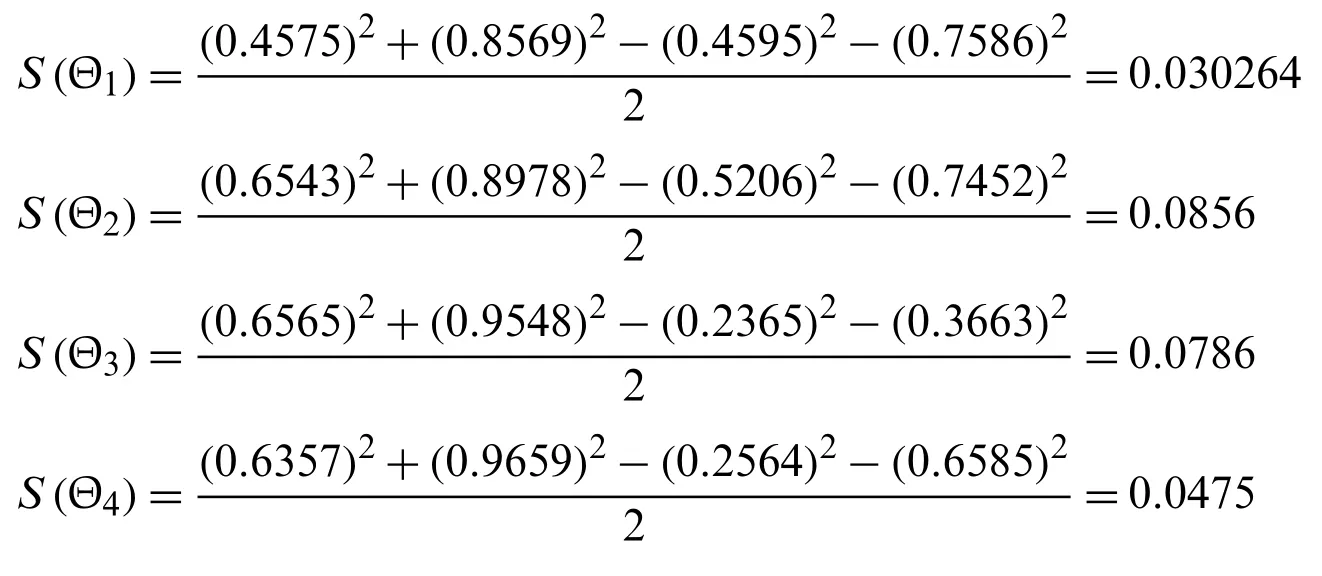
Step-5: Ranking of alternatives,S(Θ2)＞S(Θ3)＞S(Θ4)＞S(Θ1).So,I2＞I3＞I1＞I4.Hence,the best alternative is I2.

Similarly,we can get the outcomes utilizing several other existing operators for comparative studies.

5.3 Comparative Analysis

To verify the effectiveness of the proposed method,we compare the obtained results with some existing methods under the environment of IVPFS and IVIFSS.A summary of all results is given in Table 9.Zulqarnain et al.[17] developed aggregation operators for IVIFSS that are unable to accommodate the decision-makers choices when the sum of upper membership and nonmembership values of the parameters exceeds one.Peng et al.[27] interval-valued Pythagorean fuzzy weighted average operator and Rahman et al.[28] interval-valued Pythagorean fuzzy weighted geometric operator cannot handle the parametrized values of the alternatives.Furthermore,if only one parameter is supposed rather than more than one parameter,the interval-valued Pythagorean fuzzy soft set reduces to the interval-valued Pythagorean fuzzy set.Similarly,if the sum of upper values of membership and nonmembership degree is less or equal to 1.Then,IVPFSS reduced to IVIFSS.Thus,IVPFSS is the most generalized form of interval-valued Pythagorean fuzzy set.Hence,based on the above-mentioned facts,admittedly,the proposed operators in this paper are more powerful,reliable,and successful.

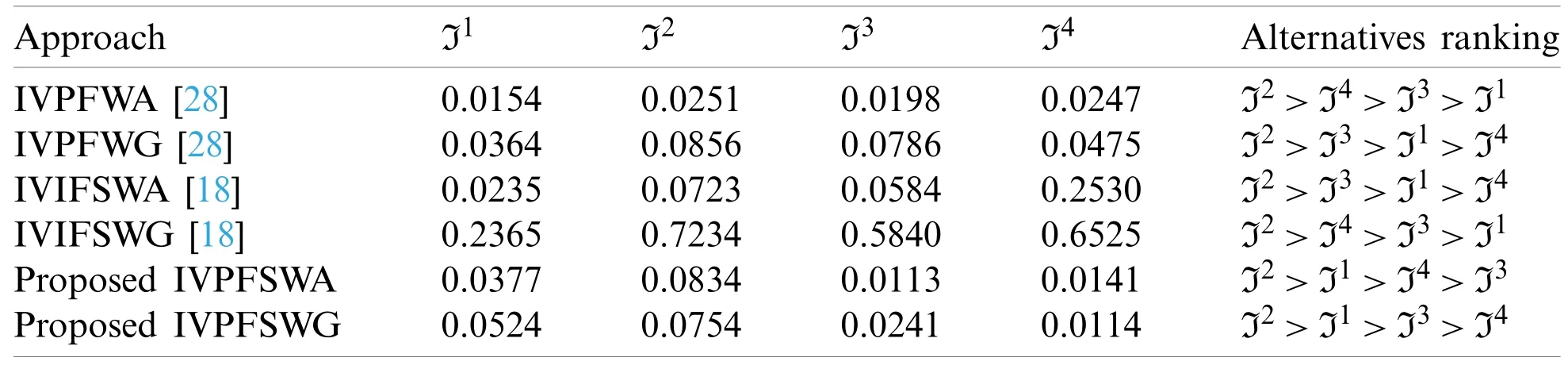
Table 9:Comparison of proposed operators with some existing operators

6 Conclusion

In this work,we have introduced two novel aggregation operators such as IVPFSWA and IPFSWG operators.Firstly,we defined operational laws under an interval-valued Pythagorean fuzzy soft environment.Based on these operational laws,we developed the aggregation operators for IVPFSS such as IVPFSWA and IVPFSWG operators with their desirable properties.Furthermore,a DM approach has been established to resolve multi-attribute group decision-making (MAGDM)problems based on presented aggregation operators.To ensure the validity of the established technique,a comprehensive numerical example has been presented.To verify the effectiveness of the proposed method,a comparative analysis with some existing methods is presented.Finally,based on obtained results,it has been concluded that the proposed method in this research is the most feasible and successful method for the MAGDM problem.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.