External blast load factors for dome structures based on reliability

Sho-bo Qi , Gung-yn Hung , Xu-ong Zhi , Feng Fn , Richr G.J.Fly

a State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing,100081, PR China

b Key Lab of Structure Dynamic Behaviour and Control of the Ministry of Education, Harbin Institute of Technology, Harbin,150090, China

c Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters of Ministry of Industry and Information Technology, Harbin Institute of Technology, Harbin,150090, China

d Department of Mechanical Engineering, University of Auckland, Private Bag 92019, Auckland,1142, New Zealand

Keywords:Dome structure Airblast variability Deterministic design Assurance factor Reliability-based blast load factor Structural damage levels

ABSTRACTDome structures have been used extensively for industrial, residential, and military infrastructure.Therefore, it is necessary to understand the damage risk potential for such structures for blast-resistant design considerations.This paper investigates the effect of blast load variability on the design value and the structural dynamic response.Therefore,the sources of uncertainty in the external blast load on dome structures were discussed firstly.Then based on the probabilistic blast load model for the dome, the rationality of a deterministic mass-increase safety method was assessed.It was found that previous deterministic design method cannot provide a consistent and sound assurance factor or reliability index on the entire dome roof.In addition, it was also proved that the assurance-based load method fails to ensure compliance with structural safety design standards on the dome roof when compared with the reliability-based blast method.A sensitivity analysis on the probabilistic blast load was conducted, and the results indicate that stand-off distance and explosive mass both act as dominant sources to influence the mean and variability of blast load.Therefore, based on the Latin hypercube sampling method, a reliability-based external blast load factor technique was proposed.This technique was further used to estimate structural damage levels of a single-layer reticulated dome under different reliability requirements, associated with a low, medium, and high level of protection grades for a specific explosion scenario, and it indicated that this technique can be useful in the building design to achieve a higher structural anti-explosion capacity.This study herein can serve as a reference for the calculation method of designed blast load.

1.Introduction

Performance-based or reliability-based design is a common approach to protect various infrastructure from natural or anthropogenic hazards.It can be used to determine the structural vulnerability and to estimate the probability of damage, failure, or collapse of infrastructure.The approach considers structural and blast load uncertainties using probabilistic assessment [1,2]in the structural blast-resistance theory in order to obtain cost-benefit analyses of protective measures.

Previous studies[3-12]have shown that the variability of blast loads has a significant effect on the structural dynamic response performance.Stewart[13]investigated the effects of coefficients of variation of explosive mass and stand-off, with each varying from 0.0 to 0.3.They also suggested that a lower certainty level regarding model error and input parameters can lead to more severe levels of damage to infrastructure by using two illustrative examples of reinforced concrete columns and glazing.Thus, it is necessary to conduct a statistical analysis of blast load variability and to describe the character of the probability distribution before being able to estimate the design load and thus make damage predictions.Based on four detonations of a general-purpose(GP)bomb,Twisdale et al.[14]recommended a coefficient of variation of 0.30 for an incident overpressure and 0.25 for impulse, and proposed a 5th to 99th percentile of the blast load for reliability-based design of GP bombs.To undertake probabilistic analysis, sufficient information about the experimental samples is required for a reliable statistical investigation.Bogosian et al.[15]collected nearly 300 individual reflected measurements of small cubicles and other samples of larger buildings at various scaled distances and reported that the observed variability for peak reflected pressure is 0.23.Based on public military test data [16,17], Netherton et al.[18]developed a probabilistic blast-load model for scaled distances ranging from 0.58 m/kgto 6.0 m/kg.The incident blast load was assumed to behave as a normal distribution, giving an observed overpressure variability of 0.069,and an impulse within 0.165 to 0.036.Razaqpur et al.[19]conducted a field test by detonating ANFO (a mixture of ammonium nitrate and fuel oil)and targeted a number of full-scale steel,reinforced concrete,and masonry specimens in the open air.A total of 118 incident overpressures and 190 reflected overpressures were recorded within scaled distances varying from 1.24 m/kgto 18.71 m/kg.The statistical analysis performed by Campidelli et al.[20,21]demonstrates that most of the incident and reflected overpressure and the impulse, are best represented by a normal distribution.In their study, the variability of each wave front parameter incident on different reflecting surfaces exhibited significant differences ranging from 0.1072 to 0.613.Besides these experimental investigations, a few studies [22,23]that compared the blast wave parameters produced by computer codes and a few available semi-empirical relations reported significant variations as the average coefficient of variation of the reflected overpressures and impulses were 0.24 and 0.18, respectively.Because of substantial economic and labour consumption involved in full-scale explosion tests, experimental blast load data are rarely reported.The limited data that are available span over decades and were not obtained under the same field conditions.Thus, their statistical analysis can vary both with intrinsic and extrinsic factors.Probability characteristic analysis requires data from repeatable tests,all with the same explosive mass and stand-off.To better describe the characterisation of parameter variability, Netherton et al.[24,25]conducted explosive field trials aimed at examining the repeatability of the explosive mass, detonator location, and the distance between the explosion and the instruments.They developed a new probabilistic blast load model from 32 detonations and more than 224 recorded time-pressure data.Reliability-based design requires that the design load meets a specified reliability level or nonexceedance probability.Hence, the reliability-based design load is calculated by multiplying the nominal load by a load factor, for a given reliability level.Accordingly, Stewart et al.[13,25]proposed non-exceedance-based load factors estimated for quantile levels in the range from 0.05 to 0.99.Different reliability indices were used to derive the blast load factors by Campidelli et al.[20,21],and the comparisons indicate that reliability-based results are more reliable than using the percentiles of the most representative probability distribution functions.

Previous statistical studies focused on airblast and infinite plane reflection; however, some military and civilian structures, such as stadiums, storage units, and industrial buildings, typically adopt a spherical shell form.Because of the high-occupant density and safekeeping of essential supplies, these structures might suffer from bomb threats from accidental explosions and bombings such as terrorist attacks or military action.The dynamic response of a single-layer reticulated dome subjected to external blast loading are discussed in Refs.[26,27], and the blast load applied to the structure was produced by using the arbitrary Lagrangian-Eulerian method using ANSYS/LSDYNA [28].In addition, a modified empirical blast load based on CONWEP[29,30]was also used to study the elastic and inelastic dynamic responses,and it proved to be feasible for a preliminary analysis of the results from a single-layer reticulated dome subjected to blast loads in a series of field experiments.However, these deterministic approaches neglect the actual variability and uncertainty associated with the parameters used in the predictive model.The structural reliability analysis and prediction for the single-layer reticulated dome is rather sensitive to the variability of blast load.As the precondition for reliable disaster prevention and reduction, a series of field tests have been conducted in the present research programme to analyse the blast wave propagation process along a spherical dome roof [31,32].In addition, semi-empirical equations based on ANSYS/LSDYNA have also been proposed to describe the temporal and spatial blast load distributions on the dome structure.As stated above,it is important to consider these variations in structural response analysis in order to get more reliable assessments of structural performance under blast loading.Several repeated explosive field trails on a laboratoryscale spherical dome structure were also conducted by Zhi et al.[33],who discussed the variability of the reflected blast load on the roof.The statistical analysis demonstrates that the normal distribution was the best fit for describing each blast load parameter in that case.Moreover, it was found that the variability of each blast load parameter on the dome roof decreases with increasing scaled distance.Thus,a probabilistic model of the blast load as a function of the scaled distance for dome roof was developed.

In this paper, the main origin of uncertainty in external blast load on dome structures was first analysed.Then, the accuracy of explosive mass-increased method as a safety factor in UFC3-340[1,2], were evaluated.Several input parameters, such as explosive mass and stand-off distance,which are used as random variables in the common probabilistic blast load models, were further investigated by using a sensitivity analysis.In addition, the concept of reliability and the Latin hypercube sampling method were also used to derive blast load factors, considering the inherent uncertainties of inevitable variability, stand-off distance, and explosive mass.In the final section, the damage levels of the mean and reliability-based design blast load applied on a single-layer reticulated dome were then compared.The importance of the specification of the reliability-based design load was thus demonstrated.This research can be used as the basis to determine the external blast loads on the protective dome structure and the defensive technology against terrorist bombing attacks.

2.Uncertainty and variability in blast load models

Previous studies[13,18,24]have indicated that the variability in blast loads on dome structures usually stems from a few input parameters and some inevitable uncertainties in blast loading from unknown and unquantifiable parameters.The input parameters usually include the field conditions, explosive, structural strength,and scale parameters.A schematic diagram of the dome structure and explosive parameters discussed in this paper is shown in Fig.1.In practice, quantifiable explosive parameters such as shape, size,density,mass(),detonation height,and the distance between the explosive and the structure (), as well as the structural scale parameters,such as the span()and rise()of the dome roof and the height of the supporting structure () can be subject to measurement and manufacturing errors when compared with the actual specified values used in calculations.The values of these parameters are typically affected by manufacturing techniques,transportation, storage conditions, and field operation.Inaccuracy in specifying these input parameters can introduce uncertainty in the load prediction before the actual explosion occurs.Moreover,the generation and propagation of blast waves during the explosion can be affected by even more uncertainties, such as geographical and meteorological conditions.Their influence cannot be easily controlled and/or avoided, so they are inevitable uncertainties.Statistical analyses of the present repeatable explosive field trials on a dome roof (Fig.2) have demonstrated that the blast load follows a normal distribution [33].

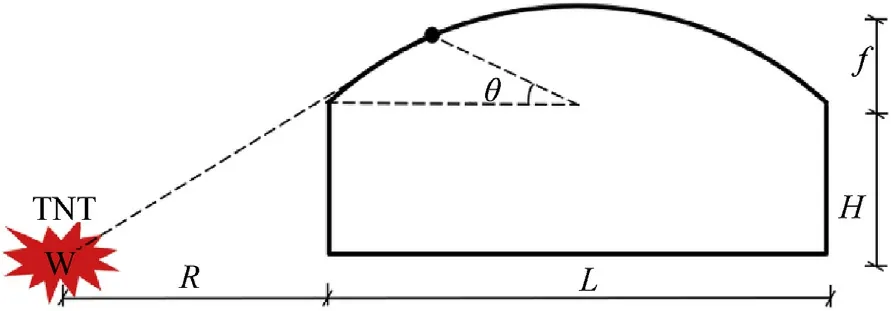
Fig.1.Schematic diagram showing the structural and explosive parameters [32].

Moreover,the coefficients of variation(COV)of positive impulse()and overpressure()representing the inevitable uncertainties on the dome roof can be described by Eqs.(1) and (2) [33].

where θ is the structural angle,is the nominal scaled distance calculated as Eq.(3),

By using the experimental data and numerical techniques, the mean of each blast load parameter(and)can be obtained by the multiplication of the deterministic semi-empirical Eqs.(4) and (5)[32]and the mean of the model error Eqs.(6) and (7) [32].

Fig.2.Repetitive field explosion test [33].

where a,b,c,a,b,c,,,andare shape parameters for the structure, which can be represented byand are given by Eq.(8) [32].

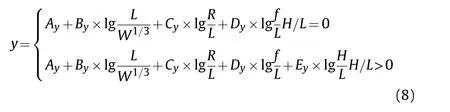
The parameters A, B, C, D, and E, are fitting constants for describing the shape parameter (), and their values are listed in Table 1.

3.Assessment of deterministic mass-increase safety method

For the design of structures, the design manual UFC-3-340-02[2]suggests that the TNT equivalent weight should be increased by a factor of 1.2 to cope with the unknown factors that can cause an overestimation of a structure’s load carrying capacity when subject to an explosion.The UFC-3-340 design manual [1,2]yields relevant deterministic blast load models for dome roofs.Figs.3 and 4 compare various predictions with the present experimental results of the reflected overpressure and the impulse distributed on the dome roof when=3.57 m/kg.The upper and lower bounds represent 5%-fractile and 95%-fractile, respectively.The reflected overpressure obtained by using the mass-increase safety concept provides a significant overestimation of the loading, especially on the front dome roof (where structural angle(θ) is less than 90, as shown in Fig.1) which almost maintained at the 95%-fractile.In addition, the predicted impulse on the whole reflector is higher than the 95%-fractile, given a stable and overestimation on the whole dome roof, as shown in Fig.5.

Figs.5 and 6, show the various probability distributions of the reflected overpressure using statistical parameters from Eqs.(2),(5)and (7), as well as the mass-increase safety factor values when=3.57 m/kgconsidering the reflected overpressure distributed on the dome roof.The design values for the reflected overpressure set by the charge mass-increase method are 399.2 kPa(Fig.5)and 65.2 kPa(Fig.6)respectively at the locations θ=4and 71.Figs.7 and 8 show that the probabilities of the reflected overpressures exceeding the UFC design values are less than 3% for gauge 1(θ = 4) and more than 54% at gauge 3 (θ = 71), based on both probability distributions.

The assurance factors based on quantile for the reflected overpressure using the mass-increase method along the dome roof both fall off rapidly from more than 97%-0%, with an increase of structural angle when= 3.57 m/kg, as shown in Figs.7 and 8 and listed in Table 2.However,the assurance factors for the impulse are close to 100% based on the normal and Gumbel distributions, asshown in Table 2.Actually, applying a safety factor to the design load would be expected to skew the mean appropriately [18].Besides the probability of non-exceedance (assurance factor), the rationality and adaptability of the universal 20% increase in mass should be further evaluated by reliability level.

Table 1Parameters for the blast load model [32].

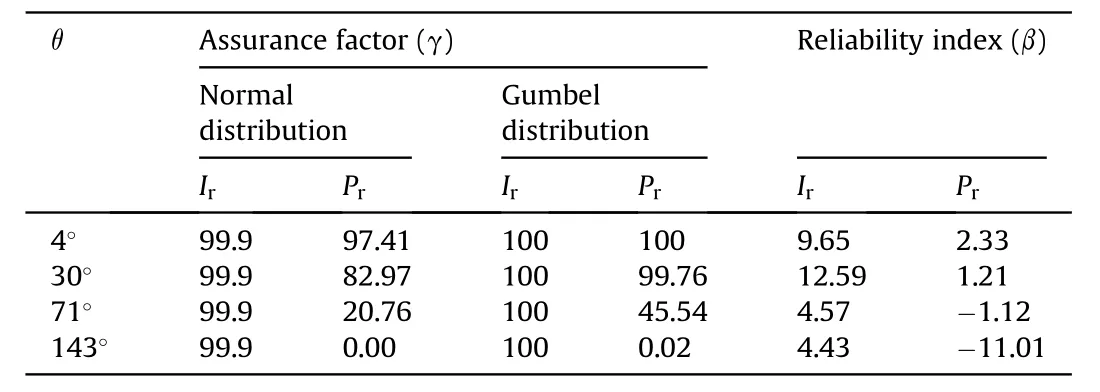
Table 2Probabilities of blast load exceedance (assurance factor) and reliability indices for impulse and reflected overpressure based on mass-increase safety factor of 20%when Z= 3.57 m/kg1/3.

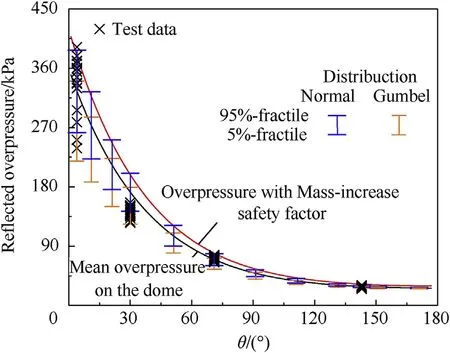
Fig.3.Pr on the dome roof when Z = 3.57 m/kg1/3.

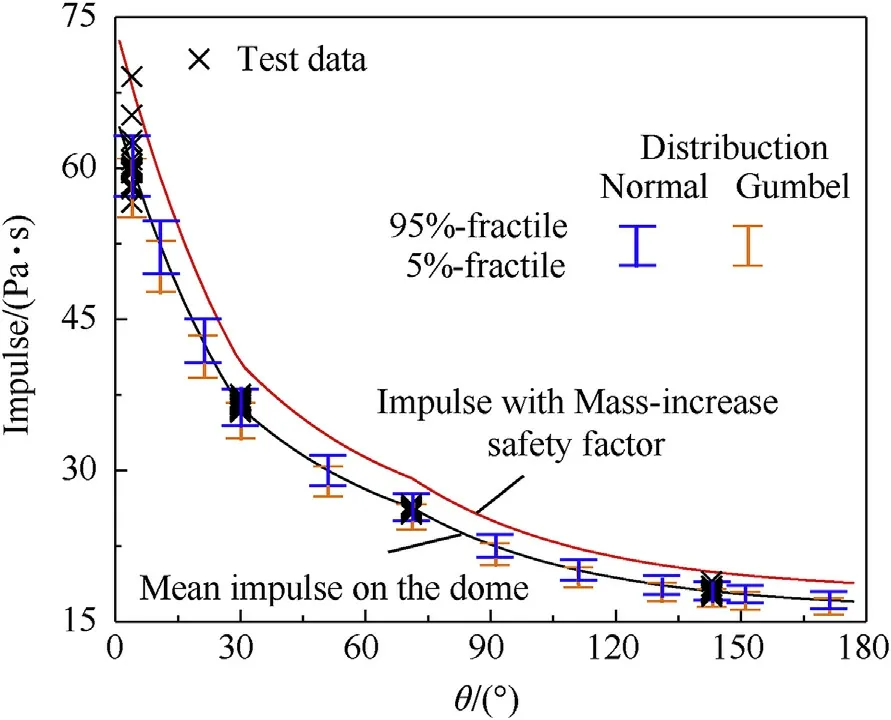
Fig.4.Ir on the dome roof when Z = 3.57 m/kg1/3.

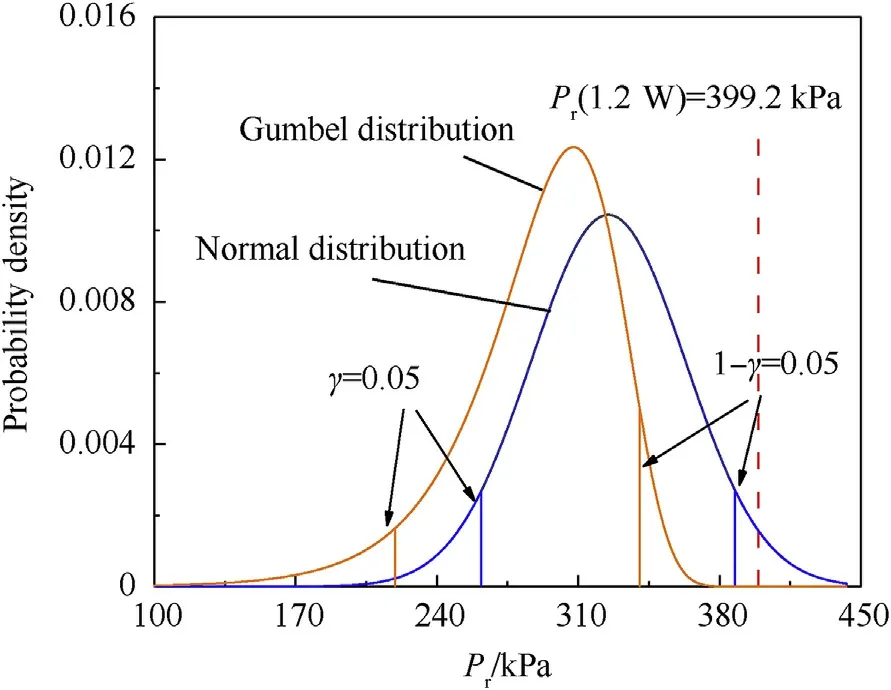
Fig.5.Various PDFs of Pr and comparison with various design load values when Z = 3.57 m/kg1/3 and θ = 4°.

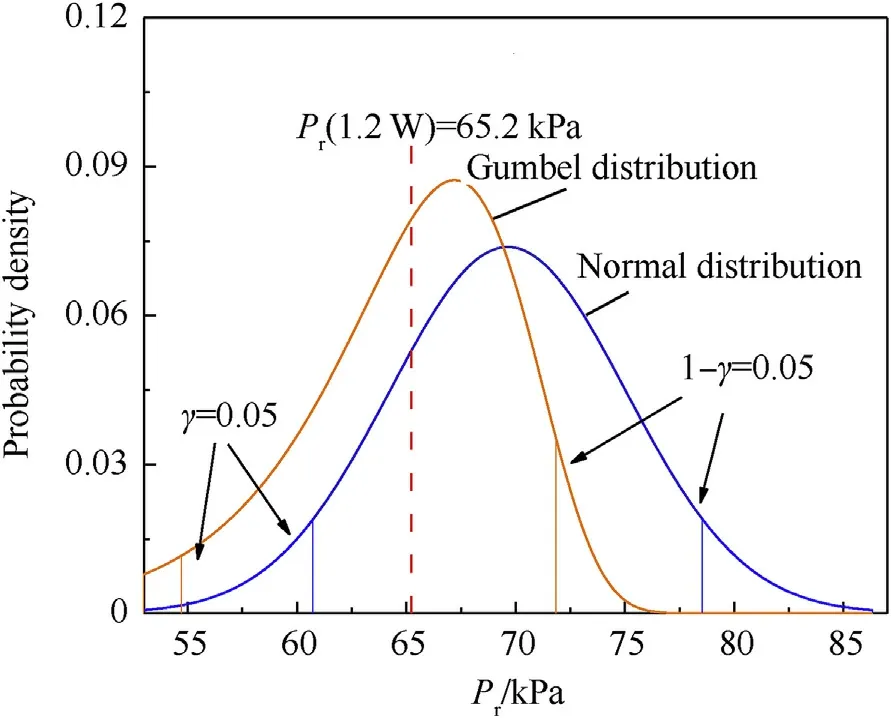
Fig.6.Various PDFs of Pr and comparison with various design load values when Z = 3.57 m/kg1/3 and θ = 71°.

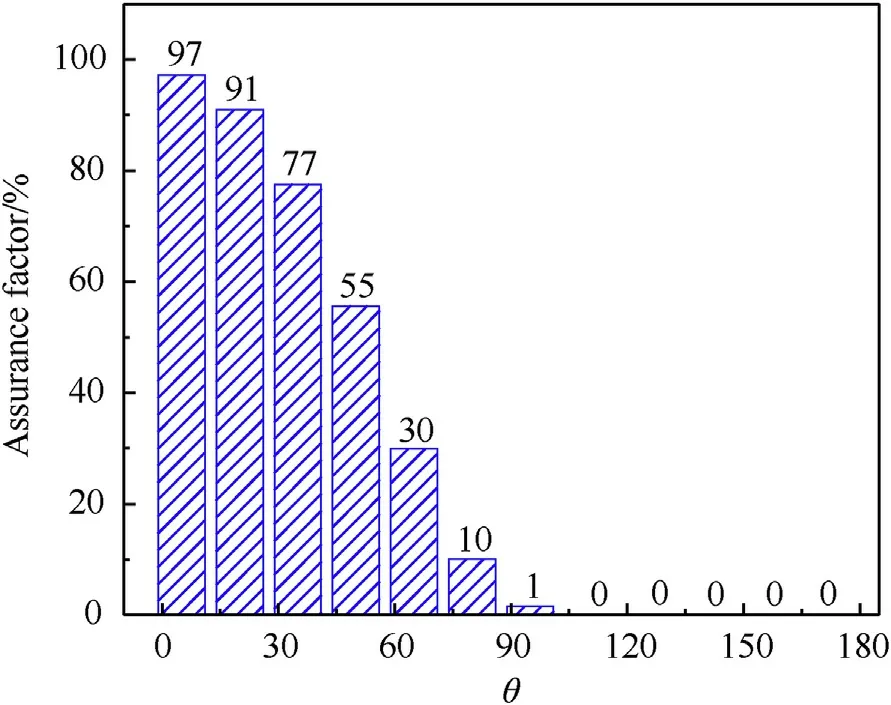
Fig.7.Assurance factors of Pr by mass-increase method with Normal distribution along the dome when Z = 3.57 m/kg1/3.

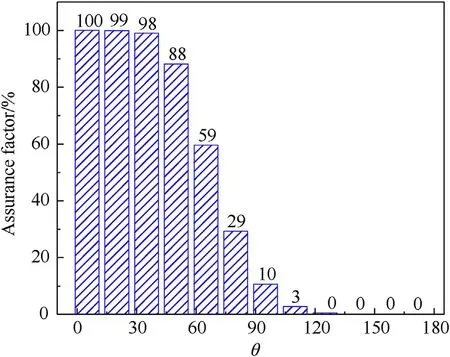
Fig.8.Assurance factors of Pr by mass-increase method with Gumbel distribution along the dome when Z = 3.57 m/kg1/3.

There is a corresponding relationship between the probability offailure()and the reliability index(β).According to a study[20]on approximation and simplification,the reliability index(β)based on the assumption of a normally distributed load and resistance can be defined as Eq.(9)

where the coefficient ζ is defined as Lind’s separation function and is assumed to be equal to 0.75 to obtain an error less than 6%[34].The variablerepresents the model error of each blast load parameter, and COVand Meanrepresent the coefficient of variation and mean,respectively.The coefficient λ is the load factor that refers to the factor that is applied to the nominal value to obtain its design value.Reliability indices for the impulse and reflected overpressure results based on the mass-increase safety method are listed in Table 2 for the case where=3.57 m/kg.As blast load parameters may be represented by a Gumbel distribution, the load factors calculated by Eq.(11) can be used as approximate relative reference values, but lower accuracy in them is inevitable.Accordingly,the reliability index of the recommended results by the mass-increase safety method for the impulse range from 4.43 to 12.59 for typical structural angles when= 3.57 m/kg.Conversely,the reliability index for the reflected overpressure is less than 2.33 and even negative when structural angle is greater than a certain critical value.

Consequently, the assurance and the reliability evaluation demonstrate that the 20% safety factor results exhibit an inconsistent safety factor (irrespective of the assurance factor or reliability index) along the dome roof when= 3.57 m/kg.It also over-estimates the actual impulse along the entire dome roof and under-predicts the reflected overpressure along most of the roof.From Eqs.(5)-(8)it can be seen that the probability model for blast loads on a specified structure is determined by each input explosive parameter, such as charge mass and stand-off distance.Although the design method proposed in UFC focuses on safety, it may not perform as conservatively and reliably as expected.Therefore, this is unacceptable when a reasonably safe design is required.

4.Reliability-based factors for external blast loads on the dome roof

4.1.Comparison between assurance and reliability-based load design methods

The reliability-based design method for buildings requires that the blast load employed in the protection design and military action should be such to meet a specified reliability level or probability of non-exceedance (assurance).The reliability-based blast load on a dome roof can be achieved where the mean blast load suggested by Qi et al.[32]is multiplied by a load factor (λ) to account for the uncertainty effect.For safety protection design, the design blast load should exceed the mean value, resulting in a more conservative structural design.One option is to take a certain percentile(γ)of the probability distributions for each blast load parameter as a reference when the probability distributions of both the resistance and load parameters need to be considered,which can then yield an assurance-based load factor(λ).Another option is to introduce the reliability index by considering the probability of failure,and then a reliability-based load factor (λ) can be defined.

A 95% assurance factor with a 5% probability of exceedance is typically accepted and desirable in structural design, so a 0.95 assurance level for the impulse and reflected overpressure along the dome roof is evaluated by using γ=0.95.Then the assurancebased load factor (λ) can be defined by Eq.(10).

For the normal distribution, the coefficient ψ as a quantile function of the standard normal distribution can be calculated by using Eq.(11).

For the Gumbel distribution,the coefficient ψ can be calculated by using Eq.(12).

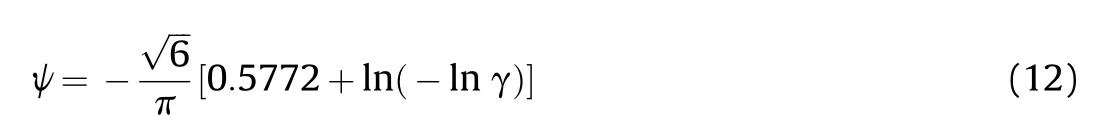
Load factors for the impulse and reflected overpressures for the 0.95 assurance factor with the normal and Gumbel probabilistic blast load models along the dome roof at typical scaled distances of 3.12,3.57,and 4.03 m/kgwere obtained and are shown in Figs.9 and 10.According to Eqs.(1)and(2),the variability of the reflected overpressure decreases with the increase of structural angle and scaled distance,while the variability of the impulse decreases only with increase in scaled distance.Therefore,Figs.9 and 10 show that the load factors increase with scaled distance,decreasing under the same assurance rate.In addition, the load factor of the reflected overpressure decreases linearly when the load factor of the impulse remains constant along the dome roof.Moreover, the rightskewness distribution given by the Gumbel probability density function promotes a higher load factor than the normal distribution function for an assurance factor of 0.95.

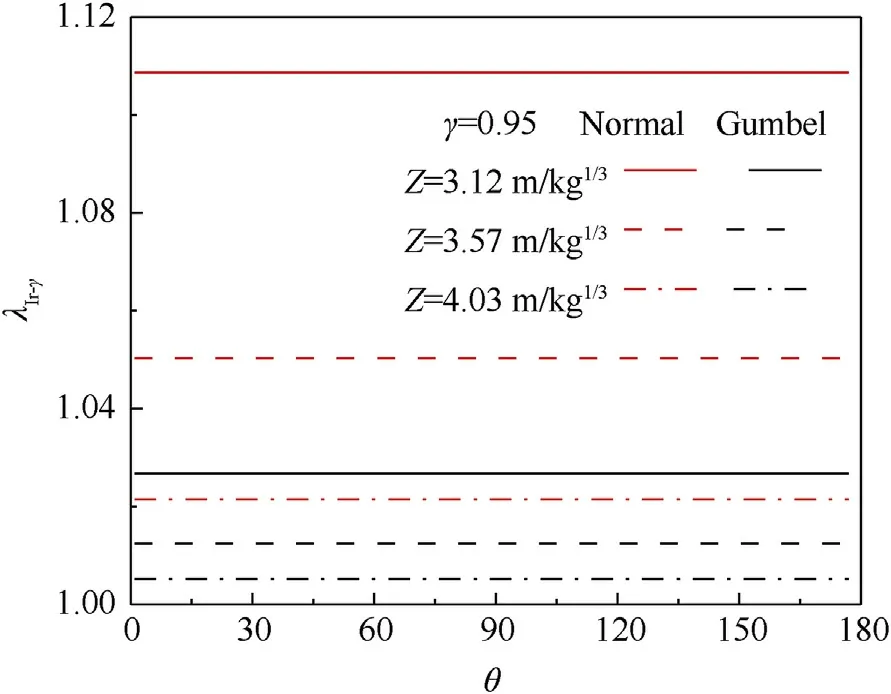
Fig.9.Load factor estimates of Ir for γ = 0.95 assurance factor with various probabilistic blast load models along the dome roof.

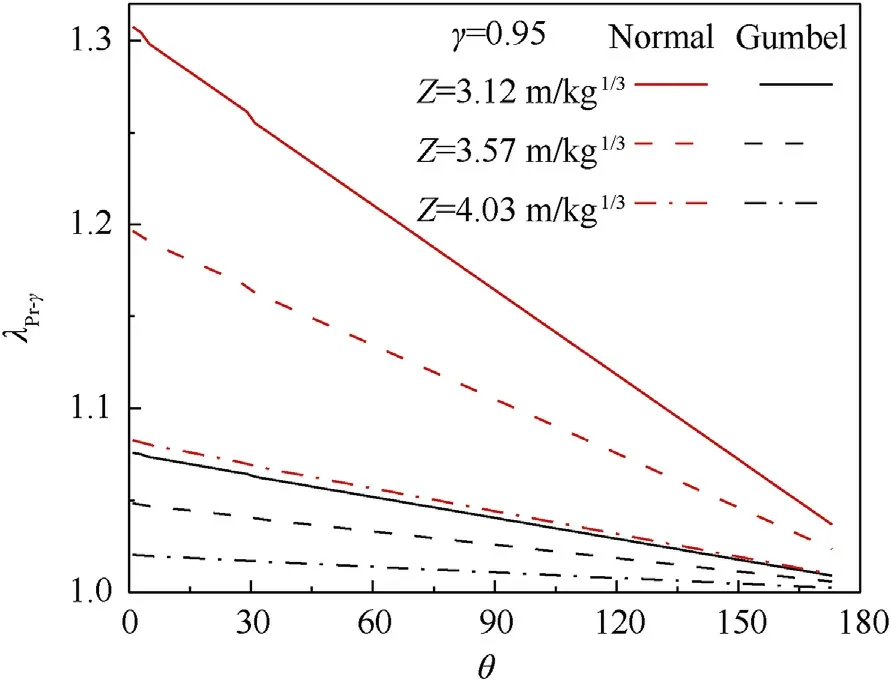
Fig.10.Load factor estimates of Pr for γ = 0.95 assurance factor with various probabilistic blast load models along the dome roof.

According to the Chinese unified standard for reliability design of building structures GB 50068 [35], three safety grades are classified, based on the importance of the industrial and civil construction.These grades correspond to low,medium,and high levels of protection.The reliability indices for the ultimate limit state design are also suggested separately for ductile and brittle fracture,ranging from 2.7 to 4.2, as shown in Table 3.

In addition,the blast load model with an assurance factor of 95%should be assessed using the reliability index to assess whether or not it can be used in reliability-based design.From Eq.(12), the reliability indices of the load factor for the impulse and reflected overpressures from both the normal and Gumbel probabilistic distributions at typical scaled distances of 3.12, 3.57, and 4.03 m/kgwere determined,and are presented in Table 4.It can be seen from Table 4 that the reliability indices calculated for the impulse and reflected overpressure increase with scaled distance, and indices are not always uniform along the dome roof, especially when based on the normal distribution.Moreover, the reliability level of design blast load based on the normal distribution are much higher than those from the Gumbel distribution, which also indicates that the former method is relatively more conservative.However, the reliability indices corresponding to the 0.95 percentile range from 0.52 to 2.17,which are far below the recommended values in the Chinese unified standard GB 50068.These low values are unacceptable in anti-explosion protection design for structural safety,both for brittle and ductile failure.The assurance-based load method based on the probability distribution has a clear physical concept and is able to reflect the variability character of each blast load parameter.Nevertheless, the assurance-based load method only focuses on its variability,and it fails to ensure compliance with structural safety design standards.

For structural risk analysis under explosion, a reliability-based load factor (λ) under a given reliability level (β) can be rewritten as Eq.(13), derived from Eq.(9).

Tables 5 and 6 separately list the blast load factor estimates ofthe impulse and reflected overpressures for different reliability indices as recommended by GB 50068 when= 3.57 m/kg.In addition, these tables also include blast load factors calculated for low, medium, and high levels of protection as recommended by Campidelli [20]and MacGregor [36], whose corresponding reliability indices are 3.5, 4.0, and 4.5.The results show that the impulse load factor is around 1 for the different reliability indices,which indicates a relatively small change.When the reflected overpressure is considered,as shown in Table 6,the load factors can be significantly different for different reliability indices compared to the impulse, owing to the larger scatter in the reflected overpressure.For a general-purpose design subject to explosion, a relatively low probability of collapse or of local failure is required in a particular blast event.Therefore, a higher reliability index is required.

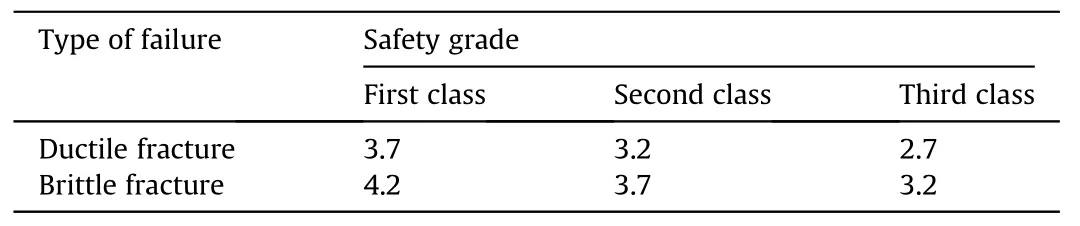
Table 3Reliability indices in Chinese unified standard GB 50068 [35].

Table 4Reliability index estimate for 0.95 assurance factor.

Table 5Blast load factor estimates of Ir for different reliability indices when Z=3.57 m/kg1/3.

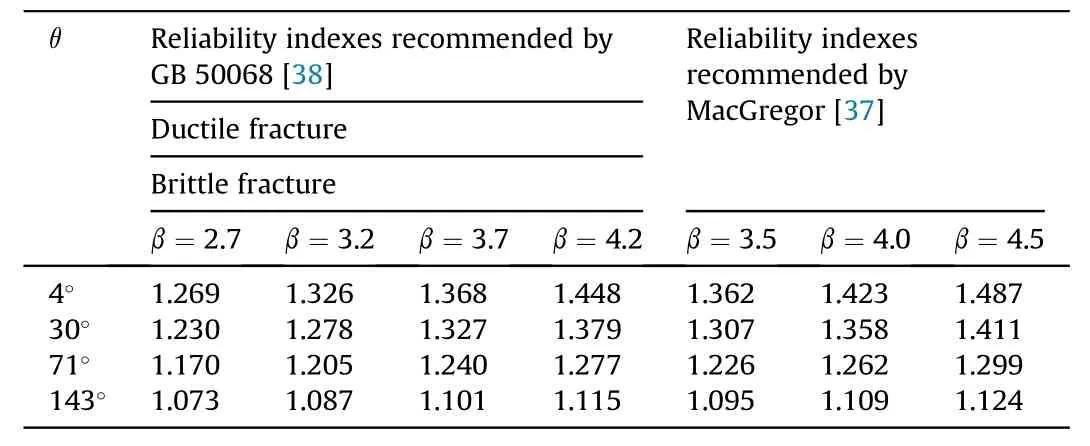
Table 6Blast load factor estimates of Pr for different reliability indices when Z=3.57 m/kg1/3.

In the following analysis,the reliability indices associated with a low,medium,and high level of protection[20,36](β=3.5,4.0,and 4.5, respectively) are required.More importantly, these reliability indices are obtained from the probability of failure during a building’s service years,which are more reasonable.In Figs.11 and 12, the reliability-based load factor estimates of the impulse and reflected overpressures along the dome roof at typical scaled distances of 3.12,3.57,and 4.03 m/kgare shown.Compared with the 0.95 percentile load factor estimates distributed on the dome roof shown in Figs.9 and 10, these reliability-based load factors demonstrate a significant difference from the assurance-based load factor values.The 0.95 probability of non-exceedance results in blast load factors ranged from 1.005 to 1.109 and 1.002 to 1.308 for impulse and reflected overpressures, respectively, whereas the recommended reliability levels result in blast load factors with the range of 1.035-1.250 and 1.020-1.880, respectively.Thus, the reliability-based load method clearly offers a more reliable and reasonable approach in probability limit state design for considering the effects of blast loads.

4.2.Sensitivity analysis and reliability-based blast load factors

As described in section 2,some input parameters can also act as the dominant sources of variability.Previous studies [18]on freefield blast loading suggest that the results are quite insensitive to variations in the air temperature and pressure compared to variability in other random variables.Eqs.(1)-(8) show that the variability of explosive mass () and stand-off distance (), influence not only the deterministic load model but also affect the model error and intrinsic variability.In this paper, the desired mass and the equivalent factor in terms of a mass of TNT are regarded as deterministic,and the coefficient of variation of the explosive mass only arises from user factors associated with the explosive delivery error.In addition,it is also assumed that the structural parameters are deterministic,and the variability of the explosive positions only results from human causes [13].Explosive mass () and stand-off distance()are assumed to be normally distributed and statistically independent random variables [13,18].In terrorist vehicle-borne improvised explosive device (VBIED) scenarios for GPS-guided systems, it is summarised that Mean() = 1, Mean() = 1,COV() = 0.102 and COV() = 0.100.Accordingly, a sensitivity analysis should be conducted to investigate the effects on the probabilistic blast load model due to changes of these two random input variables ().A reliability-based blast load method could then be proposed, which could include the uncertainty and variability in the model error,inevitable variability,explosive mass,and stand-off distance.

Local sensitivity analysis primarily investigates the effect of a single uncertain factor on the output.For this study the standarddeviation of a specific input variable is respectively increased and reduced to zero,while the other input variables are kept unchanged at their mean values.The result,i.e.change of output(Δy)divided by the nominal or mean output (), can then be used as an index to measure the specific parameter sensitivity (s), Eq.(14).

Fig.11.Reliability-based load factor estimates of Ir along the dome roof.

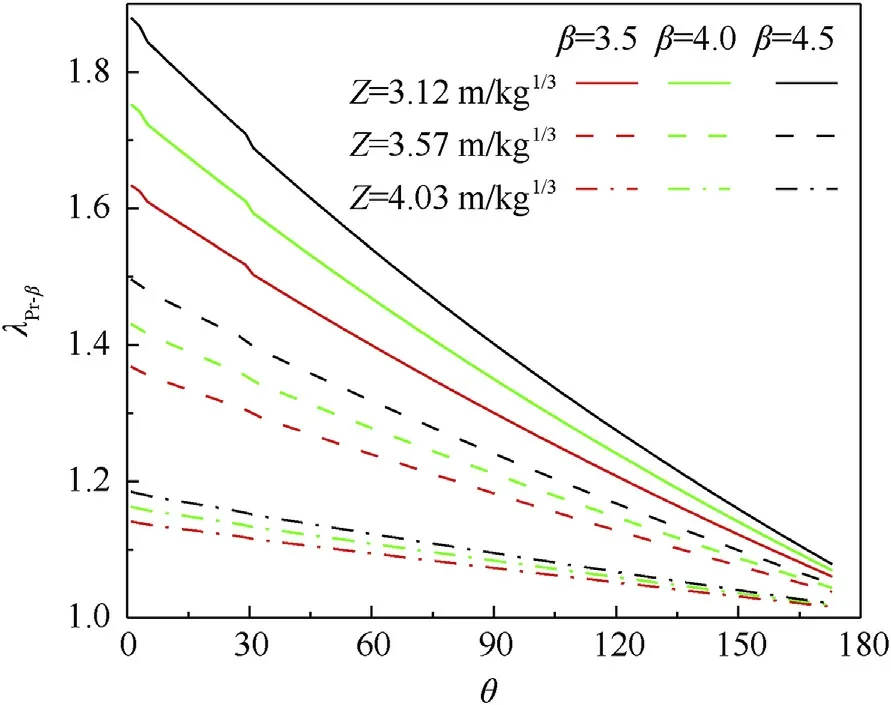
Fig.12.Reliability-based load factor estimates of Pr along the dome roof.

The results of this kind of sensitivity study are shown in Figs.13 and 14, where the sensitivity of explosive mass () and stand-off distance () to the mean of the impulse and reflected overpressures along the dome roof for a typical scaled distance are calculated.Taking the mean of the blast load along the dome roof when= 4.03 m/kgas an example, it can be seen that the influence range of the stand-off distance and the explosive mass on the impulse are from 4% to 18.5% and 13%-16%, respectively(Fig.13).Similarly, the influence ranges for the reflected overpressure are from 17.5%to 43%and 18%-24%,respectively(Fig.15).The influence range of the stand-off distance on mean blast load is clearly greater than the explosive mass, and the sensitivity of the blast load to variations in the explosive mass decreases slightly along the dome roof.It is also evident that the mean value of the reflected overpressure is more sensitive than the impulse to the effects of changes in these two random variables.Comparisons of impulse sensitivity between Figs.13 and 14 and the sensitivity of reflected overpressure between Figs.15 and 16 show that the larger the scaled distance, the higher the sensitivity of the blast load parameters to variations in the stand-off distance and explosive mass.Interestingly, the sensitivity of the blast load to the stand-off distance decreases rapidly with an increase in the structural angle,approaching zero at the top of dome roof,as shown in Figs.15 and 16.On the rear dome roof(θ>90),the sensitivity to the stand-off distance increases gradually with increase in the structural angle.The sensitivity of explosive mass () and stand-off distance () to the coefficient of variation (COV) of the impulse and reflected overpressure for some typical scaled distances are also shown in Fig.17.The sensitivity of COV() to the explosive mass () and stand-off distance () increases with scaled distance whereas the sensitivity of COV() increases initially and then decreases.

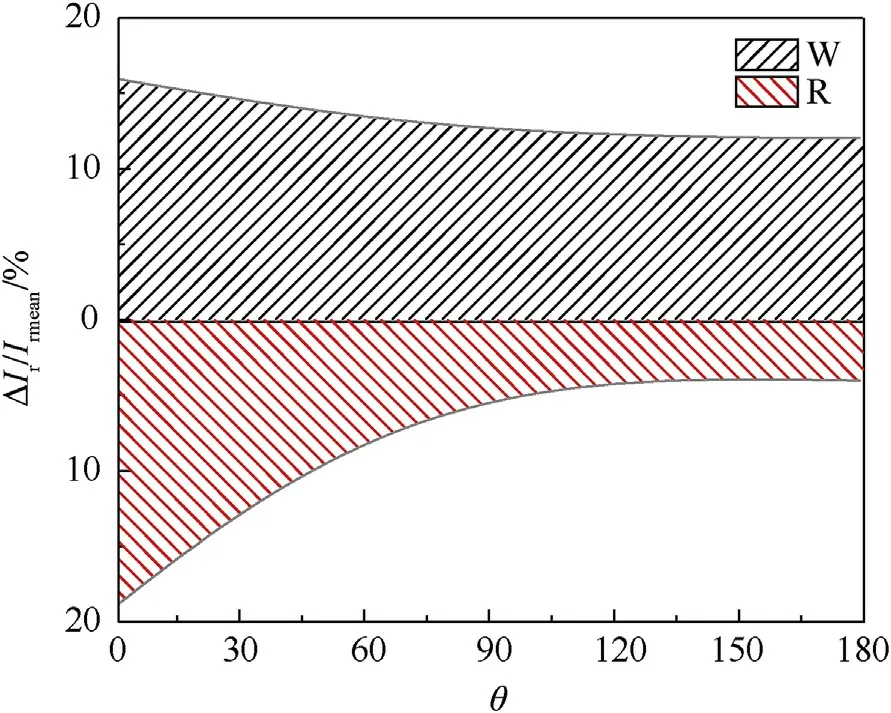
Fig.13.Local sensitivity analysis for mean of Ir along the dome roof when Z=4.03 m/kg1/3.

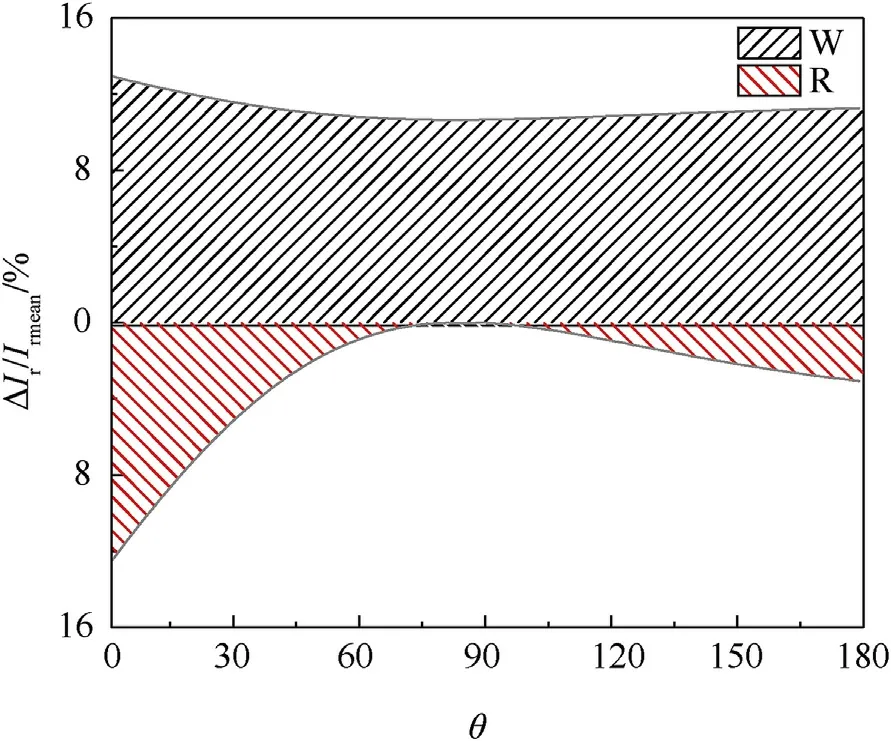
Fig.14.Local sensitivity analysis for mean of Ir along the dome roof when Z=3.12 m/kg1/3.

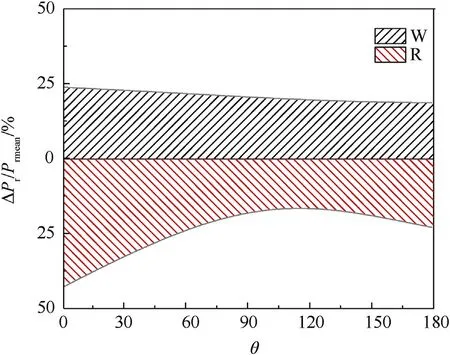
Fig.15.Local sensitivity analysis for mean of Pr along the dome roof when Z=4.03 m/kg1/3.

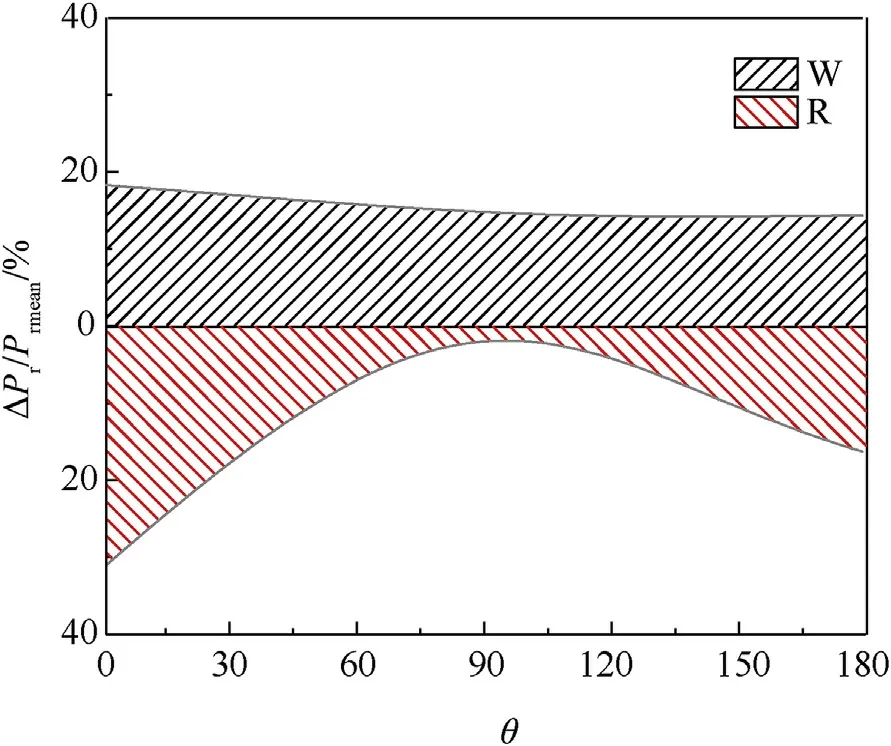
Fig.16.Local sensitivity analysis for mean of Pr along the dome roof when Z=3.57 m/kg1/3.

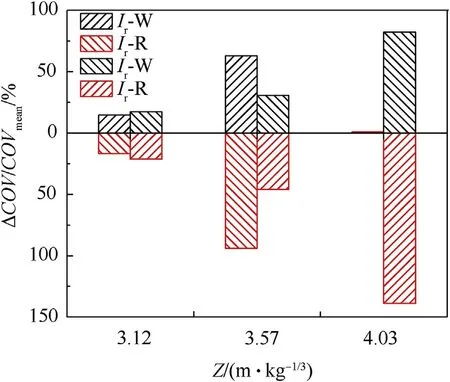
Fig.17.Local sensitivity analysis on the coefficient of variation for some typical scaled distances.

The sensitivity analysis of the mean of each blast load parameter within the range of two standard deviations of each random variable shows that the effect of the stand-off distance on the mean value of the blast load is more significant than the explosive mass when the structural angle is less than 10.Furthermore, the sensitivity of the stand-off distance fluctuates greatly along the dome,whereas the effect of explosive mass is relatively stable.The effect of the stand-off distance and explosive mass on the mean of the reflected overpressure is higher compared with the effect on the impulse.This proves that stand-off distance has a more significant effect than explosive mass on the coefficient of variation of each blast load parameter within the range of two standard deviations of each random variable.

The sensitivity analysis suggests that both the stand-off distance and the explosive mass have a non-negligible influence on the blast load along the dome roof.Thus,an improved reliability-based blast load factor with greater confidence, considering the model error,inevitable variability, and the uncertainties of stand-off distance and explosive mass should be developed.In this paper, the Latin hypercube sampling (LHS) method [34]is employed to generate near-random samples.LHS method ensures that the set of random numbers is representative of the real variability compared with the traditional random sampling method.Foremost, the input parameters,including the explosive mass()and stand-off distance (),are specified as the random variables and are assumed to be statistically independent.Subsequently,random samplings are generated forandbased on the LHS method to follow their probability distribution functions.The simulated values ofandare used to estimate the first two moments of the blast load statistical parameters, including the impulse () and reflected overpressure().Since each sample is also a random variable,a further m × n random samples of the blast load can be produced.As a result, m × n mean values of the blast load have been taken as random samples, noting that they adequately cover different possible load conditions.Based on this, relevant statistical parameters of the first two moments(Mean and COV)have been obtained,and then, a reliability-based blast load factor (λ) has been calculated.

The accuracy of λmainly depends on the sample size.Thus, a suitable sample number should be selected considering both the computational efficiency and acceptable confidence.Figs.18 and 19 show the relationship between the coefficients of variation and the sample size of each statistical parameter on blast load model in the two typical cases that are calculated.The results indicate that the sample size has a specific effect on the dispersed extent of statistical parameters, but that the coefficient of variations gradually tend to converge and become stable when the sample size exceeds 150.To confirm the accuracy and reliability in all cases, the sampling process has been repeated for 200 simulation runs using following uncertainty analysis.

The computational steps for calculating REBLFs along the dome roof can be described as follows.For example,when the=3.12 m/kg, L/W= 2.623 m/kg,= 0.755,= 0.217,= 0.311,COV= 0.102, and COV= 0.10, the REBLFs forandalong the dome roof can be calculated:

1.Two hundred samples forandare generated as normally distributed random variables by the LHS method, respectively.

2.The mean and the coefficient of variation forandare calculated based on Eqs.(1)-(8).Therefore, there are 200 statistical load parameters (Mean and COV) samples for each structural angle.

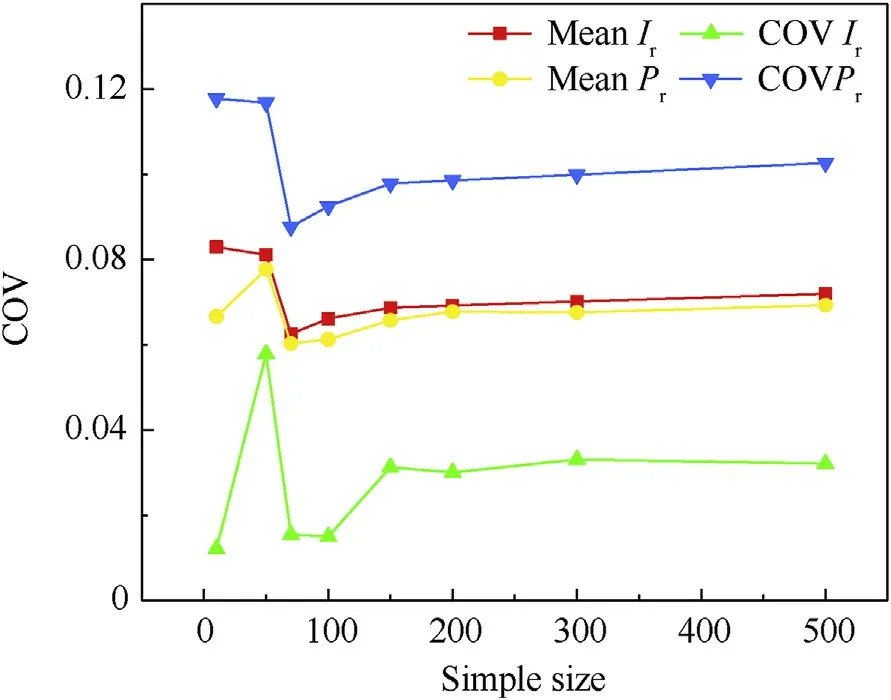
Fig.18.Relationship between coefficient of variation and sample size of each statistical parameter on blast load model when Z = 2.90 m/kg1/3 and θ = 10°.

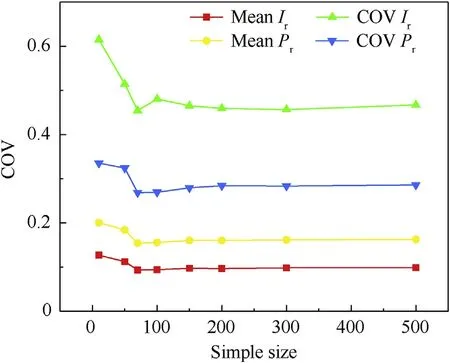
Fig.19.Relationship between coefficient of variation and sample size of each statistical parameter on blast load model when Z = 3.57 m/kg1/3 and θ = 10°.

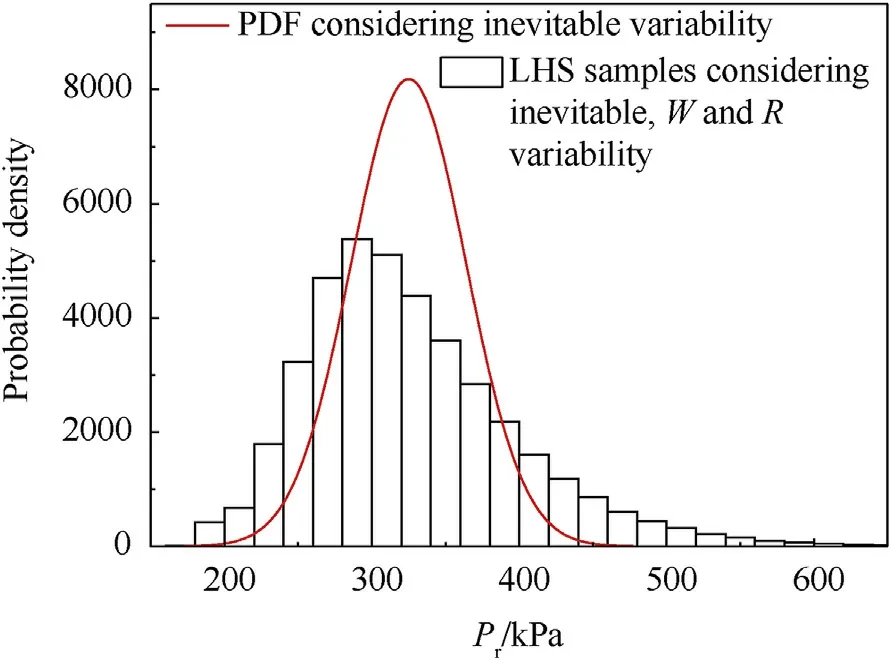
Fig.20.Simulation histogram of Pr with COV(W) = 0.102, COV(R) = 0.10 when Z = 3.12 m/kg1/3 and θ = 4°.

4.Based on the first two statistical moments (Mean, COV), the reliability-based blast load factors along the dome roof can be calculated using Eq.(14).Table 8 shows the blast load factor(λ)results considering the variability of explosive mass(),standoff distance (), and difference (δ) compared with the deterministic results for several typical structural angles.The comparison shows that the reliability-based blast load factors which consider multiple variabilities increase significantly, ranging from 10.7% to 40.2%.

4.3.Application to the dynamic structural response assessment

The probability of occurrence of different damage levels or even collapse of the structure under blast loading can be estimated by using structural reliability analysis.The reliability-based load factor approach aims at establishing a certain safety reserve for the structure and achieving a desired reliability level.To investigate the influence of the reliability-based load factor on prediction of the structural dynamic response, the effect of different blast load models under mean and different reliability levels for the reticulated dome’s damage factor () are compared.Theare an indexes that are used to quantify the structural damage level and collapse limit state.In this section, the explosion scenario considered is a terrorist VBIED with an explosive weight of 1000 kg TNT parked 20 m away from a single-layer Kiewit 8 system reticulated dome with a span of 40 m and rise-span of one-fifth, as shown in Fig.21.Using structural damage theory and critical dynamic response indices,an empirical equation forhas been proposed in Ref.[37]based on the dynamic response behaviour of this singlelayer reticulated dome, given here in Eq.(15):

whereis the displacement of structural apex, and rrepresents the ratio of the leastintegration points of members that have yielded.Therefore,represents the ratio of number of members that have entered the yield stage compared to the total number of members, whereasdenotes the ratio of members whose whole sections have yielded,as shown in Fig.22.Five damage levels for a single-layer reticulated dome under external explosion and the correspondingranges are also recommended in Ref.[37]and are listed in Table 9.

Table 7Model error statistical parameters results considering and without considering the variability of explosive mass(W)and stand-off distance(R),and the difference(δ)between them at a few typical structural angles when Z = 3.57 m/kg1/3.

Table 8Blast load factor(λβ)estimates considering the variability of explosive mass (W) and stand-off distance (R) and difference (δ)with Tables 5 and 6 at a few typical structural angles when Z = 3.57 m/kg1/3.

Table 9Damage states and corresponding damage factor ranges for a single-layer reticulated dome.

Fig.22.Plasticity development of shell member.

According to the methods for blast load testing and devices for pressure measurement [38], the thick of small scaled model designed in this study [32,33]is 30 mm, so the stiffness of the scaled model is large enough to ignore the influence of structural elastic-plastic deformation response on blast load.In addition,this section focuses more on the structural response rather than the fluid-solid coupling effect, so the blast load model obtained from rigid specimen can be used as a conservative consideration.Based on the reliability-based blast load calculation procedure described in section 4.2.2,the REBLFs forandalong the dome roof under low-, medium-, and high-reliability levels that consider the inevitable variability, and the uncertainties in stand-off distance and explosive mass can be calculated, as shown in Fig.23.Next, the reliability-based blast load models are applied to the single-layer reticulated dome structure with three different roof weights, and thefor each reliability level based on Eq.(14)are determined,as shown in Fig.24.According to the definition of damage level, the single-layer reticulated dome structure will experience moderate damage based on predictions simply using the mean blast load(β = 0).However, the predicted structural damage level will be higher and could even escalate from moderate to severe under reliability-based blast load model in Figs.25 and 26.It clearly demonstrates that a higher requirement of structural reliability can yield higher reliability-based load factors, and also increase the probability of severe levels of damage.That is,improved reliabilitybased blast load factor method can contribute to a more reliable structural design.

5.Conclusions

Based on the newly developed probabilistic model of external blast loads on a spherical dome structure, a reliability-based blast load factor which considers the variability and uncertainty of explosions has been proposed in this study.It also has made a preliminary attempt at applying a reliability-based blast load method for dynamic response predictions.The following conclusions can be drawn from this detailed study:

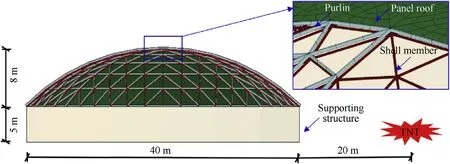
Fig.21.A single-layer Kiewit 8 system reticulated dome structure.

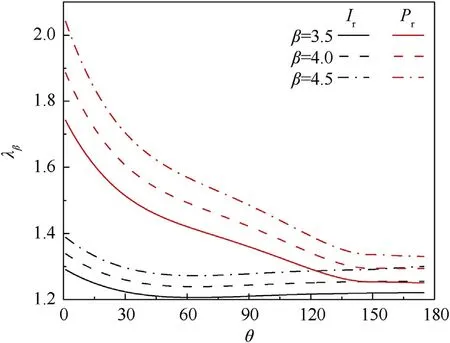
Fig.23.REBLFs for Ir and Pr along the dome roof for three different reliability levels.

(1) The deterministic design concept to obtain a safer load model has emerged from UFC-3-340-02, which suggests a mass-increase safety factor of 20%; Using this approach, the assurance can be as low as 0.00 and up to 100 on the dome roof, and the reliability levels range from -11.01 to 12.59.This was found that mass-increase method cannot give a consistent safety factor (assurance factor and reliability index) over the entire dome roof.

(2) The assurance-based load method based on the probability distribution has a clear physical basis and can reflect the variability character of each blast load parameter.However,it fails to ensure compliance with structural safety design standards.The reliability indices corresponding to the 0.95 percentile are far below the recommended values for structural design in the Chinese standard.The newly proposed reliability-based load method can offer a more reliable and reasonable approach by considering the blast load effect in probability limit state design and can serve reasonably adequately for various levels of protection.

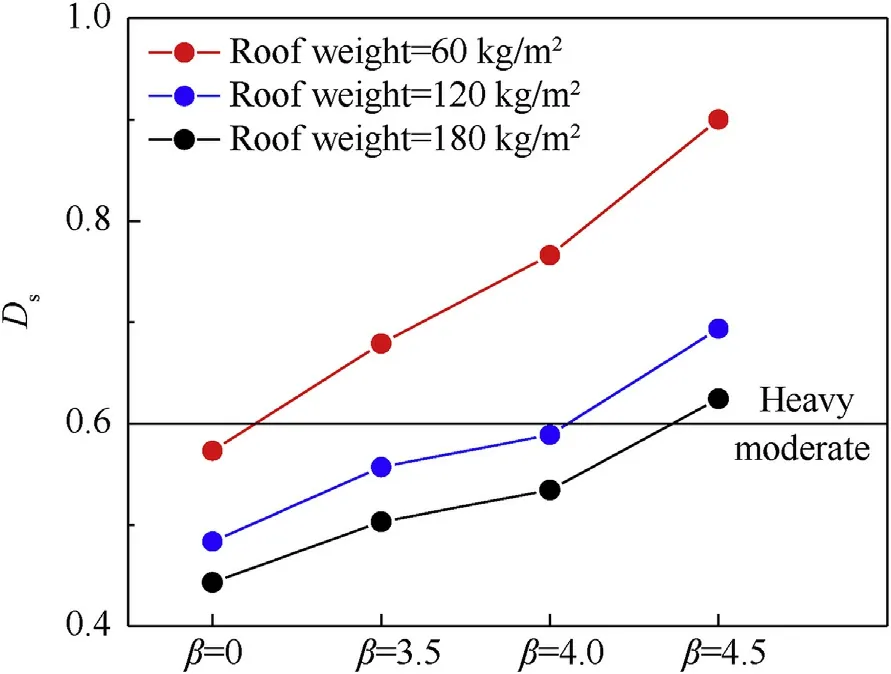
Fig.24.Reticulated dome structure’s damage factors for three different reliability levels and three different roof weights.

(3) The sensitivity analysis shows that both stand-off distance and explosive mass have a significant effect on the blast load distribution on the dome roof that has been studied here in much detail.Based on the Latin hypercube sampling method and statistical results, reliability-based load factor that considers the inevitable variability, and the uncertainties of stand-off distance and explosive mass were provided for designed load value taken.

(4) A dynamic response case study, using the approach described in the paper, has been carried out on a typical single-layer reticulated dome.The results showed that a higher structural reliability requirement gives a higher reliability-based load factor, and this reliability-based blast load factor method can be further used to design stronger buildings that will resist the possible explosion risks.

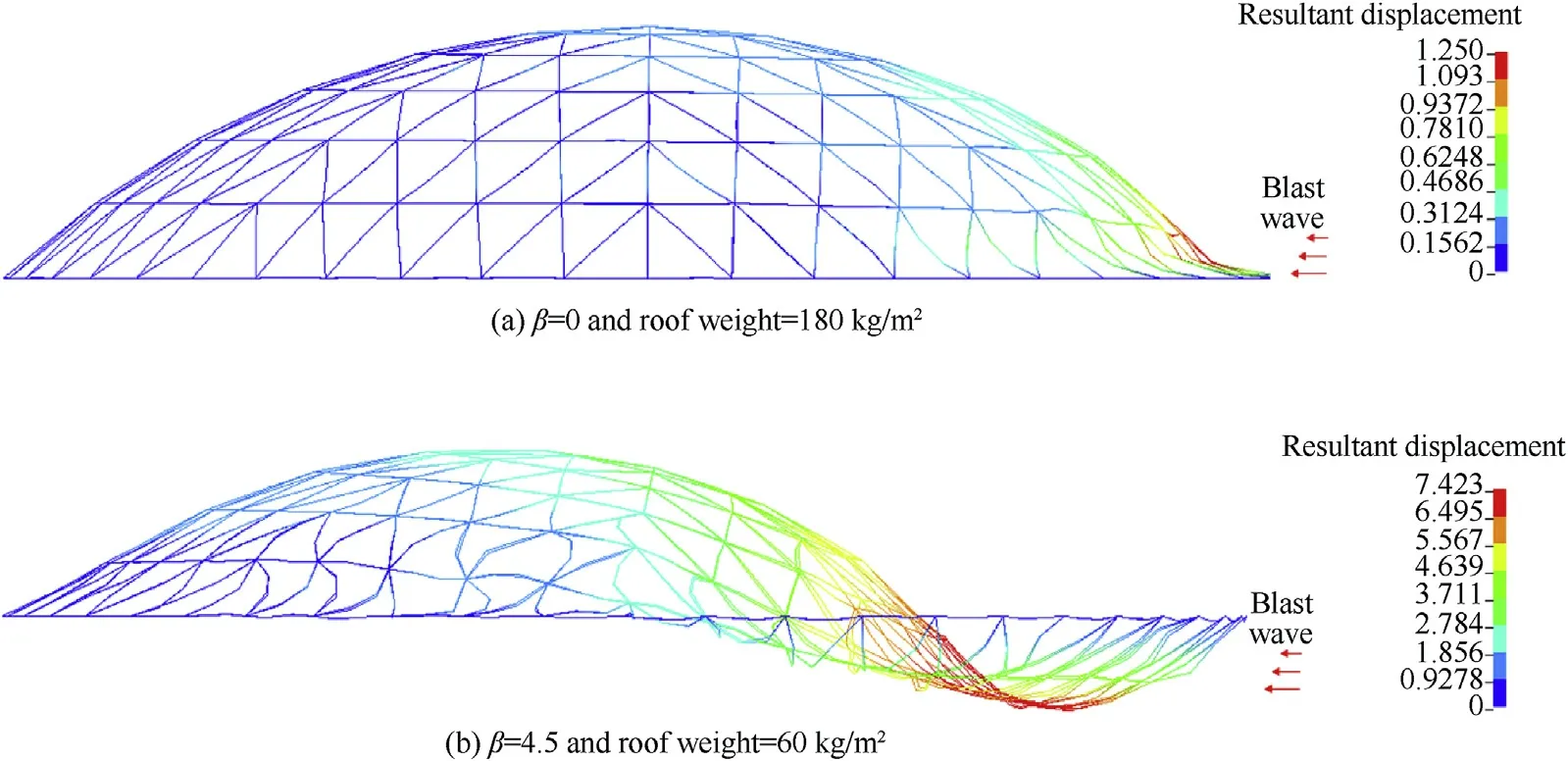
Fig.25.Displacement response of the shell member.

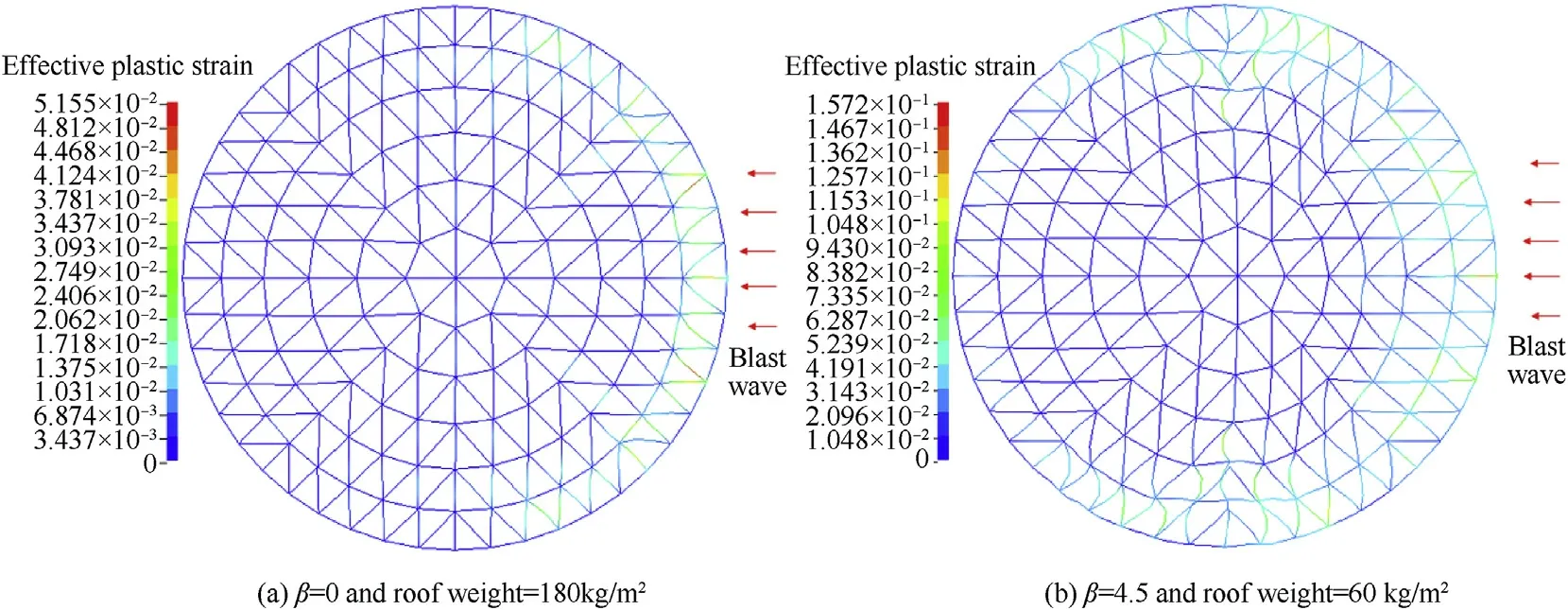
Fig.26.Plastic strain response of the shell member.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

The authors wish to thank the financial supports from and National key research and development program of China(project No.2018YFC0705703) and the National Natural Science Foundation of China (project No.51708521, 51778183).