Dispersion and damping rate of Langmuir wave in space plasma with regularized Kappa distributed electrons
Yong LIU (劉勇) and Xu CHEN (陳旭)
1 School of Sciences, Nantong University, Nantong 226019, People’s Republic of China
2 Xinglin College, Nantong University, Nantong 226019, People’s Republic of China
Abstract The dispersion of Langmuir wave (LW) in an unmagnetized collisionless plasma with regularized Kappa distributed electrons is investigated from the kinetic theory.The frequency and damping rate of LW are analyzed for the parameters relating to the source region of a type III solar radio burst.It is found that the linear behavior of LW is greatly modified by the suprathermal index κ and the exponential cutoff parameter α.In the region κ<1.5,the damping rate of LW will be much larger than the one with Maxwellian distributed electrons.Hence, the nonlinear process of LW in low κ region may exhibit different properties in comparison with the one in large κ region.
Keywords:Langmuir wave,Kappa distribution, damping rate,exponential cutoff, space plasma
1.Introduction
The particles in space plasmas often take a non-Maxwellian distribution, owning a superthermal high energy tail.There are some models describing the nonthermal behavior,such as kappa (κ) distribution, Cairns distribution, nonextensive distribution,and so on.Kappa distribution was firstly introduced to fit the electric currents in the magnetosheath [1] and the electron spectral in the magnetosphere [2].Nonextensive distribution, which has a similar behavior as the one of the Kappa distribution, is a natural result of the nonextensive statistics building on the nonextensive entropy introduced by Tsallis [3].The solitary electrostatic structures in the upper ionosphere of auroral zone found by the Freja satellite can be well explained under framework of Cairns distribution [4].The distribution of plasma particles will affect the linear and nonlinear behavior of the wave dynamics greatly.
Langmuir wave (LW), which is a high frequency electrostatic wave with phase velocity much larger than the particles thermal velocity, is a fundamental wave mode in plasma.It exists in many different space environments, such as solar wind [5], Earth’s ionosphere [6], lower auroral zone[7], Venus magnetotail [8], etc.The LWs can be excited by the bump-on-tail instability induced by electron beams.They are proposed as the candidates to generate the transverse plasma waves at the electron plasma frequency ωpeand its second harmonic 2ωpe[9],which can explain the type III solar radio bursts [10, 11].The collapse of LWs was observed in the Jovian’s bow shock [12] and the source region of a type III solar radio burst [13].In situ observations provide the unambiguous evidence of the formation of Langmuir solitons [14].
LWs have attracted considerable attention in space plasmas, since they are important for the explanation of the observed radio radiation and electron acceleration [15, 16].The dispersion and damping rate of LWs will determine the linear and nonlinear processes of LWs, and the efficiency of particle acceleration by LWs.The LW dispersion relation in a plasma with Maxwellian velocity distribution was derived firstly by Bohm and Gross in 1949 [17].Whereas, the experimental results of LW showed that the linear behavior of LW could be fitted by electrons with nonextensive distribution where the nonextensive q-parameter is smaller than unity[18].The dispersion and Landau damping of LWs in an unmagnetized plasma with non-Maxwellian electrons were investigated by several authors where the electrons were assumed to take the generalized (r, q) distribution [19], the Kappa distribution[20],the distribution given by Wright and Theimer [21, 22], the κ-deformed Kaniadakis distribution[23] and so on.
The standard Kappa distribution (SKD) and its various modified forms have been used to the investigation of the collective behavior in the field of plasma [24–29].They are the most popular ones for describing the nonthermal particles with superthermal tail in the solar wind[30,31],flare[32]and corona [33], the radiation belts [34] and magnetosheath [35]of the Earth, some planetary magnetospheres [36–41], etc.The second order velocity moment of the SKD will be negative when κ<1.5.It will lead to a negative kinetic temperature which violates the fundamental physical principal.In addition,the range of κ for the different order velocity moments to be valid is different.The exponential cutoff of the high energy tail is introduced to make all the velocity moments of the Kappa distribution valid in the whole region κ>0 [42].Scherer et al (2017) named this distribution as regularized Kappa distribution (RKD), and studied the damping rate of LWs from a numerical simulation [42].Analytical solutions of the dispersion and damping rate of LWs are necessary for the investigation of the nonlinear process of the LW in turbulent state.Therefore,the dispersion and damping rate of LWs in a plasma composed by the regularized Kappa distributed electrons as well as an immobile neutralizing background of ions are analytically studied from the kinetic theory.
The paper is structured as follows.The analytical results of the dispersion and damping rate of LWs are derived from the kinetic theory in section 2.The numerical results under the parameters of the solar wind are presented the in section 3.In the last section, a brief summary is given.
2.The dispersion of Langmuir wave
For high frequency wave modes such as LWs,the ions can be seen as an immobile background.In an unmagnetized collisonless plasma,the distribution of electron in the electrostatic wave field can be described by the linearized Vlasov equation as follows
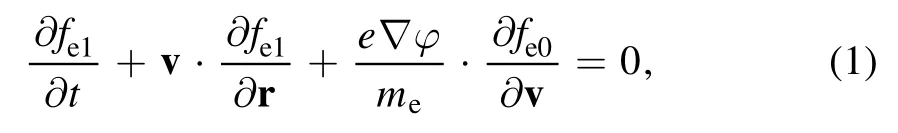
where, fe0and fe1are respectively the equilibrium and perturbed part of electron distribution; meand e are respectively the mass and the charge magnitude of electron; φ is the electrostatic potential.The collisonless plasma assumption is taken on the basis that the electron plasma frequency is much larger than the electron ion collision frequency.It is worth noting that most space plasmas belong to collisionless plasma [43].
The Poisson equation for the electrostatic potential is

where, ε0is the vacuum dielectric, ne1=n0∫fe1dv is the perturbed electron density, n0is the equilibrium number density of electrons.It is worth noting that the ions are assumed singly positively charged.Hence, the equilibrium electron density equals the equilibrium ion density due to the quasineutrality condition.
Assuming the frequency and the wave vector to be ω and k, and considering the perturbed solution ∝e xp ( ? ik · r),from equations (1) and (2) the dispersion of LW can be obtained from
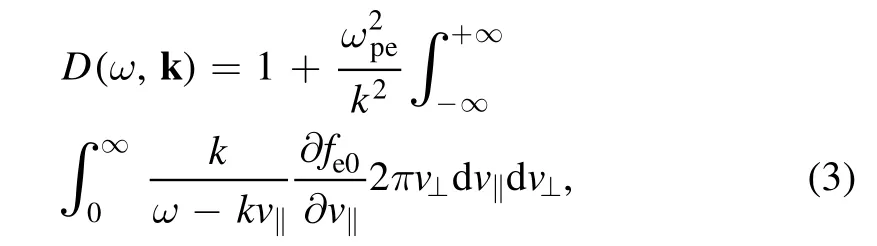
The superthermal electrons are considered to follow the RKD which has a form as [42]
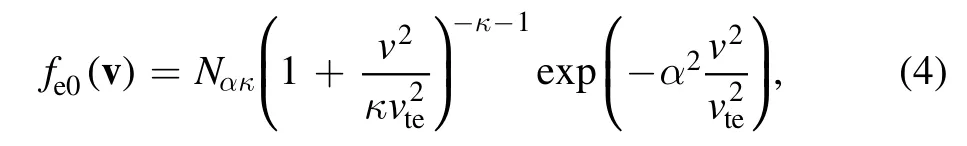
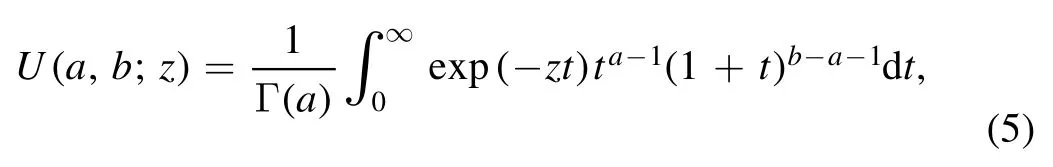
where, Γ is the standard Gamma function.
In order to show the effects of the cutoff parameter α on the Kappa distribution, the velocity distributions 4πv2vtefe0with respect to v/vtefor κ=5 (a), 1.6 (b), and 0.8 (c) are shown in figure 1, where solid lines denote Maxwellian distribution, the dotted dash lines, the dash lines, and the dotted lines correspond to α=0, 0.01, and 0.1.From figure 1 one will find that the decrease of the spectral index κ results in the enhancement of the energetic electron.Comparing to the Maxwellian distribution, the SKD has a superthermal tail.In comparison with SKD, the exponential cutoff of the RKD leads the probability of low energy electron to increase and the high energy electron to reduce.The lager cutoff parameter α means that there are less energetic electrons.Therefore,the finite α can make the concentration of the electron with velocity faster than the vacuum light velocity be negligible small.
As to the definition of the temperature in ideal gas, the effective electron temperature (EET) can be obtained as follows [42, 45]
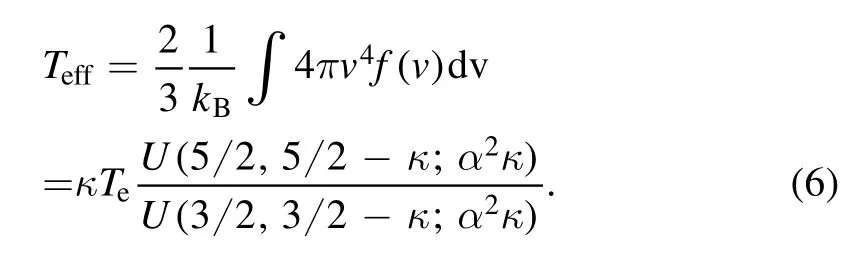

Figure 1.The velocity distribution 4πv2vtefe0 with respect to v/vte for κ=5 (a), 1.6 (b), 0.8 (b), in which solid lines correspond to Maxwellian distribution, the dotted dash lines, the dash lines, and the dotted lines correspond to α=0, 0.01, and 0.1.
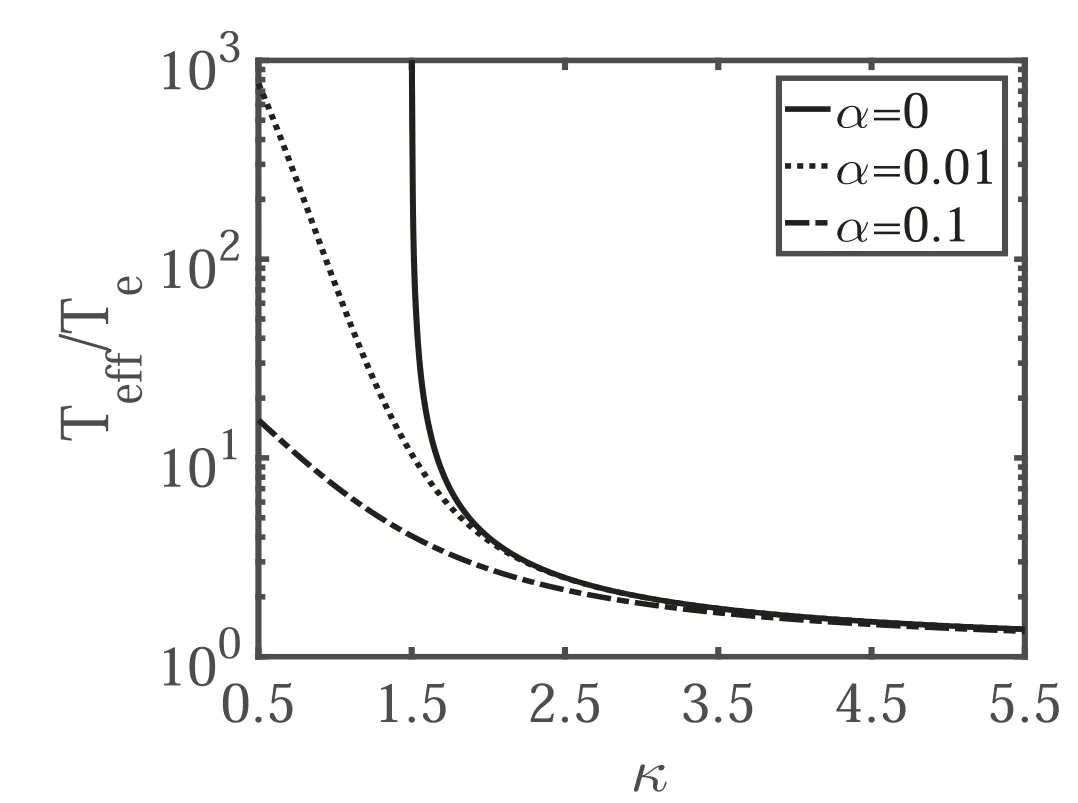
Figure 2.The normalized EET versus the spectral index κ for α=0.1 (dotted dash line), 0.01 (dotted line), and 0 (solid line).
When α=0, RKD will be reduced to the SKD.Correspondingly, the EET will beTo make the EET be finite and positive, the spectral index κ in the case should be larger than 3/2.When α=0 and κ →∞,the RKD reduces to the well known Maxwellian distribution, and one will come to Teff=Te.
In order to analyze the effects of the exponential cutoff on the EET, the EETs with respect to the κ for α=0 (solid line),0.01(dotted dash line)and 0.1(dotted line)are given in figure 2.Figure 2 indicates that the EET increases with the decrease of the cutoff parameter α for the same value of κ.The difference of the EETs for different α becomes larger when the spectral index κ reduces.In the case α=0, the effective temperature of the SKD approaches to infinitely at κ →1.5.It is due to the facts that there are too much electrons with velocity larger than the speed of light.Therefore, α should be big enough to lower the concentration of the superluminal electrons and small enough to fit the space observation [46].
Integrating the equation (4) with respect to v⊥yields where the incomplete gamma function[47]

Now, inserting equation (4) into equation (3), and considering equation (7), the integrating of equation (4) with respect to v⊥gives
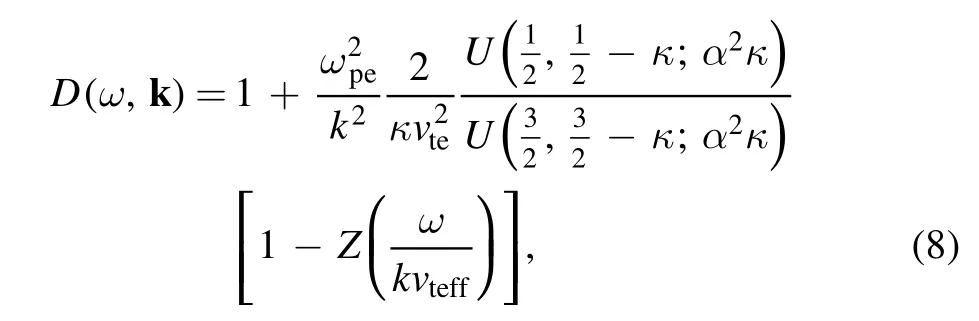
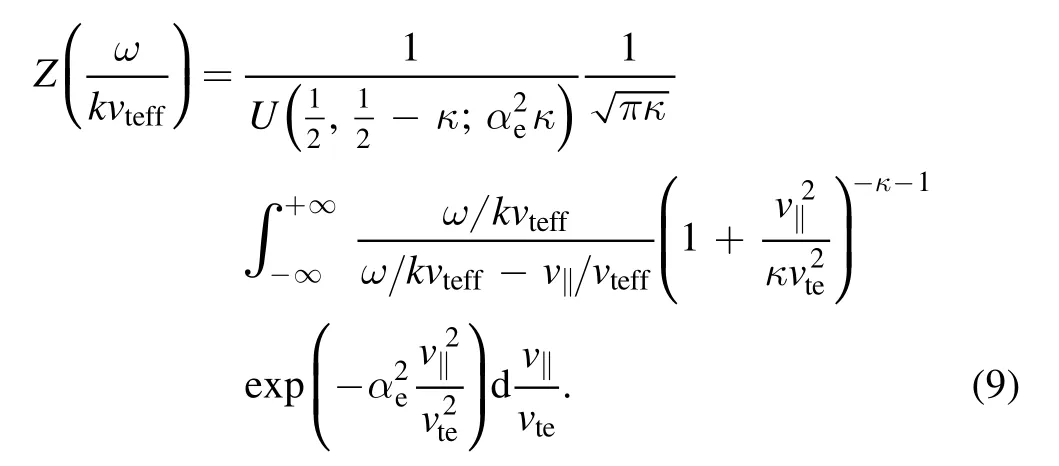
According to the Plemelj formula,the imaginary and real parts ofZ(ωkvteff)are respectively

where P.V.denotes the Cauchy principal value.
Considering the facts that the characteristic electron parallel velocity is about the electron effective temperature,i.e.v‖/vteff~1, in the case ω/kvteff?1, the real part ofZ(ωkvteff)will be
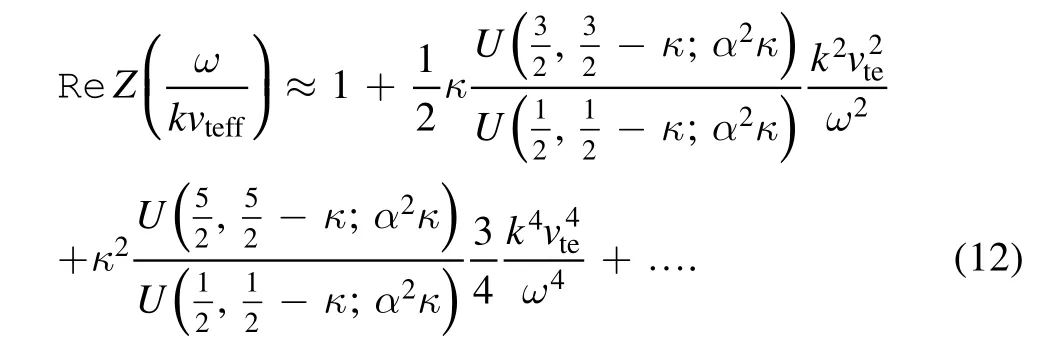
Inserting equations (10) and (12) into equation (8), the longitudinal dielectric can be written as
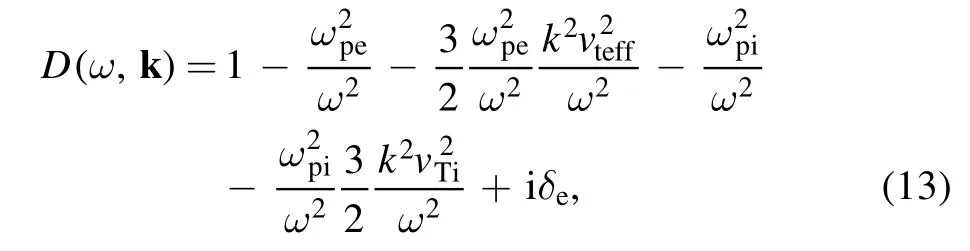
where,
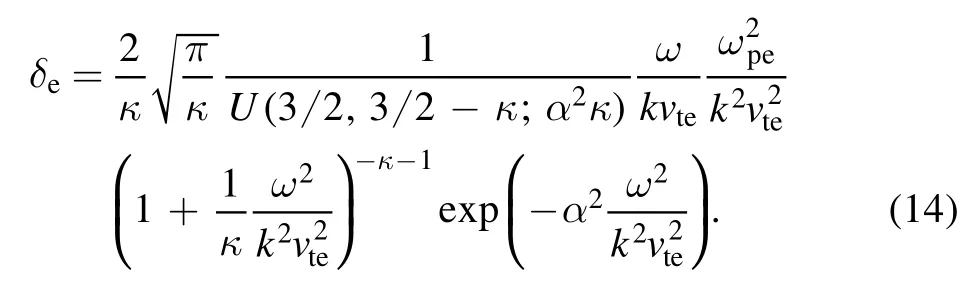
In the case, the wave length is much smaller than the effective electron Debye length deff(=vteff/ωpe), i.e.kdeff?1, the dispersion relation of LW in a plasma with electrons obeying regularized κ-distribution can be obtained from ReD(ω, k)=0, which is
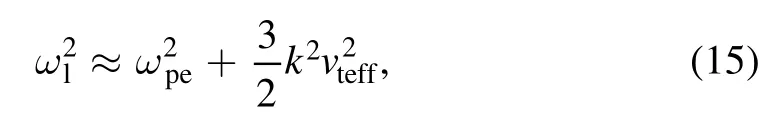
where the subscript l denotes the LW.The dispersion relation(15) has the same form as the one in a plasma with Maxwellian distributed electrons, except the electron thermal velocity is replaced by the effective electron thermal velocity.
Expressing the real and imaginary parts of ω in equation(13)as ωland γ,the damping rate of LW in the limitωl? ∣γ∣can be obtained as following

It is worth noting the the imaginary part γ<0 denotes the Landau damping which stems from the wave particle resonant interaction.
Inserting equation (13) into equation (16), the damping rate of LW takes the form as

where,δe(ωl)denotes the value of δeat ω=ωl.
3.Numerical results
LWs in the source region of a type III solar radio burst have been obtained by the STEREO WAVES experiment [13].In the region,the electron plasma frequency is much larger than the electron cyclotron frequency [13].Therefore, the electron cyclotron frequency imposes little effect on the dispersion of the LW[48],and the unmagnetized approximation is suitable.As[13],we take electron density n0=3.1×106m?3and the electron temperature Te=105K.
Figure 3 shows the frequency f(=ωl/2π),damping rateγ~(=γ/2π), and normalized parallel wave number kdeffof LW versus the superthermal index κ for different cutoff parameters α in subfigures (a), (b), and (c) respectively.We take the wave number of LW,which is 1.1×10?3m?1,estimated by Thejappa and MacDowall(2018)for the source region of a type III solar radio burst [13].Figure 3(c) shows that the normalized wave number kdeffinitially increases gradually with the decease of the spectral index κ.Whereas, it rises sharply when κ decreases to a value smaller than 2.Correspondingly,the frequency of LW has a similar behavior as the one of the normalized wave number kdeff(see figure 3(a)).In addition,the kdeffand the frequency of LW decrease with the increase of α for a fixed value of κ.This feature becomes evident when κ<2.In fact, these properties result from the variation of the EET by the parameters κ and α.
Figure 3(b) indicates that with the lowering of κ, the damping rate of LW for SKD (α=0) firstly increases, then decreases around the κ →1.5.However, it is worth mentioning that when κ →1.5, one will find kdeff>1 which violates the condition in the derivation of the LW dispersion(15).Furthermore, if α ≠0, the damping rate of LW will increase with the decrease of the κ in the whole region κ>0.In addition, the damping rates of LW in the cases α=0.01 and α=0 are almost the same, except the damping rate for α=0.01 takes a finite value in the region κ<1.5.Whereas,the damping rate of LW at α=0.1 is much smaller than the ones of α=0.01 when κ<2.It is due to the fact that the number of energetic electrons for α=0.1 is much smaller than the ones in the case α=0.01.
In order to analyze the effects of wave number on the LWs’ frequency and damping, we take the wave number k=2.1×10?3m?1in figure 4,other parameters are the same as the ones in figure 3.Comparing figures 4 and 3, it can be found that the increase of the wave number leads to the increase of the kdeff, correspondingly the damping rate and the frequency of LW increase.In this case,the decrease of the phase velocity of LW enhances the number of the electron,satisfying the resonant condition.Figures 3 and 4 show that the damping rate of LWs is comparable to the frequency of LW when kdeff~1.It means thatis the upper limit of the wave number of LW.The definition of the effective Debye length deffindicates that deffgrows with the decrease of κ and α.Correspondingly, the lower limit of the LW wavelength will be larger.
4.Conclusions
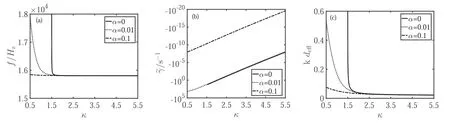
Figure 3.The frequency f (a), damping rate γ~ (b), and normalized parallel wave number kdeff (c) of LW versus the spectral index κ when k=1.1×10?3 m?1 for α=0 (the solid lines), 0.01 (the dotted lines), and 0.1 (the dotted dash lines).
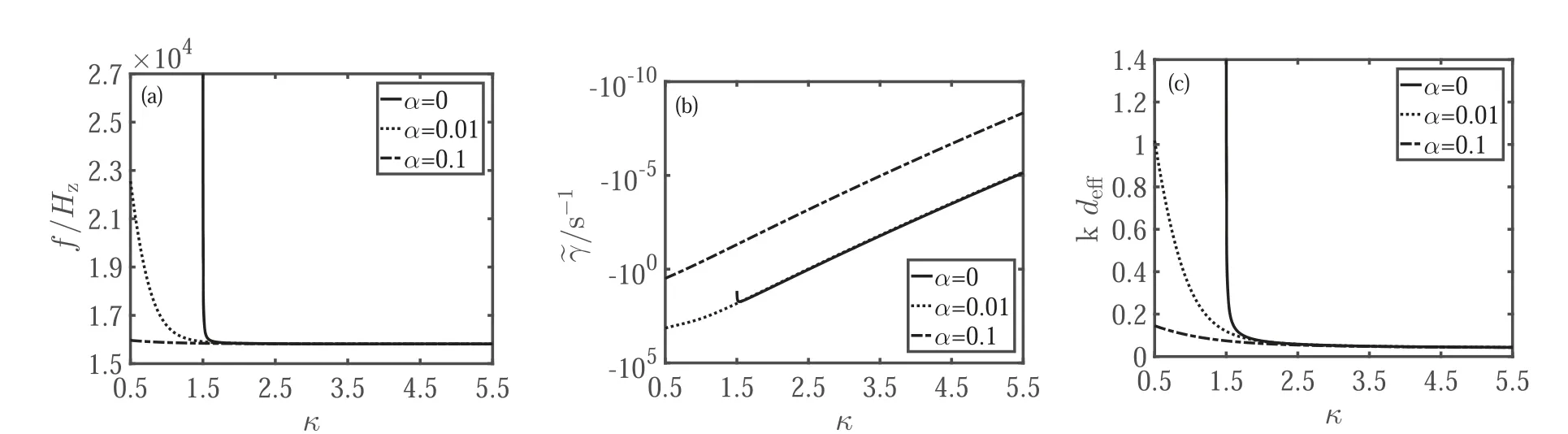
Figure 4.The frequency f (a), damping rate γ~ (b), and normalized parallel wave number kdeff (c) of LW versus the spectral index κ when k=1.1×10?3m?1 for α=0 (the solid lines), 0.01 (the dotted lines), and 0.1 (the dotted dash lines).
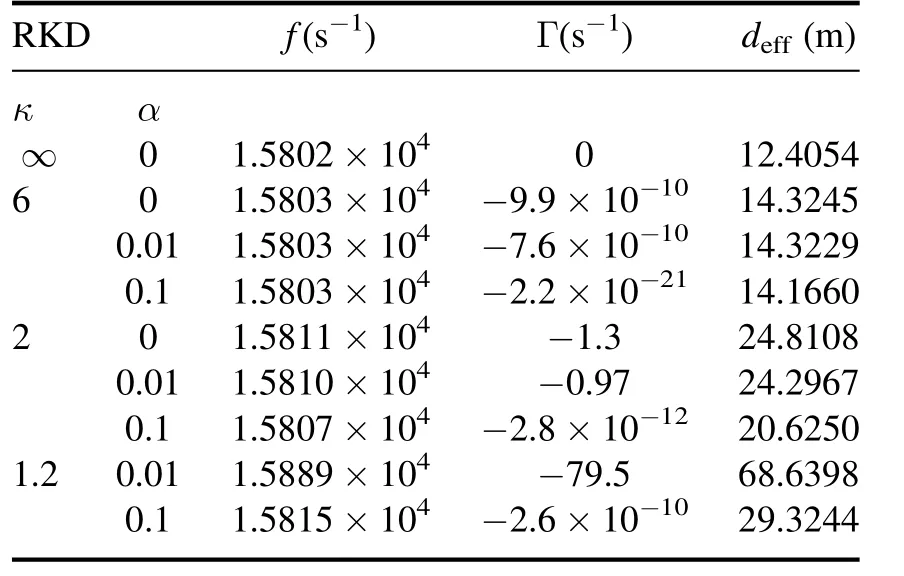
Table 1.The frequency,damping rate and effective Debye length for different α and κ, all the parameters are the same as the ones in figure 1.
In order to show the effects of the cutoff parameter α on the properties of LW in solar wind in detail, the values of frequency,damping rate and effective Debye length for different α and κ are shown in table 1.For the Maxwellian distributed electrons(κ=∞,α=0),the damping rate is about zero,and the Debye length is smaller than the effective Debye length in a plasma with superthermal electrons.The difference of the frequency of LW for different superthermal index κ and cutoff parameter α is rather small.But the damping rate and the effective Debye length are much lager than the one with Maxwellian distributed electrons, especially when κ is less than 1.5 and the cutoff parameter α takes a value as small as 0.01.
It is worth noting that if the distribution of the background electrons deviates the Maxwellian one into a low κ region with small cutoff parameter,the effects of the damping rate on the nonlinear process of the Langmuir turbulence may not be neglected.It will play an important role in the development of Langmuir turbulence which may exhibit a unique observation feature.As mentioned in the [42], the observed SKDs with κ ≤1.5 have been ruled out as they lie in an un-physical parameter region [49].However, when the exponential cutoff is taken into consideration the parameter κ can be as low as 0.2 [50].
 Plasma Science and Technology2022年1期
Plasma Science and Technology2022年1期
- Plasma Science and Technology的其它文章
- Design of improved compact decoupler based on adjustable capacitor for EASTICRF antenna
- W fuzz layers: very high resistance to sputtering under fusion-relevant He+irradiations
- Discharge and post-explosion behaviors of electrical explosion of conductors from a single wire to planar wire array
- Influence of anode temperature on ignition performance of the IRIT4-2D iodine-fueled radio frequency ion thruster
- Experimental study on plasma actuation characteristics of nanosecond pulsed dielectric barrier discharge
- A novel double dielectric barrier discharge reactor with high field emission and secondary electron emission for toluene abatement
