Non-Hermitian Weyl semimetals: Non-Hermitian skin effect and non-Bloch bulk–boundary correspondence
Xiaosen Yang(楊孝森), Yang Cao(曹陽), and Yunjia Zhai(翟云佳)
Department of physics,Jiangsu University,Zhenjiang 212013,China
Keywords: non-Hermitian skin effect,Weyl semimental,bulk-boundary correspondence
1. Introduction
Topological phases are characterized by bulk topological invariant. Examples include topological insulators,[1-10]topological superconductors/superfluids,[11-18]and Weyl semimetal.[19-31]For equilibrium closed systems, described by Hermitian Hamiltonian, the topological invariants are defined in terms of the Bloch Hamiltonian.[3-5]The Hermitian Hamiltonian has real eigenenergies and a set of orthogonal eigenstates. The bulk topological invariants dictate the existence of robust edge states at the boundary. This bulkboundary correspondence is a ubiquitous guiding principle to the topological phases. The bulk-boundary correspondence is also applicable when the bulk is gapless,by virtue of point touching of nondegenerate conduction and valence bands.[19]The gapless bulk band structure has paired Weyl points with opposite chirality and topological charge. The massless Weyl fermions near the Weyl points are stable against perturbations.
Recently, considerable efforts have been devoted to explore the properties of nonequilibrium open systems, especially non-Hermitian systems.[32-60]The non-Hermitian systems include optical and mechanical systems with gain and loss,[61-70]solid state systems with finite quasiparticle lifetimes for non-Hermitian self energy.[71-76]The non-Hermitian systems exhibit many impressive features, such as non-Hermitian skin effect,[77-87]bulk Fermi arcs connecting exceptional points[71,72,88,89]and biorthogonality.[90-93]Specifically, the non-Hermitian skin effect[77-82]means that all energy eigenstates can be localized at the boundary of non-Hermitian systems.[94-106]The interplay between the topology and non-Hermiticity can lead to the breakdown of the Bloch bulk-boundary correspondence.[77,78,81,82,105-109]The topological properties of the non-Hermitian systems can not be precisely predicted by the Bloch eigenstates under open boundary conditions. Furthermore, the real topological invariant is defined in non-Bloch Hamiltonian instead of Bloch Hamiltonian. The non-Bloch winding (Chern) number, defined in the generalized Brillouin zone (GBZ), has been introduced to characterize the topological properties of onedimensional(two-dimensional)systems.[77,78,80,106]The non-Bloch topological invariants strictly characterize the chiral edge modes and provide the non-Bloch bulk-boundary correspondence.
For three-dimensional non-Hermitian systems, the Weyl points can be spread into exceptional lines and even exceptional surfaces. Examples of non-Hermitian Weyl semimetals have been considered in Refs. [40,48,110-117], however,their novel bulk-boundary correspondence has not been uncovered and clarified yet, which is the focus of the present paper. In this work, we investigate the topological properties of the non-Hermitian Weyl semimetal in the presence of gains and losses. We analyze the shape of the exceptional rings by Bloch band theory under periodic boundary condition and give the topological phase diagram. Furthermore,the Weyl semimetal can be regarded as a stack of layers of twodimensional Chern insulator inkzmomentum space in the absence of gains and losses. Thus,we can bring insight into the topological properties of the non-Hermitian Weyl semimetal by the non-Bloch Chern number. We extend the Bloch momentum spaceT3(k) into complex momentum space ?T3(?k)to derive the three-dimensional non-Bloch Hamiltonian. For a fixed momentumkz, the three-dimensional complex momentum space ?T3(?k) is reduced to two-dimensional ?T2(?k⊥) in which the non-Bloch Chern number can be defined. We find a new non-Bloch bulk-boundary correspondence for the non-Hermitian Weyl semimetal. The non-Bloch Chern number can predict the topological edge modes. As such, the Bloch band theory and the conventional bulk-boundary correspondence break down for the non-Hermitian skin effect, which fundamentally affects the topological phase diagram. The validity of non-Bloch Chern number is confirmed by comparing its prediction to numerical results of real space energy spectra and edge-states transport.
2. Non-Hermitian Bloch Hamiltonian
We consider a non-Hermitian Bloch Hamiltonian of a semimetal on a cubic lattice
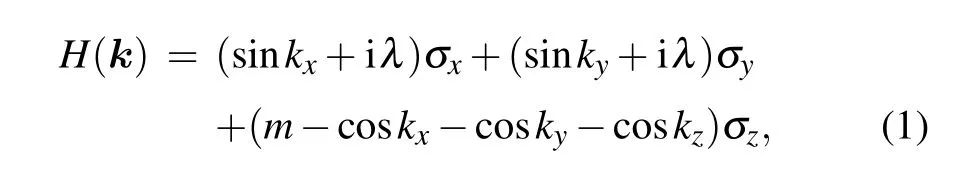

whereσx,y,zare the Pauli matrices. The real parametersΛ=(λ,λ,0) are the non-Hermitian strengths.[77,118]In the absence of non-Hermitian parts (Λ=0), the eigenvalues of the system areE±(k)=±h(k) withh(k)=|h(k)| andh(k)=(sinkx,sinky,m-coskx-cosky-coskz). A pair of Weyl points withZ2topological charge are stable when|m|< 3.The topological nontrivial phase is Weyl semimetal. When|m|>3, the two Weyl points will annihilate with each other and the phase is gapped insulator. There is a topological phase transition between Weyl semimetal and insulator at|m|=3.Therefore,we will focus onmbeing close to 3.that of any other bands in the complex-energy plane,while it is called gapless(or inseparable)if the complex-energy is degenerate with other bands.[96]For our non-Hermitian system,the Bloch bands are gapless whenm

Fig. 1. Topological phase diagram for Λ = (λ,λ,0). The blue-dotted curve,determined by the real space energy spectra of cubic open boundary,is the topological phase boundary between non-Hermitian Weyl semimetal and insulator. The left non-Hermitain Weyl semimetal has gapless bulk and gapless topological edge modes. The right insulator has gapped bulk and gapped edges. The open-boundary spectra for the three marked points are given in Fig. 3. The topological phase boundary closely approximates to the boundary based on non-Bloch Chern number (red-solid curve with m=3+λ2). This non-Bloch phase boundary is fundamentally different from the phase boundaries based on the Bloch theory (black-dashed lines with m± =3±√2λ). According to the Bloch band theory, the phase is non-Hermitian Weyl semimetal when m < m- and trivial semimetal for m-

Fig.2. Illustration of the exceptional rings in Bloch Brillouin zone with λ =0.2 for(a)m=2.6,(b)m=2.7172,and(c)m=3.05. In the presence of the non-Hermitian part, the paired Weyl points are spread into a pair of Weyl exceptional rings with opposite charge. As m increases, the two Weyl exceptional rings will merge into one uncharged exceptional ring at m=m-. The uncharged exceptional ring will disappear when m>m+.
3. Phase diagram based on non-Bloch Chern number
In Hermitian systems,Weyl semimetals are characterized by topologically protected Fermi-arcs. The chiral/helical gapless edge states exist in a finite region in momentum space and should be determined by the properties of Bloch Hamiltonian.The Bloch bulk-boundary correspondence is a key property of Weyl semimetals. However, the Bloch bulk-boundary correspondence is not applicable to the topological properties of the non-Hermitian system for non-Hermitian skin-effect. Therefore, the topological phase diagram based on the Bloch band theory will generate pronounced deviation to the real phase diagram. Thus,we draw the phase boundaries by the non-Bloch Chern number and the real space energy spectra.
The non-Bloch Chern number is defined in a complex momentum space instead of Bloch momentum space.[78]To determine the topological phase boundary, we consider the low-energy continuum case inx-yplane of our non-Hermitian Bloch Hamiltonian Eq.(1), which can be rewritten as following:




which is shown in Fig.1. The non-Hermitain Weyl semimetal phase on the left of the topological boundary has gapless bulk and gapless topological edge modes. The insulator phase on the right has gapped bulk and gapped edge modes. There is a dichotomy between the two topological phase diagrams based on the non-Bloch Chern number and the Bloch band theory.The exact topological phase boundary is only a single curve and the phase diagram has no topological trivial semimetal.Interesting, in sharp contrast to the Hermitian systems, the conventional bulk-boundary correspondence is broken down in the non-Hermitian Weyl semimetal phase. The topological edge modes of the non-Hermitian Weyl semimetal are determined by the non-Bloch Chern number of the bulk bands. The breakdown of the Bloch band theory is caused by the non-Hermitian skin effect.
To check the valid of the topological phase diagram based on non-Bloch Chern number, we calculate the real space energy spectra under cubic open-boundary condition(lattice sites sizeL×L×L). Figures 3(a)-3(c)show the spectra for(a)m=2.7172,(b)m=3.05,and(c)m=3.2828 withλ=0.2(three indicated points in Fig. 1). Considering the size effects, we make the lattice size scaling of the gap in Figs. 3(d)-3(f) for Figs.3(a)-3(c),respectively. The gap is given by the intercept ofΔ-1/Lline. In Bloch theory, the three spectra are gapless and have exceptional rings/point in the spectra. As shown in Figs. 3(a) and 3(b), the gap vanishes form=2.7172 andm=3.05 whenL →∞. Remarkably, there is a clear gap at the spectra ofm=3.2828. According to the spectra of cubic open-boundary condition, there is a topological phase transition between the gapless non-Hermitian Weyl semimetal and gapped insulator phase atm=3.05 forλ=0.2. We draw the gapless-gaped phase boundary under cubic open-boundary condition as the blue-dotted curve in Fig. 1. The two curves base on the open-boundary energy spectra and the non-Bloch Chern number are very close. Therefore,the non-Bloch Chern number is valid to our three-dimensional non-Hermitian Weyl semimetal.

Fig. 3. Real space energy spectra under cubic open-boundary condition: (a) m=2.7172, (b) m=3.05, and (c) m=3.2828 (three values of parameters indicated in Fig.1)with λ =0.2 and lattice site size L=20. Panels(d)-(f)show the magnitude of the gap Δ as functions of 1/L for(a)-(c),respectively. L is the lattice site size in x,y,z direction. The intercept of Δ-1/L line gives the gap in large scale limit(L →∞). The gap is zero for(d),(e)and nonzero for(f).
4. Non-Hermitian skin effect and unidirectional edge motion
Different from the Hermitian Hamiltonian, the eigenstates are non-orthogonal for the non-Hermitian cases. Therefore, all the eigenstates can be exponentially localized at the boundary for our non-Hermitian system. To illustrate the non-Hermitian skin effect, Fig. 4 shows the bulk states inx-yplane by adding upz-direction for (a)m= 3.2828 and(b)m= 2.7172 withλ= 0.2. The bulk states are localized at the boundary for both the non-Hermitian Weyl semimental and topological trivial gapped insulator phases. The usual bulk-boundary correspondence is invalid for our non-Hermitian systems.
For topological nontrivial phase,the localized eigenstates have Fermi-arc edge modes and gapless bulk states. However,there is no Fermi-arc edge mode in the topologically trivial regime. The chirality of the Fermi-arc edge modes will affect the wave pocket time evolution in topological nontrivial phases. To reveal the topological properties and the Fermiarc edge modes, we investigate the wave pocket time evolution. The time dependent wave satisfies the non-Hermitian Schr¨odinger equation


Fig.4. Non-Hermitian skin effects. Left panel: total normalized eigenstates N0 ∑n|uRn〉under cubic open-boundary condition for(a)m=3.2828 and(b)m=2.7172 with λ =0.2 and lattice sites size L=20.Right panels:wave pocket evolutions.The initial wave pocket takes the Gaussian form ψ(t =0)=N exp[-(ix-10)/20-(iy-1)/10-(iz-10)/20](1,1)T, normalized by N. The modulus squared intensity of|ψ(t)〉is normalized and shown for t =0,5,15 in x-y plane by adding up in z-direction. The wave packet fades into the bulk in up row. There has unidirectional edge motion in down row.
For an initial wave|ψ(t=0)〉, the time dependent wave function is|ψ(t)〉=∑nexp(-iEnt)|uRn〉〈uLn|ψ(t=0)〉.For simplicity, the initial wave takes Gaussian wave pocket withψ(t=0)=Nexp[-(ix-10)/20-(iy-1)/10-(iz-10)/20](1,1)T, normalized byN. As shown in Fig. 4, the wave pocket quickly spreads into the bulk for topological trivial insulator phase withm=3.2828. However, there is clear chiral edge motion for the topological non-Hermitian Weyl semimetal withm=2.7172. This can be explained as following. Despite the eigenstates are localized at the boundary for topological trivial phase,there is no robust chiral edge mode. Thus, the wave pocket evolves to the bulk states by quickly entering into the bulk without any topological constrain. For topological nontrivial phase,there are robust chiral edge modes with zero energy. The chirality of the edge modes will constrain the wave pocket evolution along the edges. The existence/absence of the unidirectional edge motion can be used to determine the non-Hermitian topological nontrivial phases in theory and future experiment.
5. Conclusion
We investigated the novel features of three-dimensional non-Hermitian Weyl semimetals by non-Bloch Chern number,Bloch band theory,open-boundary energy spectra and dynamics. We showed that the non-Hermitain Weyl semimetals have gapless bulk and gapless Fermi-arc edge modes. We uncovered the non-Bloch bulk-boundary correspondence for the non-Hermitian Weyl semimetal. The topological edge modes of the non-Hermitian Weyl semimetal are strictly determined by the non-Bloch Chern number of the bulk bands. Thus,the conventional bulk-boundary correspondence breaks down for the non-Hermitian skin effect. The non-Hermitian skin effect also generates pronounced deviation of the phase diagram from the Bloch band theory. The topological phase transition between nontrivial and trivial phases does not occur at the two Bloch phase boundaries. The topological phase boundary is only a single curve in the phase diagram.The valid of the non-Bloch Chern number is confirmed by the cubic open-boundary energy spectra. Furthermore, we showed that the topological edge modes can manifest as the unidirectional edge motion.
Acknowledgments
We would like to thank Zhong Wang for fruitful discussion. Project supported by the National Natural Science Foundation of China(Grants No.11504143).
——深入采訪實(shí)用小技巧
- Chinese Physics B的其它文章
- Role of compositional changes on thermal,magnetic,and mechanical properties of Fe–P–C-based amorphous alloys
- Substrate tuned reconstructed polymerization of naphthalocyanine on Ag(110)
- Anti-PT-symmetric Kerr gyroscope
- Information flow between stock markets:A Koopman decomposition approach
- Cascading failures of overload behaviors using a new coupled network model between edges
- High efficiency ETM-free perovskite cell composed of CuSCN and increasing gradient CH3NH3PbI3

