Fulde–Ferrell–Larkin–Ovchinnikov states in equally populated Fermi gases in a two-dimensional moving optical lattice?
Jin-Ge Chen(陳金鴿) Yue-Ran Shi(石悅?cè)? Ren Zhang(張仁) Kui-Yi Gao(高奎意) and Wei Zhang(張威)
1Department of Physics,Renmin University of China,Beijing 100872,China
2School of Physics,Xi’an Jiaotong University,Xi’an 710049,China
3Beijing Key Laboratory of Opto-electronic Functional Materials and Micro-nano Devices,Renmin University of China,Beijing 100872,China
Keywords: FFLO state,optical lattice,ultracold Fermi gas,superfluid
1. Introduction
After its first proposal in 1960s,the search for the unconventional pairing Fulde–Ferrell–Larkin–Ovchinnikov(FFLO)states[1,2]persists for more than half a century. The original idea of the previously studied FFLO state is to look for a compromised candidate for superconducting states which can sustain a finite magnetization. This exotic pairing state is characterized by a superconducting order parameter with one or more nonzero components of a finite momentumq, hence breaks both translational and rotational symmetry and forms a crystal of pairing order. In the past several decades,the existence of FFLO states was studied in various systems,[3]including heavy fermions[4]and dense quark matter.[5]
Recent progress of the preparation and manipulation of ultracold Fermi gases provides an ideal experimental platform of quantum simulation, which features a super clear system with unprecedented controllability, such that the single particle properties, the external environment and the inter-atom coupling can be tuned to a large extent.Thus,motivated by the first realization of pairing states in resonantly interacting alkali atoms with population imbalance,[6,7]a tremendous amount of effort has been devoted to the search of FFLO states in these systems. Many theoretical studies focused on the stable region of FFLO state in a uniform Fermi gas,and gave different conclusions by using various methods and approximations. In particular,some works claimed a fairly wide range of interaction covering both the weakly interacting Bardeen–Cooper–Schrieffer (BCS) regime and the Bose–Einstein condensate(BEC)regime for a stable FFLO phase,[8–10]while some others concluded a much narrower regime restricted within the BCS side of a narrow[11]and a wide[12]Feshbach resonances.Further studies also took realistic experimental conditions of finite temperature and harmonic trapping potential under consideration, and found that a stable FFLO state can only exist in a small region of a trap and at low temperatures with weak interaction.[13]With the consideration of these strict conditions,an unambiguous evidence for FFLO state is still lacking in polarized Fermi gases trapped in harmonic traps.
Another route towards the observation of FFLO state in ultracold Fermi gases is to implement an optical lattice. The presence of a lattice potential can assist the stabilization of FFLO states owing to two aspects. Firstly, the band structure generated by the lattice can feature von Hove singularities at an appropriate filling, leading to a nesting effect with significantly enhanced density of states to assist pairing.[14–16]Besides, the optical lattice can also provide an environment of reduced dimensionality,where a wider stable FFLO region is suggested.[17–24]Under this consideration,various methods have been proposed for detecting the FFLO state in optical lattices.[25–28]However,the FFLO state has so far eluded definite observation in ultracold atomic gases.
In this paper,we propose a scheme to stabilize the FFLO state in a two-component Fermi gas with equal population.We consider a two-dimensional(2D)Fermi gas trapped in a moving square optical lattice. In the frame moving with the lattice,the Cooper pairs acquire a finite external pair momentum,and the superconducting state becomes unstable towards the normal state at a critical velocity. For systems around half filling,the underlying Fermi surface has nesting effect, such that the critical velocity acquires significant anisotropy and reaches its maximum when the velocity is parallel to the nesting vectors.When the external velocity is tilted from this optimal direction,we find that a spontaneous pair momentum ofqscan be generated to take advantage of the nesting effect, leading to a possibility of a stable FFLO state in this equally polarized Fermi system.[29]
The remainder of this manuscript is organized as follows: In Section 2, we consider an equally populated twocomponent Fermi gas in a uniform two-dimensional square lattice,and present the formalism to derive the thermodynamic potential. By comparing the thermodynamic potential of the normal state and the super conducting state, we discuss the critical velocity of the system in Section 3. Specifically, we find that around half-filling where the system acquires nesting effect,the critical velocity is significantly enhanced when the lattice is moving along the nesting vector. In Section 4, we discuss the case where the lattice velocity is tilted away from the nesting vector,and show that the nesting effect can also be remarkable as it may spontaneously generate a pair momentum and lead to an FFLO state. We also map out the phase diagram of the system, and show the parameter region where the FFLO phase is stable against BCS and normal states. The main conclusions are summarized in Section 5.
2. Formalism
We first consider an equally populated Fermi gas confined in a static optical lattice and a quasi-two-dimensional trap,as described by the Hamiltonian(with natural units ˉh=m=1)

Assuming the optical lattice is strongly confined in thez-direction, the atoms are localized within a single layer and all the excited degrees of freedom along thez-direction are frozen out.Then,this system can be described by a 2D Fermi–Hubbard model

whereasis the s-wave scattering length between two spin components,ER=(2π/λ)2/2 is the recoil energy withλthe laser wavelength, andsi=V0i/ER(i=x,y,z) labels the dimensionless height of the lattice potential. In the following discussion,we consider a 2D square lattice withtx=ty=tandλ=1064 nm,which is realized as a layer within an anisotropic quasi-2D optical lattice withsx=sy= 2 andsz= 10. We set the scattering lengthas=?151.25aB=?8.004 nm withaBthe Born radius, which corresponds to the case ofU/t=?4.1649 and can be easily realized in experiment near a broad Feshbach resonance.
The Fermi–Hubbard model Eq. (2) cannot be solved exactly in the sense of thermodynamic limit. By adopting the mean-field approximation,the interacting term can be written as



with Θ(x)the Heaviside step function.
The thermodynamic potential is apparently a function of three parameters,i.e.,the order parameterΔ,the pair momentumq,and the chemical potentialμ. For a given filling factorn=N/MwithMthe total number of lattice sites, the equilibrium state can be obtained by minimizingΩas a function ofΔandq, while the chemical potential is determined selfconsistently via the number equation

wheref(x)=1/(eβx+1)is the Fermi function. The solution withΔ=0 is by definition the normal state,while the one with finite order parameter is the pairing superfluid state. The latter category can be further distinguished as the BCS or FFLO state,which corresponds to a zero or finite pair momentumq.We stress that the mean-field approach outlined above is commonly used to study the pairing physics in Fermi gases in traps or optical lattices.[13,15]Such a treatment can give a qualitative understanding about the stability of different pairing states in optical lattices, provided that the center-of-mass momentum remains small and higher band effect is not significant.
Next,we extend the discussion to a moving optical lattice with velocityq?. A moving optical lattice can be realized by inducing a small frequency detuning between the lasers forming the lattice,and has been successfully implemented with an acousto-optical modulator driven by phase-locked frequency generators.[30,31]Owing to the Galilean invariance, such a setup is equivalent to a superfluid with center-of-mass momentum?q?flowing in the lattice frame. Thus, we can still use the formalism above to obtain the thermodynamic potential as Eq.(15). However,one should bear in mind that a BCS state can not be considered in any sense as an FFLO state by such a frame transformation,as the center-of-mass velocity of the superfluid is imposed externally from the single-particle dispersion. An authentic FFLO state, on the other hand, is a result of interaction effect and should be spontaneously emerged.
3. Anisotropic critical velocity
The fact that the Fermi surface can be shifted by a particular vector to nest with another part of the Fermi surface is called Fermi surface nesting effect, and the particular vector is called the nesting vector,which is(±π/d,±π/d)for a 2D square lattice. Nesting effect can significantly alter the thermodynamic properties of the system when the lattice is filled properly. On one hand,the density of states of a 2D square lattice would acquire a divergence at half filling(i.e.,n=1),such that the pairing instability can be drastically enhanced. On the other hand, when the optical lattice is moving at a given velocity,it is also natural to expect a lower energy if the velocity is parallel to the nesting vector than any other directions. As a consequence,the critical velocity of the superfluid state would be anisotropic owing to the anisotropy of the Fermi surface.
To show the anisotropy of critical velocity, we plot in Fig. 1 the amplitude of the critical velocityqc=|qc| for an optical lattice moving along different directions with filling factorn=0.9,1.0,and 1.1. The critical velocity is determined by comparing the thermodynamical potential between the pairing state with a finite order parameter and a normal state withΔ=0. For all filling factors, the critical velocity increases drastically asθchanges from zero toπ/4. Here,θis defined as the angle between the moving direction and one of the lattice principal axis,say thexdirection. Thus,whenθ →π/4,the moving velocity is aligned with the nesting vector, and the critical velocity diverges owing to the diverging density of states. One can also notice that the results ofn=0.9 andn=1.1 are exactly identical as required by the particle–hole symmetry,and are always below then=1.0 case of a perfect nesting. To further analyze the effect of filling factor,we show in Fig. 2 the critical velocity as a function ofnfor two different moving directions. Notice that the line ofθ=0.156 is always higher than the one ofθ=0.0,and both curves reach their corresponding maximum at half fillingn=1.
These results clearly suggest that when the system is moving along the nesting vector ofθ=π/4, the superfluid state would benefit more from the enhancement of density of states, and can survive at a higher velocity. Since the moving velocity is equivalent to the center-of-mass velocity of the pairing order parameter,one would expect that an FFLO state can be favored if the pair momentum is tilted along the nesting vector.More interestingly,if an external movement of velocityqxis applied to the lattice along thex-direction, it is possible to have a spontaneously generated wave vectorqyalong the perpendicular direction,which tilts the originalqxtowards the nesting vector to reduce energy. The system is then stabilized at an FFLO state which features a modulating order parameter along they-direction. Naively, one may expect that when the induced wave vector is equal to the external one,i.e.,qx=qy,the overall momentum becomes parallel to the nesting vector,and the pairing state would be optimally favored. However,this scenario also has a maximal amplitude of the overallq,which is detrimental to the survival of superfluidity. As a consequence, the true ground state of the system is determined by the competition between the nesting effect and the velocity induced energy increase.
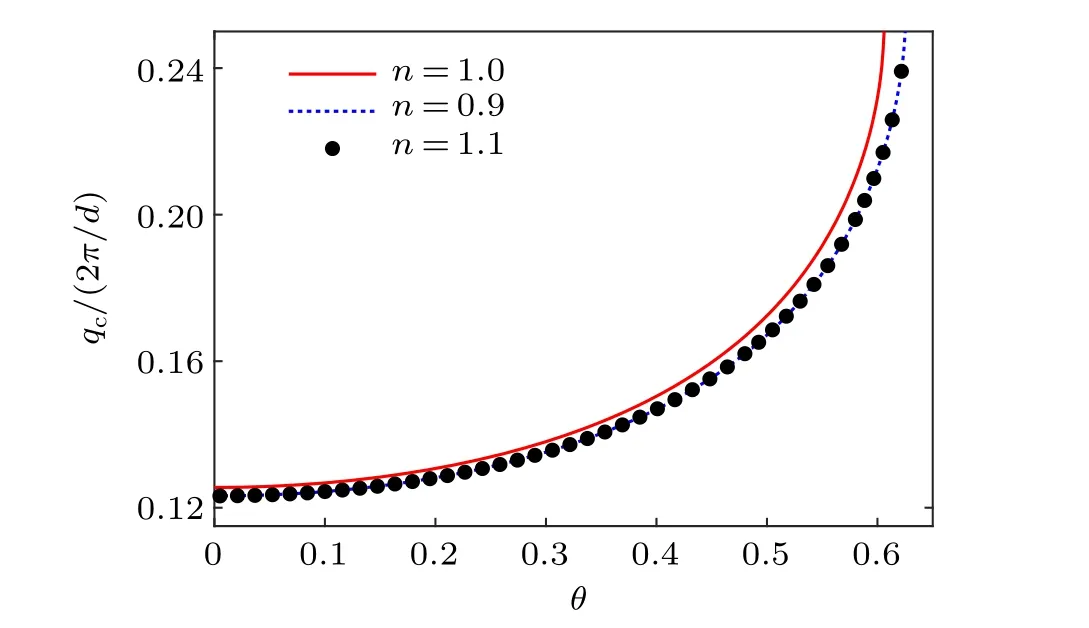
Fig.1.The critical velocity at different moving directions.For filling factors n=0.9,1.0,and 1.1,qc increases monotonically with increasing θ. When the lattice is moving along the nesting vector with θ =π/4,the critical velocity becomes divergent. The results for n=0.9 and 1.1 are identical as required by the particle-hole symmetry of this system.
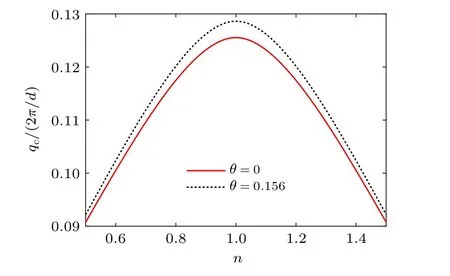
Fig. 2. The critical velocity of different moving directions with respect to the filling factor. Notice that the anisotropy of qc reaches its maximum at half filling n=1.0,at which a perfect nesting is reached.
4. FFLO states induced by moving lattice
To investigate the existence and property of the FFLO state as mentioned above,in this section we calculate the zero temperature thermodynamic potentialΩof the system, when subjected to an external velocityqxand a spontaneously generated modulationqy. In Fig.3,we show the contour plots of thermodynamic potential for different choices ofqxby varying the order parameterΔandqy,where the filling factor is fixed atn=1 by solving the number equation(16)self-consistently.The value ofΩfor different panels are shifted to zero at their corresponding ground state, such that a clear comparison can be made.
When the external velocityqxis small, there is only one minimum of the thermodynamic potential with a finite order parameterΔandqy=0 as shown in Fig. 3(a), indicating a conventional BCS state. As increasingqxbeyond a certain value,another minimum starts to appear atΔ/=0 andqy/=0.However, this FFLO state is only metastable as depicted in Fig. 3(b), and the true ground state of the system is still the BCS state.Whenqxis further elevated,the difference between the FFLO and BCS state is reduced,and finally the two states become energetically degenerate.A first order phase transition would take place at this critical point as shown in Fig. 3(c).Notice that the value ofqy ≈0.6134qxat the phase transition point, which corresponds to an angle ofθ ≈0.55, and is significantly deviated from the nesting vector withqy=qxandθ=π/4. Beyond this transition point,the FFLO state remains as the global minimum with even largerqx,as depicted in Fig.3(d).

Fig. 3. The false color plots of zero temperature thermodynamic potential Ω by varying the order parameter magnitude Δ and pair momentum along the y direction qy. In this figure,the filling factor is n=1.0,and the external velocity is (a) qx =0.126, (b) qx =0.130, (c) qx =0.13189 and(d) qx =0.137. In each panel, the value of Ω is shifted to be zero at the corresponding ground state.
According to the analysis above,it is clear that the phase transition between BCS and FFLO states is of first order,characterizing by a sudden change of the order parameter. In Fig.4,we show the amplitude of order parameter at zero temperature with respect to the variation of the external velocity by fixingn=1.0. It can be seen that when the external velocity is less than the critical value, i.e.,qx ≈0.13189, the order parameter of the BCS phase almost has no response to the variation ofqx. However,by crossing the transition point,a sharp jump occurs which is a doubtless evidence of a first order phase transition. As we continue to increase the external velocity, the amplitude of the order parameter decreases, but does not tend to zero even whenqxreaches the boundary of the Brillouin zone. This implies that the system will not enter the normal phase, which is a natural expectation for a meanfield approach of a system with perfect nesting and diverging density of states.
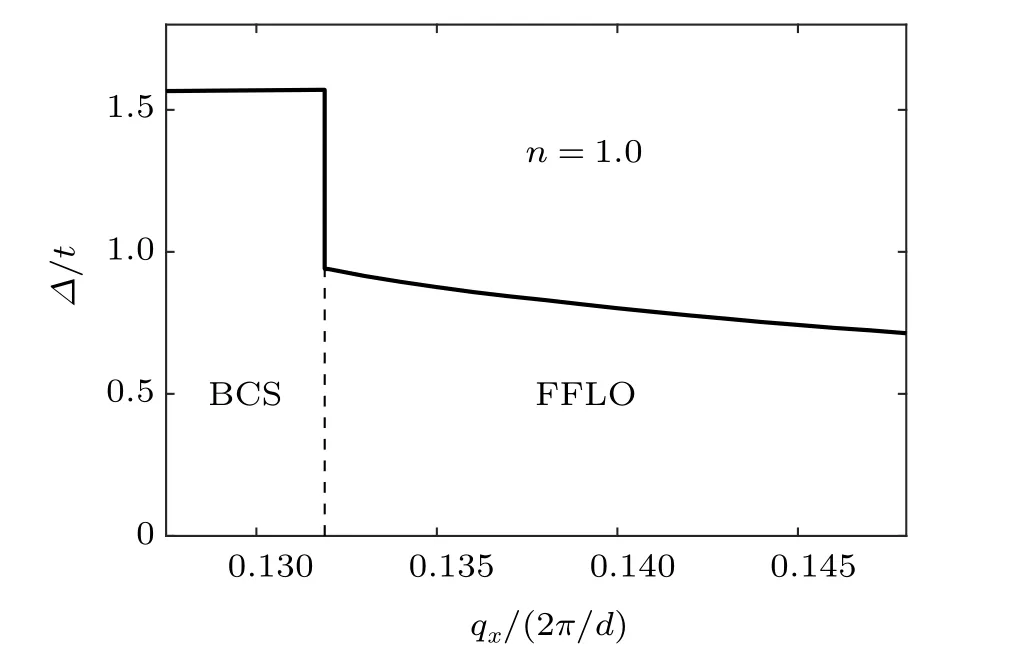
Fig.4. The change of order parameter by crossing the first order transition from BCS to FFLO states, showing an abrupt change at the critical point(dashed line).
The first order transition between BCS and FFLO states can also be characterized by the direction of the pair momentumq. As shown in Fig. 5, a local minimum of FFLO state starts to emerge atqx ≈0.1276 with a momentum tilting ofθ ≈0.4363. By increasing the external velocity, the angleθis also increased monotonically, but the FFLO state remains metastable until the first order transition point is reached. Beyond the phase transition,θalso increases withqx,indicating that the system tends to take advantage of the perfect nesting effect atθ=π/4. This result implies that although a modulation of the order parameter along they-axis tends to enhance the magnitude of the overall wave vectorqand is usually considered to be detrimental to the superfluid state,in the present case the nesting effect will become more crucial with increasingqx.

Fig.5. The change of the direction of pairing order parameter with respect to the external velocity. With increasing qx,a metastable FFLO state with a finite θ (black solid line)starts to appear at qx ≈0.1276,which becomes the true ground state(red solid line)beyond the critical point(dashed line).
With the understanding of the emergence FFLO state atn=1.0,we generalize the discussion to other filling factors.In Fig.6,we show the phase diagram of the system by varying the external driving velocityqxand the filling factor 0.2 When the filling factornis less than 0.59 (or symmetrically higher than 1.41), a first order phase transition would take place from the BCS state to the normal phase asqxincreasing. By crossing the transition point,the order parameter features a sudden change,leading to a discontinuous behavior in many thermodynamic properties. As a result, a phase separation regime exists between the BCS and normal states to minimize the free energy in the canonical ensemble.When the filling factornmoves towards half filling with 0.59n0.82(or symmetrically 1.18n1.41), an FFLO phase can be stabilized as increasingqxfrom the BCS state, and eventually gives its way to the normal phase with even higherqx.While the BCS–FFLO transition is also of the first order with a phase separation region between the BCS and FFLO states,the transition from the FFLO to the normal phase is of the second order. For filling factor even closer to half filling,0.82n1.18, the FFLO state can persist untilqxreaches the boundary of the Brillouin zone, owing to the significant enhancement of density of states induced by the nesting effect.From this phase diagram,we can clearly notice that the FFLO phase only exists when the filling factor is around half filling.This observation gives a further evidence that such an exotic pairing state crucially relies on the nesting of Fermi surface,which is significant only near half filling. Fig. 6. The phase diagram of the system at zero temperature. By varying the filling factor and external velocity, four different phases can be located by minimizing the thermodynamic potential,including the BCS state(pink),the FFLO state(yellow),the normal phase(light blue),and a narrow region of phase separation(cyan). We consider a two-component Fermi gas loaded in a twodimensional square optical lattice, which is dragged to move with a certain velocityqxalong one of the principal axis(e.g.,x-axis). Within a mean field approach, we determine the ground state of such a system by minimizing the thermodynamic potential at zero temperature. We find that for a filling factor around half filling, an FFLO state with a finite centerof-mass paring momentum can be stabilized when the moving velocityqxexceeds a critical value. This exotic pairing state is characterized by a spontaneously generated modulation with wave vectorqyalong the perpendicular direction,such that the total pair momentum of the order parameter is tilted towards the nesting vectorQ=(±π/d,±π/d). By doing so,the pairing state can be energetically favorable owing to the enhancement of density of states. We characterize the first order phase transition between the BCS and the FFLO states with increasingqx, and map out the phase diagram for a wide range of filling factor. The stability region of the FFLO state may be even enlarged when considering a more general state with a combination of multiple pairing momenta, which is usually energetically more favorable than the single-component solution.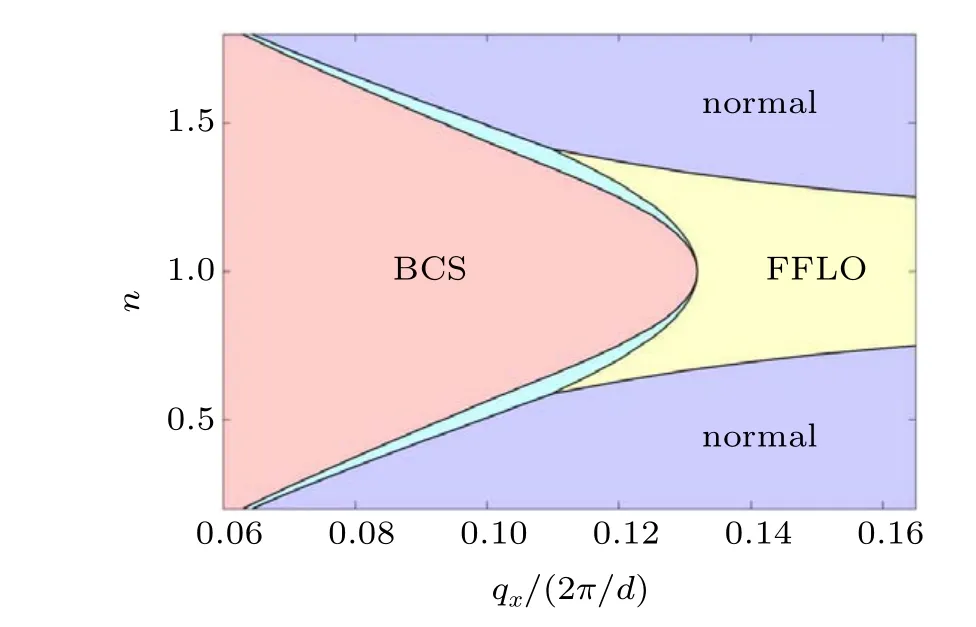
5. Conclusion
- Chinese Physics B的其它文章
- Physical properties of relativistic electron beam during long-range propagation in space plasma environment?
- Heterogeneous traffic flow modeling with drivers’timid and aggressive characteristics?
- Optimized monogamy and polygamy inequalities for multipartite qubit entanglement?
- CO2 emission control in new CM car-following model with feedback control of the optimal estimation of velocity difference under V2X environment?
- Non-peripherally octaalkyl-substituted nickel phthalocyanines used as non-dopant hole transport materials in perovskite solar cells?
- Dual mechanisms of Bcl-2 regulation in IP3-receptor-mediated Ca2+release: A computational study?

