Driven injection of a polymer into a spherical cavity:A Langevin dynamics simulation study?
Chao Wang(王超) Fan Wu(吳凡) Xiao Yang(楊肖) Ying-Cai Chen(陳英才) and Meng-Bo Luo(羅孟波)
1Department of Physics,Taizhou University,Taizhou 318000,China
2Department of Physics,Zhejiang University,Hangzhou 310027,China
Keywords: polymer,injection,simulation,free energy
1. Introduction
Polymers (such as DNA and RNA) can be driven to translocate through nanopores from thecisspace to thetransspace. It relates to many biological processes and technological applications,such as ejection of DNA from a virus capsid into host cells,[1]transportation of proteins,and RNA through channels in biological membranes,[2–4]DNA packaging,[5–8]genome mapping,[9–12]gene therapy,[13]new method for DNA sequencing and separation,[14–23]etc. Accordingly, the dynamical properties of the translocation process have been studied extensively in the last two decades.
Since the size of the pore connecting thecisspace and thetransspace is much smaller than that of the polymer in the free space,it is very difficult for the polymer to translocate through the pore spontaneously. Therefore, polymer translocation is often driven by an external force,which can be provided by the electrical field,[20–23]the flow of fluid,[24,25]binding particles,[26–28]the attraction of the membrane on thetransside,[29,30]or the spatial confinement,[31–37]etc.In the studies of polymer translocation,the dependence of the translocation time(τ)on related parameters have attracted lots of attention.
For the case that both thecisspace and thetransspace are half-infinite,it was found thatτas a function of the polymer lengthNand the driving forcefcan be expressed asτ∝Nα f?β. For driven translocation by a transmembrane force,Kantor and Kardar predictedα=1+ν,whereνis the Flory exponent.[38]However,based on the idea of tensile force propagation theory,the value ofαwas found to range between 2νand 1+ν,depending on the strength of the driving force.[39–41]Recent simulation results showed thatαchanges from 1.37 for faster translocation to 1+νfor slower translocation.[42–44]The value ofαwas also found to be dependent on the polymerpore interaction. Specifically,α=1.35 for a noninteracting pore,andα=1.22 for strong attraction pores.[45]For the exponentβ,it was predicted thatβ~1 for small driving forces andβ~0.8 for large driving forces.[46–48]
The translocation time is also influenced by the confinement of thecisspace and thetransspace. For polymers in a confinedcisspace, the confinement of thecisside is conducive to the translocation process, and the polymer can escape from thecisside spontaneously by the so-called entropic force.[31]Park and Sung have first studied the escape of an ideal polymer from a spherical cavity through a small hole via the mean first passage time, and found that the confinement gives rise to the asymmetries of the entropic free energy landscape and then drives the polymer to the outside of the sphere.[32]It was found that there is a simple scaling relation between the translocation time(τ)and the polymer length(N),i.e.,τ~N2,for small spheres.[32]However,when the excluded volume interaction between polymer segments is taken into account,the confinement effect of the sphere on the polymer is strengthened,and several different scaling relations between the translocation time,the polymer length,and the initial volume fraction were found.[49,50]Recently, Huang and Hsiao performed an elaborate simulation study on the ejection of polymer from a spherical cavity, and showed clearly that the ejection process comprises mainly three stages: the prior stage,the confined stage,and the nonconfined stage.[37]In the confined stage and the nonconfined stage,the ejection velocity shows different scaling relations on the number of monomer in the sphere,respectively.[37]
On the contrary, when a polymer moves into a confinedtransspace,it will lose lots of accessible configurations,leading to a large reduction of the conformation entropy. Therefore, the confinement of thetransside will produce an effective resistive force on the polymer during the translocation process,and the successful translocation can be achieved only under large external driving forces.[5–8]By using the stochastic rotation dynamics algorithm, Aliet al.have investigated the packaging of flexible polymers into a capsid.[51]It was found that there are several pauses during the packaging process due to the motor losing grip of the monomers and the capsid’s resistive force, and the packaging rate shows an approximately linear decrease with the number of packed monomers, which is in consistence with the experimental findings.[5]Moreover,the force needed to pack the chain was found to increases sharply near the full packaging.[51]Zhang and Luo have studied the driven translocation of a polymer into a circular confinement through a small pore, and found that the scaling exponent of the translocation time with the polymer length is dependent on the driving force and the monomer density of the whole polymer in the circular confinement.[52]Other studies indicated that the packaging of polymers into a cavity is a complex dynamical process, which is affected by many other factors, such as the attractive interaction between the polymer and the inner wall of the cavity,[30]the geometry of the cavity,[53–55]the flexibility of the polymer,[51,56]the temperature of the solvent,[57]the topology of the polymer,[58]etc.
Though the injection of polymer into a small spherical cavity has been studied by several groups, most of the works are based on an assumption that the polymer can be injected into the confinement completely under the driving force. In fact,under a constant driving force,whether the complete injection occurs or not is dependent on the polymer length and the radius of the cavity. In our recent work, we have studied the spontaneous injection of a flexible polymer into a spherical cavity from a long channel.[59]It was found that there is an obvious transition for polymer from the partial injection to the complete injection with increasing the radius of the cavity.However,the transition is not clear yet for forced cases.
In this work, the driven injection of a polymer into a spherical cavity is studied by using Langevin dynamics simulation.The transition radius of the cavity,at which the polymer changes from a partial injection state to a complete injection state, is defined based on the variation of the complete injection probability with the radius of the cavity. The dependence of the transition radius as well as the complete injection time on the polymer length and the driving force are mainly investigated. Several scaling relations are found and further confirmed by the free energy analysis and a simple kinetic model.
2. Simulation model and method
Simulations are carried out in three-dimensional (3D)space. Figure 1 shows a sketch of the model system. A half infinite space (thecisside) and a spherical cavity (thetransside)with radiusRare connected by a short cylindrical channel with radiusRpand lengthL. The boundary of the model system(the wall,the channel and the cavity)is continuous.

Fig.1. A sketch of the simulation model system. The cis side(a half infinite space)and the trans side(a spherical cavity with radius R)are connected by a short cylindrical channel with radius Rp and length L. Inside the channel,each monomer of the polymer is driven by a constant force f in the direction of the x axis.
In our simulations,the polymer is modelled by a coarsegrained off-lattice bead spring model, in which the polymer with lengthNis composed ofNidentical monomers connected by bonds sequentially. The interaction between monomers is described by the repulsive Weeks–Chandler–Andersen(WCA)potential,

wherekis the spring constant,randR0represent the bond length and the maximum bond length,respectively.
The interactions between monomers and the boundary of the simulation system (the wall, the channel, and the cavity)are also described by the WCA potential(Eq.(1)),whererrepresents the nearest distance between monomers and the boundary of the system.Besides,any monomer inside the cylindrical channel experiences a driving forcefdr=f?x. Here,fis the driving force strength,and ?xis a unit vector in the direction of thexaxis. Therefore, the polymer is driven to inject into the spherical cavity.
The motion of each monomer is described by the Langevin equation

wheremis mass of the monomer,ηis the friction coefficient, andFTis the random force with〈FT(t)〉= 0 and〈FT(t)·FT(t′)〉= 6ηkBTδ(t ?t′), wherekBis the Boltzmann constant andTis the temperature. For the numerical integration of Eq. (3), we use the velocity Verlet algorithm with a time step ?t=0.005.
At the beginning of the simulation,the polymer is generated at thecisside with the head monomer in the middle of the cylindrical channel. We at first setf=0 and run a long time (>106) of Brownian motion to equilibrate the polymer under the constraint that the head monomer is fixed. Once the polymer is at the equilibrium state, we switch on the driving force and release the head monomer, and let the polymer run a long enough time (te>107) to reach the final steady-state,at which the number of packed monomers will no longer increase. We then counter the number of monomers(min)in the cavity. Ifmin In this work,σ,m, andkBTare chosen as the units of length, mass, and energy, respectively. So, the time scale and the force scale are given bytLJ= (mσ2/kBT)1/2andf0=kBT/σ, respectively. In the simulation, we fixε0=1,k=15,R0=2,η=1. Besides,to ensure the monomers of the polymer move across the channel one by one,we adopt a narrow and short cylindrical channel withRp=1.5 andL=2. In our model,the short-range repulsive interaction between polymer and the spherical cavity is WCA potential (Eq. (1)) withrcutoff=21/6σ, so the distribution of monomers in the cavity with radiusRis roughly confined in a spherical space with radiusR ?rcutoff/2≈R ?0.56,i.e., the effective radius of the spherical cavity isRe≈R ?0.56. This correction becomes important for the calculation of the monomer density in the cavity and the theoretical analysis in our work. Though the polymer is driven by a driving force in our work,it is not necessary that the polymer can be injected into the cavity completely. For the given polymer length and driving force,whether the complete injection could occur or not is dependent on the radius of the cavityR. Qualitatively, whenRis small, there is no enough space for the cavity to accommodate the whole polymer,so it is difficult for the polymer to enter into the cavity completely. Only whenRis large enough,can the whole polymer be driven into the cavity. Figure 2 shows the dependence of the complete injection probabilityPinon the radius of the sphereRfor different polymer lengthsNatf=0.5. We can see two polymer states: a partial injection state withPinroughly zero at smallRand a complete injection state withPinroughly 1 at largeR. There is an obvious sharp transition from the partial injection state to the complete injection state at a specialR. To give approximately the radius of the spherical cavity where the transition occurs,we here define the transition radiusRCat whichPin=0.5,[59]as shown in Fig.2,and the corresponding effective transition radius isReC=RC?0.56. Fig. 2. The dependence of the complete injection probability Pin on the radius of the sphere R for different polymer lengths N,where the driving force f =0.5. The radius where Pin=0.5 is defined as the transition radius RC. The effective transition radius of the cavityReCincreases withNincreasing,because long polymers need large cavities to accommodate all the monomers. The monotonous increase ofReCwithNis presented in Fig. 3 for differentf. We find thatReCas a function ofNcan be specifically expressed by a simple scaling relationReC∝N0.34. This is different from the well known relation between the average radius of gyration(Rg)and the polymer lengthRg~Nν,with the Flory exponentν=0.6 for self-avoiding polymer and 0.5 for ideal polymer.The value ofνis related to the excluded-volume interactions between different monomers and also the configurations of the polymer.In our study,when the whole polymer is injected into the spherical cavity with radiusRec, the polymer is squeezed and then the excluded-volume interaction between monomers will be partially screened,meanwhile,the polymer configurations withRglarger than the radius of the sphere will be forbidden, which results thatRecis smaller thanRgand the scaling exponent (0.34) forRecwithNis smaller thanν. Quantitatively,the scaling relation betweenRecandNcan be obtained from the free energy landscape based on the blob theory which will be shown below. Fig.3.The log–log plot of the effective transition radius ReC versus the polymer length N for different driving forces f. ReCis also dependent on the driving forcef. Figure 4 shows the dependence ofReConffor differentN. Withfincreasing,ReCdecreases and saturates gradually at largef. In our study,due to the confinement of the cavity,the number of the configuration of polymer inside the cavity decreases,leading to an entropic force.The entropic force plays a role as a resisted force for the injection process,so the external force must be bigger than the entropic force to drive the whole polymer into the spherical cavity. Qualitatively, the entropic force is related to the radius of the spherical cavity. For large cavities,the entropic force is small,and then a relatively small driving force can driven the whole polymer into the cavity. While for small cavities,the entropic force is big,and then a large driving force is needed to complete the injection. Therefore, we find that the transition radius of the cavity decreases with the driving force increasing,i.e.,larger force leads to smaller transition radius for a given polymer. Specially,ReCas a function offcan be expressed asReC∝f?δin both small and moderatefregions. In the smallfregion (f<0.15),δ~0.27,while in the moderatefregion(0.15 For any givenNandf, we have also calculated the monomer densityφC=Nσ3/8R3eCwhen the whole polymer is in the spherical cavity with the corresponding effective radiusReC.φCis nearly independent ofN,but it increases withfincreasing and saturates gradually at largef,as shown in the inset of Fig.4. This indicates that the polymer in the cavity is compressed gradually withfincreasing. Whenfis large,φCis big,and then the polymer can not be compressed further,resulting thatφCandReCsaturate gradually at largef,as shown in Fig.4. In small and moderatefregions,φCas a function offcan also be expressed by a scaling relationφC∝fκ. Specifically,κ~0.8 in the smallfregion(f<0.15)andκ~0.5 in the moderatefregion(0.15 Fig.4. The log–log plot of the effective transition radius ReC versus the driving force f for different polymer lengths N. The inset shows the log–log plot of the monomer density φC versus the driving force f for different polymer lengths N. whereC0is a constant andνis the Flory exponent (ν=0.6 for self-avoiding polymer, and 0.5 for ideal polymer). In Eq. (4), the first term represents the increase in free energy due to the cost of confiningmmonomers in the spherical cavity with effective radiusRe,[60]and the second term is the decrease in free energy due to the work of the driving force. For any givenN,R, andf, the free energyFreaches its minimum at the final steady-state, and the corresponding number of monomers (min) in the spherical cavity is determined by(?F/?m)m=min=0,i.e., Obviously, the polymer can be completely injected only whenRe≥ReC. Based on the results ofRCin Subsection 3.1, we next study the complete injection timeτfor polymer injecting into spherical cavity with radiusR>RC. To check our simulation results, we at first calculate the complete injection time (τ0)for the extreme caseR →∞,which corresponds to the driven translocation of a polymer through a small pore connecting two half-infinite spaces. As an example, figure 5 shows the dependence ofτ0on the polymer lengthNfor different driving forcesfand a very largeR=10000. We can see thatτ0is dependent onNandf, and it as a function ofNandfcan be specifically expressed asτ0∝N1.36f?1, which is in good agreement with the simulation results of Luoet al.[44] Fig. 5. The dependence of the product fτ0 on polymer length N for different driving forces f, where τ0 represents the injection time for very large R=10000. Figure 6 shows the dependence of the injection timeτon the radius of the cavityRfor different polymer lengthsN. We can see thatτdecreases monotonously with increasingR,due to the decrease of the confinement effect of the sphere on the polymer withRincreasing. For givenfandR,τincreases monotonously with increasingN,because long polymers have more monomers to be injected into the cavity. In addition,τdecreases with increasingf(results not shown),i.e.,the polymer moves faster and faster with the driving force increasing. Fig.6. The dependence of the injection time τ on the radius of the cavity R for different polymer lengths N, where the driving force f =0.5. The inset shows the product (1 ?τ0/τ)f as a function of the monomer density in the cavity φ. The dependence ofτonR,N, andfcan be roughly understood by the following kinetic model. From Eq. (4), the increase of the free energy (?F) when the whole polymer is injected into the cavity can be expressed as Substitutingν=0.6 into Eq.(12),we have(1?τ0/τ)f∝φ1.25, which is in good agreement with the simulation result at smallφ(< 0.1), as shown in the inset of Fig. 6. Whenφis big,the excluded-volume interaction between monomers is screened, and the value ofνshould be 0.5,[34]leading to(1?τ0/τ)f∝φ2, which is also in good agreement with the simulation result at bigφ(>0.1), as shown in the inset of Fig.6. Using Langevin dynamics simulation,we investigate the injection of a self-avoiding polymer into a spherical cavity under a driving force.With increasing the radius of the cavity,the polymer undergoes a sharp transition from the partial injection to the complete injection at the transition radius (ReC). The dependence ofReCon the polymer length(N)and the driving force(f)can be described by a scaling relationReC∝N1/3f?δwithδ~4/15 for smallfandδ~1/6 for moderatef. In addition, the monomer density (φC) of the whole polymer in the cavity with radiusReCis nearly independent ofN,but increases with increasingf,which can be specifically expressed asφC∝fκwithκ~4/5 for smallfandκ~1/2 for moderatef. The scaling relations can be understood by using the free energy landscape, and the changes of values ofδandκwithfare found to be attributed to the screening of the excludedvolume interaction between monomers. The complete injection time(τ)is also calculated and found to show monotonous dependence on the polymer length, the driving force, and the radius of the cavity, which can be interpreted by a simple kinetic model.3. Results and discussion
3.1. Complete injection probability and transition radius of the cavity



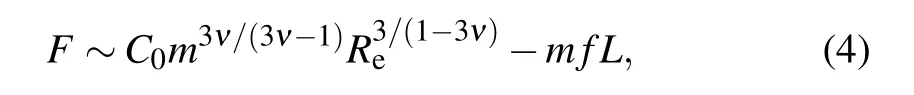



3.2. Complete injection time




4. Conclusion

