Novel energy dissipative method on the adaptive spatial discretization for the Allen-Cahn equation*
Jing-Wei Sun(孫竟巍) Xu Qian(錢旭) Hong Zhang(張弘) and Song-He Song(宋松和)
1Department of Mathematics,National University of Defense Technology,Changsha 410073,China
2State Key Laboratory of High Performance Computing,National University of Defense Technology,Changsha 410073,China
Keywords: moving mesh,energy dissipative,average vector field method,Allen-Cahn equation
1. Introduction
Phase-field models are usually constructed to reproduce a given interfacial dynamics. For instance, in solidification problems, the front dynamics is given by a diffusion equation for either concentration or temperature in the bulk and some boundary conditions at the interface, which constitutes the sharp interface model. In the past few decades,phase-field models have been widely applied in image analysis, material science, engineering, fluid mechanics, and life science, etc.(e.g.,Refs.[6,8,13-15])Among them,one fundamental model is the Allen-Cahn model,which is originally introduced to describe the non-conservative phase variables in the phase separation process. The Allen-Cahn model is recognized as gradient flow systems, for which there exists a Lyapunov function, known as the free energy. From a modeling view, given a specified Lyapunov function or a free energy function, the Allen-Cahn type equations can be derived as theL2gradient flow. This generality makes the Allen-Cahn type equations extremely useful in modeling many interfacial or multiphase problems. In this paper,we are concerned with numerical solutions of the following Allen-Cahn equation:
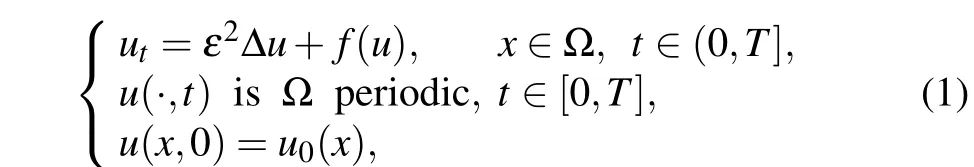
where Ω is a domain in R, Δ is the Laplacian operator, andu,ε,f(u)=u-u3represent the difference between the concentrations of the two mixtures’ components, the interfacial width, and a polynomial double-well potential, respectively.The Allen-Cahn equation was originally introduced by Allen and Cahn in Ref. [1] to describe the motion of anti-phase boundaries in crystalline solids. After that,it has been widely extended to model various phenomena in nature,such as phase transitions,[2]image analysis,[3]mean curvature flows,[4]and crystal growth.[5]It is well known that the Allen-Cahn equation possesses nonlinear stability due to its time-dependent dissipation, i.e., it can be viewed as theL2-gradient flow of the Ginzburg-Landau free energy functional

Besides the dissipation property, another is that the Allen-Cahn equation admits the maximum principle preserving(MPP)property:[9,16]if the initial value and the boundary conditions are bounded by constantβ(β=1 for Eq.(1)),then the entire solution is also bounded byβ, i.e.,||u(·,t)||L∞≤β,?t >0.
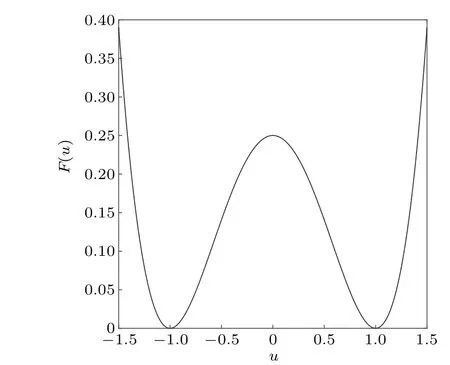
Fig.1. A double well potential F(u)=0.25(u2-1)2.
Since available theoretical solutions for the Allen-Cahn equation are still very limited, numerical investigation is an important tool to understand the physical behavior of this system. In particular, the average vector field (AVF) method[17]was proposed to simulate Hamiltonian ordinary differential equations(ODEs)due to their long time simulation and good preservation properties of conservative quantities of the original problem. It is a kind of B-series method which can be used to analyze the accuracy of the scheme by using the root series theory. There have been a number of works solving various PDEs by using the AVF method in time discretization.Gong, Jianget al.[18,19]extended the original second-order AVF scheme to the higher-order schemes. This is undoubted because of the satisfactory performance of the AVF method in maintaining the high-order accuracy of energy.
There are many ways to solve the problem of energy conservation, including the symplectic and multisymplectic method (e.g., Refs. [7,35,36]), the high-order Runge-Kutta method (e.g., Refs. [10,34]), the wavelet method (e.g., Refs.[11,12]), and especially the AVF method for time-dependent PDE systems(e.g.,Ref.[38]),etc.These systems usually have a structure that has significantly evolved as the integration of PDEs proceed,including interfaces,shocks,changes of phase,and high vorticity or regions of complexity,etc. They are further associated with small length or time scales, rapid movement of the solution feature, and the possibility of blow-up of solution. Although researchers have adapted the finite element, finite volume, finite difference, or collocation method and achieved satisfactory numerical results,one problem is inevitable, that is, small enough time and space steps are required to achieve the desired accuracy, which takes a lot of computing costs. The adaptive moving mesh method has a favorable characteristic that could overcome this problem.However,as far as we know,there is no related work on how to extend the AVF method to preserve energy dissipative property on the nonuniform meshes.
Adaptive methods for solving PDEs can be roughly divided into three fundamental categories:h-refinement method,p-refinement method, and r-refinement method. For hrefinement method, it starts with an initially uniform mesh and then locally coarsens or refines it by the inclusion or deletion of mesh points. For p-refinement method, finite element discretization of the PDE is used with local polynomials of some particular order. And for r-refinement method, it starts with a uniform mesh and then moves the mesh points, keeping the mesh points fixed as the solution evolves. The mesh points are then concentrated into regions where the solution has individual behavior, usually typified by a rapid variation of either the solution or one of its higher derivatives. Compared with other methods,there are several significant advantages of r-refinement methods in various applications such as computational fluid mechanics, phase-field models, and convective heat transfer,etc. (e.g.,Refs.[20,21])For instance,it is convenient to work with the same number of mesh points.This makes linear algebra rather easier because the matrices considered have a constant sparsity structure. Moreover, the discretization strategy on the mesh is also easier. The third advantage of r-refinement methods is that under certain conditions, the mesh movement strategy coupled with the discrete PDE can be regarded as a large dynamical system that would be easier for theoretical analysis.
Our main proposal is to achieve a balance among effectiveness, high efficiency, and structure preservation. We are committed to extending the AVF method to nonuniform meshes via the r-refinement method. The extension is based on the “mapping method” which is the most popular one among the moving mesh method, and the change of coordinates plays an important role. Recently,Yaguchi extended the discrete variational derivative method to nonuniform grids[22]and proved that this method could likewise do the structurepreserving on nonuniform grids. A summation by parts formula is introduced on one-dimensional nonuniform grids since it plays a very important role in the discrete variational method. We also use this method as a reference to prove the theorem. In a recent study,[23]an hr adaptive method is proposed to get the spatial and temporal adaptation effect and then to solve the nonlinear Schr¨odinger equation(NSE).Nevertheless, the proposed method only involves r-refinement and explores the adaptation in space.
The rest of this paper is organized as follows. In Section 2, we review the idea of the mapping method and two approaches of discretization for the PDE.In Section 3,we introduce our mesh movement strategy,including the mesh density function and its corresponding smoothing method. The dissipative moving mesh scheme based on the classical AVF method is defined in Section 4, and relevant theorems and proofs are given. Section 5 contains numerical experiments and results of the application of the scheme proposed. Conclusion and outlook are discussed in Section 6.
2. Discretization and mesh adaptation
Notice that the Allen-Cahn equation as one of the Hamiltonian PDEs

whereSis a negative semi-definite differential operator, and?denotes a certain energy functional,such as the Hamiltonian or free energy. Equation(5)can be rewritten as the following form:[24]
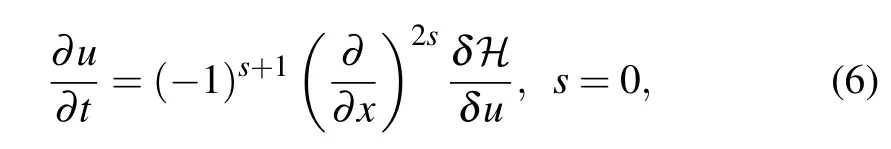
which will be a general form for later discretization and theorems.
2.1. Spatial discretization
For simplicity of notation, we define the following finite difference operators:

whereD(κ)=diag(κ0,...,κN-1)is anNbyNdiagnoal matrix.
In order to introduce mesh movement,Eq.(6)is rewritten with respect to a moving reference frame, and the problem is recast in terms of the independent variablesξandt,by using the transformation
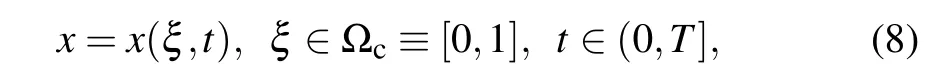
from computational space Ωc×(0,T]to physical space Ωp×(0,T]. A uniform mesh covering Ωcis given by
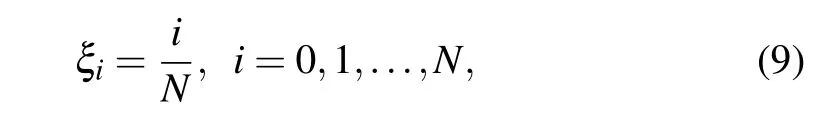
and the corresponding nonuniform mesh on Ωpis
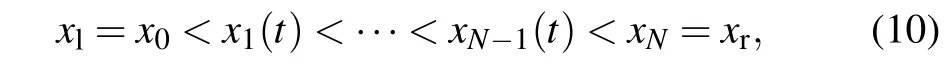
where
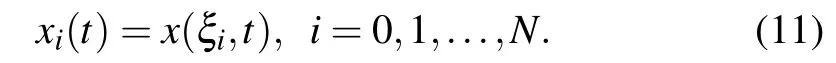
Equation(6)is rewritten in the computational domain Ωc
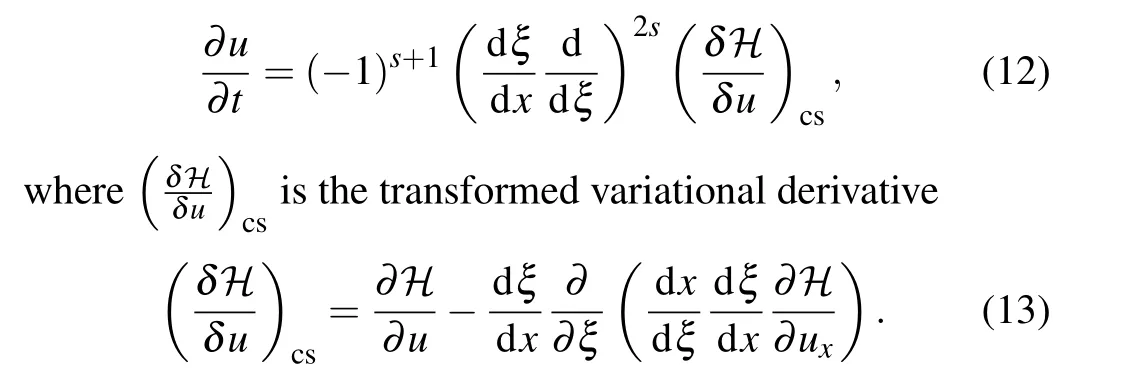
This is a natural form of the variational derivative in the computational space. Yaguchiet al.[22]have proved that the variational structure is retained in the computational space. To make it convenient for the theoretical analysis,we decompose Eq.(12)to the following form:

The following theorem explains that in the computational domain, Eq. (12) also has the dissipation property. It is worth mentioning that although the theorem gives special boundary conditions, it also applies to periodic boundary conditions. It can refer to Ref.[22].
Theorem 1[22]Suppose that the boundary condition satisfies

The effect of mesh movement in the time discretization of the physical PDE system can be treated with either the quasi-Lagrange approach or the rezoning approach. We would give the quasi-Lagrange approach as a reference. The latter one will be highlighted and applied to the adaptive method.
2.1.1. Quasi-Lagrange approach
With the quasi-Lagrange approach, the mesh points are considered to move continuously in time, and physical time derivatives are transformed into time derivatives along mesh trajectories supplemented with a convective term reflecting mesh movement. This approach mainly use the chain rule,i.e., denoting the transformed variablev(ξ,t)=u(x(ξ,t),t),we have

2.1.2. Rezoning approach
The rezoning approach, as its name implies, is going to update the mesh at each time step by using certain mesh equations or generators, and the mesh points are considered to move intermittently in time. It is an integrated process that involves solving alternately for the physical solution and the mesh. The physical solution is interpolated from the old mesh to the new one,and the physical PDE is then discretized on the new mesh, which is held fixed for the current time step. This is the main difference from the quasi-Lagrange approach, and Fig.2 gives an intuitive display. As can be seen,the mesh points are considered to move continuously for the quasi-Lagrange approach of temporal discretization of physical PDEs, while the mesh is considered to vary only at time instants for the rezoning approach of temporal discretization of physical PDEs. Interpolation of the physical solution determines the success of this method, and it is often necessary to use a conservative interpolation scheme that preserves some solution quantities and properties. We will show the detail in later chapters.
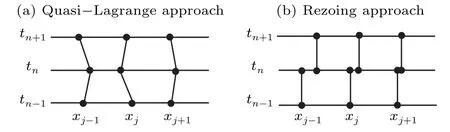
Fig. 2. Two different mesh movement approaches with time varying in Ref.[25].
In fact,for a moving mesh method,the discrete physical PDE and the mesh equation give a coupled system. Moreover,on account of high coupling,the mesh can respond promptly to any change occurring in the physical solution. Unfortunately,coupling leads to a highly nonlinear equation that is difficult to solve due to its more complicated structure. Therefore we choose the rezoning approach to strive for maximum decoupling. Since the time lag effect brought and the computational cost by the rezoning approach cannot be ignored, we have to take a smaller time step.
3. Mesh movement strategy
Since only the one-dimensional problem is concerned in this paper, the de Boor’s equidistributing algorithm could not be more appropriate. Given a continuous functionρ(x), typically depending on the first or second order derivatives of the underlying solutionuto be adapted, the number of grid pointsN-1 and the bounded domain[0,L]whereuis defined,equidistribution needs to find a gridXh:x0=0<x1<···<xN=Lsuch that
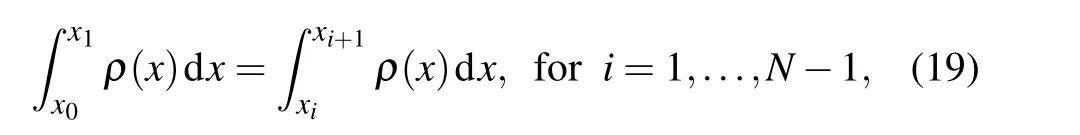
where the functionρ(x)is to minimize the error of the numerical approximation,which is currently called the mesh density function(e.g.,Refs.[25,26]). To ensure that the equidistribution is unique,assume that the mesh density function is strictly positive,i.e,
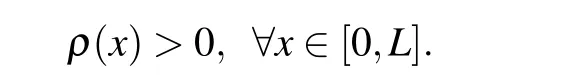
A typical and simple choice ofρ(x) is the arc-length mesh density function

In this case,the meaning of the equidistribution principle is that the weighted arc length ofuover each interval is equal.That means that bothuandρare approximate values. In addition,notice that ifuis not smooth,the discrete mesh density function computed this way can often change abruptly and unnecessarily slow down the computation. To obtain a smoother mesh and also make Eq. (19) easier to integrate, a common practice is to smooth the mesh density functionρ(x). A simple but effective smoothing method is given as follows:[25]
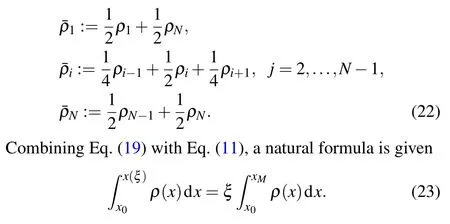
After twice differential with respect toξ,a classical equation yields

4. Adaptive energy dissipative method
Lemma 1 in Ref.[27]indicated that the operator ?as the standard gradient could replace the variational derivative in a finite number of dimensions,i.e.,

where the notations ˉ?and ˉu,which are different from the notation ˉρas mentioned earlier,denote the discrete values of?anduand ˉ?′= ˉ?D(κ). The following two lemmas are given for later proof.
Lemma 1[22]Suppose that a solution of Eq.(6)satisfies the condition

4.1. Design of schemes for dissipative equations

Theorem 2Let ˉSbe any negative-definite matrix approximation toSand ˉ?be any finite difference approximation to?. Let

where (xξ)k,jandδkcan be chosen arbitrarily (k=1,...,s),andsis equivalent tosof Eq.(6).
Theorem 3If the periodic boundary condition is satisfied,then Eq.(33)has an energy dissipation law,i.e.,

Substituting Eq.(33)and applying the summation by parts in Ref.[22]gives
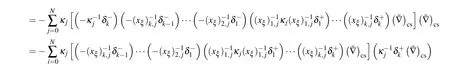
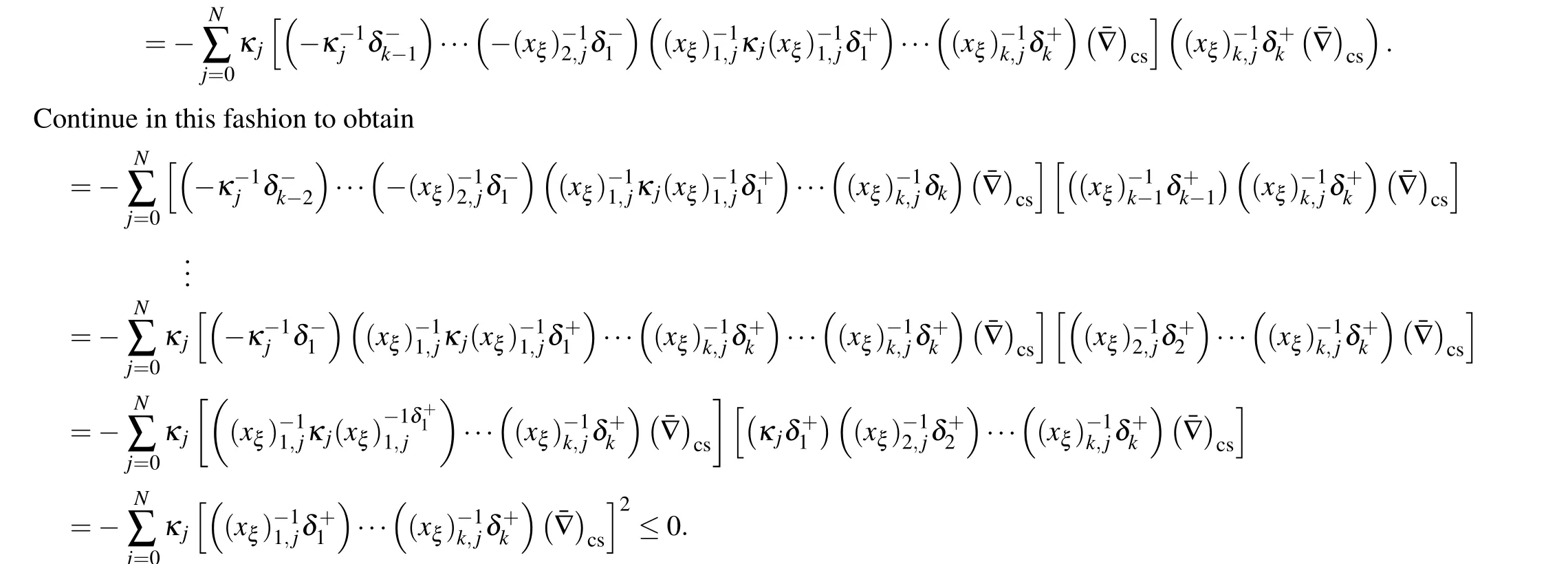
4.2. A complete r-algorithm based on rezoning approach


Algorithm 1 The r-algorithm based on rezoning approach 1: Initialize variables;select all parameters including Δx and Δt,etc.2: Give a uniform mesh over the physical domain and determine u0 based on initial condition φ0 3: Utilize the mesh density function ω(x)and de Boor’s equidistribution principle to compute an initial grid x0.4: for n=0:NT-1 do 5: Set reltol=1.0e-10 and abstol=1;6: while abstol >reltol do 7: Compute the approximately equidistributing grid xn+1 from xn and un 8: Compute ?u=ψ(xn+1,xn)un,for a given interpolation operator ψ(xn+1,xn) mapping from xn to xn+1.9: Solve Eq.(33)where U(n)j is replaced by ?Uj on the new mesh xn+1images/BZ_138_447_2554_467_2587.pngimages/BZ_138_515_2554_535_2587.pngimages/BZ_138_720_2554_740_2587.pngimages/BZ_138_740_2554_760_2587.png10: abstol=maxabs U(n+1)j -U(n)j 11: end while 12: Set n:=n+1 13: end for
As mentioned before, the key step is to select the appropriate interpolation operatorψ. In Ref.[28], Huang gave the detailed process and error analysis of linear interpolation on the adaptive moving mesh. However,in the actual calculation,we observe that the cubic interpolation operator (the MATLAB built-in functionpchip) works best with respect to the error between the numerical solution and the exact solution.
5. Numerical experiments
According to Eq.(33),we obtain the full-discrete scheme of the Allen-Cahn equation on the nonuniform mesh
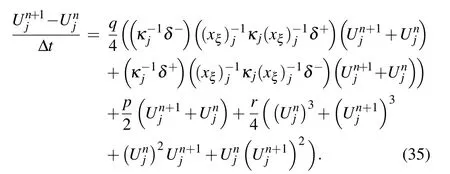
Next,we choose two pairs of initial solutionu0(x)and parameterεto verify the validity of the scheme.
Example 1Consider the following initial value
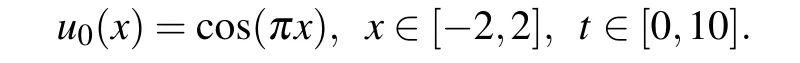
We also setε=0.01,Δt=0.01 and Δx=0.02. In Fig.3,two intuitive top views are given att=0 s andt=10 s to show that the phase has been completely separated. The mesh trajectories and energy change are shown in Fig.4 to indicate that the r-adaptive component of the adaptive algorithm performs well tracking the movement of the front throughout the time integration period,and the discrete energy drops very quickly in the first two seconds,and att=3 s it is at a stable state.
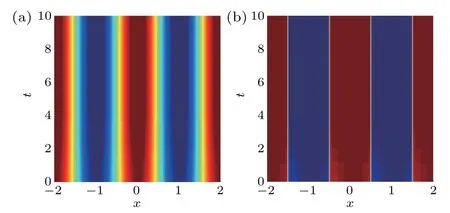
Fig.3. Snapshots of(a)initial time T =0 s and(b)terminus time T =10 s.
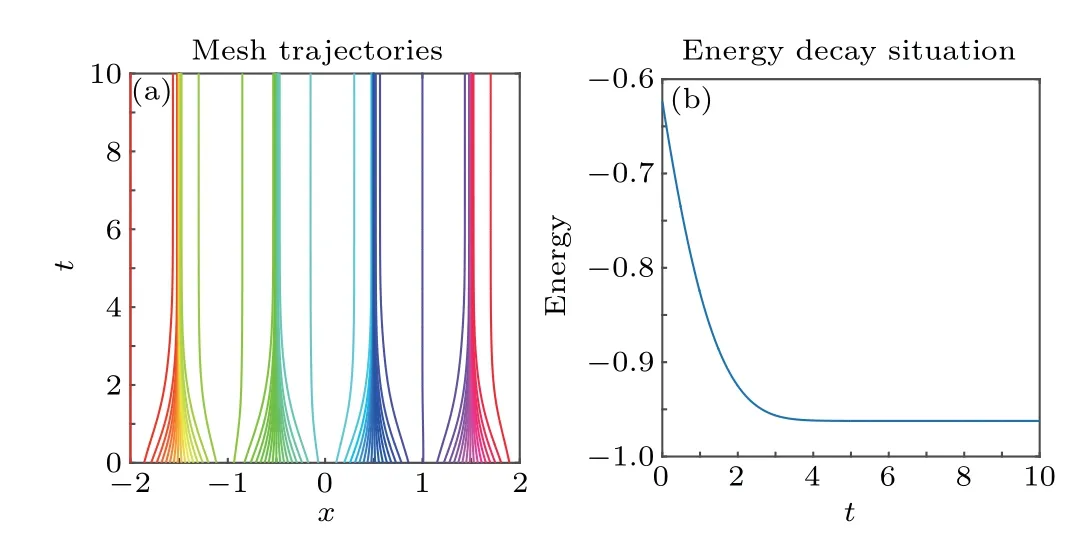
Fig.4. (a)Grid movement-each line represents the path of one grid point in time. (b)AC equation’s energy decay case.
Next, we test the accuracy of the proposed method by choosing a reference solution with a small time step Δt=5×10-4. TheL2-norms andL∞-norms of the errors of numerical solutions are presented respectively in Table 1.It indicates that the moving mesh method can achieve almost the same accuracy as the uniform method. Fixing space step Δx=0.02 and setting time step Δthalf each time,we obtain the numerical results shown in Table 2. Note that in the uniform mesh method,L2error can be kept the second-order convergence while it can not be in the moving mesh method. Referring to the previous literature,there is no convergence analysis for the moving mesh method. This is because even if the same number of grids are taken each time, the grid position will also bring a small change due to the r-algorithm. We also notice that in Table 2, there is no numerical result for the uniform mesh method when taking Δt=0.25 or 0.125. This is because the traditional uniform mesh method is limited by the step ratio Δx/Δt. However,the moving mesh method can break through this limit and tend to perform well in a large step, although there is no theory to verify whether it is unconditionally stable. Another point we have to mention is that using the moving mesh method costs more computational time, especially when the space or time step is very small. This phenomenon is also caused by the r-refinement method. In the beginning,the physical domain Ωpis mapped to Ωc,and it needs to solve alternately between two domains all the time. In addition,we compare the total energy with different time steps with the reference solution for theL∞error, and the line chart is shown in Fig. 5. It is worth noting that when Δt=0.5, the energy error reaches around magnitude 10-2, and Δt=0.001 corresponds to magnitude 10-6. In addition, the error decreases very quickly before the time grid numbers reach 500. It again verifies the solution stability of large time steps and the advantage of the proposed scheme.
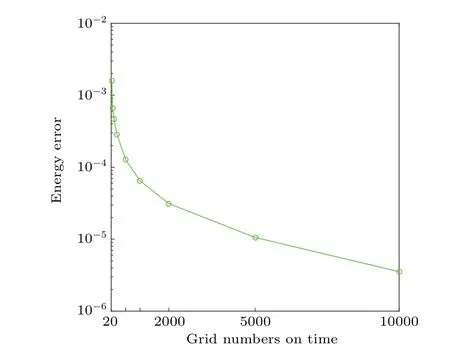
Fig.5. Different time step’s energy error with reference solution.

Table 1. Numerical results for the AC equation(example 1),Δx=0.01.

Table 2. The L2 error and L∞error between the current time step and the previous time step(example 1),Δx=0.02.
Example 2Consider the following initial value:
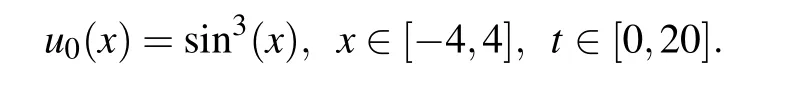
Four different parametersε2=0.001,0.002,0.003 and 0.004 are tested for this example. We also set Δx=0.02=Δt. Figure 6 shows the phase cases at the terminal timeT=20 s.Furthermore,in order to reflect the difference in phase change caused by different parameters, the magnified results of the four local areas are shown in Fig.7. It can be seen that as the parameterεbecomes larger, the width of the interfacial becomes longer,and phase separation gets coarser. This is consistent with the actual phase separation.Figure 8 illustrates intuitively the parameterεaffects the steady-state energy value and energy dissipation rate and verifies Eqs.(2)and(3).
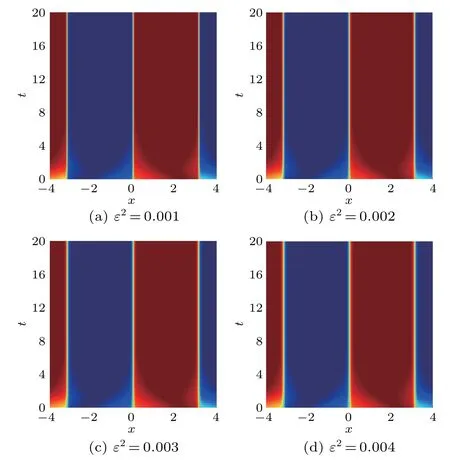
Fig.6. Different parameter ε2s’snapshots at T =20 s.
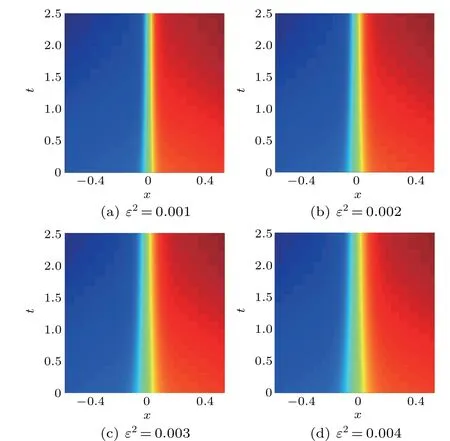
Fig. 7. Enlarged images in part of the phase area, with x ∈[-0.4,0.4] and T =20 s.
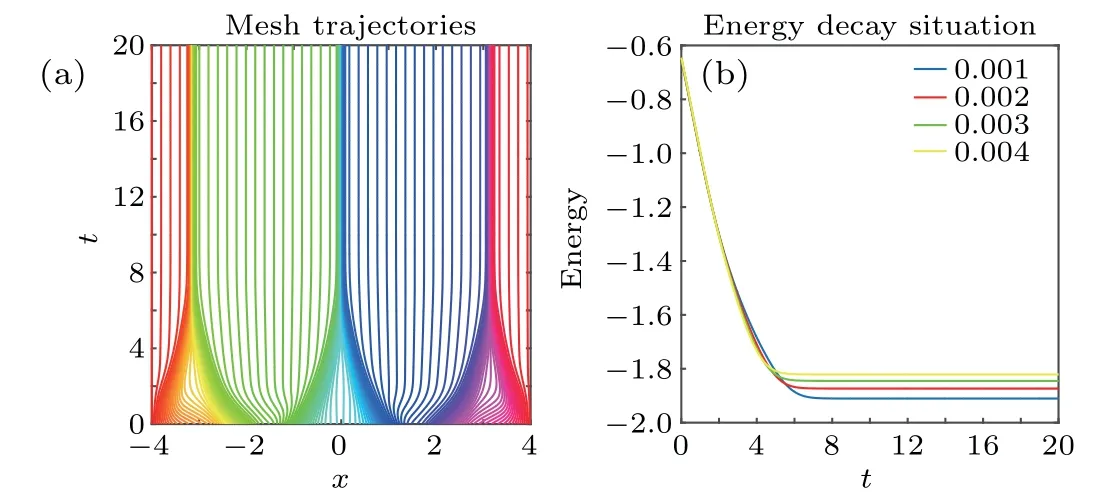
Fig. 8. (a) Grid movement with ε2 =0.001 and (b) different ε2s’ energy decay cases.
6. Conclusion and outlook
In this paper, we introduce a dissipative scheme and extend the average vector field method to nonuniform meshes.Our extension borrows from Yaguchi’s thought that the dissipation properties obtained from the variational structure still holds after the change of coordinates. The de Boor’s equidistribution principle and appropriate monitor function make the grid reasonably clustered in the region where the solution needs to get the effect of adaptive mesh. By using the rezoning approach, we get the discretization process of PDE solving. The numerical experiments confirm that the scheme can work well under the large step and step ratio Δx/Δtthat much less than 1. Although we have considered the only onedimensional case, the scheme can also be derived for twodimensional case by transforming the differential operators to Since the quasi-Lagrange approach and rezoning approach each has its advantage, in the near future, we may propose a two-dimensional scheme by using the quasi-Lagrange approach and try to apply it to other phase-field models such as the Cahn-Hilliard equation and molecular beam epitaxy,etc.
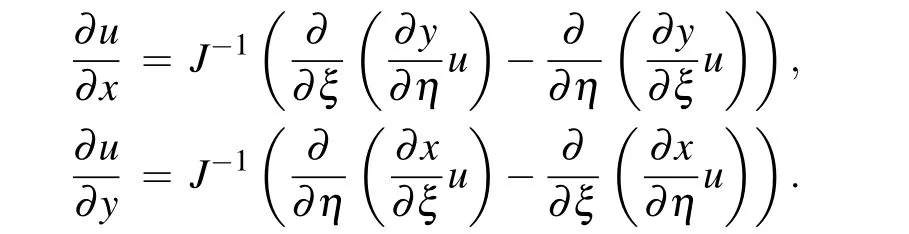
- Chinese Physics B的其它文章
- Numerical simulations of partial elements excitation for hemispherical high-intensity focused ultrasound phased transducer*
- Magnetic-resonance image segmentation based on improved variable weight multi-resolution Markov random field in undecimated complex wavelet domain*
- Structure-based simulations complemented by conventional all-atom simulations to provide new insights into the folding dynamics of human telomeric G-quadruplex*
- Dual-wavelength ultraviolet photodetector based on vertical(Al,Ga)N nanowires and graphene*
- Phase-and spin-dependent manipulation of leakage of Majorana mode into double quantum dot*
- Deep-ultraviolet and visible dual-band photodetectors by integrating Chlorin e6 with Ga2O3

