Explicit structure-preserving geometric particle-in-cell algorithm in curvilinear orthogonal coordinate systems and its applications to whole-device 6D kinetic simulations of tokamak physics

Jianyuan XIAO (肖建元)and Hong QIN (秦宏)

1 School of Nuclear Science and Technology, University of Science and Technology of China, Hefei 230026, People’s Republic of China

2 Plasma Physics Laboratory, Princeton University, Princeton, NJ 08543, United States of America

Abstract Explicit structure-preserving geometric particle-in-cell(PIC)algorithm in curvilinear orthogonal coordinate systems is developed.The work reported represents a further development of the structure-preserving geometric PIC algorithm achieving the goal of practical applications in magnetic fusion research.The algorithm is constructed by discretizing the field theory for the system of charged particles and electromagnetic field using Whitney forms, discrete exterior calculus,and explicit non-canonical symplectic integration.In addition to the truncated infinitely dimensional symplectic structure, the algorithm preserves exactly many important physical symmetries and conservation laws, such as local energy conservation, gauge symmetry and the corresponding local charge conservation.As a result, the algorithm possesses the long-term accuracy and fidelity required for first-principles-based simulations of the multiscale tokamak physics.The algorithm has been implemented in the SymPIC code,which is designed for highefficiency massively-parallel PIC simulations in modern clusters.The code has been applied to carry out whole-device 6D kinetic simulation studies of tokamak physics.A self-consistent kinetic steady state for fusion plasma in the tokamak geometry is numerically found with a predominately diagonal and anisotropic pressure tensor.The state also admits a steady-state subsonic ion flow in the range of 10 km s?1,agreeing with experimental observations and analytical calculations Kinetic ballooning instability in the self-consistent kinetic steady state is simulated.It is shown that high-n ballooning modes have larger growth rates than low-n global modes,and in the nonlinear phase the modes saturate approximately in 5 ion transit times at the 2%level by the E×B flow generated by the instability.These results are consistent with early and recent electromagnetic gyrokinetic simulations.

Keywords: curvilinear orthogonal mesh, charge-conservative, particle-in-cell, symplectic algorithm, whole-device plasma simulation

1.Introduction

Six dimensional (6D) particle-in-cell (PIC) simulation is a powerful tool for studying complex collective dynamics in plasmas[1–3].However,as a first-principles-based numerical method, 6D PIC simulation has not been employed to study the dynamical behavior experimentally observed in magnetic fusion plasmas, mainly due to the multiscale nature of the physics involved.The technical difficulties are two-fold.Firstly, the span of space-time scales of magnetic fusion plasmas is enormous, and numerically resolving these spacetime scales demands computation hardware that did not exist until very recently.Secondly, even if unlimited computing resource exists, the standard 6D PIC algorithms do not possess the long-term accuracy and fidelity required for firstprinciples-based simulations of magnetic fusion plasmas.For example, the most commonly used 6D PIC scheme is the Boris–Yee scheme, which solves the electromagnetic fields using the Yee-FDTD [4] method and advances particles’position and velocity by the Boris algorithm[5].Even though both Yee-FDTD method [6] and the Boris algorithm [7–12]themselves do have good conservative properties, their combination in PIC methods does not [2, 3, 13].Numerical errors thus accumulate coherently during simulations and long-term simulation results are not trustworthy.

Recent advances in super-computers [14] have made 6D PIC simulation of magnetic fusion plasmas possible in terms of hardware.On the other hand,much needed now is modern 6D PIC algorithms that can harness the rapidly increasing power of computation hardware.A family of such new 6D PIC algorithms[15–25]has been developed recently.Relative to the conventional PIC methods, two unique properties characterize these new PIC algorithms: the space-time discretization is designed using modern geometric methods,such as discrete manifold and symplectic integration, and the algorithms preserve exactly many important physical symmetries and conservation laws in a discrete sense.For this reason, these algorithms are called structure-preserving geometric PIC algorithms.The long-term accuracy and fidelity of these algorithms have been studied and documented by different research groups [17, 22, 26–35].

Discrete symplectic structure and symplectic integration are two of the main features of the structure-preserving geometric PIC algorithms.Up to now, the only explicit symplectic integrator for the non-canonical symplectic structure of the discrete or continuous Vlasov–Maxwell system is the splitting method developed in[19],which splits the dynamics symplectically into one-way decoupled Cartesian components.The requirement of the Cartesian coordinate system creates a hurdle for applications in magnetic fusion plasmas,for which cylindrical or toroidal coordinate systems are more convenient.Most simulation codes, such as GTC [36, 37],XGC [38, 39] and GEM [40–42] adopted curvilinear coordinate systems.In the present study, we extend the structurepreserving geometric PIC algorithm to arbitrary curvilinear orthogonal coordinate systems,in particular,to the cylindrical coordinate system for applications in tokamak physics.We show that when a sufficient condition (40) is satisfied, which is the case for the cylindrical mesh, the structure-preserving PIC algorithm can be made explicitly solvable and highorder.For easy implementation and presentation, we first present the algorithm as a discrete field theory [43–48] specified by a Lagrangian discretized in both space and time.It is then reformulated using a generalized version of the discrete Poisson bracket developed in [17] and an associated explicit symplectic splitting algorithm, which generalizes the original algorithm designed in[19]in the Cartesian coordinate system.In particular, the technique utilizing the one-way decoupling of dynamic components is generalized to arbitrary curvilinear orthogonal coordinate systems satisfying condition (40).

The algorithm has been implemented in the the SymPIC code and applied to carry out whole-device 6D kinetic PIC simulations of plasma physics in a small tokamak with similar machine parameters as the Alcator C-Mod [49, 50].We numerically study two topics: self-consistent kinetic steady state in the tokamak geometry and kinetic ballooning instability in the edge.Simulation shows that when plasma reaches a self-consistent kinetic steady state, the pressure tensor is diagonal, anisotropic in 3D, but isotropic in the poloidal plane.A sub-sonic ion flow in the range of 10 km s?1exists, which agrees with experimental observations [51, 52]and theoretical calculations [53, 54].In the self-consistent kinetic steady state,it is found that large-nkinetic ballooning modes(KBMs)grow faster than low-nglobal modes,and the instability saturates nonlinearly at the 2% level by theE×Bflow generated by the instability.These results qualitatively agree with previous simulations by electromagnetic gyrokinetic codes [55–57].

Because the algorithm is based on first-principles of physics and constructed in general geometries, the wholedevice 6D kinetic simulation capability developed is applicable to other fusion devices and concepts as well, including stellarators, field reserve configurations and inertial confinement.It is also worthwhile to mention that the structurepreserving geometric discretization technique developed for the 6D electromagnetic PIC simulations can be applied to other systems as well, including ideal two-fluid systems [58]and magnetohydrodynamics [59–63].Structure-preserving geometric algorithms have also been developed for the Schrdinger–Maxwell [64] system, the Klein–Gordon–Maxwell system [65–68], and the Dirac–Maxwell system [69],which have important applications in high energy density physics.Another noteworthy development is the metriplectic PIC integrators for the Landau collision operator [70].Recently, a field theory and a corresponding 6D structurepreserving geometric PIC algorithm were established for lowfrequency electrostatic perturbations in magnetized plasmas with adiabatic electrons [25].The long-term accuracy and fidelity of the algorithm enabled the simulation study of electrostatic drift wave turbulence and transport using a 6D PIC method with adiabatic electrons.

The paper is organized as follows.In section 2 we develop the explicit structure-preserving geometric PIC scheme in arbitrary orthogonal coordinate systems, and the algorithm in a cylindrical mesh is implemented in the SymPIC code.In section 3, the code is applied to carry out whole-device 6D kinetic PIC simulations of tokamak physics.

2.Explicit structure-preserving geometric PIC algorithm in curvilinear orthogonal coordinate systems

2.1.The basic principles of structure-preserving geometric PIC algorithm

The procedure of designing a structure-preserving geometric PIC algorithm starts from a field theory, or variational principle,for the system of charged particles and electromagnetic field.Instead of discretizing the corresponding Vlasov–Maxwell equations, the variational principle is discretized.

For spatial discretization of the electromagnetic field,discrete exterior calculus[71,72]is adopted.As indicated by its name,a PIC algorithm contains two components not found in other simulation methods: charge and current deposition from particles to grid points,and field interpolation from grid points to particles.Note that these two components are independent from the field solver, e.g.the Yee-FDTD method, and the particle pusher, e.g.the Boris algorithm.In conventional PIC algorithms[1–3],the function of charge and current deposition and the function of field interpolation are implemented using intuitive techniques without fundamental guiding principles other than the consistency requirement.It was found [15, 24] that a systematic method to realize these two functions is to apply the Whitney interpolation (differential)forms[73]and their high-order generalizations[17]on the discrete Lagrangian.

The application of Whitney forms is a key technology for achieving the goal of preserving geometric structures and conservation laws.It stipulates from first principles how charge and current deposition and field interpolation should be performed [15–25].It also enabled the derivation of the discrete non-canonical symplectic structure and Poisson bracket for the charged particle-electromagnetic field system[17].At the continuous limit when the size of the space-time grid approaches zero, the discrete non-canonical Poisson bracket reduces to the Morrison–Marsden–Weinstein(MMW)bracket for the Vlasov–Maxwell equations [74–77, 26].(The MMW bracket was also independently discovered by Iwinski and Turski [78].) To derive the discrete Poisson bracket,Whitney forms and their high-order generalizations are adopted for the purpose of geometric spatial discretization of the field Lagrangian density as an 1-form in the phase space of the charged particle-electromagnetic field system, whose exterior derivative automatically generates a discrete noncanonical symplectic structure and consequently a Poisson bracket.As a different approach,Heet al[21]and Krauset al[22] used the method of finite element exterior calculus to discretize the MMW bracket directly, and verified explicitly that the discretized bracket satisfies the Jacobi identity through lengthy calculations, in order for the discretized bracket to be a legitimate Poisson bracket.If one chooses to discretize the MMW bracket directly [32, 31], such verification is necessary because there are other discretizations of the MMW bracket which satisfy the numerical consistency requirement but not the Jacobi identity.On the other hand, the discrete Poisson bracket in [17] was not a discretization of the MMW bracket.It was derived from the spatially discretized 1-form using Whitney forms and is naturally endowed with a symplectic structure and Poisson bracket, and reduces to the MMW bracket in the continuous limit.The advantage of this discrete Poisson bracket in this respect demonstrates the power of Whitney forms in the design of structure-preserving geometric PIC algorithms.

To numerically integrate a Hamiltonian or Poisson system for the purpose of studying multiscale physics, symplectic integrators are necessities.Without an effective symplectic integrator,a symplectic or Poisson structure is not beneficial in terms of providing a better algorithm with longterm accuracy and fidelity.However, essentially all known symplectic integrators are designed for canonical Hamiltonian systems [43–47, 79–98] except for recent investigations on non-canonical symplectic integrators [99–112] for charged particle dynamics in a given electromagnetic field.Generic symplectic integrators for non-canonical symplectic systems are not known to exist.Fortunately, a high-order explicit symplectic integrator for the MMW bracket was discovered[19] using a splitting technique in the Cartesian coordinate system.The validity of this explicit non-canonical symplectic splitting method is built upon the serendipitous one-way decoupling of the dynamic components of the particle-field system in the Cartesian coordinate system.It is immediately realized [17] that this explicit non-canonical symplectic splitting applies to the discrete non-canonical Poisson bracket without modification for the charged particle-electromagnetic field system.This method was also adopted in [21, 22] to integrate the discretized MMW bracket using finite element exterior calculus.See also [113, 114] for early effort for developing symplectic splitting method for the Vlasov–Maxwell system.It was recently proven[24]that the discrete non-canonical Poisson bracket [17] and the explicit noncanonical symplectic splitting algorithm [19] can be equivalently formulated as a discrete field theory [48] using a Lagrangian discretized in both space and time.

The geometric discretization of the field theory for the system of charged particles and electromagnetic field using Whitney forms [73, 15, 17], discrete exterior calculus[71, 72], and explicit non-canonical symplectic integration[19,17]results in a PIC algorithm preserving many important physical symmetries and conservation laws.In addition to the truncated infinitely dimensional symplectic structure, the algorithms preserves exactly the local conservation laws for charge [15, 24] and energy [23].It was shown that the discrete local charge conservation law is a natural consequence of the discrete gauge symmetry admitted by the system[15, 24, 115].The correspondence between discrete spacetime translation symmetry [116, 117] and discrete local energy-momentum conservation law has also been established for the Maxwell system [118].

As mentioned in section 1, the goal of this section is to extend the explicit structure-preserving geometric PIC algorithm,especially the discrete non-canonical Poisson bracket[17]and the explicit non-canonical symplectic splitting algorithm [19], from the Cartesian coordinate systems to curvilinear orthogonal coordinate systems that are suitable for the tokamak geometry.

2.2.Field theory of the particle-field system in curvilinear orthogonal coordinate systems

We start from the action integral of the system of charged particles and electromagnetic field.In a curvilinear orthogonal coordinate system(x1,x2,x3) with line element

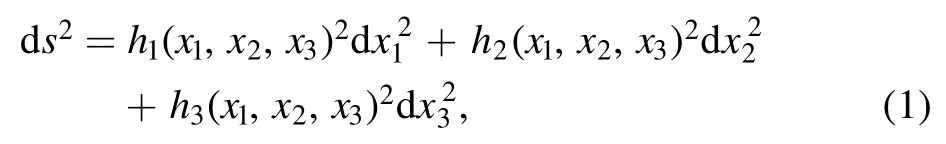
the action integral of the system is

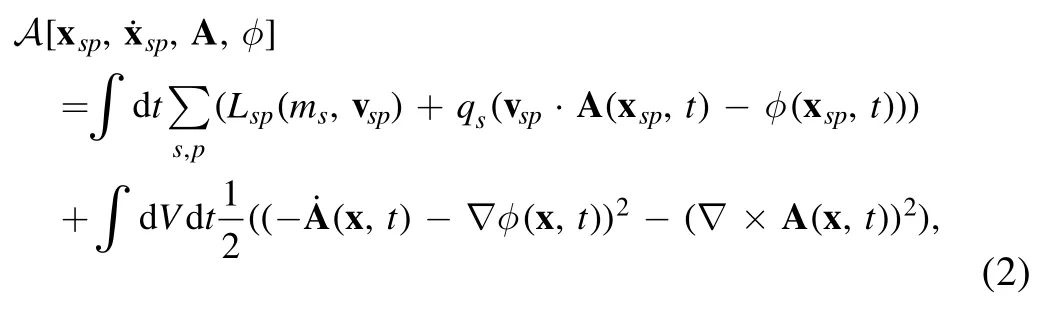
where x=[x1,x2,x3] and dV=∣h1(x)h2( x)h3( x)∣dx1dx2dx3.In this coordinate system, the position and velocity of the vsp=[x˙sp1h1( xsp),x˙sp2h2( xsp),x˙sp3h3( xsp)].Lspis the freepth particle of speciessare xsp=[xsp1,xsp2,xsp3] and Lagrangian for thepth particle of speciess.For the non-relativistic caseLsp=ms|vsp|2/2, and for the relativistic caseLsp=Here, we set both permittivity ?0and permeability μ0in the vacuum to 1 to simplify the notation.The evolution of this system is governed by the variational principle,

It can be verified that equations (3) and (4) are the Maxwell equations, and equation (5) is Newton?s equation for thepth particle of speciess.

2.3.Construction of the algorithm as a discrete field theory

According to the general principle of structure-preserving geometric algorithm, the first step is to discretize the field theory [15, 17, 24, 25].For the electromagnetic field, we use the technique of Whitney forms and discrete manifold[73, 71].For example, in a tetrahedron mesh the magnetic field B as a 2-form field can be discretized on a 2-simplex σ2(a side of a 3D tetrahedron mesh)as·B Sd ,where S is the unit normal vector of σ2.Note that σ2is a common side of two tetrahedron cells.In a mesh constructed using a curvilinear orthogonal coordinate system,which will be referred to as a Curvilinear Orthogonal Mesh(COM),such discretization can be also performed.Let

To discretize the particle-field interaction while preserving geometric structures and symmetries,Whitney interpolating forms [73] and their high-order generalizations [17] are used.Akin to previous results on Whitney interpolating forms in a cubic mesh [17], interpolating formsfor 0-, 1-, 2- and 3-forms can be constructed on a COM as follows,

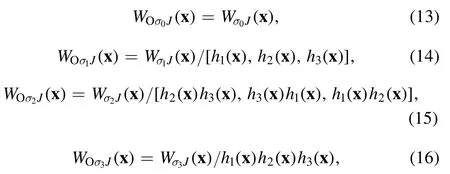
whereWσiJ(x ) , 0≤i≤3are the interpolating forms in a cubic mesh defined in [17] and the quotient (product) of vectors means component-wise quotient (product), i.e.

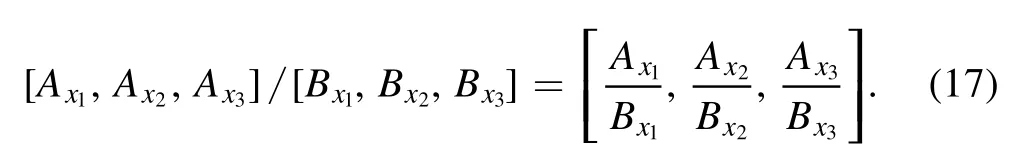
With these operators and interpolating forms, we discretize the action integral as

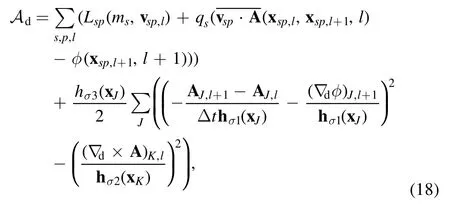
wherelis the index for the temporal grid,JandKare the index vectors for the spatial grid,i.e.,J=i,j,kandK=i′,j′,k′,and

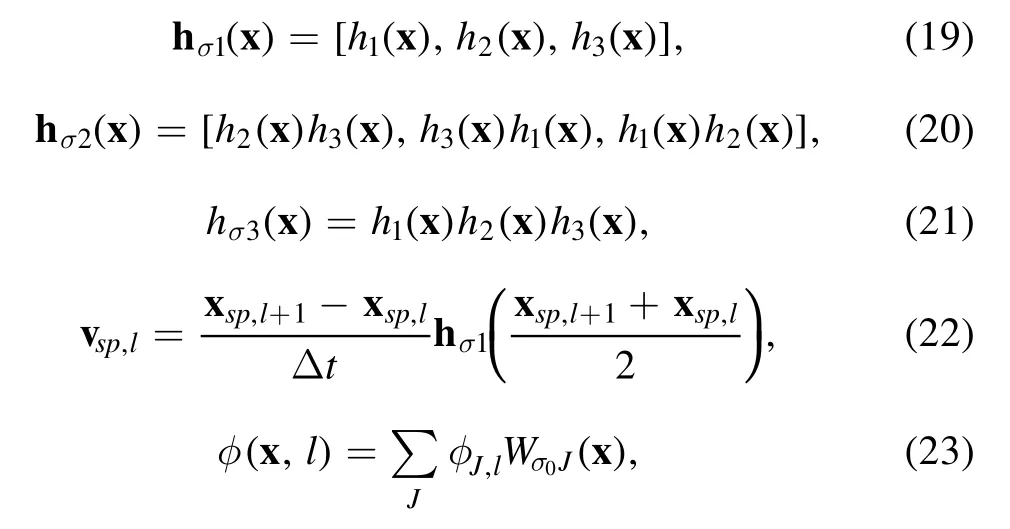
Finally,the time advance rule is given by the variation of the action integral with respect to the discrete fields,

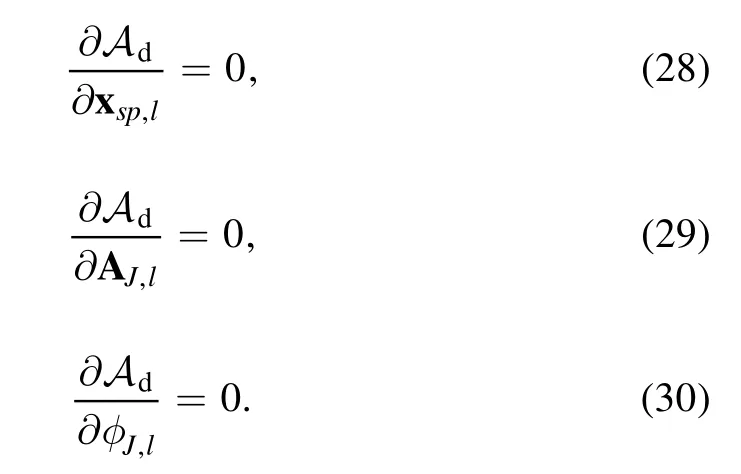
From equation (28), the variation with respect to xsp,lleads to

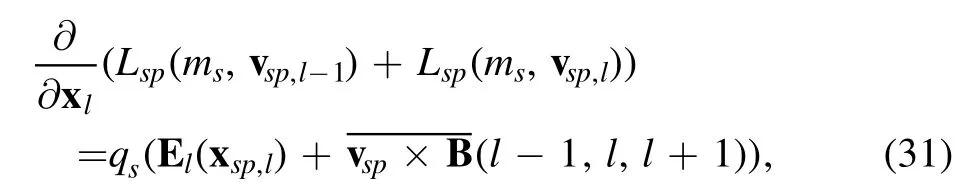
where

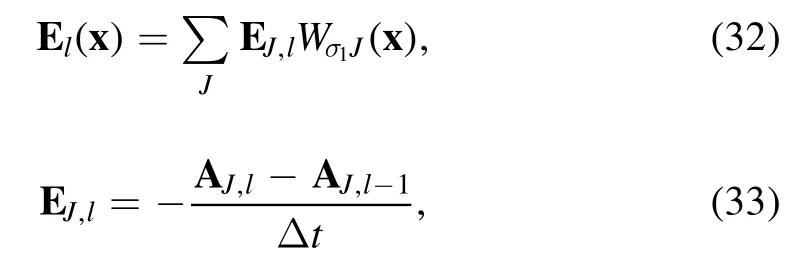
To reduce simulation noise,we use 2nd-order Whitney forms for field interpolation.The concept of 2nd-order Whitney forms and their constructions were systematically developed in [17].In general, only piece-wise polynomials are used to construct high-order Whitney forms, and it is straightforward to calculate integrals along particles’ trajectories.These integrals can be calculated explicitly even with more complex Whitney interpolating forms, because these interpolating forms contain derivatives that are easy to integrate.

From equation (29), the discrete Ampere?s law is

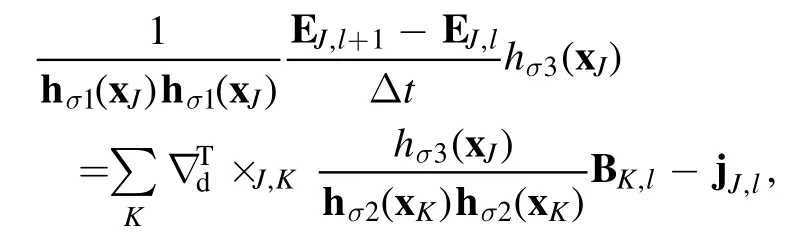
where

and the integral pathCsp,l,l+1is defined as a zigzag path from xsp,lto xsp,l+1, i.e.

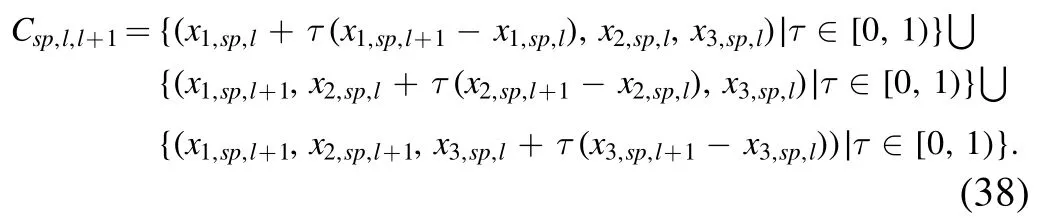
Using the definition of BK,l, i.e.equation (36), we can obtain its discrete time evolution,

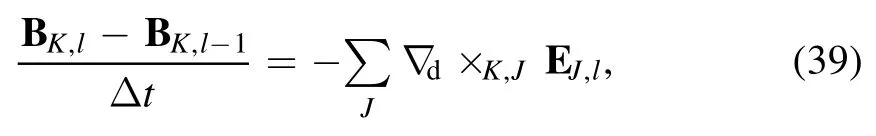
which is the discrete version of Faraday?s law.

Generally the above scheme is implicit.However, if particles are non-relativistic and the line element vector h of a curvilinear orthogonal coordinate system satisfies the following condition

then high-order explicit schemes exist in the COM constructed using this coordinate system.The cylindrical coordinate is such a case.In section 2.5 we derive the 2nd-order explicit scheme for the non-relativistic Vlasov–Maxwell system in the cylindrical mesh.

2.4.Poisson bracket and its splitting algorithm in a COM

For the structure-preserving geometric PIC algorithm presented in section 2.3, there exists a corresponding discrete Poisson bracket.When particles are non-relativistic and condition (40) is satisfied, an associate splitting algorithm,which is explicit and symplectic, can be constructed.The algorithm is similar to and generalizes the explicit noncanonical symplectic splitting algorithm in the Cartesian coordinate system designed in [19].Since the algorithm formulated in section 2.3 is independent from these constructions, we only list the results here without detailed derivations.

In a COM built on a curvilinear orthogonal coordinate system, we can choose to discretize the space only using the same method described above to obtain

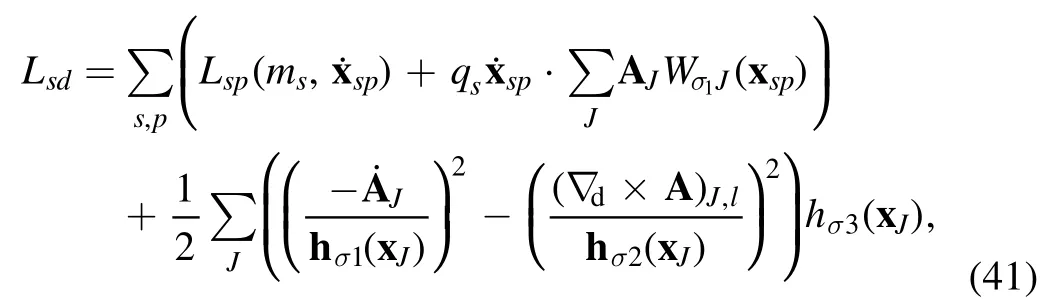
where the temporal gauge (φ=0) has been adopted.Following the procedure in[17], a non-canonical symplectic structure can be constructed from this Lagrangian, and the associated discrete Poisson bracket is

where( )vdiag means the diagonal matrix

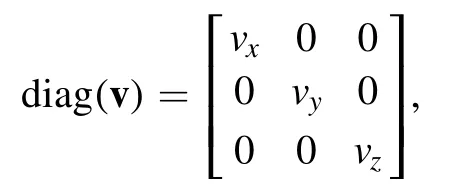
and the corresponding Hamiltonian is

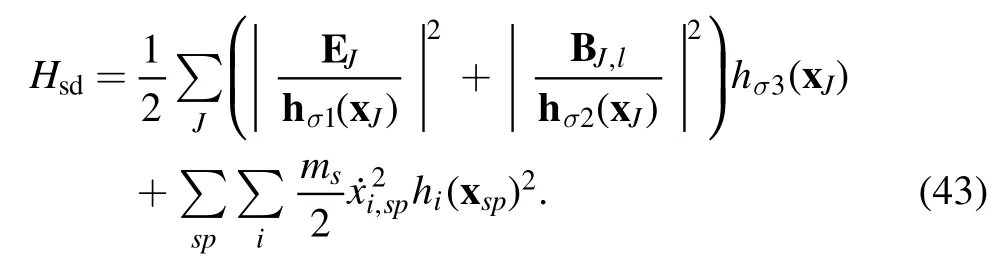
Here particles are assumed to be non-relativistic and EJ, BKare spatially discretized electromagnetic fields defined as

The Poisson bracket given by equation(42)generalizes the previous Cartesian version[17]to arbitrary COMs.It automatically satisfies the Jacobi identity because it is derived from a Lagrangian 1-form.See [17] for detailed geometric constructions.

The dynamics equation, i.e.the Hamiltonian equation, is

where

To build an explicit symplectic algorithm, we adopt the splitting method [19].The HamiltonianHsdis divided into 5 parts,

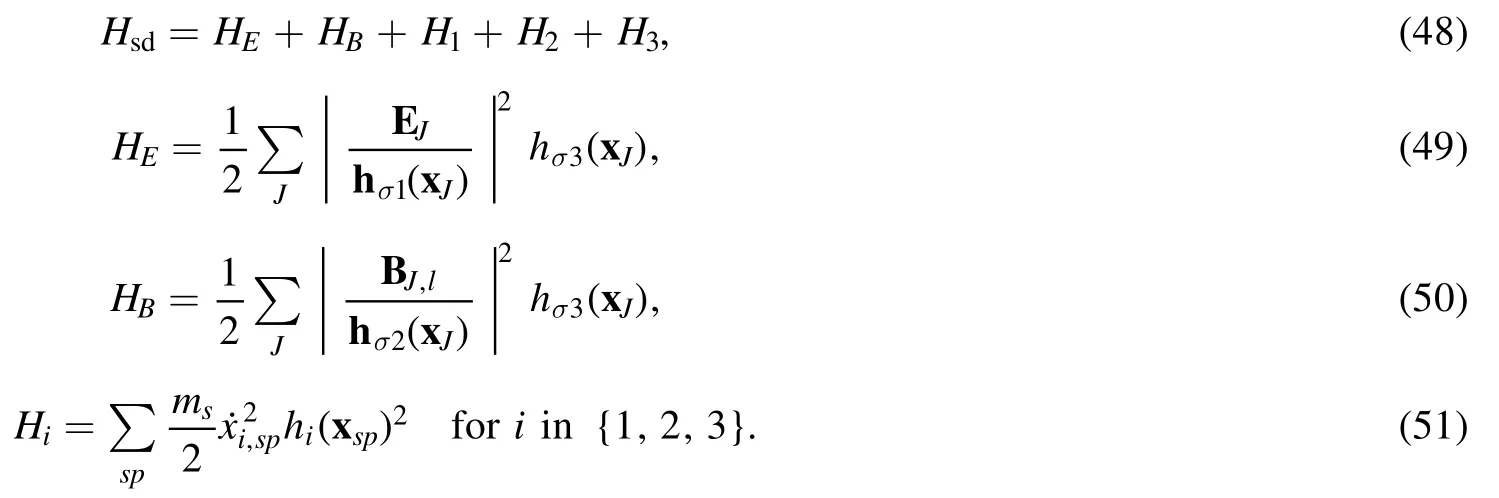
Each part defines a sub-system with the same Poisson bracket (42).It turns out that when condition(40)is satisfied the exact solution of each subsystem can be written down in a closed form,and explicit high-order symplectic algorithms for the entire system can be constructed by compositions using the exact solutions of the sub-systems.ForHEandHB, the corresponding Hamiltonian equations are

i.e.

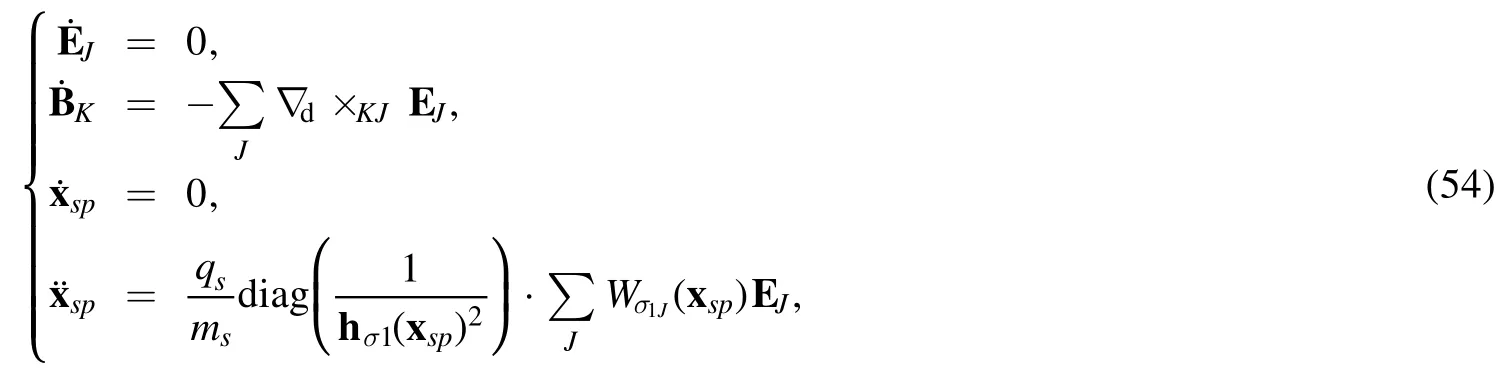
and

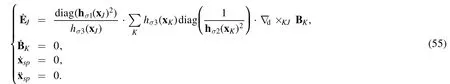
Their analytical solutions are

ForH1, the dynamic equation isor more specifically,

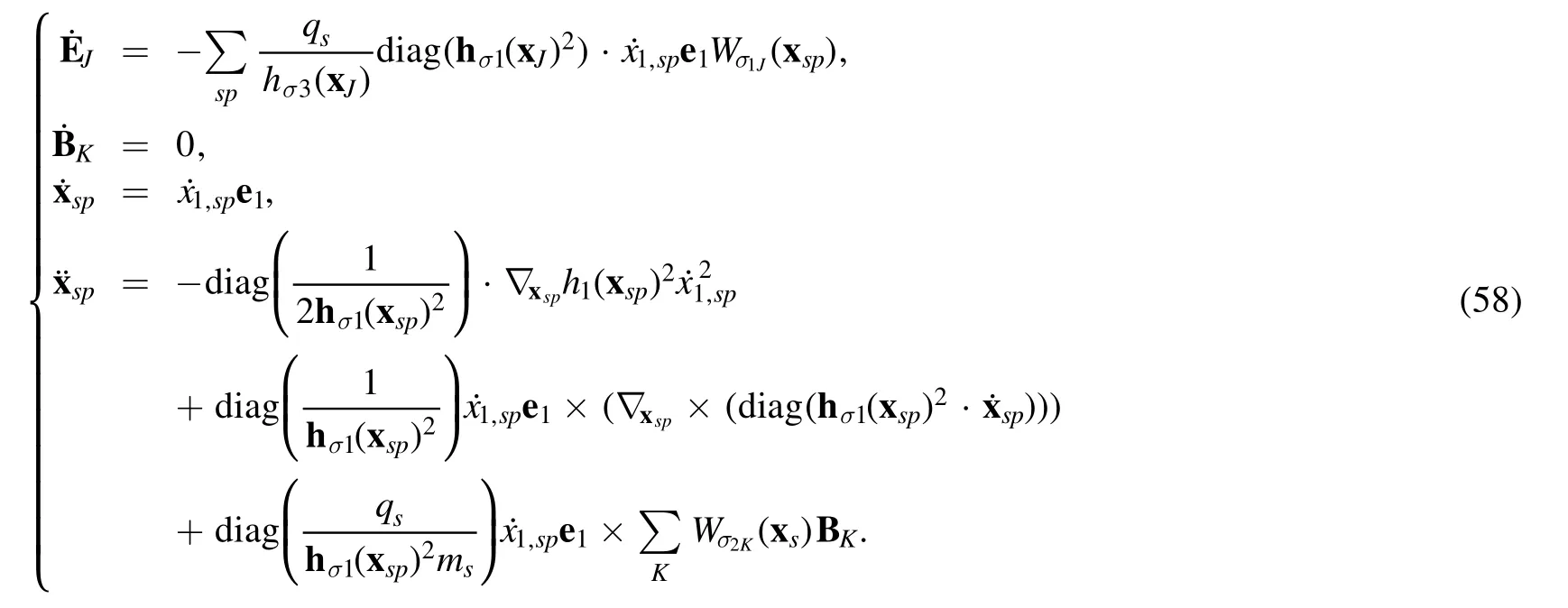
Because the equation forx1,spcontains bothexplicitly, equation (58) is difficult to solve in general.However,when ?h1(x)?x1=0, i.e.

the dynamics equation for particles in equation (58) reduces to

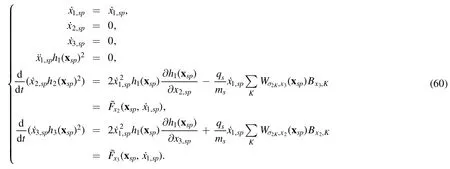
In this case, equation (58) admits an analytical solution,

Similarly,analytical solutions Θ2(Θ3)forH2(H3)can be also derived whenFinally,we can compose these analytical solutions to obtain explicit symplectic integration algorithms for the entire system.For example, a first order scheme can be constructed as

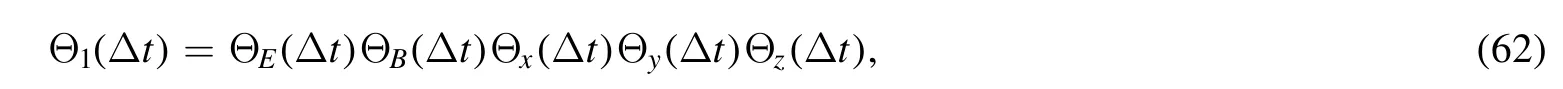
and a 2nd-order symmetric scheme is

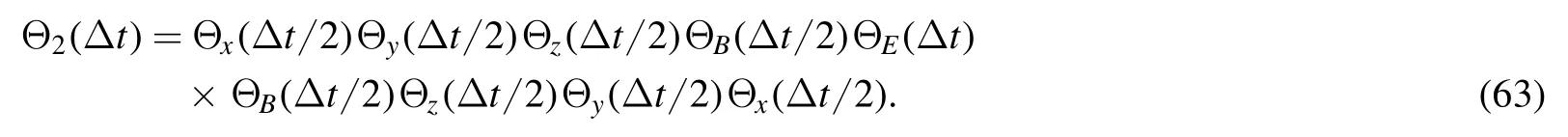
An algorithm with order 2(l+1) can be constructed in the following way,

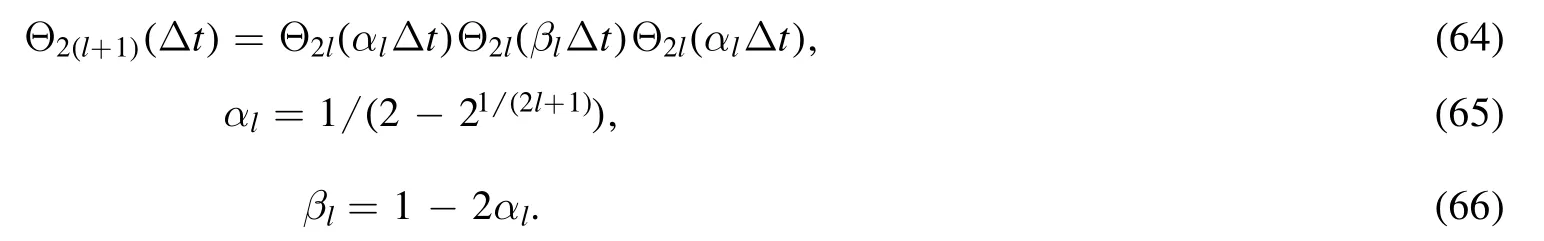
2.5.High-order explicit structure-preserving geometric PIC algorithm in a cylindrical mesh

Magnetic fusion plasmas are often confined in the toroidal geometry,for which the cylindrical coordinate system is convenient.We now present the high-order explicit structure-preserving geometric PIC algorithm in a cylindrical mesh.In this coordinate system, the line element is

whereR0is a fixed radial length,r+R0is the radius in the standard cylindrical coordinate system,andR0ξ is the polar angle coordinate normalized by 1/R0.For typical applications in tokamak physics,R0is the major radius and ξ is called toroidal angle.To simplify the notation, we also refer to (r,R0ξ,z) as (x,y,z).

For non-relativistic particles in the cylindrical mesh, if the discrete velocity in equation (22) is changed to

then the 1st-order scheme given by equation (28) will be explicit.To construct an explicit 2nd-order scheme, the 2nd-order action integral can be chosen as

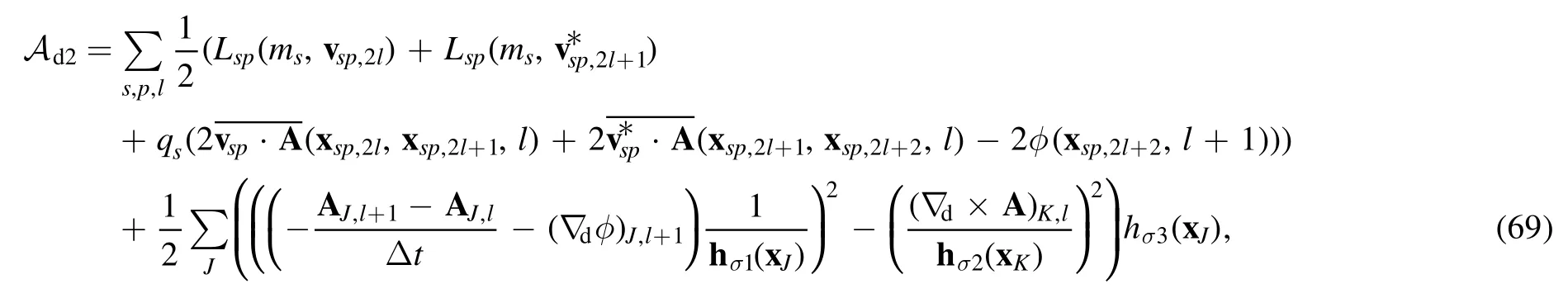
where

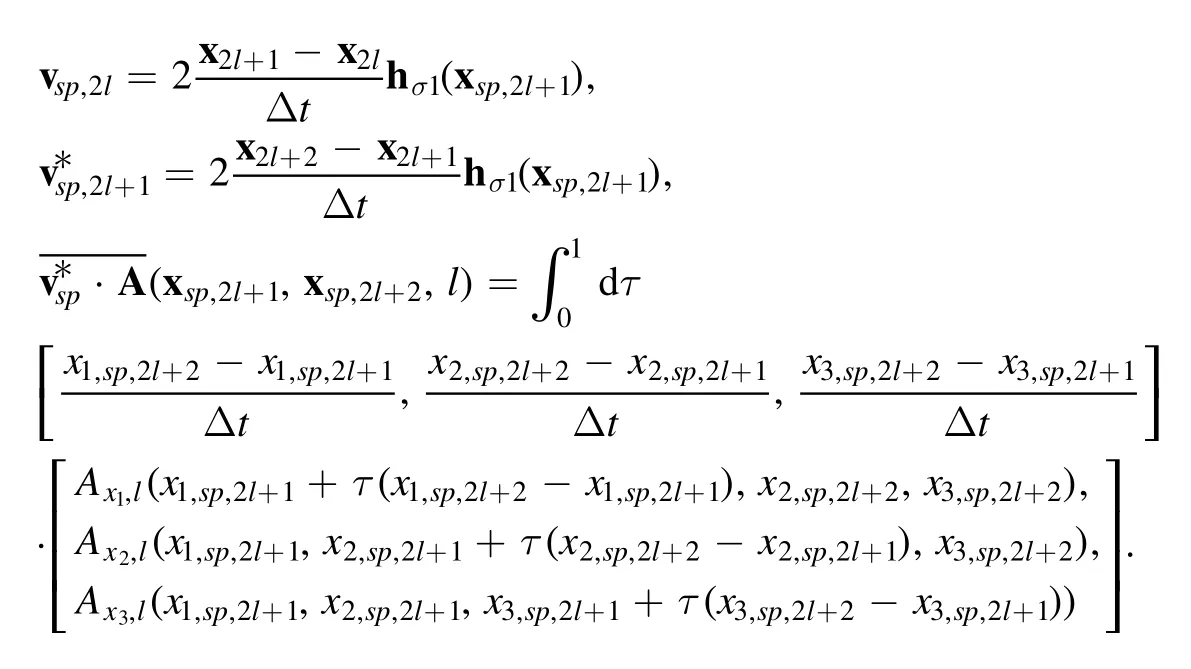
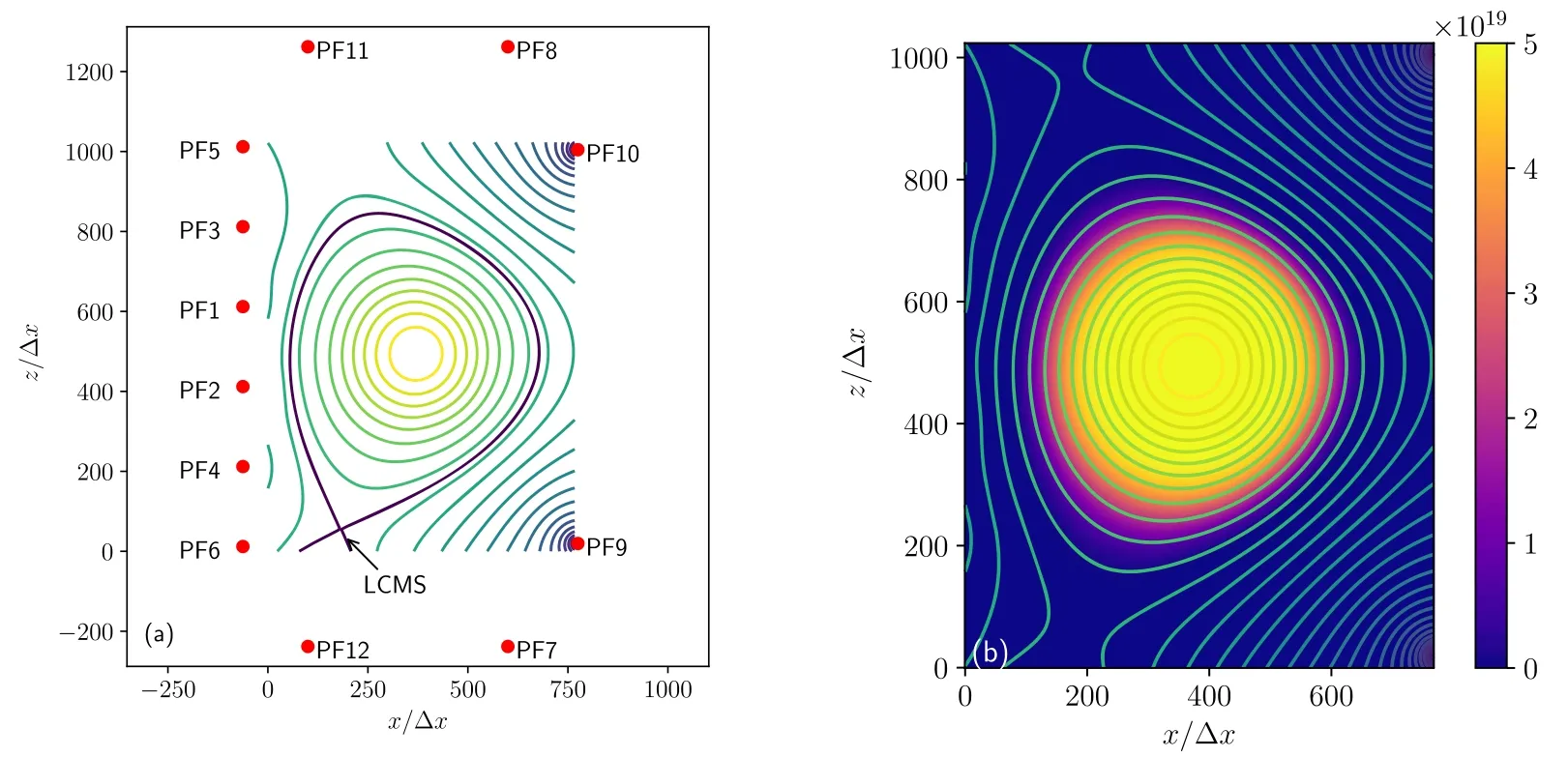
Figure 1.Poloidal field locations (a) and initial density profile for electrons (b).

Table 1.Machine parameters of the simulated tokamak.This set of parameters is similar to those of the Alcator C-Mod tokamak.

Taking the following discrete variation yields discrete timeadvance rules,

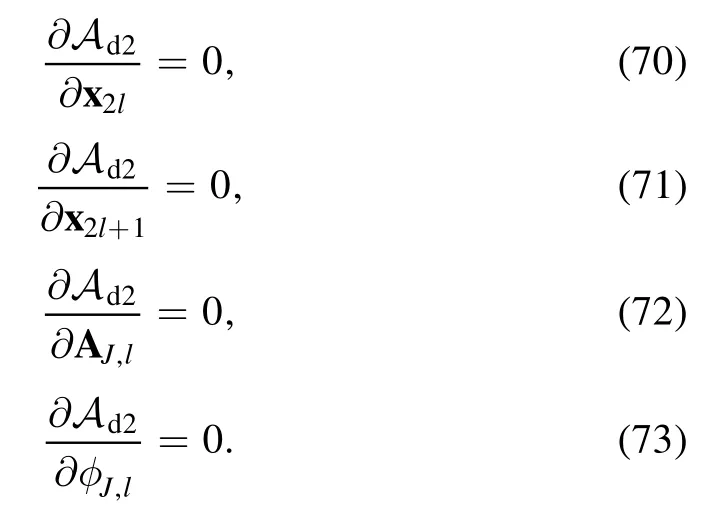
The explicit expressions for these time-advance are listed in appendix B.Higher-order discrete action integral for building explicit schemes can be also derived using a similar technique, or using the splitting method described in section 2.4.

In addition, we have also implemented the 1st-order relativistic charge-conserving geometric PIC in the cylindrical mesh.However the particle pusher in the relativistic scheme is implicit, and it is about 4 times slower than the explicit scheme.When studying relativistic effects, the implicit relativistic algorithm can be applied without significantly increasing the computational cost.

3.Whole-device 6D kinetic simulations of tokamak physics

The high-order explicit structure-preserving geometric PIC algorithm in a cylindrical mesh described in section 2.5 has been implemented in the SymPIC code, designed for high-efficiency massively-parallel PIC simulations in modern clusters.The OpenMP-MPI version of SymPIC is available at https://github.com/JianyuanXiao/SymPIC/.The algorithm and code have been used to carry out the first-ever whole-device 6D kinetic simulations of tokamak physics.In this section, we report simulation results using machine parameters similar to those of the Alcator C-Mod tokamak [49, 50].Two physics problems are studied,the self-consistent kinetic steady state and KBM instabilities in the self-consistent kinetic steady state.

3.1.Axisymmetric self-consistent kinetic steady state in a tokamak

Kinetic equilibrium is the starting point for analytical and numerical studies of kinetic instabilities and associated transport phenomena.Because no self-consistent kinetic equilibrium is known in the tokamak geometry,most previous studies adopted non-self-consistent distributions as assumed kinetic equilibria, especially for simulations based on the δfmethod.Here, we numerically obtain an axisymmetric selfconsistent kinetic steady state for a small tokamak using parameters similar to those of the Alcator C-Mod tokamak[49,50].The machine parameters are tabulated in table 1.The device is numerically constructed with poloidal field (PF)coils displayed in figure 1(a).

At the beginning of the simulation, non-equilibrium distributions for deuterium ions and electrons are loaded into the device.The initial density profile in the poloidal plane is shown in figure 1(b).The 2D profiles of the external field and initial velocity and temperature profiles for both species are plotted in figure 2.Simulation parameters are chosen as

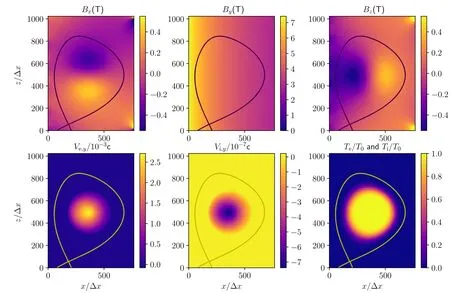
Figure 2.Tokamak external magnetic field and initial profiles of flow velocities in the ey direction and temperatures.

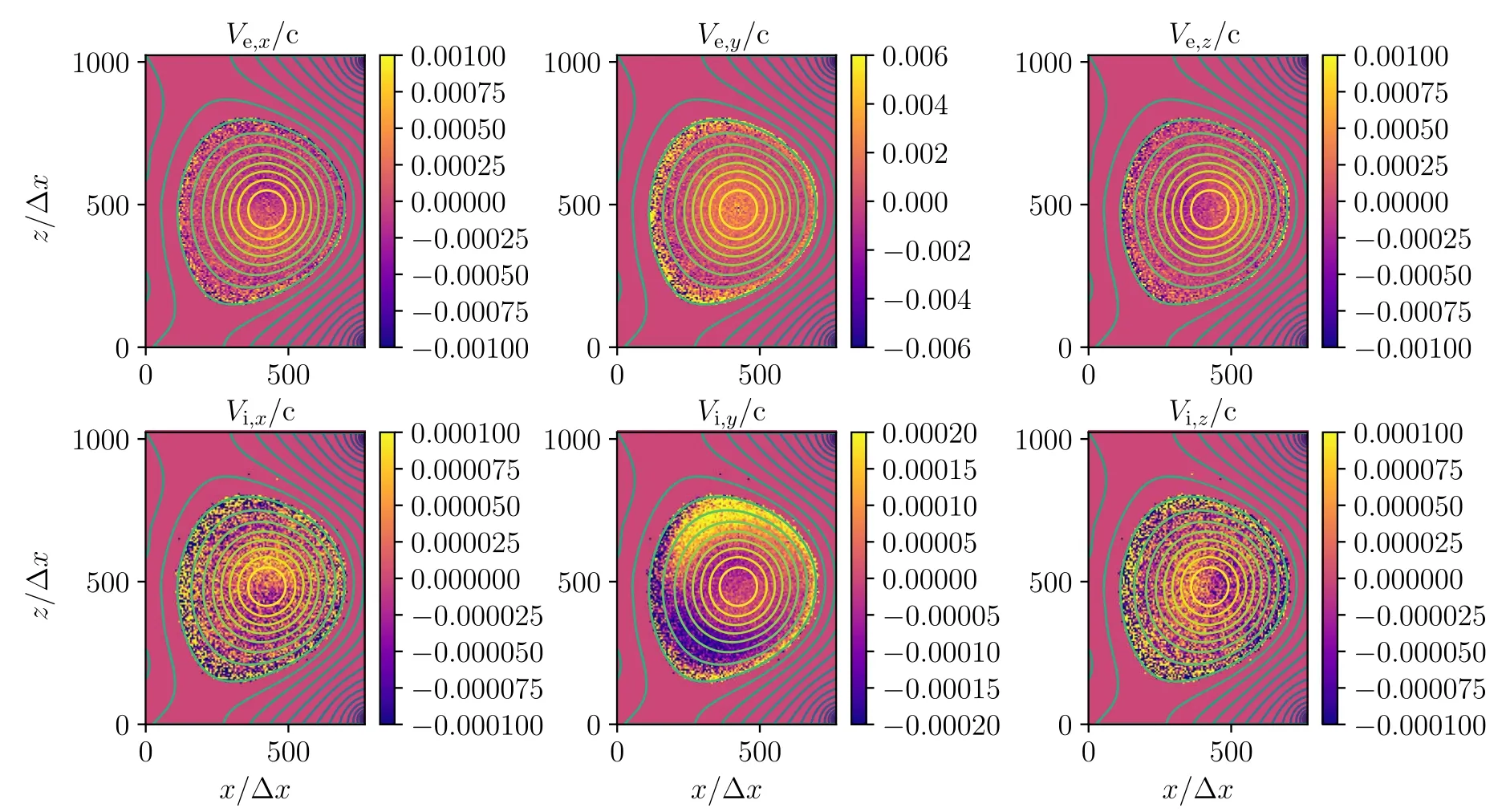
Figure 3.Flow velocity distributions for electrons and ions at the steady state.

Detailed calculation of the external magnetic field, initial particle distributions, and boundary setup are outlined in appendix A.Simulations show that the system reaches a steady state after 1.6×107time-steps.At this time, the amplitude of magnetic perturbation at the middle plane of the edge(x=0.48 m andz=0.41 m)is smaller thanB0/200,and the oscillation of position of plasma core is very small.Therefore, we can treat this state as a steady state.One such calculation requires about 1.3×105core-hours on the Tianhe 3 prototype cluster.Profiles of flow velocities, densities,temperatures of electrons and ions as well as electromagnetic field at the steady state are shown in figures 3–6.

Figure 4.Density and temperature profiles of electrons and ions at the steady state.

From figure 3,the flow velocity of ions at the steady state is in the range of 10 km s?1, which is consistent with experimental observations [51, 52] and theoretical calculations[53, 54].This ion flow is much slower than the thermal velocity of ions and thus is negligible in the force balance for the steady state, which can be written as

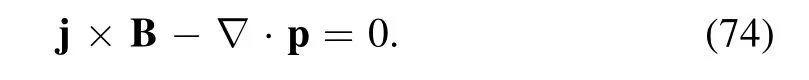
Here, p is the pressure tensor.Equation (74) is obtained by the familiar procedure of taking the second moment of the Vlasov equation, subtracting the flow velocity and summing over species.From the simulation data, thepijcomponent of the pressure tensor is calculated as

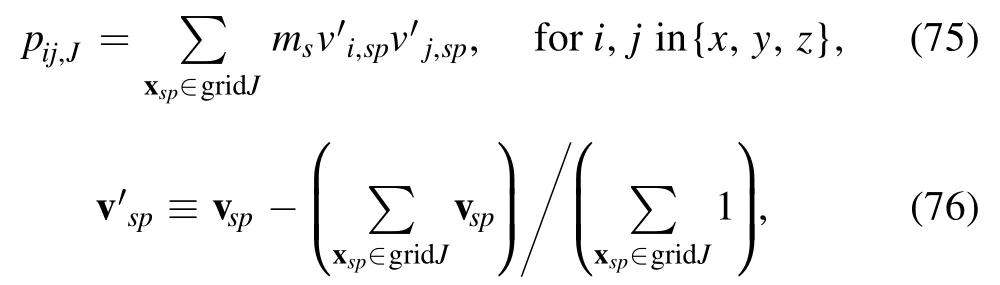
To verify the force balance of the steady state,the four terms in equations(77) and (78) are plotted in figure 8.For comparison, the components of ?pyy/?xand ?pyy/?zare also plotted.Figure 8 shows that the force balance is approximately satisfied for the numerically obtained steady state,which can be viewed as a self-consistent kinetic steady state.

Figure 5.Electromagnetic field profiles at the steady state.

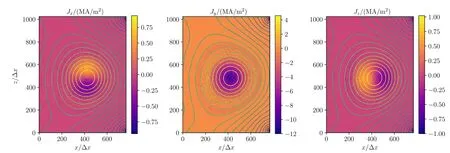
Figure 6.Current profiles at the steady state.

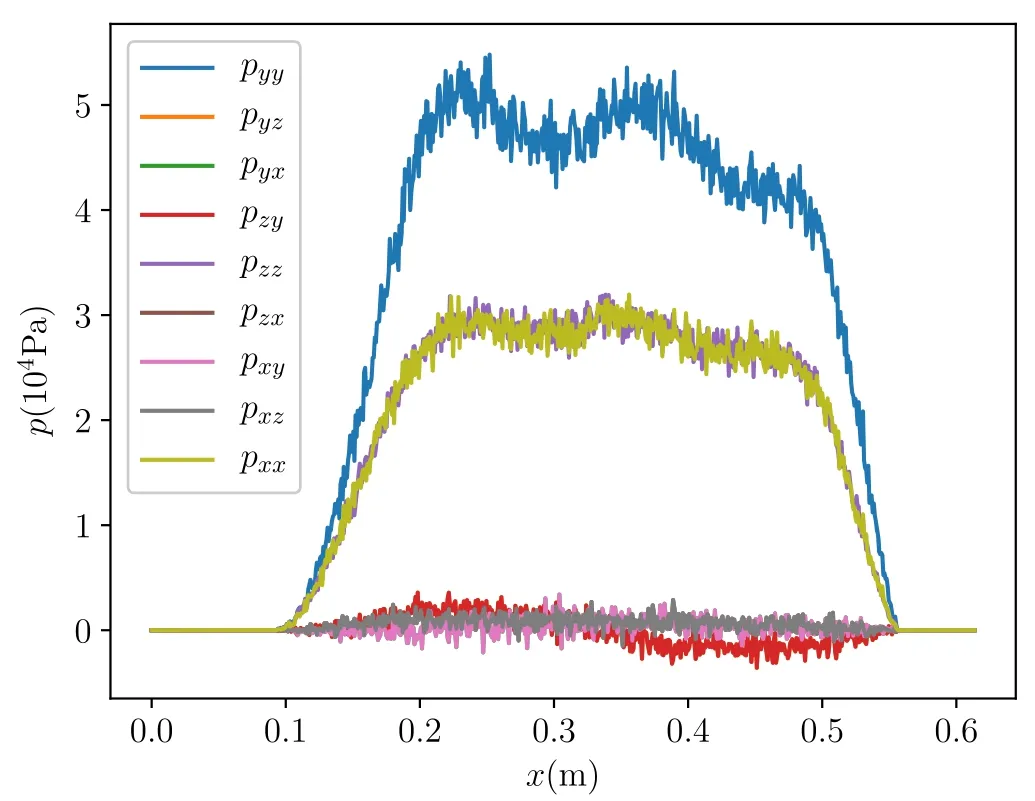
Figure 7.Pressure tensor profile at z=0.41 m.

To verify the energy conservation in the simulation, we have recorded the time-history of the total energy in figure 9.The total energy drops a little,because some particles outside the last closed magnetic surface hit the simulation boundary,and these particles are removed from the simulation.

Before reaching the kinetic steady state, the plasma oscillates in the poloidal plane.It is expected that this oscillation can be described as an MHD process whose characteristic velocity is the Alfvn velocityTo observe this oscillation, we plot in figure 10 the evolution of the magnetic field atx=600Δxandz=512Δx.From the parameters of the simulation, the characteristic frequency of the oscillation is

which agrees with the frequency of theBxoscillation in figure 10.

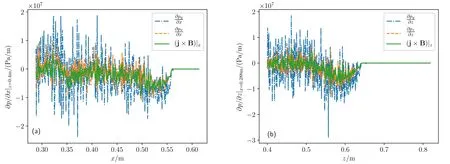
Figure 8.Pressure gradient ?·p and Lorentz force j×B in the ex (a) and ez (b) directions.

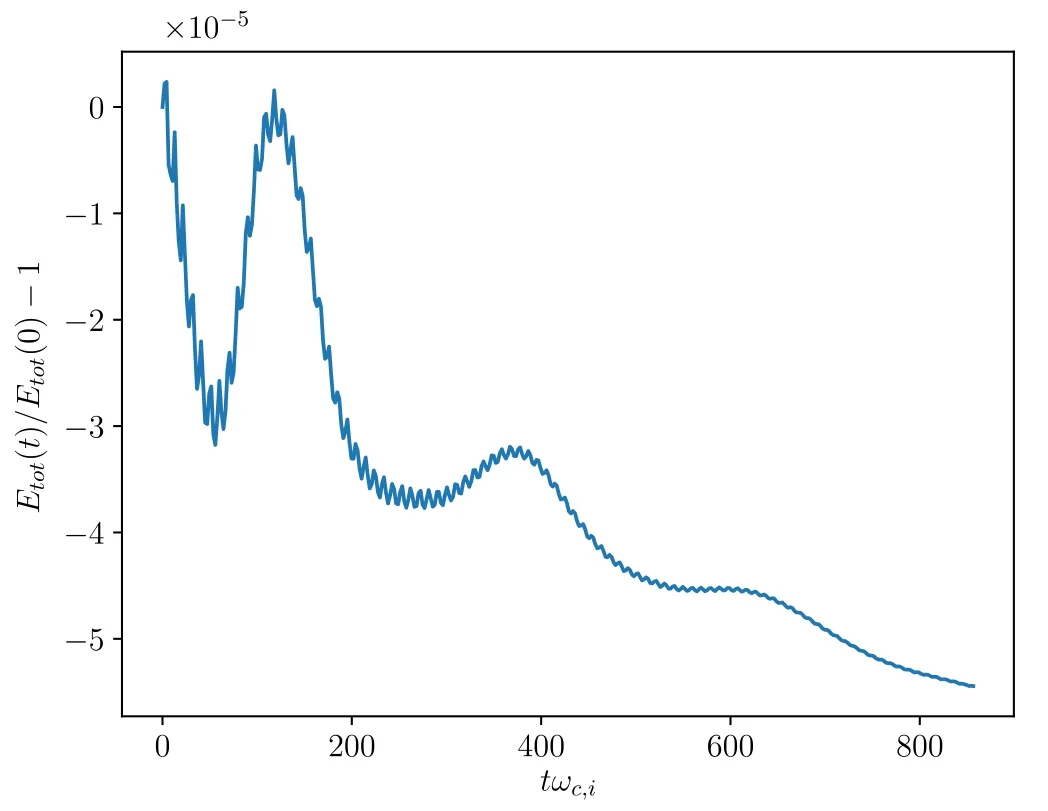
Figure 9.Evolution of total energy.

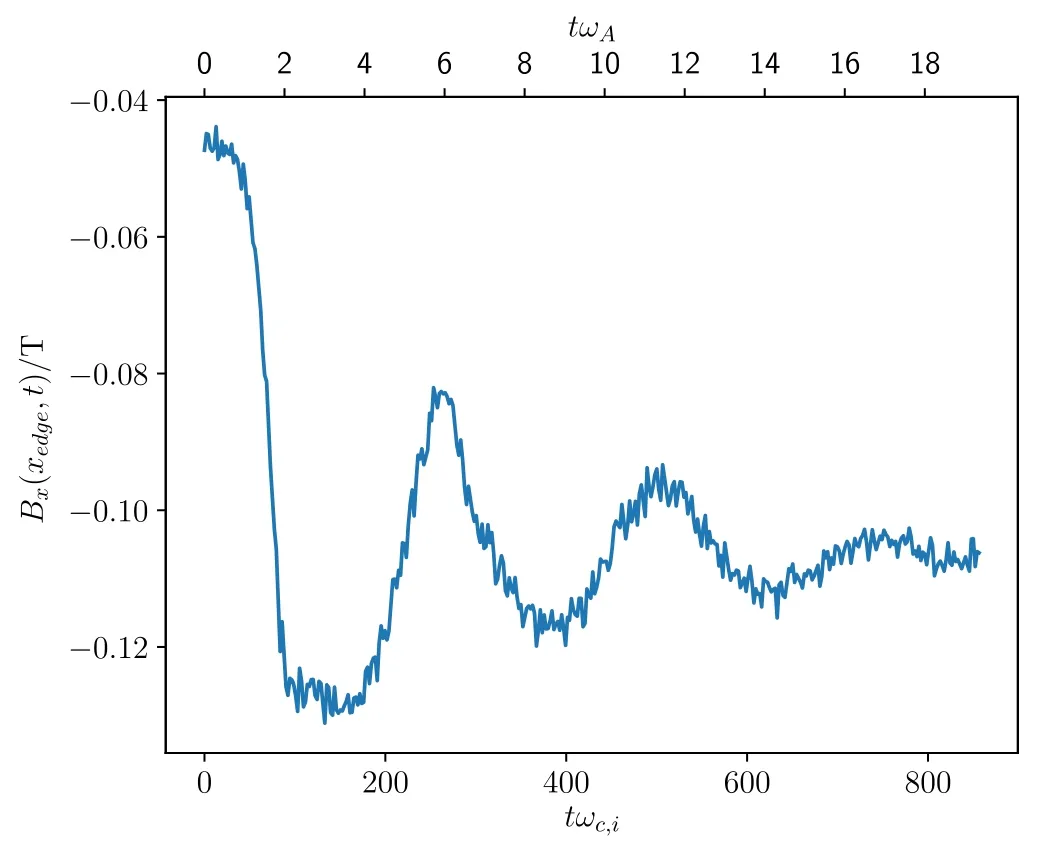
Figure 10.Evolution of Bx(600Δx, 0, 512Δx).

3.2.KBM in tokamak

KBM [119], characterized by both electromagnetic perturbations of the MHD type and nontrivial kinetic effects, plays an important role in tokamak edge physics.Traditionally, it has been simulated using electromagnetic gyrokinetic codes such as the Kin-2DEM[55,56],LIGKA[120],GTC[37,57]and GEM [42].However, for edge plasmas, the gyrokinetic ordering [56, 121–124] may become invalid under certain parameter regimes for modern tokamaks.For instance, the characteristic length in the edge of the H-mode plasma simulated by Wanet al[133,134]can be as short as about 5 times of the gyroradius of thermal ions, and in this situation,the gyrokinetic density calculation may be inaccurate.We have applied SymPIC code developed to carry out the first whole-device 6D kinetic simulations of the KBM in a tokamak geometry.

The machine parameters are the same as in section 3.1.To trigger the KBM instability, we increase the plasma density ton0=1×1020m?3, and the rest of parameters are

Herermis the mass ratio between the deuterium and electron,cnis the speed of light in the simulation andrcis the ratio betweencnand the real speed of light in the vacuumc.For real plasmas,rm≈3672 andrc=1.Limited by available computation power, we reducermandrcin some of the simulations.Such an approximation is valid because the low frequency ion motion is relatively independent from the mass of electron and the speed of light, as long asrm?1 andIn the present work, we takerm=100 andrc=0.16 to obtain long-term simulation results.Short-term results forrm=300,rc=0.5 andrm=3672,rc=1 (in this case Δt=0.1Δx/c) are also obtained for comparison.The simulation domain is a 192×64×256 mesh, where perfect electric conductor is assumed at the boundaries in thex- andz-directions, and the periodic boundary is selected inydirection.

Figure 11.Profiles of the kinetic steady state at z=0.41 m.

Because of the steep pressure gradient in the edge of the plasma, the threshold βcritfor ballooning mode instability is low.An estimated scaling for βcritis [135]

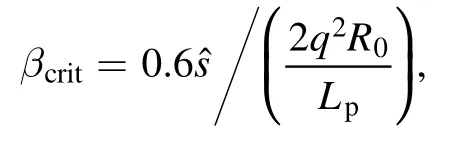
To obtain a self-consistent kinetic steady state, we first perform a simulation as described in section 3.1 and obtain the 2D kinetic steady state.The profiles of temperature,safety factor, number density, pressure, toroidal current and bulk velocity of this steady state atz=0.41 m are shown in figure 11.

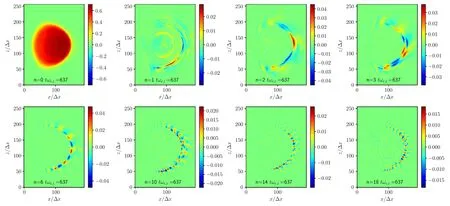
Figure 12.Mode structures of the electron density at t=637/ωc,i=2.85a/vt,i.

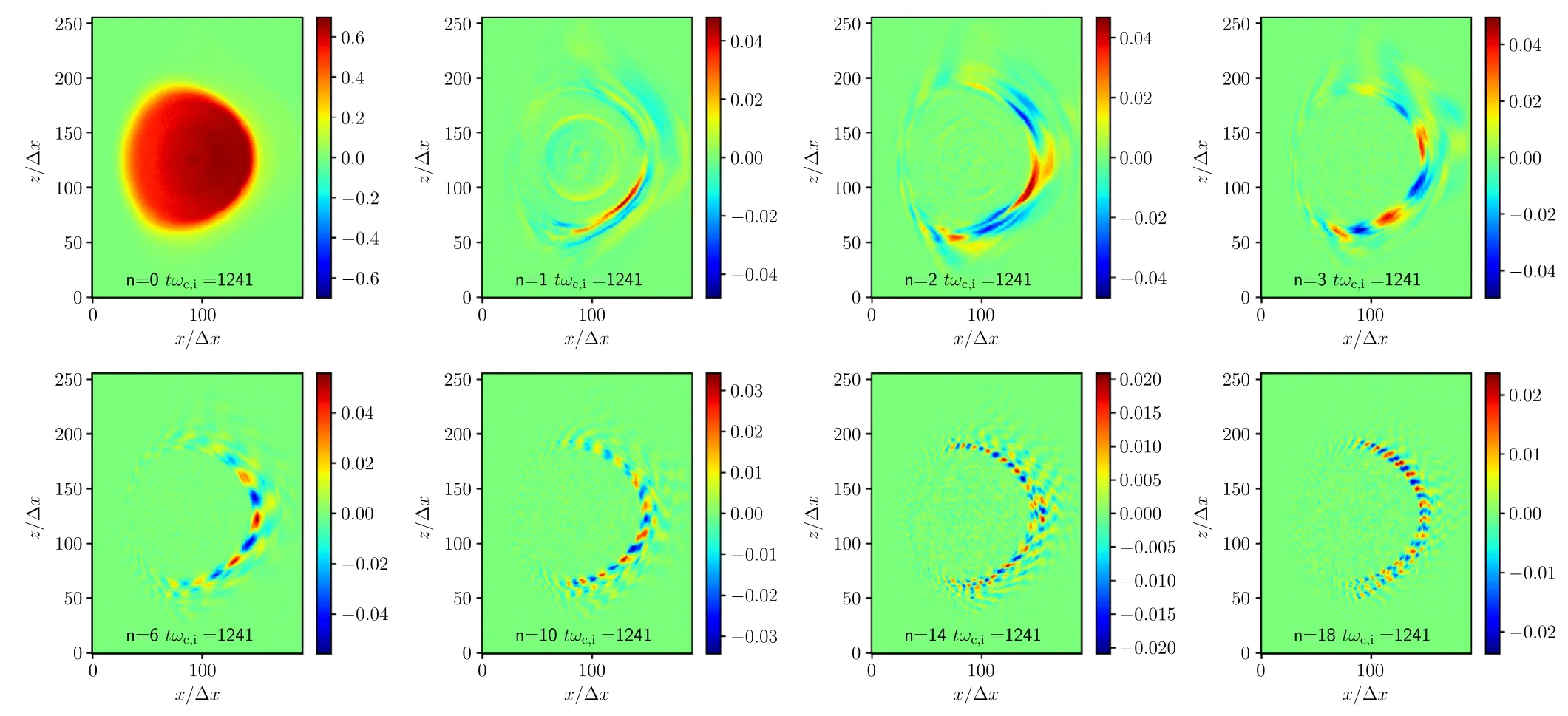
Figure 13.Mode structures of the electron density at t=1241/ωc,i=5.55a/vt,i.

A random perturbation is then added in as the initial condition of the 6D simulation.The total simulation time isFor one such simulation it takes about 3×105core-hours on the Tianhe 3 prototype cluster.The resulting mode structures of ion density for toroidal mode numbern=1,2,3,6,10,14,18 are shown in figures 12, 13 and 14 fortωc,i=637, 1241 and 9693.It is clear that the unstable modes are triggered at the edge of the plasma, and the ballooning structure can be observed for modes with largen.The growth rate as a function ofnis plotted in figure 15.For comparison, the grow rate obtained usingrc=0.5,rm=300 andrc=1,rm=3672 are also plotted.It is clear that the growth rate has little correlation with the reduction ofrcandrm.Figure 15 shows that the growth rate increases withn, consistent with the early gyrokinetic simulation results obtained using the Kin-2DEM eigenvalue code[55,56].Because the number of grids in the toroidal direction is 64 and the width of interpolating function is 4 times the grid size,the results for modes withn＞16 may not be accurate.The results displayed here are thus preliminary.In the next step, we plan to perform a larger scale simulation with more realistic 2D equilibria to obtain improved accuracy.

The time-history of the mode amplitude is shown in figure 16.The unstable mode saturates approximately att≈5a/vt,i, and the saturation level is in the range of 2%.Recent nonlinear gyrokinetic simulation [57] suggested that the instability is saturated by theE×Bzonal flow generated by the instability.To verify this mechanism in our 6D fully kinetic simulation, the toroidally averaged E,E×Bvelocity and the measured phase velocity of then=12 mode atz=128Δxandt=8a/vt,iare compared in figure 17.TheE×Bvelocity at the edge correlates strongly with the phase velocity of the perturbation in terms of amplitude and profile.As a result, theE×Bflow for the background plasma generated by instability interacts coherently with the mode structure, significantly modifies the space-time structure of the perturbation relative to the background plasma and reduces the drive of the instability.For this case simulated,the nonlinear saturation mechanism agrees qualitatively with the nonlinear gyrokinetic simulation [57].

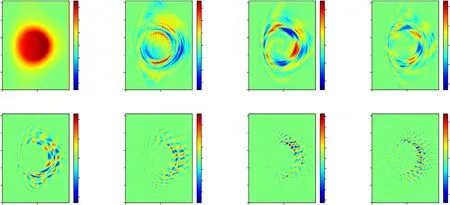
Figure 14.Mode structure of the electron density at t=9693/ωc,i=43.35a/vt,i.

Figure 15.Growth rate as a function of toroidal mode number for different values of rc and rm.

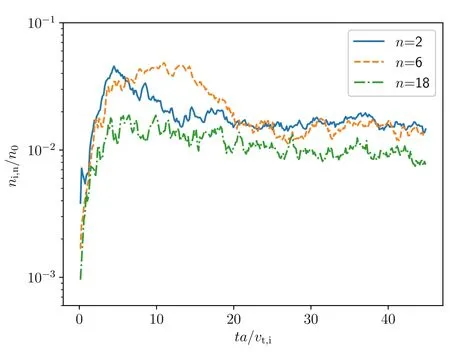
Figure 16.Time-history of ion densities for different toroidal mode number n.

4.Conclusions

Even though 6D kinetic PIC method is a classical simulation tool for plasma physics, up to now it has not been applied to numerical studies of tokamak physics in spite of continuous improvement [27–30, 33–35, 136–160].In the present study,we have developed an explicit structure-preserving geometric PIC algorithm in COMs, in particular the cylindrical mesh,and apply it to carry out whole-device 6D kinetic simulation studies of tokamak physics.The work reported represents a further development of the structure-preserving geometric PIC algorithm [15–25], achieving the goal of practical applications in magnetic fusion research.

Along with its predecessors[15–25],the algorithm extends the symplectic integration method for finite dimensional canonical Hamiltonian systems developed since the 1980s [43–47,79–98], and preserves an infinite dimensional non-canonical symplectic structure of the particle-field systems.In addition,other important geometric structures and conservation laws,such as the gauge symmetry,the local charge conservation law[15, 24, 115] and the local energy conservation law [23], are preserved exactly as well.These preserved structures and conservation laws improve the accuracy and fidelity of large-scale long-term simulations on modern computing hardware [14].

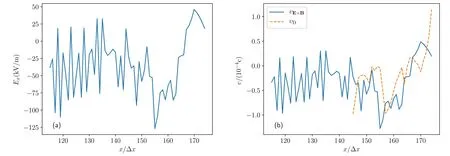
Figure 17.The toroidal averaged electric field in ex direction (a).The E×B velocity vE×B and measured phase velocity vD for the n=12 mode in the ez direction at z=128Δx and t=8a/vt,i (b).

Through the whole-device 6D kinetic simulation, we numerically obtained a self-consistent kinetic steady state for fusion plasma in the tokamak geometry.It was found that the pressure tensor of the self-consistent kinetic steady state is diagonal, anisotropic in 3D, but isotropic in the poloidal plane.The steady state also includes a steady-state sub-sonic ion flow in the range of 10 km s?1, which agrees with previous experimental observations [51, 52] and theoretical calculations[53,54].Kinetic ballooning instability in the selfconsistent kinetic steady state was successfully simulated.In the linear phase, it was found that high-nballooning modes have larger growth rates than low-nglobal modes.In the nonlinear phase, the modes saturate approximately in 5 ion transit times at the 2% level by theE×Bflow generated by the instability.These results qualitatively agrees with early[55, 56] and recent [57] simulations by electromagnetic gyrokinetic codes.In addition, compared with conventional gyrokinetic and reduced Braginskii [161–163] fluid simulation methods, more physical effects, such as fully kinetic dynamics and the self-consistent radial electric field, are naturally included in the present method.These effects can be crucial for edge plasmas and will be investigated in the next step.

It worth mentioning that in the present work we can not directly control the 2D kinetic steady state because it is numerically evolved from a given initial condition.In the future, we plan to solve this problem by adopting MHD equilibrium solutions as the initial conditions.Because a MHD equilibrium should be at least close to a lowest order kinetic steady state, it is expected that a kinetic steady state can be obtained by a short time evolution.

The present work can be also extended to describe more complex physical processes in tokamak plasmas.For example, we can add energetic particles to investigate their interactions with the background plasma.An antenna can be also modeled as a current source to study the wave heating and current drive [33].To simulate collision related physics, we can include Monte-Carlo Collision [164] processes.It should be noted that due to the lack of marker particles in PIC simulations, the numerical collision frequency is usually larger than the real collision frequency of the plasma.More investigations are needed to determine the proper method to simulate collisions in the present scheme.Adding more physical effects to the geometric structure preserving PIC simulation framework will help us to better understand the tokamak physics.These topics will be addressed in the future study.

Acknowledgments

J Xiao was supported by the the National MCF Energy R&D Program (No.2018YFE0304100), National Key Research and Development Program(Nos.2016YFA0400600,2016YFA0400 601 and 2016YFA0400602), and National Natural Science Foundation of China (Nos.11905220 and 11805273).J Xiao developed the algorithm and the SymPIC code and carried out the simulation on Tianhe 3 prototype at the National Supercomputer Center in Tianjin and Sunway Taihulight in the National Supercomputer Center in Wuxi.H Qin was supported by the U.S.Department of Energy (DE-AC02-09CH11466).H Qin contributed to the physical study of the self-consistent kinetic equilibrium and the KBMs.

Appendix A.External magnetic field of the tokamak,initial particle loading, and the boundary setup

In this appendix we describe the setup of external magnetic field of the tokamak,initial particle loading,and the boundary setup for the simulation study.The normalization of quantities are listed in table A1.

The magnetic field is divided into three parts,

where B0,eis the external magnetic fields generated by poloidal coils, B0,tis the magnetic field generated by toloidal coils, i.e.

and they do not evolve with time.B0,pis the magnetic field generated by the plasma current.The current j and the vector potential A are related by

Initially,the current is in they-direction and depends only onxandz.In the adopted cylindrical coordinate(x,y,z)the lineelement is

Table A1.Normalization for quantities.

Table A2.Locations of tokamak poloidal field coils.

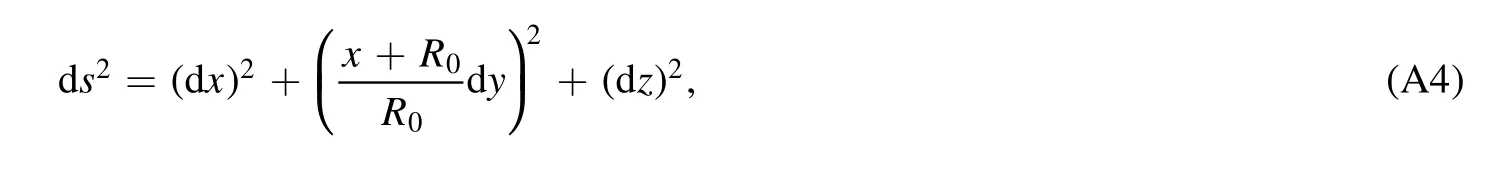
and equation (A3) becomes

where

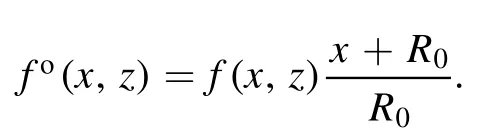
which is a standard 2D Poisson equation.Its solution for the coil current at (x0,z0) withI0=1 is

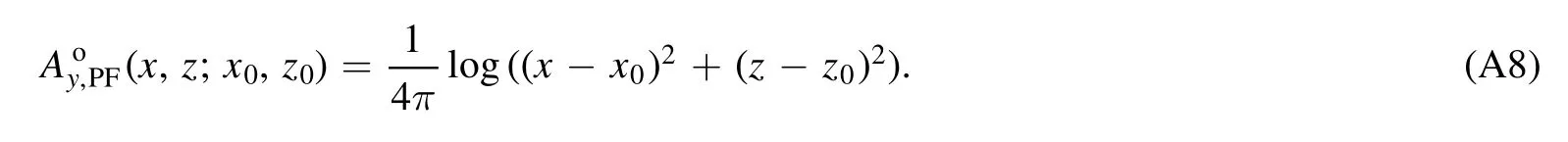
Here,dimensionless variables have been used to simplify the notation.The total external vector potential generated by poloidal field coils is

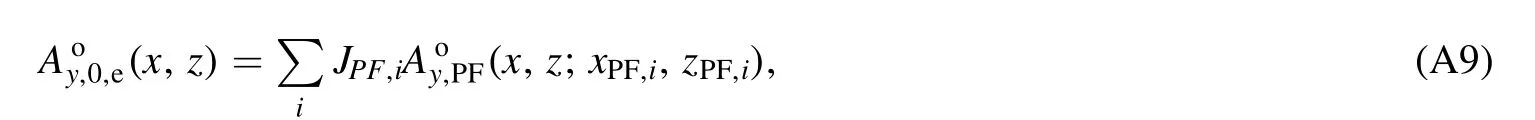
where the locations of poloidal field coils are displayed in table A2.

For B0,pand the corresponding plasma current j0,we first construct a vector potential Ay,0,pand then use this potential to obtain B0,pand j0.The constructedAy,0,pis

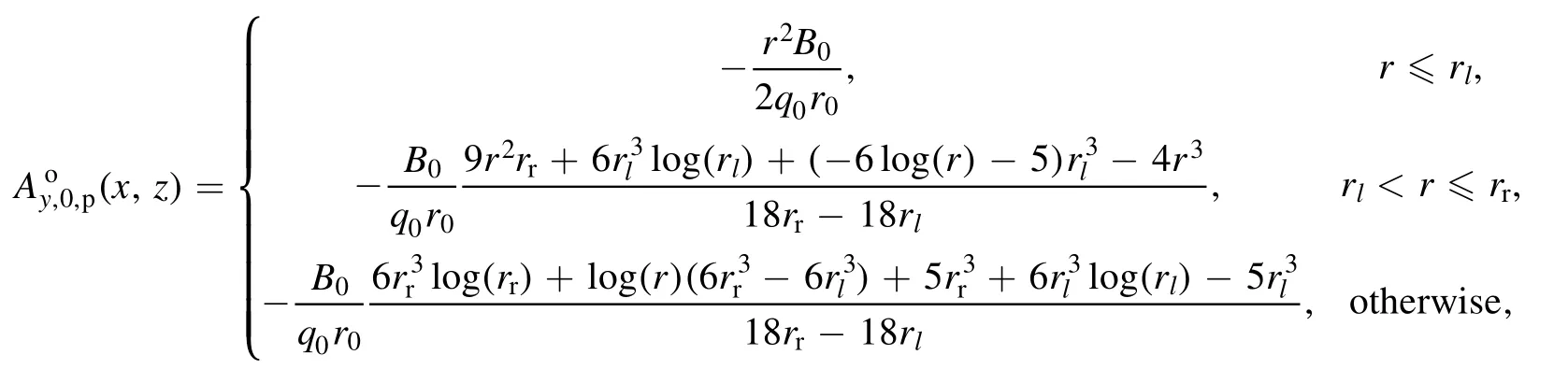
and the discrete current density is obtained from

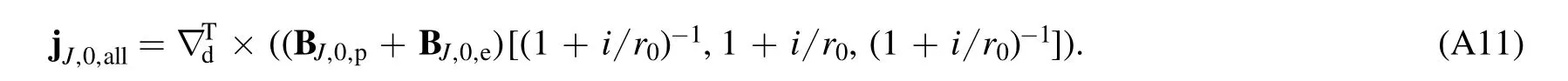
The final plasma current is chosen as

Density and temperature are calculated fromWe introduce a reference functiongrdefined as

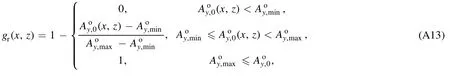
where

The initial density and temperature for electrons and ions are

In this work,ions are all deuterium ions,and the initial velocity distribution for each specie is Maxwellian with a flow velocity,i.e.

where

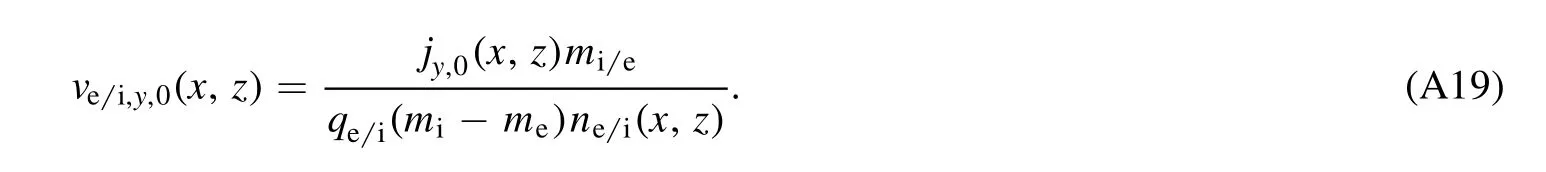
The boundaries of the simulations are configured as follows.The boundaries atx=0,x=NxΔx,z=0,andz=NzΔzare chosen to be perfect electric conductors for the electromagnetic fields.For particles, we introduce a thin slow-down layer,

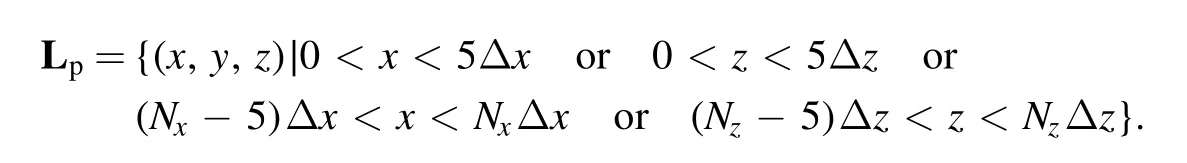
If a particle is inside Lpat a time-step,its velocity vpwill be reduced to 0.98vpat the end of this time-step,and the particle will be removed when vpis smaller than 1×10?5c.Periodic boundaries for both particles and electromagnetic fields are adopted in they-direction.The plasma is confined inside the last closed flux surface mostly,and the shape of plasma is not directly related to the simulation boundaries.

Appendix B.Explicit 2nd-order structure-preserving geometric PIC algorithm in the cylindrical mesh

In this appendix, we list the detailed update rule for the 2nd-order structure-preserving geometric PIC algorithm in the cylindrical mesh introduced in section 2.5.It updates previous particle locations and discrete electromagnetic fields {xsp,2l?2,xsp,2l?1, EJ,l, BK,l} to the current ones {xsp,2l, xsp,2l+1, EJ,l+1, BK,l+1},

where