A path integral approach to electronic friction of a nanometer-sized tip scanning a metal surface

Yang Wangand Yu Jia

1 School of Physics,Zhengzhou University,Zhengzhou 450001,China

2 International Laboratory for Quantum Functional Materials of Henan,and School of Physics and Microelectronics,Zhengzhou University,Zhengzhou 450001,China

3Key Laboratory for Special Functional Materials of Ministry of Education,and School of Materials and Engineering,Henan University,Kaifeng,475001,China

Abstract In this work,we study the dissipation mechanism and frictional force of a nanometer-sized tip scanning a metal surface via a path integral approach.The metal,with internal degrees of freedom(c,c?)and a tip with an internal degree of freedom (d,d?) couple with one another by means of an exchanged potential,V.Having integrated out all internal degrees of freedom,we obtain the in-out amplitude.Moreover,we calculate the imaginary part of the in-out amplitude and the frictional force.We find the imaginary part of the in-out amplitude to be positive,and correlated to the sliding velocity in most cases.The frictional force is proportional to the sliding velocity for the case where v ＜0.01.However,for cases where v ＞0.01,the frictional force demonstrates nonlinear dependence on sliding velocity.

Keywords: path integral,electronic friction,quantum field

1.Introduction

Electron friction has been the subject of intensive study in recent years.Due to surface force apparatus techniques[1]such as scanning probe microscopy [2],frictional drag experiments involving 2D electron systems have been performed successfully.Electronic friction is the naive damping force that nuclei experience when they move near to or within a manifold of metallic electrons[3].Generally speaking,the mass of a nucleus is much bigger than that of an electron; this results in nuclear motion being slow in comparison to electronic dynamics.As such,the Born–Oppenheimer approximation can be introduced.For instance,nuclear dynamics can be considered in terms of classical(or semi-classical)motion,whereas electron dynamics is a quantum feature.As a result,a nuclear equation of motion(EOM) can be expressed via the Langevin equation [4]:

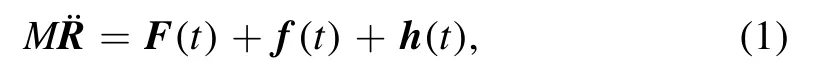
where t denotes time,f is the frictional force acting on the nucleus,F is the mean force,and h denotes the random force.There are various of approaches to obtaining this EOM.The main idea is to focus on the time evolution of the density operator for the electrons,and to trace over the electrons’degrees of freedom[5].The electronic friction can be derived from the EOM.The more precise approach is via the path integral and influence functional.In this approach,the random force presented as a background field and can be considered as a mean field when focusing on the classical dynamics.Via this method,the electronic friction is calculated based on the short time dynamics of the nucleus [6].Taking into account the total Hamiltonian of the system,it always contains the following terms:

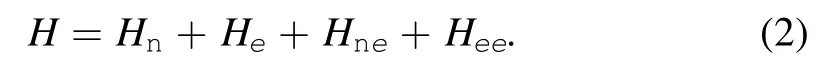
The first term refers to the kinetic energy of nucleus,the second term to the kinetic energy of electrons,the third term to the interacting energy between the nucleus and the electrons,and the fourth term to the interacting energy between electrons.The in-out amplitude of the system can be written as

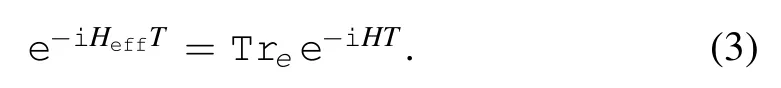
T denotes a sufficiently large time interval.Treis the partial trace over the electrons’ degrees of freedom.Thus the effective Hamiltonian reads

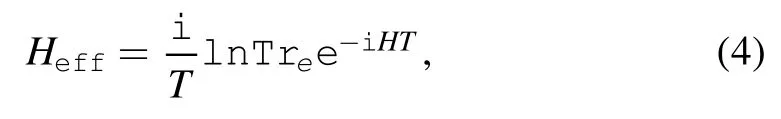
Via a Hamiltonian canonical equation,we find the EOM,which is similar to equation (1).In [4],the frictional force is proportional to the relative velocityhowever,in the general case,the fluctuation effect makes all interactions mixed.As such,the frictional force may be not proportional to v[7].For constant velocity,the left hand side(LHS)of(1)is zero;this implies that the value of frictional force equals the value of other forces.In this case we can calculate the frictional force via the dissipation process.Considering that the dissipated energy excites the electrons’ degrees of freedom,the dissipated energy can then be written in the following form [8]:

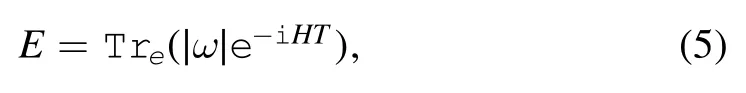
where ω denotes single particle energy.From this viewpoint we can calculate the dissipated energy involved in all possible quantum processes (i.e.,a one-loop diagram).As a result of energy balance,the frictional force is expressed as

A remarkable example of electron friction is the frictional force induced by tunneling electrons between a particle in the tip and a metal surface.Yoichi Shigeno studied a similar model,whereby a nano-scale molecule,having a single energy level,links with an external electrode,and vibration occurs at the linkage bond [9].This model clarified the rapidity of molecule vibration damping due to the presence of electronic current at nano-contact interfaces,from a microscopic viewpoint.Feng Chen provided a more general argument for current-induced friction using near-equilibrium statistical theory [10].Federico derived general expressions for current-induced forces,using a friction coefficient via real-time diagrammatic approach [11].Niels Bode employed the scattering-matrix approach to quantum transport in order to develop a unified theory of nanoelectromechanical systems out of equilibrium,finding that in out-ofequilibrium situations,current-induced forces can destabilize mechanical vibrations,resulting in limit cycle dynamics[12].All of the above works are related to dissipation effects,and their corresponding theories can be regarded as forms of linear response theory.These works focus on the frictional coefficient,owing to the linear dependence of velocity.In this paper,we consider a model consisting of a 2D metal substrate and a scanning tunneling microscope(STM)tip.The tip slides relative to the 2D metal at a constant velocity.We employ the functional approach to derive the expression of the imaginary part of the inout amplitude for the model,which is related to the dissipation effect.In addition,we obtain the expression of the frictional force and the function graph between frictional force and relative velocity.

2.Model Hamiltonian

The model considered in this paper consists of a 2D metal and a scanning tunneling microscope(STM)tip.The tip moves parallel to the metal surface at a constant velocity,v,with no contact between the two.We select the rest frame of the substrate to be

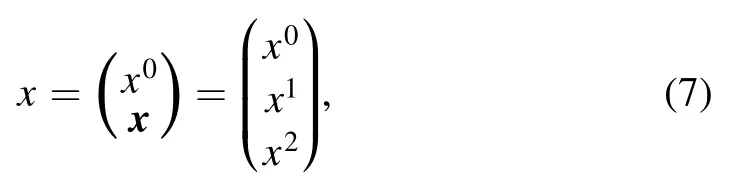
where x0is time coordinate,and x1and x2are the two-dimensional Cartesian coordinates of the metal surface

The schematic diagram of the system is shown in figure 1.We label the corresponding Fourier momentum coordinates via

At any time x0,the coordinate of the tip reads

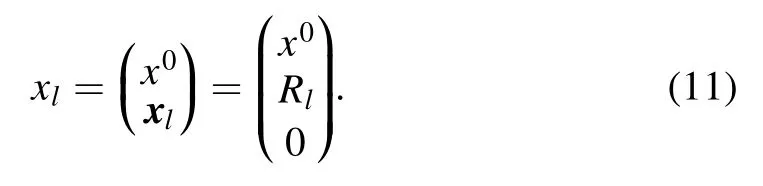
The Hamiltonian of the system reads

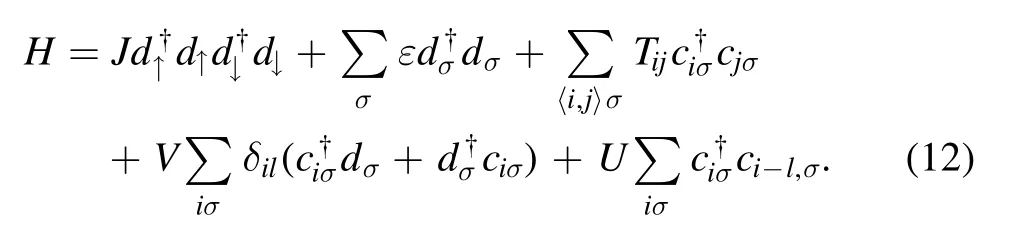
Here,the first and second terms are the energies of electrons in the tip;ε is a tip-site energy,while J denotes the repulsion energy between electrons.The third term is the tight-binding Hamiltonian of conducting electrons in metal,and the angle bracket indicates that the summation runs over the nearest neighbor lattices;Tijis the hopping energy in-between.The fourth term is the so-called Anderson s-d model,representing the contribution from the interaction between the metal electrons and the tip electrons[13],and the delta function indicates that the s-d interaction only exists at the tip location.Here,the energy U,corresponding to the so-called surface potential experienced by the metal electrons,is taken into account.This energy causes the on-site energy of the metal electrons to change,via Fourier transformation:

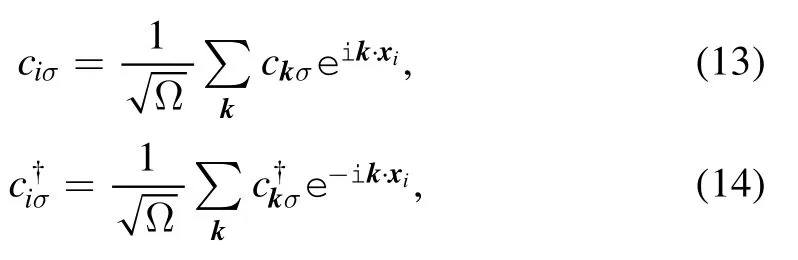
where the Hamiltonian of the system reads

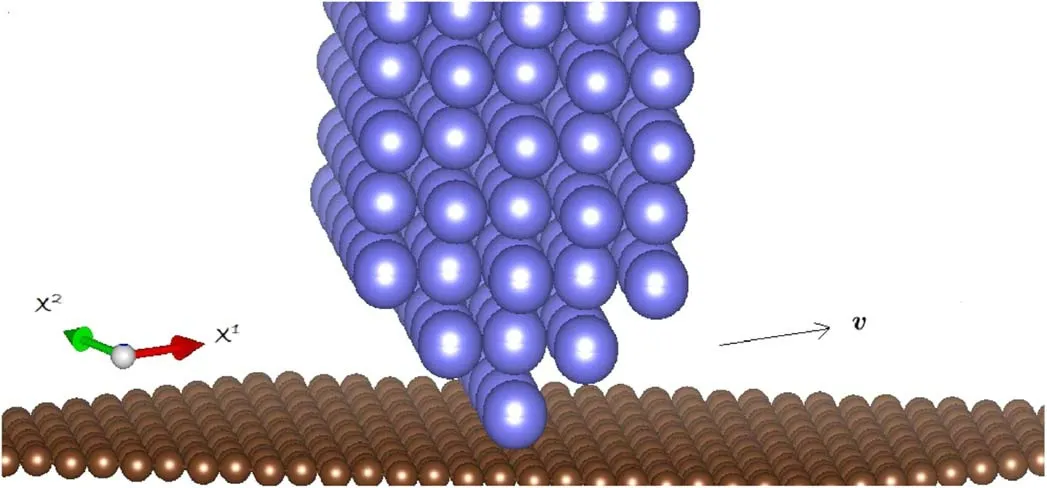
Figure 1.The model: a nanometer-sized tip scanning a metal surface.

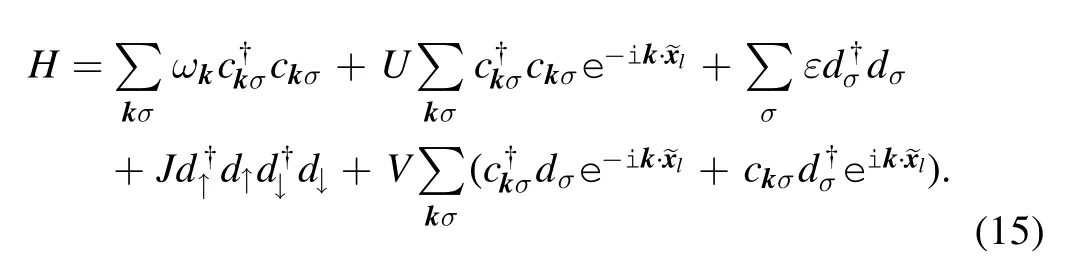
Without loss of generality we choose the relative velocity v along the x1axis to be

and introduce the Galilean boost matrix along the x1axis,

where its corresponding matrix is

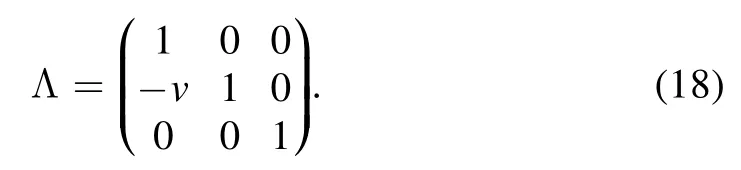
This leads to the coordinate transformation

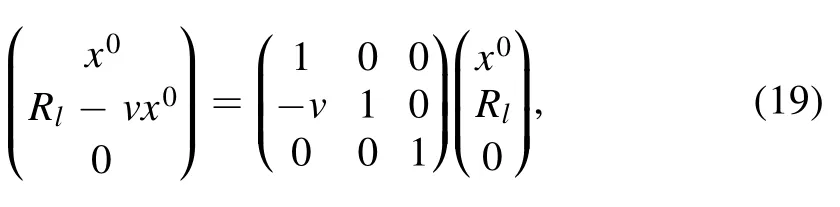
such that the spatial coordinates of the tip become

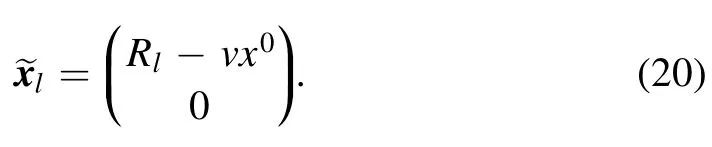
Therefore,the inner products of the space vector on the exponential in the Hamiltonian are

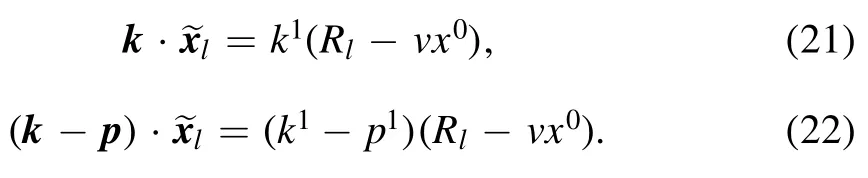
The Hamiltonian becomes

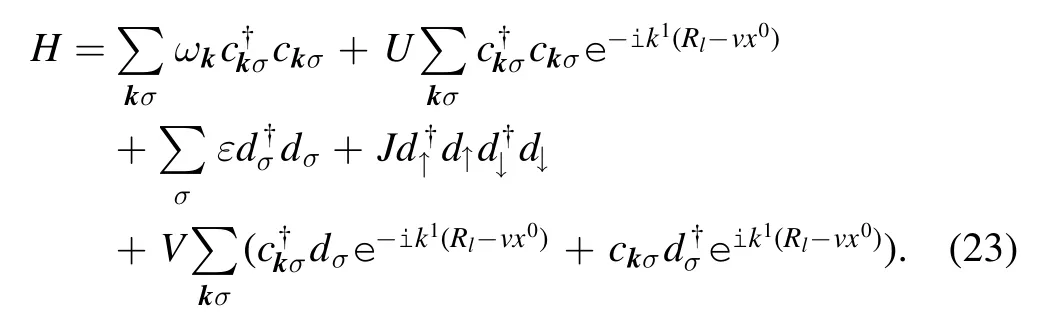
3.The effective action

By introducing a Legendre transformation,the action of the system can be written as

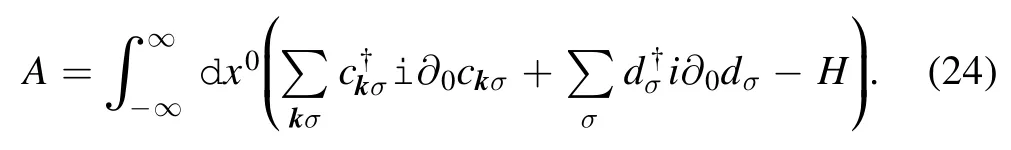
There is a quartic term in this action,via the following transformation [14]:

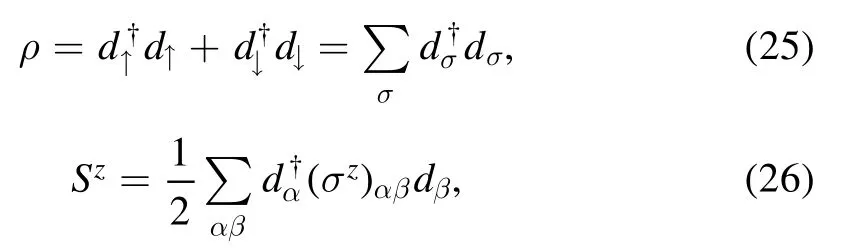
The quartic term can be written as

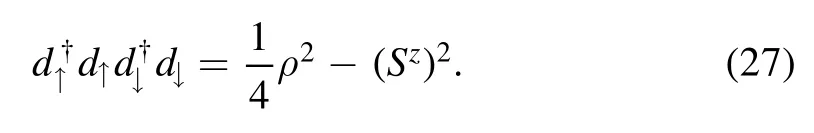
Therefore the action reads

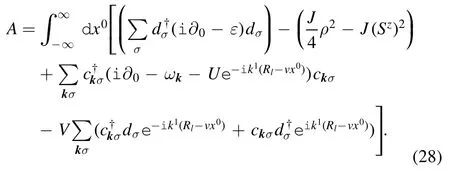
We introduce the mean field approximation by means of a Hubbard–Stratonovich transformation [15]:

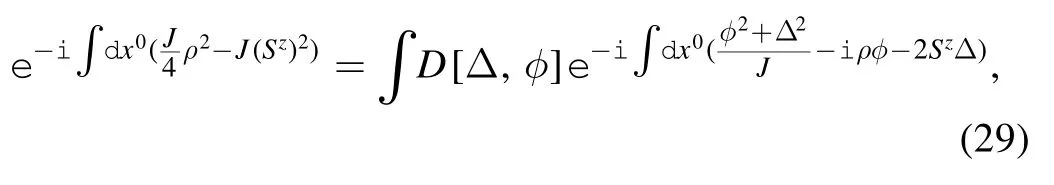
The in-out amplitude can be written as a functional integral.Here,we use the natural unit

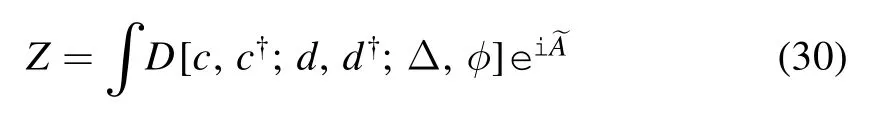
and the new action reads

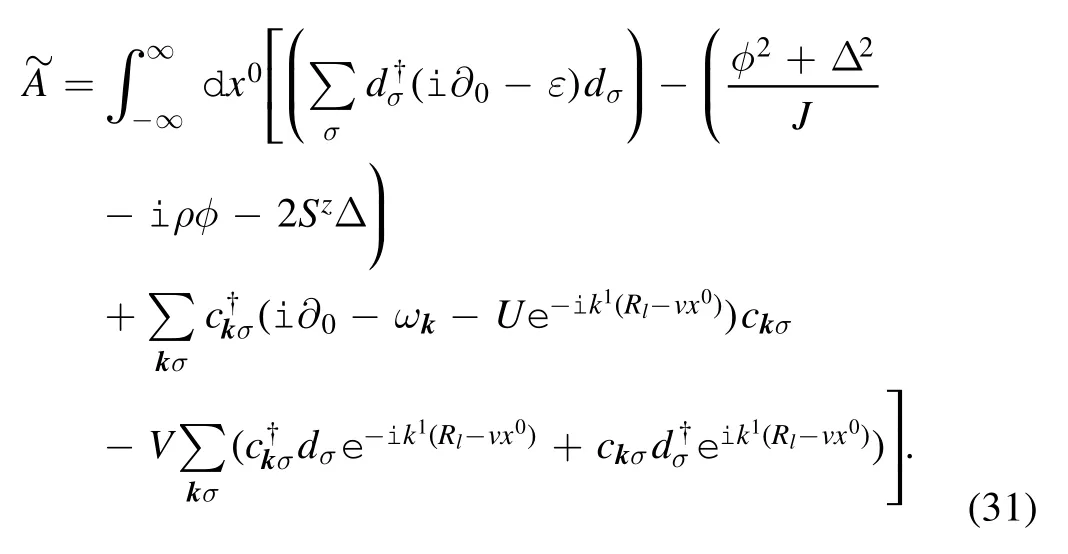
The mean field approximation suggests that the two auxiliary fields are equal to their mean values; thus the following selfconsistent equations hold [15]:

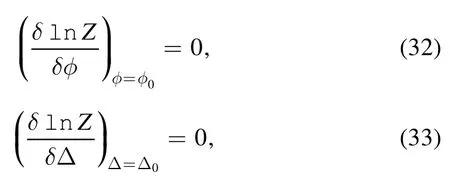
Here,the electron single occupancy condition is taken into account,such that

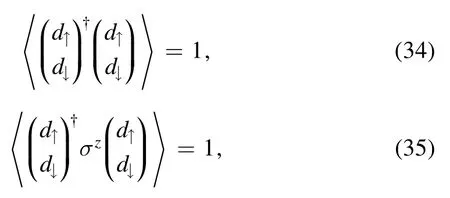
Using (26)–(29)we obtain

We then obtain the effective action under the mean field approximation as

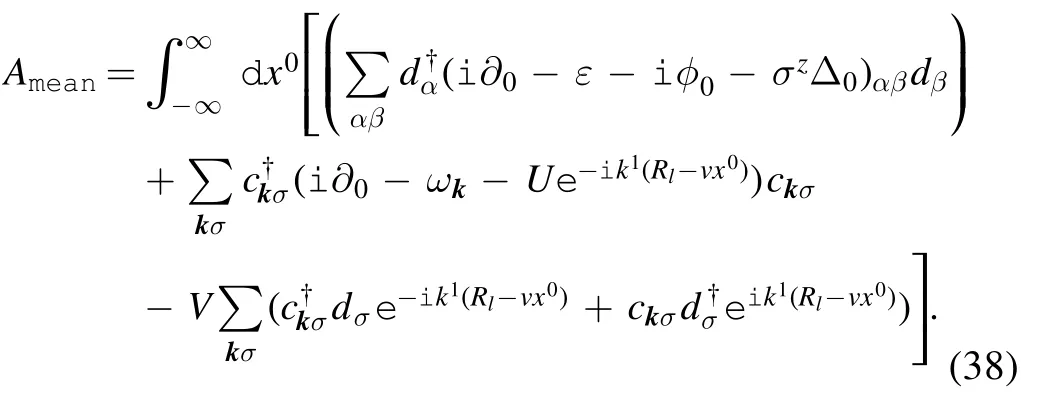
4.The in-out amplitude

In the case where v=0,the model exhibits the corresponding socalled in ground state [16],so that there is no excitation of internal degrees of freedom.If we add an external force on the tip to make it slide,the internal degrees of freedom in the tip and the metal around the slip line are temporally excited; thus the total energy rises.Subsequently,the system transfers to the so-called out ground state[16]and the total energy therefore decreases.As the result of these two competing effects,the system exhibits a non-equilibrium steady state,dependent on the sliding velocity,v.Here,we refer to the transition amplitude between in ground state and out ground state as the in-out amplitude.The in-out amplitude equation (3) can be written as a functional integral

Here,Γ is the amplitude contributed by the one-particle irreducible Feynman diagram[17].If the system has no dissipation,Z must can be normalized.Thus Γ must have a real value.If the system is a dissipative system,Z must not be normalized,and therefore Γ must contain an imaginary component [17].Having integrated out the degrees of freedom c and d,the connected inout amplitude is

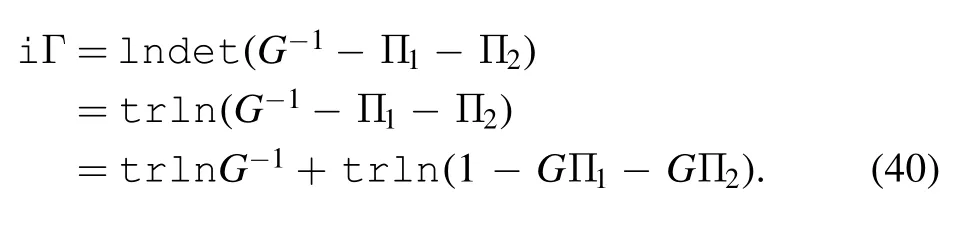
where the functions are

Dropping a factor which does not depend on relative velocity v,we obtain

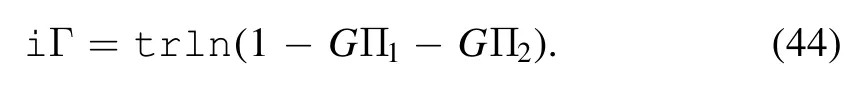
If we assume that the coupling constants U and V are small enough,the last term can be perturbatively expanded,and up to the second order of UV2,the in-out amplitude then becomes

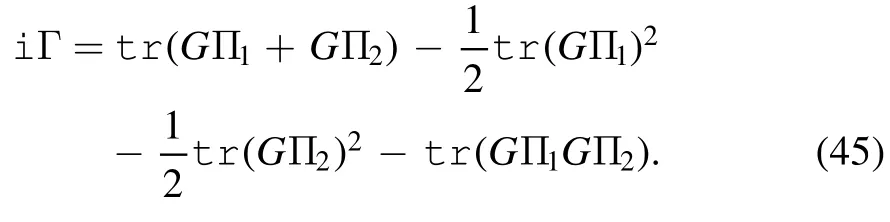
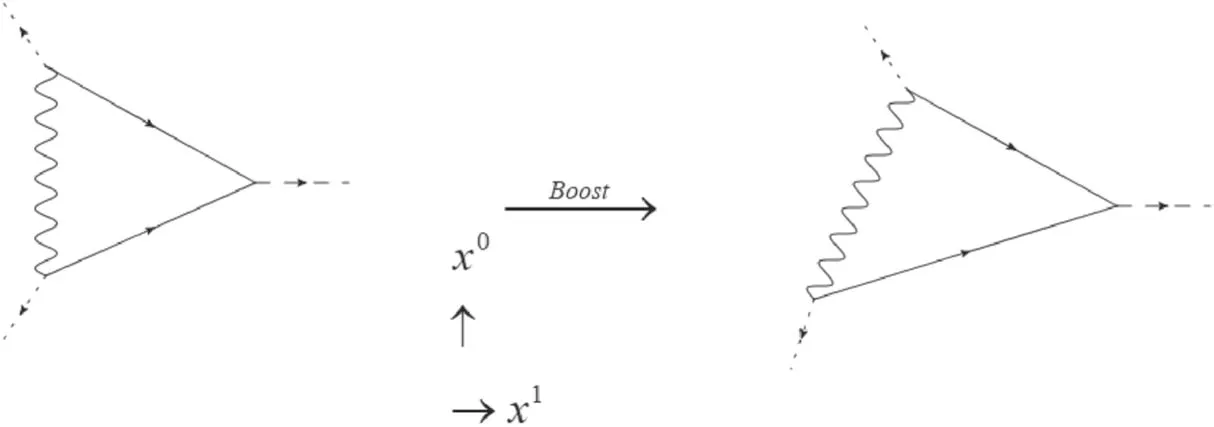
Figure 2.Galilean boost of the in-out amplitude.

Via Fourier transformation,the in-out amplitude can be written in frequency space.By means of straightforward calculation,the leading order terms are as follows:

and the second order terms are

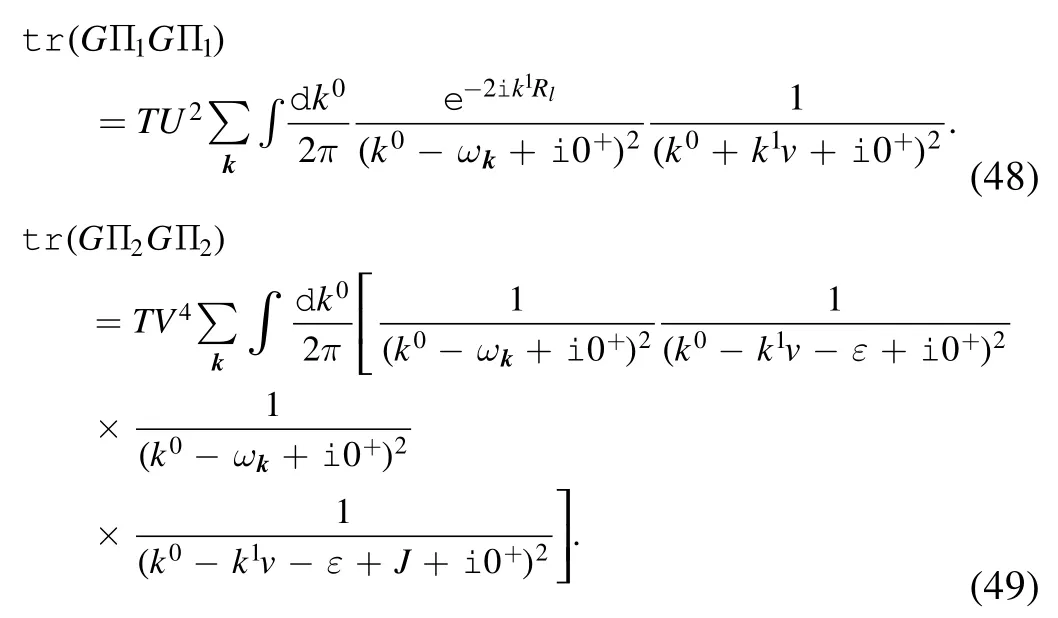
These terms are known as the symmetric terms.In addition,

We call this term the cross term.T is the total time.Here,we note that the Galilean boost transforms the in-out amplitude;the corresponding Feynman diagram is shown in figure 2.

5.Imaginary part of the in-out amplitude

The imaginary part of the in-out amplitude represents the excitation of the internal degree of freedom on the metal and the tip,and this excitation leads to dissipation.In this section,we obtain the expression of the imaginary part of the in-out amplitude,and study the relationship between the imaginary part of the in-out amplitude and the sliding velocity.In order to perform the integral over k0,we choose a closed contour formed by the real axes,and a half circle with very large radius on the bottom half complex plane.For the first order terms,using Cauchy’s theorem,we find that these terms vanish.For the second order terms,Cauchy’s theorem indicates that the symmetric terms also vanish.As such,the only nontrivial contribution to the in-out amplitude is the cross term.We rewrite this as

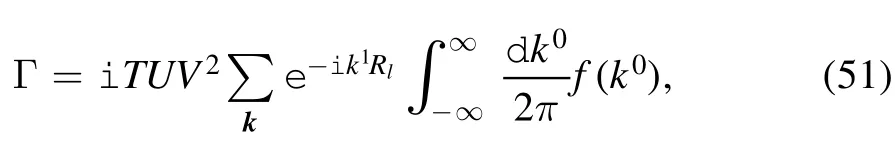
where the integrand

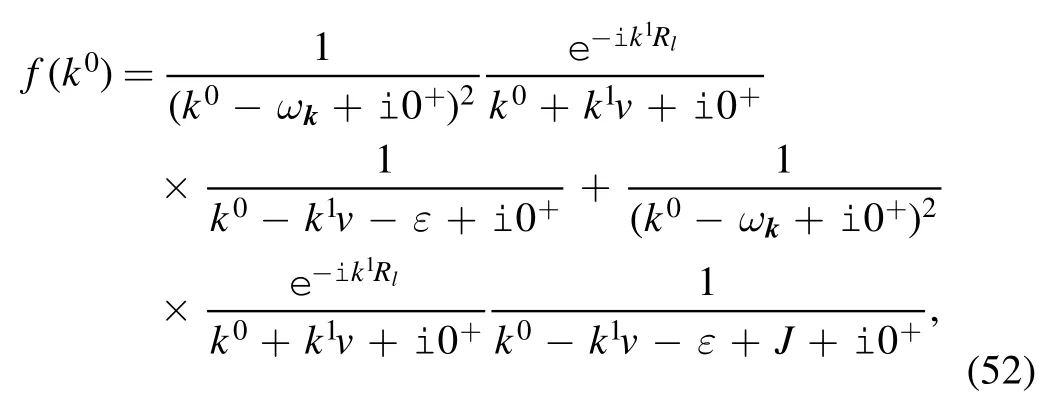
has four poles on the bottom half plane:

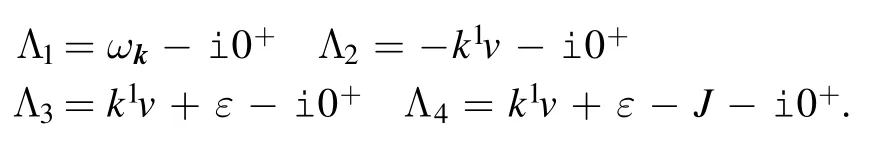
We perform the Cauchy integral along the closed contour.Since perturbative expansion can also lead to an imaginary part which independent of the tip’s velocity,we focus only on the tip velocity-dependent imaginary part.Therefore we only select poles 2,3,and 4.The corresponding residues are

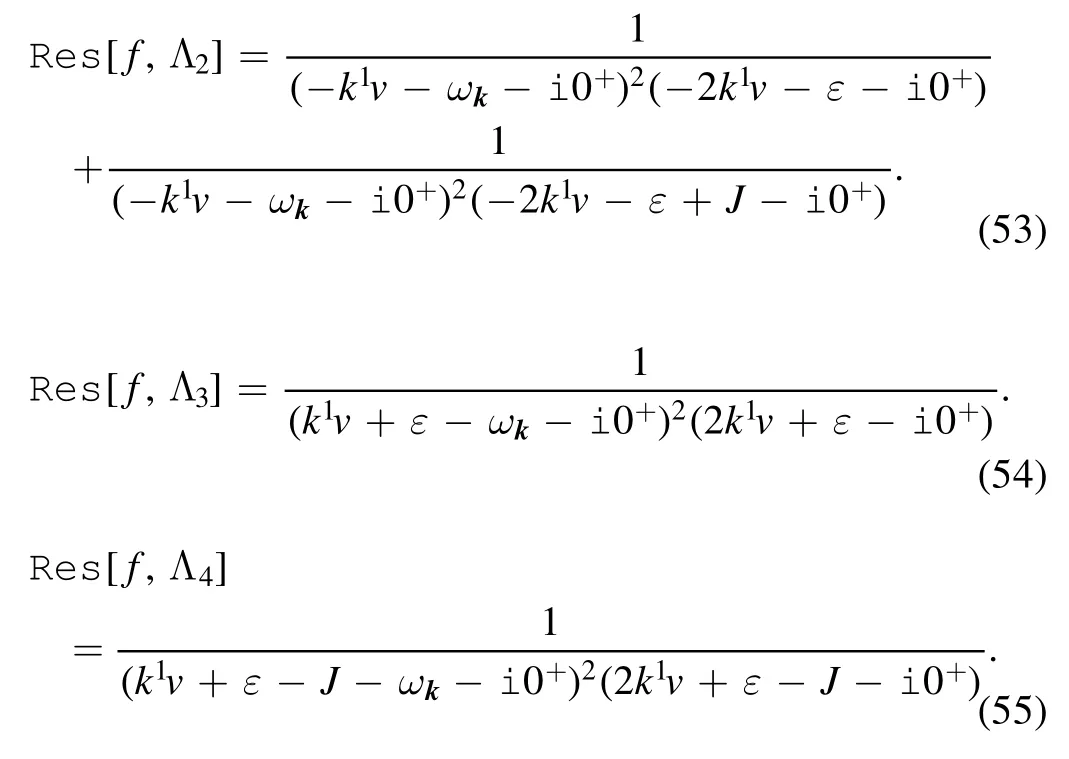
Taking into account the continuous limitation,the summation over momentum k can be replaced by the integral.Thus the inout amplitude becomes

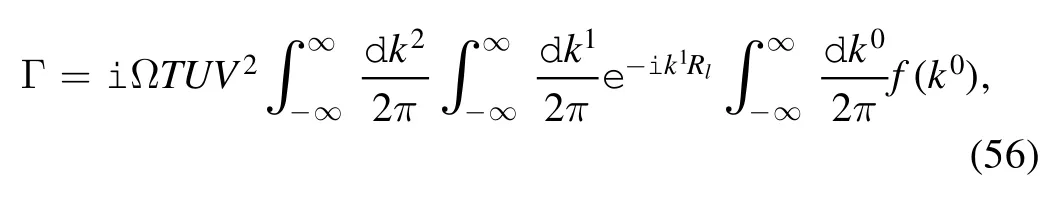
where Ω is the total area of the substrate.We can set Rl=0 without loss of generality.The in-out amplitude reads

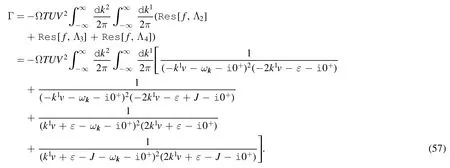
Taking into account all of the above,and using the identity

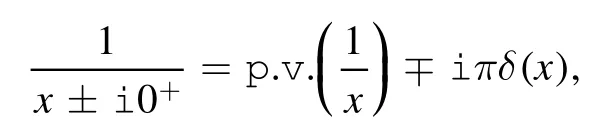
the imaginary part of the in-out amplitude can be calculated as follows:

The numerical results are shown in figures 3 and 4.It can be seen that the imaginary part of the in-out amplitude and the sliding velocity are positively correlated for different J in figure 3.J=0.3 is a special case,as shown in equation (57).When J=0.3,the second and the last terms of equation(57)give two very large contributions ofwhere N is a very large constant.Moreover,when v →0,this result is divergent.This implies that there must be extra dissipation caused by some new degrees of freedom.Here,J=0.3 means J=ε.Actually,this implies the formation of a local magnetic moment relating to the electrons on the tip.The new degree of freedom is therefore the local spin on the tip.Generally speaking,this large term with respect to the imaginary part of the in-out amplitude does not contribute to frictional force.We will expand on this point in the next section.

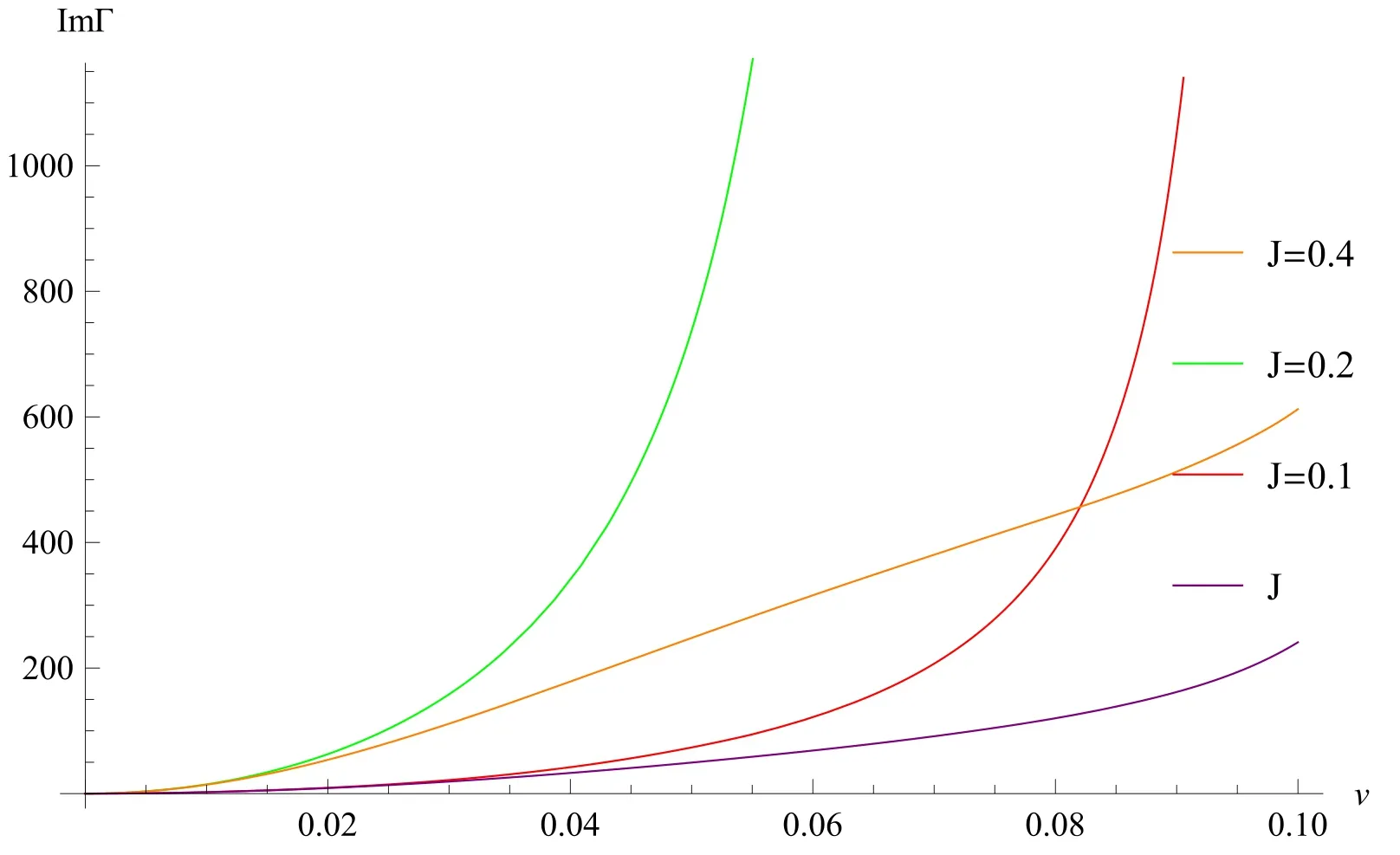
Figure 3.The imaginary part of the in-out amplitude as a function of the relative velocity,v,for the typical caseε=0.3,J=0.1,0.2,0.4,0.5,=0.3,in units of 4πUV2ΩT.

6.Dissipation and frictional force

The transition probability is

Therefore,the in-out probability contributed only by the connected diagrams is

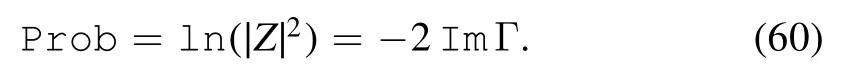
On the other hand,dissipation arises when the in ground state of the system becomes unstable against the production of onshell c-electrons and on-shell d-electrons [18].As such,the transition probability can be written as

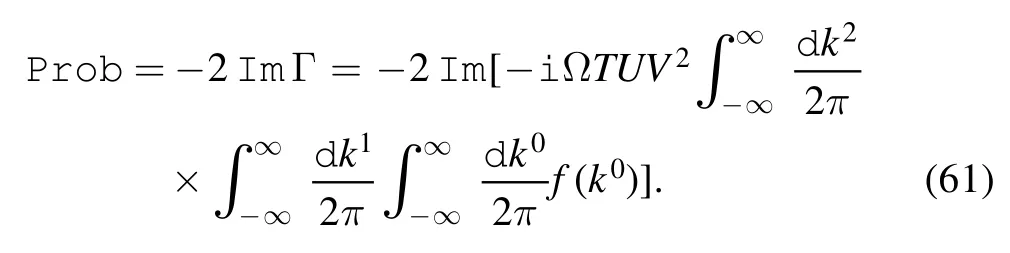
f(k0)is the probability amplitude of creating an electron with energy and momentum k per unit time and area.The dissipation energy during time T is

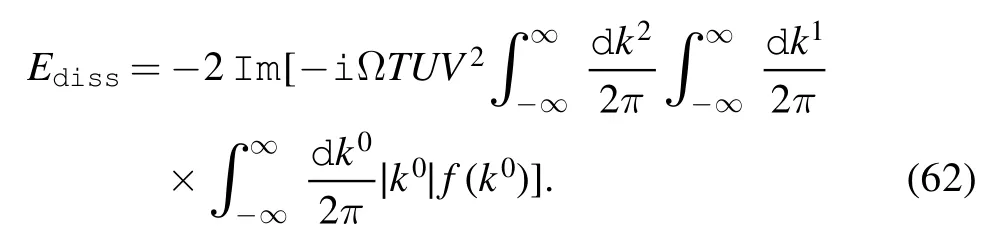
The dissipative power per unit area is

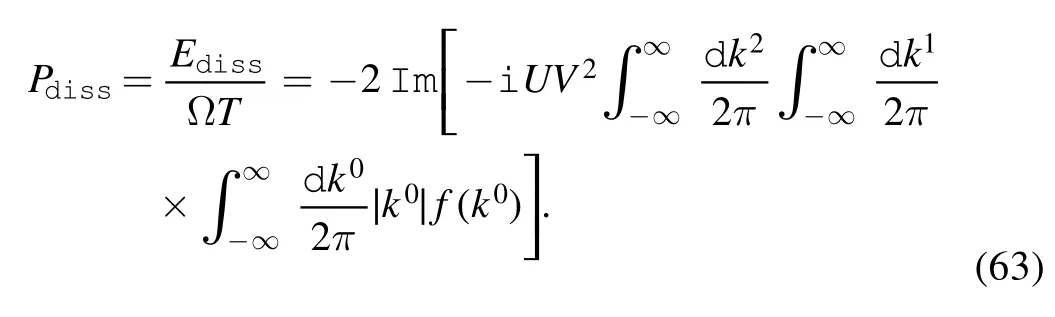
The dumped power is provided by an external source,which keeps the tip moving at a constant velocity,against the frictional force.Thus the energy balance is

and the expression of frictional force is

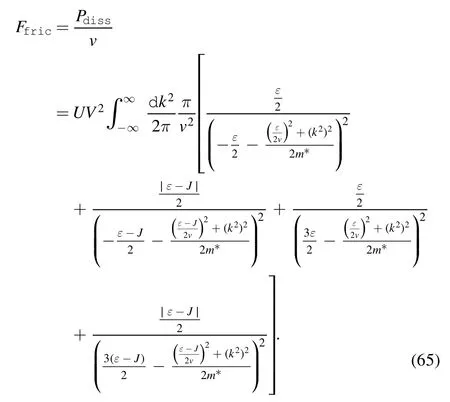
The numerical result is shown in figure 5.The frictional force is proportional to the sliding velocity when v ＜0.01 for different J.In contrast,for the case where v ＞0.01,the frictional force exhibited nonlinear dependence on sliding velocity.This phenomenon may be justified as follows: let us consider the momentum and energy balance in a time interval ΔT,assuming that in the first period of time both the frictional force and the dissipated energy are driven by the excitation of c-electrons.The change in the c-electrons’momentum reads as

the change of the on-shell c-electrons energy reads

the condition of c-electrons being excited reads

and therefore

when v ＜0.01,ΔP1＜0.033;as such,only c-electrons with a momentum of less than 0.033 are excited.When v ＞0.01,celectrons with a momentum greater than 0.033 are excited.This leads to vΔP1＞ε.Therefore,d-electrons on the tip are excited,and are interacting with c-electrons.This leads to a sharp increase in dissipated power.The dependence of frictional force on velocity will change.Moreover,J=0.3 is still a special case.In equation(63),J=0.3 means that the second and the last terms will vanish.This implies that the large term,of the imaginary part of the in-out amplitude does not contribute to frictional force,unless we consider the new degrees of freedom caused by the formation of a local magnetic moment on the tip.

7.Conclusions and outlooks

In this paper,we have studied the dissipation mechanism and frictional force of a nanometer-sized tip scanning a metal surface,via a path integral approach.The interaction between the 2+1d spinor field in the 2D metal and the 0+1 spinor field in the tip has been taken into account via the coupling constant V.We have seen that the relative motion may generate an imaginary component in the in-out amplitude.Dissipation arises here due to the in ground state of the system being unstable due to the production of on-shell c-electrons and onshell d-electrons.These internal degrees of freedom in the tip and the metal around the slip line are temporally excited,and thus the total energy rises.Subsequently,the system transfer to the out ground state,and thus the total energy decreases.As a result of these two competing effects,the system exhibits a non-equilibrium steady state,which depends on the sliding velocity,v.We also compute the frictional force.

The numerical results of the in-out amplitude show that the imaginary part of the in-out amplitude and the sliding velocity are related in quadratic function.In addition,the frictional force is proportional to the sliding velocity for the case v ＜0.01.In contrast,for the case where v ＞0.01,the frictional force demonstrates nonlinear dependence with respect to sliding velocity; we have provided a classical explanation for this phenomenon.

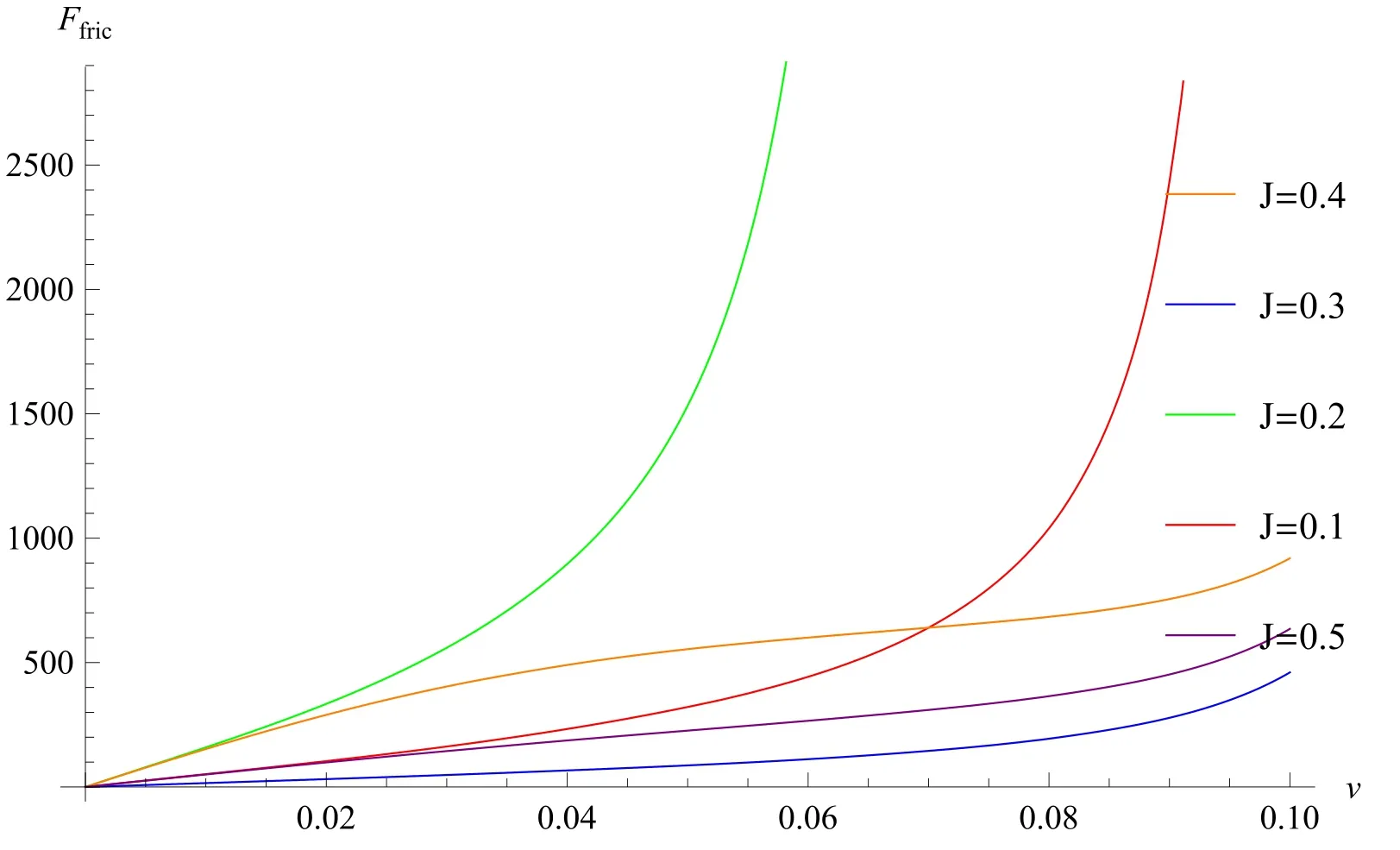
Figure 5.Frictional force as a function of relative velocity,v,for the typical case ε= 0.3,J= 0.1,0.2,0.3,0.4,0.5=0.3,in units of 4πUV2.

In [18],the dissipation mechanism was attributed to the production of on-shell fermion pairs induced by some timedependent external source.Via relative motion,the vacuum state of the electromagnetic field plays the role of a time-dependent external source.In our paper,however,there is no vacuum electromagnetic field; instead,there are two coupling constants,U and V.Equation (23) shows that the relative motion causes U and V to acquire a time-dependent phase factor,eik1vx0,for every momentum k.In this instance,the relative motion causes U and V to become two timedependent external sources.Therefore the system becomes an open system,and the internal degrees of freedom are excited by the time-dependent external source.This leads to energy and momentum flowing into or out of the interacting vertices,as shown in figure 2.

In one of our ongoing works relating to sliding friction between a magnetic tip and a ferromagnetic surface,we are employing a similar approach to that employed in this work.We started from an anisotropic Heisenberg Hamiltonian

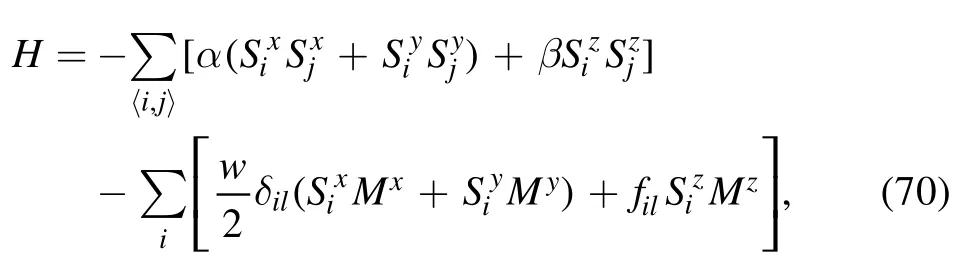
where the first term is the magnetic exchange energy between spins in the ferromagnetic surface,and the second term is the magnetic exchange energy between the tip spin and the surface spin located on the i-th site.The surface potential induced by the magnetic tip always has the formBy means of a boost transformation between the tip and the substrate,a Holstein–Primakoff transformation,and a Fourier transformation,we obtain a Hamiltonian similar to that in equation (23):

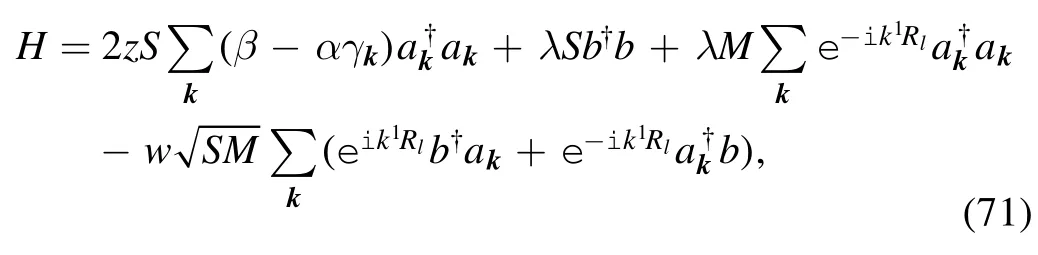
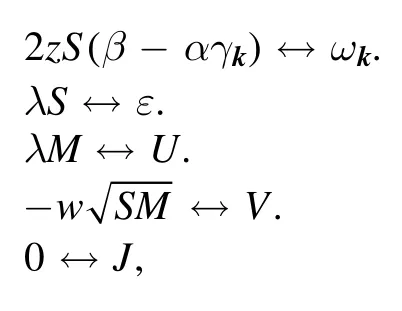
equations (23) and (69) will then be similar to one another.We therefore conclude that the sliding friction in this system may have the same v-dependence as the sliding friction in the electronic system.In[7],Fusco and Wolf simulated this kind of magnetic friction,and their results were similar to ours.Although the sliding friction in electronic systems and the sliding friction in magnetic systems originate from different physics,the interaction terms in their Hamiltonians have a similar form to the Anderson s-d model.This kind of interaction always results in sliding friction with a linear dependence on v,if |v| is small.

Acknowledgments

We would like to thank Qiang Sun,Kai Li,and Fei Wang for valuable insights and discussions.

ORCID iDs