Oblique propagation of nonlinear ionacoustic cnoidal waves in magnetized electron-positron-ion plasmas with nonextensive electrons
Muhammad KHALID,Ghufran ULLAH,Mohsin KHAN,Sheraz AHMAD,Sardar NABI and Daud KHAN
1 Department of Physics, Government Post Graduate College Mardan, Mardan 23200, Pakistan
2 Department of Physics, Islamia College Peshawar (Public Sector University), Peshawar 25120, Pakistan
3 Department of Physics, Government Post Graduate College Nowshera, Nowshera 24100, Pakistan
Abstract Theoretical investigation of nonlinear electrostatic ion-acoustic cnoidal waves (IACWs) is presented in magnetized electron-positron-ion plasma with nonextensive electrons and Maxwellian positrons.Using reductive perturbation technique, Korteweg-de Vries equation is derived and its cnoidal wave solution is analyzed.For given plasma parameters, our model supports only positive potential (compressive) IACW structures.The effect of relevant plasma parameters (viz., nonextensive parameter q, positron concentration p, temperature ratio σ,obliqueness l3) on the characteristics of IACWs is discussed in detail.
Keywords: ion-acoustic cnoidal waves, KdV equation, q-distribution
1.Introduction
The behavior of linear and nonlinear phenomena in electronpositron-ion (EPI) plasma contain a huge amount of interest and active field of study for many researchers.Large number of investigations on structures with nonlinear properties viz.,cnoidal waves (CWs), solitary waves (SWs), vortices etc, is reported in linear and nonlinear plasmas with various distribution of charged particles [1-5].The electron-positron plasma is produced naturally by phenomena of pair production.It also shows its presence in processes with high energy like neutron stars, in early universe [6], in active galactic nuclei[7]and in atmosphere of stars[8].The plasma of roomtemperature having the composition of 107positrons with 103s lifetime is led by positron trapping technique mentioned by Greaves et al [9].Majority of laboratories and astrophysical plasma [10] become a mixture of EPI (electrons,positrons and ions) as a result of long life of positrons.Therefore, the positron concentration plasma study is important to seize the behavior of every laboratory and astrophysical plasma.The existence of positrons has also been confirmed in laboratory plasmas [11].
The Boltzmann, Gibbs and Shannon (BGS) entropy study received a great attention from last few decades and become a field of considerable interest for many authors.Renyi [12] in 1955 was the first who presented the nonextensive generalization of the Boltzmann-Gibbs statistics entropy and then in 1988 it was forwarded by Tsalli [13].Large number of systems with long range interactions follows this new statistics.Maxwellian distribution is not applicable for system having non-equilibrium stationary states and interactions of long-range, such as gravitational systems and plasmas.Tsalli proposed a new statistical approach which is the generalization of the BGS entropy [13], in which q is the nonextensive parameter, which defines the measure of the nonextensivity of the system under consideration.Nonextensive statistics (q-distribution) was applied to numerous cosmological scenarios and astrophysics including stellar polytropes [14], problem of solar neutrino [15].As a special case when q →1, the nonexensive distribution reduces to Maxwellian distribution.
In plasma physics the study of nonlinear periodic waves gain a valuable interest[16-26]for so many researchers.The CW solution which is the solution of Korteweg-de Vries(KdV) nonlinear equation have been presented by Korteweg and de Vries in 1895.The sharper crests and flatter troughs successfully explains the characteristics of periodic (cnoidal)waves.The solution of CW can be expressed in term of Jacobi-elliptical function such as cn, sn and dn.Recently,Rahman et al studied the ion-acoustic cnoidal waves(IACWs) in unmagnetized electron-ion plasma with Cairns distributed electrons.They showed that nonthermality of electron significantly affects both compressive and rarefactive cnoidal structures [27].The effect of positrons concentration on the behavior of IACWs in unmagnetized Maxwellian EPI plasma was studied by Chawla and Mishra[28].The IACWs in two electron temperature plasma was studied in [29].Farhadkiyaei and Dorranian discussed the dynamics of IACWs in an unmagnetized EPI plasma having Tsallis electrons and Maxwillian positrons [30].
The phase portrait analysis of nonlinear periodic waves gain a considerable interest for so many researchers, few of them are highlighted here.Saha and Tamang reported the positron-acoustic(PA)waves in EPI plasmas with Kaniadakis distributed hot electrons and hot positrons[31].The dynamics of supernonlinear periodic PA waves in EPI plasmas with nonextensive hot electrons and hot positrons was investigated by Tamang and Saha[32].The dynamics of ion-acoustic(IA)waves in plasma with Tsallis electrons and positrons was studied by Ghosh et al[33].Most recently,the supernonlinear IA in a multicomponent plasma with q-distributed electrons is investigated in[34].Abdikian et al discussed the dynamics of electron-acoustic supernonlinear waves in multicomponent plasma with nonexensive hot electrons [35].
Recently,our aim is to study the dynamics of IACWS in magnetized EPI plasmas having nonextensive electrons and Maxwellian positrons, we follow the range of nonextensive parameter q as suggested by Verheest [36].
The paper is arranged in the following manner.Model equations for the system have been presented in section 2.In section 3, KdV equation has been calculated by using reductive perturbation technique (RPT).CW solution is obtained in section 4.Numerical analysis is carried out in section 5 and the conclusion of main results is discussed in section 6.
2.Basic equations
Considering a collisionless multicomponent magnetized plasma composed of ions, nonthermal electrons and Maxwellian positrons, the electrons follow Tsallis distribution[13, 36] and positron are Maxwellian.The plasma is assume to be immersed in a constant magnetic fieldB=B0z?.The dynamics of ions can be characterized by the following set of normalized fluid equations:
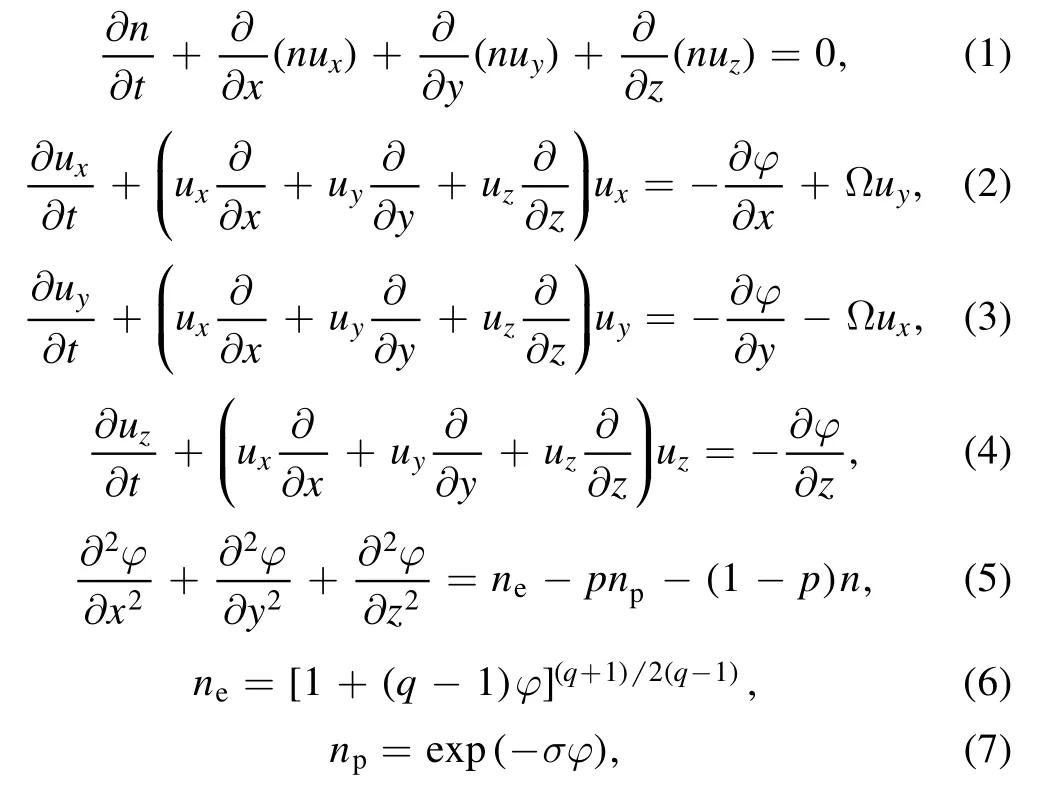
for small φ, equations (6) and (7) can be expanded respectively as;
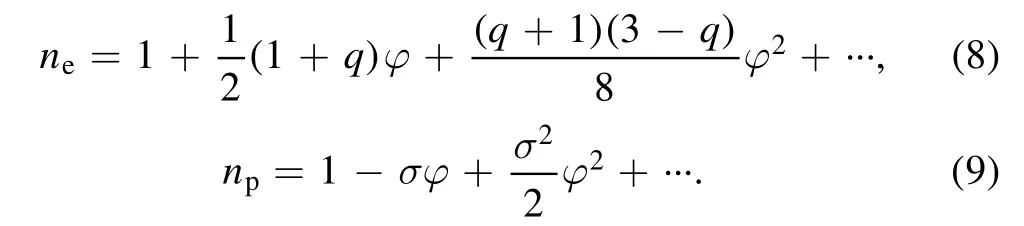
Here n is the number density of ions normalized by its equilibrium value n0, the ion fluid velocity u which is scaled by IA speedand the normalized electrostatic wave potential is denoted byTeand Tprepresent the temperatures of electron and positron respectively,is the temperature ratio.np0(ne0) represents the equilibrium number density of positron (electrons), =pis the positron concentration.is the gyrofrequency of ion, and the quantityis dimensionless.The space and time variables have been normalized by Debye lengthandrespectively.ux, uyand uzare the ion fluid velocity components along x, y and z axes respectively.
3.KdV equation
In order to calculate the KdV equation, using RPT, we introduce the new stretching as,
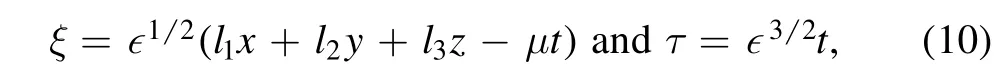
where the phase velocity is μ.The direction cosines along x,y and z axes respectively represented by l1,l2and l3,they must satisfy
Now the dependent variables can be expanded as:

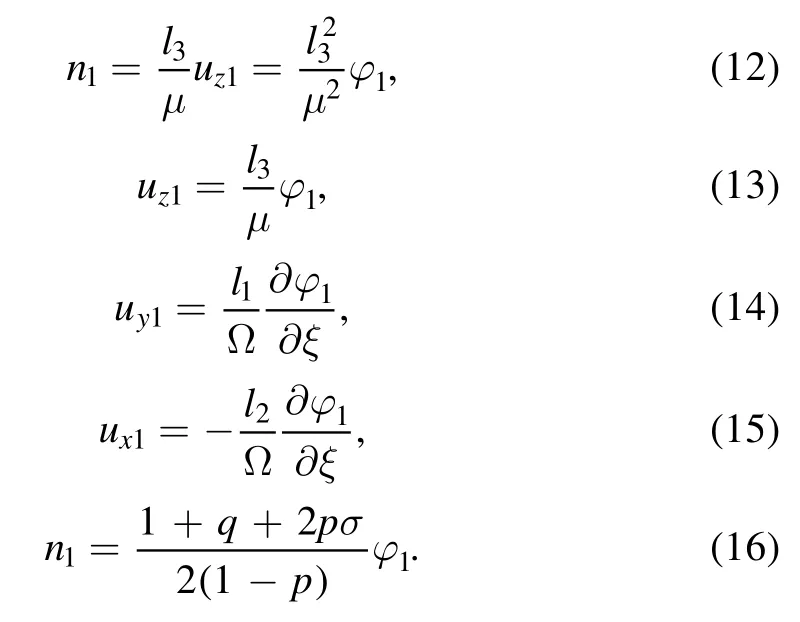
Comparing equations (12) and (16), we obtain the phase velocity as
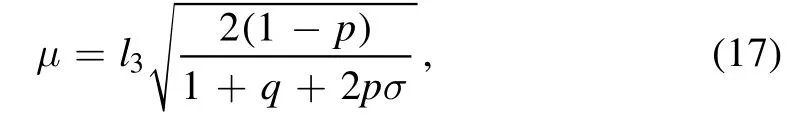
from equation(17)it is seen that phase velocity μ depends on q, p, σ and l3.
Following the same procedure, proceeding to the next order of ?and eliminating the second order quantities, we obtain the standard KdV equation as
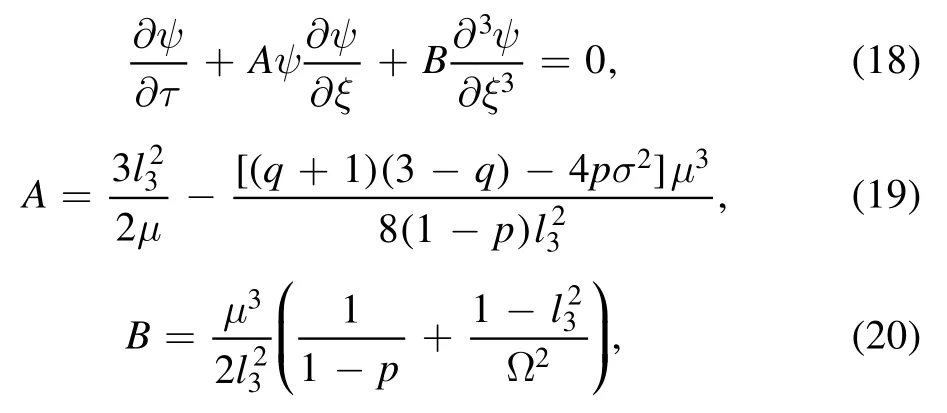
it is clear that the nonlinear coefficient A and dispersion coefficient B of KdV equation are functions of q,p,σ,l3and Ω, respectively.In equation (18) we have replaced φ1by ψ.As a special case,the coefficients for A and B reduce to that of[28] when l3=1 and q →1.
4.CW solution
To solve equation (18), let define the transformation χ=ξ ?u0τ,where u0is the constant velocity of the nonlinear structure, thus equation (18) becomes
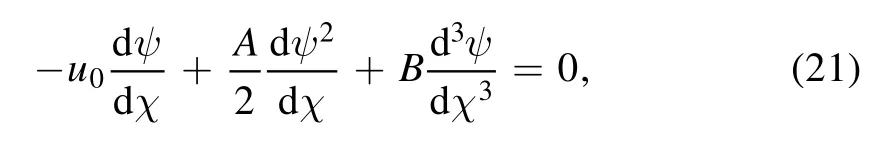
integrating two times equation(21)with respect to χ,we have
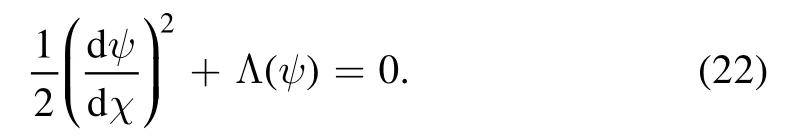
The Sagdeev potentialΛ(ψ) is defined as
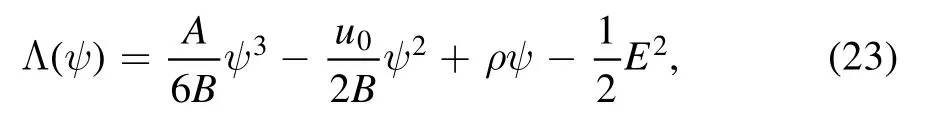
Equation (23)Λ(ψ) has two points of extremum e1,2and can be calculated by differentiating equation (23) with respect to ψ and put it equal to zero, i.e.,which gives:
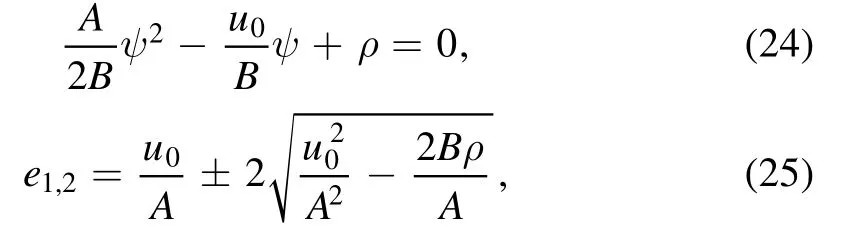
hence we have two states of equilibrium,e2is the saddle point and e1is the center.e1and e2should always be real.This is possible only iftherefore we can choose ρ in such a way that the conditionis satisfied.These equilibrium points strongly depends on A and B.The potential well must fulfill the following condition
To find the nonlinear periodic solution, using initial conditionsψ(0)=α,and,in equation(23),we can find
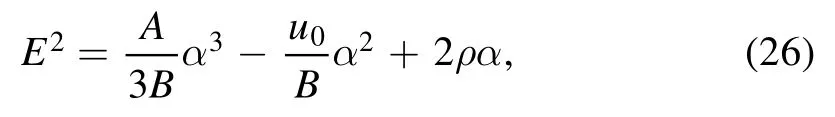
substituting equations (23) and (26) in equation (22) and simplifying, we get
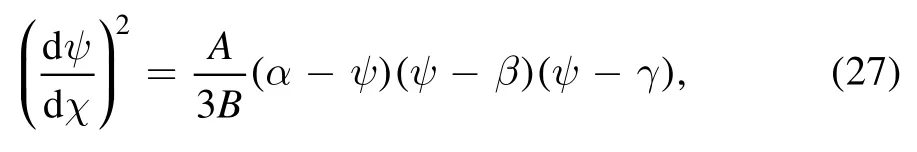
where β and γ are defined as;
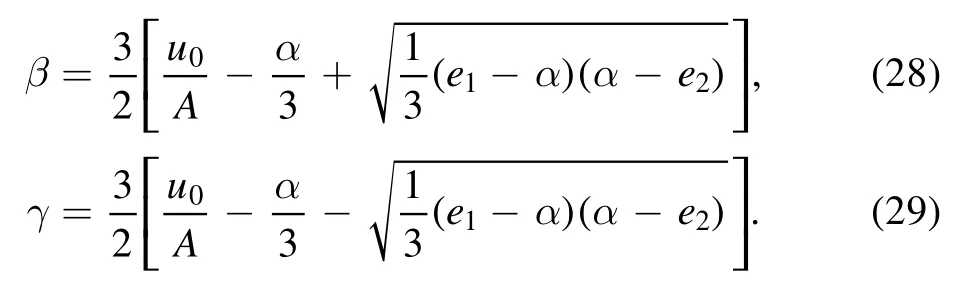
In order to find the nonlinear CW solution, the following conditions must hold: e2≤α ≤e1or e1≤α ≤e2.The nonlinear CW solution of equation (22) is given as [27]
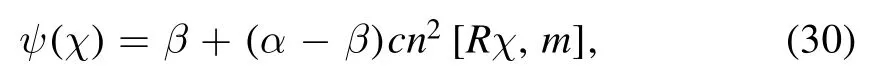
here the Jacobian elliptic function is cn.The parameter m is called modulus which measures the nonlinearity and the quantity R in terms of real zeros (α, β and γ) of Sagdeev potential is respectively defined as;
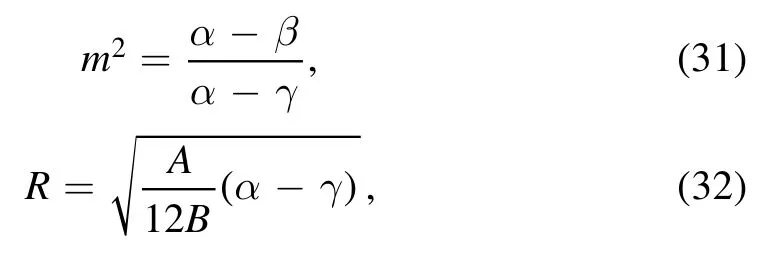
the nonlinear coefficient A >0 for α >β >γ and A <0 for α <β <γ.The amplitude Ψ and wavelength λ of the IACW can be defined as;

and
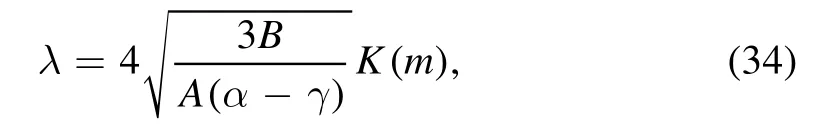
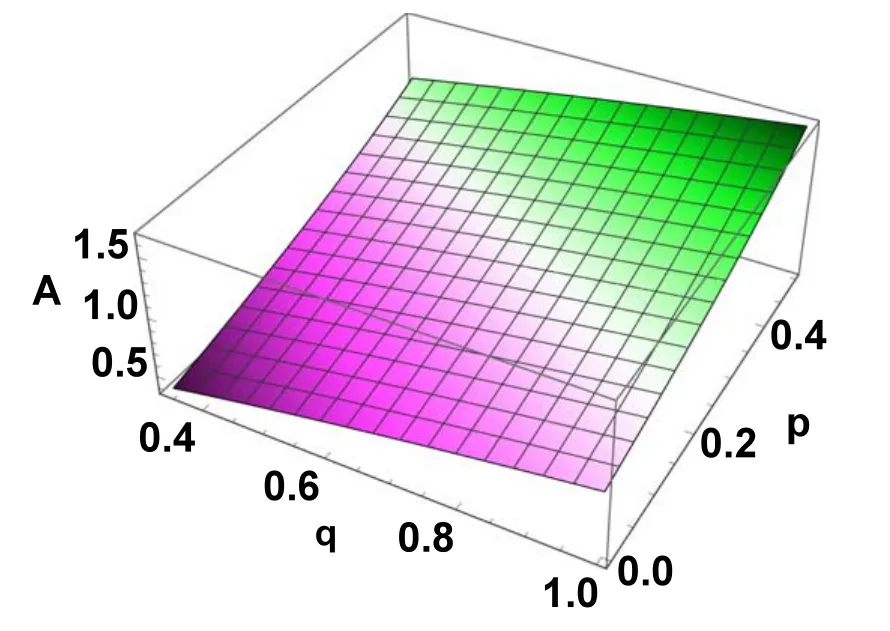
Figure 1.Variation of A against q and p, while l3=0.90, σ=0.1.

Figure 2.Sagdeev potentialΛ( ψ)is plotted against ψ with l3=0.90,u0=0.1, Ω=0.3, p=0.1, σ=0.1.The solid curve corresponds to ρ=0.02 and E=0.04 while dashed curve corresponds to ρ=0 and E=0.
where the first kind complete elliptical integral is K(m).Now when ρ=0 and E=0, then β=γ=0, so m →1, the CW solution deduce to SW solution.Therefore, equation (30)takes the form,
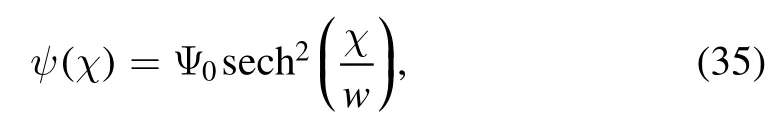
5.Numerical analysis
The nonlinear coefficient A and dispersion coefficient B are functions of various plasma parameters(viz l3,Ω,p,σ and q)as appear in KdV equation (18).The values of these coefficients strongly affect the structural characteristics of IACWs.So it is important to study the effect of these parameters on the characteristic propagation of IACWs.It is important to mention here that the polarity of nonlinear structures can be determined on the basis of nonlinear coefficient A.Since in present case nonlinear coefficient A is positive (A >0) as shown in figure 1, therefore, only positive potential IACWs are observed in our present plasma configuration.
To study the dynamics of IACWs in the present system,the Sagdeev potentialΛ(ψ) is plotted against ψ as shown in figure 2.It is clear that Λ(ψ)≠0 at ψ=0 for IACW (see solid curve) and on the other hand Sagdeev potential Λ(ψ)= 0at ψ=0 corresponds to IASW(see dashed curve).
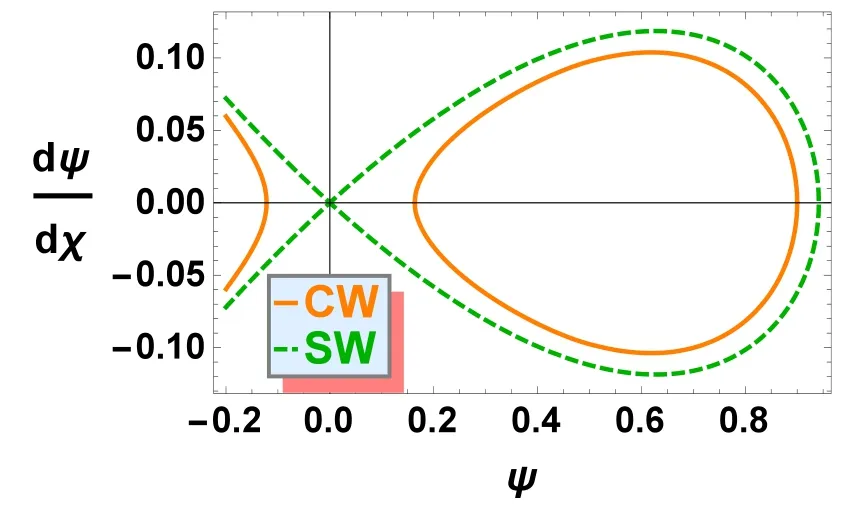
Figure 3.Phase plot dψ/ dχ is plotted against χ with l3=0.90,u0=0.1, Ω=0.3, p=0.1, σ=0.1.The solid curve corresponds to ρ=0.02 and E=0.04 while dashed curve corresponds to ρ=0and E=0.
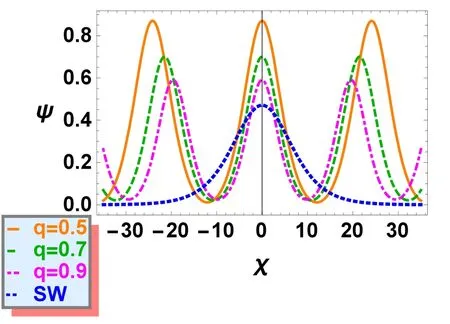
Figure 4.CW solution ψ versus χ is plotted for different values of q while σ=0.1, u0=0.1, Ω=0.3, l3=0.90, p=0.1, ρ=0.02 and E=0.04, while dotted curve corresponds to q=0.95, ρ=0 and E=0.
The phase curves using equations (22) and (23) have been plotted against ψ as shown in figure 3.The curves (see solid curves) confined to the inner side are for IACWs with[(ρ,E) ≠0], while the solid outer curve (see dashed curve)represents the SW with[(ρ,E)=0].It can be observed from figure 3 that the phase plot consists of two set of orbits.The homoclinic orbit (dashed curve) corresponds to SW, whereas the periodic orbit (solid curve) stands for periodic CW.
The variations of CW solutionψ(χ) versus χ for different values of q are depicted in figure 4 having fixed values of all other parameters.It is found that there is reduction in the amplitude and width of IACWs structures with increasing values of nonextensive parameter q, the blue dotted curve represents soliton.
Figure 5 explores the effect of positron concentration p on IACWs structures by plotting equation (30) against χ for different values of p and keeping all other parameters fixed.It is noted that increasing values of p causes attenuation in the amplitude and width of IACWs.
The variations of equation (30) versus χ for different values of temperature ratio σ (keeping all other parameters fixed)are presented in figure 6.Clearly it is found that higher values of σ leads to reduce the amplitude and width of IACWs structures.
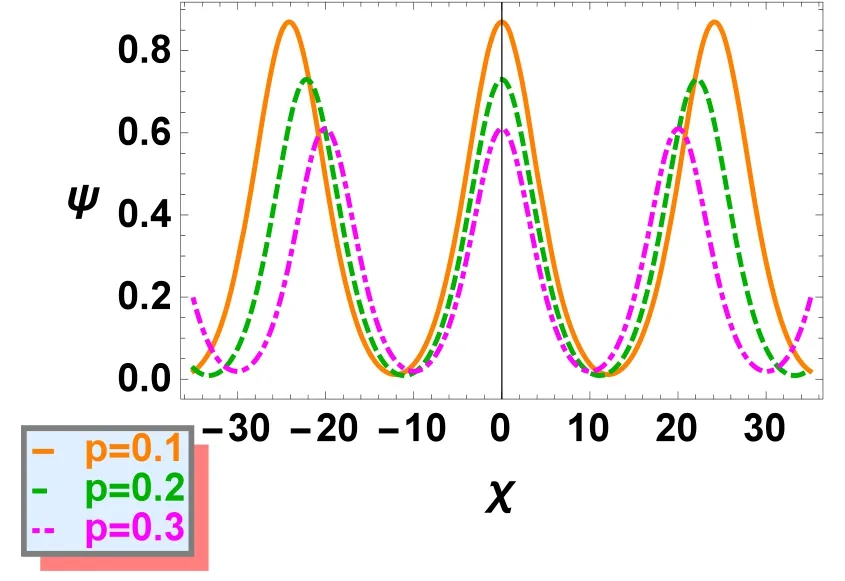
Figure 5.Variation of CW solution ψ versus χ for different values of p while σ=0.1, u0=0.1, Ω=0.3, l3=0.90, q=0.5, ρ=0.02 and E=0.04.
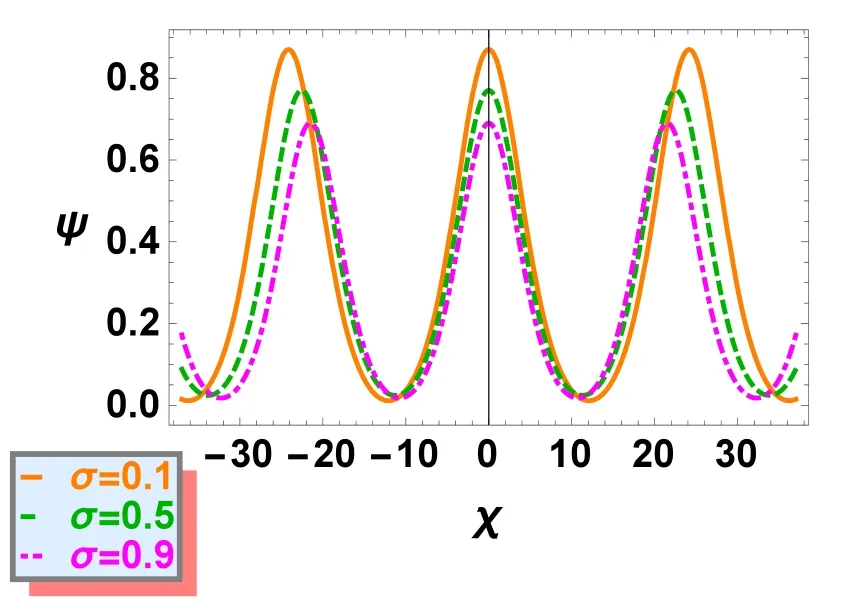
Figure 6.Variation of CW solution ψ against χ for different values of σ while q=0.5, u0=0.1, Ω=0.3, l3=0.90, p=0.1, ρ=0.02 and E=0.04.
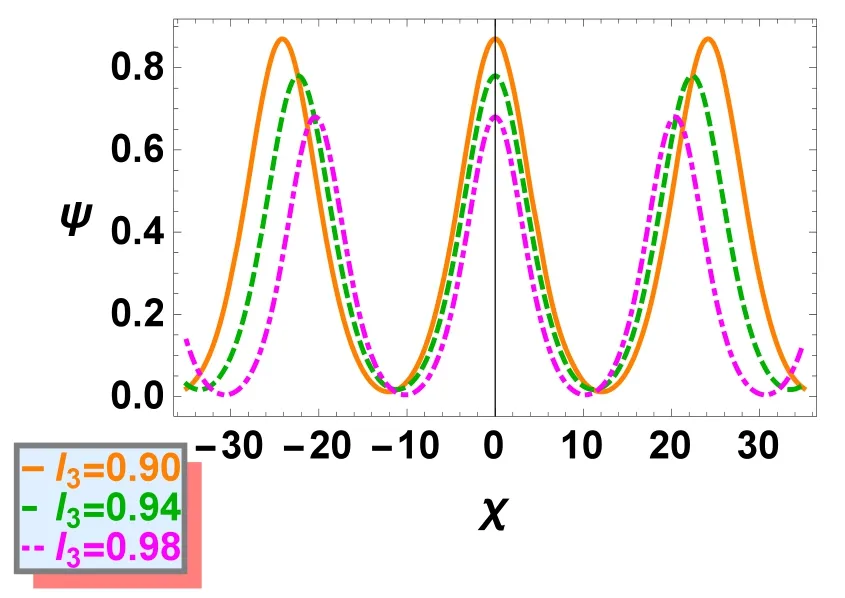
Figure 7.Variation of CW solution ψ versus χ for different values of l3 while q=0.5, u0=0.1, Ω=0.3, σ=0.1, p=0.1, ρ=0.02 and E=0.04.
Finally the effect of obliqueness angle as manifested via l3(related byl3=cosθ) on IACWs is presented by plotting CW solutionψ(χ)versus χ as shown in figure 7.It is clearly found that lower values of θ or higher values of l3give lower amplitude IACW profiles.
6.Conclusion
To summarize, the propagation of nonlinear electrostatic IA periodic waves is studied in magnetized EPI plasmas with electrons following a nonextensive distribution and Maxwellian positrons.By employing RPT, the KdV equation has been obtained and its CW solution is analyzed.Due to the variation of given plasma parameters, our model only supports the compressive nonlinear IACW structures.Further, it is concluded that both amplitude and width of the IACWs decrease with increasing values of q, p, σ and l3.
Our results clarify the nonlinear periodic electrostatic structures that propagate in space and astrophysical environments, where magnetized EPI plasma with nonextensive electrons and Maxwellian positrons may exist, like stellar polytropes [14], pulsar magnetosphere [37] and protoneutron stars [38].
Appendix.Derivation of equation (30)
Let define
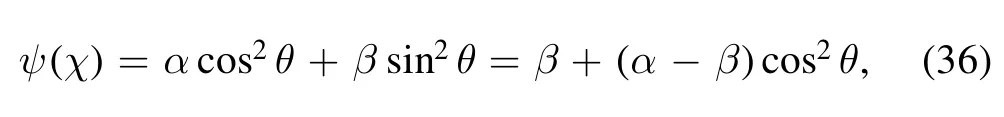
where θ is a function of χ,i.e.θ θ χ= ( ),using equation (36)in equation (27), we get:
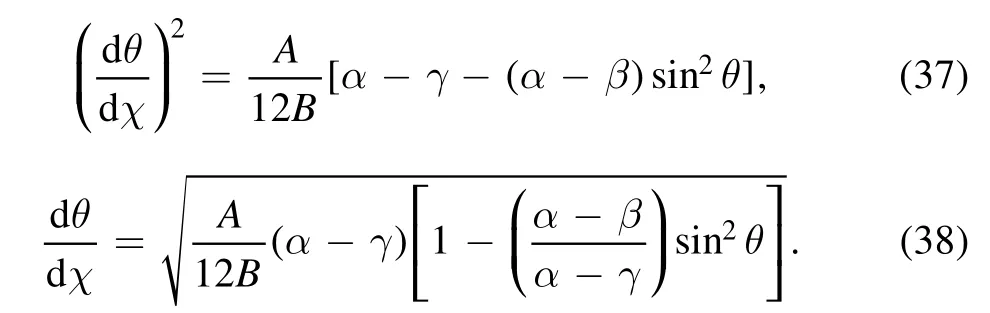
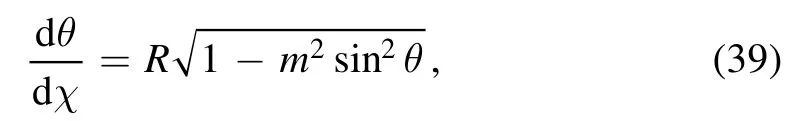
using separation of variables method and integrating,we have
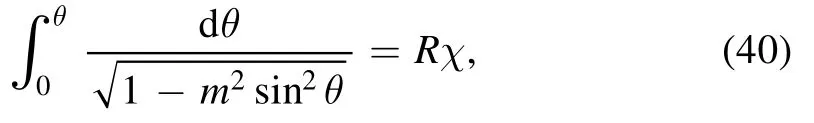
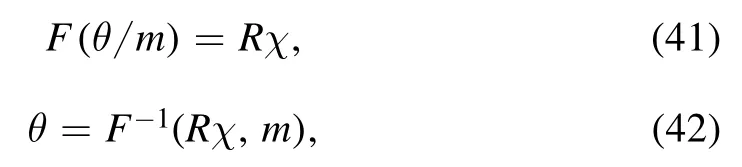
put equation (42) in equation (36), we get

 Plasma Science and Technology2021年3期
Plasma Science and Technology2021年3期
- Plasma Science and Technology的其它文章
- In-situ reduction of silver by surface DBD plasma:a novel method for preparing highly effective electromagnetic interference shielding Ag/PET
- Preliminary study of an open-air watercontacting discharge for direct nitrogen fixation
- Simulations of standing wave effect, stop band effect,and skin effect in large-area very high frequency symmetric capacitive discharges
- Experimental study of ELM-induced filament structures using the VUV imaging system on EAST
- Nonlinear evolution and secondary island formation of the double tearing mode in a hybrid simulation
- Experimental study of sheath potential coefficient in the J-TEXT tokamak
