Simultaneous optimization of even flow and land and timber value in forest planning:a continuous approach

José M.González-González,Miguel E.Vázquez-Méndez and Ulises Diéguez-Aranda*

Abstract

Keywords: Even-aged forest management,Forest-level optimization,Continuous optimization,Gradient-type algorithms

Background

A forest can be considered a set of stands, which are contiguous communities of trees sufficiently uniform in composition, age-class distribution and site quality,to distinguish each community from its adjacent ones(Helms 1998). In forest planning, decision-making processes often use optimisation approaches for developing optimal harvest schedules that will best meet the objectives of the landowners or land managers (Kaya et al.2016).The main issue consists in determining when(and how) to harvest each stand during the planning horizon(nextPyears),to achieve the proposed objectives.To formulate this problem, it is necessary to have a simulator that allows predicting the development of forest stands efficiently and accurately.In the last decades,many papers have been devoted to this topic (see, for instance García 1994; Castedo-Dorado et al. 2007; álvarez-González et al. 2010), and for any well-know species can be assumed that output functions are available,given,for example,the timber volumeVj(y)(volume/area) of the standjalong the time. To clearly show the novelty and interest of this work,we begin by analyzing different formulations of the forest planning problem in the optimization framework.For simplicity,we assume that maximizing timber volume is the main objective.Without any additional hypothesis,denotingAjthe area of standj, the problem is to determine the harvest ratehrj(y)(area/time)of each stand over time(Heaps 1984;2015),such that

Within the framework of the binary linear programming(BLP), the exact solution of (4) can be obtained by the branch and bound or cutting plane methods,as long as the problem does not exceed a certain relatively small dimension (Bettinger et al. 1999). For large problems, a spatial application of the RC method can be also useful(Pukkala et al.2009).Additionally,problem(4)also accepts a combinatorial formulation in the frame of non-linear integer programming(NLIP),by considering the harvest instants y =(y1,...,yns)as the decision variables.In this case,(4)is equivalent to find vector y such that

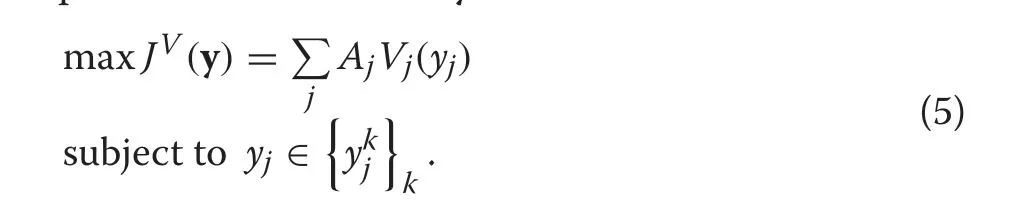
This formulation is more appropriate if a heuristic method is used to solve the problem (which generates a solution within a reasonable amount of time, although of uncertain quality(Davis et al.2001,p.741;Bettinger et al.2009,p.172).

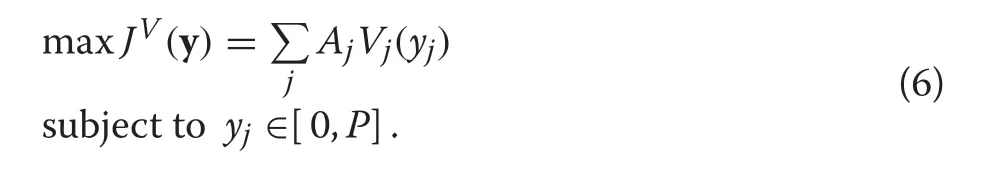
If hypothesis H1 is not considered,then H2 is equivalent to assume thathrj(y)=Ajδ(y-yj),and without any additional assumption,problem(1)changes into the following non-linear problem(NLP)Now,hypothesis H1 can be understanding as a discretization of the continuous variable of this NLP, and if it is assumed (what may be necessary if the dimension of the problem –number of stands–, is high and the available methods do not work in a reasonable time), problem (6) becomes straightly the previous NLIP problem(5). Equivalences and transformations between all these formulations are summarized in Fig.1.

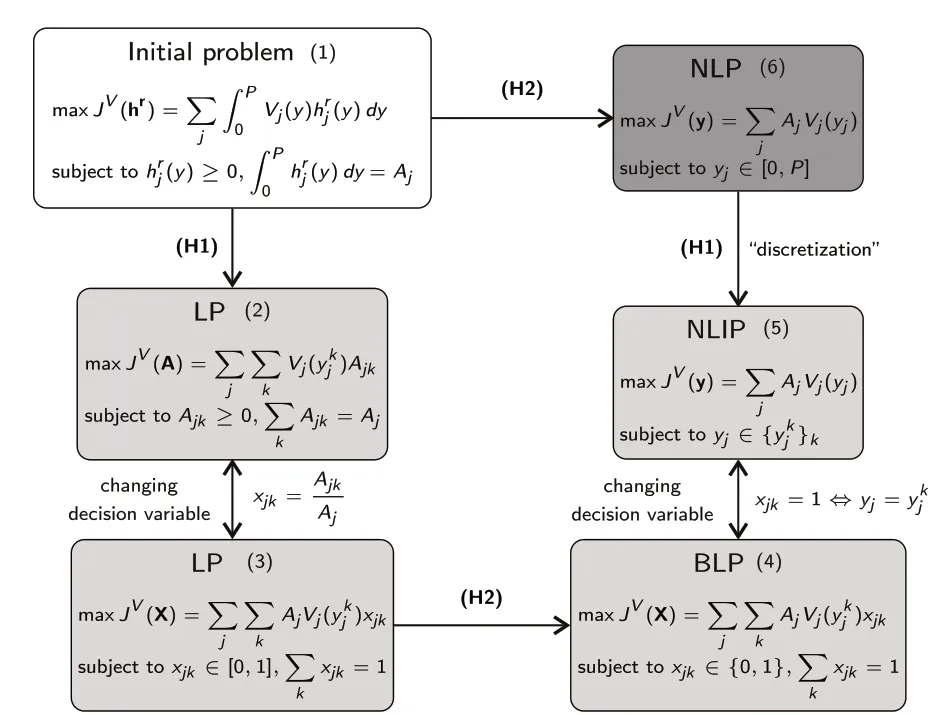
Fig.1 Equivalences and transformations between different formulations of the forest planning basic problem(harvest scheduling problem)

Problems(3)-(6)can be improved by considering more sophisticated goals,such as land and timber value(LTV).They can also be completed with additional objectives and/or constraints related to even flow of products (EF),size of contiguous area harvested(spatial constraints),etc.There are many papers dealing with models based on formulations (3)-(5), and Table 1 includes some examples classified by the formulation type,and the objectives and constraints considered. On the contrary, due to the inheritance of the original LP formulation, and to the apparent absence of suitable methods for numerical resolution,models based on the continuous formulation given in problem (6) have been much less explored (see, for instance, Roise 1990). The aim of this work is to help fill this gap in the forestry literature, by presenting a novel continuous bi-objective model in forest planning.

In recent papers,Arias-Rodil et al.(2017)and González-González et al. (2020) presented rigorous mathematical analysis of two continuous metrics for measuring,respectively,land expectation value(LEV)and EF.In this work,without losing their good properties for working with gradient-type methods, these metrics are appropriately modified to deal with the scheduling harvest problem of a forest, assuming future rotations based on economically optimal management prescriptions at stand level. These modifications include a novel way to estimate the planning horizon in an automatic manner, and the possibility that a stand is harvested several times.The combination of these new metrics leads to a biobjective model,which can be efficiently solved by using gradient-type techniques, does not require to set management prescriptions in advance,and avoids the division of the planning horizon into periods, therefore resulting an useful tool for the decision-making processes in forest planning.

The paper is organized as follows.In Methods section,the new metrics are detailed in a suitable mathematical framework, and the forest planning problem is formulated by means of the new continuous bi-objective model,which is studied from a cooperative point of view,proposing a numerical method to obtain its Pareto-optimal frontier.The efficiency and accuracy of the numerical method is shown in Results and discussion section,where results in someEucalyptus globulusLabill. forests are presented and discussed. Finally, some interesting conclusions are summarized in Conclusions section.

Methods

Mathematical framework

To formulate the forest planning problem, we need a growth simulator which allows prediction of stands development. To that end, we used the dynamic systemsbased framework (frequently referred to as “state-space”approach),first used in forestry by García(1994).Particularly,our approach is based on:

(i) Each standjis characterized by three state variables:mean height of dominant trees in the stand(Hj,inmeters),number of stems per hectare(Nj),and stand basal area(Gj,in m2/ha).

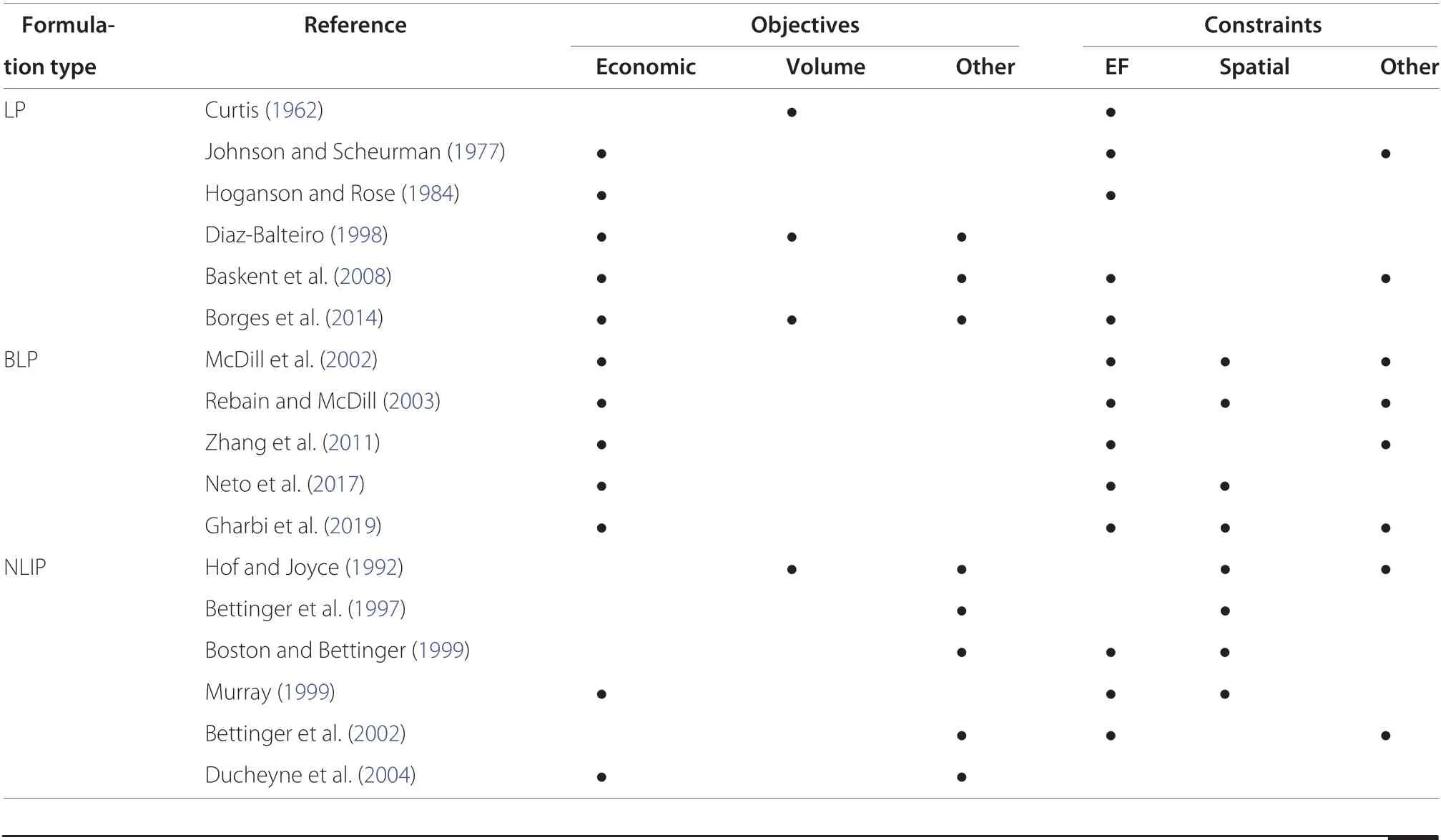
Table 1 Literature review:some references dealing with optimization models for forest planning.They are grouped by the formulation type and classified according to the objectives(columns 3-5)and constraints(columns 6-8)considered

(ii) Outputs can be obtained from the predicted values of these state variables.For example,the timber volume(in m3/ha)is given by a known species-specific functionvj(H,N,G).

Economic metric:the land and timber value(LTV)

The economic value of the forest is the sum of the value of each standj,which depends on:

wherer∈(0,1]is the interest rate,andRj(ˉtj)andCj(ˉtj)represent,respectively,functions of present values of revenues and costs.

The land and timber value (LTV) can be defined as the present value of the sum of the timber value at the first clearcutting and the LEV just after clearcutting. For each standj, it depends not only on the time of the first clearcutting (yj), but also on the future rotation age (ˉtj).We only seek foryjand, consequently, ˉtjhas to be set in advance.We assume future rotations based on the optimal management prescription at stand level,in such a way thatˉtjis the solution of the following optimization problem

The regularity properties ofJLTVare given by the properties of functionshj,nj,gjandvj,and we can assume that it is smooth enough(Arias-Rodil et al.2017).

Even flow(EF)metric

Even flow (EF) and sustained yield are two of the oldest objectives of forest management. The first has been related to the concept of maintaining a stable timber supply (nowadays provisioning ecosystem services) through appropriate forest planning and management techniques.There are numerous examples of how to address the even flow issue in harvest scheduling. Some studies use constraints that ensure volume levels in each period within some upper and lower limits (O’Hara 1989; Murray and Church 1995) or that allow a certain variation in volume between periods(McDill et al.2002;Constantino et al. 2008), while others include even flow as an objective in which volume variations between periods should be minimized (Kao and Brodie 1979; Brumelle et al. 1998;Ducheyne et al.2004).

In this study we recover the concept of harvest rate(now volume/time) and seek for a constant rate during a period ofTyears, named tentative planning horizon for even-flow. It represents the period for which, clearcutting all stands at least once time, a stable timber supply is desired. The value ofTis a technical decision, which depends on the species,site qualities,stand ages...of the forest.

We consider that interventions may not begin at the present time if, for example, the forest is too young. We denote bylj ＞0, in years, the minimum harvest age for each standj, in such a way thattj≥ljshould be verified. From these bounds, the instanta≥0 (years) when harvests can begin in the forest is given:it will be zero if any stand can be harvested now, otherwise it will be the minimum time guaranteeingtj≥lj.Specifically:

Taking into account that a management prescription can be greater thana+T, and assuming that all stands have to be harvested at least once during the planning horizon,its upper limit must be automatically computed by

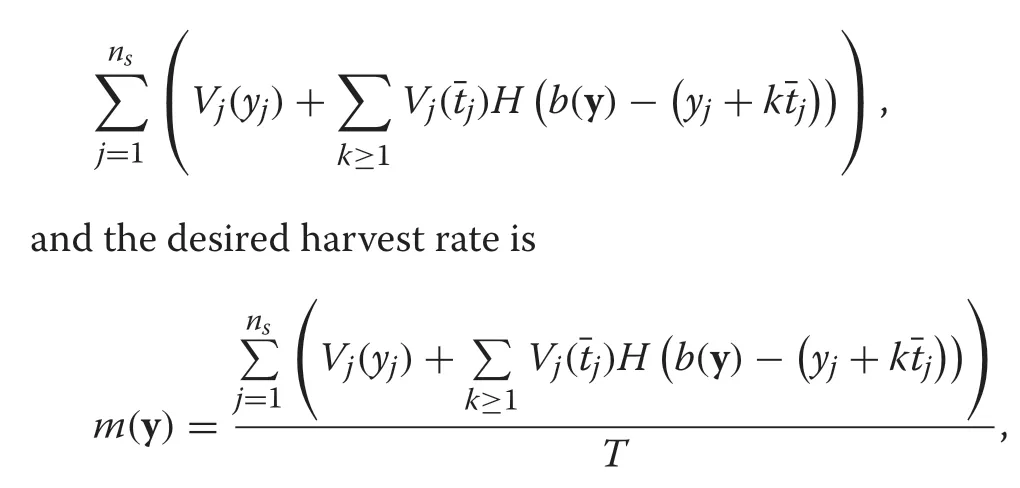
whereH(y)is the Heaviside function(Oldham et al.2009,Ch.9).Therefore,from the EF point of view,the objective is to achieve the next goal harvest rate function(see Fig.2)

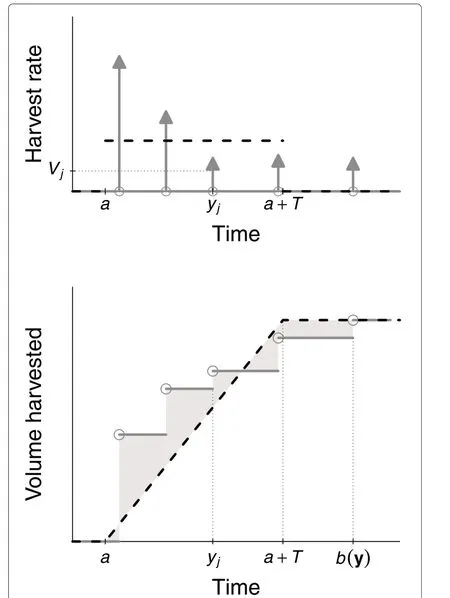
Fig.2 Example of harvest rate(top)and volume harvested(bottom).The grey solid lines represent real instant harvests(top,Eq.(10))and real volumes harvested(bottom,Eq.(12)),while the black dashed lines represent goal harvest rate functions(top,Eq.(9))and goal volume harvested functions(bottom,Eq.(11))

The Dirac delta is not a function in the traditional sense,so the comparison between expressions(9)and(10)is not appropriate. Instead of comparing harvest rates we propose to compare the volumes harvested (goal and real),which are obtained by integrating those expressions (9)and(10):

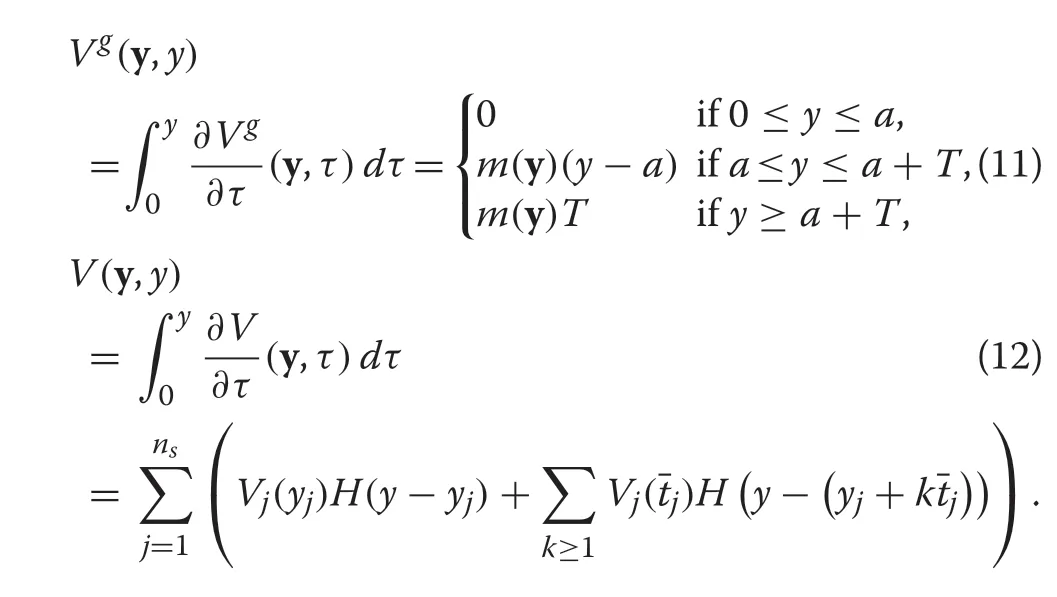
The EF metric must measure the distance between both functions for the planning horizon[a,b(y)].By using the associated distance to theL2norm(Adams 1975),for any planning strategy y ∈Yad,it is given by

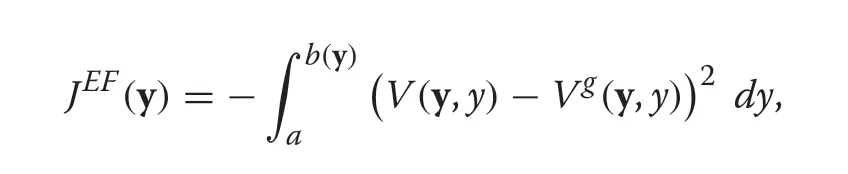
where the minus sign is included precisely so that a higher value ofJEF(y)corresponds to a greater similarity of the functionV(y,.)to the goal functionVg(y,.),which is what is meant by a higher even flow.

Following (González-González et al. 2020), it can be proved that functionJEFhas continuous derivatives in almost all points,and an explicit expression for its gradient can be obtained.

Bi-objective model

In this work, it is assumed that the main goal of forest planning is to determine the management prescriptions to be applied to each stand (i.e., to determine y ∈Yad) to get the best profitability(i.e.,to maximizeJLTV)with the highest possible even flow(i.e.,to maximizeJEF).Hence,the following Bi-objective Optimization Problem(BOP)is considered:

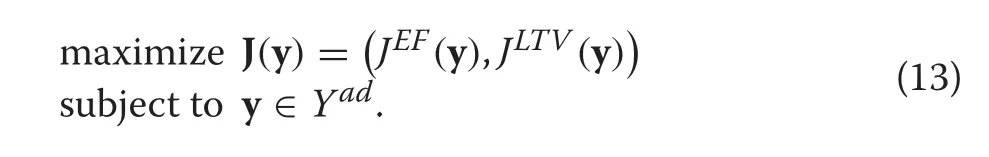
This problem must be studied from a cooperative point of view, looking for non-dominated admissible vectors,also known as efficient solutions or Pareto optima. An admissible vector y ∈Yadis said dominated if there exists a better admissible vector, in the sense that it improves at least one objective, without making the other worse.If y ∈Yadis non-dominated (Pareto optimum), the corresponding objective vector J(y)∈R2is also known as Pareto-optimal, and the set of Pareto-optimal objective vectors is known as Pareto frontier (see Fig. 3). A more detailed definition can be seen,for instance,in Miettinen(1998,p.11).

As commented above,the final aim is to determine the management prescription to be applied to each stand.Therefore, a satisfactory solution must be chosen within the set of Pareto optima.A satisfactory solution is the best compromise for the preferences of the decision maker.These preferences may be articulated prior to the analysis(allowing to reformulate the BOP into a single objective problem through weights or/and treating some objectives as constraints),after graphing the Pareto frontier,or interactively in a progressive way (requiring to compute only some Pareto optima) (Miettinen 1998, pp. 61-65). In the next section we propose a numerical method for obtaining the set of Pareto optima and graphing the Pareto frontier.It allows to articulate preferences a posteriori,resulting in a very interesting tool for the decision-making process in forest planning.

Numerical resolution

Regarding BOP (13), to take advantage of the regularity properties ofJLTVandJEF, we propose to obtain the Pareto frontier by the weighting method (Miettinen 1998, pp. 78-84), solving each single-optimization problem by a gradient-type method, combined with a random multi-start if local minima are detected. It is also advisable to normalize the objective functions so that their objective values are of approximately the same magnitude. For the results presented in the next section, both objectives were normalized using the ideal objective vector (that obtained by maximizing each of the objective functions individually subject to the constraints of the problem) and an estimation of the nadir objective vector (given by the value of each objective function at the point where the other objective function reaches its maximum) (Miettinen 1998, pp. 15-19),weights were taking equally spaced, and the L-BFGS-B algorithm was used again without any multi-start procedure. To check this approach, BOP (13) was also solved by the evolutionary algorithm NSGA-II(Deb et al.2002), widely used in multi-objective optimization, and already implemented in the Python library Inspyred 1.0(Tonda 2020).

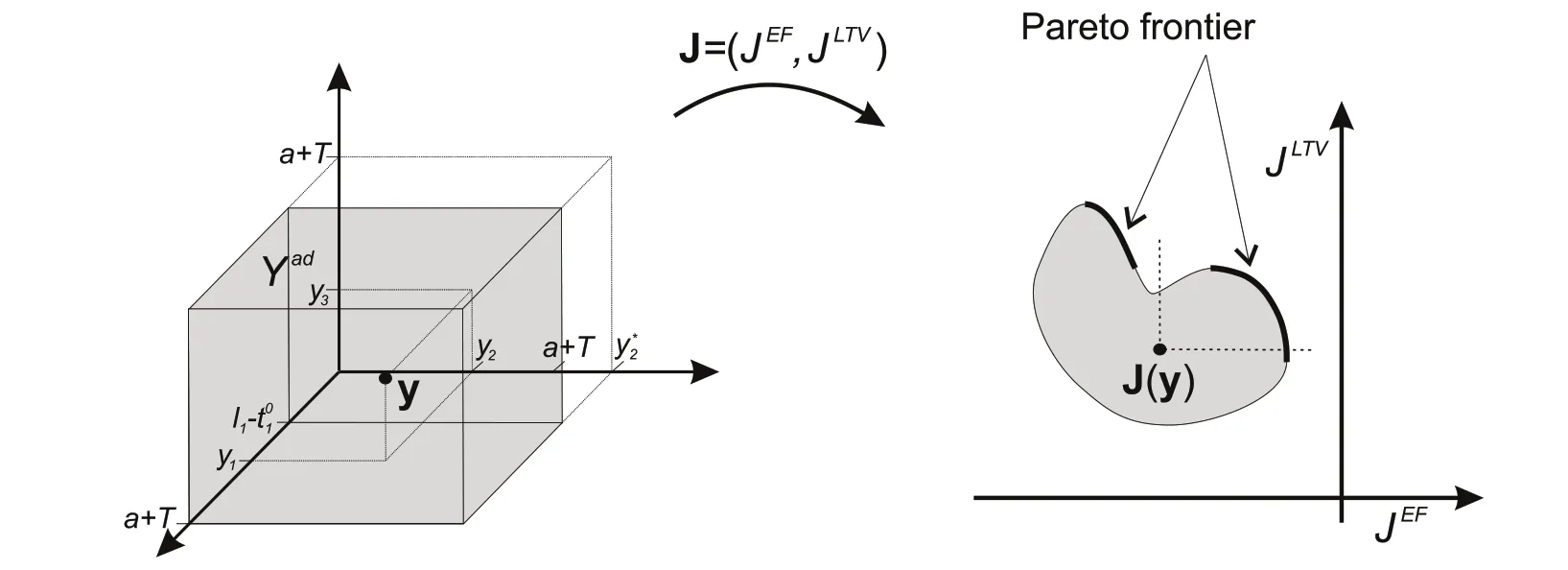
Fig.3 Example of an admissible set Yad ?R3(corresponding with ns =3)and an image set J(Yad)?R2,where the Pareto frontier is highlighted

Results and discussion

We analyzed the usefulness of our approach in a real forest ofEucalyptus globulusLabill. located in the municipality of Xove (Galicia, NW Spain), considering a tentative planning horizon for even flow ofT= 13.5 years. The forest comprisesns= 51 stands whose area and inventory data can be seen in Table 2. From these data, the state variables until clearcutting are computed from the specific transition functions given by (García-Villabrille 2015).Specifically:

After clearcutting,we assume no changes on site quality (site index) and a constant plantation density of 1333 trees/ha for all stands.Under this hypotheses,by using an appropriate function for initializing the stand basal area(García-Villabrille 2015),we predicted the data at one year after clearcutting(see Table 2).These data were used for computing the state variables (and outcomes) after the first clearcutting. To further test our approach in a forest with a different structure,we also used these data for simulating a hypothetical forest(hereinafter the simulated young forest)with 51 stands of the same species,area and site index,but all at one-year age.

For the real forest of the case study, Fig. 4 shows the Pareto fronts obtained with the weighting method and with the NSGA-II, for a population size ofP=200 individuals andG=500 generations. Additionally, this figure also shows the comparison between real and goal volumes corresponding to all (ten) Pareto optima obtained with the weighting method. The corresponding results for the simulated young forest can be seen in Fig. 5. In view of these results, it can be highlighted that:

· Both methods,although using different techniques,provide the same Pareto fronts,which warrants the appropriateness of our approach.

· The continuous approach works well for forest with very different stand structures,as suggested from the results of the real forest(which has many mature stands of different ages)and the simulated young forest(in which all stands are of the same age).

· Figures 4 and 5 are very useful for the decision-making process:

– In the top graphs,the normalized-JLTVisJLTV/JLTV(y*),i.e.,the LTV divided by its best value.This way of proceeding allows an intuitive comparison of the different optimal management strategies:for the real forest,there was a reduction of about 8%in LTV between the best solutions from the economic and even flow perspectives(points 1 and 10 in the Pareto front,respectively),while for the simulated young forest it was of only 5%.

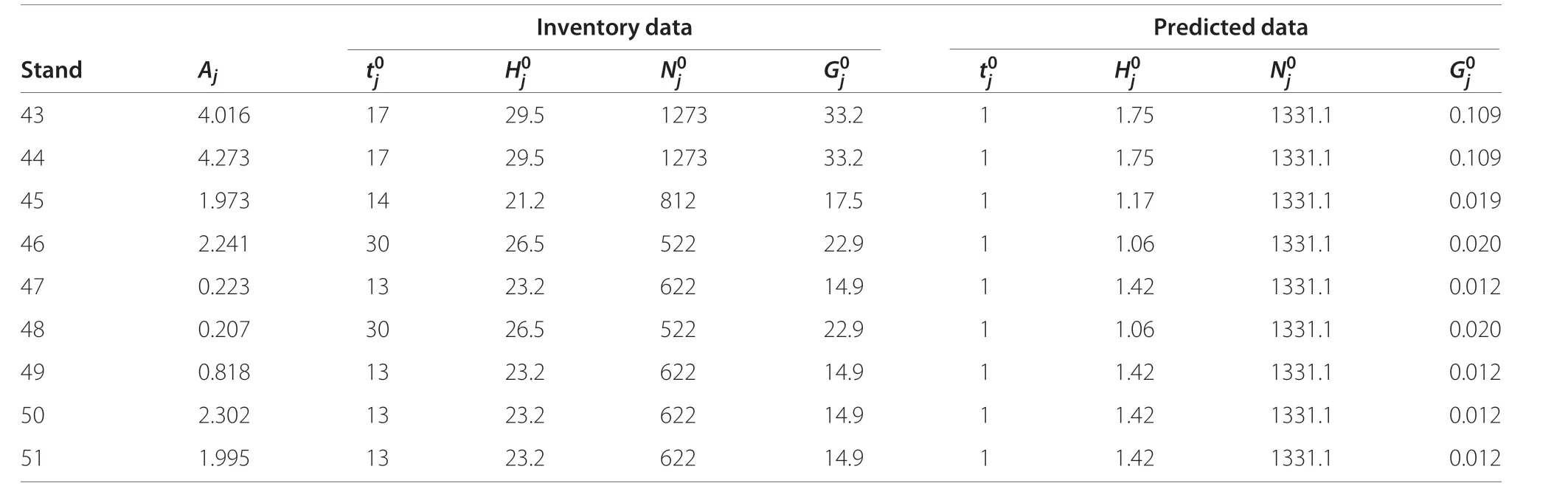
Table 2 Inventory data and hypothetical predicted data at one year after clearcutting for the forest of the case study.Aj:stand area in hectares,t0j:stand age in years,H0j:dominant height in meters,N0j:number of trees per hectare,G0j:stand basal area in m2/ha(Continued)

– The even flow metric has not such an easy interpretation in terms of numerical values,but the grey area of the bottom graphs of the figures clearly indicates the achievement of the even flow objective as well as the moment in which the clearcuts are done.Additionally,these graphs also show the total harvest volume of each Pareto optimum,which is reduced as the even flow objective is improved.

Finally, to analyze our continuous approach in larger forests, we simulated two new hypothetical forests: one with 204 stands and other with 1632 stands. They were obtained by replicating the stands of the real forest 4 and 32 times,respectively,and randomly generating their area between the minimum and maximum real-area values.Then,we solved the problem on the simulated forest with 204 stands and observed that the weighting method captured the complete Pareto front in a very reasonable time (about half a minute), but the NSGA-II needed a greater number of generations than the previous experiments with the 51-stand forests and, consequently, a higher computation time.This fact was confirmed by the results obtained on the simulated forest with 1632 stands,where the weighting method kept providing the complete Pareto front in an acceptable time(about seven minutes),but the NSGA-II withG=2000 generations only captured a small arc(see Fig.6),with a computation time of about eleven hours. Table 3 summarizes the computation time of all performed experiments.

The use of non-linear continuous models to formulate the forest management problems has been scarce.In the framework of optimal control theory, Heaps(1984; 2015) studied the general problem of determining the harvest rate of each stand over time, but did not address with examples how the continuous forestry age class model he proposed could be solved numerically. Tahvonen (2004) discussed the use of discrete or continuous variables in describing time and age class structure in models for optimization of forest harvesting.Roise (1990) proposed and solved a continuous model,but without performing a mathematical analysis of the objective and constraint functions,applying optimization techniques that may not be the most adequate to solve the problem.On the contrary,the continuous model proposed in this paper uses functions with appropriate regularity properties, that guarantee a successful numerical resolution using gradient-type methods.

In this study we have dealt with a species whose main use is pulp production, therefore the land and timber value has been calculated on the basis of the stumpage price times the volume at the harvest instant. Nevertheless,for other species which require merchantable volume estimates,a more sophisticated method must be used.For example, in a study of optimization at stand level, Arias-Rodil et al. (2015) evaluated two alternative methods of estimating the merchantable volume of a stand at a given age: (i) a disaggregation system, which involves aggregating the merchantable volume previously predicted by diameter classes,and(ii)a stand volume ration function.The latter considers a top diameter limit for classifying the volume by timber assortments,while the former also allows specification of long length requirements.The use of alternative (i) may cause discontinuities in theJLTVfunction, which makes a gradient-based search challenging.However,alternative(ii)does not present any problem and,although will provide slightly higher optimal values ofJLTV,may even be more accurate(Arias-Rodil et al.2016).

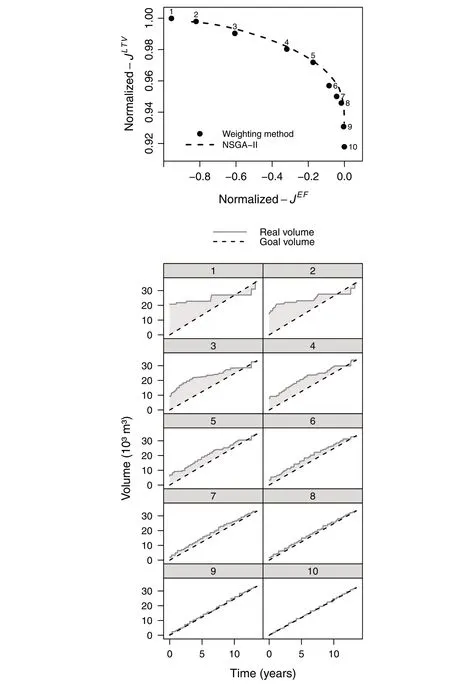
Fig.4 Results for the real forest:normalized Pareto front obtained with the weighting method and the NSGA-II(top),and comparison between real and goal volumes for the points obtained with the weighting method(bottom)

Fig.5 Results for the simulated young forest:normalized Pareto front obtained with the weighting method and the NSGA-II(top),and comparison between real and goal volumes for the points obtained with the weighting method(bottom)

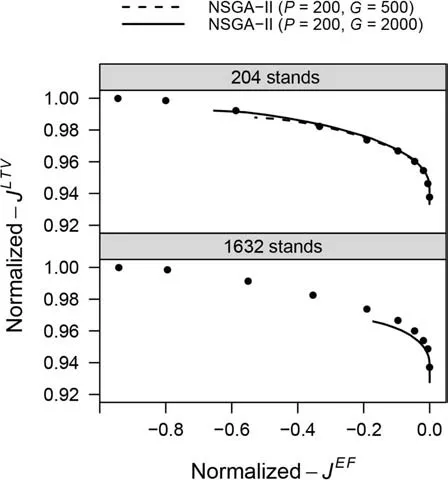
Fig.6 Normalized Pareto fronts obtained with the weighting method(·)and the NSGA-II,for two simulated forest comprising 204 stands(top)and 1632 stands(bottom).The Pareto fronts obtained with NSGA-II correspond with a population size of P=200 individuals and a number of generations of G=500(dashed line)and G=2000(solid lines)

Our proposal provides a graphical tool to analyze the relationship(trade-off)between the two objectives,helping the landowners to choose a suitable weighting after seeing the effect of even-flow requirement on economic profitability. This methodology can include constraints and be extended to other objectives, in pairwise comparison or considering three or more objectives. In the latter case,despite a posteriori techniques combined with special visualization methods have been used in forest management problems (Borges et al. 2014), interactive techniques can also be useful (Diaz-Balteiro 1998). In any case, the features of the problem and the capabilities and type of the decision maker have to be considered before selecting the most appropriate solution method(Miettinen 1998,pp.227-231).

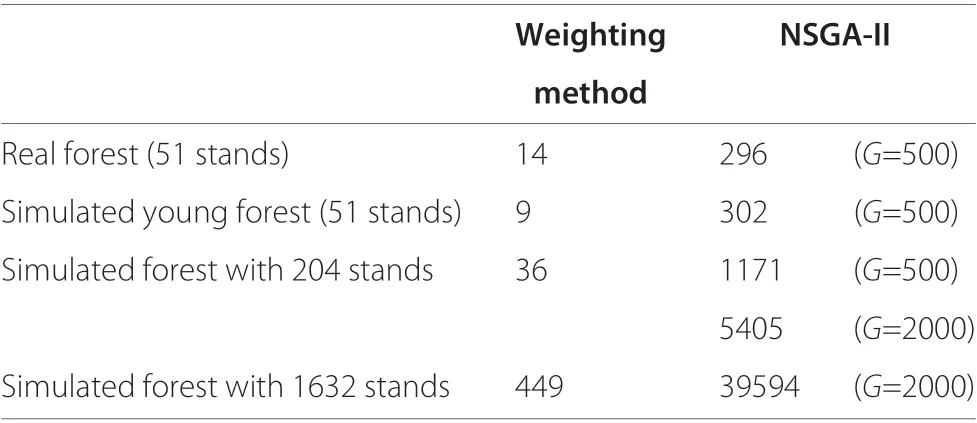
Table 3 Computation times(seconds)for obtaining the Pareto fronts shown in Figures 4,5 and 6 on an Intel?CoreTM i7 Processor 4 GHz iMac.Comparison,on forest with different structure or number of stands,between the weighting method and the NSGA-II with a population size of P=200 individuals and different number of generations(G)

Conclusions

In this paper we present a novel continuous bi-objective model (economic vs. even flow) in forest planning.According to the results obtained,it is worth highlighting the following aspects:

· The planning horizon is not set in advance and only a tentative value is required.It is involved in the optimization process and obtained as an output of the model.

· The LTV and EF functions have smooth enough properties,which allows the use of gradient-type methods for its optimization,behaving in a more efficient,effective and robust way than many other gradient-free methods commonly applied in forestry.

· The continuous formulation does not require to set management prescriptions in advance and avoids the division of the planning horizon into periods,providing solutions which may be better than those obtained with traditional combinatorial formulations.

· This model allows forest-level problems to be treated with continuous decision variables,in a way similar to that used generally with stand-level problems.As envisaged in previous works,the performance of the continuous approach combined with gradient-type methods improved as the forest size(the number of decision variables)increased.

· With this approach,it is not necessary to articulate the preferences of the decision maker a priori.Furthermore,the graphical outputs of our numerical method provide the Pareto front and other useful trade-off information in an intuitive way,which makes the proposed continuous bi-objective model a very interesting tool for the decision-making process in forest planning.

· This model was successfully used in forests comprising single-species,even-aged stands which are intended to be managed with the rotation forest management system.The applicability of the model in forests with more complex structures and dynamics(forests consisting of mixed stands,which have gradual advance regeneration,and are treated with partial cuttings)is the topic of an ongoing research.

Abbreviations

BLP:Binary linear programming;BOP:Bi-objective optimization problem;EF:Even flow;LEV:Land expectation value;LP:Linear programming;LTV:Land and timber value;NLIP:Non-linear integer programming;NLP:Non-linear problem;NW:North West

Acknowledgements

Not applicable.

Authors’contributions

All authors have contributed similarly in research planning,analysis,and writing of the manuscript.

Authors’information

JMG-G is a PhD Student focused in forest management planning with optimization methods.MEV-M is Associate Profesor and his research interests are optimal control of partial differential equations and numerical optimization with applications in engineering and environment.UD-A is Associate Profesor interested on quantitative methods for forest management(growth modelling,forest inventory and forest management planning).Currently,the three are working together on forest management planning within the framework of continuous optimization.

Funding

Not applicable.

Availability of data and materials

All data generated or analyzed during this study are included in this published article.

Declarations

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare that they have no competing interests.

Author details

1 Departamento de Enxe?aría Agroforestal,Universidade de Santiago de Compostela.Escola Politécnica Superior de Enxe?aría,R/Benigno Ledo,27002 Lugo,Spain.2Departamento de Matemática Aplicada,Instituto de Matemáticas,Universidade de Santiago de Compostela.Escola Politécnica Superior de Enxe?aría,R/Benigno Ledo,27002 Lugo,Spain.

Received:9 April 2021 Accepted:1 June 2021