ASYMPTOTIC STABILITY OF A BOUNDARY LAYER AND RAREFACTION WAVE FOR THE OUTFLOW PROBLEM OF THE HEAT-CONDUCTIVE IEAL GAS WH SY*
Lili fan(范麗麗)
School of Mathematics and Computer Science,Wuhan Polytechnic Unversity,Wuhan 430023,China E-mail:fll81@buve.cn
Meichen HOU(侯美晨)
School of Mathematical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China E-mail:meichenhou@amss.ac.cn

is a fundamental system to describe the motion of a compressible gas without the viscosity phenomenon,and it has many applications.Here the constantκ>0 is the coefficient of the heat conduction.Throughout this article,we will concentrate on the ideal polytropic gas
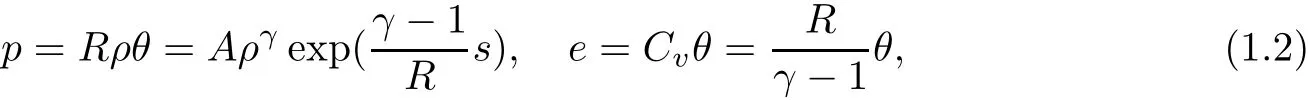
wheresis the entropy,γ>1 is the adiabatic exponent andA,Rare both positive constants.
As far as we know,most of the existing results in this field concern the analysis of the global-in-time existence and stability of the elementary wave for the heat-conductive ideal gas with viscosity;that is,there are many works on the large-time behavior of solutions to the compressible Navier-Stokes equations towards the viscous versions of the three basic wave patterns:rarefaction wave,contact wave,and shock wave,as well as their linear superpositions.We refer to([3–5,8,11,13,14,18,25,32])and some references therein for the Cauchy problem.
As for the initial-boundary value problem(IBVP),the boundary layer solution(BL solution)may appear.In[19],Matsumura considered the IBVP problem for the isentropic Navier-Stokes equations(the pressurep=Aργfor some constantA)and proposed a complete classification for the large time behavior of solutions.After that,many authors studied the IBVP problem for viscous and heat-conductive gas.For the isentropic case,Matsumura-Nishihara[22]studied the stability of the inflow problems of the boundary layer and its superposition with a rarefaction wave in different regions.Since then,Huang-Matsumura-Shi[9]proved the stability of the superposition of the boundary layer and the shock wave.Fan-Liu-Wang-Zhao[1]obtained the asymptotic stability of both the boundary layer solution and the supersonic rarefaction wave for a certain class of large initial perturbation.
For the non-isentropic case,the system for the viscous and heat-conductive gas is modelled by
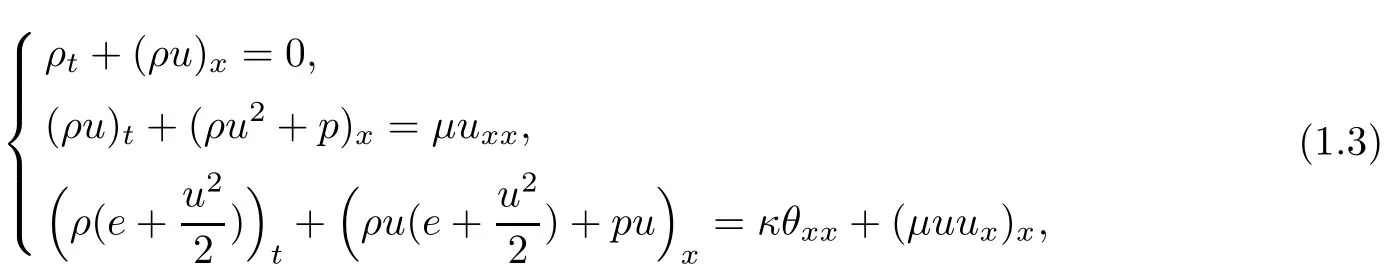
whereμ>0 stands for the coefficient of viscosity.According to the sound speed,the phase space is divided into the following regions to study the initial and boundary value problems:
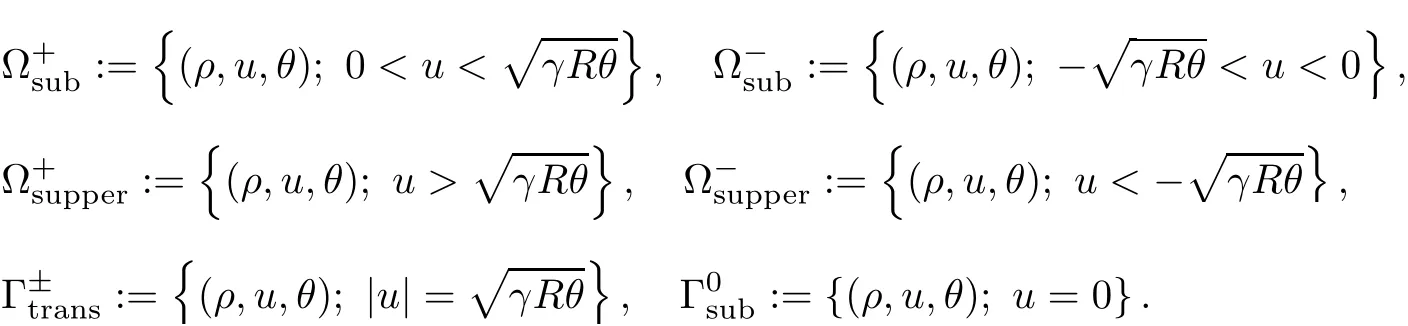
For different regions,there are different results.Huang-Li-Shi[7]studied the asymptotic stability of the non-degenerate boundary layer and its superposition with a 3-rarefaction wave for the inflow problems.Qin-Wang([27,28])studied the stability of the BL-solution and its superposition with a viscous contact wave and a rarefaction wave.For the outflow problems,Kawashima-Nakamura-Nishibata-Zhu[15]performed an existence and stability analysis of the boundary layer.Wan and Wang[31]also proved the stability of the stationary solution under a kind of larger initial perturbation.Recently,Nakamura-Nishibata[24]have proven the existence and stability of the boundary layer for a kind of general symmetric hyperbolic-parabolic system.For other works related to the IBVP problems of the compressible Navier-Stokes equations,we refer to([2,6,10,12,16,17,21,26,29]).
Motivated by these works,we will continue the study of the outflow problem for the system(1.1);this is the second in our series of articles on the initial-boundary value problem for the equations of heat-conductive ideal gas without viscosity in one-dimension.Here we will consider the outflow problem in the Eulerian coordinates governed by the system(1.1)in a half space with the initial data
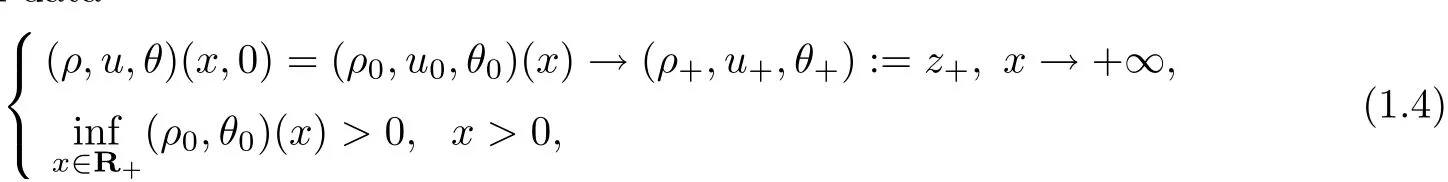
and where the condition on the boundaryx=0 is

Hereρ+>0,u+<0,θ±>0 are given constants,and the initial value(1.4)and the boundary condition(1.5)satisfy the compatible condition at the origin(0,0).In this manuscript,we will investigate the existence of a boundary layer solution(see Lemma 2.2)for problem(1.1),(1.4)and(1.5).Then the stability of the degenerate boundary layer,the 3-rarefaction wave,and the superposition wave to the system will be shown;this extends the result of[24]for this model.In this case,the strict monotonicity of the corresponding degenerate boundary layer solution and the 3-rarefaction wave play a crucial role.
It is well-known that,depending very much on the sign of the eigenvalues,different types of boundary states yield different possible configurations of the asymptotic states,which could consist of the rarefaction wave,the viscous shock wave,the viscous contact wave,the stationary boundary layer,or some combination of these.To simplify this problem,we investigate the solutions of(1.1)in a small neighborhood ofz+,which is denoted asU(z+),so the eigenvalues at the boundaryx=0 keep the same sign as at the far fieldx=+∞.Hence,as in[20],we divide the phase spacez=(ρ,u,θ)into new six regions:

Here we will consider the case that the solutionz=(ρ,u,θ)is in the shaded area as shown in Figure 1,i.e.,

Just under the assumption(1.6),two eigenvalues of the hyperbolic part of(1.1)are less than zero,i.e.,
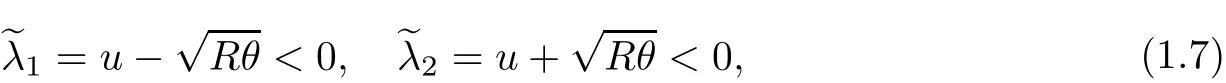
so the boundary conditions of(ρ,u)are unknown.We give the boundary condition(1.5)in order to make the problem well-posed,while(ρ,u)(0,t)cannot be assigned.Lack of these boundary conditions makes the outflow problem more challenging to analyse than the inflow problem.Firstly,due to the lack of boundary condition of velocity,we cannot investigate the outflow problem in the Lagrangian coordinates simply.Moreover,the lack of boundary conditions on density and velocity also prevents us from applying the integration by parts directly,so the trace of density and velocity on the boundary need to be handled by some subtle analysis.In particular,we use the interior relations between functions and the character of the domain itself(see(4.36),(5.7)),which is very helpful.We remark that in the study of the inflow or outflow problem,even for the scalar model,behaviors of solutions with a boundary effect are also complex and need to be handled with subtle techniques.

Figure 1
Furthermore,our arguments apply an elementary energy method to establish the a priori estimates.While system(1.1)as a hyperbolic-parabolic system is less dissipative than the viscous system(1.3),we need more subtle estimates to recover the regularity and dissipativity for the components of the hyperbolic part,and just to overcome this difficulty,more regularity on the solutions is required to enclose the energy estimates.We also need our solution to belong toC(H2),which is different from the viscous system inC(H1).
This article is organized as follows:in Section 2,we obtain the existence of the boundary layer foru+<0,list some properties of the boundary layer and the viscous rarefaction wave,and state our main results.In Section 3,we reformulate the system and establish the local existence of the reformulated problem.Then a series of a priori estimates are established and the main Theorem,2.5,is proved in Sections 4 and 5,respectively.
NotationsThroughout this article,candCdenote some positive constant(generally large).A?Bmeans that there is a generic constantC>0 such thatA≤CBandA~BmeansA?BandB?A.For function spaces,Lp(R+)(1≤p≤∞)denotes the usual Lebesgue space onR+with norm‖·‖Lp,andHk(R+)the usual Sobolev space in theL2sense with norm‖·‖p.We note‖·‖=‖·‖L2for simplicity.Ck(I;Hp)is the space ofk-times continuously differentiable functions on the intervalI,with values inHp(R+).L2(I;Hp)is the space ofL2-functions onIwith values inHp(R+).
2 Boundary Layer Solution and Main Results
In this section,we will construct the boundary layer,the smooth rarefaction wave for(1.1),and then state our main results.
2.1 Boundary layer



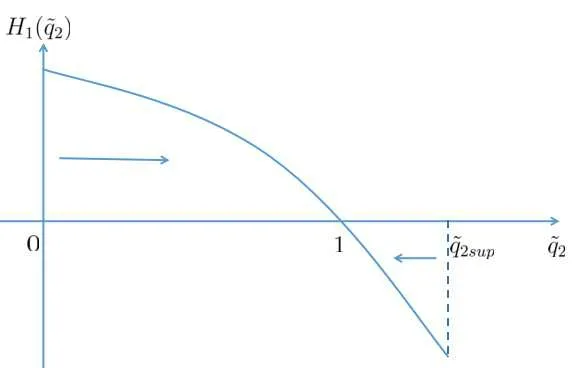
Figure 2
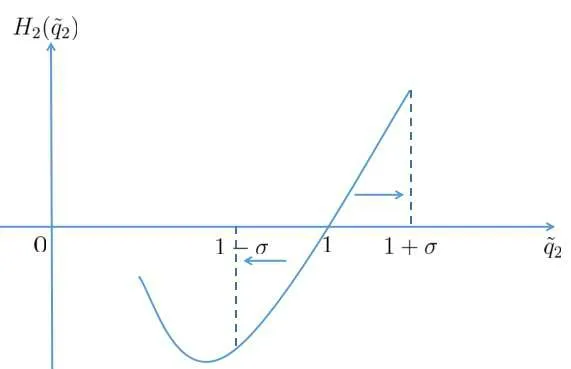
Figure 3

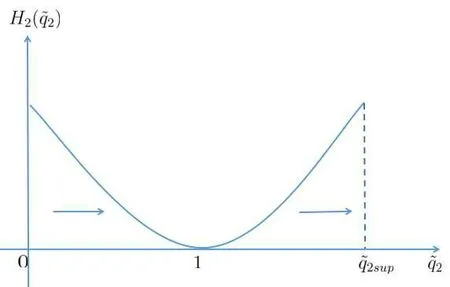
Figure 4
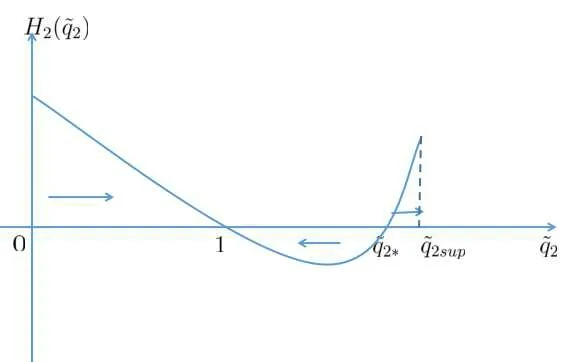
Figure 5

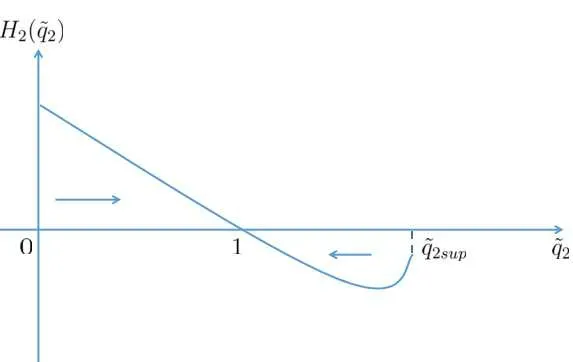
Figure 6
Summarizing(1)to(5),we have following proposition:
Proposition 2.1Whenu+<0,for the boundary value problem(2.11),we have following conclusions:




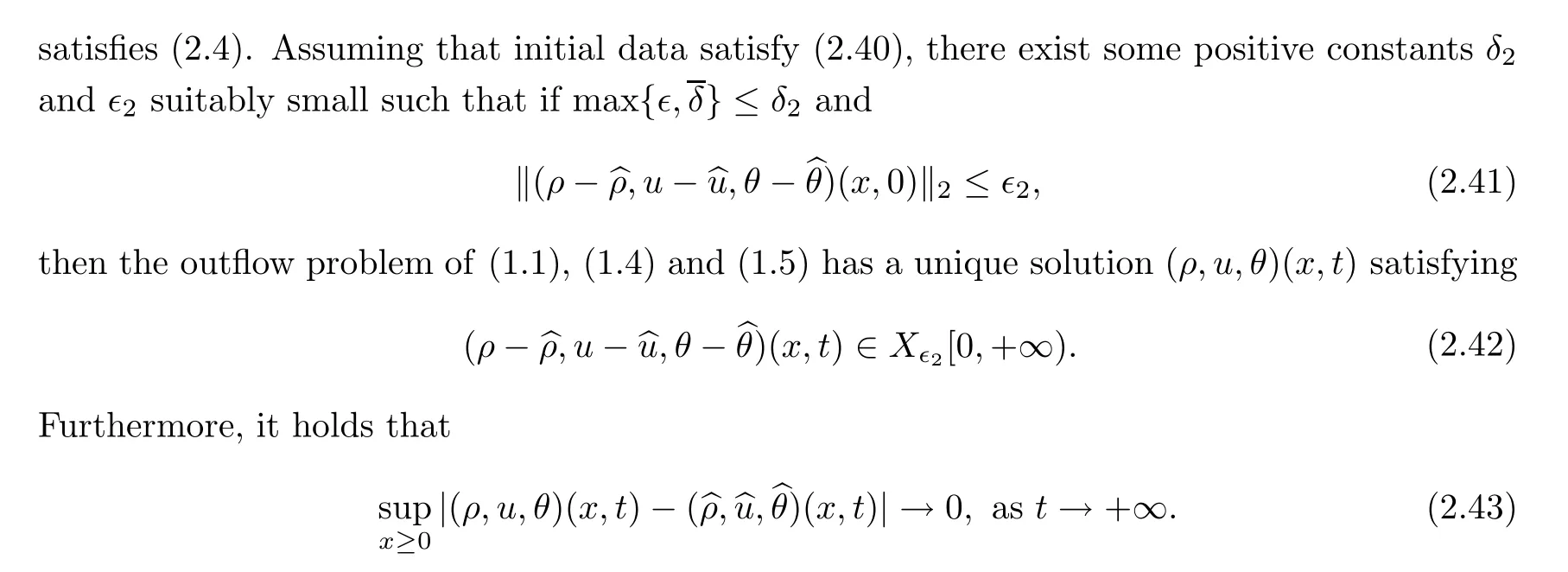
Remark 2.6Ifzm=z?,this result also implies that the 3-rarefaction wave solution is stable.
3 Reformed System and Propositions

then the reformulated problem is
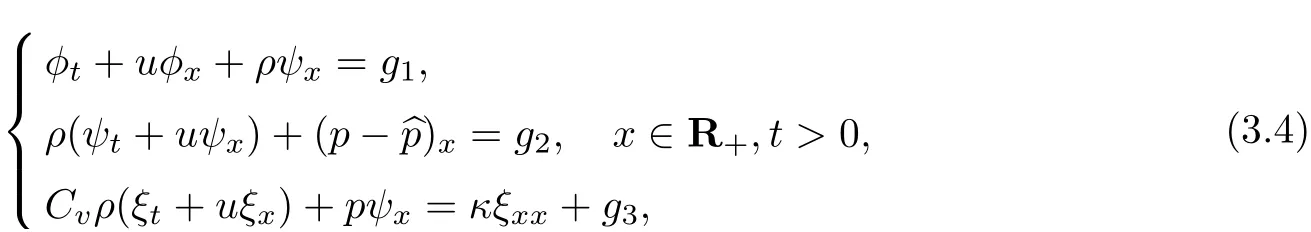
with the initial data and boundary condition
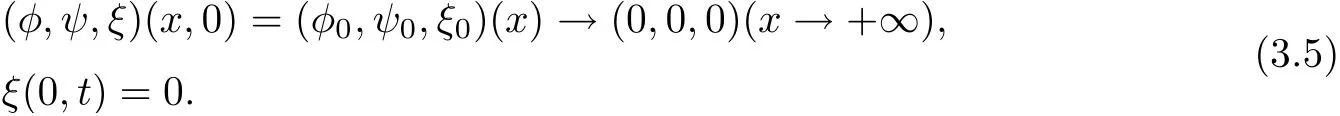
and
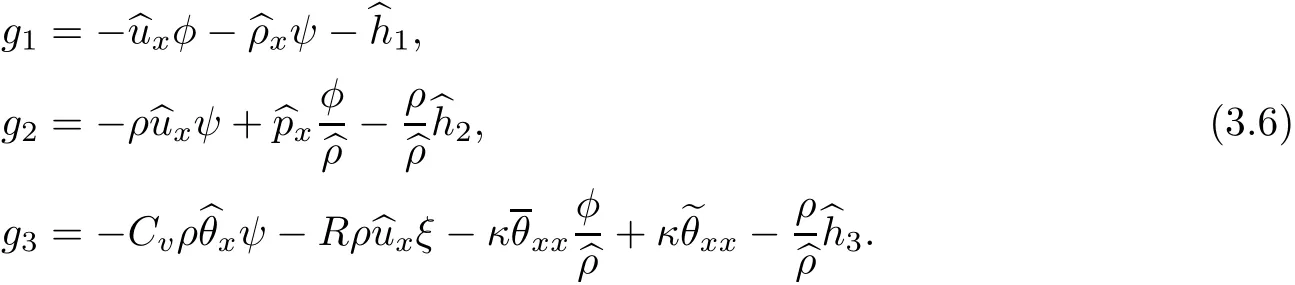
To prove our main result,the local existence of the solution to the problem(3.4)is stated in the following proposition:

and
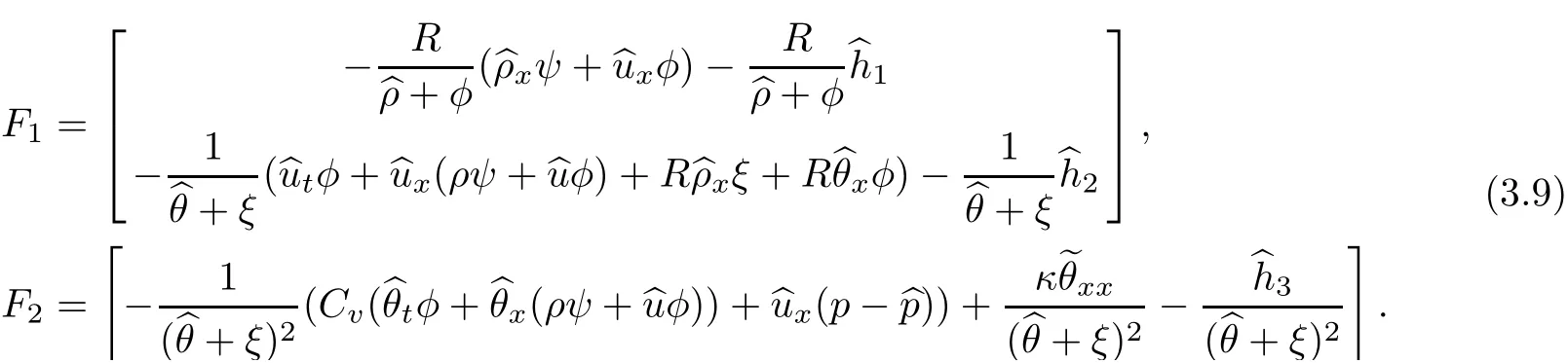
Then the local existence of solution for(3.7)in spaceXM(0,T)has been proven in[23]by the iteration method;we omit the details here for the sake of brevity.
Suppose that(φ,ψ,ξ)(x,t),obtained in Proposition 3.1,has been extended to some timeT(>t0),and we want to obtain the following priori estimates to get a global solution:

which,together with the Sobolev’s inequality,leads to the asymptotic behavior(2.43)in Theorem 2.5.
4 Basic Energy Estimate
In the next part of this section,we mainly prove the a priori estimates.Note that through our construction,the local solutionsare uniformly positive such that

for some positive constantm,which will be used later.Proposition 3.2 is proved by a series Lemmas.
Lemma 4.1Under the assumptions in Proposition 3.2,ifδ, ε ,N(t)are suitably small,then it holds fort∈[0,T]that
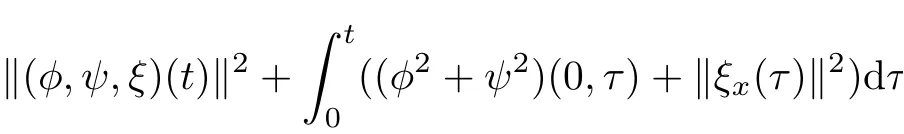






Integrating(4.34)overR+×[0,t],and using the results of(4.36)–(4.41)and Lemma 4.1,we can obtain(4.33)and complete the proof of Lemma 4.2.
Lemma 4.3Under the assumptions in Proposition 3.2,ifδ, ε,N(T)are suitably small,then it holds fort∈[0,T]that
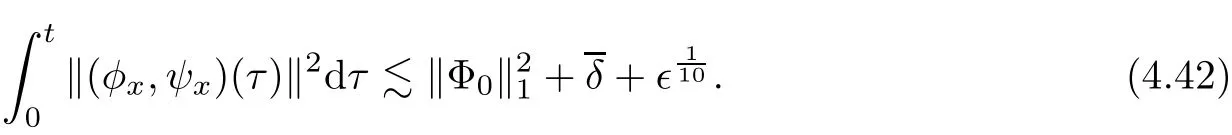
ProofWe multiply(3.4)2byand(3.4)3byψx,and combining these together,we get that
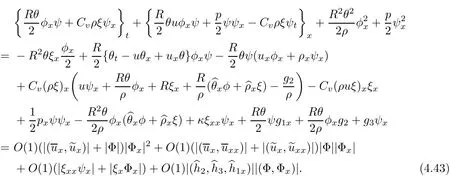
After integrating(4.43),using the results of Lemma 4.1–4.2,and similar to those estimates ofJ1,J2,J3,J4,we get(4.42),and omit the details.
Combining the results of Lemma 4.1–4.3,it holds that
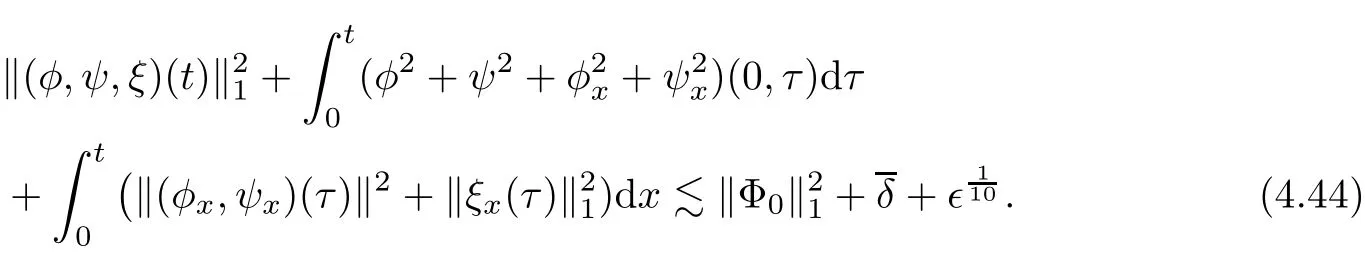
5 Higher Order Energy Estimate
In this section,in order to close the energy estimate,we consider the estimate of the second order derivative,and the following computations are formally obtained.One can verify all of them through the methods of the difference quotient in thexdirection and mollifiers in thetdirection:
Lemma 5.1Using the same assumptions listed as in Proposition 3.2,if,ε,N(t)are suitably small,it holds fort∈[0,T]that

ProofWe obtain this Lemma by three steps.
Step 1Multiplying(3.4)1xxbyRθφxx,we get
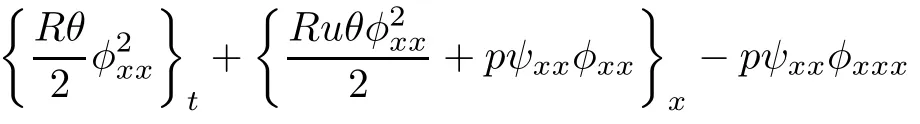


At same time,sinceφtx+(uφx)x+(ρψx)x=g1x,we see that
Inserting(5.20)into(5.19)and integrating the result onR+×[0,t],we obtain
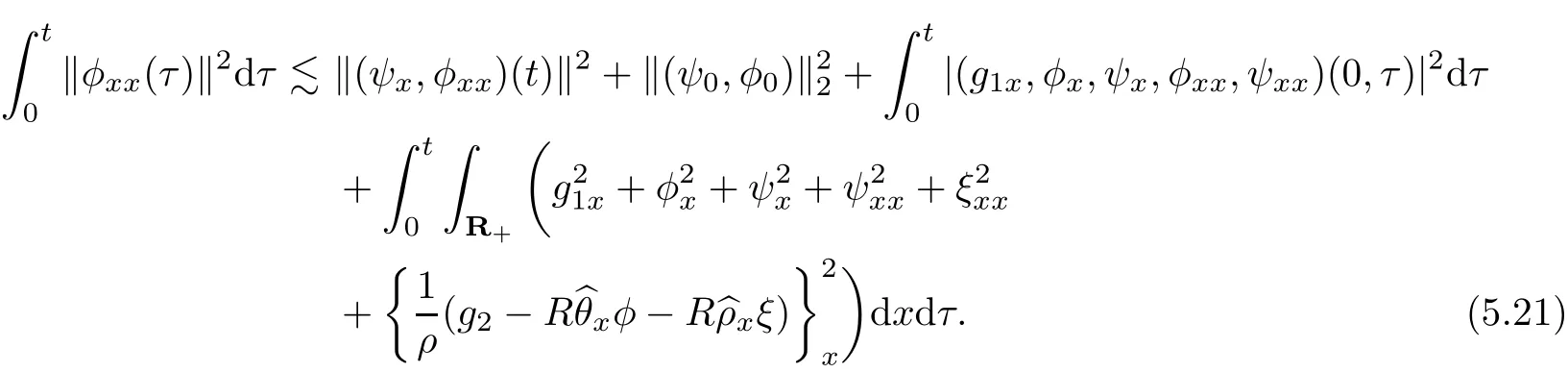
Combining the results(5.13),(5.17)and(5.21),and after choosing 0 Combining the estimates(4.44)and(5.1)together,we obtain(3.11).This completes the proof of Proposition 3.2. AcknowledgementsThe authors are grateful to Professors S.Nishibata,Feimin Huang and Huijiang Zhao for their support and advice.
 Acta Mathematica Scientia(English Series)2020年6期
Acta Mathematica Scientia(English Series)2020年6期
- Acta Mathematica Scientia(English Series)的其它文章
- IT?O DIFFERENTIAL REPRESENTATION OF SINGULAR STOCHASTIC VOLTERRA INTEGRAL EQUATIONS?
- ON THE NUCLEARITY OF COMPLETELY 1-SUMMING MAPPING SPACES*
- EXISTENCE AND UNIQUENESS OF THE POSITIVE STEADY STATE SOLUTION FOR A LTKA-VTE PEDPY MD WIH CING*
- ASYMPTOTICS OF THE CROSS-VARIATION OF YOUNG INTEGRALS WITH RESPECT TO A GENERAL SELF-SIMILAR GAUSSIAN PROCESS?
- THE DECAY ESTIMATES FOR MAGNETOHYDRODYNAMIC EQUATIONS WITH COULOMB FORCE*
- VAR AND CTE BASED OPTIMAL REINSURANCE FROM A REINSURER'S PERSPECTIVE*
