ASYMPTOTICS OF THE CROSS-VARIATION OF YOUNG INTEGRALS WITH RESPECT TO A GENERAL SELF-SIMILAR GAUSSIAN PROCESS?
Soukaina DOUISSI
Laboratory LIBMA,Faculty Semlalia,University Cadi Ayyad,40000 Marrakech,Morocco
Department of Statistics and Probability,Michigan State University,East Lansing,MI 48824,USA E-mail:douissi.soukaina@gmail.com
Khalifa ES-SEBAIY
Department of Mathematics,Faculty of Science,Kuwait University,Kuwait E-mail:khalifa.essebaiy@ku.edu.kw
Soufiane MOUSSATEN
Faculty of Sciences Mohamed first University,Oujda,Morocco
E-mail:moussaten.ump@gmail.com
Abstract We show in this work that the limit in law of the cross-variation of processes having the form of Young integral with respect to a general self-similar centered Gaussian process of orderβ∈(1/2,3/4]is normal according to the values ofβ.We apply our results to two self-similar Gaussian processes:the subfractional Brownian motion and the bifractional Brownian motion.
Key words self-similar Gaussian processes;Young integral;Breuer-Major theorem;subfractional Brownian motion;bifractional Brownian motion
1 Introduction
In the present paper we study the asymptotic distribution of a sequence of random processes having the form of a product of Young integrals with respect to a self-similar centered Gaussian process which does not necessarily have stationary increments.Our results obtained in this work can be seen as a generalization of the work of Nourdin and Zintout[1],when one replaces the two dimensional fractional Brownian motion(B(1),B(2))having identical Hurst parameterHby anyβ-self-similar Gaussian processes(G(1),G(2)).
Namely,the processes(G(1),G(2))are constraint to additional assumptions on their covariance structures(chosen to be equal)and their increments are assumed to satisfy fori=1,2;ss→0,forα=2β,that we call,inspired by[2],the increment exponent.Those kind of processes are of importance in practice,typically in mathematical modeling,when the data are shown to have exotic non-stationary correlation structures.
The main result of the paper is based on two major theorems:The first one is the recent work of Nualart and Harnett[2],which gives a version of the Breuer-Major theorem for functionals of generalized self-similar Gaussian processes,and the second one is a theorem proved by Corcuera,Nualart and Podolskij[3]which sets the convergence in law of weighted random sums.
The limit in law that we obtained is in the Skorohod spaceD([0,T]),whereTis a fixed positive time horizon and it’s discussed according to the value of the self-similarity orderβof the driving Gaussian process.This discussion came from the fact that the central limit theorem proved in[2]requires that the increment exponentαshould be strictly less than 2?1/dwheredis Hermite rank of the functionfwhich belongs toL2(R,μ),whereμstands for the standard Gaussian probability measure,that is,dx,for every Borel setA.As we worked with a function havingd=2,namely which is equal to the second Hermite polynomialH2,the exponent incrementαis supposed to be less than 3/2.Here,we also prove a central limit theorem for this function for the limit caseα=3/2,which will be presented in the preliminaries and proved in the appendix.The main result is presented in Section 3,while in Section 4,we apply the results obtained to two Gaussian processes with non-trivial covariance functions:The two-dimensional subfractional Brownian motion(S(1),S(2))with Hurst indexHand the two-dimensional bifractional Brownian motion(B(1),B(2))with parametersHandK.We proved in details that those two processes satisfy the required assumptions for which the main theorem holds.
2 Preliminaries
In this section,we recall some elements of Malliavin calculus along with some fundamental theorems that we will need in the proofs of our main results.For more details about the topic,we refer the reader to[14]and[7].
2.1 Malliavin calculus and elements of Gaussian analysis
Let H be a real separable Hilbert space with inner product
?An isonormal Gaussian process over H is a centered Gaussian familyG=of random variables defined on a probability space(?,F,P)such that E[G(?)G(ψ)]=H for every?,ψ∈H.F is assumed to be generated byG.In the following,the symbols H?pand H⊙pfor any integerp1,will denote thep-th tensor product and thep-th symmetric tensor product of H respectively.
?The Wiener chaos of orderpassociated withGwhich will be denoted by Hpis by definition the closed linear subspace ofL2(?)generated by the random variables{Hp(G(?)):?∈H,whereHpis thep-th Hermite polynomial defined by
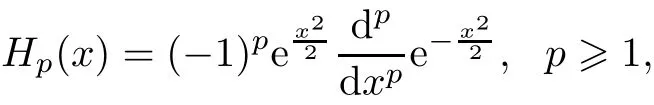
andH0(x)=1.
?It can be shown(see for instance[14],Proposition 2.2.1)that ifU,V~N(0,1)are jointly Gaussian,then for allp,q∈N,

?Thep-th multiple integral of??p∈H⊙pis defined by the equalityIp(??p)=Hp(G(?))for any?∈H with ‖?‖H=1.Moreover,the mapIpis a linear isometry between H⊙pequipped with the norm√p!‖.‖H?pand Hpunder theL2(?)’s norm.
?The Wiener chaos expansion.For anyF∈L2(?),there exists a unique sequence of functionsfp∈H⊙psuch that
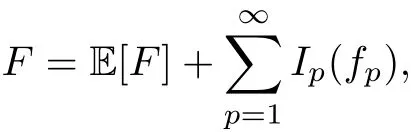
where the terms are all mutually orthogonal inL2(?)andfp∈H⊙pare uniquely determined byF.
?Product formula.For any integersp,q≥1 and symmetric integrandsf∈H⊙pandg∈H⊙q,
2.2 Young integrals
FixTas being the horizon time.We denote by C1([0,T])the set of functionsg:[0,T]→R that are differentiable and whose first derivative is continuous.We also use the common convention that C0([0,T])denotes the set of continuous functionsg:[0,T]→R.
For anyγ∈[0,1],we denote by Cγ([0,T])the set ofγ-H¨older continuous functions,that is,the set of functionsf:[0,T]→R such that

2.3 Central limit theorem for functionals of self-similar Gaussian process
We consider a centered Gaussian processG={Gt,t≥0}that is self-similar of orderβ∈(0,1).Namely,the process{a?βGat,t≥0}has the same distribution as the processGfor anya>0.Consider the functionφ:[1,∞)→R given by

This function characterizes the covariance function.Indeed,for 0 Let us recall the assumptions of[2]on the functionφdefined above,and on its derivatives,whereα∈(0,2β]: (A1)φhas the formφ(x)=?λ(x?1)α+ψ(x),whereλ>0 andψ(x)is twice-differentiable on an open set containing[1,∞),and there is a constantC≥0 such that for anyx∈(1,∞) 1.|ψ′(x)|≤Cxα?1; 2.|ψ′′(x)|≤Cx?1(x?1)α?1; 3.ψ′(1)=βψ(1),whenα≥1. (A2)There are constantsC>0 and 1<ν≤2 such that for allx≥2, Remark 2.5The constantα∈(0,2β]satisfies E[(Gt+s?Gs)2]~sαas it is proved in[2],where it is called the increment exponent.For example,whenGis a fractional Brownian motionBHwith Hurst parameterH,the increment exponent is exactly 2H,which means that in this caseα=2β.From now on,we will consider self-similar centered Gaussian processesGthat are similar to the fractional Brownian motion,namely their increment exponentαis equal to 2β,but their covariance structures are non-trivial.In the last section,we give typical example of such processes. Based on the previous theorem,we have in the following theorem two central limit theorems where we extend the result of Theorem 2.4,to the limit caseα=3/2 for an Hermite rank of the functionfequalsd=2.More precisely,we have the following result. Theorem 2.6LetGbe a self-similar centered Gaussian process of indexβ∈(0,1)satisfying the assumptions(A1)and(A2)above and having an increment exponentα=2β.Then We recall now a theorem of Corcuera,Nualart and Podolskij,see[3],which sets the convergence in law of weighted random sum,and that will play an important role in the proof of the main theorem of the paper. Theorem 2.8([3])The underlying probability space is(?,F,P).Let?={?t}t∈[0,T]be a H¨older continuous process with indexγ>1/2,and letζ={ζk,n}n≥1,1≤k≤∟nT」be a family of random variables.Set Assume the following two hypotheses on the double sequenceζ: LetT>0 be a fixed time horizon and let(?,F,P)be a complete probability space where we considerG=(G(1),G(2))two independentβ-self-similar centered Gaussian processes such thatG(1)law=G(2),we also assume that for allε∈(0,β),G(1)andG(2)have versions with H¨older continuous paths of order(β?ε).Throughout the text,the constantβis assumed to be in(1/2,1). Letγ∈(0,1)and define two more stochastic processesη(i):?×[0,T]→R,i=1,2 such that fori=1,2,η(i)has H¨older continuous paths of orderγ. In this work,we are concerned with the asymptotic behavior of the following sequence of stochastic processes whereCβis the constant defined in(2.6)and(2.7)depending on the value ofβ,andWis a standard Brownian motion independent of F. Remark 3.3If one considersG=(G(1),G(2))to be a two dimensional fractional Brownian motionBH=(B(1,H),B(2,H))withB(1,H),B(2,H)having the same Hurst indexH>1/2 defined on the probability space(?,F,P),then under the required assumptions(H1),(H2)above,Theorem 3.2 corresponds to Theorem 1.2 of[1],sinceβ=Hin this particular case.Hence Theorem 3.2 generalizes Theorem 1.2 of[1],to the case where the Gaussian processesG(1),G(2)don’t necessarily have stationary increments and have more complex correlation function than the one of the fractional Brownian motions.In[1],the authors studied the case where the convergence is not Gaussian which typically corresponds toH>3/4 for the fractional Brownian motionsB(1,H),B(2,H),we won’t investigate in this work the case where non-normal asymptotic limits occur. We will need the following Lemma and Proposition in the proof of Theorem 3.2. Lemma 3.4LetG(i)andη(i),i=1,2,βas before.Then,there is a constantC=C(γ,β,T,η)>0 such that for alln≥1,k∈{1,.···,∟nT」}and for anyi=1,2,we have ProofSee Appendix. Proposition 3.5Let?={?t}t∈[0,T]be a H¨older continuous process with index in(1/2,1).Set Letanbe given by(3.4).Then,asn→∞, whereCβis the constant defined in(2.6)and(2.7)depending on the value ofβ,andWis a standard Brownian motion independent of F. ProofWe give now the proof of Proposition 3.5.Inspired by the proof of Proposition 3.1 of[1],we extend it to any Gaussian processes satisfying the required assumptions mentioned before.We will check that(h1)and(h2)of Theorem 2.8 hold for both cases 1/2<β<3/4 andβ=3/4. We set To check(h1),we consider two Gaussian processes constructed fromG(1)andG(2)by a rotational trick as follows so that The processesg(1)andg(2)are two independent Gaussian processes self-similar with indexβ.Therefore(h1)is satisfied by applying Corollary 2.7 for the values ofanaccording to those ofβfor 1/2<β<3/4 and forβ=3/4. For the assumption(h2),by the hypercontractivity property on fixed Wiener Chaos,see[4]for more details,here it’s the second Wiener chaos,it suffices to check the existence of a constantC>0 such that,for any 1≤i Using the expression ofζk,ngiven in(3.9)and the independence ofG(1)andG(2)and their equality in law,we have where we put For 1/2<β<3/4,we havean=n?1/2,then under the inequalities(3.2)and(3.3)of Assumption(H3),and using theβ-self-similarity ofG(1),we get where we used for the last inequality the fact thatβ<3/4.Therefore the assumption(h2)holds for this case.Forβ=3/4,we havean=n?1/2log(n)?1/2,and forn≥3 Hence the convergence holds in law.Finally,applying Proposition 3.5 toanfn,1(t),we get directly the desired result. The sub-fractional Brownian motionSH:={SHt,t≥0}(subfBm for short)with Hurst parameterH∈(0,1),first introduced by Bojdecki et al in[9],is an extension of the Brownian motion that preserves also many properties of the fractional Brownian motion except the stationarity of its increments.SHis defined as a centered Gaussian process with covariance function By Kolmogorov’s continuity criterion and(4.1),SHhas H¨older continuous paths of orderH?ε,for everyε∈(0,H). Assumptions(A1)and(A2)of Theorem 2.6 hold forSH,the reader may consult[2,Section 4.2]for a detailed proof.Therefore,it suffices to check Assumptions(H2)and(H3)of Theorem Combining(4.2),and the fact thatSHis Gaussian with(4.1),one deduce that the process|SH|γhas moments of all orders,so(H2)is satisfied. Checking Assumption(H3) Letnandktwo integers withn1 andwe have by(4.1) Thus the trajectories of the processBH,Kare(HK?ε)-H¨older continuous for anyε∈(0,HK),due to Kolmogorov’s continuity criterion. Assumptions(A1)and(A2)are satisfied by[2,Section 4.1].Therefore,Theorem 2.6 holds for AcknowledgementsWe would like to thank Professor David Nualart for many valuable discussions on the subject. Appendix We first prove(ii)of Theorem 2.6.For this aim we will need the following lemma. Lemma A.1Lett>0 andGa Gaussian process self-similar of indexβequal toβ=3/4.We define fort>0 andn≥1,

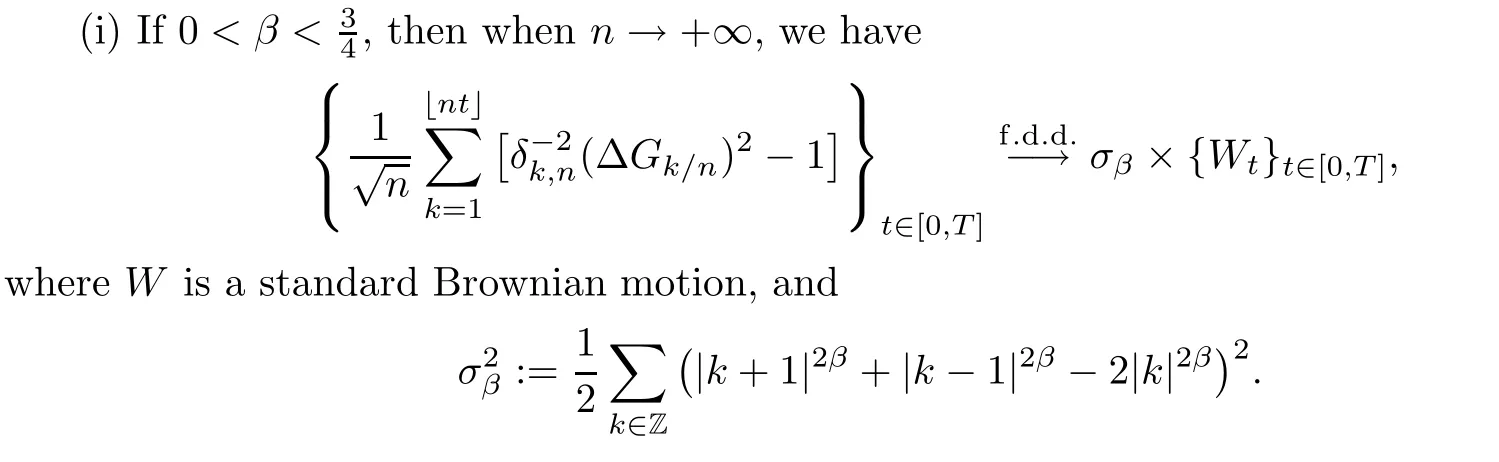

2.4 Asymptotic behavior of weighted random sums
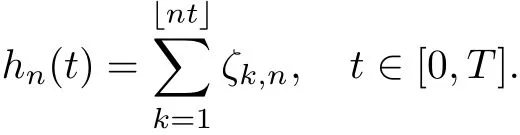

3 Presentation of the Problem












4 Examples

4.1 G is a two-dimensional subfractional Brownian motion




4.2 G is a two-dimensional bifractional Brownian motion










 Acta Mathematica Scientia(English Series)2020年6期
Acta Mathematica Scientia(English Series)2020年6期
