分?jǐn)?shù)階q-差分方程多點(diǎn)邊值問題解的存在性與唯一性
閆雅雯, 侯成敏
(延邊大學(xué)理學(xué)院, 吉林 延吉 133002)
邊值問題是微分方程理論中的重要分支, 它具有深刻的物理背景和廣泛的理論應(yīng)用[1-3], 近年來許多學(xué)者對(duì)整數(shù)階、分?jǐn)?shù)階微分方程邊值問題進(jìn)行深入研究, 取得了豐碩的成果[4-6], 但具有q-積分邊值條件的分?jǐn)?shù)階q-差分方程多點(diǎn)問題的研究卻很少見.Graef等[7]利用Banach壓縮映像原理和Schauder不動(dòng)點(diǎn)定理, 得到含有分?jǐn)?shù)階導(dǎo)數(shù)的高階多點(diǎn)含參數(shù)q-差分邊值問題
正解的存在性和唯一性, 其中Dq是Riemann-Liouville型分?jǐn)?shù)階q-導(dǎo)數(shù),f:[0,1]×R→[0,∞)是連續(xù)函數(shù),q∈(0,1),m≥1,n≥2是整數(shù),n-1 解的存在性, 其中f:[0,1]×R→R是連續(xù)函數(shù);n-1<α≤n, 整數(shù)n≥3;βi,γi>0, 0<η1<η2<…<ηm-2<1, 1≤i≤m-2, 整數(shù)m≥3.受上述研究的啟發(fā), 本文考慮如下分?jǐn)?shù)階q-差分方程的邊值問題: (1) 定義1κ是Banach空間, Α:κ→κ是映射. 若存在連續(xù)非減函數(shù)ψ:R+→R+, 使|f(t,x)|≤p(t)ψ(‖x‖),ψ(0)=0,ψ(α)<α, 且對(duì)任意α>0, ‖Αx-Αy‖≤ψ(‖x-y‖), ?x,y∈κ, 則A被稱為壓縮算子. 引理2設(shè)h:[0,1]→R是連續(xù)函數(shù), 則分?jǐn)?shù)階q-差分方程 (2) 等價(jià)于積分方程 (3) (4) Banach空間κ=C[0,1]的范數(shù)定義為‖x‖=sup{|x(t)|,t∈[0,1]}, 由引理2知 (5) 算子A的不動(dòng)點(diǎn)x即為問題(1)的解.為計(jì)算方便, 令 定理1設(shè)連續(xù)函數(shù)f:[0,1]×R→R滿足Lipschitz條件: ?x,y∈κ,t∈[0,1], 有|f(t,x)-f(t,y)|≤L|x-y|, 其中L是Lipschitz常數(shù). 若LΘ<1, 則邊值問題(1)存在唯一解. 2) 存在x∈?U和λ∈(0,1)使得x=λAx. 引理4[10]令κ是Banach空間, Α:κ→κ是非線性壓縮算子, 則A在κ中有唯一的不動(dòng)點(diǎn). 例1考慮如下分?jǐn)?shù)階q-差分邊值問題 例2對(duì)于邊值問題 例3對(duì)于邊值問題 同理, 0.506 784≤Δ1≤0.552 99,Δ2=2.55,Δ3≈-0.368 31, 取函數(shù)g(t)=exp(-t2)/6, 得到φ=0.890 77.又|f(t,x)-f(t,y)|≤g(t)(ln(1+|x|)-ln(1+|y|))≤g(t)φ-1ln(1+|x-y|), 由定理3知, 此邊值問題在區(qū)間[0,1]上有唯一解.1 預(yù)備知識(shí)
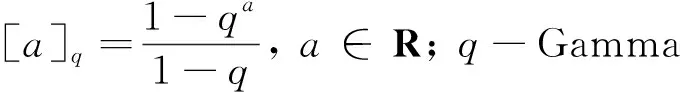
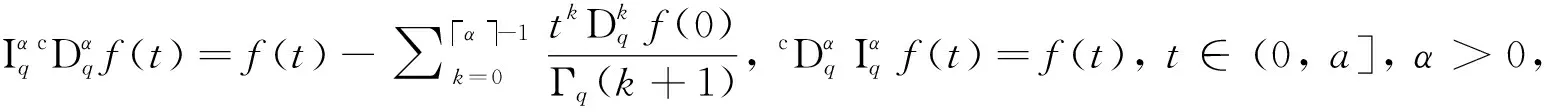
2 解的存在性和唯一性

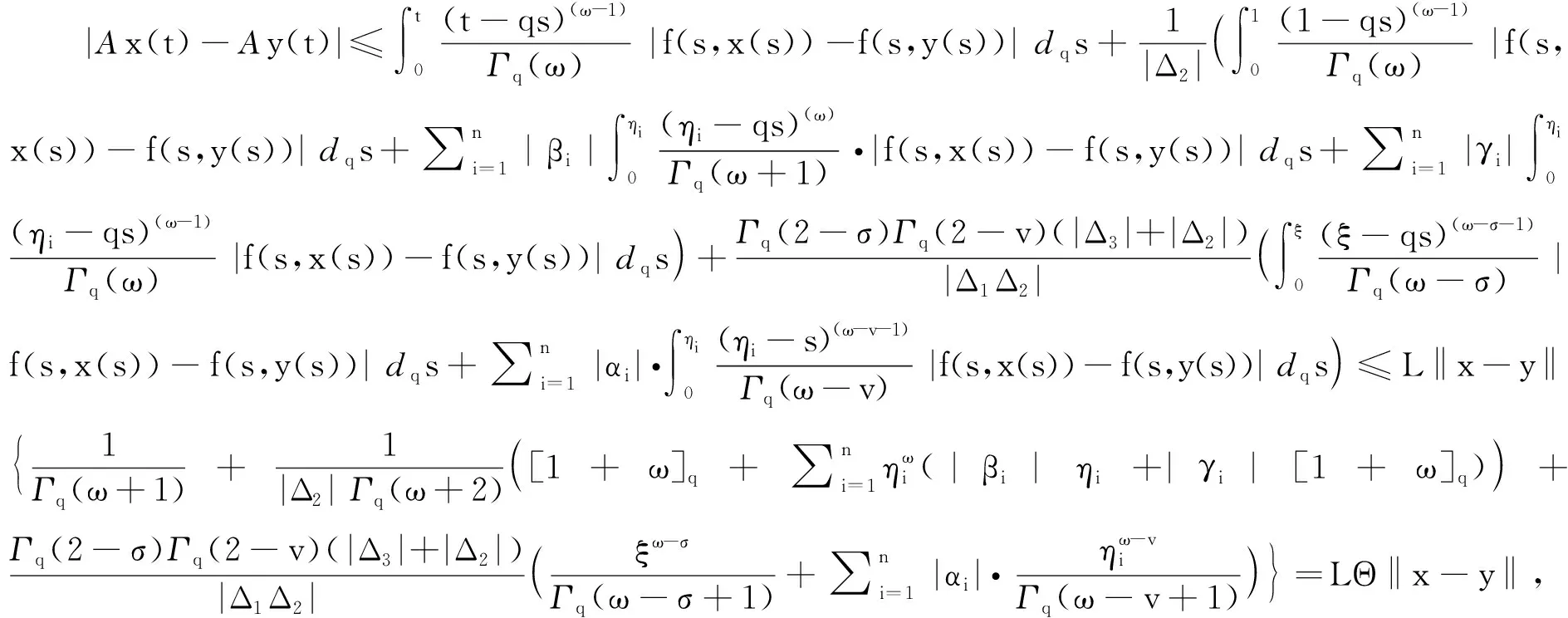
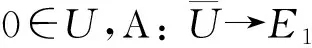
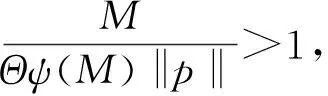
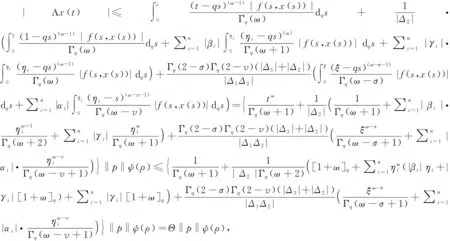
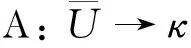
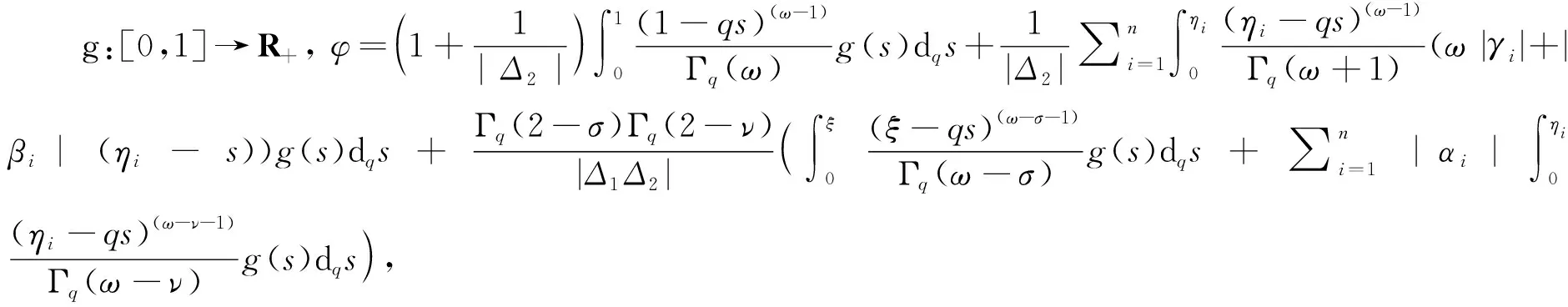
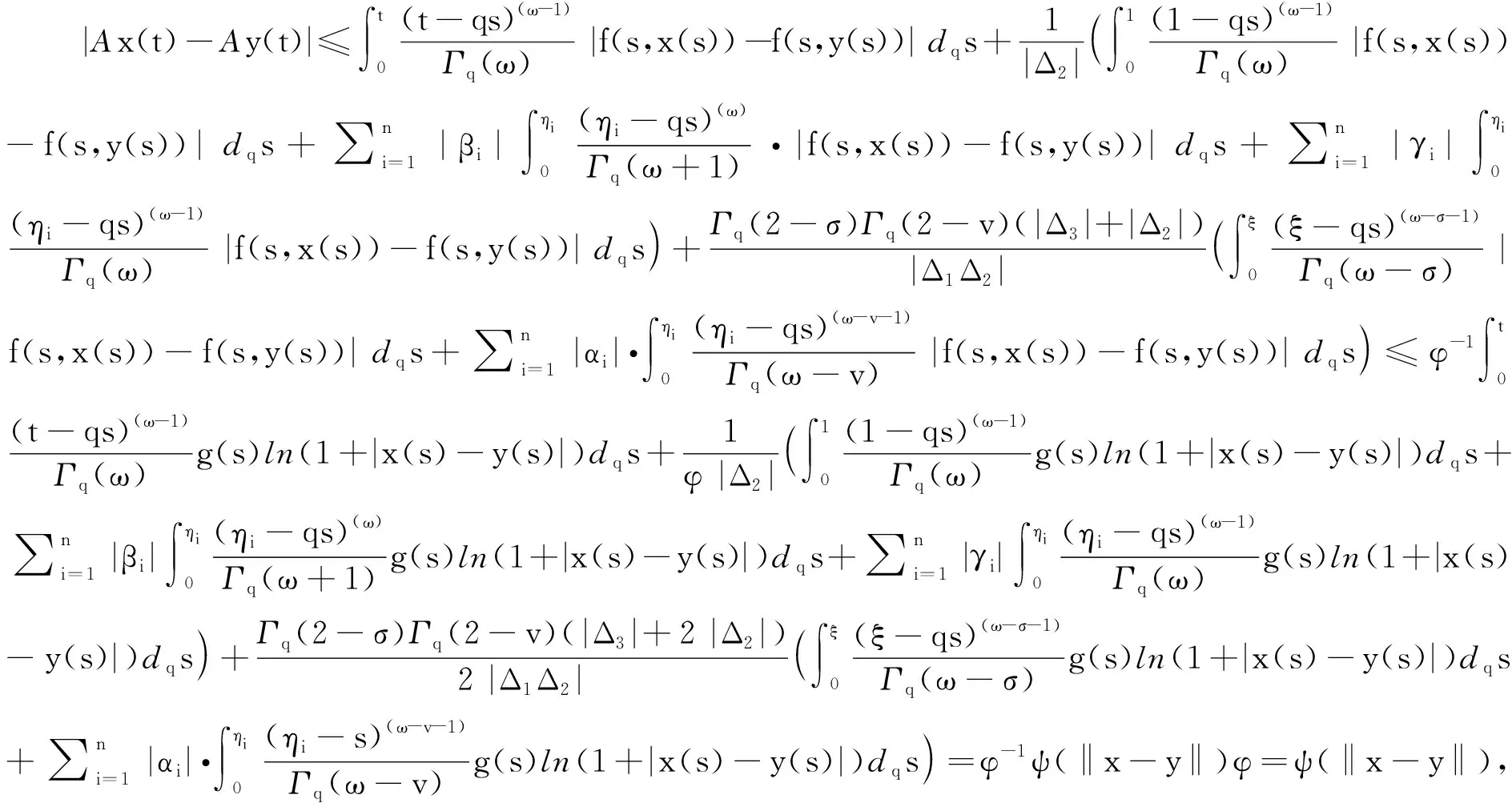
3 算例