GLOBAL NONEXISTENCE FOR A VISCOELASTIC WAVE EQUATION WITH ACOUSTIC BOUNDARY CONDITIONS?

Jiali YU(于佳利)Yadong SHANG(尚亞東) Huafei DI(狄華斐)

1.School of Science,Dalian Jiaotong University,Dalian 116028,China

2.School of Mathematics and Information Science,Guangzhou University,Guangzhou 510006,China

E-mail:yujialigz@163.com;gzydshang@126.com;dihuafei@yeah.net

Abstract This paper deals with a class of nonlinear viscoelastic wave equation with damping and source termswith acoustic boundary conditions.Under some appropriate assumption on relaxation function g and the initial data,we prove that the solution blows up in finite time if the positive initial energy satis fies a suitable condition.

Key words viscoelastic wave equation;Global nonexistence;Acoustic boundary conditions

1 Introduction

In this work,we investigate the following viscoelastic wave equation with acoustic boundary conditions

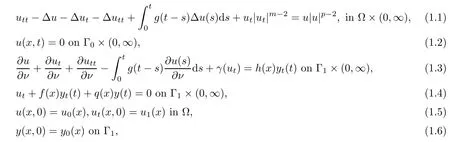
where ? is a regular and bounded domain of Rn(n ≥ 1)with a smooth boundary?? = Γ0∪Γ1.

Here Γ0,Γ1are closed and disjoint with meas(Γ0)>0 anddenotes the unit outer normal derivative to Γ.p>m,the functions f,q,h:Γ1→ R+are essential bounded and q(x)≥ q0>0.g represents the kernel of the memory term,the function γ:R→R is monotone and continuous.The initial conditions(u0,u1,y0)belong to a suitable space.

The problem(1.1)–(1.6)is related to noise control and suppression in practical applications.This type of eq.(1.1)usually arises in the theory of viscoelasticity,describes a variety of important physical processes,such as the analysis of heat conduction in viscoelastic materials,viscous flow in viscoelastic materials[1],nonlinear bidirectional shallow water waves[2],vibration of nonlinear elastic rod with viscosity[3]and so on.It is well known that viscoelastic materials have memory e ff ects,which is due to the mechanical response in fl uenced by the history of the materials themselves.From the mathematical point of view,these damping e ff ects are modeled by integro-differential operators.Hence,differential equations with memory e ff ects have become an active area of research in recent years.We can refer to the recent works in[4–16].

The boundary conditions(1.3)–(1.4)are a generalization of the acoustic boundary conditions which exhibit some reaction and variable(h(x)6=constant)porosity of the materials of the walls,ceiling and fl oor.The models with acoustic boundary conditions were introduced by Morse and Ingard[17]in 1968 and developed by Beale and Rosencrans in[18],where the authors proved the global existence and regularity of the linear problem.Recently,some authors studied the existence and decay of solutions for a viscoelastic wave equation with acoustic boundary conditions(see[19–28]).In particular,Boukhatem and Benabderrahmane[20]considered the nonlinear viscoelastic wave equation with acoustic boundary conditions as follows

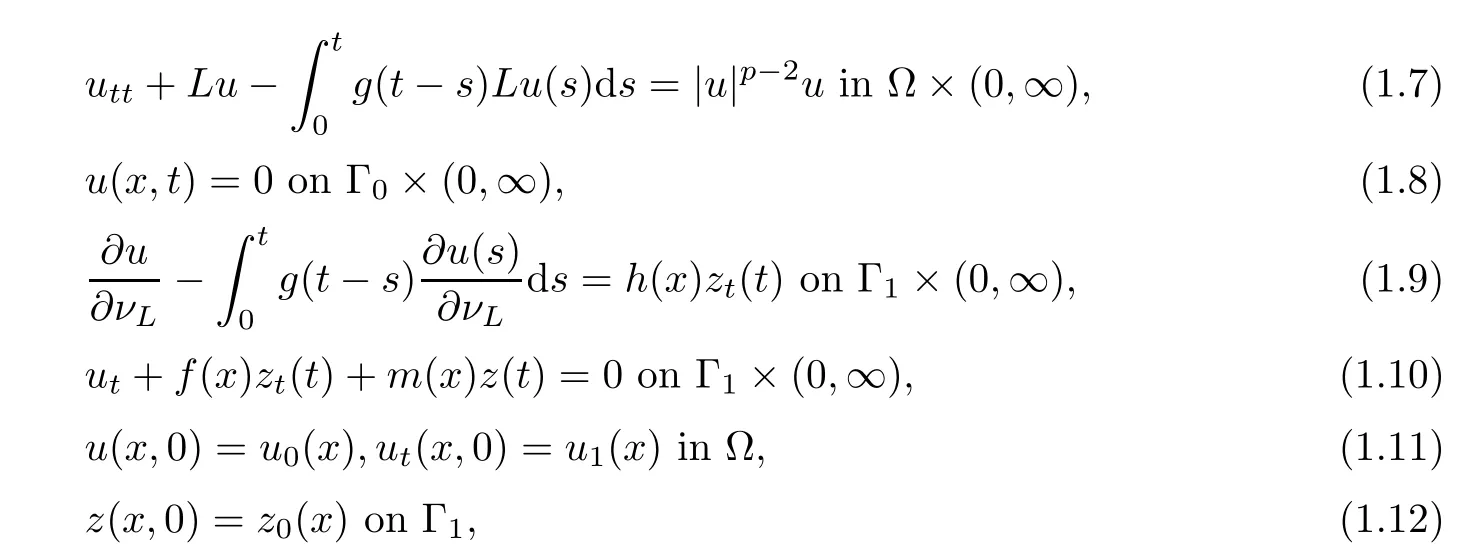
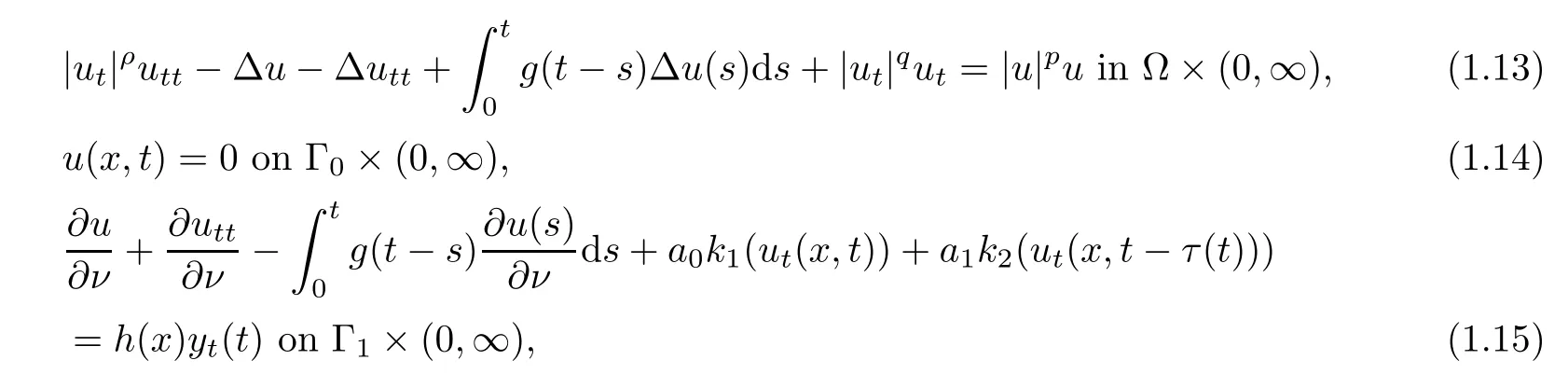
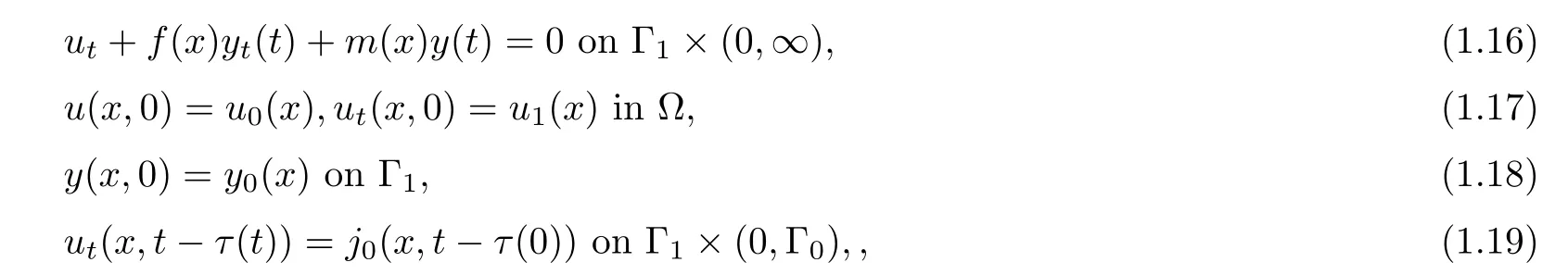
where ? be a bounded domain of Rn,n ≥ 1 with a smooth boundary Γ = Γ0∪Γ1of C2.Here ρ,p,q>0.The functions f,m,h:Γ1→ R are essential bounded,k1,k2:R → R are given functions,a0,a1are real numbers with a0>0,a16=0,τ(t)>0 represents the time-varying delay.In another work by Xu et al.[30],the authors studied an initial boundary value problem for nonlinear viscoelastic wave equation with strong damping and dispersive terms

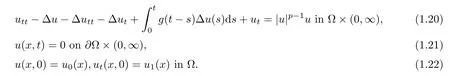
By introducing a family of potential wells they obtained the invariant sets and proved existence and nonexistence of global weak solutions with low initial energy.In high energy case,they also established a blow-up result with arbitrary positive initial energy.Later,Peyravi in[31]investigated a system of viscoelastic wave equations with nonlinear boundary source term of the form

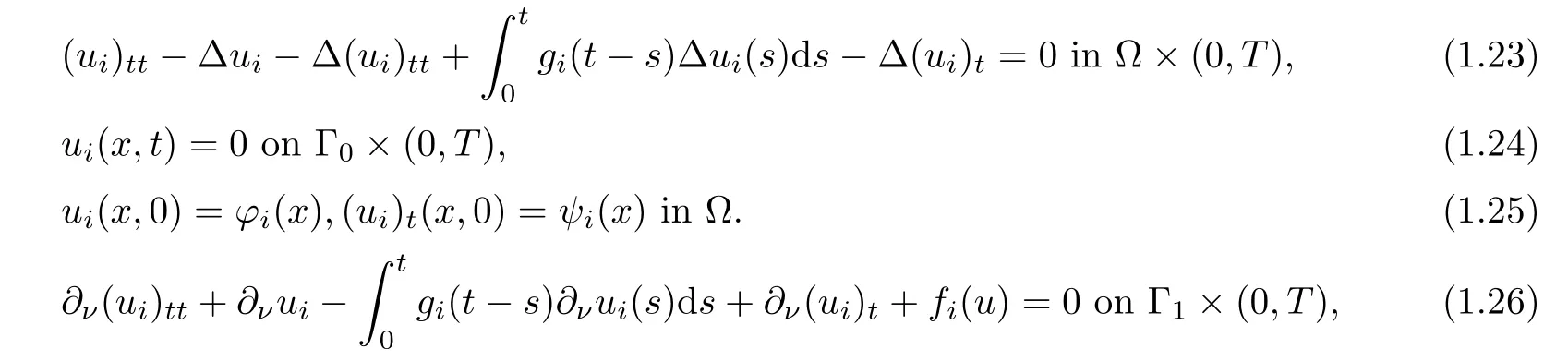
where i=1,···,l(l ≥ 2).They established general decay and blow up results associated to solution energy.Estimates for lifespan of solutions were also given.More recently,Kang et al.[32]considered with the following quasi-linear viscoelastic wave equation with acoustic boundary conditions

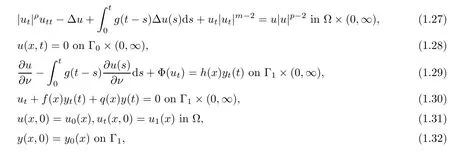
where ? is a regular and bounded domain of Rn(n ≥ 1)and ?? = Γ0∪Γ1.The functions f,q,h:Γ1→ R+are essential bounded and q(x) ≥ q0>0.The function Φ :R → R is monotone and continuous.They studied the global nonexistence of solutions for(1.27)–(1.32).

Motivated by the previous works[30–32],in this paper,we study the global nonexistence of solutions for the nonlinear viscoelastic problem(1.1)–(1.6).To the best of our knowledge,there is no results of nonlinear viscoelastic wave equation(1.1)with acoustic boundary conditions.

Thus this work is signifi cant.The outline of the paper is the following.In Section 2,we give some notations and materials for our works.In Section 3,we prove our main results.

2 Preliminaries and Main Results

In this section,we begin with some notations,assumptions and lemmas to be used throughout this article.We denote byand,the Lp(?)-norm and Lp(Γ1)-norm respectively and inner scalar productin L2(?).We introduceNow,we make the following assumptions on the problem(1.1)–(1.6).

(A1) For the nonlinear terms,we have

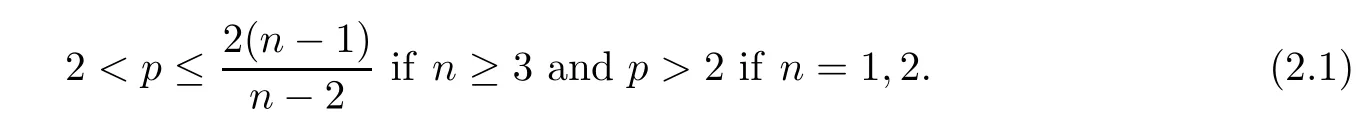
(A2) g:R+→R+is a differentiable function such that

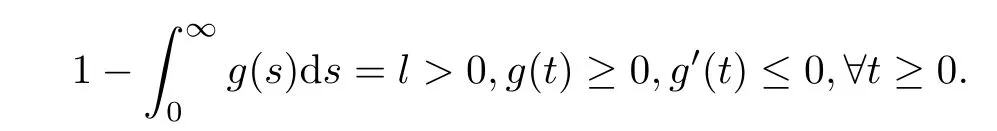
(A3) γ:R→R is monotone,continuous and there exist positive constants m1and m2such that

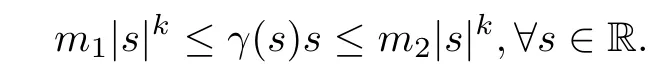
(A4) The functions f,q,h are essentially bounded such that

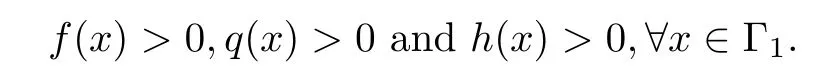
We state,without a proof,a local existence result which can be established by combing arguments of[29,31].

Assume that(A1)–(A4)hold.Then for any given u0(x)∈(?),u1(x)∈(?)and y0(x)∈ L2(Γ1),the problem(1.1)–(1.6)has a weak local solution(u,y)such that

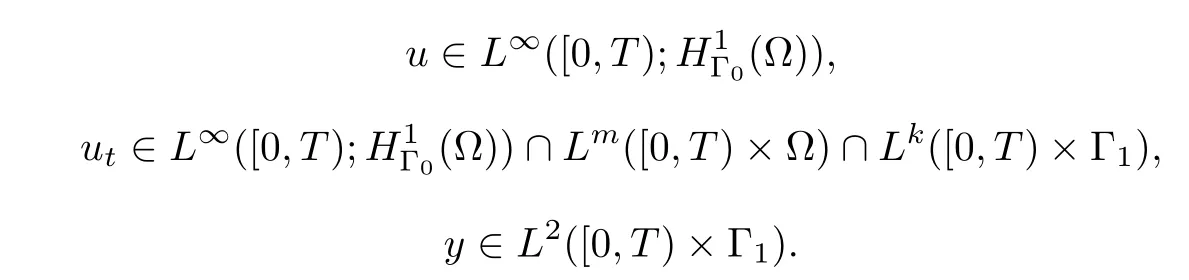
De fine the functional

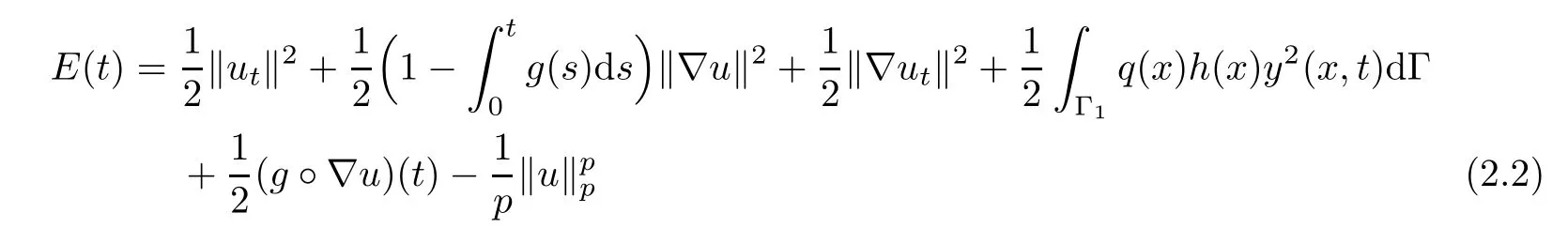
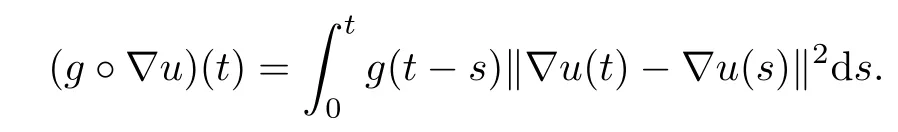
Lemma 2.1Assume that(A1)–(A4)hold.Let u(t)be a solution of problem(1.1)–(1.6).Then the energy functional E(t)of problem(1.1)–(1.6)is non-increasing.Moreover,the following energy inequality hold

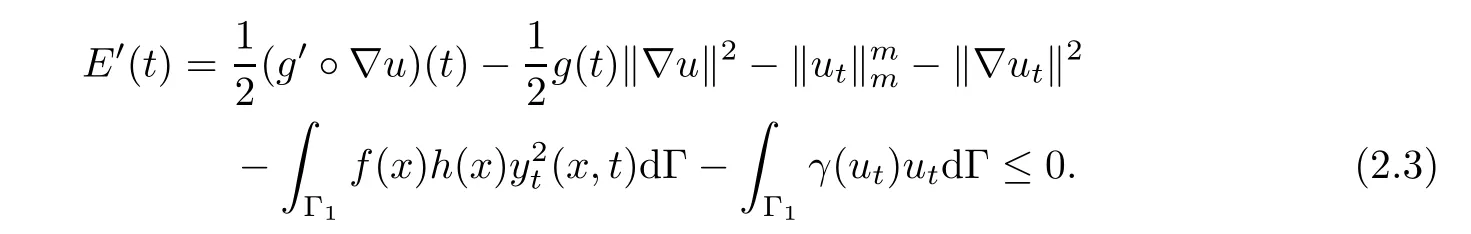
Lemma 2.2Assume that(A1)–(A4)hold.Suppose that

and

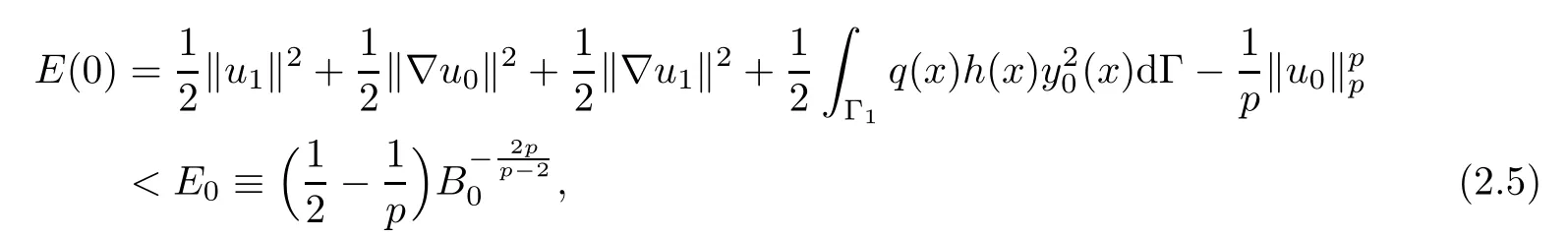
where B0=and B is the optimal constant of the Sobolev embedding

Then there exists a constant β > λ0such that

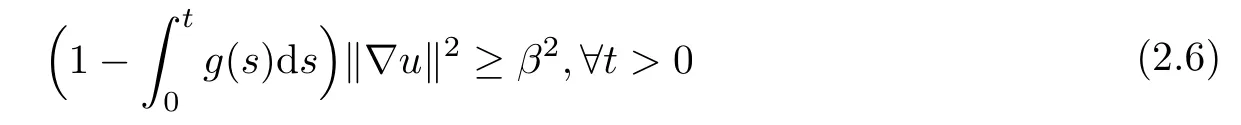
and

ProofBy virtue of(2.2),one has

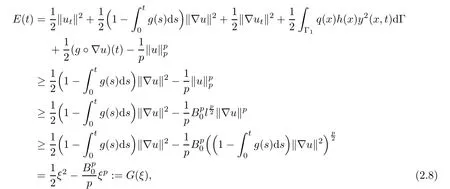
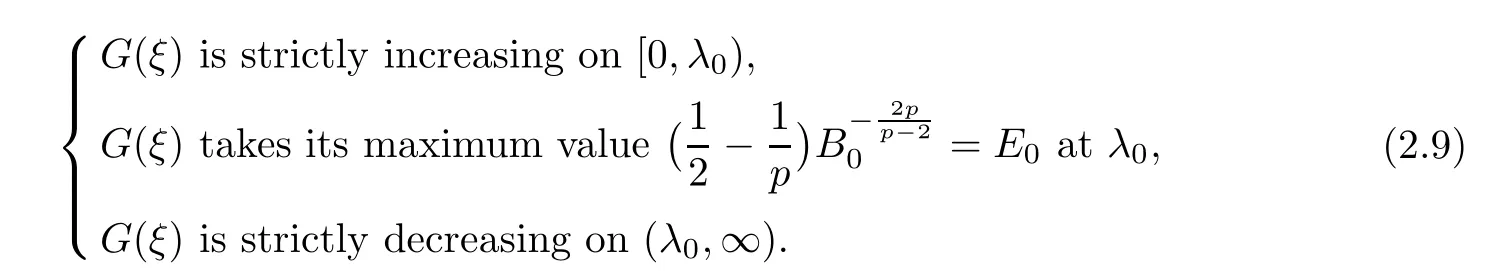
Since E0>E(0),there exists β > λ0such that G(β)=E(0).By virtue of(2.4)and(2.8),we have G()≤ E(0)=G(β),which implies that> β.To prove(2.6),we suppose on the contrary that

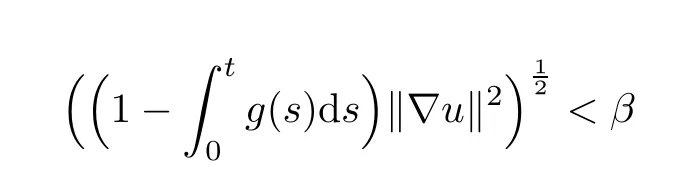
for some t=t0>0.By the continuity of,we may choose t0such that

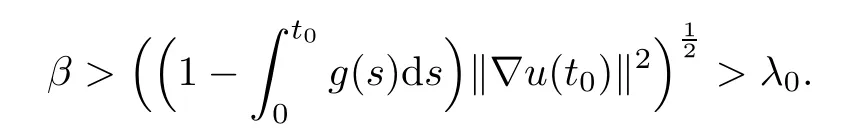
Then it follows from(2.8)that

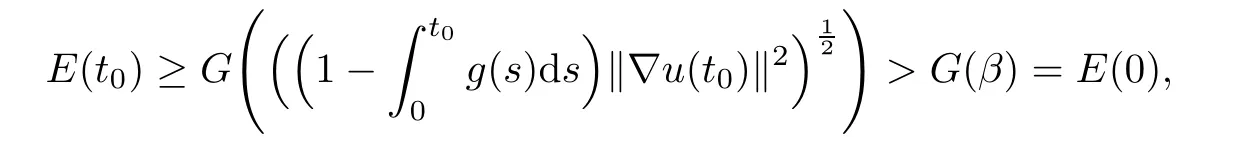
which contradicts Lemma 2.1.Hence(2.6)is proved.Now we go to the proof of(2.7).From Lemma 2.1,(2.2)and(2.6),it follows that

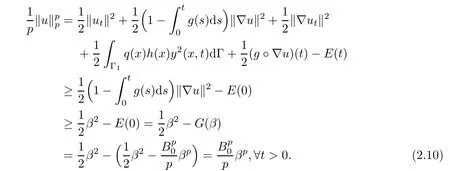
Thus the proof of Lemma 2.2 is completed.

Similar to the proof of Lemma 2.2,we can get the result as follows.

Corollary 2.3Suppose that the conditions of Lemma 2.2 hold,then there exists a constant β > λ0such that

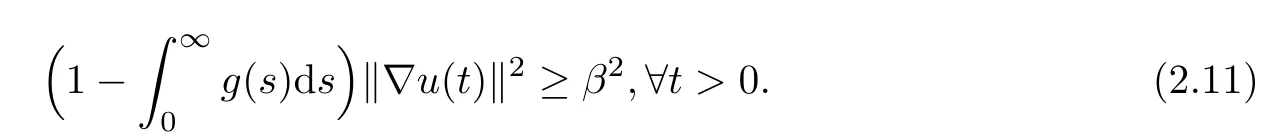
Theorem 2.4Assume that m>2,k≥2,p>max{m,k,5?2/l}and Lemma 2.2 hold.Suppose that

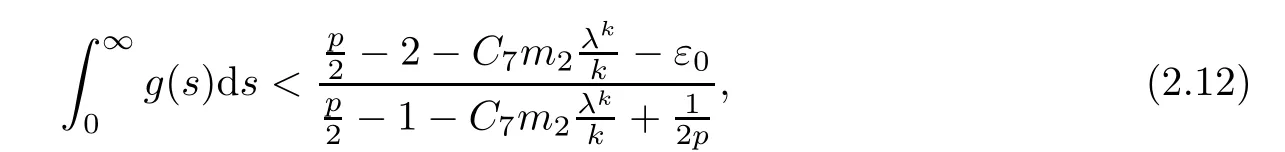
0< ε0

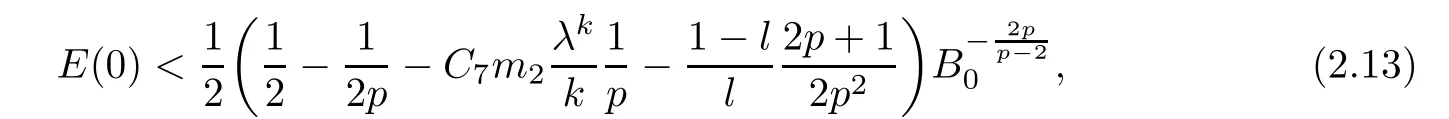
where λ,C7are some positive constants to be determined in(3.17),(3.22),respectively.

3 Proof of Theorem 2.4

Assume that the solution u(x,t)of(1.1)–(1.6)is global.Then,for any T0>0,we may consider functional M:[0,T0]→R+de fined by

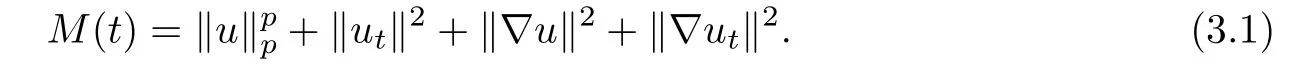
As M(t)is continuous on[0,T0],there exists,C0>0,such that≤M(t)≤C0.Let

where the constant E1∈(E(0),E0)shall be chosen later.Then it is clear that H(t)is an increasing function of time,H(0)>0.Then,for t≥s≥0,we have

From(2.2),we get

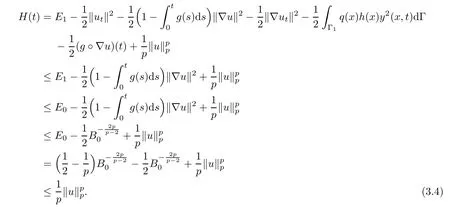
Set a function Φ(t)as

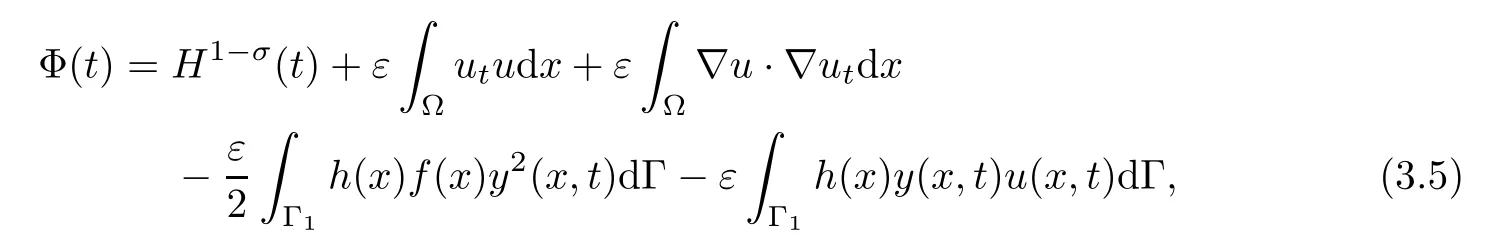
where the constants 0< σ<1,ε>0 shall be chosen later.

Taking the derivative of Φ(t),we have

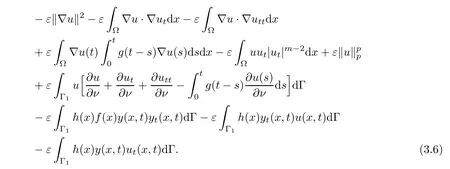
Making use of conditions(1.3)and(1.4),we get

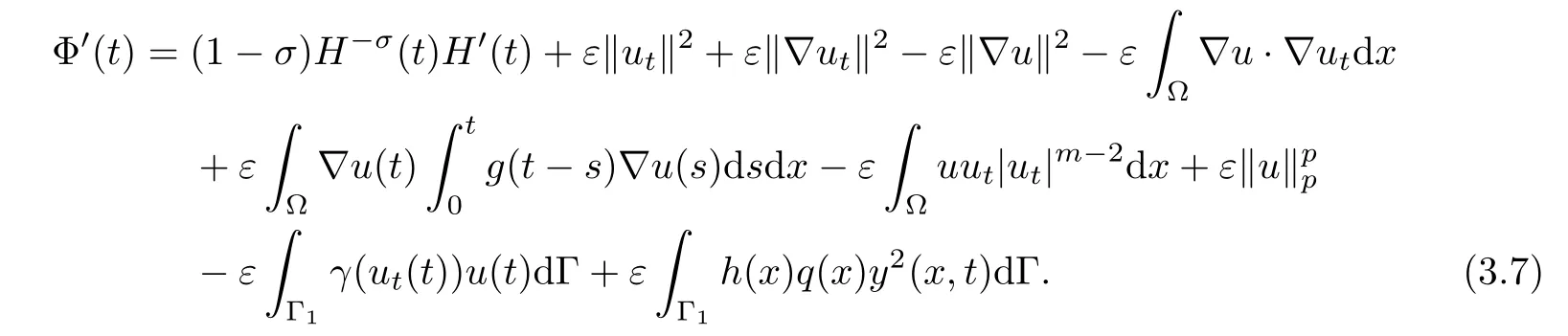
Exploiting H?lder’s and Young’s inequality,for any ε1(0< ε1<1),we obtain

Thus from(3.7)and(3.8),we arrive at

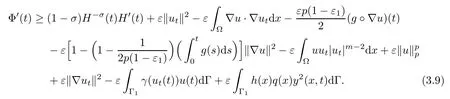
From Lemma 2.1 and(3.9),we deduce that

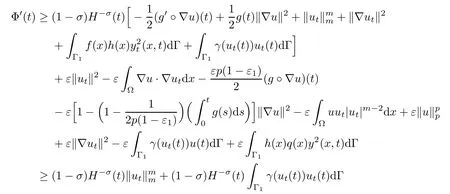
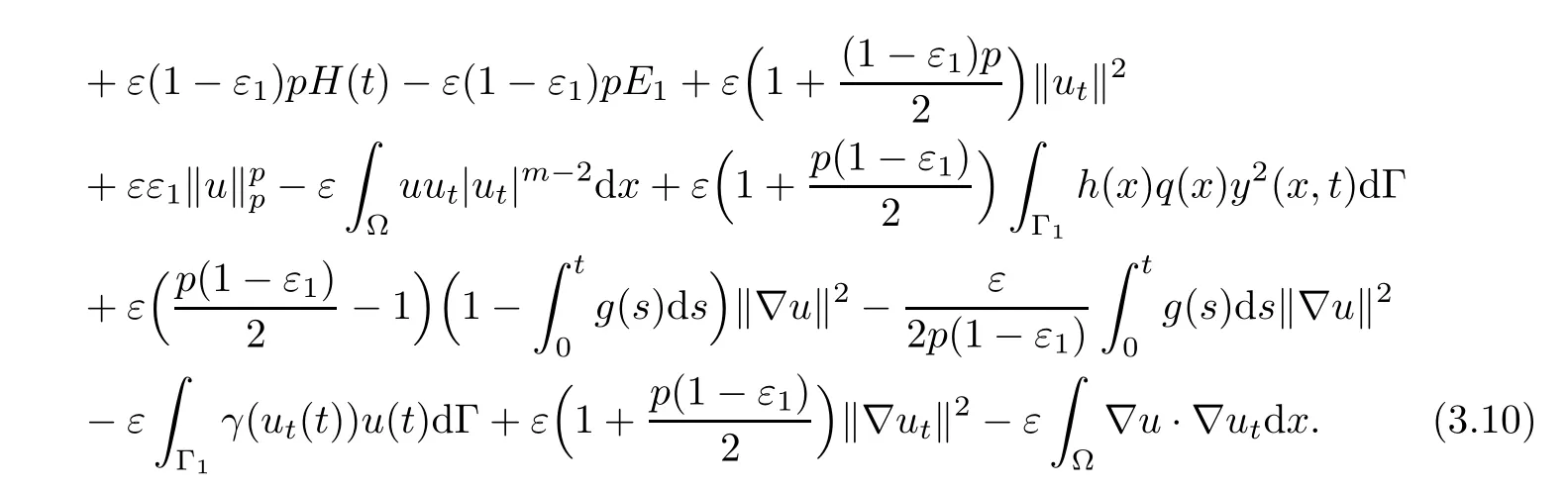
From H?lder’s and Young’s inequality,the condition m

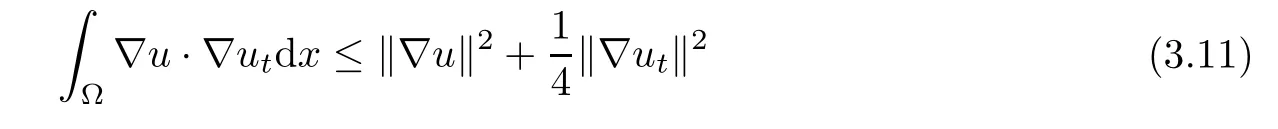
and

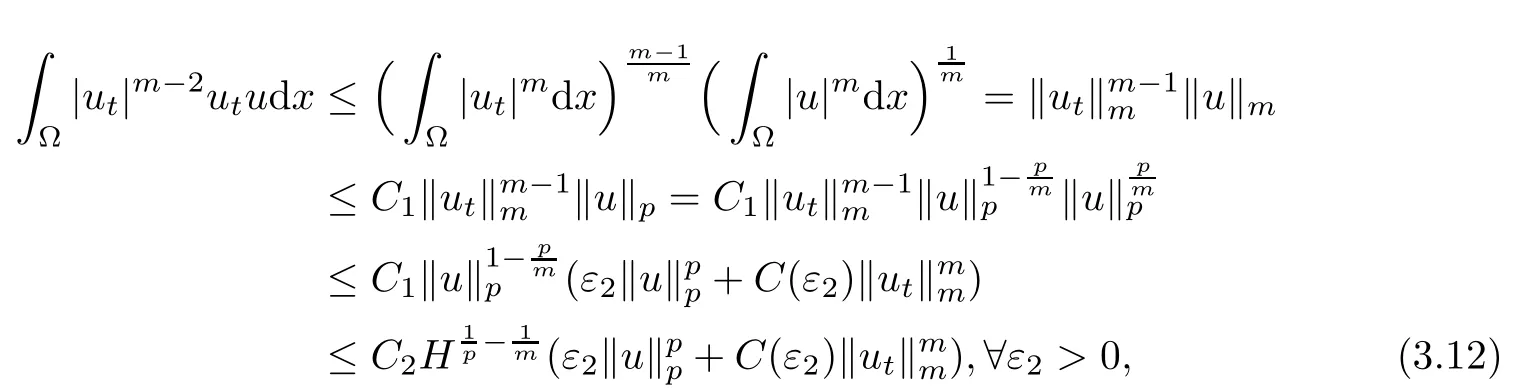
where C1is the optimal constant of the embeddingand C2=C1p1/p?1/m.

Here we choose

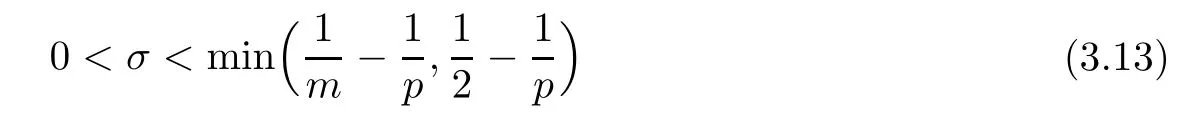
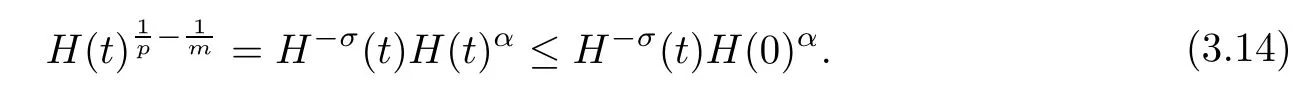
Thus,from(3.12)and(3.14)it follows that

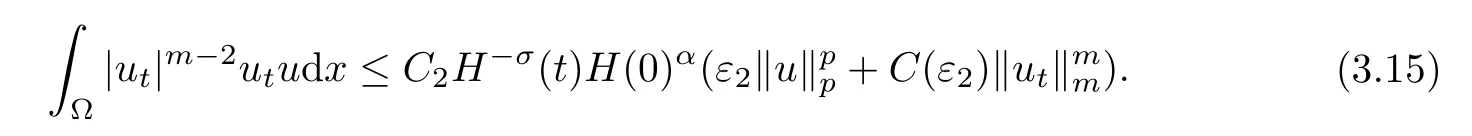
Moreover,from assumption(A3),it follows that

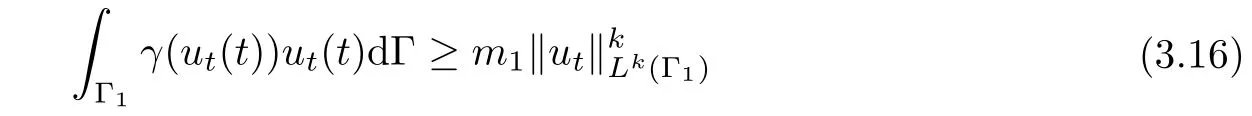
and using Young’s inequality and assumption(A3),we have

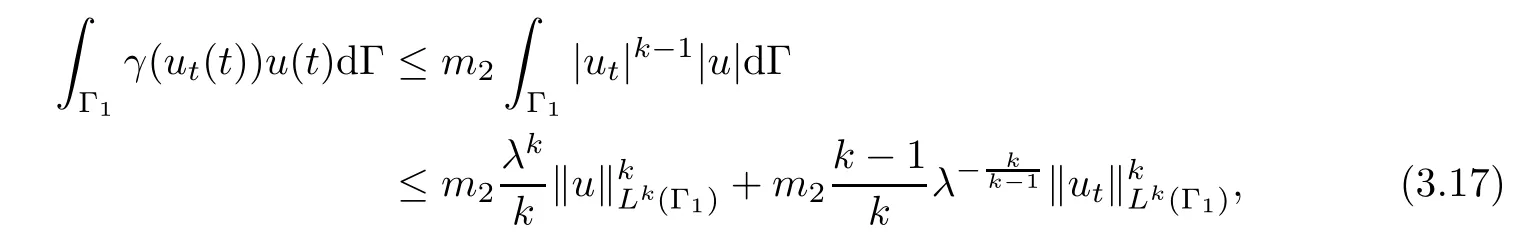
where λ is a positive constant.From(3.10),(3.12),(3.11)and(3.15)–(3.17),we deduce

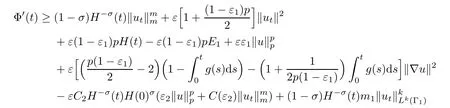
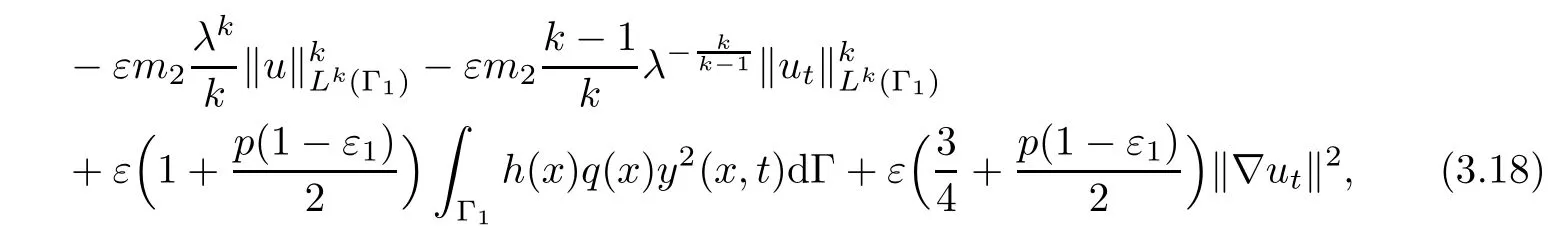
where λ >0.We also use the embedding theorem

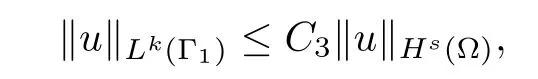
where C3is the optimal constant,0≤ s<1 and s≥?>0.Using the interpolation inequality,we have

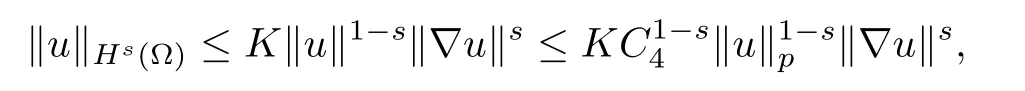
where K=K(s,n)and C4is the optimal constant of the embedding

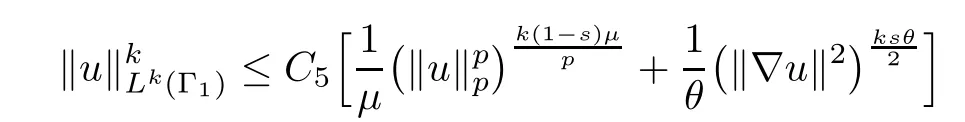
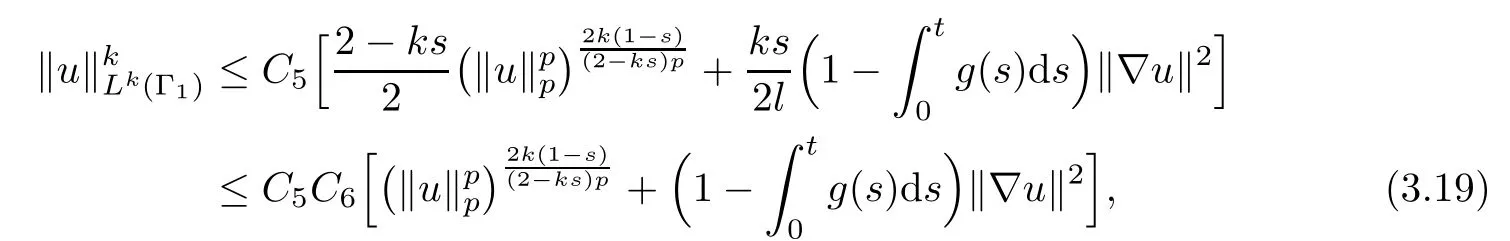
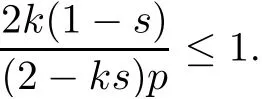
Moreover,in this case,due to algebraic inequality

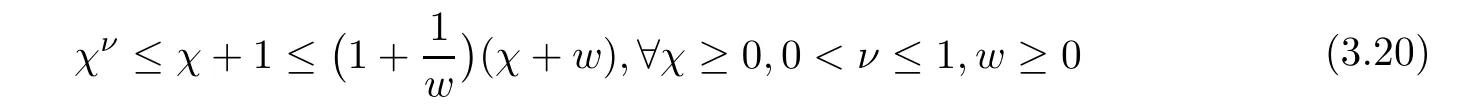
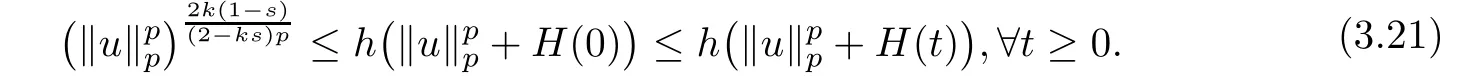
From(3.19)and(3.21),we have

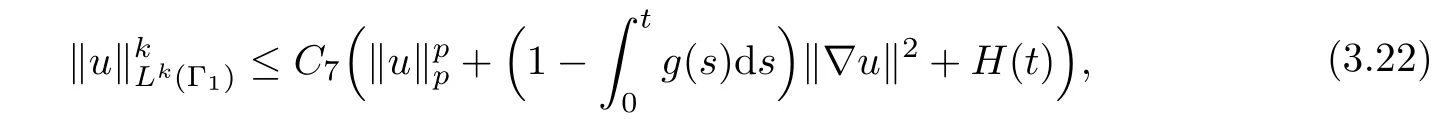
where C7=C5C6h.By inserting(3.22)into(3.18),using(2.6)and(2.11),we deduce that

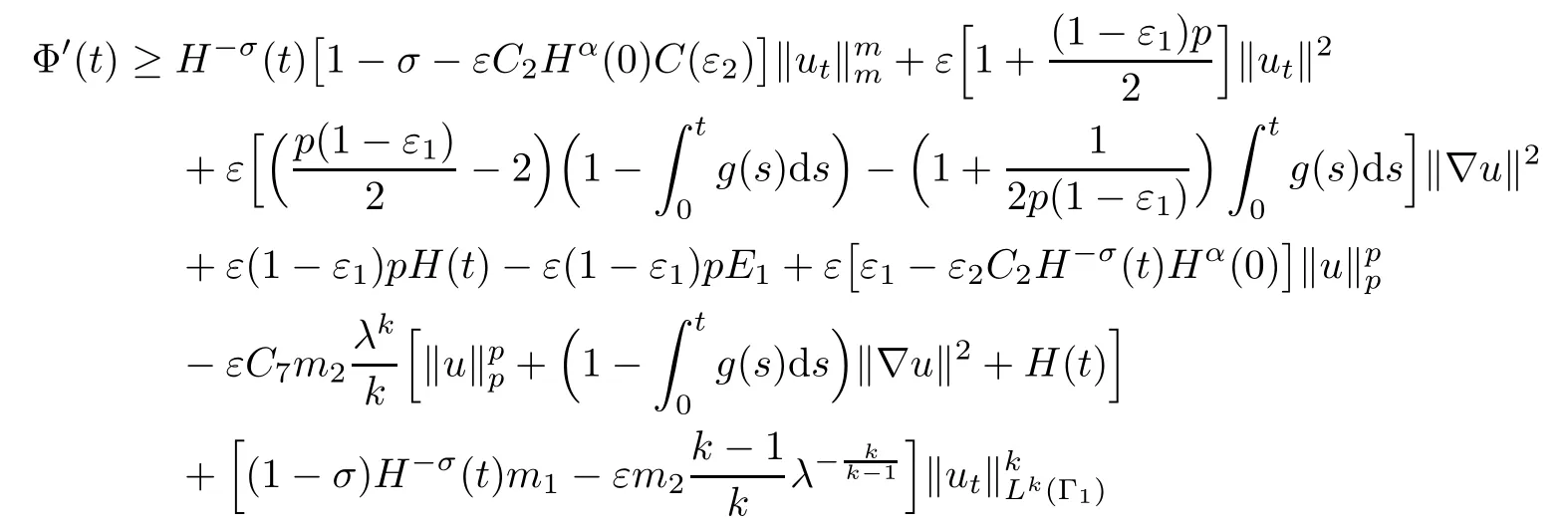
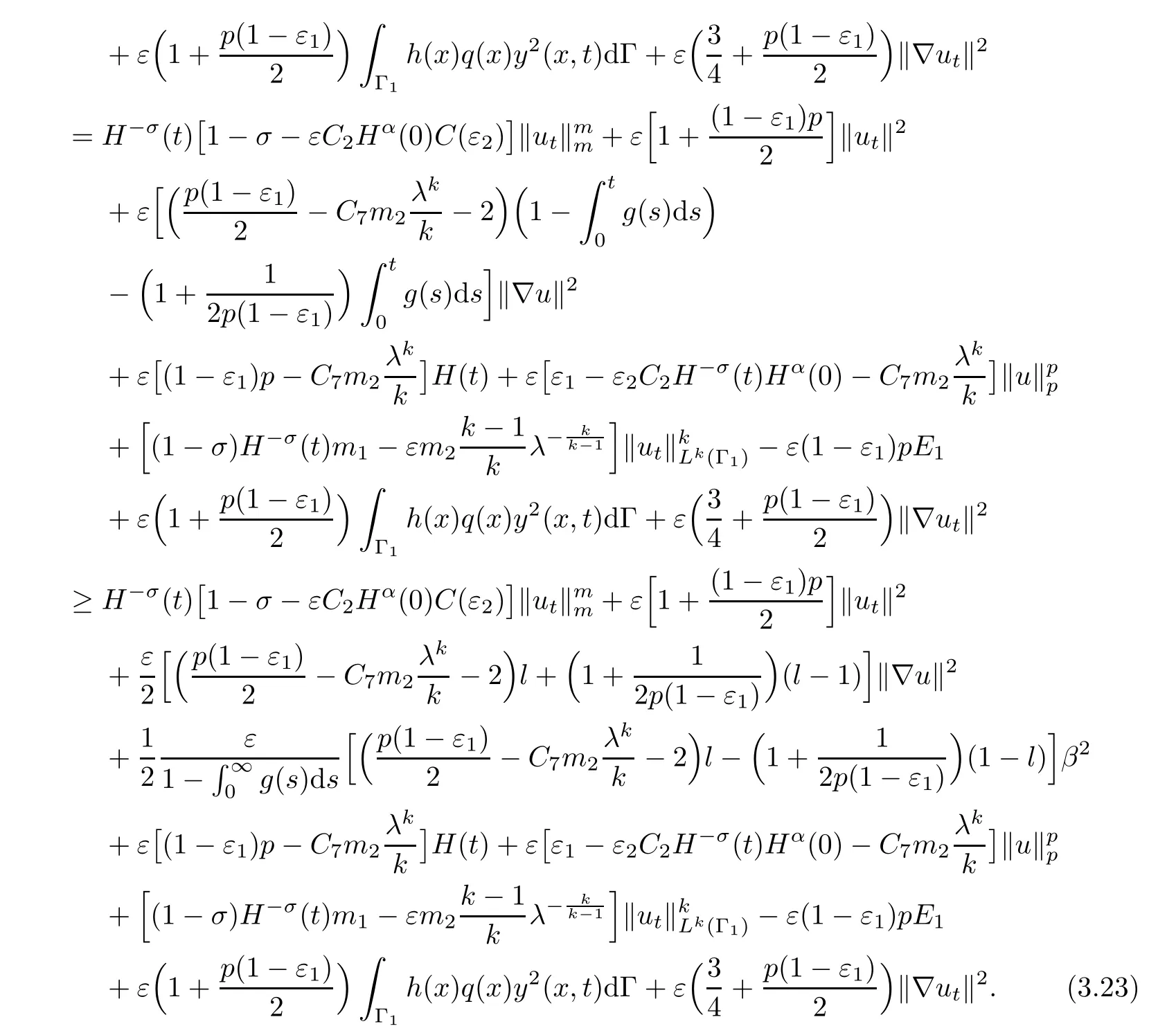
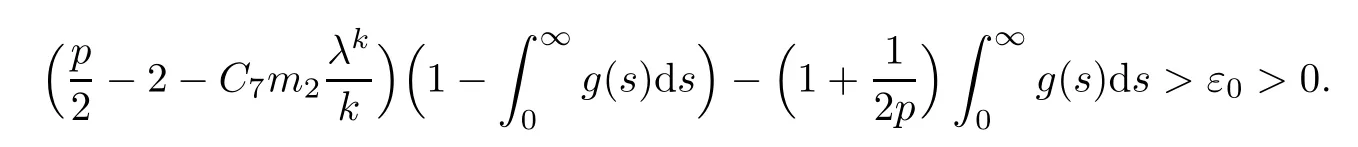
It is easy to see that there exists>0,and T0>0 such that for 0< ε1<:=1 ?,0< ε0T0,

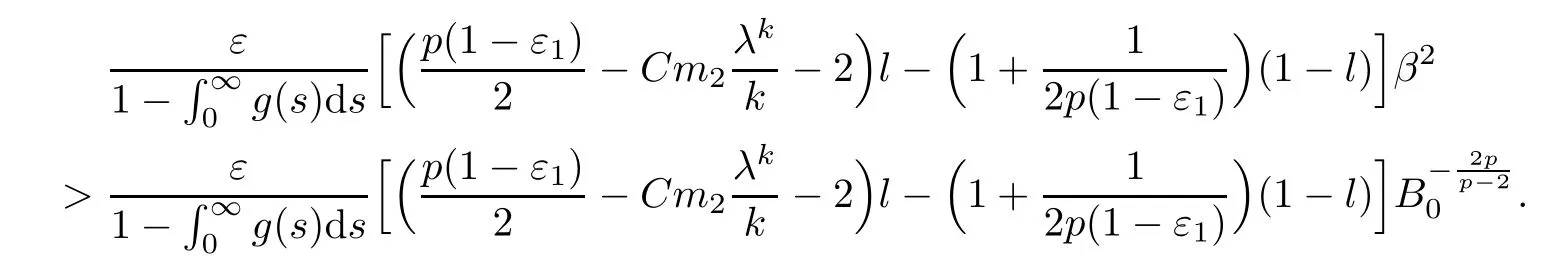
Now,we choose ε1>0 sufficiently small and E1∈ (E(0),E0),sufficiently near E(0)such that

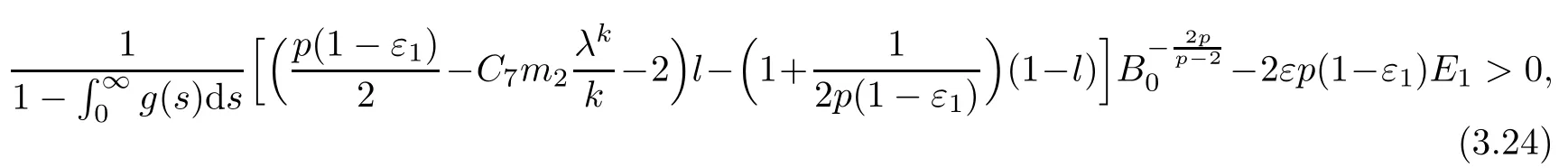
since

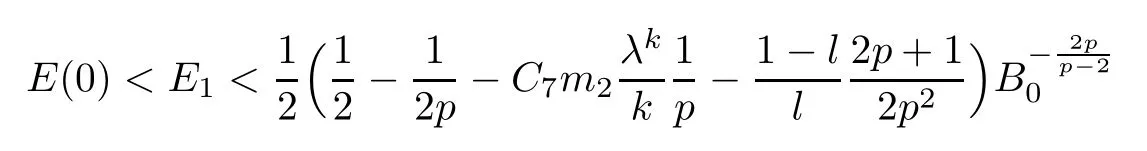
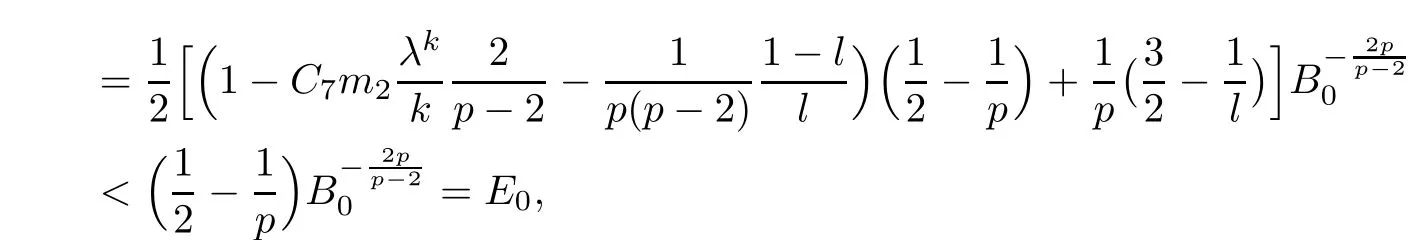
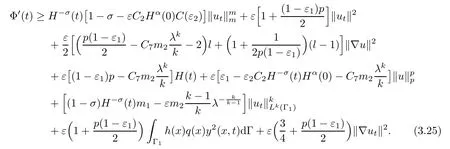
At this point,for ε2C2H?σ(t)Hα(0)< ε1<1,we can take λ sufficiently small such that

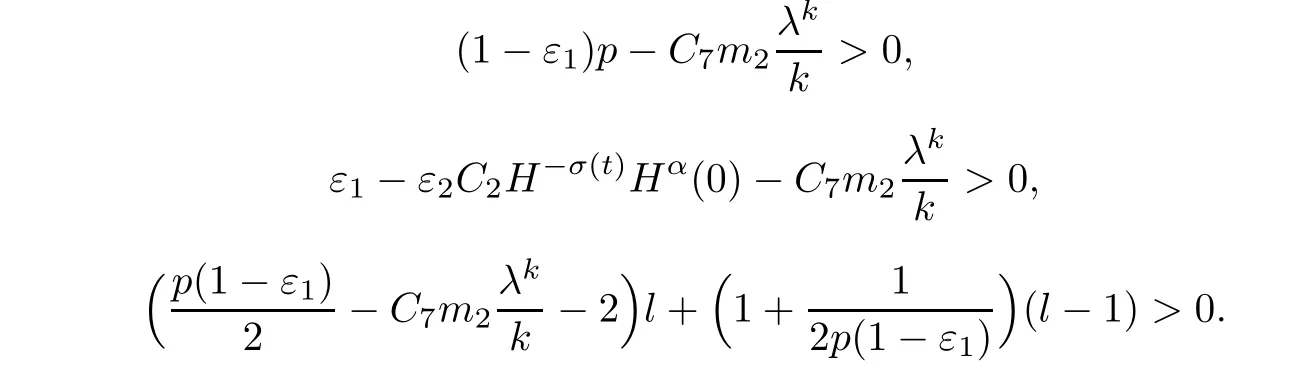
Once again,we take ε small enough such that

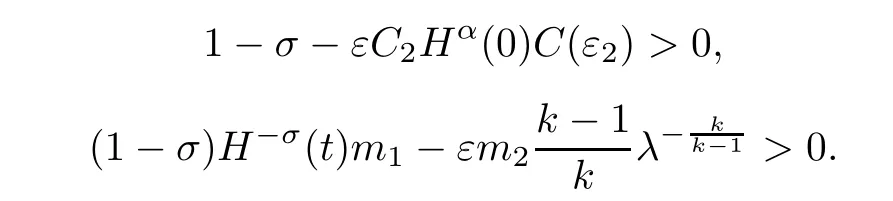
Then from(3.25),there exists a positive constant K1>0 such that the following inequality holds

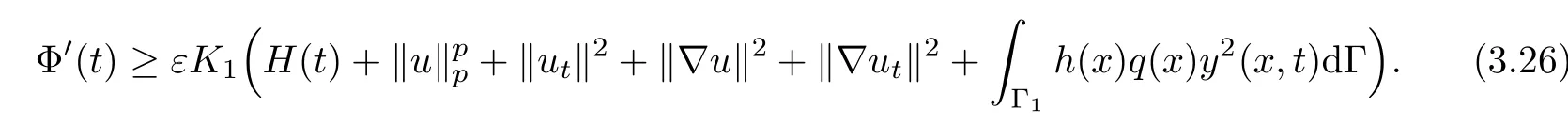
On the other hand from de finition(3.5)and assumption(A4),we have

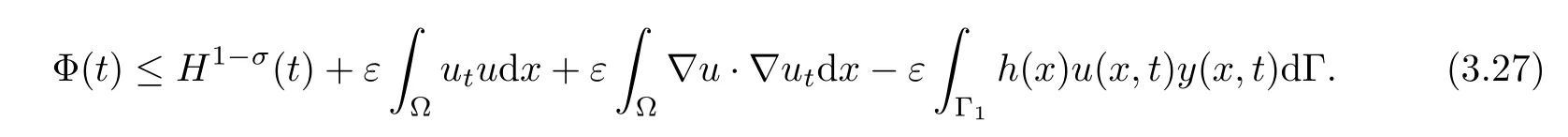
Consequently,from the above inequality,it follows that

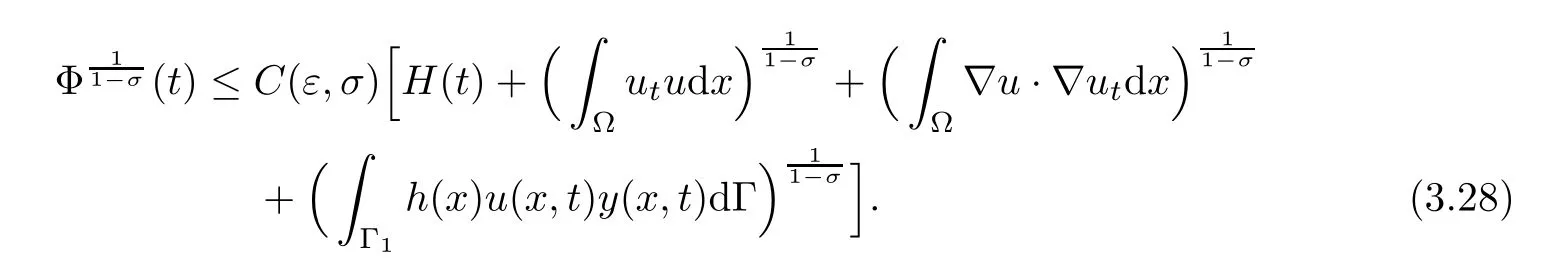
Using Young’s inequality,we now estimate

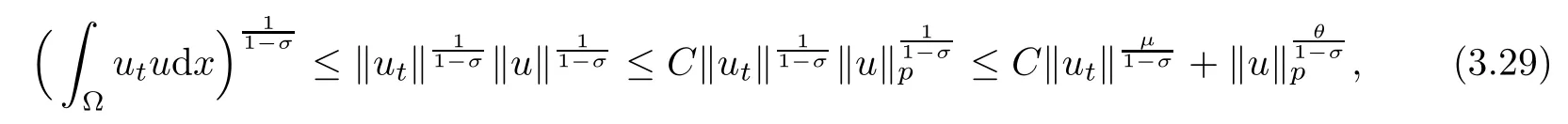
We choose μ =2(1?σ)>1,to get θ=.Using(3.13),we have

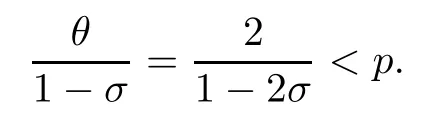
Then from(3.4),we can deduce

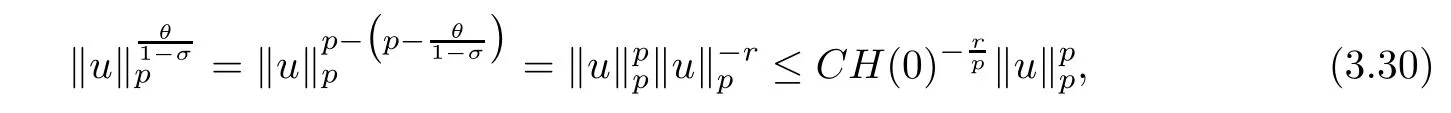
Using Young’s inequality again,we now estimate

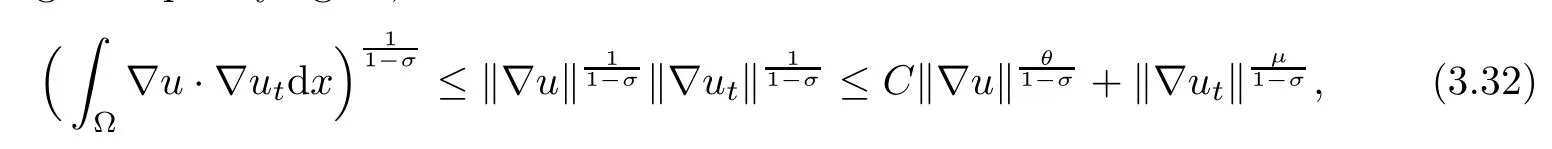
Thus,we obtain

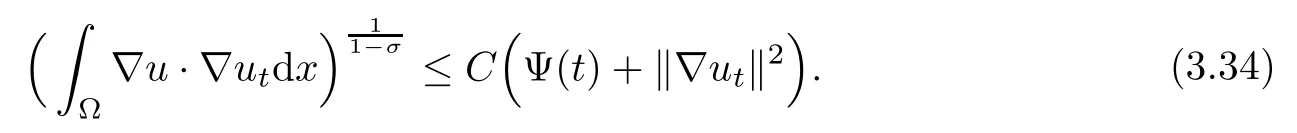
On the other hand,using H?lder’s inequality,we obtain

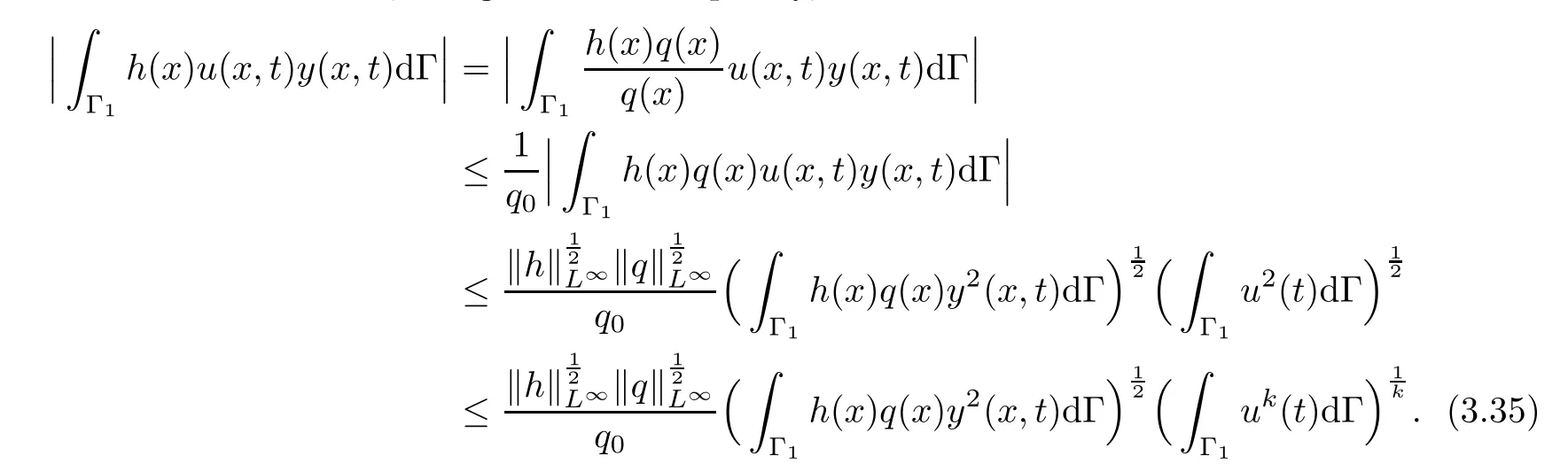
Thus,there exists a positive constantsuch that

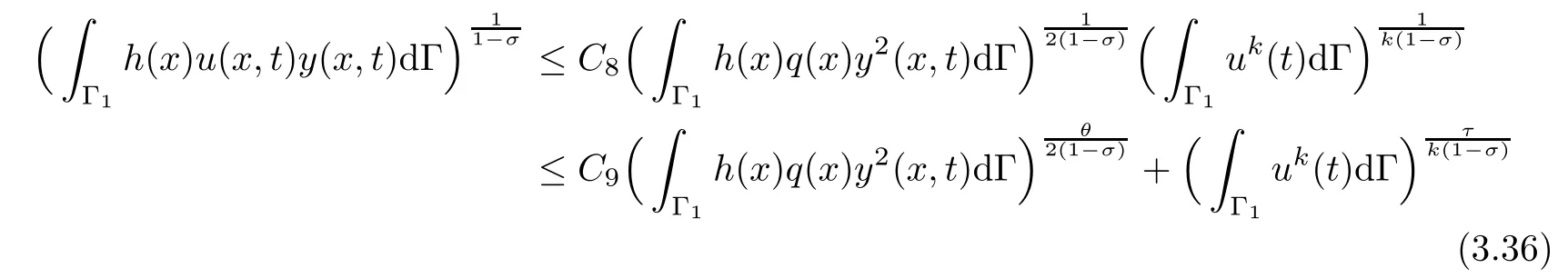
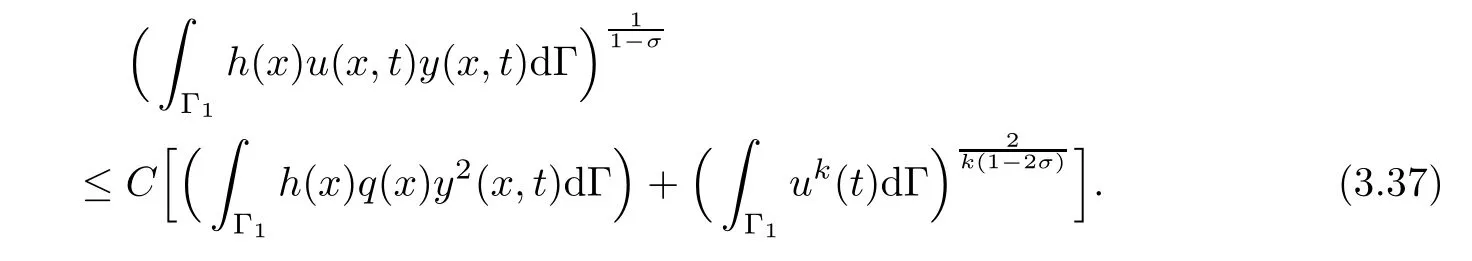
By using(3.13)and the algebraic inequality(3.20)withand,the condition(3.13)ensures that 0< ν <1,we can obtain

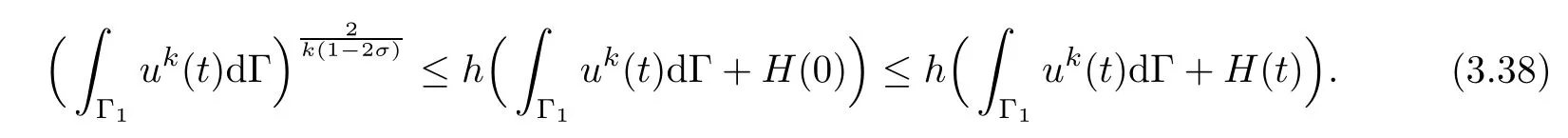
From(3.37)and(3.20),it follows that

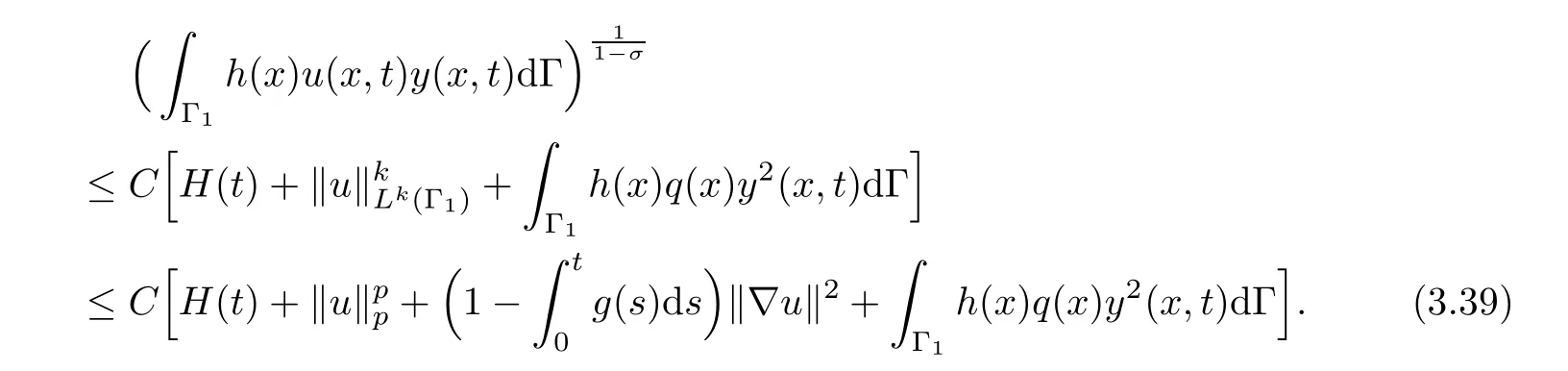
Therefore,from(3.28),(3.31),(3.34)and(3.39),there exists a positive constant K2>0 such that

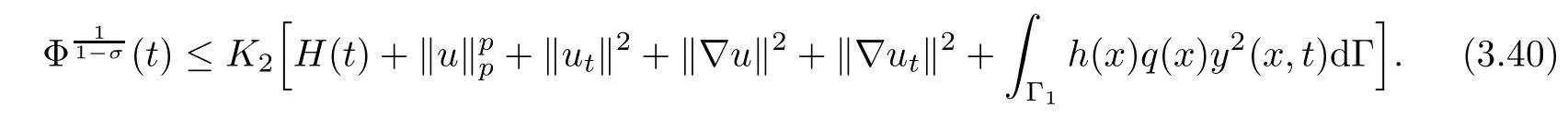
Consequently combining(3.26)and(3.40),we obtain

where ζ is a positive constant depending only on C,ε,σ and p.A simple integration of(3.41)over(0,t)yields

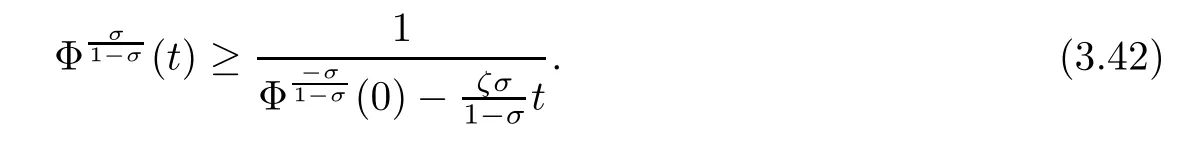
For(3.42)with positive initial data,Φ(t)goes to in fi nity as t tends to some time t1,with

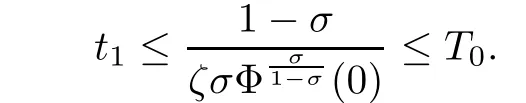
Thus the proof of Theorem 2.4 is completed.

Remark 3.1From the above estimate of the blow-up time t1,it can be seen that the larger of Φ(0),the faster the blow-up solution happens.