Robust Control of a Bevel-Tip Needle for Medical Interventional Procedures

Surender Hans and Felix Orlando Maria Joseph,

Abstract—In minimally invasive surgery, one of the main objectives is to ensure safety and target reaching accuracy during needle steering inside the target organ. In this research work, the needle steering approach is determined using a robust control algorithm namely the integral sliding mode control (ISMC) strategy to eliminate the chattering problem associated with the general clinical scenario. In general, the discontinuity component of feedback control input is not appropriate for the needle steering methodology due to the practical limitations of the driving actuators. Thus in ISMC, we have incorporated the replacement of the discontinuous component using a super twisting control (STC)input due to its unique features of chattering elimination and disturbance observation characteristics. In our study, the kinematic model of an asymmetric flexible bevel-tip needle in a soft-tissue phantom is used to evaluate stability analysis. A comparative study based on the analysis of chattering elimination is executed to determine the performance of the proposed control strategy in real-time needle steering with conventional sliding mode control using vision feedback through simulation and experimental results. This validates the efficacy of the proposed control strategy for clinical needle steering.

I. INTRODUCTION

IN minimal invasive surgeries involving biopsy and brachytherapy procedures, needle is a commonly used tool employed for treatment. In such procedures, accuracy is a major requirement for the needle in reaching the target tissue region in spite of perturbations from neighboring tissues during needle maneuvering. Generally, medical imaging modalities are helpful for providing feedback to obtain the actual position of the needle during the steering procedures. From [1],[2], it has been observed that the effectiveness in the minimal invasive procedures decreases where there is divergence of the needle from its prescribed preplanned plane of motion towards the target. In the current clinical scenarios, the target accuracy is limited by several factors mostly due to fatigue and human error. Also, during the needle insertion, physicians face several challenges such as the patient's movement,tissue deformation, and dependence of human hand-eye coordination to insert the needle. Therefore there is a need to develop an enhanced needle steering approach involving robust control strategies to ensure stability, disturbance and chattering avoiding capability.

To address the aforementioned requirement, the most widely investigated approach involving a passive flexible needle with an asymmetric tip was proposed by Taylor and Stoianovici [3]. During insertion, due to the beveled tip, an asymmetric force is applied by the tissue on the needle,causing the needle tip to bend. Generally, during needle steering, base manipulation involves both spinning and insertion degrees of freedom. Thus, the spinning of the needle shaft alone controls the direction of the tip bending. Likewise,the insertion of the needle causes its tip to bend due to the tissue reaction force thereby following a curvilinear path.These bevel-tip needles generally have higher maneuverability compared to conventional rigid straight needles.

In this paper, the robust control strategy proposed is based on sliding mode control, for the elimination of chattering in bevel-tip-steered needles while maneuvering inside the tissue region in spite of disturbances. The merits of sliding mode based robust control strategies involve disturbance rejection,parameter uncertainty, and unmodeled dynamics, which are essential for addressing any practical applications. However,undesirable chattering emerges due to the discontinuous component of the SMC control law. In order to suppress chattering, the following methods are considered [4], 1) The discontinuous control law can be replaced by either sigmoid or saturation functions, thereby yielding continuous control and elimination of chattering. However, in these approaches,even though the chattering is eliminated, robustness to the disturbances suffers. 2) By deploying the sliding mode control techniques with higher orders thereby assurings,s˙,...,sn1=0. However, in higher order sliding mode control techniques, complete information involving the sliding variable and its higher order time derivatives are necessary.Furthermore, the second order sliding mode control technique such as the super twisting algorithm (STA) [4], [5] requires only the information of the sliding variable.

A. Related Work on Needle Steering Control

For the past two decades, several researchers have proposed various needle steering strategies involving robotic systems for needle base manipulations [1]-[3], [6]-[30]. In order to drive a robot guided bevel-tip needle steering system to the desired target region [7], a computer calculates the optimum trajectory that is free from the obstacles and also hits the targets. An imagebased control strategy is suggested to reach the 2D target with obstacle avoidance [8], [9]. One step ahead in the progressing direction, the motion planners for bevel-tip flexible needles [10]is presented with the 3D environment including obstacles.Based on the duty cycle spinning of the needle [11], paths with different curvatures, i.e., changing from straight line movement to normal curvature can be achieved. Furthermore, the two methods for duty cycle spinning have been presented [12] to overcome the hardware limitations such as cable wind-up.More specifically in the control of bevel-tip needles, an observer-based feedback controller has been described [13] that stabilizes the position of the needle tip from the desired plane of interest. In the presented system, the activation of the needle at its base to rotate through a series of 180° is decided by the planner. Recently, the sliding mode control technique is used[14] to steer a flexible bevel-tip needle for both set point and path tracking tasks within the tissue region. Steering bevel-tip needles to stationary locations in soft tissue in a 2-D and 3-D environment is performed with appropriate switches in the bevel orientation with 180-degree axial rotation while the needle has been inserted. Furthermore [15], [16] presented a robust sliding mode controller to drive the passive bevel tip in a 2D environment in regulating the position of the needle tip at a static point. Overall, the developments on the new needle designs [17]-[21] which is helpful to achieve inaccessible targets, imaging modalities [22] like CT-scan, ultrasound,fluoroscopy, and MRI which play an important role for accessing the target points, needle-tissue interactive nonholonomic models used for steering the passive flexible bevel tip needle specifically for hard tissue [23], [24], and path planning [25]-[29] are discussed more elaborately in the recent survey on passive needle steering by Abolhassaniet al. [30].

B. Objectives and Contributions

The main objectives of this paper are two-fold: 1) First, to propose a robust control technique which rejects the disturbance and provides accuracy of the passive flexible needle during the insertion inside the tissue. In general, the sliding mode controller is well suited, but due to the discontinuous control input which creates chattering, it becomes impractical to apply this controller to actuator driven needling systems for percutaneous interventions. 2) Second, to avoid chattering, a continuous control is designed, which is based on integral sliding mode control, where the discontinuous part of ISMC is replaced by super twisting control. The proposed controller is continuous due to the combination of two continuous controls which ensures all the main properties of first order sliding mode control. Hence, chattering is mitigated,and the controller will be practically applicable for clinical scenarios. To the best of the author’s knowledge, the proposal of continuous STA based SMC for needle steering applications has not been reported in the literature so far. Thus the motivation for this study is to control needle steering so that there is no chattering; thereby it is clinically acceptable for maneuverability in biological tissues.

The rest of the paper is organized as follows: in Section II,methods involved in our study such as the kinematic model of the flexible needles, robust control studies, and proposed control strategies with ISMC based on STA are explained.Section III is devoted to the presentation of simulation results.Next, the experimental results are presented in Section IV.Section V includes the discussion and finally, concluding remarks are made in Section VI.

II. METHODS

A. Kinematic Model of Bevel Tip Needle

The kinematic model of the needle considered in our study is the generalized nonholonomic unicycle model presented by Websteret al. [24]. The insertion velocityi1and the rotational velocityi2are the two inputs of the passive needle kinematic model where it is assumed that the torsional compliance of the needle shaft is neglected. Thus, the needle has two DOF including both independent insertion and rotation. As shown in Fig. 1, framePis the inertial world reference frame, and frameQis the needle tip. With reference to universal frameP,parameter θ is the front wheel angle depending on insertion length. The position and orientation of frameQ, relative to framePcan be described precisely by a 4 × 4 homogeneous transformation matrix.

where

Here, the curvature attained by the needle during insertion is given ask=tanθ/l1. Due to insertion inputi1, the needle moves forward along thez-axis direction and also curves its path around they-axis of the body reference frame, which represents the orientation of the needle tip. The combined insertion and the passive curvature of the needle are depicted in Fig. 1. In our study, spinning of the needle is the primary input which causes it to follow the straight path whereas, the insertion is considered as the secondary input and is assumed to be constant.

The body-frame velocity is given bywhere

Thus the kinematic model of the bevel-tip passive flexible needle further simplifies to

The statesxandzdo not necessarily need to be controlled to stabilize the needle in thex-zplane. Moreover, the remaining needling system states are not perturbed by specific states(x,z). Fig. 2 depicts the reduced order system states. Fig. 2 (a)shows the first states1, which is the distance away from the desired plane of interest. Likewise, Fig. 2 (b) and 2 (c) denote the second and third statess2ands3, which correspond to the angles aroundzandx-axes, respectively. Hence, we can define the reduced order system’s state vector as:

Note that

is the desired equilibrium point of the system which corresponds to placing the needle in thex-zplane. Tracking the needle tip from the imaging system gives us only the position of the needle, not the orientation which is simply the distance from thex-zplane. The insertion velocity remains constant throughout the motion, which is equivalent to settingi1=1.The rotation of the needle needs to be controlled to keep it in the desiredx-zplane. Indeed, the resulting system is

In general,

which can be represented as follows:

The non-linear model of needling system (5) is transformed into an equivalent linearized form using the following transformation as follows:

Here,Lf h(s) stands for the Lie derivative ofh(s) along the vector fieldf, whereis the Lie derivative ofLf h(s)along the vector fieldf.

Finally, the state equations in the feedback linearized form are

B. Robust Control Study

1)Sliding Mode Control: A nonlinear control technique that, by the application of discontinuous control, changes the nonlinear system dynamics to the desired system dynamics where the order is lower than the given system model. The main strength of sliding mode control (SMC) is its robustness because many times, we do not have the exact model of the system. Thus, we need a robust control system to address model uncertainty.

SMC exhibits two-phase motion, namely, a reaching phase(in which the system trajectory moves from any initial state towards to the sliding surface) and a sliding phase (in which once it is on the surface, will slide along the surface and move towards the equilibrium point). In order to design the sliding variable and to provide the sliding motion in the sliding mode,two main conditions must be satisfied. First, the sliding surface should be the first order. Second, the control law should be designed in such a way that it drives the sliding variable to zero [32], [33]. Once the system state trajectory is reached on the sliding surface, the disturbance does not affect on the system model.

where,

The sliding surface is as follows,

It is clear that the parameterc1=10,c2=5,K=6, and η=4 give a desired rate of convergence of states to zero.

2)Motivation to Use the STA in ISMC Design: The motivation behind the use of the STA in ISMC is clearly understood by a simple first-order system. Let us consider,

where, andare the state, control input, and matched non-vanishing disturbance, respectively. It has been already explained in the literature that states are converging only when the magnitude ofKis greater than the upper bound of the disturbance. When the state converges towards zero, the equivalent value of the control input is obtained by setting. Once, the system state reaches the sliding surface, the equivalent control is applied to the system.This control signal ensures that the system state stays on the surface afterward. From (19), the disturbancedis given byd=Ksign(r)and can be observed directly fromu. The disturbance observation property by this method has one drawback where the control inputuhas a discontinuous nature.This discontinuous nature of control input is not suitable for practical implementations due to chattering. To resolve this problem of chattering, the STA is involved in the control law.In STA we exploit the continuous nature of the control input and the disturbance observation property. Mathematically, the expression of STC is

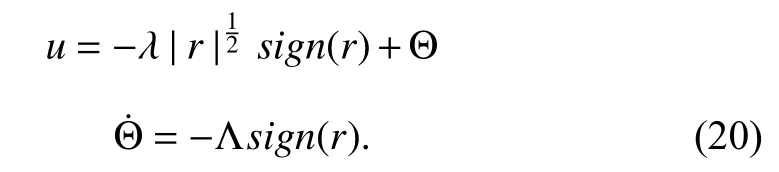
After substituting the control input (20) into (19), one can write

The above-derived theory motivates us to use the STA in ISMC as a disturbance observer and a mostly chattering free control input. Thus, we replace the discontinuous part of ISMC with STA such that the overall control is continuous.

3)Continuous Control With and Without Disturbance: In this section, we move one step forward towards continuous control. References [35], [36] prove the existence of a continuous finite time stabilization feedback control for a chain of integrator systems. For the system given by (17), the following theorem is given for finite time stabilization without disturbance.

Theorem 1 [35]: Leta1,...,an＞0 be such that the polynomialis Hurwitz, and there exists ? 2(0,1) such that, for everyb2(1 ?,1), the origin is a globally finite-time stable equilibrium for system (17) under feedback controli=g1(r)[uf(r)] by assuming,

whereb1,...,bnsatisfy

withbn+1=1 andbn=b.This control law (24) is not able to suppress the disturbance.It is continuous control which gives the state convergence in finite time. To understand the need for ISMC, first, we applied this control law in the system (18), wherer=[r1,r2,r3]Tis the state vector,u=unominalis the control input, anddis a disturbance. For the same system, controlu=unominalbecomes

where controller gains are chosen for the simulation asa1=15,a2=23,a3=9,b1=1/4,b2=1/3,b3=1/2 and a disturbance of 2sin(t)+3 is applied through the control input.But when we apply the disturbance, the states are not converging in finite time to the equilibrium point. Although our states are converging, the control input gives finite time convergence without disturbance. Thus we intend to design ISMC with a discontinuous control input.

4)ISMC With Discontinuous Control: In ISMC, the control inputuconsists of two parts. First is the continuous control component known as (unominal) (25). Second is discontinuous control (udiscon). The discontinuous control term takes care of the disturbance while the nominal control term is responsible only for the performance of the system. It is stated that the equivalent value of the discontinuous control is equal to the negative of the disturbance. So when we apply this controluto a system with disturbance, the discontinuous control rejects the disturbance, and all the states converge to the equilibrium by the application ofunominal. The controller design is explained as follows:

Consider the control input of the formu=unominal+udisconwhereudiscondefined as

wherer30is the initial value of stater3such that the system trajectory starts from the sliding surface. Thus the equivalent control law is expressed as,

Substituting the value ofudisconfrom (26), we can write

But again we face the same problem of discontinuous control as in the conventional sliding mode control. The control inputuin ISMC has discontinuous control which again is cause of chattering and again is not suitable from the practical implementation point of view. To remove chattering, we introduce continuous ISMC, in which the discontinuous part is replaced by the super twisting algorithm, which is proposed in the next subsection of the paper.

C. Proposed Continuous Controller Involving ISMC With STC to Remove Chattering

1) Concept of Higher-Order Sliding Mode Control: To begin with, let us briefly present the higher-order sliding mode controller concept applied to continuous time systems [37].Consider a smooth dynamic affine system of the form

wherer2 Rnis the system state,u2 R is the scalar control,ψ is the only measured output, andf(t,r) andg(t,r) are some smooth functions. Here, the objective is to make the sliding variable ζ approaches zero in finite time and to haveζ ≡0 with the help of a discontinuous feedback control. Higher-order sliding manifolds can be represented by is a nonempty set and can be understood in the Filippov sense,such that all the trajectories, i.e., the sliding variable and its successive time derivative converge to zero in finite time.Here, we presumed that the relative degreesmis known.Equation (31) is themth order sliding mode where the controluappears for the first time in themth time derivative of the sliding variable along the trajectories of (30). We have

where the functions

are certain anonymous smooth functions. Consider the inequalities

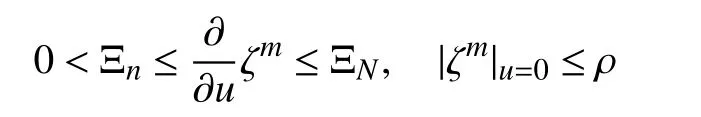
which hold globally for someand where ρ ＞0 implies the differential inclusion

Hence, finding the feedback control is a nontrivial task

such that all the trajectories of (33) and (34) go to zero in finite time. There are several simple and popular controllers for solving this problem in the continuous time domain like the twisting controller, sub-optimal algorithm, control law with prescribed convergence law, terminal sliding mode controller and super twisting controller. Out of these, the most popular controller is the super twisting algorithm.

It has the accompanying points of interest:

i) It remunerates uncertainties/perturbations which are theoretically Lipschitz in time on the system trajectories.

ii) We require just the information about the sliding variable ζ. As in other higher order algorithms, the control input requires the information of the sliding variable as well as it's consecutive time derivative.

iii) It gives simultaneously the finite time convergence of the sliding variable in addition to its consecutive time derivative.

iv) More importantly, it provides the continuous and consistent control input signal and, subsequently rectifies chattering.

2) Proposed Methodology: Here, the control input is given byu=unominal+uS TC, whereunominalis a nominal control term (25) anduS TCis the super twisting algorithm given as

Here, the sliding variable ζ is designed the same as in (27), so that system starts from initial time. Differentiating (27), we get

After putting the proposed control law ofu, we obtain

Let us defineRewrite (38), after putting the value ofO

From (39), after choosing the suitable value of gainsanda6=1.1τ1, we can conclude that in finite time, we can get ζ=O=0. By using the STC in integral sliding mode control, both the control signals are continuous in nature, and we achieve a chattering free response from the control input.

Proof:First, it is required to show thatFrom (39),by the selection of proper values [5], [34] ofanda6=1.1τ1. It is observed that in finite time in spite of disturbances, we can get ζ =O=0 , which givesTherefore, from (36)

We replaceu+din the chain of integrator form (18) withunominalwhich is free from disturbances (25). We then put the proposed control law in (40),

Thus,uS TCis the negative of the disturbance and hence, cancels out the disturbance. Now, when the system state trajectory is on the sliding surface, the dynamics of the system is governed by the nominal control input which is stable by its inherent design [35].

Remark 1: The sliding variable was chosen such that it starts from the initial condition of the state, thus, when the disturbance affects the system, it will be cancelled out byuS TC. By the proper choice [5], [34] ofuS TCgains,a5anda6,we get thein finite time irrespective of disturbance..Once the system is on the sliding surface, the closed-loop system governed by the nominal control which is stable by design.

Remark 2: The proposed controller involving ISMC with STC consist of two parts:

The nominal control term is responsible only for the performance of the system; it is not accountable for disturbance rejection. TheuS TCcontrol term takes care of the disturbance and model uncertainty. Designing of both control inputs is independent of each other. Thus, when the proposed control inputuis applied to a system with disturbance, theuS TCcontrol term rejects the disturbance, and all states converge to the equilibrium by the application ofunominal.

III. SIMULATION RESULTS

The proposed needle steering control strategy ensures stability is first tested with extensive simulations conducted through customized MATLAB 2018b/SIMULINK platform with a sampling time of 0.0001 s. The application of conventional SMC strategy to the passive needling system is first explained elaborately in this section. The system states arer1,r2andr3, where,r1is the distance to be minimized andr2andr3are the yaw and roll angles. The needle is simulated to insert to a depth of 10 cm inside the tissue phantom medium and is given a sinusoidal disturbance signal represented byd=3+2sin(t). It is a well-known fact and also mentioned in the literature that gains of the controller must be greater than the bound of the disturbance. If the bound of disturbance is a larger value, then the gain value must be greater than that. Furthermore, the magnitude (gain) of the discontinuous control law is the cause of the high-frequency component. The greater the amplitude, the greater the switching of the high-frequency component. Thus, if our proposed methodology is able to reject high-frequency components, then it will also work for scenarios with less disturbance. We have taken the matched disturbance (18),which is lipschitz continuous and assumed to be bounded kd(t)k ≤dmwith a known upper bounddm＞0 andNote that here the disturbance considers the patient’s movement, tissue deformation, and dependence of human hand-eye coordination during needle insertion. As mentioned in the methods section, coordinate (0, 0, 0) is the equilibrium point for the convergence of respective system states. First,we performed the simulation of our needling system with conventional SMC strategies. With this control algorithm, the asymptotic convergence of the three states is clearly observed in Fig. 3(a) and Fig. 3(b). This clearly indicates that the beveltip passive needle lies in the desired plane of interest using SMC. The finite time convergence of the sliding surface is observed clearly from Fig. 3(c) which is assured using conventional SMC. However, as shown in Fig. 3(d) , the control input has high-frequency chattering, which is not suitable for any practical applications. More precisely, in percutaneous interventional procedures, using flexible needles, the control input leading to spinning and insertion of the needles inside the tissue environment must be smooth and continuous with feasible magnitude. In conventional SMC, the chattering problem is a major limitation which needs extreme attention to address. Hence, to address this issue, we approach it in a hierarchical manner with the following cases and compare the performance of the existing needle steering control approaches with our proposed methodology:

Case 1: Here, the control input is only the nominal control which is in a continuous mode as given by

and it excludes the discontinuous control portion which addresses the disturbance involved in the system. Fig. 4 gives the convergence of states in finite time without disturbance.The nominal control input takes care of the performance of the system as observed in Figs. 4(a) and 4(b). Fig. 4(c) indicates that the control input is without chattering. However, this control case is not the typical robust type, as it does not involve disturbance (Figs. 4(a) and 4(b)). Thus, as a concluding remark for this case, the advantage is that it provides a chattering free control input, whereas the disadvantage is that there is a lack of disturbance during the performance observation.

Case 2: Here, in this case, the system with the same nominal continuous input as in Case 1 is introduced to address the system disturbance. As seen in Figs. 5(a) and 5(b) the performance of the needling system is affected due to the presence of a disturbance. Furthermore, it is noted that, due to the non-convergence of the states to the equilibrium position,the main objective of controlling the needle to stay within the desired plane of interest is not fulfilled, even though the control input is chattering free (Fig. 5(c)). Thus, there is a chattering free control input but the system states do not converge because the needle is out of the plane.

Case 3: To overcome the limitations of Case 1 and 2, we consider a control input consisting of two terms involving the continuous control input (as in Case 1 and 2) and a discontinuous control to address the disturbance and model uncertainty. Thus,u=unominal+udiscon. This control strategy is known as integral sliding mode control (ISMC). From Fig.6, the states converge to the equilibrium point in finite time in the presence of a disturbance. The chosen controller gains for the simulation study area1=15,a2=23,a3=9,a4=10,b1=1/4,b2=1/3,b3=1/2 with the disturbance as 2sin(t)+3. With the help of this controller with the aforementioned parameters, system states convergence is well-observed in spite of the disturbance as shown in Figs.6(a) and 6(b). But still, high-frequency chattering exists in the control input (Fig. 6(c)). As it is observed from the above three states where the needle lies within the desired plane of interest, there exists the problem of chattering in the control signal leading to the practical application of this strategy in the real clinical scenarios involving percutaneous cancerous interventions. Thus, we proposed a novel chattering free control strategy to regulate the needle and keep it within the plane of interest.

Case 4: As the final case, here consider the control input given by,u=unominal+uS TC. Here, in our proposed control scheme, as discussed in Section II, the discontinuous term of the control signal is replaced by the super twisting control term (35). The motivation behind this idea is as follows. First,the smooth convergence of the needle states is observed in Fig. 7 with the controller gains asa5=0.13,a6=300. Second,the control inputuwhereunominalanduS TCboth are the continuous control terms, which make the proposed controllerucontinuous. Thus, we achieve chattering free control that can be applied successfully for the needling system used in the clinical environment. The overall control performance of the conventional control strategies with the one proposed in state convergence and control input nature is tabulated in Table I.For a comparative simulation study it is observed from the Figs. 8 (a), (b) and (c) that our proposed control strategy in needle steering involving ISMC based on STC yield improved performance in real-time applications. The different control strategies were simulated with same initial states:r1(0)=0.3,r2(0)=0.5 andr3(0)=0.2. Furthermore, with the experimental study, we justify that our methodology in needle steering assures good practicality in a clinical scenario for percutaneous cancerous interventions.

IV. EXPERIMENTAL RESULTS

After the simulation study, the in-tissue phantom experiments are performed with an online vision feedback using the LabVIEW 2015 platform using customized programming. The experimental setup consists of a DC stepper motor, dc servo motor, stereo vision system, NI-DAQ Card 6212, and motor driver (experimental circuitry). The stepper motor is vertically mounted on the screw with a nut slider. The DC servo motor is mounted on the stepper motor platform as seen in Fig. 9. The stepper motor is used for insertion of the passive needle inside the tissue phantom, and the servo motor is used for rotation of the passive needle which allows the needle to move in a straight direction. The passive needle utilized in our experimental study is made up of polyamide PA 2200 with SLS (Selective laser sintering)technology. The needle is beveled at 45 degrees and has a 200 mm length and 3 mm diameter as seen in Fig. 10. The base of the needle is attached to the rotatory shaft of the servomotor.As the stepper motor moves, the needle advances into thetissue with a spinning movement which is carried by a servo motor. From the experiment, the value of 1/k=56.7 cm is used so that the needle follows the curvature after insertion of 10 cm into the tissue.

Control strategy Control input Convergence of states Chattering existence Conventional SMC Discontinuous Asymptotic convergence Yes Nominal control without disturbance Continuous Finite time convergence No Nominal control with disturbance Continuous No convergence No ISMC Discontinuous Finite time convergence Yes ISMC based on STC Continuous Finite time convergence No

The image to cartesian coordinate system transformation is shown in Fig. 11, where the scale parameters are customized.Transparent petroleum wax (for visual tracking of the needle tip) with a refractive index 1.4 and a volume of 800 cm3is utilized as a tissue phantom in our study. A customized pattern recognition LabVIEW program is developed to track the needle tip using the stereo vision system made up of two identical Logitech C270 USB Webcams. During the insertion(Fig. 12), the amount the passive needle moves away from the desired plane of interest corresponds to the first state of the needling system which is shown in Figs. 13 (a), 14(a) and 15(a). Deflection away from the plane can be directly measured from the stereo vision camera, which gives the distance in mm (i.e., z-direction) away from thex-yplane and is depicted in Fig. 11 (b). From Figs. 13 (a), 14(a) and 15(a), it is clearly understood that prior to 4 cm of insertion, the proposed controller controls the first state during left side,right side, and straight movement in the tissue phantom,respectively. Figs. 13 (b), 14(b) and 15(b) give the second and third states which are rotation around ofx-axis andy-axis w.r.t. needle insertion distance, respectively. Rotation around thex-axis is the angle in degrees between the two planesandvx2= [0,y,z], and rotation around they-axis is the angle in degrees between the two planesvy1=[1,0,0] andwherex,y, andzare the coordinates calculated directly from the stereo vision camera. To be more specific positivexis a movement towards right side inside the tissue,negativexis movement towards left side inside the tissue,yis insertion distance into the tissue andzis the distance away from thex-yplane. The left sided movement, right sided movement, and straight movement of the second and third state are shown in Figs. 13(b), 14(b) and 15(b), respectively.

V. DISCUSSION

In this paper, we have proposed a novel control technique based on sliding mode control that stabilizes the passive bevel-tip needle within the desired plane of interest. The novelty of control in our needling system application lies in the fact that the control law assures performance and allows the needle to be free from chattering, which is the major accomplishment in our research study. In clinical scenarios,the factors that affect target reaching accuracy include tissue deformation, internal organ’s movement due to patient respiration, and so on. These factors need to be addressed during percutaneous interventional procedures to achieve successful results. Thus the target reaching accuracy of the needling system with simultaneous disturbance avoidance capabilities could be achieved by a highly robust control technique. In our study, the main advantage of the proposed control strategy is the decreased number of times the passive needle’s bevel tip rotates in the presence of a disturbance. The proposed control law which was fed to the actuator (DC motor) is smooth and continuous due to the replacement of discontinuous term of ISMC by the super twisting algorithm.Chattering caused by the spinning of the needle in conventional SMC damages both actuators and the tissue phantom, which leads to piercing of tissue. The results obtained from the proposed control methodology are compared with that of a conventional first-order sliding mode controller to study the betterment of the proposed methodology in needle steering approaches. The future direction of our work involves addressing the limitations mentioned in our present study.

A. Limitations and Future Work

The limitations associated with our current study involves the following:

1) We have considered only the 2D path of the needle in convergence. An immediate future study will involve the 3D trajectory tracking of the needle tip.

2) Also, the dynamics of the needle tissue interaction has not been considered in our current study as we deal with a robust control algorithm implementation.

3) Furthermore, only a tissue phantom is considered in our study, whereas biological ex-vivo tissues are to be used in our immediate further study.

VI. CONCLUSIONS

The article proposes the super twisting algorithm with integral sliding mode control to make the control input signal completely continuous. By replacing the discontinuous term in integral sliding mode control with the super twisting algorithm, chattering has been eliminated in our needle steering study. Through a comparative study, the efficacy of the proposed control strategy is evaluated by both simulation and experimental results. From the results of our study, it is observed that the approach used is suitable to face challenges such as external disturbances and chattering leading to perturbations. Thus, the approach is suitable for needle steering in the real clinical scenarios. In the near future, we will be studying 3D trajectory tracking of the needle in an invivo tissue environment comprising the dynamics of the needle-tissue interactive modeling.