Numerical simulation on dynamic behaviors of bubbles flowing through bifurcate T-junction in microfluidic device?
Liang-Yu Wu(吳梁玉),Ling-Bo Liu(劉凌波),Xiao-Tian Han(韓笑天),Qian-Wen Li(李倩文),and Wei-Bo Yang(楊衛(wèi)波),?
1School of Hydraulic,Energy,and Power Engineering,Yangzhou University,Yangzhou 225127,China
2Key Laboratory of Energy Thermal Conversion and Control of Ministry of Education,School of Energy and Environment,Southeast University,Nanjing 210096,China
Keywords:microfluidic,T-junction,bubble break-up,numerical simulation
1.Introduction
Bubbles or droplets flowing in microchannel with bifurcate T-junction are significant in various industrial and pharmaceutical applications such as drug delivery,[1,2]fusion energy,[3,4]controlled release,[5,6]electronic cooling,[7]and chemical reaction.[8,9]The size and uniformity of the bubbles are essential particularly when the bubbles or droplets act as carrier vessels for active ingredients.[10,11]A thorough investigation of the dynamic behaviors of bubbles in the T-junction is beneficial to the optimization of the microfluidic device and has attracted widespread attention in the past decade.[12–14]
According to the pioneering work of Taylor,[15]droplets break when the strain rate of the continuous fluid reaches a certain value in an unconfined space. However,droplets or bubbles carried by the continuous phase in the confined microchannels show distinct hydrodynamic characteristics.[16,17]To answer questions,for example,how strong continuous flow is required to break up the bubbles at a T-junction or what the underlying mechanisms of break-up and non-break behaviors are,experimental,theoretical and numerical investigation have been carried out.[18–20]Single and series of bifurcate Tjunctions were employed by Link[21]to explore the passive break-up of droplets experimentally.Controllable asymmetrical break-up can be accomplished precisely by adjusting the relative length of the branches.And the volume of the daughter droplets was found to be proportional to the length ratio between the branches. The range of capillary number studied was extended to 4×10?4to 2×10?1shown by Jullien et al.[22]in a symmetrical PDMS T-junction.Two classes of break-up are distinguished and the experimental results of the tunnel break-up accord well with the results from the analytical theory of Leshansky and Pismen.[23]To further explore the dynamics of the fluids,a high-speed camera equipped with a micro-particle image velocimetry(micro-PIV)system was utilized by Fu et al.[6]to examine the break-up of N2bubbles in T-junction. Flow fields around the bubbles were reconstructed to show the characteristics of different flow patterns.Especially,a power-law relationship between the extension and capillary number was proposed to describe the transition of break-up and non-break regime.Numerical investigations have been conducted to study the dynamics of interfaces in T-junction as well.A three-dimensional(3D)color-gradient lattice Boltzmann method was proposed by Ba et al.[24]to examine the droplet formation in both symmetric and asymmetric T-junctions with high numerical accuracy.Both dripping regime and squeezing regime were examined in detail and the upstream pressure and viscous force were found to dominat the droplet formation process in T-junction.Combined with phase-field,a two-dimensional(2D)lattice Boltzmann model was developed by Liu and Zhang[25]and the droplet formation in a T-junction was studied.The effects of various flow parameters were examined systematically,and the transition from squeezing to dripping was found to occur at a critical capillary number of 0.018. Gas bubble formation under Taylor flow in T-junctions with different configurations was examined by Lim et al..[26]A theoretical model has been proposed to predict the size of the bubbles based on the junction angle and flow rates.The mechanisms behind the non-break behavior of bubbles were investigated further by Chen and Deng through using a phase-field lattice Boltzmann method.[27]It was found that the vortexs inside the droplets and tunnels between the droplets and channel walls lead to non-break behaviors.The asymmetrical behavior of droplets was studied by Bedram et al.[28]through using a T-junction with adjustable valves downstream of the branches.The results show that the volume of the daughter droplets after break-up is dependent on the pressure difference between branches.Non-break-up was also observed when the valve ratio was less than 0.65. Especially,the contact angle hysteresis during the break-up of droplet in a T-junction was examined in detail by Liu et al.[29]through using a multiphase lattice Boltzmann method(LBM).It was found that the difference between the channel surfaces of the branches also leads to asymmetrical break-up of droplets.Less volumes of the droplet enter the branch with nonideal surface,leading a smaller daughter droplet to be produced.
As mentioned above,extensive efforts have been devoted to the study of bubble behaviors in bifurcate T-junction and plenty of valuable results have been obtained.[30–33]However,most of the existing studies focused on the behaviors of one bubble at the T-junction[34]dominated by the viscous force from the continuous phase. The continuous bubble stream which is more commonly encountered in practical application is less considered,especially in the numerical simulation work. And the effect of coalescing between bubbles in the T-junction needs further investigating.Therefore,in this work a numerical model based on the volume of fluid(VOF)method is developed to gain a further understanding of the hydrodynamics of bubble stream in microfluidic device with Tjunction.Particularly,the generation of bubbles is controlled by a user defined function(UDF)which gives extra flexibility for controlling the size and loading density of the bubbles.The behaviors of bubbles including break-up and non-break are discussed with detailed pressure distribution and streamlines.The effects of bubble length,capillary number and diameter ratio between the mother channel and branches are discussed.Particularly,a phase diagram is summarized to clarify the boundary between break-up and non-break in a coordinate system of capillary number of the continuous phase and initial extension factor of the bubbles.
2.Mathematical model
The simulation of bubble dynamics is carried out by two numerical methods,i.e.,the interface tracking method and the interface capturing method.In the interface tracking method,such as boundary integral method,[35]finite element method,[36]and front-tracking method,[37]the interface is described as a boundary layer with a thickness of 0.The mesh evolves with the interface,which requires mathematical skills to be treated while the results are of high accuracy at the onset of break-up or merging of the interface.On the contrary,the interface capturing methods,including volume of fluid(VOF)method[38]and level set method,[39]treat the interface as a thin layer with a finite thickness[40]that evolves through the meshes.Complex mesh manipulations are avoided and fixed grid can be used. Of various interface capturing methods,the VOF method is most widely used. The mass conservation has proved accurate and the parallel calculation is easy to implement.[41]Hence,the VOF method is utilized to track the development and movement of the interfaces.

Fig.1.Schematic diagram of the microfluidic T-junction.
A 2D model is developed to study the gas bubbles flowing in a liquid continuous phase in a microfluidic bifurcate T-junction. As illustrated in Fig.1,the width of the mother channel is D=300μm and the length is L0=10D=3000μm.While the width of the daughter channel is d=1/2D=150μm and the length is L1=16D=4800μm.The lengths of the two daughter branches are the same.In this work we consider the incompressible and Newtonian two-phase fluid system in which the gas is immiscible with the liquid phase.A volume fraction function αGis used to represent the ratio of gas in one simulation cell as

The volume fraction of the liquid is αLand the sum of the two fluids in a cell is 1 as shown below

The governing equation of the volume fraction can be expressed as

where t is the time and v is the velocity which is governed by the continuum equation and Navier–Stokes equation as

where the density ρ and viscosityμare obtained from the interpolation of each phase as

subscripts G and L represent the gas phase and liquid phase,respectively.
The interfacial tension is induced into the Navier–Stokes equation as the source term Fvolfollowing the continuum surface force model[42]

Velocity inlet boundary condition is applied to the inlet of the mother channel.To avoid setting up two separate inlets for the continuous phase and dispersed phase and obtain better control over the bubble size and loading density,both gas and liquid are injected through this inlet.The duration time of gas and liquid is defined by using a user defined function(UDF).The flow time is acquired by the UDF and used as the condition of the conditional statements in the loop during the numerical simulation.And the volume fraction of gas to liquid at the inlet is dependent on the returned value of the UDF.Pressure outlet is set as the boundary condition at the outlets of the daughter channels.In addition,non-slip boundary condition is applied to all channel walls with a contact angle of 18?.
3.Numerical solution
The numerical solution is conducted by using the commercial CFD code Fluent 6.3 based on a finite volume scheme.Quadrilateral cells are used to mesh the computational domain(Fig.2(a)).Since the Reynold number is very low in microfluidic devices,the laminar model is adopted. The pressurevelocity coupling is obtained by the semi-implicit method for pressure linked equations(SIMPLE)algorithm.The momentum equation is discretized by using a second-order upwind scheme while other equations are discretized by using a firstorder upwind scheme. To achieve quick convergence,the under-relaxation factors implemented are 0.2(pressure),0.3(density),0.3(source term),and 0.2(momentum).In order to reduce the computational cost,the time steps are varied automatically based on the criterion that the global courant number does not exceed 0.5.The iteration in one time step ends when the relative residuals are less than 1%.
A mesh independence study is conducted by using a fine grid(30852 cells),a medium grid(19854 cells)(Fig.2(b)),and a coarse grid(9180 cells).Simulation result comparison of the velocity at the center of the junction is presented in Fig.2.The results obtained by using the fine grid and the medium grid are similar to each other,which indicates that the medium grid has sufficient cells to produce a mesh independent solution.Therefore,the medium grid is used in our simulation considering the computational cost.
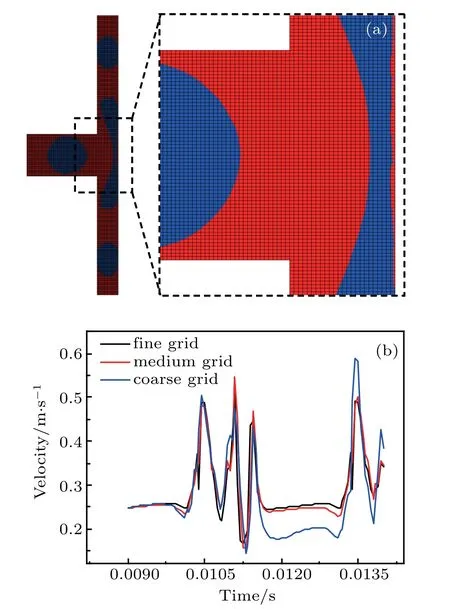
Fig.2.(a)Mesh geometry,(b)velocity in center of junction calculated by using different grids.
To verify the mathematical model developed in this paper,the simulation results are compared with the experimental result of Jullien[22]as shown in Fig.3.The evolution of the interfaces reconstructed from the numerical results is well consistent with the experimental observation.Hence,it can be verified that the numerical model is accurate enough to predict the dynamic behaviors of the bubbles.

Fig.3.Dynamics of bubble flowing through T-junction.
4.Results and discussion
Based on the aforementioned mathematical model,a numerical simulation of bubble splitting in bifurcate T-junction is conducted to clarify the underlying physics of the dynamic behaviors of the bubbles.Different flow patterns are obtained by adjusting the flow rate and the size of the bubbles.Both break-up regime and non-break regime are observed when the bubbles flow through the bifurcate T-junction.Two daughter bubbles are formed in the break-up regime and launched into the branches of the T-junction.While the bubbles are maintained entirety and flow into an arbitrary branch in the nonbreak regime.
4.1.Dynamics of bubble break-up
As mentioned above,the break-up regime can be divided into two classes,namely the obstructed break-up and the tunnel break-up.Under the obstructed break-up sub-regime,the branches of the T-junction are blocked entirely by the bubbles that the liquid film between the interface of the bubble and the channel wall is extremely thin. While under the tunnel break-up sub-regime,a visible gap namely the tunnel can be observed between the bubble and the channel wall which the continuous phase can flow through without being blocked.
4.1.1.obstructed break-up
Three classes of break-ups namely symmetrically obstructed break-up,coalescing symmetrically obstructed breakup,and coalescing asymmetrically obstructed break-up are observed under different loading densities of the bubbles.
(i)Symmetrically obstructed break-up
Figure 4 gives the pressure distribution(upper half)and the streamlines(bottom half)of a bubble splitting process in a typical symmetrically obstructed break-up regime(Ca=0.000417).The front interface of the bubble flattens when approaching to the wall of the T-junction and vortexes are observed both in front and in back of the bubble. The bubble is stretched into the two branches and the pressure in front of bubble in the branches decreases with the movement of the interface.Since the bubble is long,the branches are blocked before the back interface of the bubble enters into the junction.The pressure difference between the upstream and downstream of the bubble accumulates with time.After the bubble flows entirely into the branches,the back interface is pushed towards the junction by the continuous phase. thus bending toward the flow direction.Strong vortex in the corner of the junction is developed during this movement,thereby increasing the curvature radius of the back interface.The daughter bubbles inside the branches are connected with a thread that thins with time.The pressure inside the bubble is higher than the outside so that the gas inside the thread is drained towards both branches,leading to break-up of the thread in the center of the junction.Two daughter bubbles with the same size are formed consequently.The next bubble enters into the junction when the break-up of the previous bubble ends.

Fig.4.Symmetrically obstructed break-up(Ca=0.000417).
(ii)Coalescing symmetrical obstructed break-up
Under higher Ca,the subsequent bubble flowing behind catches up with the prior bubble at the junction and coalesces into a bigger bubble as shown in Fig.5.When the prior bubble stretches into the branches(t=0.03612 s)it cannot obstruct the branches completely.The continuous phase between the prior bubble and the subsequent bubble is drained through the gap between the bubble and the back wall of the junction as illustrated by the streamlines. Hence,the prior bubble is kept entirety when the subsequent bubble enters into the junction.The coalescing occurs when the interfaces of these two bubbles contact each other(t=0.03772 s in Fig.5)and the branches are obstructed completely thereafter.The continuous phase squeezes the bubble and leads to symmetrical break-up(t=0.04012 s–0.04252 s in Fig.5).The pressure at the front interface of the bubble increases after the break-up.

Fig.5.Coalescing symmetrically obstructed break-up(Ca=0.00139).

Fig.6.Coalescing asymmetrical obstructed break-up(Ca=0.000694).
(iii)Coalescing asymmetrical obstructed break-up
Under the condition of low Ca,coalescing is also observed when the bubbles are loaded densely.Figure 6 shows a typical case of coalescing obstructed break-up that the bubbles are split asymmetrically.To achieve the asymmetrical behavior of the bubbles,different gauge pressures are set at the outlet of the branches that the pressure at the outlet of the top branch is 200 Pa higher that of the bottom branch.Since the velocity of the continuous phase is low,the stretched bubble stagnates at the junction(t=0.0672 s–0.0816 s)and swings between the branches due to low pressure in the branches.The pressure inside the bubble decreases during this stage,and the vortexes at the back of the bubble evolve forward into the front of the bubble inside the branch.Before the bubble enters the junction,a subtle discrepancy is observed between the two vortexes behind the bubble. This asymmetry of streamline develops quickly,leading to asymmetrical pressure distribution in the branches.The subsequent bubble flows into the junction and coalesces with the prior bubble,thus causing further asymmetry of the fluid flow.The volumes of the bubble in the two branches are unequal as can be seen from t=0.0920 s in Fig.5,and the strong vortex develops in the upper corner of the junction outside the bubble. This vortex leads to further unequal distribution of the gas phase in the branch so that the bubble in the upper branch shrinks and the upper branch turns into being incompletely obstructed(t=0.0960 s).The pressure difference between the upstream of the bubble and downstream of the branches accumulates as the fluid flows,and thus finally causing the bubble to be broken up. Since the evolution of the bubble is asymmetrical in the branche,the breaking does not happen in the center of the junction.
4.1.2.Tunnel break-up
When none of the smaller bubbles can obstruct the branches completely,visible gaps namely tunnels are observed between the bubbles and the channel walls during the breakup. Similarly,two classes of tunnel break-up,namely,the symmetrical tunnel break-up and asymmetrical tunnel breakup,are obsedrved.
i)Symmetrical tunnel break-up
Since the volume of the bubble is insufficient to fill the branches in the tunnel break-up mode,the continuous phase circumvents the bubbles through the tunnels into the branches as illustrated in Fig.7.Before the bubble enters into the junction,the streamlines are almost parallel to the channel wall and no vortex is observed. When the bubble enters into the junction at t=0.0096 s,the streamlines are bent towards the bubble due to the interfacial tension. And the gap between the bubble and the corner of the junction is relatively narrow so that high pressure difference is observed between the upstream and downstream of the corner.After the back interface of the bubble enters into the junction,the viscous force from the continuous phase stretches the bubble into the branches and pushes the bubble clinging to the front wall of the junction. The distance between the bubble and the channel wall increases,and the tunnels open.The streamlines are bent towards the wall when passing through the tunnel,and the pressure of the continuous phase decreases(t=0.0102 s in Fig.7).The bubble is broken up into two daughter bubbles after being stretched.Strong vortexes are observed in both the front and back of the bubble due to the unsmooth interface shape after being broken up.The vortexes disappear after the interface of the daughter bubbles has deformed into a smooth shape.

Fig.7.Symmetrical tunnel break-up(Ca=0.00417).
ii)Asymmetrical tunnel break-up
Asymmetrical tunnel break-up occurs under the condition of higher loading density of the smaller bubbles as shown in Fig.8.The pressure at the outlet of the bottom branch is 200-Pa higher than at the top branch.Comparing with the symmetrical tunnel break-up stated in class i),the distances between the bubbles are closer,hence the squeezing from the continuous phase to the bubble is weaker and the pressure difference inside and outside the bubble is almost zero when the bubble is flowing in the mother channel.Under this flow condition,little perturbation in the flow field can lead to an asymmetrical pressure distribution.The pressure inside the upper branch is lower than that of the bottom branch,hence the pressure difference is higher between the upper branch and the mother channel.As a result,the position of the bubble is already deviated from the center of the mother channel before entering into the junction. After entering into the junction,the pressure inside the bubble increases and the bubble diverges into the upper branch driven by the unequal pressure difference.At first,the difference between the volumes of the bubble inside the two branches are small(t=0.01009 s). However,this difference leads the upper branch to be obstructed and the bottom branch with a narrow tunnel to be partially open The pressure difference between the bubbles of the continuous phase upstream and the branches grows higher,resulting in growing divergence of the bubble volume distribution in the branch(t=0.01049 s).The subsequent bubble enters into the junction before the previous bubble is split which gives rise to strong squeeze on the previous bubble and finally leads the the previous bubble to be broken up.The breaking happens almost in the center of the junction due to the small size of the bubble.Two daughter bubbles with different sizes and the pressure inside the branch increase due to the release of the upstream pressure after being broken up.

Fig.8.Asymmetrical tunnel break-up(Ca=0.00417).
4.1.3.Non-break
Under a moderate loading density of the bubbles and low flow rate of the continuous phase,the non-break mode is observed no matter what the bubble size is.The pressure at the outlet of the top branch is 200 Pa higher than at the bottom branch in the case shown in Fig.9.Like the asymmetrical tunnel break-up,the difference between the pressure inside the bubble and that outside the bubble is low before entering into the junction,and increases as the bubble deforms inside the junction.The vortexes behind the bubble evolve into the bubble and move towards the two fronts of the bubble. Strong vortex is developed in the bottom corner of the junction where the bigger volume of the bubble is in the bottom branch.This vortex drags all the gas in the bubble to the bottom branch and weakens after the bubble has entered into the bottom branch entirely.

Fig.9.Non-break(Ca=0.000694).
Under a higher loading density of the bubbles,the distances between the bubbles are short and the subsequent bubble catches up with the prior bubble in the corner of the junction at t=0.06646 s(the pressure at the outlet of the top branch is 200 Pa lower than that at the bottom branch)as shown in Fig.10.Since the distances between the bubbles are short,the flow is chaotic so that the streamlines are no longer parallel to the channel wall in the mother channel and vortexes occur in most places near the interface.After the coalescing of the bubbles,strong vortexes are observed at the back of the bubble due to interfacial tension which weakens quickly after the bubble has deformed into a smooth shape. After the bigger bubble flows into the upper branch,the pressure difference between the mother branch and the bottom branch is higher.Hence,the next bubble enters into the bottom branch,and the subsequent coalescing with the prior bubble happens in the bottom branch as well.In this non-break mode,bubbles coalesce and flow into the two branches alternatively.

Fig.10.Coalescing non-break(Ca=0.000694).
4.2.Regime diagram
The behaviors of the bubbles at the junction are mainly determined by the viscous force of the continuous phase,the loading density of the bubbles and the length of the bubbles.The competition between the viscous force and the interfacial tension can be represented by a capillary number Ca as follows:

in which U(in units m/s)is the inlet velocity of the continuous phase,μ(in units Pa·s)is the viscosity of the continuous phase,and σ(in units N/m)is the interfacial tension coefficient.
To study the break-up behavior of the bubble quantitatively,an initial extension factor of the bubble before entering into the junction is defined as

in which l0and w0are the length and width of the bubble before entering into the junction,respectively. After the bubble enters into the junction,the shape of the bubble deforms,
which is described by the transit extension factor as

in which leand weare the length and width of the bubble after entering the junction(measured as shown in Fig.1).It is found by Link et al.[21]that the bubbles are always in break-up state when ε is larger than 1,which is in agreement with our numerical result.

Fig.11.Phase diagram of break-up and non-break.
Based on the numerical results,the behaviors of the bubbles are summarized in a coordinate system of Ca and ε0as shown in Fig.11.Generally speaking,the bubbles are more likely to be broken up when both Ca and ε0are high. Under low Ca,bubbles with low initial extension factor ε0,such as spherical bubbles with ε0=1/π,are less likely to be broken up than the bubbles with high ε0in the same T-junction.While the bubbles are always in break-up state under the condition of high ε0(ε0>0.7)no matter what the value of Ca is.The behavior of the bubbles with constant length transits from non-break to break-up with the increase of Ca which is attributed to the intensified viscous force acting on the bubbles at the junction.While under the same Ca,the non-break bubbles turn into break-up with the increase of bubble length due to the increased pressure accumulates in the upstream bubble at the junction.It can follow from Fig.11 that there is a critical capillary number Cacdividing the non-break and breakup behaviors,which is related to the length of the bubbles and the geometry of the T-junctions. As can be seen,Cacdecreases with the increase of initial length of the bubble l0.When the bubbles are not long enough to obstruct the channel,break-up occurs only when the viscous force overcomes the interfacial tension.Hence,a high velocity of the continuous phase is required to introduce the break-up,thus leading to high Cac. While the pressure difference between the upstream and downstream bubbles at the junction cooperates in pushing the bubbles and thus leading them to be broken break when the branches are obstructed by bubbles with ε0>1/π.Consequently,the viscous force is required to be less and the Cacto be lower under high ε0. Note that the behaviors of continuous bubble stream are different from those of a single bubble that flows through a T-junction.The distance between the bubbles decreases with the increase of loading density of the bubbles,which gives rise to the probability of coalescing.Hence,the boundary between the non-break and break-up in the phase diagram differs under different value of loading density of bubbles.

Fig.12.Behaviors of bubbles under bubbling flow condition in channels with different diameter ratios(D1=300μm,Ca=0.00417).
4.3.Effect of diameter ratio
The geometry of the T-junctions determines the local flow field and thus affects the dynamics of the bubbles.In this subsection,the behaviors of bubbles under the bubbling flow condition(short bubbles)and the slug flow condition(long bubbles)are examined under the same Ca(=0.00417)in channels with different diameter radios between the mother channel and branch(d=D1/D2).
Bubbles with low ε0are loaded under the condition of bubbling flow.The diameter of the bubbles is smaller than the width of the mother channel so that the mother channel is not obstructed by the bubbles.As shown in Fig.12(a),when d=1 the bubble does not contact any channel wall in the T-junction and the transit extension factor ε is low so that only slight deformation is observed when the bubble flows into a branch(pressure at the outlet of the top branch is 100 Pa lower than that at the bottom branch).The prior bubble is caught up by the subsequent bubble in the corner and coalesces into a bigger bubble that flows into a branch without being broken up.With narrower width of the branches,(d=1.5,Fig.12(b)),the bubbles are deformed more obviously at the junction.However,the tunnels can still be formed between the bubble and channel wall,and the viscous force from the continuous phase is insufficient to lead to the break-up. The tunnel width decreases with d increasing(Fig.12(c)),and the viscous force increases correspondingly so that the bubbles can be split under the tunnel break-up regime. The analytical results from Link et al.[21]show that ε increases with d increasing and contributes to the break-up of the bubbles which accords with our numerical simulation.

Fig.13.Behaviors of bubbles under slug flow condition in channels with different diameter ratios(D1=300μm,Ca=0.00417).
Compared with the bubbling flow,the slug flow is loaded for bubbles with ε0>1/π as shown in Fig.13(pressure at the outlet of the top branch is 100 Pa lower than at the bottom branch).Under low d(Fig.13(a)),the fluid slows down when entering into the branches due to the sudden increase in the flow section.The bubble stagnates at the junction and coalesces with the subsequent bubble.However,the viscous force is still insufficient until the third bubble merges into the bubble at the junction.The thread connecting the bubbles inside the branches thins with the coalescence and finally is broken up under the joint action of viscous force and pressure difference.Like the bubbling flow,the tunnel between the channel wall and bubble narrows with d increasing.Since the bubble is long enough under the slug flow condition,the tunnel is narrow enough to introduce high viscous force at d=1.5 at which the bubbles are split in the symmetrical tunnel break-up mode(Fig.13(b)).With the further increase in d,the branches are obstructed entirely,and the bubbles are split under symmetrically obstructing break-up mode as shown in Fig.13(c).It can be concluded that increasing d is beneficial to the break-up of bubbles under the same capillary number.However,unlike the head of the bubbles with ε0=1/π,the head of the bubbles with ε0>1/π expands inside the branch and higher pressure difference between upstream and downstream of the bubble is introduced.The pressure difference plays a more significant role in breaking up the bubbles under slug flow than under the bubbling flow.
To sum up,in applications where equal-sized bubbles are required to be produced in the branches,high diameter ratio between the mother channel and the branch is beneficial to the symmetrical break-up.Especially when bubbles are short,at least a diameter ratio of d=2 is required in order to introduce the obstruction into the branches.
5.Conclusions
Based on the VOF method,a transit 2D model is developed to investigate the gas–liquid two-phase flow in the microfluidic device with a T-junction that the bubbles enter into from the mother channel.The behaviors of the bubbles and the evolution of the interfaces are examined in detail.The mechanisms of break-up are discussed in particular and different flow patterns are distinguished.The effect of geometry is explored by examining the dynamics of bubbles in T-junctions with different diameter ratios.The configuration of channels which is beneficial to bubble break-up is obtained.The conclusions can be summarized below.
(I)Both break-up behavior and non-break behavior of the bubble are observed at the T-junction.Bubble with ε0>1/π flowing under slug flow condition is easy to split in the Tjunction due to the obstruction of the branch which introduces high pressure difference between upstream and downstream bubble.While the bubble with ε0=1/π flowing under bubbling flow condition is less apt to be broken up.The bubble remains integrity and flows into an arbitrary branch when the flow rate of the continuous phase is low. The break-up can only be observed when the viscous force from the continuous phase overcomes the interfacial tension.
(II)Under the condition of low capillary number(Ca<0.001),spherical bubble(ε0=1/π)is less likely to break than bubble with higher ε0in the same T-junction.With constant length,the behavior of the bubble transits from non-break to break-up with the increase of Ca.Bubble with ε0>0.7 is always in break-up state in the T-junction no matter what the value of Ca is.
(III)High diameter ratio between the mother channel and branch is beneficial to both symmetrical and asymmetrical break-up of the bubbles.At least a diameter ratio of 2 is required to break up the spherical bubble with ε0=1/π.
- Chinese Physics B的其它文章
- Theoretical analyses of stock correlations affected by subprime crisis and total assets:Network properties and corresponding physical mechanisms?
- Influence of matrigel on the shape and dynamics of cancer cells
- Benefit community promotes evolution of cooperation in prisoners’dilemma game?
- Theory and method of dual-energy x-ray grating phase-contrast imaging?
- Quantitative heterogeneity and subgroup classification based on motility of breast cancer cells?
- Designing of spin filter devices based on zigzag zinc oxide nanoribbon modified by edge defect?

