Extraordinary transmission and reflection in PT-symmetric two-segment-connected triangular optical waveguide networks with perfect and broken integer waveguide length ratios*

Jia-Ye Wu(吳嘉野), Xu-Hang Wu(吳栩航), Xiang-Bo Yang(楊湘波), and Hai-Ying Li(李海盈)

1Guangzhou Key Laboratory for Special Fiber Photonic Devices,School of Information and Optoelectronic Science and Engineering,South China Normal University,Guangzhou 510006,China

2Laboratory of Nonlinear Fiber Optics,School of Electronic and Computer Engineering,Peking University,Shenzhen 518055,China

Keywords:parity-time symmetry,optical waveguide network,integer broken ratios

1.Introduction

In the recent two decades,a kind of absorbing artificial optical structures to control and confine the propagation of electromagnetic(EM)waves,the-symmetric systems,have been widely investigated. In quantum mechanics,the eigenvalues of observable mechanical quantities must be real numbers,therefore their operator matrices should be Hermitian ones. Bender et al.[1–4]found in the year 1998 that for a-symmetric system,even if its Hamiltonian is non-Hermitian,when the potential function is smaller than a certain threshold,all energy eigenvalues are still real numbers.When the potential function is larger than this threshold,its energy eigenvalues appear complex numbers.This threshold is called spontaneous-symmetric breaking point.In 2007,El-Ganainy et al.[5–9]introduced the concept of-symmetry into optical system through paraxial approximation.Similar to the-symmetric mechanical system,-symmetric optical systems can produce extraordinary optical features and phenomena near the spontaneous-symmetric breaking point.Subsequently,-symmetric optical systems,such as-symmetric optical lattices,[6–10]optical waveguides,[11–29]inhomogeneous nonlinear optical media,[30]and graphene,[31,32]have been widely investigated and some extraordinary optical characteristics,for instance,birefringence,[6]unidirectional invisibility,[8,9]ultrastrong absorption,[31]and singlemode lasing,[33,34]have been found.

Optical waveguide networks(OWNs)[35–52]are another type of novel artificial optical structures to manipulate the propagation of EM waves.It is found that they can produce ultrastrong photonic localization,[31]extreme wide photonic bandgap(PBG),[38,41,44]interesting comb-like optical transmission spectrum,[45,46]rich photonic attenuation mode,[49]and so on.However,studies that combine the idea of opticalsymmetry and OWNs are quite rare.

Recently,our research group designed a-symmetric aperiodic Thue–Morse optical waveguide network[53]and asymmetric periodic ring waveguide network,[54]whose waveguide length ratios are perfect integer ratios(i.e.,1:1,1:2,1:3,...).Although seemingly similar,the difference betweensymmetric optical lattices[6–10]andsymmetric optical waveguide networks are fundamental.The former possesses a pair of gain and loss waveguides which are coupled perpendicularly to the directional of light propagation;the latter arranges the gain and loss profiles alternately along the length,whose waveguide segments and unit cells are all physically linked and connected.

In this study,we investigate the propagation properties of EM waves in one-dimensionalsymmetric two-segmentconnected triangular optical waveguide networks with perfect and broken integer waveguide length ratios.It is found that the number and the corresponding frequencies of the extremum spontaneoussymmetric breaking points are dependent on the degree of brokenness δ. Near the extremum breaking points,ultrastrong extraordinary transmissions are created and the maxima can arrive at 2.4079×1014and 4.3555×1013in the two kinds of networks,respectively,which are several orders of magnitude larger than those in thesymmetric Thue–Mose waveguide networks[53]andsymmetric periodic waveguide-ring networks.[54]However,bidirectional invisibility can only be produced by the networks with broken integer waveguide length ratios,whose mechanism is explained in detail from the perspective of photonic band structure. The findings of this work can be useful optical characteristic control in the fabrication ofsymmetric optical waveguide networks,which possesses great potential in designing optical amplifiers,optical energy saver devices,and special optical filters.

This paper is organized as follows.In Section 2,our designed model,the main theory,and the methods for analytical deduction and numerical calculation are demonstrated and introduced.In Section 3,we show the distribution of photonic modes. The numerical and analytical discussions of the extremum breaking points,the transmission and reflection characteristics of the networks with perfect and broken integer waveguide length ratios are demonstrated.Section 4 gives the conclusion of this work.

2.Model and methods

2.1.The optical structure

In this article,the schematic diagram of our designed structure is plotted in Fig.1. In this model,every two adjacent nodes of the same unit cell are connected by the two waveguide segments with the lengths of d1and d2,respectively,with the shortest segment d1defined as a unit length“1”,and the lengths of the other segments are expressed as a normalized value relative to d1.Hence the waveguide length ratio is expressed as d1:d2=1:t,where it is called perfect integer ratio when 1:t=1:z and z itself is a small integer;broken integer ratio when a small positive number δ is subtracted and 1:t=1:z ?δ. For example,the waveguide length ratios of d1:d2=1:1,1:2 are perfect integer ratios and d1:d2=1:0.999,1:1.99 are broken integer ratios with corresponding degrees of brokenness δ=10?3and 10?2,respectively. In this study,without loss of generality,the simplest form,the smallest odd and even numbers,z=1,2 are used to investigate the transmission and reflection behaviors in our designed model. In order to measure conveniently,d1is set to be related to the communication wavelength λC=1550 nm.In Subsection 3.2,from Fig.2 one can see that νGBP≈0.693=c/d1,where νGBPis the frequency of the spontaneoussymmetric generalized breaking point(GBP)of the networks with d1:d2=1:1,therefore we set νGBP=c/λC,and consequently,d1=0.693λC≈1074 nm.Each waveguide is composed of three subsegments whose lengths m are all the same for simplicity,as shown in Fig.1(b),and the refractive index of each waveguide segment is defined as follows:where nR=nSiO2=1.4430,[55,56]the optimal nIvalue is determined by the extremum spontaneoussymmetric breaking point in Subsection 3.2,and silicon dioxide(SiO2)is chosen to be the material of the three subsegments.aij,bij?aij,and lijare,respectively,the lengths of the first sub-segment,the second sub-segment,and the whole waveguide segment between nodes i and j.

Fig.1. Schematic diagram of the optical structure. (a)The optical waveguide network with three unit cells,one entrance,and one exit,where EI,ER,and EO are,respectively,the input,reflected,and output EM waves.Each black thick dashed line represents two segments of symmetric waveguides with the lengths of d1 and d2,respectively,and the black thick solid curves at the entrance and exit representsymmetric waveguides with the length of d1.(b)symmetric waveguide composed of three subsegments,where the lengths of the three subsegments are the same.

2.2.Network equation

In this research,each waveguide in the networks is composed of three materials,therefore,a three-material network equation is needed to study their photonic modes,transmissions,and reflections.As is known to all,the EM wave function in 1D waveguide segment between nodes i and j can be regarded as a linear combination of two opposite traveling plane waves

with the wave vector ku=ωnu/c(u=1,2,3).By means of the continuities of the wave function,its differential quotient and energy flux conservation,one can deduce the following three-material network equation:[53]

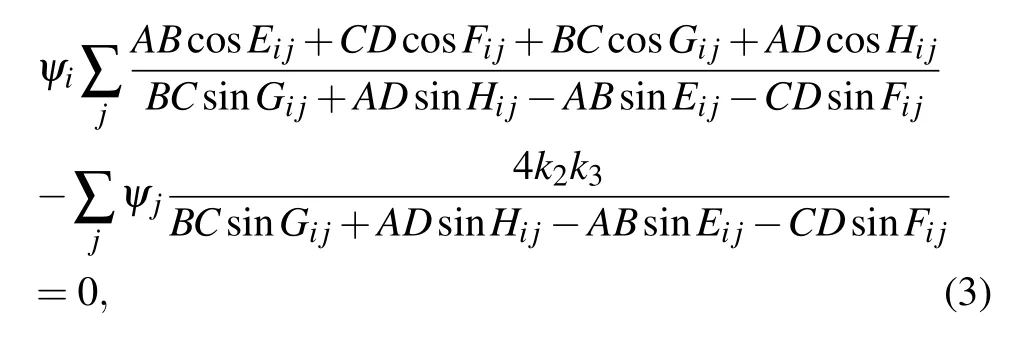
where ψiand ψjare the wave functions at nodes i and j,respectively,

In the next section,by use of three-material network equations(3)and(4),the distribution of photonic modes,transmissions,and reflections of the networks are calculated and plotted.

3.Results and discussion

3.1.Photonic mode distribution

The generalized Floquet–Bloch theorem,[39]can be used to assess the photonic mode distribution. In a periodic optical waveguide network,the difference between the wave functions of the N-th and the(N+T)-th unit cell is a phase factor ofWhenis real,is also real.Therefore,the amplitude of the wave function is kept constant,while the phase changes by a factor of.This mode is called ordinary propagation mode(OPM).[49]Whenis a complex number,is also complex.Subsequently,not only the phase changes by a factor of,but also the amplitude changes by a factor ofWhenthe amplitude of the wave function attenuates;when,the amplitude gains.These two photonic modes are called,respectively,attenuation propagation mode(APM)and gain propagation mode(GPM),which are the non-propagation modes.

For infinite-unit-cell networks, based on the threematerial network equations(3)and(4),and the generalized Floquet–Bloch theorem,the following dispersion relation can be deduced:

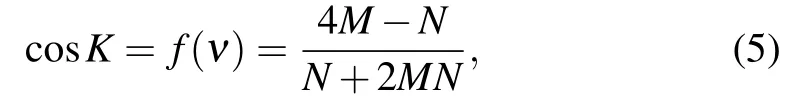
where

From Eq.(5),it can be found that,for 1D vacuum or dielectric triangular optical waveguide networks,[47,48]where the refractive indices of the materials are all real,the dispersion function f(ν)must be real. Therefore,for f(ν)being real and|f(ν)|<1,from Eqs.(5)and(6)it can be deduced that the Bloch wavevector K of the structure possesses real solutions,EM waves with the corresponding frequencies propagate as OPM and form passbands.For|f(ν)|>1,it can be deduced that K possesses a pair of complex conjugate solutions.Mathematically,EM waves within this frequency range operate simultaneously as APM and GPM.However,in vacuum or dielectric optical waveguide networks,there exists only attenuation but no gain mechanism.Consequently,from a physical perspective,the corresponding EM waves will propagate only as APM and create stopbands.This shows that|f(ν)|=1 is a critical point for the transition of the photonic modes in vacuum or dielectric optical waveguide networks.

Recent research found that|f(ν)|=1 can be chosen to be the critical value for different photonic modes insymmetric networks. The reason is that from Eqs.(5)and(6),when|f(ν)|is small,Im()might also be small,and extraordinary transmission with T>1.0 can not be created.Only when f(ν)is sufficiently large,can Im()be very large and the extraordinary transmission with T>1.0 be produced.Moreover,we define both APM and GPM produced by thesymmetric waveguide network corresponding to|f(ν)|≤1 as weak propagation modes(WPMs),and those corresponding to|f(ν)|>1 as strong propagation modes(SPMs). By this condition,spontaneoussymmetric breaking points of the networks are defined as the imaginary part of the refractive index,nI,located between WPM and SPM.

3.2.Extremum spontaneous symmetric breaking point

Generally,extraordinary optical characteristics of the system can be found near the spontaneous breaking points,the boundary between WPM and SPM.We define the extremum spontaneous breaking points as follows: (i)when|f(ν)|=1;(ii)the dispersion function f(ν)is continuous and nondifferentiable.From numerical results,the systems will produce increasing extraordinary transmissions and reflections at the extremum breaking points,so the optical propagation characteristics near the extremum breaking points are mainly studied here.

Fig.2.Distribution of photonic modes in the network with d1:d2=1:1,where SPM represents strong propagation mode,and WPM denotes weak propagation mode.(a)Overall figure;(b)enlarged figure of(a),where GBP indicates generalized breaking point.

By use of dispersion relation Eqs.(5)and(6),we can determine the photonic modes in the networks with perfect and broken integer waveguide length ratios.Since there are infinite configurations of networks with integer waveguide length ratios,for simplicity and without loss of generality,as a representative of the minimal odd number and the minimal even one,we study the networks with,respectively,d1:d2=1:1 and 1:2,whose photonic mode distributions are plotted in Figs.2 and 3,where the yellow and red areas represent WPM and SPM,respectively. It can be seen from Fig.2 that at the frequency of ν=0.693000694c/d1,there exists one extremum spontaneous breaking point,where nI=1.32×10?8.From Fig.3, at the frequencies of ν=0.57750053c/d1,0.693000694c/d1,and 0.80850075c/d1,there exist three extremum spontaneous breaking points,where nI=1.02×10?6,1.25×10?8,1.34×10?6,respectively.

Fig.3.Distribution of photonic modes in the network with d1:d2=1:2:(a)overall figure;(b)–(d)enlarged figures of(a).

Through the previous study,[39]it is found that,for vacuum or dielectric OWNs,the width of the narrow band is proportional to the degree of brokenness δ in the broken integer waveguide length ratio.When δ decreases,the width of the narrow band will shrink and the characteristics of the networks will change dramatically.Therefore,in this work,we concentrate on the networks with δ<10?2as an example.However,there are infinite configurations of networks with broken integer waveguide length ratios.As an extension of the above two examples of perfect integer ratios,we study the networks with,respectively,d1:d2=1:0.99 and 1:1.99(indicating δ=10?2),whose photonic mode distributions are plotted in Fig.4.

When d1:d2=1:1 changes to 1:0.99,the result is plotted in Fig.4(a).From Fig.4(a),one can see that the extremum breaking point near ν=0.6930c/d1disappears. When d1:d2=1:2 changes to 1:1.99,the result is plotted in Fig.4(b).From Fig.4(b),one can see that the extremum breaking point near ν=0.6930c/d1also disappears. The extremum breaking points originally located at ν=0.57750053c/d1and 0.80850075c/d1are right-shifted,where ν becomes,respectively,0.57942376c/d1and 0.81120487c/d1. Besides,the values of nIof the extremum breaking points also change from 1.02×10?6and 1.34×10?6to 7.20×10?7and 1.82×10?6,respectively.

Fig.4.Distribution of photonic modes in the networks with(a)d1:d2=1:0.99,δ=10?2;and(b)d1:d2=1:1.99,δ=10?2;(c)and(d)enlarged figures of(b).

Comparing Figs.2–4,it is known that within the same frequency range,when the waveguide length ratios change from perfect to broken integer ratio,not only the number of the extremum breaking points reduces,but also the frequencies and the corresponding nIof the extremum breaking points change.In Subsection 3.3,we will determine the optimal nIaccording to the positions of the extremum breaking points,and then calculate the transmission and reflection near the corresponding frequency.

3.3.Extraordinary transmission and reflection in network with perfect integer waveguide length ratio

When d1:d2=1:1,the results are shown in Fig.5(a).From Fig.5(a),one can see that(i)at the frequency of ν=0.693000691c/d1,for the left-incident EM waves,the maximal transmission arrives at 2.4079×1014;(ii)at the frequency of ν=0.693000695c/d1,for the right-incident EM waves,the maximal transmission arrives at 1.2074×1013;(iii)at the frequency of ν=0.693000693c/d1,for both left-and right-incident EM waves,the minimal transmission arrives at 9.0025×10?10.

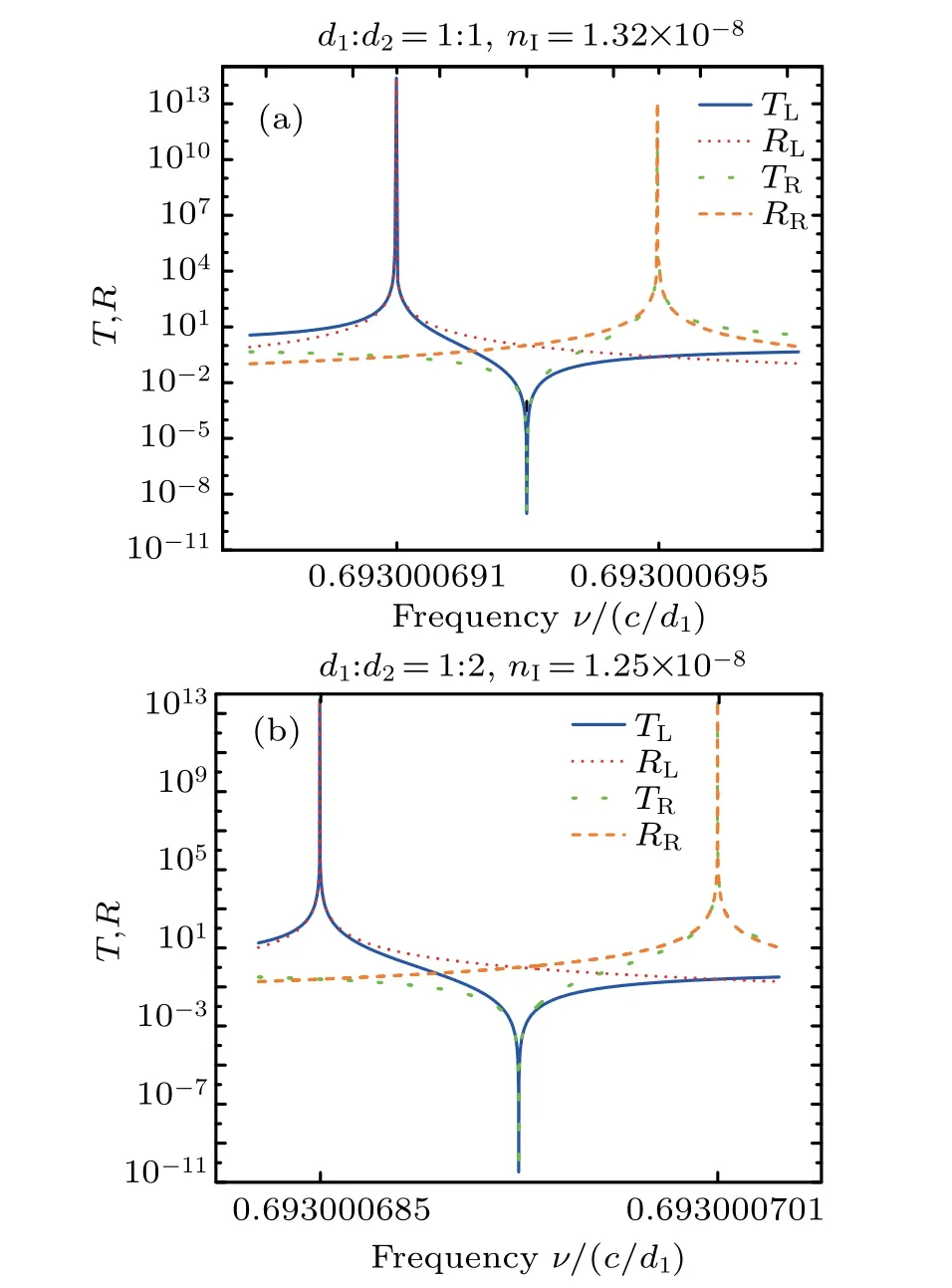
Fig.5.Transmission and reflection spectra of the networks with perfect integer waveguide length ratios at extraordinary point,where the blue solid line,thin red dotted line,thick green dotted line,and brown dashed line represent the left-incident transmission and reflection and the rightincident transmission and reflection,respectively:(a)d1:d2=1:1 and nI=1.32×10?8;(b)d1:d2=1:2 and nI=1.25×10?8.

When d1:d2=1:2,the results are shown in Fig.5(b).From Fig.5(b),one can see that(i)at the frequency of ν=0.693000685c/d1,for the left-incident EM waves,the maximal transmission arrives at 5.2412×1013;(ii)at the frequency of ν=0.693000701c/d1,for the right-incident EM waves,the maximal transmission arrives at 4.2044×1013;(iii)at the frequency of ν=0.693000693c/d1,for both left-and right-incident EM waves,the minimal transmission arrives at 9.0036×10?10.It means that the networks possess ultrastrong extraordinary transmissions and ultrastrong PBG attenuation characteristics. Obviously,these networks may possess potential in designing optical filters,optical amplifiers,optical energy saver devices,and so on.

Similar to transmission,for both left-and right-incident EM waves,the transmission and reflection peaks totally overlap,no matter whether d1:d2=1:1 or 1:2.The difference between transmission and reflection is that the networks produce transmission valleys,but no reflection valley.These characteristics are completely different from those in the networks with broken integer waveguide length ratios shown in Subsection 3.4.Besides,for both transmission and reflection spectra,the left-incident curves do not coincide with the right-incident ones,these networks show typical nonreciprocity of EM wave propagation.

Regarding the reason why this structure can generate the extraordinary transmission and reflection,we believe it is a result of the extraordinary photonic modes mentioned in Section 3 and the gain-and-loss coupling resonant effect.(i)From the analysis on the photonic modes in Subsection 3.2,it is known that in our designed models,there exists no OPM,but two simultaneous non-propagation modes APM and GPM.These two modes are different from not only the OPM but also the non-propagation modes in normal dielectric waveguide networks.Therefore,in our models,neither passband nor stopband can be created,leading to completely different transmission and reflection spectra from those of dielectric ones.(ii)Insymmetric networks,the pure gain and loss effects on photons of both gain and loss materials are all trivial and in subordinate roles,which means that they will neither cancel nor weaken one another,but strengthen and couple with each other. The gain and loss materials in such structure can be regarded as that they form a coupling resonant cavity and exhibit strong coupling resonant effect on APM and GPM photons,which,results in sharp transmission and reflection peak and valley,whose frequencies are determined inherently by the network structure as discussed in Section 3.

3.4.Extraordinary transmission and reflection in network with broken integer waveguide length ratio

In the above subsection,it is found that the networks with perfect integer waveguide length ratios can produce ultrastrong extraordinary transmission and reflection. Do the networks with broken integer waveguide length ratios possess the same characteristics?In this section,we discuss and analyze the propagation behavior of the networks with broken integer waveguide length ratios. In order to obtain increasing extraordinary transmission and reflection,we further reduce the degree of brokenness δ to produce an ultra-narrow photonic band.Without loss of generality,in this section we choose a very small δ=10?8to indicate a situation that the ratios are near-perfect,and design one-unit-cell networks with waveguide length ratios of d1:d2=1:1 ?δ and 1:2 ?δ,(δ=10?8),with nI=1.35×10?8and 1.26×10?8,respectively.

When d1:d2=1:1 ?δ,δ=10?8,the result is shown in Fig.6.From Fig.6,one can see that(i)at the frequencies of ν=0.693000689c/d1and 0.693000703c/d1,for the leftincident EM waves,the transmissions arrive at,respectively,2.3127×1013and 4.3555×1013;(ii)for the right-incident EM waves,there is no transmission peak.

Fig.6. Transmission and reflection spectra of the network with d1:d2=1:1?δ,δ=10?8 at extraordinary point,with nI=1.35×10?8,where the blue solid line,green dot line,yellow dot line,and red solid line indicate the left-incident transmission and reflection and the rightincident transmission and reflection,respectively.

When d1:d2=1:2 ?δ,δ=10?8,the result is shown in Fig.7.From Fig.7,one can see that(i)at the frequencies of ν=0.6930006892079c/d1and 0.6930006935281c/d1,for the left-incident EM waves,the transmissions arrive at,respectively,3.77056×1013and 3.29120×1012;(ii)at the frequencies of ν=0.6930006935961c/d1and 0.693000696363c/d1,for the right-incident EM waves,the transmissions arrive at,respectively,3.88015×1012and 6.86564×1013.Obviously,the networks with broken integer waveguide length ratios also produce ultrastrong transmission and reflection,which also possess the potential in designing high efficiency optical filters,optical amplifiers,optical energy saver devices,and so on.

For both left-and right-incident EM waves,the transmission and reflection peaks totally overlap,no matter whether d1:d2=1:1 ?δ or 1:2 ?δ. The networks with broken integer waveguide length ratios not only generate transmission and reflection peaks,but also produce reflection valleys which are absent in networks with perfect integer length ratios. From Fig.6,one can see that there exists a reflection valley at the frequency of ν=0.693000721c/d1,for leftand right-incident EM waves,where the reflections arrive at 3.5966×10?13and 4.0859×10?13and the transmissions arrive at 0.99995 and 1.00005,respectively.From Fig.7,one can see that there exists a reflection valley at the frequency of ν=0.6930006935551c/d1,for left-and right-incident EM waves,where the reflections arrive at 3.31537×10?11and 1.59481×10?13and the transmissions arrive at 0.99995 and 1.00005,respectively.It means that this kind of networks have bidirectional invisibility characteristics,which may be useful in designing structures that are invisible to certain frequencies of EM waves.

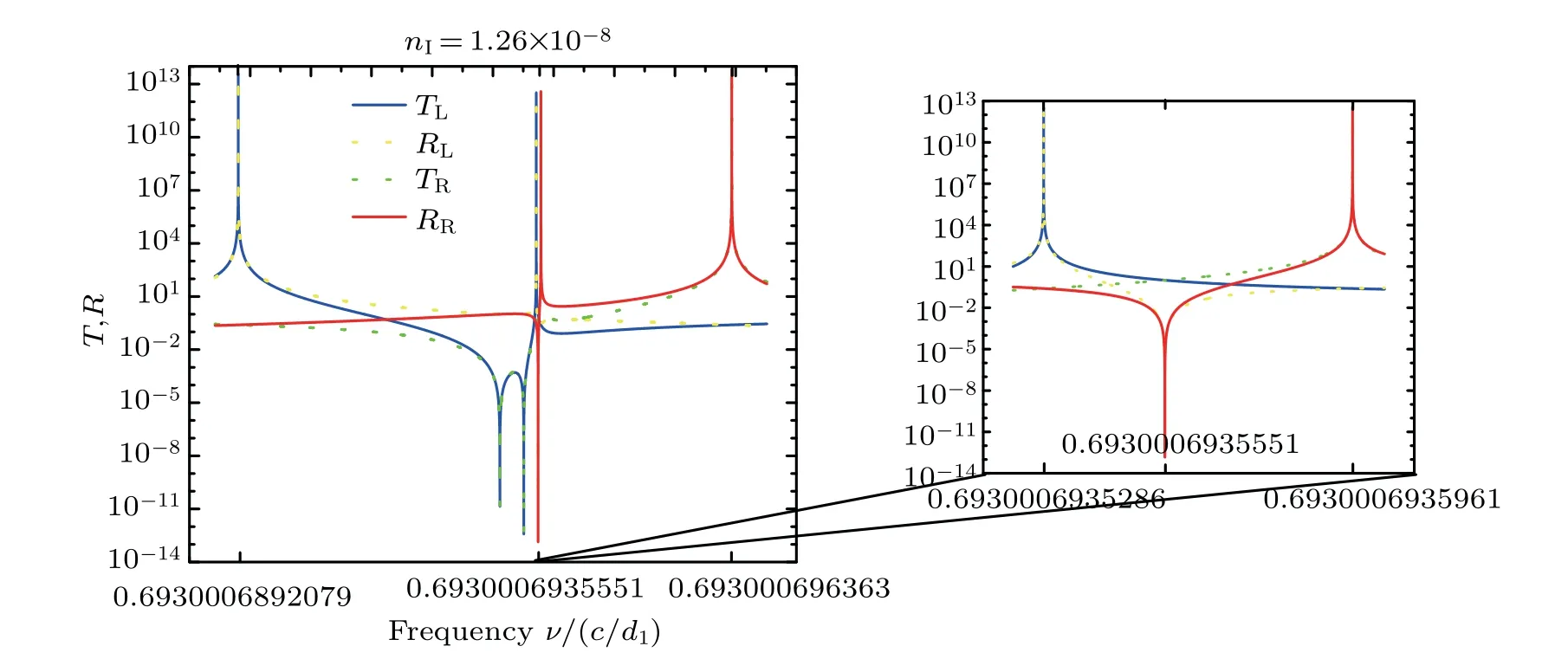
Fig.7.Transmission and reflection spectra of the network with d1:d2=1:2?δ,δ=10?8 at extraordinary point,with nI=1.26×10?8,where the blue solid line,green dot line,yellow dot line,and red solid line donate the left-incident transmission and reflection and the right-incident transmission and reflection,respectively.

Comparing Figs.5–7,it is found that the networks with perfect integer length ratios can produce reflection valleys while those with perfect integer length ratios cannot.By use of dispersion relation Eqs.(5)and(6),we plot the band structure diagram of one dimensional two-segment connected triangular optical waveguide networks with uniform SiO2waveguide segments in Fig.8,where d1:d2=1:1,1:0.99(δ=10?2),1:2,and 1:1.99(δ=10?2),respectively,to aid the explanation in the case of δ=10?8.Based on the band structure diagram,the reflection valleys of the broken integer length ratio networks can be explained.

From Figs.8(a)and 8(c),one can see that there exists a wide passband near the point of ν=0.693c/d1when d1:d2=1:1 and 1:2. When the networks are composed of uniform SiO2,at the wide passbands,the transmission generally satisfies 0.01 ≤T ≤1 and changes slightly;the reflection commonly satisfies 0.01 ≤R+T ≤1 and also changes slightly. Consequently,the network can not produce a deep reflection valley. Therefore,when the uniform SiO2is replaced by thesymmetric materials,the networks possess no enormously deep reflection valley as well.From Figs.8(b)and 8(d),one can see that there exist a narrow stopband near the point of ν=0.693c/d1when δ=10?2.The previous research[39,48]found that the width of the stopband is proportional to the degree of brokenness δ. Therefore,when δ=10?8,we speculate that there exists an ultranarrow stopband near the frequency of ν=0.693c/d1. The boundary between ultra-narrow stopband and wide passband can be regarded as ultra-narrow passband for the reason that their transmission spectra are similar. When the networks are composed of uniform SiO2,the propagation behaviors of extremely narrow passband and wide passband are different.Although the transmissions in wide and ultra-narrow passbands are both in the range of 0.01–1,with the variation from the ultra-narrow stopband to the ultra-narrow passband,the transmission changes enormously,therefore,the reflection also changes greatly. When the networks are composed ofsymmetric materials,the resonance coupling effect of the gain and loss materials cause these changes in reflection to be magnified.This magnifying effect leads the reflection within the ultra-narrow passband to be exceedingly small,which results in an enormously deep reflection valley.It can be seen that the band structure is not only suitable for the optical waveguide network of vacuum/ordinary dielectric material,but also suitable for thesymmetric optical waveguide network.Due to the same mechanism,similar transmission and reflection behaviors can be found in networks with a negative degree of brokenness δ,with the same number of transmission peaks and valleys and the same amount of spectral shift in opposite directions.

Fig.8.The frequency band structure of one-dimensional two-segment connected triangular optical waveguide networks with perfect and broken integer waveguide length ratios:(a)d1:d2=1:1;(b)d1:d2=1:0.99(δ=10?2);(c)d1:d2=1:2;(d)d1:d2=1:1.99(δ=10?2);(e)–(h)enlarged figures of(a)–(d).

4.Conclusion

In this paper, we design the one-dimensionalsymmetric two-segment-connected triangular optical waveguide network and investigate its extraordinary optical characteristics.We obtain the network equation of the general threematerial OWN and then thoroughly investigate the photonic modes in our designed networks with perfect and broken integer waveguide length ratios based on this network equation and the generalized Floquet–Bloch theorem.According to the photonic modes redivided as WPM and SPM,we find the extremumsymmetric breaking points in periodic networks and study the transmissions and reflections near the extremumsymmetric breaking points.

It is found that: (i)no matter whether the waveguide length ratios are perfect or broken integer ratios,the networks possess extremumsymmetric breaking points.When the waveguide length ratios change from perfect or broken integer ratio,somesymmetric extremum breaking points disappear,the frequencies and nIof thesymmetric extremum breaking points change as well.(ii)The maximal transmission in the waveguide network with integer waveguide length ratio reaches 2.4079×1014and the maximal reflection reaches 1.2074×1013.These networks can produce extraordinary ultrastrong transmissions and reflections and they may possess potential application in the designing of all-optical devices,such as efficient photonic energy storages,optical amplifiers,optical filters,and so on.(iii)The networks with broken integer waveguide length ratios can not only produce extraordinary ultrastrong transmissions and reflections,but also generate reflection valleys,where the maximal transmission and reflection reach,respectively,3.77056×1013and 6.86564×1013,and the minimal reflection reaches 4.0859×10?13. It may be useful in designing structures that are invisible to certain frequencies of EM waves.

Finally,we explain the phenomena that reflection valleys appear in networks with broken integer waveguide length ratios based on the band structure diagram of one dimensional two-segment connected triangular optical waveguide networks with uniform SiO2. It may deepen the community’s understanding onsymmetric optical waveguide networks.