Benchmarking the simplest slave-particle theory with Hubbard dimer?

Wei-Wei Yang(楊薇薇), Hong-Gang Luo(羅洪剛),2, and Yin Zhong(鐘寅),?

1Center for Interdisciplinary Studies and Key Laboratory for Magnetism and Magnetic Materials of MOE,Lanzhou University,Lanzhou 730000,China

2Beijing Computational Science Research Center,Beijing 100084,China

Keywords:slave particle theory,Hubbard dimer,strongly correlated physics

1.Introduction

Correlation is a crucial ingredient responsible for many exotic phenomena, such as the Mott insulator–metal transition,[1,2]heavy fermions,[3]unconventional superconductivity,[4,5]and ultra-cold atoms in optical lattice.[6]However,these phenomena are difficult to study by traditional methods that base on independent particles approximation.Now we know that this challenge results from the entanglement of multiple degrees of freedom such as spin,charge,and orbit that can not be captured by the independentparticle representation.

Fortunately,the invention of slave-particle concept enlightens physicists to a novel method to systematically comprehend strong correlation physics. The main idea in the method is to enlarge the Hilbert space with auxiliary degrees of freedom so that the charge and spin degrees of freedom could be disentangled and thus many above-mentioned phenomena could be studied at a mean-field level. In the past several decades,slave-particle method was developed into several different forms,such as slave boson,[7–9]slave rotor,[10–12]and slave spin.[13,14]These different slaveparticle representations have their own advantages and are pioneered in tackling various strongly correlated electron problems,[7–10,13–22]e.g.,Anderson and Kondo models,[7,9,23]Mott localization,[10,13–15]quantum spin Hall effect,[24,25]and high temperature superconductivity.[26]

In spite of these successful applications,the accuracy of these methods is uncontrollable due to the mean-field approximation or Gaussian fluctuation,and their reliability has not been studied quantitatively yet. As far as we know,there is neither a systematic scheme nor detailed analysis to investigate the accuracy and limitation of the slave-particle method.We believe that these are important for any unconventional method. Therefore,we will try to fill in this gap by studying a two-site Hubbard model with a specific slave-particle approach. In this paper,we consider the simplest Z2slavespin method,because it is easy to study due to the finite Hilbert space of slave spin.Its extension to other slave-particle method is straightforward. This method has predicted some new physics,such as orthogonal metals[27,28]and fractionalized Chern insulator,[29]and the former one has been confirmed in a recent quantum Monte carlo simulation.[30]We aim at making an explicit evaluation of the Z2slave-spin method by comparatively analyzing aspects of properties in this two-site Hubbard model,which is exactly solvable so that the benchmark is ready-made and we can evaluate slave spin fairly.

Here,we have two important conclusions.(i)Some specific symmetries,e.g.,particle–hole symmetry,can play important roles in reproducing the exact behavior in the slavespin mean-field approach.(ii)The accuracy of slave particle is ensured if only we can exclude all unphysical states by enforcing gauge constraints.

We demonstrate the reliability of the slave-spin method both on mean-field level and with gauge constraints at zero and finite temperature.It turns out that the slave-spin meanfield method performs perfectly well in the static properties of the ground state,whereas its accuracy does not sustain at finite temperature.Since unphysical states are mixed in the eigenstates in this enlarged slave-spin representation,the mean-field approximation cannot access dynamical or thermal dynamic behavior accurately.Fortunately,this ill-defined behavior can be fixed with enforcing gauge constraints exactly,i.e.,excluding the unphysical states completely. Besides,the result of ground state also shows that the slave-spin mean-field method is effective in both a small U regime and a large U regime,but it fails in the regime where U is comparable to hopping integral t.For the latter case,the result either diverges or deviates far from the exact solution. By taking thisslavespin method as an example,we hope to uncover the nature of slave-particle theory and give some suggestions on the application and regime where the slave-particle method can work effectively and accurately.

The outline of this paper is as follows:at first we present the general formulation ofslave-spin method in Hubbard model in Section 2. In Section 3,we introduce three theoretical approaches involved in the next context.We describe the exact diagonalization method in Subsection 3.1,theslave-spin mean-field method in Subsection 3.2,and the slavespin method with exact gauge constraints in Subsection 3.3.In Section 4,we demonstrate and analyze our results with the above-mentioned three methods for different context:in Subsection 4.1 and Subsection 4.2,the zero temperature situation,whereas in Subsection 4.3 and Subsection 4.4 the finite temperature situation.Within this section,the static,dynamical,and thermal dynamic properties are discussed in various regimes of U.Finally,we conclude in Section 5.

2.Introduction to slave-spin method

As a starting point,we introduce the main idea ofslave spin in the single-orbital Hubbard model.[31–36]The Hamiltonian can be written as follow:

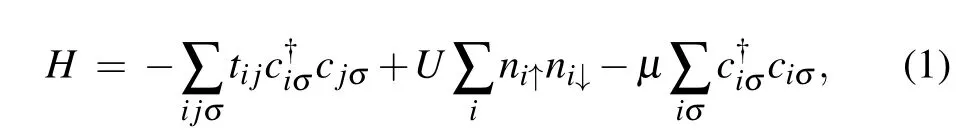
where ciσis the electron annihilation operator on site i with spin σ;niσis the occupancy number of electrons which satisfiesis the hoping integral between sites i and j;andμis the chemical potential.In the strongly correlated regime,the approximate methods based on independent particles are invalid. Therefore,we introduce the slave-spin method to solve this dilemma. In the slave-spin representation,the physical electron operator is written as[14,18]

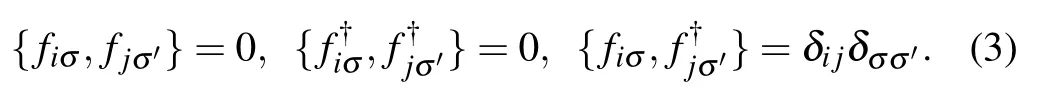
As shown in Fig.1,with the discretegauge symmetry,the Hilbert space is twice as large as the original one,i.e.,in therepresentation,only half of the states are physical

while the other four states are unphysical

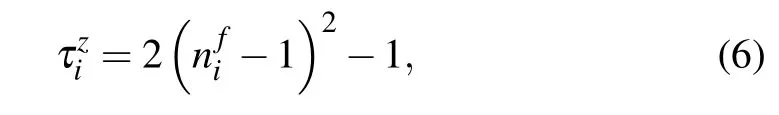
which can also be written as

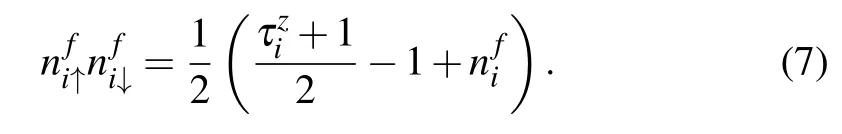
Here this non-linear constraint turns out to be a crucial ingredient to tackle with the cumbersome interaction term

In this slave-spin formulation,we can write the partition function as

where PIis the projection operator onto the physical Hilbert space

with

while only the states satisfying Qi=0 are corresponding to physical states.

Fig.1.The schematic illustration of slave-spin representation.The physical state of one site(left column)can be represented by pseudospin and pseudofermion. In the enlarged Hilbert space,half of states are physical(middle column)and the other half are unphysical(right column).It is twice as large as the original one.

Now the complex strong correlation effect of this system is merely reflected in the dependence between the hopping integral t of f fermions and the coupling strength of pseudospins.Here,this transformed formalism is exact,but it looks cumbersome due to the complicated hoping term.Generally,there are three methods to proceed.

(i)Upon most occasions,we can perform some meanfield approximations,with which the original Hamiltonian could be divided into three independent parts and then solved by an iteration method.

(ii)For some small systems,we can make exact diagonalization and directly access all properties.

(iii)For a considerable large system,quantum Monte Carlo simulation is widely used to obtain credible results.

For some extremely simple cases,such as the two-site model,it is also possible to apply slave spin with exact gauge constraints.In the next section,we set the second scheme to be the benchmark to justify the validity of slave spin at meanfield level and slave spin with gauge constraints.

3.Three approaches to two-site Hubbard model

To further simplify the two-site model,we regard the system as a canonical ensemble,i.e.,the chemistry potential should satisfy the constraintμ=0. Now we start with the Hamiltonian

3.1.The analytical solution

The analytical solution is directly derived from exact diagonalization without special skill.In this subsection,we will neglect the simple non-half-filled situation but focus on the half-filled case,in which the slave-spin mean-field approach surprisingly reproduces the behavior of exact solution. We hope to uncover the nature of this coincidence by discussing all methods at different cases in detail.Now the starting point of our discussion of the canonical ensemble is the half-filling property,which means there should be two electrons in total.Thus we can directly list the entire basis vectors in the occupation number representation

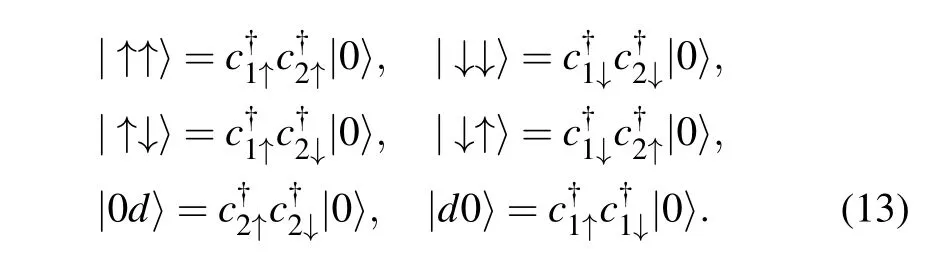
where E=0,we can neglect them in the subsequent analysis.Thus,the other four states constitute a 4-dimensional Hilbert space and the basis vector is

which is straightway to derive the Hamiltonian matrix in this occupation number representation

By diagonalizing this Hamiltonian,we obtain four eigenenergies

As shown in Eq.(17),the minimal energy solution,i.e.,the ground-state energy,is.Thus we get the analytical solution for this 2-site Hubbard model.In principle,with the help of Hellmann–Feynman theorem,now we can deduce most physical quantities in the ground state.For example,the double occupancyand bond orderof physical electrons can be derived directly from the analytical expression

3.2.The slave-spin mean field

In this subsection,we will explore the 2-site Hubbard model with theslave-spin mean-field method. With Eqs.(2)and(7),the 2-site Hubbard Hamiltonian can be transformed into the slave-spin representation

To tackle with the four operatorin this new Hamiltonian,we take the mean-field approximation

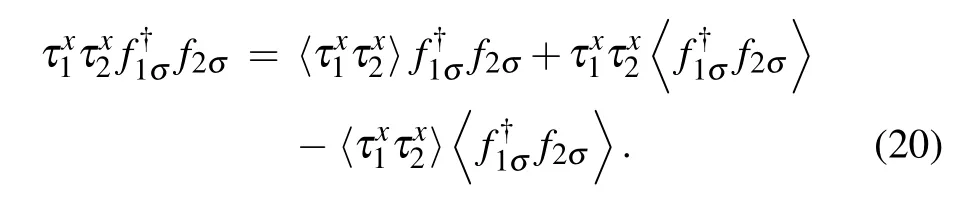
Thus the auxiliary Ising spin operator and the auxiliary fermion operator are decoupled with each other. Generally,it is hard to deal with the constraint precisely on every site,so we can also take the constraint condition into account at meanfield level,i.e.,adding some Lagrangian multipliers in original Hamiltonian

Due to the translation invariance of the Hamiltonian,in this 2-site situation we simply assume λi(i=1,2)=λ.Now the Hamiltonian takes the formwhere

Here the mean-field parametersand χ12=Note that at half filling,λ should be zero to respect the particle–hole symmetry,where the energy spectrum is symmetric only if λ=0.Under this assumption,the Hamiltonian can be written as

In the physical ground state,the pseudo-fermions term Hfshould be self-consistent with the pseudo-spins HIsing.In order to achieve this self-consistency,at first we have to set an initial value for I12.With this I12we can derive the Hamiltonian of the f fermions at a specific U.Afterwards,we calculate the eigenstatesand thenwith which we can deduce the Hamiltonian matrix and thus the eigenstates of pseudo spinsNext we get a new.Now we update the initial I12with the new one calculated from the pseudo-spins system.By repeating these steps mentioned above,we can finally get a selfconsistent result in the required accuracy range. Generally,for this simple two-site half-filling model it takes less than 30 steps to reach the convergence.

Note that,the ground-state energy could be directly written as

From the constraint Eq.(7),we can derive the double occupancy in the slave-spin mean-field level

and also the bond order of physical particles

3.3.The slave-spin method with exact gauge constraints

As mentioned above,this slave-spin representation is with respect to thegauge symmetry.[37,38]Thanks to the simplicity of both the gauge symmetry and the two-site model,in this subsection we could derive an exact solution in the enlarged Hilbert space without mean-field approximation.

Next we make exact diagonalization of the Hamiltonian(Eq.(19))in this four times enlarged representation and derive the 64 eigenstates

Here we label its eigenstates asbecause only onefourth of them are physical states. To select these physical states,we have to construct gauge transformation with appropriate formulation whose eigenstates could be utilized to distinguish physical states. Considering the constraint Eq.(6),we define a local gauge transformation at site i as the operator

Firstly,we will demonstrate the reasonability of this gauge transformation. For example, in the first term of Eq.(19),

The first equation is derived from the anti-commutation relations of pseudo-spins;the second demonstrates that the hopping terms in fact change pairity of occupied number on every site. In a similar way,the other three terms are also gaugeinvariants under this transformation,i.e.,

Thus we prove the commutative relation between the Hamiltonian and operator G(i).

Next we discuss how to accurately exclude unphysical states.Notably,

where only+1 is corresponding to the physical states.Since the operator G(i)commutes with the Hamiltonian,they must have the same set of eigenstatesHere we find such a set and select only 16 physical states which satisfyandto recover the behavior of this two-site model.

Although the Hamiltonian is gauge-invariant,the ground state has been changed when we enlarge the initial Hilbert space.The physical ground state is still one of the 64 eigenstates,but it no longer possesses the lowest energy. It will be shown in the next section that the lowest energy is invariable with different U if we simply describe the system with wave-function mixed with physical and unphysical states.Obviously,the unphysical states badly impact all aspects of behavior. If the constraint conditions are originally satisfied,the mean-field approximation could eliminate the effect of unphysical states and access some static properties effectively,such as the ground state. While it comes to the dynamical properties or finite temperature,the deviation is stubborn at mean-field level. To demonstrate the great influence caused by the unphysical states,in the next section we will also show the results of entire 64 states without gauge constraints.

4.Result and analysis

4.1.The ground-state properties and analysis

In this subsection,we demonstrate and discuss the performance of slave-spin approach by calculating the typical static properties of ground state,such as energy,double occupancy,and bond order of physical fermions.It turns out in some contexts slave spin can describe the 2-site model extremely accurate whereas in some other situations great deviation emerges.In the following,we will focus on revealing the kernel hinge which decides the efficiency of the slave-spin method by contrasting different methods in different situations,half-filled and non-half-filled.

We first address the performance of slave spin on meanfield level in the half-filling situation. Figure 2 compares different slave-spin methods and analytical solution.We provide the dependence of the static properties of ground state on U,in which the slave-spin mean-field model predicts exactly the same results with the analytical solution.The accuracy is not caused by accident but the particle–hole symmetry.As mentioned in the last section,Lagrange multipliers should be zero,i.e.,λ=0,respecting to this special symmetry. It means that the form of Hamiltonian is fixed even if we have to consider the gauge constraint.As the constraint conditions will not impact the Hamiltonian directly,we can simply start from the Hamiltonian in the enlarged Hilbert space without any gauge constraints but access the accurate behavior of the ground state.

This is not the first show of particle–hole symmetry in slave-spin method.In both Anderson impurity model[14,39,40]and infinite-dimensional half-filled Hubbard model,[41]which can map with each other with dynamical mean-field theory,[42]the partition function can be calculated with corresponding slave-spin Hamiltonian without any constraint.Since the specific form of the partition function is independent of the constraint conditions,so is the free energy.It turns out that the slave-spin method is elegant and effective in these models which possess particle–hole symmetry.

Fig.2.The comparison of ground-state energy Eg(left),double occupancy d(middle),and bond order of physical fermions χ(right)of the 2-site Hubbard model.(a)–(c)Slave-spin mean-field(MF)method(green circle)and analytical solution(red square)in half-filling situation.Besides,the bond order of pseudo-fermions(cyan circle)is also demonstrated in panels(g)–(i).(d)–(f)Slave-spin MF method(green circle)and analytical solution(red square)without particle–hole symmetry.(g)–(i)Slave-spin method with gauge constraints(GC)(blue triangle)and analytical solution(red square)without particle–hole symmetry.(j)–(l)Slave-spin method without GC(yellow diamond)and analytical solution(red square)without particle–hole symmetry.

Since this fortune results from the special half-filling situation,in more general context the slave spin cannot access such perfect results with mean-field approximation.We demonstrate the properties of the two-site model with arbitrary electron number in Figs.2(d)–2(f).Since in this situation,the constraint conditions could not be enforced exactly,deviation shows up at a small U regime. Nevertheless,the slave-spin mean-field model has a more ill-defined behavior at moderate 1

Here we also provide the result from the enlarged slavespin representation with physical and unphysical states mixed together(see Figs.2(j)–2(l)). Unfortunately,without constraints,the behavior of slave spin is badly influenced by unphysical states and the result seems to be nonsense at most regime.Therefore,in the next subsection we no longer demonstrate the result with this non-constraint slave-spin method.

As shown in Figs.3 and 4,we plot the energy spectrums of the original physical representation and the slave-spin representation at half filling and non-half filling,respectively.It turns out that all the physical states are included in the four times enlarged Hilbert space.Notably,at small U regime,the distributions of eigen-energy are almost the same in both representations,whereas at the large U limit,the fake states deviate greatly from the physical ones.As a matter of fact,the feature of energy spectrums is accounting for the the gratified results at small U regime and the ill-defined results at large U regime of slave-spin method in calculating the thermal dynamic properties(as shown in Section 4).

Obviously,in non-half-filling situation,at most large U regime,the ground state is not the physical state at all(see Fig.4).In general cases,we simply estimate the stability of the system according to the level of energy,such as in the variational Monte Carlo method.However,in some artificial representations,even the ground state may be fake states. The height of energy level should not be the only ruler to judge the ground state,where we should also ensure the inherent physical nature of the objects discussed.Conversely,guaranteed by particle–hole symmetry,at half filling,the slave-spin method reproduces the exactly right ground state as the analytical solution(see Fig.3). In both situations,the unphysical states which possess greatly deviated eigen-energies take up a much bigger proportion than the physical ones.Most excited states are unphysical so that the finite-temperature framework is not so reliable without stringent constraints,where these unphysical states will impact observables heavily,especially at large U regime.

Fig.3. At half filling,comparison of energy spectrum distribution(without MF approximation)in slave-spin representation(yellow diamond)and original physical representation(red square).

Fig.4.At non-half filling,comparison of energy spectrum distribution(without MF approximation)in slave-spin representation(yellow diamond)and original physical representation(red square).

As indicated above,the crucial ingredient to ensure the accuracy of the slave-spin approach is excluding the unphysical states by exactly enforcing gauge constraints. Next we will analyze the processing of iteration in detail to elucidate how the particle–hole symmetry plays such an important role in this slave-particle method. Due to the fact of half-filling,the total electron number should be an invariant to respect the particle–hole symmetry,i.e.,Thus in the original Hamiltonian(Eq.(23)),pseudo-fermions term Hfcould now be rewritten in an equivalent form to give

It turns out that no matter what initial value has been set for I12,the ground-state wave-function of the auxiliary fermions is unchangeable so that we get an invariant χ12.A fixed χ12also leads to a fixed ground-state wave-function for the auxiliary Ising spin degree of freedom. Thus we directly get a self-consistent ground state,while the iteration process is not indeed necessary. As shown in Fig.2,now the bond order of quasi-particle χ12is a constant irrelevant to the correlation strength U. As a result,the average bond order of physical electrons χ=I12χ12is only dependent on the auxiliary spin degree of freedom. It turns out that a bond order only depending on a single degree of freedom,i.e.,the thorough decoupling between different slave variables,is a crucial signal which suggests the slave-spin method may possess a precise solution of ground state.

As to the two-site model with arbitrary electron number,the iteration process is much more complex. Different from the half-filling context,now the Hamiltonian of pseudofermions is written as

which indicates that both Hfand HIsingin Eq.(23)are dependent on correlation strength U.Therefore,sufficient iterations are inevitably needed to achieve a self-consistent ground state.Now the physical bond order is relying on both charge and spin degrees of freedom.The entanglement between pseudo-spins and pseudo-fermions naturally leads the slave-spin solution on mean-field level deviating from the analytical solution.

4.2.Quantum fluctuations beyond mean field

In this subsection,we will additionally demonstrate some extremely intriguing properties of the slave-spin approach in half-filling situation.So far,we merely apply this slave-spin method to investigate the two-site Hubbard model on a meanfield level. Even if we have made some approximations for convenience,the slave spin still performs exactly the same with analytical solution,which makes us wonder what if we further consider the effect of quantum fluctuations beyond mean-field and whether this system would be described more accurately.

In the last several subsections,after making transformation to the slave-spin representation,we generally tackle the four operatorsterm with mean-field theory and neglect any quantum fluctuations. Now there is an alternative method to go beyond this local approximation with the perturbation theory,where we mainly consider the quantum fluctuations of the transverse Ising part after making the mean-field approximation.In order to apply the perturbation theory,it is necessary to change the Hamiltonian into the form

where H0still takes the slave-spin formulation

and the perturbation term is written as

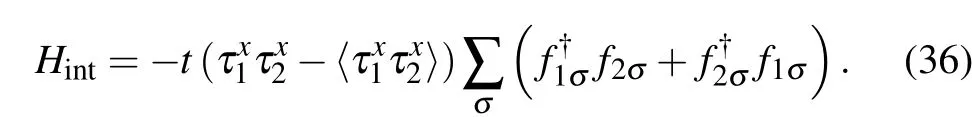
To get the ground-state properties with correction up to the second order,firstly we derive the ground wave function with first-order correction

where the index n stands for the seven excited states in the slave-spin representation,which are calculated from the nonperturbation Hamiltonianis the n-th excited eigenstate without correction.As we can see,the first-order correctionNext with the first-order corrected wave-function,we could further calculate the secondorder correction

As shown in Fig.5,we plot the energy including quantum fluctuations beyond mean-field with varying U and compare it with the original mean-field result.Intriguingly,this figure demonstrates that the quantum fluctuations beyond mean-field lead the energy deviating from the exact solution.The effect of fluctuations seems to be monotonously elevating the energy of the slave-spin mean-field solution.

Fig.5. Comparison of ground-state energy with the slave-spin MF method(green circle)and the slave-spin method including the effect of fluctuation(brown dotted-line).

In this two-site Hubbard model,there are two reasons that make the mean-field solution with fluctuation correction even worse than the mean-field solution.First of all,we only include the first-order and second-order corrections but neglect all higher-order ones.The first and second order corrections lift the ground-state energy,while these higher-order corrections sum up to a pure decline effect.As a result,if we consider the corrections of all orders,coincidently they conspire to make no difference,thus make the mean-field level solution as precise as the exact solution.What is more,we calculate the corrections in the enlarged Hilbert space,i.e.,there are some unphysical states mixed with the physical ones in the corrected ground wave function.The unphysical states make it hard to accurately calculate the excited-state wave-functions and also the effect of quantum fluctuations beyond MF.Although it has been proved that in some special situations we can access the expected value of some physical properties without accurate constraint,[39,40]the deviation somehow is unavoidable when considering fluctuations beyond mean-field or generic time evolution of observables.

4.3.Dynamics:Green function with time evolution

At last subsection,we discuss both advantages and disadvantages of slave spin in describing ground state in various contexts,which are limited to the static properties in zero temperature situations. In this subsection,we start from the single-particle Green function,and focus on how different parameters impacting the accuracy of the slave-spin method with time evolution.These parameters include temperature T,correlation strength U,and also electron number nf.The Green function generally reads

Here Ttis the time-ordering operator andis the real time.If we use the slave-spin method and consider exact gauge constraints,the Green function could be calculated with the eigenstates in the enlarged Hilbert space directly.However,to keep gauge constraints satisfied,it is necessary to get rid of unphysical states in the wave function at every period. Otherwise,if we make mean-field approximation in this slave-spin representation,equation(39)changes to

Here we have introduced some auxiliary quantities

Firstly we demonstrate the zero temperature situation,i.e.,the dynamics of ground state,in half-filled(Fig.6)and non-half-filled(Fig.7)situations.Unfortunately,only if there is no interaction between electrons,the slave-spin mean-field model could exactly reproduce the standard behavior of the exact solution.As U is increased,a great deviation shows up between them.At half filling,the behavior of single-particle Green function is unchanged versus U,while in the slave-spin mean-field theory,the Green function shows ill-defined behavior.Notably,even if the particle–hole symmetry is restored in this case,the mean-field approximation is effective merely at a small U regime.With a large U,although slave spin on meanfield level can describe the static properties of ground state of the half-filling two-site model exactly,the deviation caused by unphysical states will be magnified with time evolution.This assumption is confirmed again in the non-half-filled situation,where the slave-spin method with gauge constraints does not reproduce the desired behavior as analytical solution with all scope of U.Our paper provides some insights into the issue of how to improve the accuracy of slave spin,and the hinge is projecting the enlarged Hilbert space onto the physical one.

Fig.6.The single-particle Green function with evolution of time in zero-temperature half-filling situation: exact diagonalization(red square)and the slave-spin MF method(green circle). The results are calculated with different U.

Fig.7.The single-particle Green function G()with evolution of time in zero-temperature non-half-filled situation:exact diagonalization(red square),the slave-spin MF method(green circle),and the slave-spin method with GC(blue triangle).The results are calculated with different U.

Fig.8.The single-particle Green function with evolution of time in finite-temperature(kT/t=0.1)non-half-filled situation:exact diagonalization(red line),the slave-spin MF method(green circle),and the slave-spin method with GC(blue triangle).The results are calculated with different U.

Here we also provide the results with finite temperature in non-half-filled situation(see Figs.8 and 9).At finite temperatures,it is necessary to include time evolution of all excited states on average level,weighted by the Boltzmann factor(we take k=1 throughout this paper).It demonstrates that the availability of slave spin with mean-field approximation is merely limited to a small parameter regime,where both correlation strength and temperature are small enough compared with the hopping integral term. As shown in Fig.9,when kT/t=1,the slave-spin mean-field method accesses an incorrect behavior of dynamical properties.This is caused by unphysical states which could not be removed completely in the mean-field approximation.As we know,λ of Lagrange multiplier is dependent on T and U.In a high temperature context,the influence of thermal fluctuation is quite severe and this two-site system is instable.This instability is also reflected on λ,where a tiny deviation of λ will lead to a great distinction in Hamiltonian and destroy the gauge constraints completely.Because of the difficulty in calculating the accurate value of λ,it is impossible to satisfy the constraint conditions and access the exact behavior on mean-field level.

Fig.9.The single-particle Green function with evolution of time in finite-temperature(kT/t=1)non-half-filled situation:exact diagonalization(red line),the slave-spin MF method(green circle),and the slave-spin method with GC(blue triangle).The results are calculated with different U.

The good news is that if we could take gauge constraints into account exactly at both two sites,the slave-spin method behaves credible at most parameter regime.Only tiny deviation shows up at high temperature together with strong correlation situation(see Fig.9).It turns out that in general situation,the slave-spin method could also work well in calculating dynamical quantities as long as we can project the enlarged Hilbert space into the original physical one.

4.4.Thermal dynamic properties:heat capacity

A stringent test for slave-spin method is to compare the thermal dynamic properties. To benchmark the capacity of slave spin in studying thermal dynamic properties,next we focus on the behavior of heat capacity with all three methods.We derive heat capacity with the aid of partition function,which is obtained by summing up all configurations of this system.As a canonical ensemble,μ=0 so that the partition function reads

where Eistands for the eigen-energy on i-th level and k is the Boltzmann constant.Since in Section 3 we have introduced three methods to access the energy level distribution,with the partition function it is easy to access the average value of energyand square of energyThe heat capacity is written as

As shown in Figs.10 and 11,we demonstrate both half-filled and non-half-filled situations.Notably,in both situations,the slave-spin method with exact gauge constraints perfectly reproduce the behavior of analytical solution,while on meanfield level the results could not catch the nature of thermal dynamic properties unless the correlation strength is small enough(U/t<1). In Fig.11 we also demonstrate the result without constraint condition at all.Similar with the result of mean-field approximation,in this non-constraint situation the heat capacity calculated with mixed physical and unphysical states is well-behaved merely at small U regime,where the distribution of eigen-energy in the slave-spin representation closely resembles the original physical one.These results suggest the great influence caused by unphysical states,which could be eliminated completely with gauge constraints.The unit of axis is set as t/k,which means slave spin with gauge constraints could work well in a large temperature regime.

Fig.10.The heat capacity Cv in half-filled situation:exact diagonalization(full red line),the slave-spin MF method(full green line),and the slave-spin method with GC(blue triangle).The results are calculated with different U.

Fig.11.The heat capacity Cv in non-half-filled situation:exact diagonalization(full red line),the slave-spin MF method(green circle),the slave-spin method with GC(blue triangle),and also the slave-spin method without GC(yellow diamond).The results are calculated with different U.

5.Conclusion

We have studied the performance ofslave-spin method in describing various properties.In order to investigate the accuracy of slave spin,we choose the minimal formulation of previous slave-particle representations and the simplest correlated system,i.e.,two-site Hubbard model. Because of the simplicity of formulation and the finite Hilbert space,we directly access the analytical solution and set it as benchmark. By recovering the static, dynamical, and thermal dynamic properties with slave-spin method both with exact gauge constraints and mean-field approximation,we can eventually make a fair evaluation about slave spin.

Surprisingly,in half-filled situation,slave spin on a meanfield level can perform exactly as well as the analytical solution when investigating the static properties of ground state.It turns out that the accuracy of mean-field approximation is ensured by the particle–hole symmetry.However,in more general non-half-filled situation or when we turn to the dynamical properties and thermal dynamic properties,the slave-spin method merely works well at the regime where both U and T are small(U/t<1 and kT/t<1). Although the slavespin mean-field approach is not available in some parameter regime,we could still use it accessing accuracy behavior of all properties with gauge constraints.Considering the constraint condition exactly,only tiny deviation shows up when both T and U are extremely large.All these deviation are caused by unphysical states.At a small U and low temperature situation,the influence of unphysical states is tiny,but it would be magnified with strong correlation and strong energy fluctuation.

Our work highlights the importance of identification of physical states in the slave-particle method. As long as unphysical states are excluded completely,the slave-particle mean-field method could access the exact properties. However,most strongly correlated systems are much more complex and it is difficult to take the constraint condition into account exactly,i.e.,some unphysical states are unavoidably remaining.For all these,our work finds a way out for slave particle.In some models with specific symmetry,the gauge constraint does not change the formulation of partition functions and thus unphysical states may not impact the expected value of physical observables.As we know,the particle–hole symmetry has successfully simplified the slave-particle mean-field theory in many cases.In the future research,we could apply slave particle into this sort of models,such as periodic Anderson impurity model.Besides,some other symmetries may also work in other contexts.We hope our work can enlighten the slaveparticle method to be utilized into suitable area and motivate further investigations.

Acknowledgment

We thank Ji-ze Zhao for careful reading and useful suggestions.