Topological phases of a non-Hermitian coupled SSH ladder*
J S Liu(劉建森), Y Z Han(韓炎楨),and C S Liu(劉承師)
Hebei Key Laboratory of Microstructural Material Physics,School of Science,Yanshan University,Qinhuangdao 066004,China
Keywords:topological phase,non-Hermitian,Su–Schrieffer–Heeger(SSH)ladder,winding number
1.Introduction
A number of recent works have started to explore the topological properties of non-Hermitian systems,[1–31]since non-Hermitian effects are found applicable in a wide range of systems including open boundaries[32–40]and systems with gain and/or loss.[25,41–57]Interestingly,non-Hermitian Hamiltonian exhibits the intriguing features and many other interesting phenomena with no counterpart in Hermitian cases,e.g.,the existence of exceptional points where the Hamiltonian becomes nondiagonalizable.[25,58]A key issue of non-Hermitian systems is to find the topological invariants which are responsible for the bulk–boundary correspondence.Previous non-Hermitian topological invariants,including the Chern number,generalized Berry phase,and winding number,are formulated in terms of the Bloch Hamiltonian by employing the biorthonormal eigenvectors.[1–7,9,48]However,numerical results in a one-dimensional(1D)model show that openboundary spectra look quite different from periodic-boundary ones,which seems to indicate that the bulk topological invariants fail to be responsible for the topological edge states.[2,6]
To establish the non-Hermitian bulk–boundary correspondence,one possible way is to find a Hermitian counterpart of the corresponding non-Hermitian Hamiltonian. The Hermitian Hamiltonian can be constructed with a pseudo-Hermiticity operator. A Hermitian counterpart can have an identical fully real spectrum in the symmetry-unbroken region.[5,59–61]The other case is taking the non-Hermitian skin effect into account,where the bulk states are localized at boundaries and deviate from the extended Bloch waves.The non-Hermitian skin effect is from asymmetric tunneling amplitudes which create effectively an imaginary gauge field. Nonzero imaginary magnetic flux breaks the conventional bulk–boundary correspondence and leads to a topological phase transition.[62,63]A non-Bloch topological invariant is introduced and gives the number of topological edge modes of the non-Hermitian Hamiltonian.[63–67]
The coupled Su–Schrieffer–Heeger(SSH)systems,as the crossover from one-dimensional(1D)to two-dimensional(2D)system,host a rich phase diagram which is different from that of both 1D and 2D systems.[68–70]Then for the non-Hermitian version of the SSH ladder,what is the bulk–boundary correspondence and what is the topological invariant that determines the zero modes?In a study of the model,the winding number was defined in the generalized Brillouin zone(GBZ)and faithfully predicted the topological zero-energy edge modes.[71]We study a special non-Hermitian version of the coupled SSH model which originates from the two-row limit of the brick-wall lattices.Benefiting from the existence of the complex wave vector in GBZ,we can define the winding number in GBZ without solving the model directly.It is found that the winding number has nothing to do with the interleg hopping.The two chains are decoupled completely.We can obtain the topological phase transition point from the studies in Ref.[64].The numerical analysis is used to verify our study.
The remainder of this paper is organized as follows.In Section 2,we present the coupled-SSH chains and explain the origination of the model.Section 3 gives the theoretical and numerical analysis to prove that the interleg hopping does not modify the topological feature of the model.The phase diagram of the model is the same as that of the chain.Finally,we present a summary and discussion in Section 4.
2.Models
The system is coupled SSH chains with the two-leg ladder structure.The geometry of the system is sketched in Fig.1(a).Each ladder is a bipartite lattice system,consisting of two sublattices a and b(or c and d).The hopping amplitudes in each leg are staggered and the rung indicates the interleg hopping.The model originates from the two-row limit of the brick-wall lattice[Fig.1(b)]which is an alternative representation of the honeycomb lattice[Fig.1(c)].
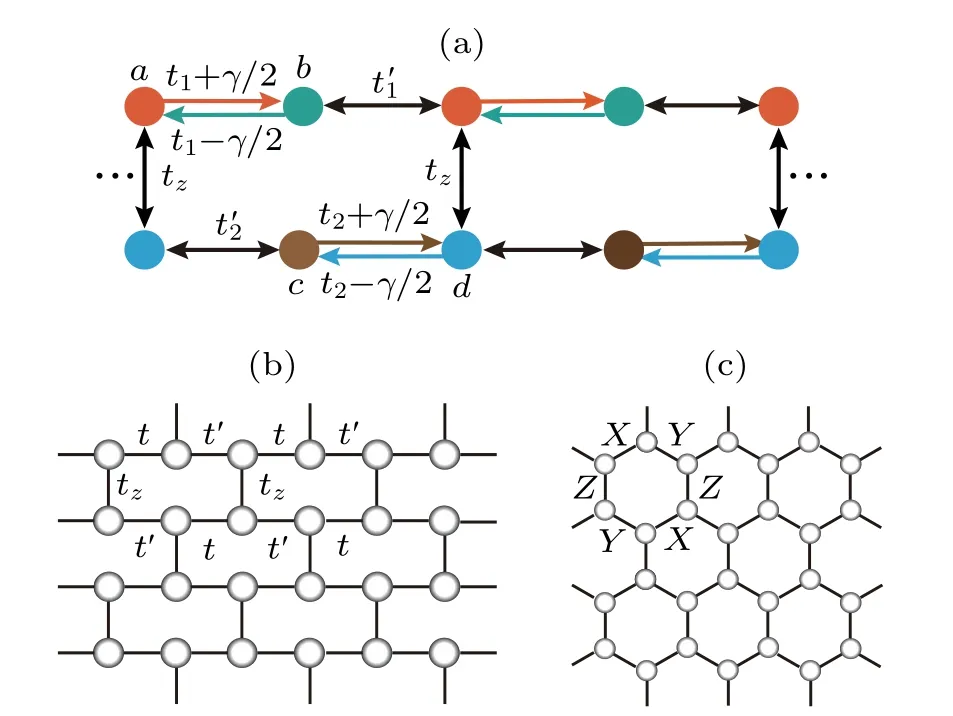
Fig.1. (a)Coupled SSH chains which are the two-row limit of the brick-wall lattice.(b)The brick-wall lattice is equivalent to(c)the honeycomb lattice.
The model is described by the Hamiltonian
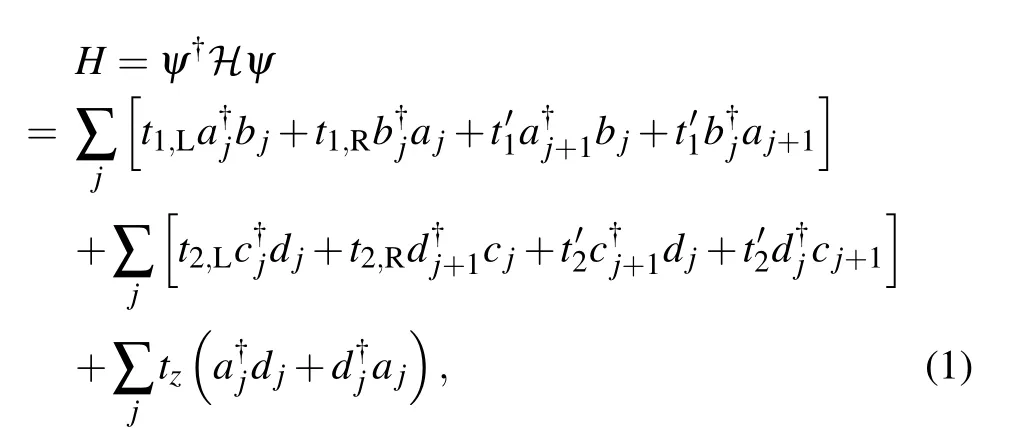
The non-Hermiticity of the Hamiltonianin Eq.(1)is due to the introduction of γ/2 which changes the hopping term in the unit cell with different hopping strengthsin the right direction andin the left direction(i=1,2). By adopting periodic boundary conditions and Fourier transformthe Hamiltonian H can be easily written asand

3.Results
The non-Hermitian skin effect determines drastically the topology of the non-Hermitian systems.The non-Bloch bulk–boundary correspondence and generalized Brillouin zone were suggested in the discussion in Refs.[64],[66],[71],and[72].In the generalized Brillouin zone,the wave number k becomes complex.The real part of the wave vector is from the the periodicity of the system according to the Bloch theorem.The non-Hermitian skin effect attributes to the imaginary part of the complex-valued wave vector. The non-Hermitian topological invariant can be constructed by replacing the Bloch phase factorbyand the value ofis confined in a loop on the complex plane.The?i time of natural logarithm values k →?i lnβ form a generalized Brillouin zone(GBZ),whereis generally not a unit circle in the complex plane.The GBZ and E can be obtained by solving the equationwhere i,j are the middle two indexes when orderingas
The existence of β gives an opportunity to find the non-Bloch topological invariants of the model according to the results given in Ref.[64]without solving the model directly.With the unitary
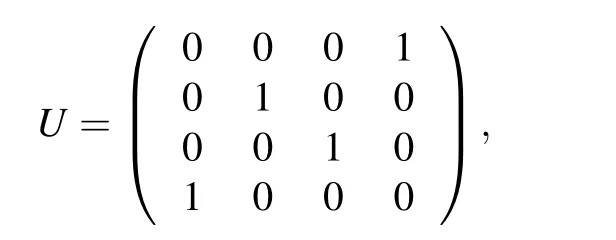
the Hamiltonian hβin Eq.(2)is brought into block offdiagonal form by the unitary transformation

where

The determinants of V1and V2are q1=DetV1=andwhich have nothing to do with tz.With the determinants q1and q2as the winding vectors,the winding number is defined by
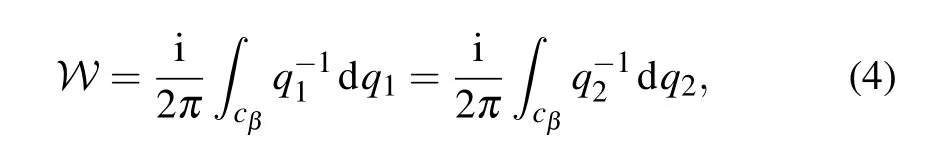
which is defined on the GBZ.The winding numbers of the winding vectors q1and q2on the GBZ cβcan be used as topological invariants to distinguish the different topological nontrivial states.
When γ1=γ2=0,the non-Hermitian skin effect disappears and the Hamiltonian in Eq.(2)becomes Hermitian.In such case,the wave vector is real quantum according the Bloch theorem.The winding number defined by the block offdiagonal Hamiltonian in Eq.(3)is still effective to distinguish the topological nontrivial phase and has nothing to do with tz.The conventional bulk–boundary correspondence governs the system.
From Eq.(4),the winding number has nothing to do with tz.It gives us a strong evidence that the two ladders are decoupled completely when discussing the topological behaviors.The augment is first reported for the Hermitian SSH ladder in Ref.[73]. Here,we obtain the argument in the non-Hermitian case which benefits from the the existence of the generalized Brillouin zone.To verify the above analysis,we diagonalizein Eq.(1)under the open boundary condition.The parameters are t1=1.3,t2=0.4,tz=1.2,γ1=4/3,and γ2=2/3.The intercell hoppings are taken to beAs shown in Fig.2(a),the energies as a function as t′are completely real-valued.The zero modes exist for1160 and.4989.We have changed tzand re-calculated the energies as a function of t′.It is found that the energies change obviously and the zero modes remain unchanged,however.To understand the four phase transition points at|t′|=1.1160 and|t′|=0.4989,we diagonalize the two ladders which are non-Hermitian SSH models,respectively.The absolute values of energies as function as t′are shown in Figs.2(b)and 2(c).Shown by four vertical lines,the four phase transition points are the same as those of individual non-Hermitian SSH I and II.The topological phase transition points have been analytically solved in Ref.[64]for the non-Hermitian SSH chain.The transition points arefor the two ladders respectively.With the parameters used in Fig.2,the transition points are t′=±0.4989 and±1.1160.

Fig.2.Energy spectra of an open chain with length L=80(unit cell)as a function of t′by numerical diagonalization of the Hamiltonian:(a)in Eq.(1),(b)of the non-Hermitian SSH model for ladder I,(c)of the non-Hermitian SSH model for ladder II.Here t1=1.3,t2=0.6,tz=1.2,γ1=4/3,and γ2=2/3.The other parameters are set to be

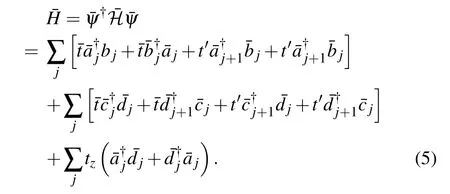
The open-boundary spectra of Hamiltonian ? in Eq.(2)andin Eq.(5)are given in Figs.3(a)and 3(b),respectively.The open chain length is L=80. The other parameters are taken to be t2=1,γ=4/3,and tz=0.3.It is interesting to see that the zero modes exist in ?3 Fig.3.(a)(b)The open-boundary spectra of Hamiltonian in Eq.(5)andin Eq.(5).The parameters are taken to be t2=1,γ=4/3,and tz=0.3.Panels(a1)–(b4)show the eigenfunctions.The x-axis is the coordinate of the chain.Panels(a1)–(a4)are the non-Hermitian cases.Panels(b1)–(b4)are the Hermitian cases.Panels(a1),(a2),(b1),(b2)show the zero-energy modes of the two chains.Panels(a3),(a4),(b3),(b4)show the non-zero-energy modes of the two chains. The wave functions are shown in Fig.3 for t=0.8.For the non-Hermitian case,figures 3(a1)and 3(a2)show the zeroenergy modes,and figures 3(a3)and 3(a4)show the non-zeroenergy modes. Due to the non-Hermitian skin effect,the eigenstates of one open chain[Figs.3(a1)and 3(a3)]and the other chain[Figs.3(a2)and 3(a4)]are found to be localized near the left boundary,which is in contrast to the Hermitian cases in Figs.3(b1)–3(b4).Figures 3(b1)and 3(b2)show the zero-energy modes of the the Hermitian cases. The zeroenergy mode in Fig.3(b1)of chain I is an asymmetry wave function duo to the symmetry of chain I.The zero-energy mode in Fig.3(b2)of chain II is a localized wave function since the chain II does not possess the symmetry. The nonzero-energy modes in Figs.3(b3)and 3(b4)are all the extended Bloch waves in the two chains. We have studied topological phases of a special non-Hermitian coupled SSH ladder where the interlegs of the special ladder are cancelled alternately. The model is different from the general ladder and originates from the brick-wall lattices in the two-row limit.With a unity transition,the Hamiltonian in GBZ is brought into block off-diagonal form.According to the calculations of the winding number defined by the determine of the block off-diagonal matrix,we find that the interleg hopping has nothing to do with the topological number of the ladder.So the special coupled SSH chain is decoupled when discussing the topological behavior.The topological properties of the model are determined by the single non-Hermitian SSH chain.This method may be useful to investigate other multi-leg ladder models.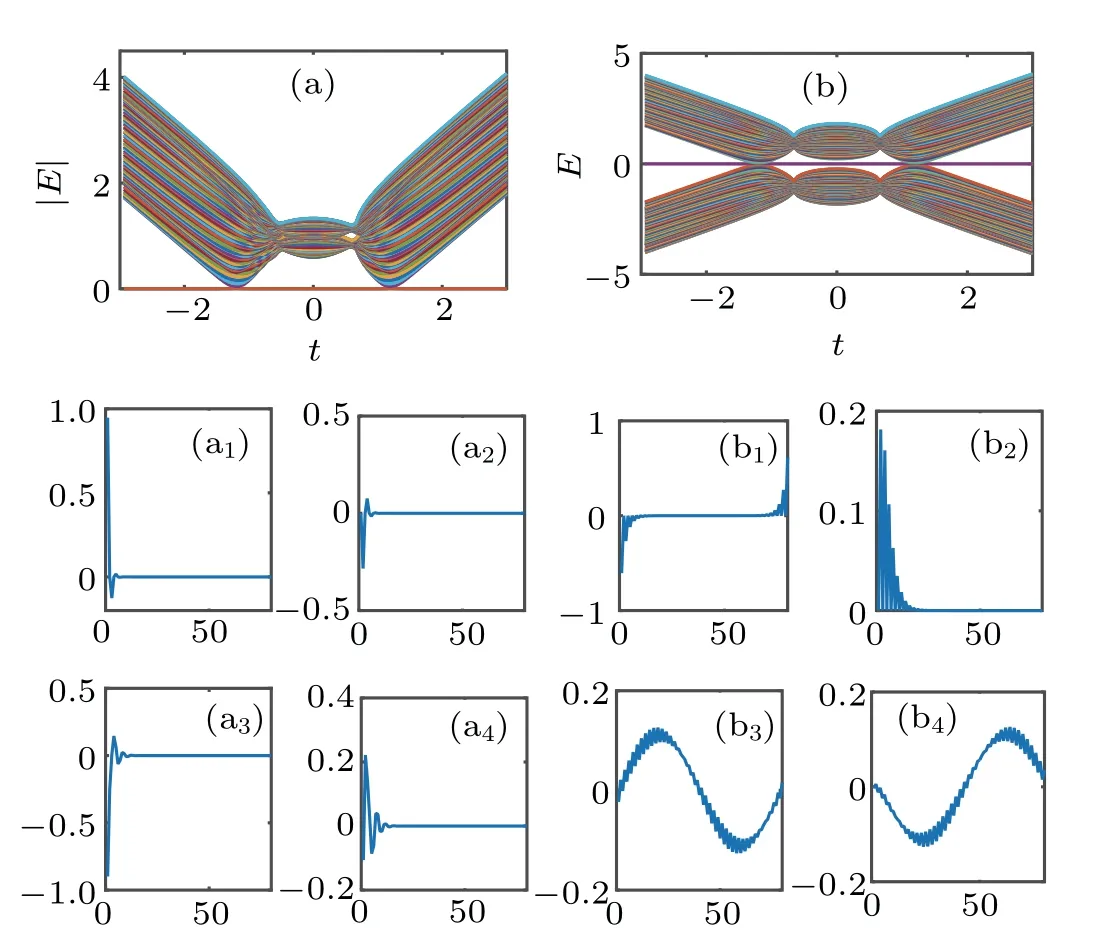
4.Summary
- Chinese Physics B的其它文章
- Theoretical analyses of stock correlations affected by subprime crisis and total assets:Network properties and corresponding physical mechanisms?
- Influence of matrigel on the shape and dynamics of cancer cells
- Benefit community promotes evolution of cooperation in prisoners’dilemma game?
- Theory and method of dual-energy x-ray grating phase-contrast imaging?
- Quantitative heterogeneity and subgroup classification based on motility of breast cancer cells?
- Designing of spin filter devices based on zigzag zinc oxide nanoribbon modified by edge defect?

