Exact solutions of a(2+1)-dimensional extended shallow water wave equation?
Feng Yuan(袁豐),Jing-Song He(賀勁松),and Yi Cheng(程藝)
1School of Mathematical Sciences,University of Science and Technology of China,Hefei 230026,China
2Institute for Advanced Study,Shenzhen University,Shenzhen 518060,China
Keywords:(2+1)-dimensional extended shallow water wave equation,Hirota bilinear method,dormion-type solution
1.Introduction
Nonlinear phenomena are ubiquitous in fields of engineering,physics,and even in social sciences. A wide variety of processes in physics can be described by nonlinear partial differential equations(PDEs).In recent decades,nonlinear science has been highly developed and applied in many areas. Integrable nonlinear systems have been interested in many mathematicians and physicists.One important task is to look for exact wave solutions of nonlinear evolution equations.These exact solutions are conducive for us to understand the physical mechanism of nature,such as solitons propagating with finite speed. Thus,in recent years,various approaches have been established to construct the exact solutions in closed form of the nonlinear PDEs,including Lie group method,[1,2]inverse scattering method,[3]Hirota bilinear method,[4–7]the tanh-function method,[8]Darboux transformation,[9–12]the Jacobi elliptic function expansion method,[13]extended Jacobi elliptic function expansion method,[14–16]and so on.Among these famous methods,the Hirota bilinear method is a direct approach to solve nonlinear PDEs.Its advantage is that if we obtain the corresponding bilinear form of the equation,the multi-soliton solutions can be constructed in a simple and algebraic way.
The shallow water wave(SWW)equation is applied to study the surface wave in shallow water.The SWW equations are well known as a flow of shallow water at the free surface under gravity,or below the surface of horizontal pressure in a fluid.[17–19]Stokes,a pioneers of hydrodynamics,derived the equation of motion of an incompressible inviscid fluid under constant vertical gravity.[19]From these basic equations,various shallow water wave models can be obtained by further simplifying assumptions.These shallow water models are widely applied in oceanography and atmospheric science.
The(1+1)-dimensional SWW equation[20,21]arises from the Boussinesq approximation is in the form
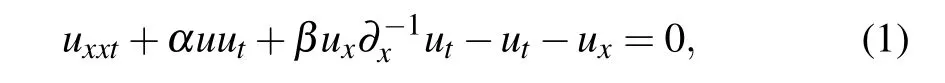
where α and β are arbitrary nonzero constants. By taking ux=v,equation(1)can be written as
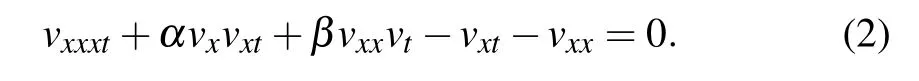
In the case α=2β,equation(2)becomes SWW–Ablowitz–Kaup–Newell–Segur(SWW–AKNS)equation,[21]while in the case α=β it becomes SWW–Hirota–Satsuma(SWW–HS)equation.[20]Both these two equations are completely integrable and exist Lax pair.[21,22]The(2+1)-D SWW equation which is a(2+l)-D generalization of the shallow water wave equation[23]has the form
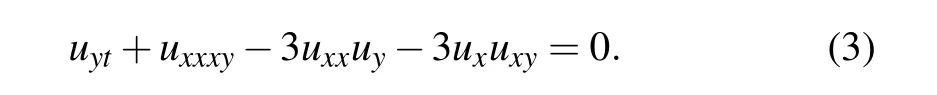
This is formulated as a nonlocal Riemann–Hilbert problem.A set of studies about Eq.(3)has been done in Refs.[24]–[26].In addition,several generalized equations about the(2+1)-D SWW equation have been studied,such as the generalized(2+1)-D SWW equation.[27]
In this paper,inspired the above results of shallow water wave equations,we study a new integrable nonlinear equation,namely a(2+1)-D extended shallow water wave(eSWW)equation,[28]and further discover new patterns of nonlinear waves due to the appearance of an arbitrary function. This newly introduced eSWW equation[28]is given by a form as
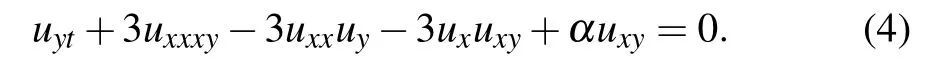
If setting x=y,v=r,and α=0,equation(4)can be reduced to KdV equation.[29]In Ref.[28],exact periodic wave solution of eSWW equation was constructed by using the generalized D-operator[30]and Riemann theta function[31]in terms of the Hirota bilinear method.In Ref.[32]Wronskian,Pfaffian,and periodic wave solutions of Eq.(4)has been given.Letting

then the eSWW equation is written as

which will be studied in the following context to get four kinds of solutions including soliton,breather,hybrid,and Jacobitype solutions.
This paper is organized as follows: In Section 2,we give the bilinear form and n-soliton of eSWW equation,i.e.,Eq.(6),and analyze the amplitudes and extreme values of bright soliton and dark soliton. In addition,we obtain the breathers and hybrid solutions by the complexification method.[33–36]In Section 3,we get new periodic solution and three kinds of dormion-type solution by setting an arbitrary function φ(y)as a Jacobi elliptic function.Note that φ(y)is appeared in the f for the bilinear form of the eSWW equation.Finally,we conclude this paper in Section 4.
2.Bilinear form and n-soliton solution
As we know,the Hirota bilinear D-operator plays a very important role in Hirota bilinear method which is defined as[4]
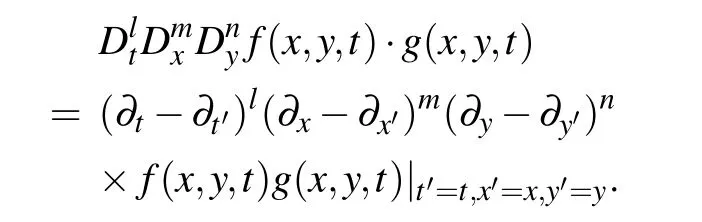

Through the dependent variable transformation equation(4)is transformed into a bilinear form
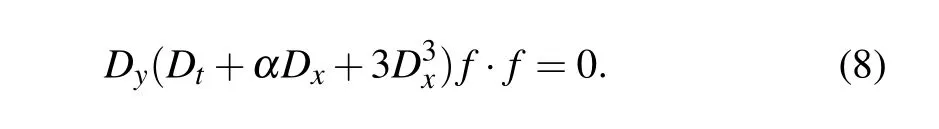
Here f is a real function of x,y,and t.The N-soliton solution of Eq.(8)is expressed as
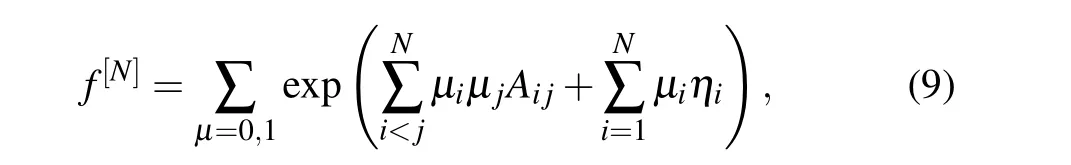
where
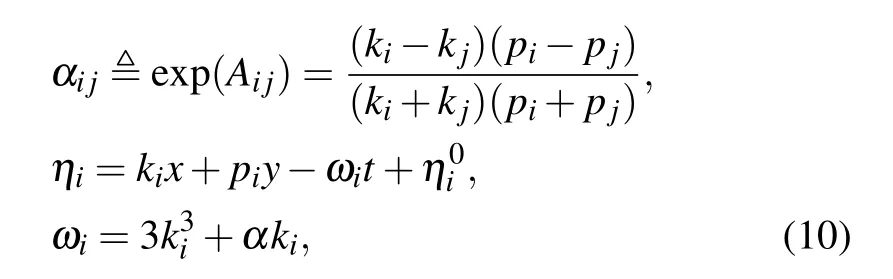
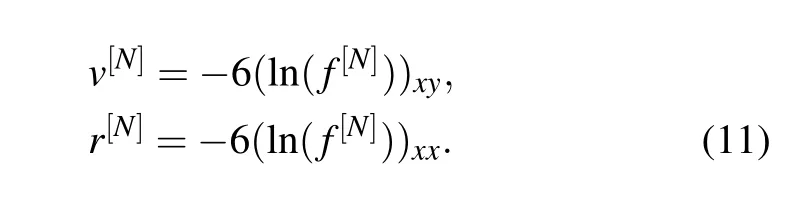
2.1.Soliton solutions
In order to obtain one-soliton solutions,we gain f[1]=by substituting N=1 into Eq.(9).Then we gain the solution from Eq.(11)as follows:
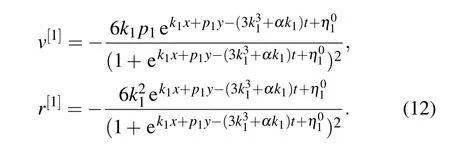
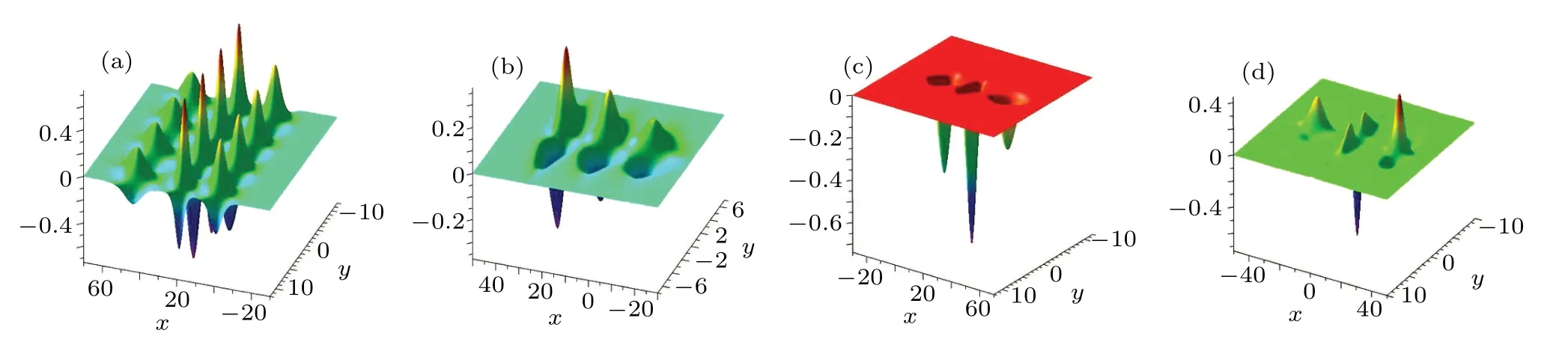
It can be seen from this formula that v[1]and r[1]have the same extreme linebut different amplitudes. The amplitude of v[1]is(3/2)k1p1,but the amplitude ofThus v[1]is a dark soliton when k1p1>0(Fig.1(a))and a bright soliton when k1p1<0(Fig.1(b)). However,r[1]generates only a dark soliton as shown in Fig.1(c). In addition, v[1]and r[1]have the same velocity on(x,y)-plane,which is given by
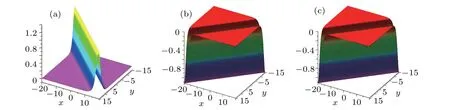
Fig.1.One-soliton equation(12)with α=1,=0,t=0.(a)Bright soliton v[1]:k1=?3/4,p1=1;(b)Dark soliton v[1]:k1=3/4,p1=1;(c)Dark soliton r[1]:k1=3/4,p1=1.
In the same way,we obtain two-soliton solution by setting N=2 in Eqs.(9)and(11).Two formulas of the solutions are given by
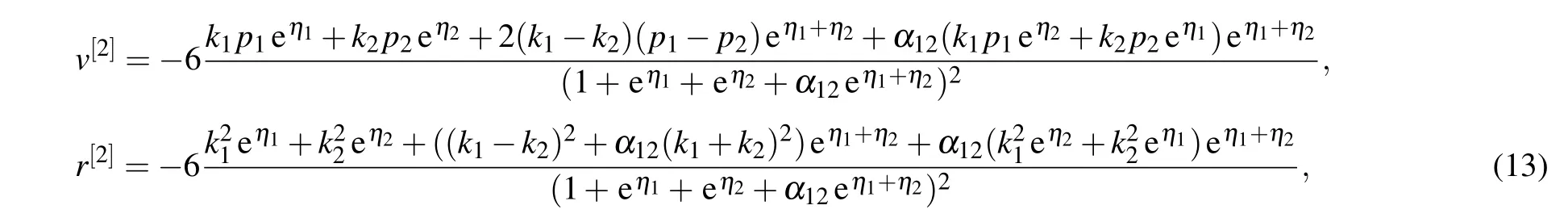
where η1,η2,and α12are given in Eq.(10).
The profiles of two-soliton given by Eq.(13)are shown in Fig.2.In this case,r[2]is always a dark soliton(Fig.2(d)),but v[2]is not.If k1p1>0 and k2p2>0,v[2]is a dark soliton(see Fig.2(a));If k1p1/k2p2<0,v[2]becomes a mixed-soliton(dark–bright form)(see Fig.2(b));and if k1p1<0 and k2p2<0,v[2]turns into a bright soliton as shown in Fig.2(c).
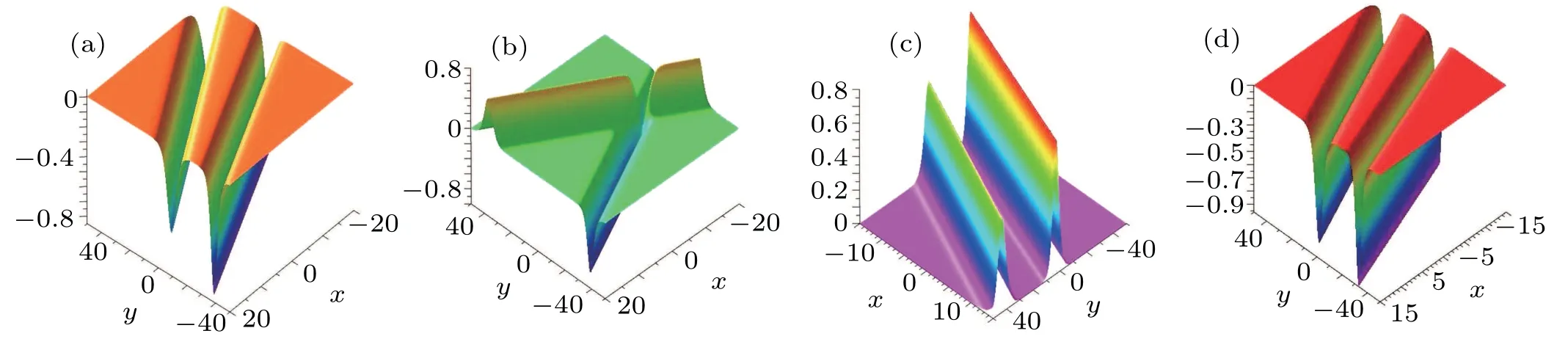
Fig.2.Two-soliton with α=?1/2,t=0,p1=1/2,=?5,p2=2/3,=10.(a)Dark soliton:v[2]with k1=3/4,k2=4/5;(b)Mixed soliton:v[2]with k1=?3/4,k2=4/5;(c)Bright soliton:v[2]with k1=?3/4,k2=?4/5;(d)Dark soliton:r[2]with k1=3/4,k2=4/5.
Similarly,we can obtain the N-dark-soliton r[N]or Nbright-soliton r[N]or N-mixed-soliton which consists of dark and bright solitons.Two examples of three-soliton are shown in Fig.3.
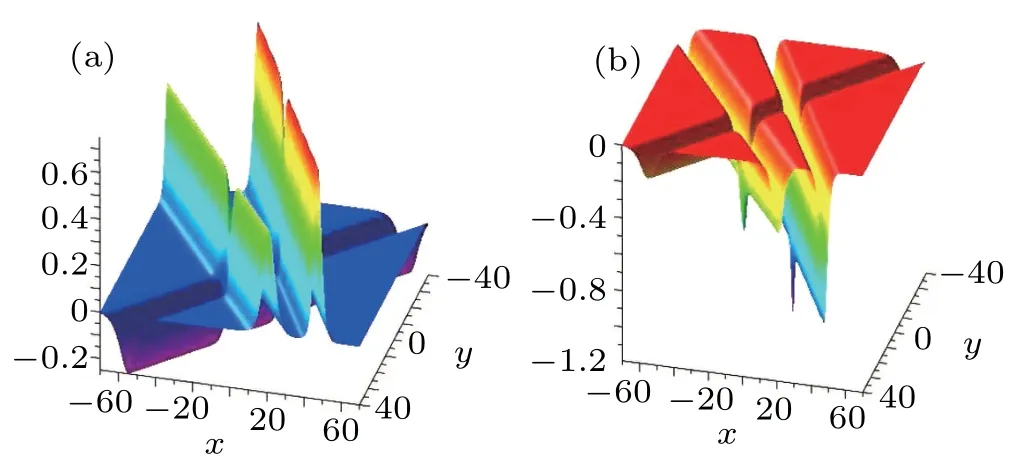
Fig.3.Three-soliton with α=1,t=0,k1=?3/4,k2=?1/2,k3=1/3,p1=2/3,p2=3/5,p3=1/2,=10,=?8,=0.(a)Mixed soliton v[3];(b)Dark soliton r[3].
2.2.Breather solutions
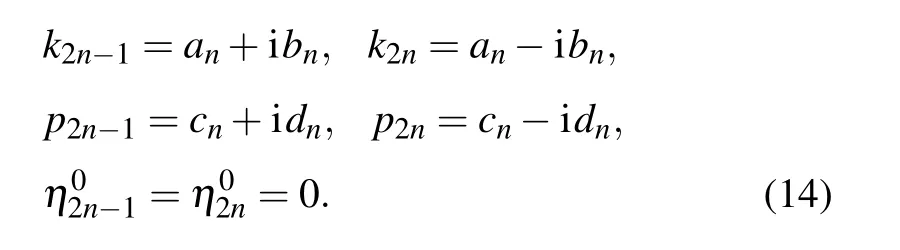
The real and imaginary parts of ηigiven in Eq.(10)are
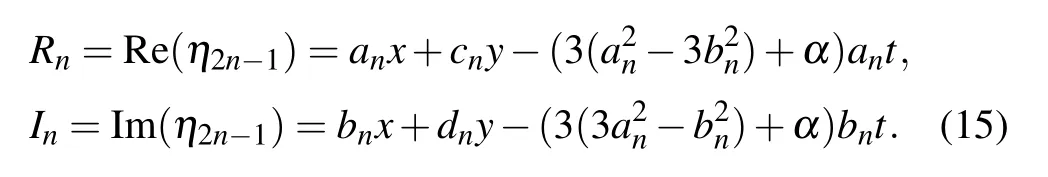
In the case N=2,the one-breather of the eSWW equation can be generated with the function f as follows:
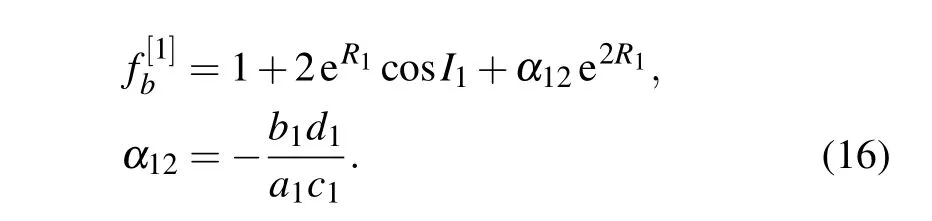
Substituting Eq.(16)into Eq.(11),we have the following expressions:
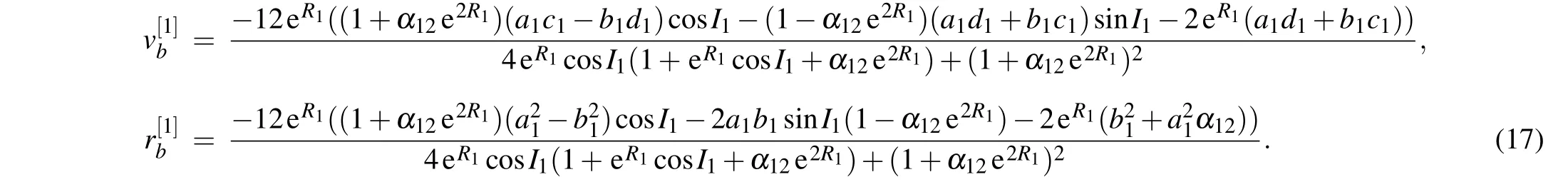
Their proflies are plotted in Fig.4.The trajectory ofandis R1=0.And through computing,we get that their period is T[x]=|2c1π/a1d1?b1c1|,T[y]=|2a1π/a1d1?b1c1|,and then the distance between two adjacent peaks is
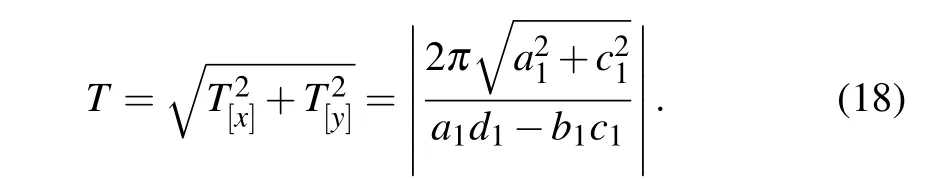
It implies that the breather moves parallelly on the(x,y)-plane as t changing,while its shape keeps unchanged.andhave the same velocityon(x,y)-plane.
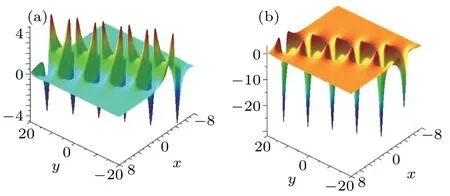
Fig.4.One-breather Eq.(12)with t=0,α=?1/2,a1=?1,b1=1/2,
In the case N=4,two-breathersandare generated by the following function through Eq.(11),namely,
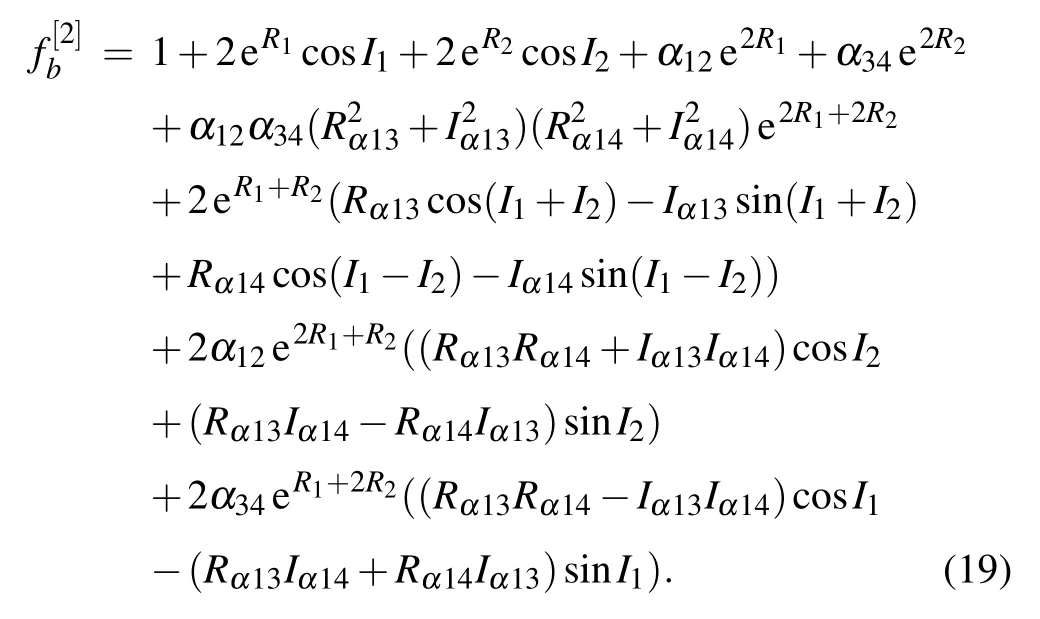
Here,

The profiles of the above two-breather solutions are plotted in Fig.5.
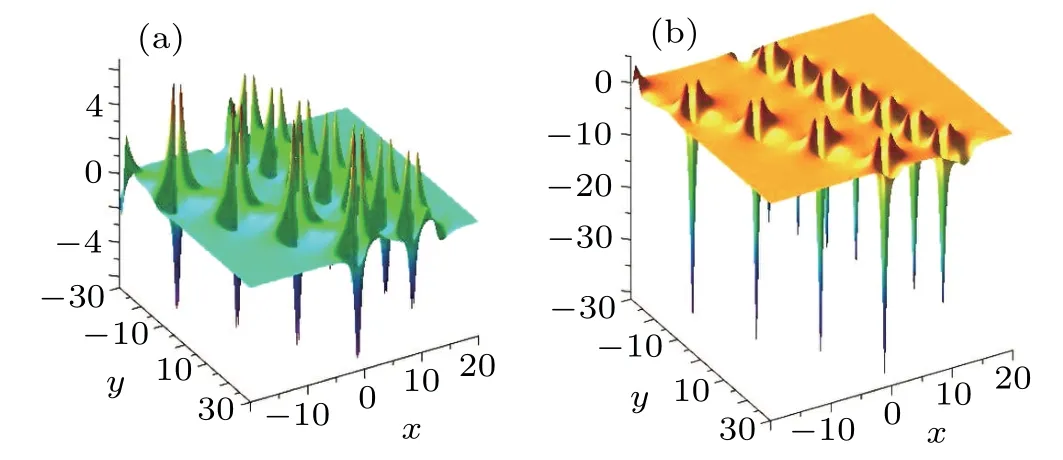
Fig.5. Two-breather solutions with t=0,α=?1/2,a1=?1/2,b1=1/3,c1=1/5,d1=1/3,a2=?1,b2=1/2,c2=1/5,d2=2/3,
2.3.Hybrid solutions
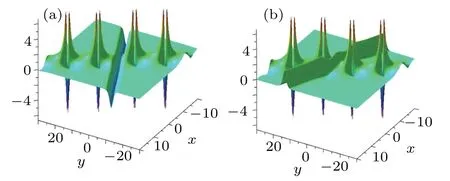
Fig.6. Hybrid solution v[3]with α=?1/2,t=0,k1=?1/2+i/3,p1=1/5+i/3,=i/4,k2=?1/2 ?i/3,p2=1/5 ?i/3,=?i/4.(a)One breather and one dark soliton with parameters k3=?1,p3=3/2,=0;(b)One breather and one bright soliton with parameters k3=1,
3.Jacobi-type solutio n
In this section,we shall give another kind of new solution.One crucial observation is that v[N]and r[N]are also solutions of the eSWW equation if we setin Eq.(10)by inserting a continuous arbitrary real function of y,i.e.,φ=φ(y).This fact is also mentioned in Ref.[37].According to this fact and setting φ be a Jacobi elliptic function,then equation(11)yieldsandwhich are hereinafter called Jacobi-type solution.We mainly discussin this section,which will provide a periodic solution and three kinds of dormion-type solutions.
3.1.Case 1:N=1
Using above modified η1with φ,the first order Jacobitype solution of Eq.(6)is in the form of
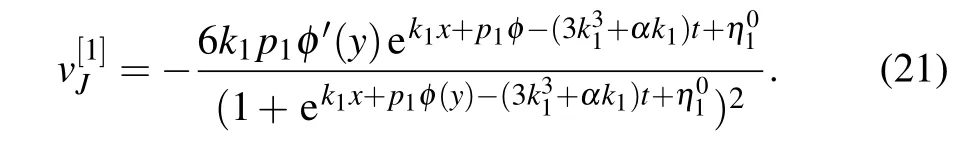
The character of the solution depends on the specific choice of φ.The velocity ofon(x,y)-plane isbecause of the termand the periodicity of φ with respect to y.That means the first order Jacobi-type solution parallelly travels along the x axis.
If we choose φ(y)=sn(y,3/10),the corresponding solution is given by
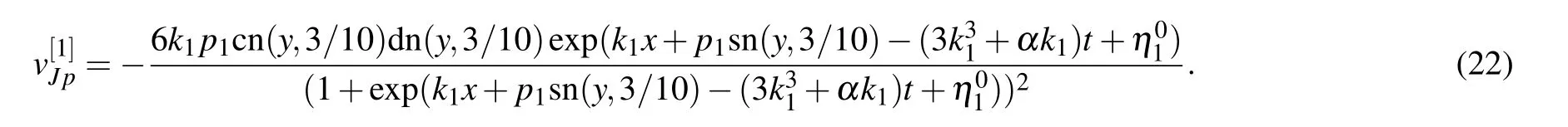
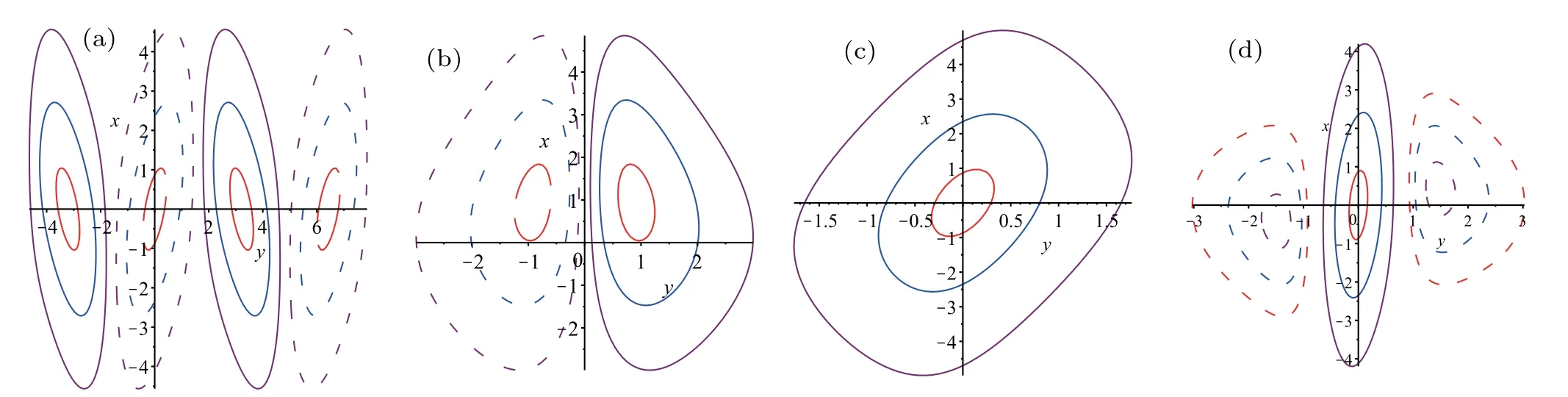
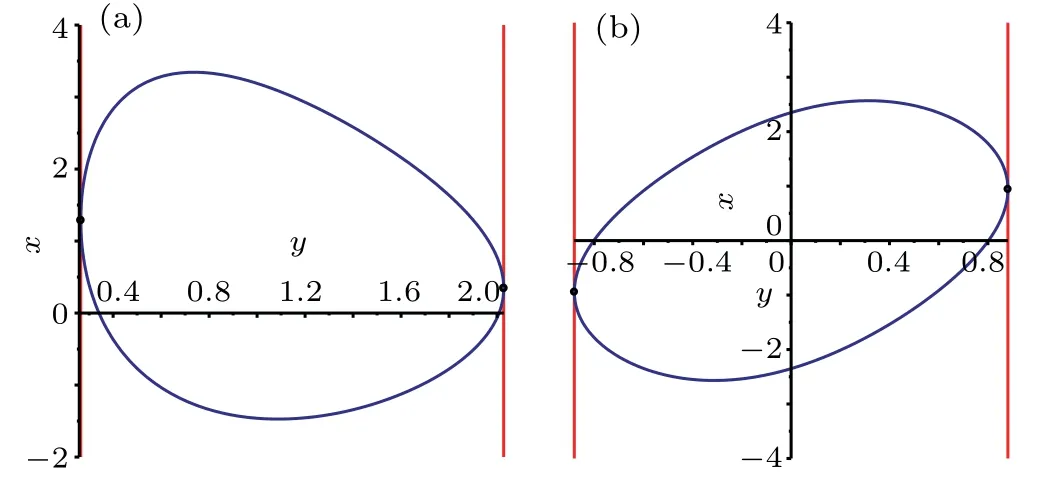
This is a periodic solution because of the appearance of elliptic functions,and its extreme value is±(3/2)k1p1,which is confirmed by Fig.7(a).The contour lines on different hights are plotted in Fig.7(a),where h is the hight and ?|(3/2)k1p1| Fig.7.with α=1,=0,t=0.(a)Periodic solution(22):φ(y)=sn(y,3/10),k1=?3/4,p1=1;(b)Dormion-type-I soliton(23):φ(y)=cn(y,1),k1=?3/4,p1=1;(c)Bright dormion-type-II soliton(26):φ(y)=sn(y,1),k1=?3/4,p1=1;(d)Dark dormion-type-II soliton(26):φ(y)=sn(y,1),k1=3/4,p1=1;(e)Bright dormion-type-III soliton(21):φ(y)=sn(y,1/2)/(1+y2),k1=?3/4,p1=1;(f)Dark dormion-type-III soliton(21):φ(y)=sn(y,1/2)/(1+y2),k1=3/4,p1=1. If we choose φ(y)=cn(y,1),and then we obtain a doubly localized solution on(x,y)plane which is called a dormion-type-I solution and is shown in Fig.7(b).The expression of this solution is given by which is traveling along y=0 with a velocityon(x,y)plane. It is interesting to note thathas one maximumlocated atarccoshand minimum ?(3/4)k1p1located atThe contour lines on different hights are plotted in Fig.8(b),where ?|(3/4)k1p1| Taking the derivative of x in Eq.(24),and making dy/dx=0,we can get two endpoints on(x,y)-plane.In addition,we obtain two tangent lines perpendicular to the y axis, Fig.8.Parameters:α=1,=0,k1=?3/4,p1=1,t=0.(a)The contour line with h=(27/20)k1p1(solid,red),h=(3/4)k1p1(solid,blue),h=(1/4)k1p1(solid,purple),h=?(27/20)k1p1(dash,red),h=?(3/4)k1p1(dash,blue),h=?(1/4)k1p1(dash,purple);(b)The contour linewith h=(27/40)k1p1(solid,red),h=(3/8)k1p1(solid,blue),h=(3/20)k1p1(solid,purple),h=?(27/40)k1p1(dash,red),h=?(3/8)k1p1(dash,blue),h=?(3/20)k1p1(dash,purple);(c)The contour linewith h=?(27/20)k1p1(red),h=?(3/4)k1p1(blue),h=?(1/6)k1p1(purple);(d)The contour line with h=?(27/20)k1p1(solid,red),h=?(3/4)k1p1(solid,blue),h=?(1/4)k1p1(solid,purple),h=(1/6)k1p1(dash,red),h=(1/4)k1p1(dash,blue),h=(1/3)k1p1(dash,purple). If we choose φ(y)=sn(y,1),and then we obtain a doubly localized solution on(x,y)plane which is called a dormion-type-II solution and is shown in Fig.7(c).The formula of this solution is given by This solution is different from dormion-type-I becausejust has one extreme value ?(3/2)k1p1located atof(x,y)plane.We can see from formula ofthat it is also a traveling wave along y=0 with the same velocity asIn addition,generates a bright dromion when k1p1<0(Fig.7(c)),and a dark dromion when k1p1>0(Fig.7(d)).The contour lines on different hights are plotted in Fig.8(c),where h is between 0 and ?(3/2)k1p1.The contour line of Eq.(26)on the hight h=?(3/4)k1p1(the half amplitude)is Using the same method as Eqs.(24)and(25),we can obtain two endpointsandon(x,y)-plane. The tangent lines perpendicular to the y axis are If we choose φ(y)=sn(y,1/2)/(1+y2),equation(21)yields a dormion-type-III solutionwhich shows very strong doubly localized feature(Figs.7(e)and 7(f))on(x,y)plane,and the profile of this solution is invariant during the propagation along y=0,although there exist Jacobi elliptic functions in the representation of solution. In other words,the periodicity ofis disappeared remarkably such that it shows behavior as a dormion,because the(1+y2)in denominator of φ(y)completely depresses the amplitude when y>10.A simple calculation shows thathas a significant extreme value ?(3/2)k1p1at centeral pointof(x,y)plane and other two small extreme values located in two sides.It is too long to write out the formulas of the above two small extreme values,but it can give approximately as 0.3568320478k1p1.Furthermore,the centeral point is a maximum if k1p1<0 which implies that this solution is a bright dromion(Fig.7(e)),however it is a minimum if k1p1>0 so that this solution is a dark dormion(Fig.7(f)).The contour lineis plotted in Fig.8(d),where h is between the peak value and valley value.Because it is too complicated to write,we do not give the figure and expressions of the end points,the tangent lines perpendicular to the y axis,and the width of the contour lines. Fig.9.The curve line is the contour line on the height of half amplitude.The two black points are the end points,and the two red lines are the tangent lines perpendicular to the y axis.Parameters:α=1,=0,k1=?3/4,p1=1,t=0.(a)The contour line is Eq.(24),and the tangent lines are Eq.(25);(b)The contour line is Eq.(27),and the tangent lines are Eq.(28). We can obtain the second order Jacobi-type solution as follows: If we choose φ(y)=sn(y,3/10),it shows obviously a periodic structure in Fig.10(a).If we choose φ(y)=cn(y,1),it is dormion-type-I solution as shown in Fig.10(b).It has two maximum values and two minimum values on(x,y)plane.If we choose φ(y)=sn(y,1),it is a dormion-type-II solution.Its extreme values have three scenarios:letting k1p1>0 and k2p2>0 it is a dark form as shown in Fig.10(c),which has only two minimum values;letting k1p1/k2p2<0 it is a mixed form as shown in Fig.10(d),which has a minimum value and a maximum value;letting k1p1<0 and k2p2<0 we can get a bright solution as shown in Fig.10(e),which has only two maximum values. Fig.11. with α=1,t=0,p1=2/3,p2=3/5,p3=1/2. (a)Periodic solution:φ(y)=sn(y,3/10),k1=3/4,k2=1/2,k3=1/3,=?10,(b)Dormion-type-I soliton:φ(y)=cn(y,1),k1=3/4,k2=1/2,k3=1/3,;(c)Dark dormion-type-II soliton:φ(y)=sn(y,1),k1=3/4,k2=1/2,k3=1/3,;(d)Mixed dormion-type-III soliton:φ(y)=sn(y,1/2)/(y2+1),k1=3/4,k2=?1/2,k3=?1/3, By setting in Eqs.(9),(10),and(11),we can obtain the third-order Jacobi-type solutionand,where By the same way used above,we obtain more kinds of solutions through choosing different function φ(y)and ηi.Part of the situation is shown in Fig.11. In this paper,we obtained the bilinear form and the nsoliton solution of an eSWW equation by using Hirota method.The solution v[1]is dark when k1p1>0 while it is bright when k1p1<0.The solution r[1]is always a dark soliton.By using complexification method,breathers and hybrid solutions are constructed which are all travelling waves. More importantly,we obtained Jacobi-type solution associated with a certain given φ(y)which is an arbitrary real continuous function appeared in f of bilinear form.It is selected by using Jacobi elliptic functions,and the character of the solutions depends on its specific choice.We stress on the case N=1.The first-order Jacobi-type solutionparallelly travels along the x axis with the velocityon(x,y)-plane. (i)When φ(y)=sn(y,3/10),equation(22)is a periodic solution and the period depends on φ(y). (ii)When φ(y)=cn(y,1),we obtained a dormion-type-I solutions. Equation(23)has one maximum(3/4)k1p1located atarccoshand one minimum ?(3/4)k1p1located at?arccosh2). The width of the contour line on the hight h=(3/8)k1p1(the half amplitude)is (iii)When φ(y)=sn(y,1),we obtained a dormion-type-II solution equation(26)which has only one extreme value?(3/2)k1p1located atof(x,y)plane.The width of the contour line on the hight h=?(3/4)k1p1(the half amplitude)is (iv)When φ(y)=sn(y,1/2)/(1+y2),we obtained a dormion-type-III solution(21)which shows very strong doubly localized feature on(x,y)plane,and the profile of this solution is invariant during the propagation along y=0. Moreover,we gave several figures of the mixture of periodic and localized solutions.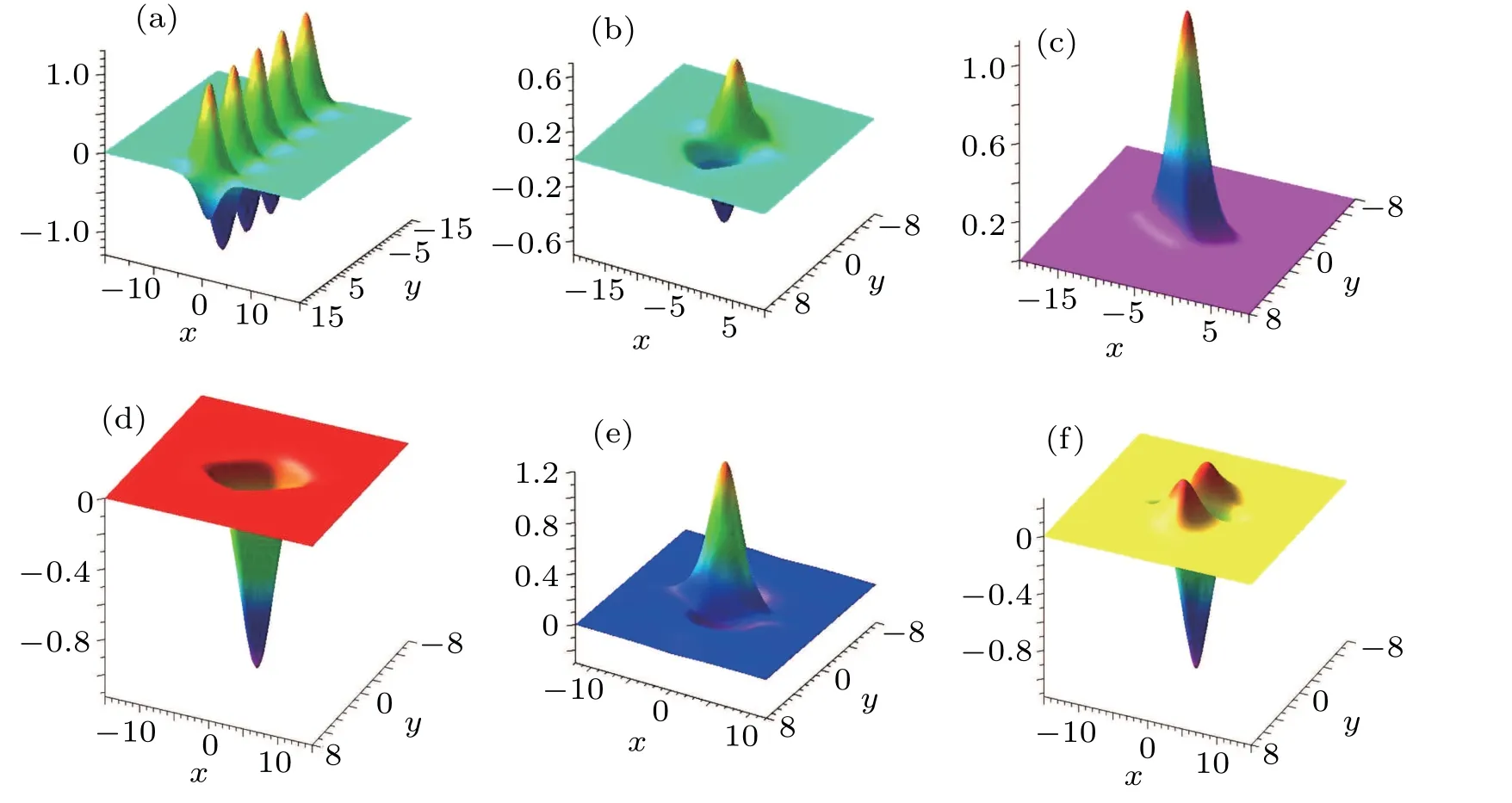
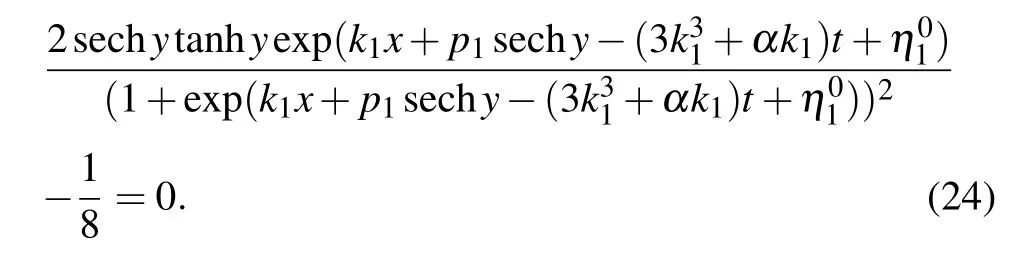
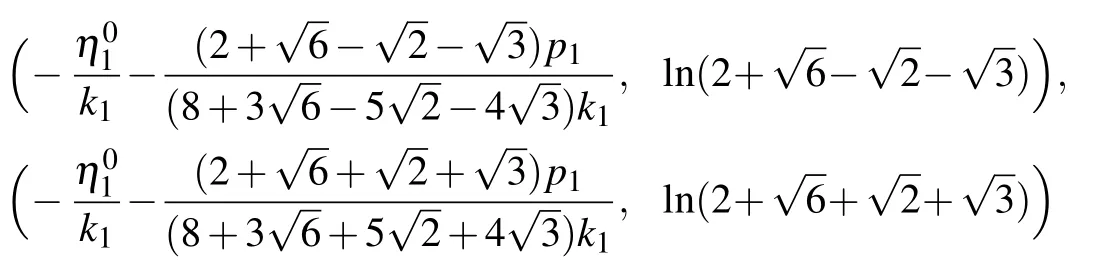
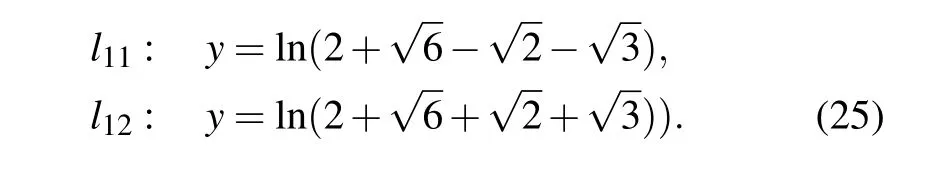
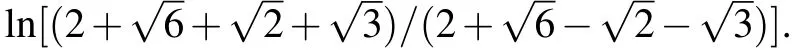
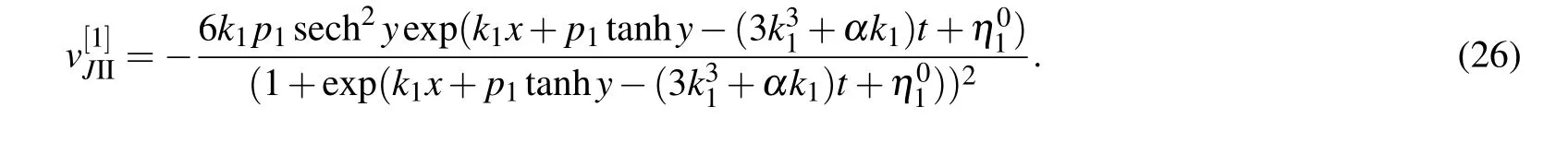
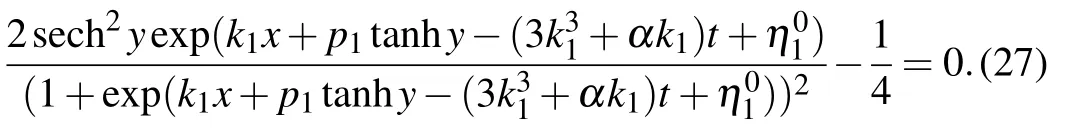
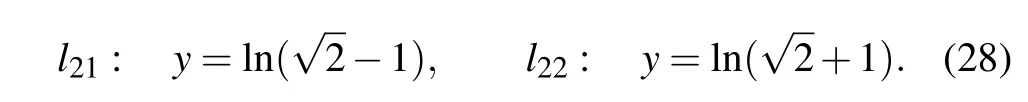
3.2.Case 2:N=2
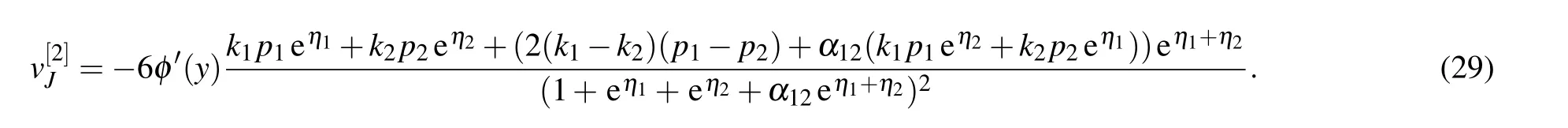
3.3.Case 3:N=3

4.Summary

