Thermodynamics Properties of Confined Particles on Noncommutative Plane
Rachid Hou?caand Ahmed JellalEquipe de Physique Thorique et Hautes Energies,Facult des Sciences,Universit Ibn Zohr,P.O.Box 806,Agadir,Maroc
2Saudi Center for Theoretical Physics,Dhahran,Saudi Arabia
3Laboratory of Theoretical Physics,Faculty of Sciences,Choua?b Doukkali University,P.O.Box 20,24000 El Jadida,Morocco
(Received March 30,2019;revised manuscript received April 30,2019)
AbstractWe consider a system of N particles living on the noncommutative plane in the presence of a confining potential and study its thermodynamics properties.Indeed,after calculating the partition function,we determine the corresponding internal energy and heat capacity where different corrections are obtained.In analogy with the magnetic field case,we define an effective magnetization and study its susceptibility in terms of the noncommutative parameter θ.By introducing the chemical potential,we investigate the Bose-Einstein condensation for the present system.Different limiting cases related to the temperature and θ will be analyzed as well as some numerical illustration will be presented.
Key words:confining potential,noncommutative plane,thermodynamics properties,Bose-Einstein condensation
1 Introduction
The noncommutative geometry[1]remains among the strongest mathematical tools that can be used to solve different problems in modern physics.For instance,interesting results were reported for the quantum Hall effect[2]due either to the charge current[3]or spin current.[4?7]To remember,the noncommutative geometry already exits and is found its application in the fractional quantum Hall effect when the lowest Landau Level(LLL)is partially filled.It happened that in LLL,the potential energy is strong enough than kinetic energy and therefore the particles are glue in the fundamental level.As a consequence of this drastic reduction of the degrees of freedom,the two space coordinates become noncommuting[8]and satisfy the commutation relations analogue to those verifying by the position and the momentum in quantum mechanics.Also various aspects of the quantum mechanics have been investigated in different ways in order to explore the role of the noncommutative parameter in the physical observables.[9?13]
On the other hand,the noncommutative geometry has been employed to study different thermodynamics systems,one may see Refs.[14–16].The main outcome is that modification of different thermodynamics quantities were obtained in terms of the noncommutative parameter θ.The Bose-Einstein condensation(BEC)was also taken part of the application of the noncommutative geometry.In fact,the thermodynamic properties of BEC in the context of the quantum field theory with noncommutative target space was studied in Ref.[17].Initially BEC was theoretically predicted in 1924[18]and experimentally observed in 1995,[19]which is a purely quantum phenomenon.Most quantum effects occur either in the microscopic domain or at low temperatures.This condensation does not deviate from the rule since it appears when one approaches the absolute zero K.
Motivated by different works mentioned above,we consider a system of N particles living on the noncommutative plane and study its thermodynamics properties.In the first stage we write the corresponding Hamiltonian using the star product definition to end up with the solutions of the energy spectrum in terms of the noncommutative parameter θ.These will be used to explicitly determine the partition function and therefore derive the related thermodynamics quantities such the internal energy and heat capacity.In analogy with the magnetic field case,we discuss the possibility of having an effective magnetization with respect to θ and also getting the associated susceptibility.We also study BEC for the present system and underline its main behavior.Finally interesting limiting cases in terms of the involved parameters will be discussed and some plots will be presented to give different illustrations of our results.
The present paper is organized as follows.In Sec.2,we consider one particle in 2-dimensional subjected to a harmonic potential and use the noncommuting coordinates to end up with its noncommutative version.This process allows us to end up with a Hamiltonian system similar to that of one particle living on the plane in the presence of an external magnetic field.The corresponding energy spectrum will be given by using the algebraic approach through the annihilation and creation operators.In Sec.3,we determine the partition function to end up with different thermodynamic quantities and study some limiting cases related to the temperature as well as θ.In Sec.4,we define an effective magnetization with respect to θ and study its susceptibility by considering some limits.We analyze BEC for the present system in Sec.5 and study its particular cases.We conclude our work in the final section.
2 Solution of the Energy Spectrum
We consider a particle of mass m living on the plane(x,y)and subjected to a confining potential.It is described by the Hamiltonian
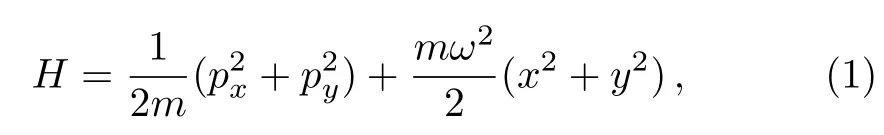
where ω is the frequency.To study the thermodynamics properties of a system of N particles described by Eq.(1)on the noncommutative plane,we have to settle all ingredients needed to tackle our issues,which can be achieved by adopting a method similar to that used in Ref.[3].Indeed,in addition the standard canonical quantization between the coordinate and momentum operators,we introduce an algebra governed by the noncommutating coordinates

where θ is a real free parameter and has length square of dimension.Without loss of generality,hereafter we assume that θ>0 is fulfilled.From the above consideration,we can now derive the noncommutative version of the Hamiltonian(1)as
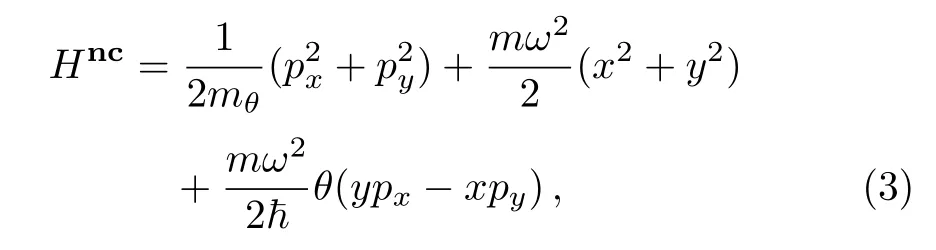
with the effective mass
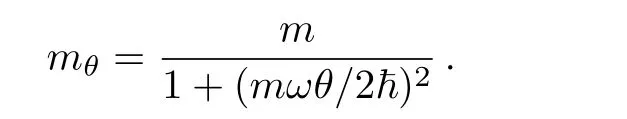
At this level,we have some comments in order.Indeed,one can use the mass mθto of fer a way of measurement of the noncommutative parameter θ and therefore give experiment evidence of the space deformation.We notice that Hncis actually sharing some common features with the Hamiltonian describing one particle moving in plane and subjected to an perpendicular magnetic field B in the symmetric gauge.This comparison allows to establish a relation between θ and B,which can also be implemented to give another laboratory test of the deformation.
The noncommutative Hamiltonian(3)can be diagonalized algebraically by introducing the annihilation and creation operators
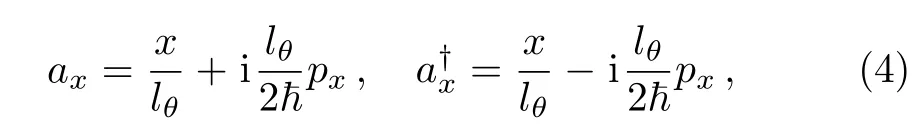
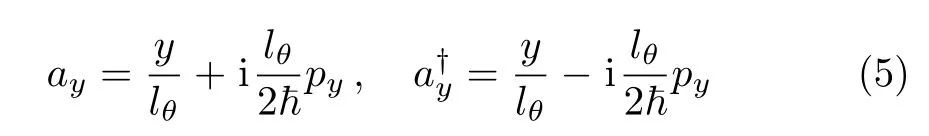
satisfying the commutation relations
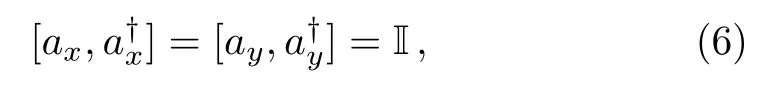

verifying

and all other commutators are vanishing.Now combining all and using the operator numbers Nd=and Ng=,to write the Hamiltonian(3)as

which has the following solution of the energy spectrum
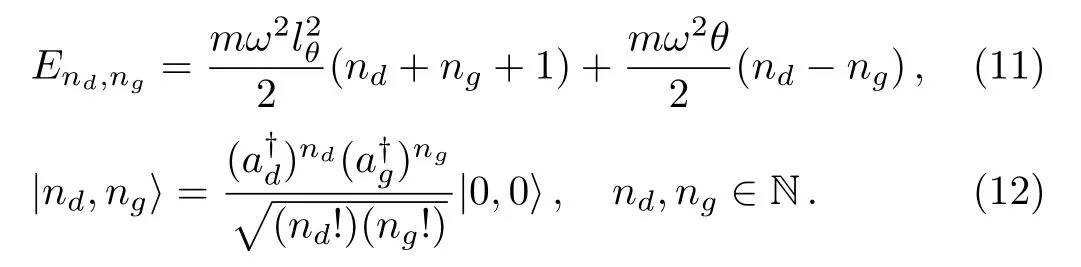
It is interesting to notice that when the condition ωθ? 1 is fulfilled,the eigenvalues(11)reduce to the following
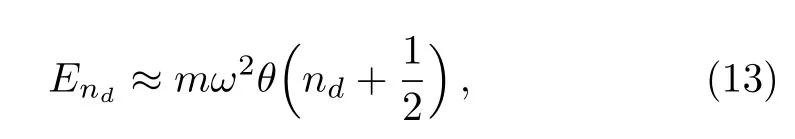
which can be compared to the Landau level energies
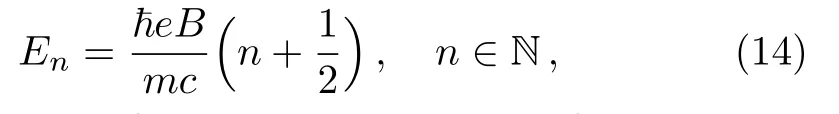
that are solutions of the energy spectrum of one particle of mass m submitted to a perpendicular magnetic field.Then one can see that the relation End=Enis satisfied if we require

showing another way to measure the parameter θ in terms of the field B.We conclude that particles moving in a noncommutative plane can be envisaged as the usual motion of particles experiencing an effective magnetic field(15).In the next we will show how the above results can be used to investigate the main thermodynamics features of the present system.
3 Thermodynamics Quantities
As usual to determine different thermodynamics quantities,one has to start from the corresponding partition function

where β=1/kBT,kBthe Boltzmann constant,T the temperature and H is the Hamiltonian for a given system.
In terms of the above solution of the energy spectrum,Eq.(16)takes the form
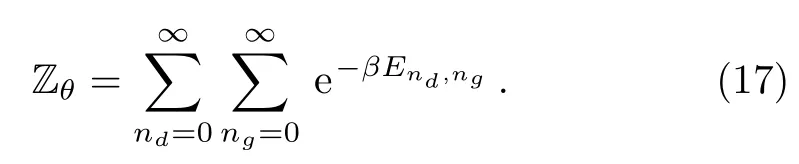
To proceed further,let us rearrange the eigenvalues(11)as

by involving two parameters θ-dependent ?θ=mω2l2θ/2 and φθ=mω2θ/2.After straightforward calculation,we end up with the partition function for one particle
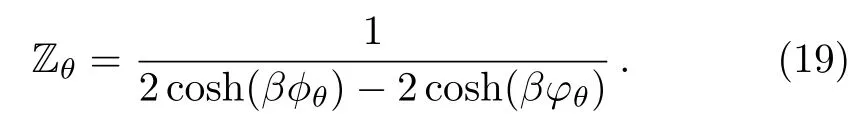
It is clearly seen that for a system of N non-interacting particles,the total partition function is simply given by the product

which is actually depending on two parameters of our theory,temperature and noncommutative parameter.These will be used to study different limiting cases and therefore characterize the present system behavior.
Having obtained all ingredients needed,now we can determine different thermodynamics quantities related to the present system.Indeed,as far as the internal energy is concerned we start from the usual definition
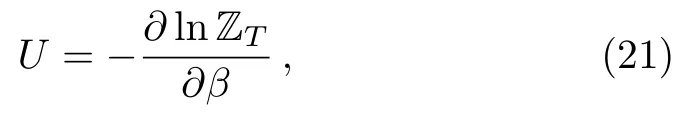
to end up with the form
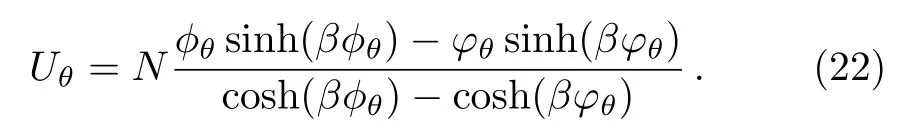
We notice that there are two limiting cases that can be considered with respect to the noncommutative parameter θ.Indeed,firstly by switching off θ,we recover the standard form

and secondly,by requiring the limit,we end up with a linear behavior in terms of temperature

Note that,Eq.(24)is independent of the noncommutative parameter,a result that will be confirmed in the next analysis.
To characterize thermally the present system let us consider the heat capacity.Then from the above result and using the relation

one gets the following heat capacity
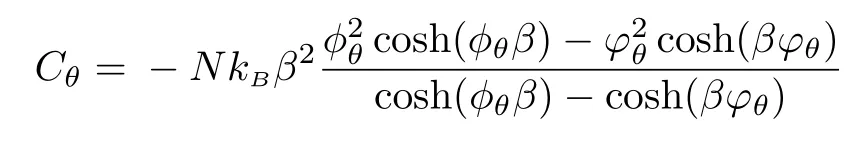
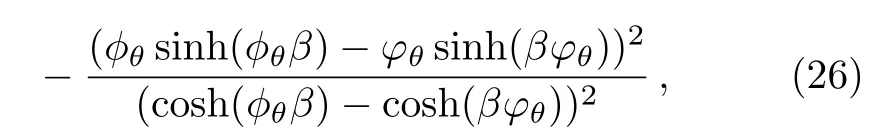
which can be studied according to different limits taken by the parameters θ and β.Indeed,for θ=0,we recover the usual result

and at high temperature limit,it reduces to the quantity

which is showing an extra term removed from the standard result 2NkBthat can be interpreted as a quantum correction to the heat capacity.This result might be interesting in dealing with the vibration of atoms in solid state physics or other systems in order to give a laboratory test of the noncommutative parameter.However,at low temperature we show that Cθvanishes that is in agreement with the standard result.
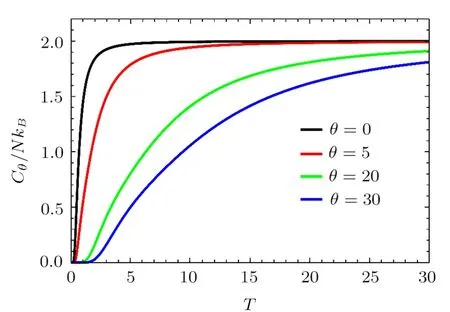
Fig.1 (Color online)The heat capacity versus the temperature T for four values of the noncommutative parameter θ=0,5,20,30,with the unit systems kB==ω=m=1.
Figure 1 presents the heat capacity Cθas a function of the temperature for four values of the noncommutative parameter θ=0,5,20,30.We observe that Cθincreases quickly toward a constant value in terms of T when θ is small.However when θ becomes large and even T increases,the heat capacity remains null,which causes a change of its origin.This behavior tells us that there a threshold value Ts(θ)of the temperature,which is θ dependent.Thus,we conclude that if T
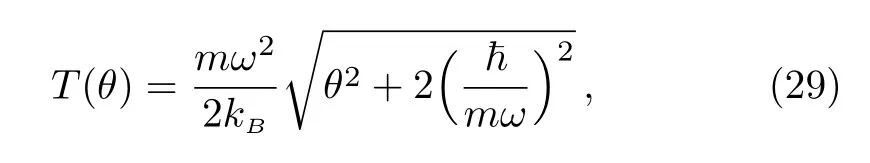
which can be used to give a measurement of the noncommutative parameter through the temperature variation and therefore argue the validity of introducing the noncommutating coordinates in the present system.
To accomplish such numerical analysis of the heat capacity Cθ,in Fig.2 we plot Cθin terms of the noncommutative parameter θ for different values of temperature T=100 K,200 K,300 K,400 K.It is clearly seen that Cθdecreases rapidly for some values of the temperature but such behavior changes once T increases giving rise different results.Thus,we conclude that the heat capacity can be controlled by changing θ together with the temperature.
4 Effective Magnetization
Recall that the present study does not include an external magnetic field but we can still talk about magnetization since θ is a free parameter.Then in analogy,we can define an effective magnetization in the same as for the case of a magnetic field and write
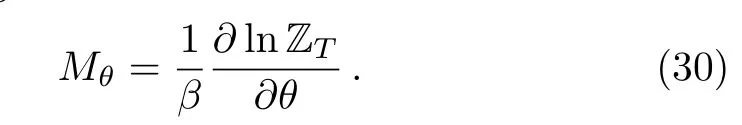
After calculation,we end up with

which is depending on θ as well as the temperature and therefore one can study some limiting cases to underline its behavior.Indeed,at low temperaturebecomes
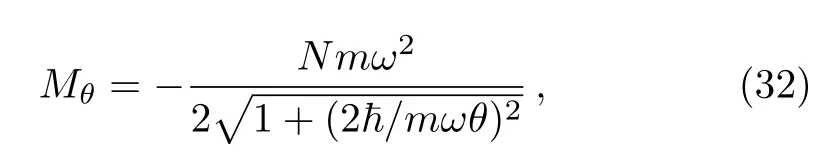
and at high temperature(β ?→ 0),we obtain a linear dependence in terms of θ
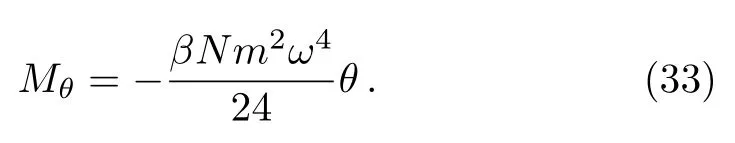
In Fig.3,we plot the effective magnetization versus the noncommutative parameter θ for different values of the temperature T.A very important point is that when the parameter θ is weak for high or low temperature,Mθvaries in a linear way.However for the case when θ is strong in low temperature Mθbecomes constant.This tells us that one may use such magnetization to measure the noncommutative parameter.
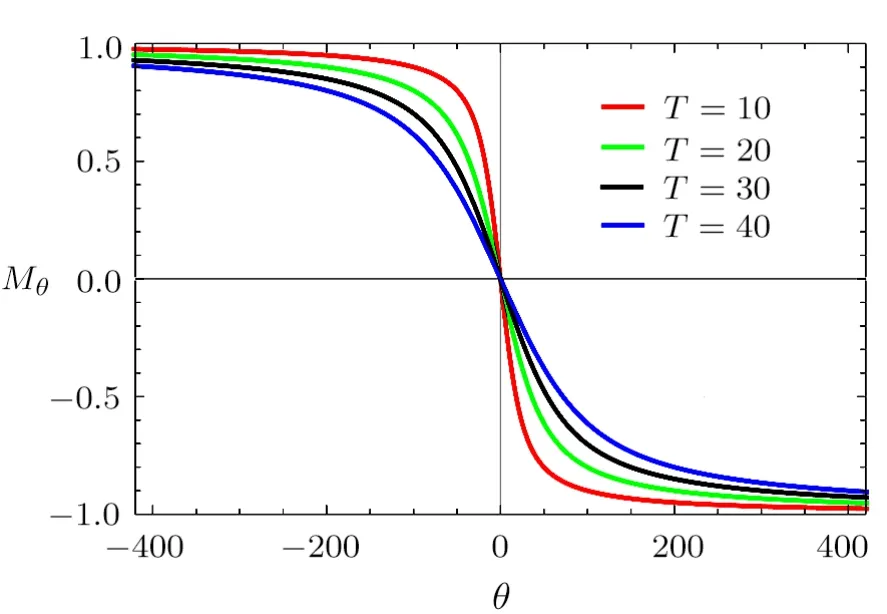
Fig.3(Color online)The effective magnetization Mθin terms of the noncommutative parameter θ for different values of the temperature T=10 K,20 K,30 K,40 K,with the unit systems kB==ω=m=1.
At this level,we can also introduce the effective susceptibility by adopting that corresponding to the magnetic field and thus have

At high temperature β ?→ 0,it can be approximated as
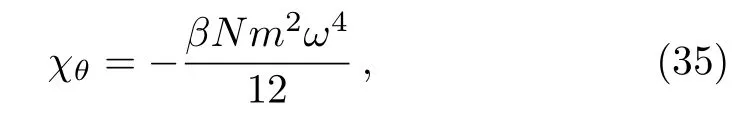
which is similar to the well-known Curie law C/T where the Curie constant can be fixed as C= ?Nm2ω4/12kB.It is clearly seen that from Eq.(35),the present system behaves like a diamagnetism and also like a superconductor if we require

These show that our results are general and can be tuned on to give different interpretations of the present system.On the other hand,one can use them to give a laboratory test of the noncommutative parameter.
5 Bose-Einstein Condensation
Let us investigate the relation between the corresponding Bose-Einstein condensation and the noncommutative parameter θ.For this we start by introducing the quantities
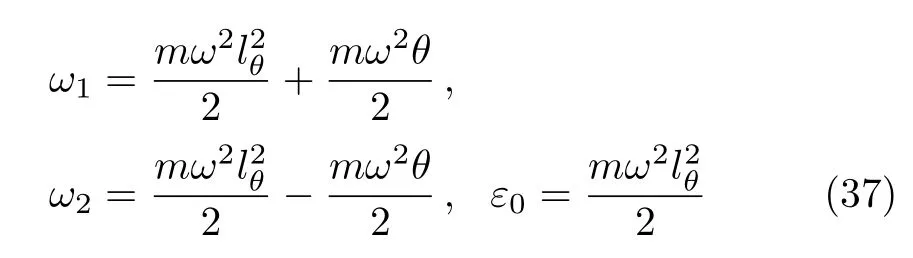
to rewrite the single-particle energy as
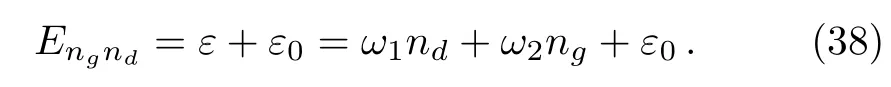
Unlike the case of fermions,any number of bosons may be placed in a particular micro-state and when the temperature of the system is null,all bosons must be in the ground-state energy ε0.Such number of bosons,that are not in the ground-state ε0,is given by
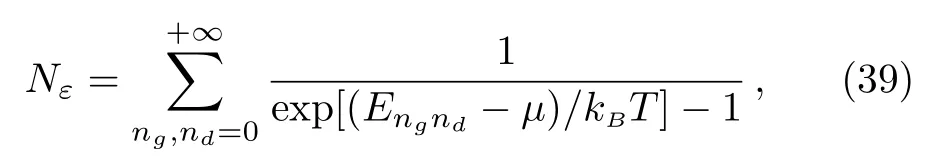
where μ is the chemical potential.Then immediately,we derive the number of bosons in the ground-state ε0
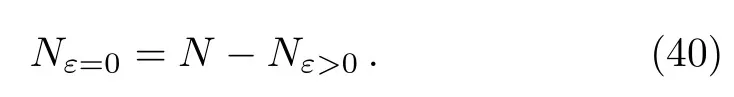
Note that,when T is high we have Nε=0? Nε>0,but at T=0 this is no longer the case because all particles are in the corresponding micro-state=0 and therefore we can write

Now we adopt a procedure similar to that applied in Ref.[20–21]in order to determine the proper density of states ρ(ε).This latter can be obtained from the number ν(ε)of states for which ε= ω1nd+ ω2ngis less than or equal to a given energy.To describe the Bose-Einstein condensation we restrict our self to the case where θ is small and therefore we can make an expansion to write a new frequency ? = ω1ω2and the ground-state energy as

which allow to end up with the desired density ρ(ε)
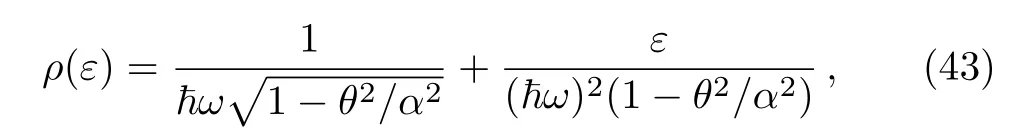
where we have defined the parameter α =2/mω that has to fulfill the condition α > θ.To go further,we replace ω1nd+ω2ngby a continuous variable ε and consider(43)to convert the summation over the quantum numbers nd,ngon integration over ε.Doing this process to obtain

which can be written in terms of the fugacity zθ=exp[(μ ? ε0)/kBT]as

or equivalently
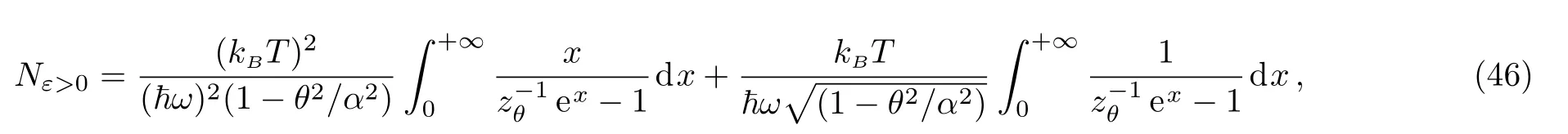
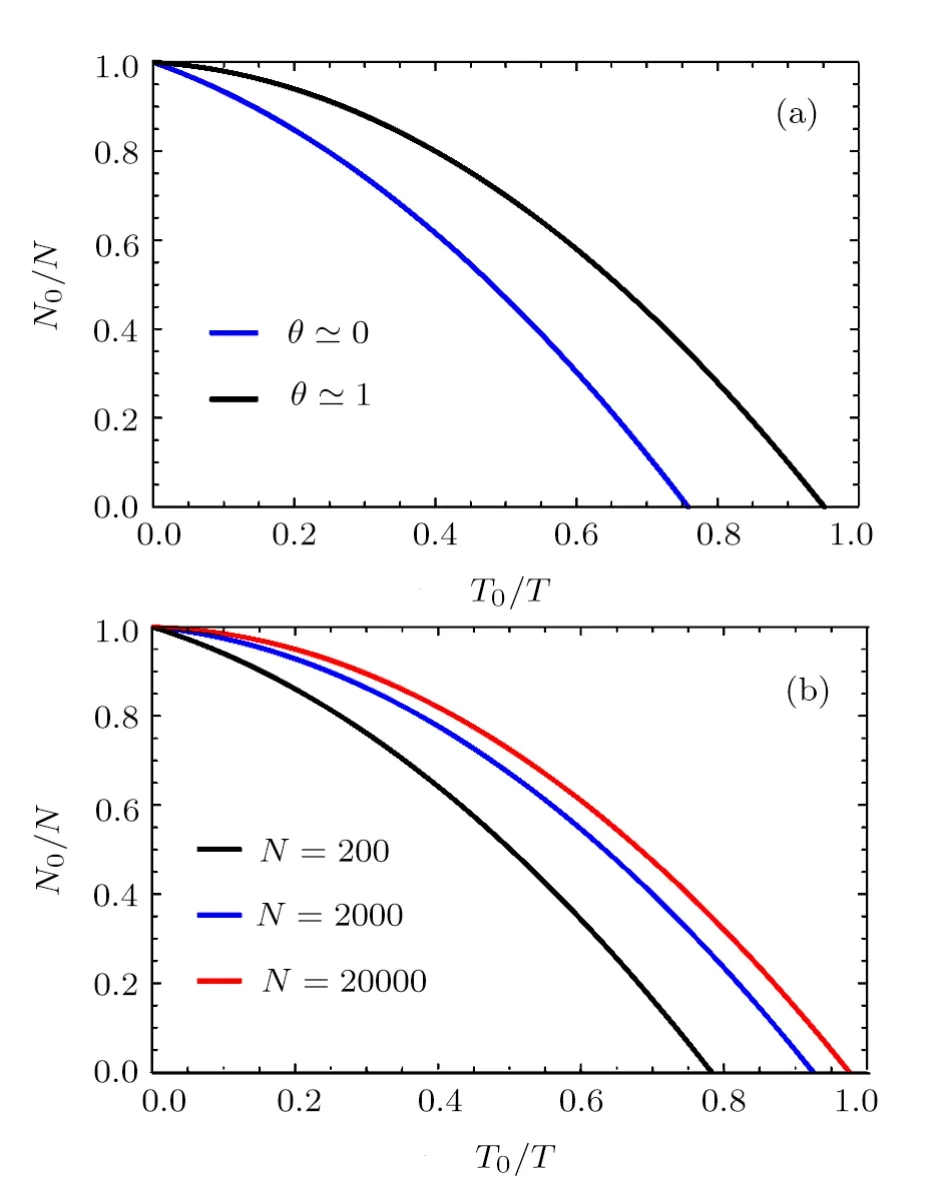
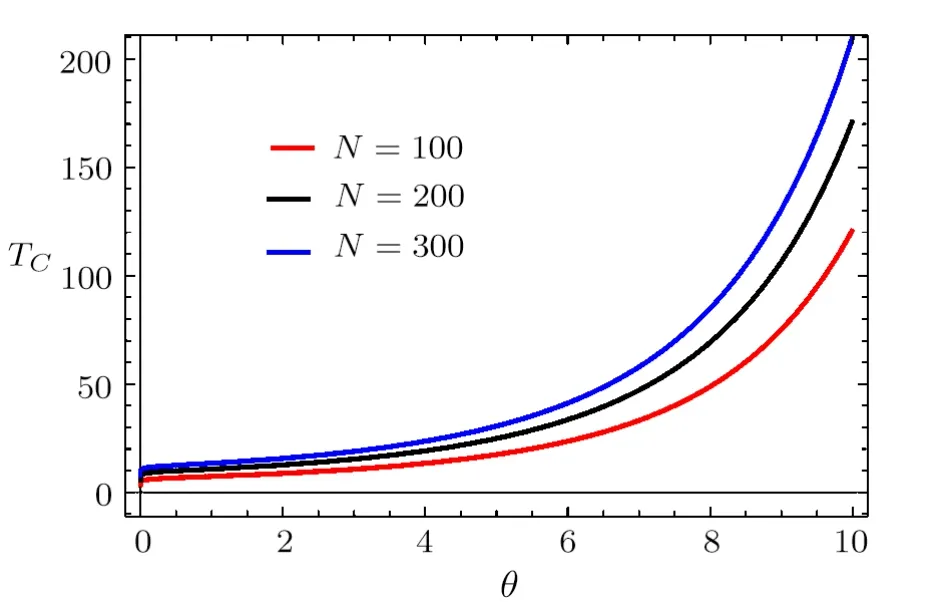
after making the change of variable x=ε/kBT.We show that both of integrals converge only when the fugacity is in the interval 0 With this,we can now integrate Eq.(46)to get where Li is the polylogarithm function.Recall that the Bose temperature TCis that for which Nε>0=N and then we have Now if the number of particles is very large,then the Bose-Einstein condensation occurs at the temperature Using Eqs.(40)and(50)to obtain the ratio which is actually θ-dependent due to the fugacityand then we can tun on such parameter to extract more information about the system behavior.For this we will analyse two interesting cases:commutative θ ? 0 and noncommutative θ? 1.Indeed,in Fig.4(a)we plot the number ratio N0/N versus the temperature ratio T/T0for θ? 0,1 and N=200.Figure 4(b)presents the same quantities but with θ?0 and tree values of particle numbers N=200,2000,20000.The shape of the Bose-Einstein condensation becomes spherical by decreasing either θ or the number of particles N,which are two parameters governing the ellipticity of the shape of the Bose-Einstein condensation.These are interesting remarks because in the physics we know that the elliptical shape is a consequence of the precise geometry of the trap in which the super fluid is maintained.Thus one can modify such shape by changing the magnetic field that creates this trap.Then in our study we can do the same job by fixing the noncommutative parameter as a magnetic field and then modify the shape of the Bose-Einstein condensation.One way to do such job is to use the relation(15)established before between θ and magnetic field B. Fig.4 (Color online)The number ratio N0/N versus the temperature ratio T/T0.(a)For commutative θ? 0 and noncommutative θ1 with N=200.(b)For θ 0 and tree different values of number of particles N =200,2000,20000,with the unit systems kB==ω=m=μ=1. Let us look for the relation between the noncommutative parameter and the condensation temperature TCto underline the behavior of the present system.This can be done by considering Eq.(48)to show that such relation is given by Figure 5 shows that the temperature of condensation is strongly depending on the noncommutative parameter θ together with the number of particles N.We observe that when θ is close to zero Tcremains almost constant but when θ increases to move away from zero Tcincrease rapidly.On the other hand,Tctends to zero when N becomes of the order of 100 but if N is of the order of 300,Tctends to a non-null value.For small values of θ,TCremains almost constant even if N changes a result that is known for the low interaction fluids.However when θ becomes large,there is a shift between different curves in Fig.5,which also a result known for fluids with strong interactions.These results tell us that the noncommutative parameter can be tuned on to play the role of an interacting force. Fig.5(Color online)The condensation temperature TC versus the noncommutative parameter θ for tree values of number of particles N=100,200,300,with the unit systems kB==ω=m=μ=1. We have studied the thermodynamic properties and analyzed the Bose-Einstein condensation for a system of N particle living on the noncommutative plane.After building the noncommutative Hamiltonian via star product definition and getting the solution of the energy spectrum,we have determined the partition function Zθin terms of the noncommutative parameter θ.This was used to derive the corresponding internal energy and therefore the heat capacity. Subsequently,we have defined an effective magnetization in similar way to that corresponding to the magnetic field.It was noticed that when the parameter θ is very low for high or low temperature regimes,the effective magnetization varies in a linear way.On the other hand,by evaluating the associated susceptibility,we have obtained a negative expression at high temperature,which showing similarity with the Curie law for a magnetic system.Finally,we have shown that to get the Bose-Einstein condensation in the present system,one has to fix the noncommutative parameter θ in a well-defined interval.This was used to establish an interesting relation between the condensation temperature and θ. The generous support provided by the Saudi Center for Theoretical Physics(SCTP)is highly appreciated by all authors.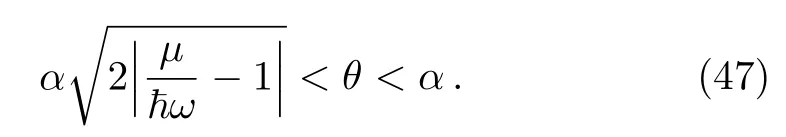

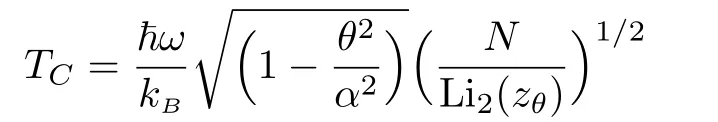


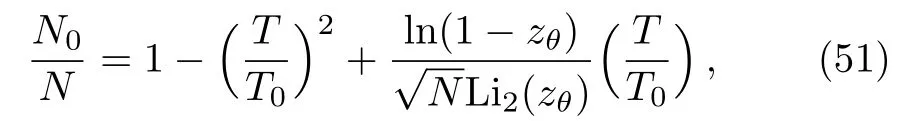

6 Conclusion
Acknowledgments
 Communications in Theoretical Physics2019年9期
Communications in Theoretical Physics2019年9期
- Communications in Theoretical Physics的其它文章
- Dynamical Analysis and Exact Solutions of a New(2+1)-Dimensional Generalized Boussinesq Model Equation for Nonlinear Rossby Waves?
- DKP Equation with Energy Dependent Potentials
- Effective Correlation of Two Holes in a Semimagnetic Quantum Well Wire:Influence of Shape of Confining Potential on Coulomb Interaction?
- Scale-Invariance Exists in the Series of Character Intervals in the Four Great Chinese Novels?
- A Statistical Mechanical Analysis on the Bound State Solution of an Energy-Dependent Deformed Hulthn Potential Energy?
- Study on the Amyloid Aβ42 with Accelerated Molecular Dynamics Simulations?
