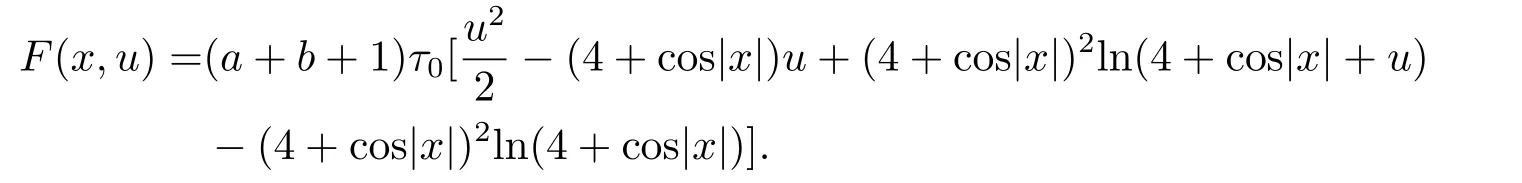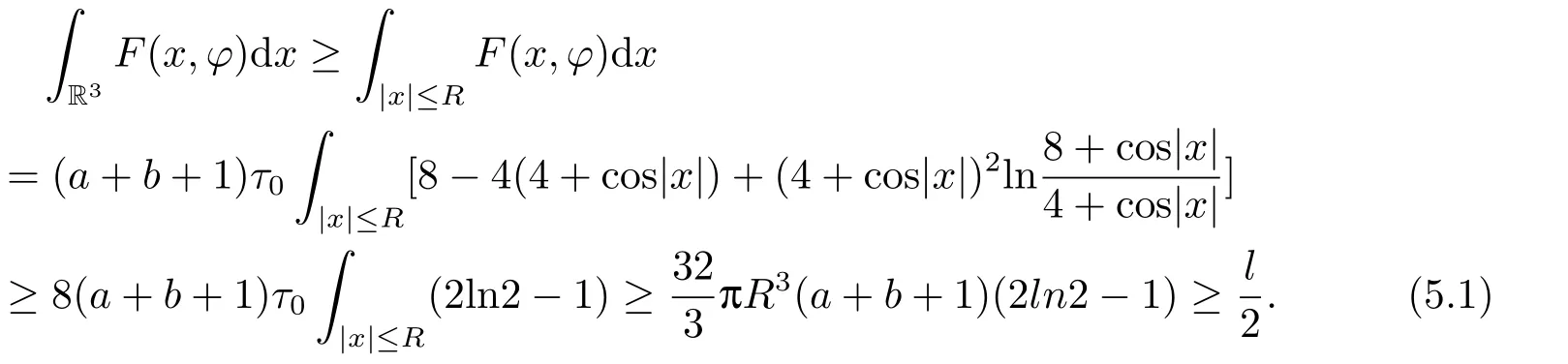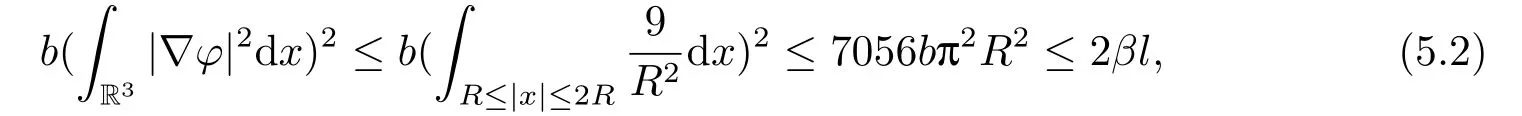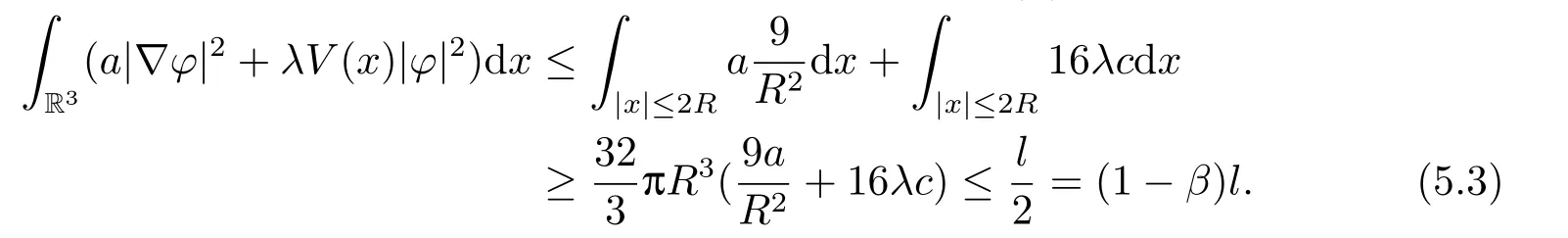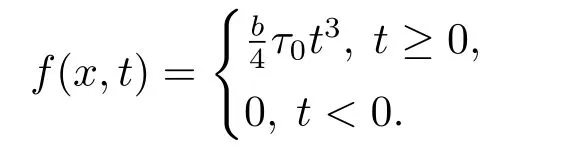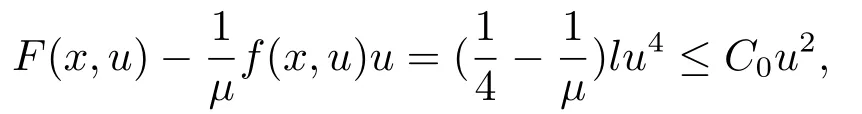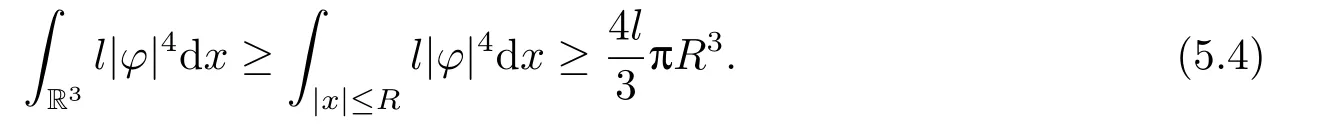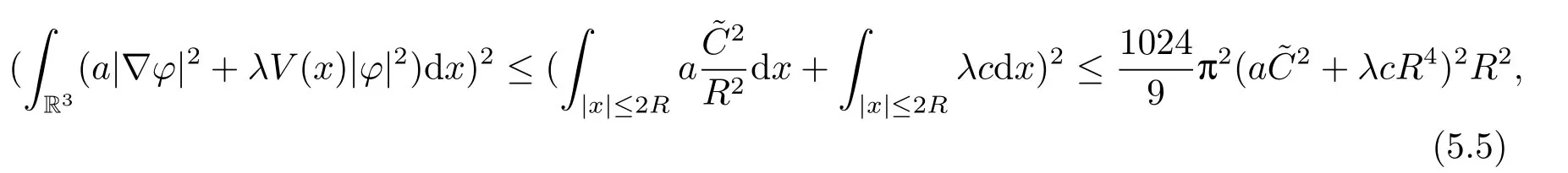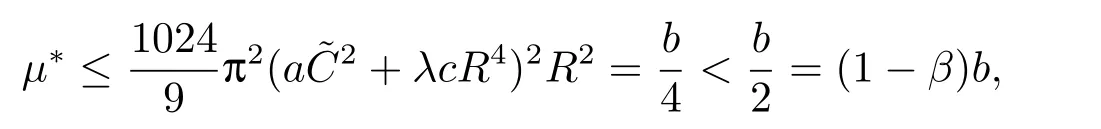Positive Solutions for Kirchhoff-Type Equations with an Asymptotically Nonlinearity
XU Liping(許麗萍),CHEN Haibo(陳海波)
( 1.Department of Mathematics and Statistics,Henan University of Science and Technology,Luoyang 471000,China;2.School of Mathematics and Statistics,Central South University,Changsha 410075,China)
Abstract: We focus on a class of nonlinear Kirchhoff-type equation.The nonlinear function f(x,u) is either asymptotically linear or asymptotically nonlinear with respect to u at infinity.Under certain conditions on the potential function V(x) and the nonlinear term f(x,u),the existence of positive solutions is obtained without using the compactness of embedding of the working space.
Key words: Kirchhoff-type equation;Asymptotically nonlinear;Variational method;Positive solution
1.Introduction and main results
In this paper,we study the existence of positive solutions for the following nonlinear Kirchhoff-type problem:
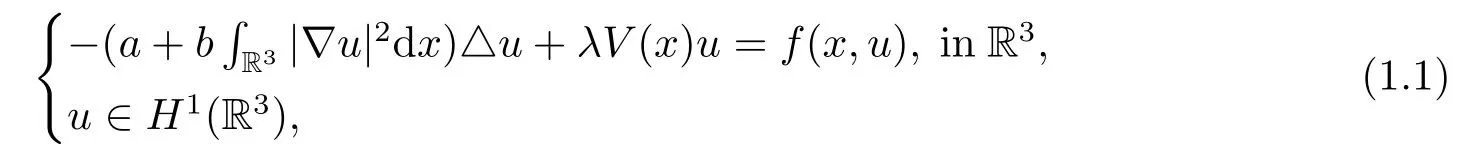
wherea,bare positive constants andλ≥1 is a parameter.We assume that the functionsV(x) andf(x,s) satisfy the following hypotheses.
(v1)V(x)∈C(R3,R) satisfiesV(x)≥0 on R3;
(v2) There existsd>0 such that the set{x∈R3:V(x)≤d} has finite measure;
(f1)f(x,s)∈C(R,R+),f(x,s)≡0 for alls<0 and
(f2)≤lwithl∈(0,+∞);
(A1) There exists a constantβ∈(0,1) such that
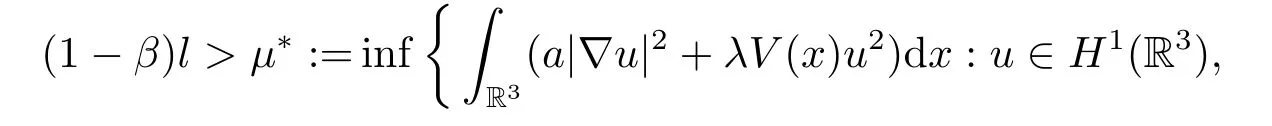
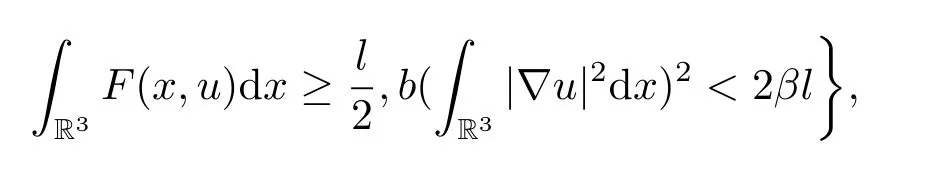
whereF(x,u):=f(x,t)dt;
(f3)
(f4) There exist 0 for alls≥0 andx∈R3,whereη2is defined by Lemma 2.1; (A2) There exists a constantβ∈(0,1) such that The problem (1.1) is related to the stationary analogue of the following equation proposed by Kirchhoff in 1883 (see [1]) to describe the transversal oscillations of a stretched string,particularly,taking into account the subsequent change in string length produced by transverse vibrations.In (1.2),udenotes the displacement,f(x,u) the external force,andbthe initial tension whileais related to the intrinsic properties of the string (such as Young,s modulus). Such a class of problem is often referred to as being nonlocal because of the presence of the integral term∫?|?u|2?udx,which means that(1.2)is no longer a pointwise identity.This makes the study of such a class of problem particularly difficulties and interesting.Similar nonlocal problems also model several physical and biological systems,whereudescribes a process which depends on the average of itself,for example,the population density(see [2-3])and the references therein.Recently,assuming that the potentialV(x) satisfies: (v′1)V(x)∈C(R3,R) satisfieswhereb1>0 is a constant. (v′2)meas{x∈R3:V(x)≤M}<∞,for anyM >0,where meas(.)denotes the Lebesgue measure in R3.The authors[4?5]obtained the existence and multiplicity of nontrivial solutions of (1.1) withλ=1.The hypotheses (v′1) and (v′2) were used in [6]to guarantee the compact embedding of the working space (see [7,Lemma 3.4]).Obviously,(v2) is weaker than (v′2),which cannot guarantee the compactness of the embedding.This situation becomes more delicate.Recently,some authors in [8-11]dealt with this cases.For example,LIANG and ZHANG[8]investigated the existence of solutions of Kirchhoff type problems with critical nonlinearity.Iff(x,u) in (1.1) is superlinear at infinity,the authors[9]proved two existence theorems of nontrivial weak solutions and a sequence of high energy weak solutions for (1.1).Particularly,SUN and WU[10]also studied the existence of ground state solutions.More recently,XU and CHEN[11]also investigated the existence and multiplicity results iff(x,u)is either sublinear or superlinear at infinity.But to the author,s knowledge,there are few works on the existence of positive solutions for(1.1),whenf(x,u)is asymptotically linear andV(x)satisfies more general conditions. The main results are the following theorems. Theorem 1.1Let (v1)-(v2),(f1)-(f2) and (A1) hold,then the problem (1.1) possesses a positive solution for largeλ>0. Remark 1.1Condition like (f1)-(f2) and (A1) on the nonlinear termfwas employed in [11-13].For example,ifV(x)=1,SUN et al.[12]obtained the ground state solutions of Schr?dinger-Poisson equations.Whenλ=1,using similar assumptions on the nonlinearityf,LIU et al.[13]proved the existence of positive solution of (1.1),assumingV(x) satisfying(v1) andTheorem 1.1 extends the main results in [12]to the Kirchhoff-type equations. Theorem 1.2Let (v1)-(v2),(f1),(f3)-(f4) and (A2) hold,then for largeλ >0 the problem (1.1) possesses a positive solution. Remark 1.2Under the conditions(f1),(f3)and(f′4):is nondecreasing foru>0,DING et al.[14]studied the existence of positive solutions for a class of nonhomogeneous Schr?dinger-Poisson system.Note that (f′4) is stronger than (f4).Theorem 1.2 also extends the main results in [14]to the Kirchhoff-type equations.To the best of our knowledge,little has been done for Kirchhoff-type equations with asymptotically linear or asymptotically nonlinear under relaxed assumptions (v1)-(v2). The rest of the paper is given as follows:in Section 2,we present some preliminary results.In Section 3 and 4,we give the proofs of Theorem 1.1 and 1.2,respectively.In the latter parts of this paper,we useC >0 to denote any positive constant. Let be equipped with the inner product and norm We also need the following inner product and norm SetEλ=(E,‖.‖λ),then we have the following lemma. Lemma 2.1Under assumptions (v1) and (v2),for 2≤r <2?,the embeddingEλLr(R3) is continuous.Hence,there isηr >0 (independent ofλ) such that where‖.‖rdenotes the usual norm onLr(R3). ProofThe proof is similar to that of Lemma 2.1 in [15],and is omitted here. It follows from (v1)-(v2) and (f1)-(f2) that the functionIλ:Eλ→R defined by is of classC1(Eλ,R),and for allu,v∈Eλ.Furthermore,the critical points ofIλare weak solutions of the problem(1.1).Thus,we only need to look for critical points ofIλonEλ.To find the critical points ofIλ,we use the following mountain pass theorem,which is a very useful tool in dealing with the asymptotically linear case. Lemma 2.2[15]LetEbe a real Banach space with its dual spaceE?and suppose thatI∈C1(E,R) satisfies for someν <η,ρ>0 ande∈Ewith‖e‖>ρ.Letc≥ηbe characterized by whereΓ={γ∈C([0,1],E):γ(0)=0,γ(1)=e} is the set of continuous paths joining 0 ande,then there exists{un}?Esuch that SetBR:={x∈R3:|x| Lemma 2.3Assume (v1) and (v2) hold.Then for anyε>0,there existsτε >0 andRε >0 such thatfor allu∈Eλandλ≥τε,where 2≤p<2?. ProofThe proof of this lemma is inspired by [18].For the convenience of the reader we sketch it here.For anyR>0 define Then For 2 Settingθ=and using the Gagliardo-Nirenberg inequality,we have According to (v2),we obtain that|B(R)|→0 asR→∞.Then,ifλandRare large enough,the term in brackets above will be arbitrarily small.This concludes the proof the Lemma 2.3. In this section,we give the proof of Theorem 1.1.In what follows,we give several lemmas which are useful to the proof of the main results. Lemma 3.1Assume(v1)-(v2),(f1)-(f2)and(A1)hold.Then the sequence{un}defined in (2.3) is bounded inEλ. ProofInspired by [17],we argue by contradiction and assume that‖un‖λ→∞asn→∞.Setωn=,then there is aω∈Eλsuch that In what follows,we will obtain a contradiction by ruling out the vanishing and nonvanishing of{ωn}. Assume that{ωn} is vanishing.Then,suppose that,for everyR>0, By (f1) and (f2),there existsC >0 such that uniformlyx∈R3.For any 0<ε<1,by Lemma 2.3,there exists aRε >0 such that Then it follows from (3.2)-(3.4) that By (2.3),one has Combining this with (3.5),we obtain which means a contradiction.Hence,non-vanishing must hold,that is,there existR,α >0 and bounded sequence{yn}?R3such that Using (3.1),we see thatω≠0.By (f2),one has It follows from Lemma 2.1 that there existsη22>lsuch that‖u‖2≤η2‖u‖λ.Then,by (2.1),(3.6) and (3.7),we obtain that Thus,by (2.3) and (3.6) which is a contradiction.This concludes the proof of Lemma 3.1. Lemma 3.2Under the assumptions (v1)-(v2),(f1)-(f2),any bounded cerami sequence ofIλdefined in (2.3) has a convergent subsequence inEλ. ProofLet{un} be a bounded sequence defined by (2.3).After a subsequence,we can assume thatun ?uinEλ.Setωn=un?u.By (f1) and (f2),for any 0<ε1 and therefore Since‖ωn‖λis uniformly bounded inEλandλ≥1,we may fix aε2>0 such that By Lemma 2.3,there existτε2>0 andRε2>0 such that Using the fact thatωn→0 in(R3) and (3.9),we have asn→∞.It follows from (2.3),(3.8) and (3.10) that which meansωn→0 inEλby the value ofε1.The proof of Lemma 3.2 is complete. Proof of Theorem 1.1The proof of this theorem is divided into three steps. Step 1 There existρ,η,m>0 such that inf{Iλ(u):u∈Ewith‖u‖λ=ρ}>η. Fix any 2 and then It follows from Lemma 2.1 that,for allu∈Eλ, Combining (2.1) with (3.11),one has Fix any 0<ε Step 2 There existsv?∈Ewith‖v?‖λ >ρsuch thatIλ(v?)<0. By (A1),in view of the definition ofμ?and (1?β)l>μ?,there existsv?∈Esuch that andμ?≤‖v?‖2λ <(1?β)l.Then,by (2.1),we obtain We chooseρ>0 small enough such that‖v?‖λ >ρ,and Step 2 is proved. Step 3Iλhas a nontrivial positive critical point inEλ. By Step 1,Step 2 and Lemma 2.2,we see that there is a Cerami sequence{un} ?Esatisfying(2.3).Thus,it follows from Lemma 3.1 and Lemma 3.2 that there exists a nontrivialu0∈Eλsuch thatI′λ(u0)=0.In what follows,we prove thatu0>0.By (f1)-(f2),we have whereu?0=max{?u0,0}.This shows thatu?0=0 andu0≥0.From the Harnacks inequality[19],we can infer thatu0>0 for allx∈R3.The nonzero critical point ofIλis the positive solution for the problem (1.1).The proof is completed. This section is devoted to the proof of Theorem 1.2.We consider the problem (1.1) with the case:asymptotically cubic case at infinity. Lemma 4.1Assume that (v1)-(v2) and (f4) hold,then the sequence{un} defined in(2.3) is bounded inEλ. ProofBy (f4) and Lemma 2.1,one has fornlarge enough.This implies that{un} is bounded inEλsince 0 Lemma 4.2Under assumptions (v1)-(v2),(f1),(f3) and (f4),any bounded cerami sequence ofIλdefined in (2.3) has a convergent subsequence inEλ. ProofPart of the proof is similar to Lemma 3.2.For the reader’s convenience,we sketch the proof here.Let{un}be a bounded sequence defined by(2.3).After a subsequence,we can assume thatunuinEλ.Setωn=un?u.By (f1) and (f3),for any 0<ε2 and therefore Since‖ωn‖λis uniformly bounded inEλandλ≥1,we may fix aε3>0 such that By Lemma 2.3 there existτε3>0 andRε3>0 such that Using the fact thatωn→0 inL4loc(RN) and (4.2),we have It follows from (2.3),(4.1) and (4.3)that which meansωn→0 inEλby the value ofε2.The proof of Lemma 4.2 is complete. Proof of Theorem 1.2The proof of this theorem is divided into three steps. Step 1 There existρ,η,m>0 such that inf{Iλ(u):u∈Ewith‖u‖λ=ρ}>η.For anyε>0,it follows from (f1) and (f3) that there existsCε >0 such that and Together (2.1) with Lemma 2.1,one has Fix any 0<ε By (A2),In view of the definition ofμ?and (1?β)b>μ?,there exists∈Esuch thatThen,by (2.1) and Fatou,s lemma,we obtain We chooseρ>0 small enough such that‖‖λ >ρ,and Step 2 is proved. Step 3Iλhas a nontrivial positive critical point inEλ. By Step 1,Step 2 and Lemma 2.2,we see that there is a Cerami sequence{un} ?Esatisfying(2.3).Thus,it follows from Lemma 4.1 and Lemma 4.2 that there exists a nontrivialu1∈Eλsuch thatI′λ(u1)=0.The proof ofu1>0 is similar to that of of Theorem 1.1,and is omitted here.The proof is complete. It is not difficult to find examples of functions which satisfy our assumptions. Example 5.1LetV(x)=c(>0),?x∈R3.And for anyτ0>0,andl=(a+b+1)τ0,let Clearly,(v1)-(v2) and (f1) hold.Simple calculation shows that foru≥0 Choose someτ0>0,0 Takingτ0=7056π2,R=1 andβ=we have and in view of the definition ofμ?,we can find constantsλandV(x)=csatisfying (5.1)-(5.3) means that (f2) and (A1) hold,and Theorem 1.1 applies. Example 5.2LetV(x)=c(>0),?x∈R3.And for anyτ0>0,andl=let It is easy to see that (v1)-(v2),(f1) and (f3) hold.Direct calculation shows that foru≥0,F(x,u)=Then,for any 0 sinceμ≥4,which means (f3) holds.For anyR >0,chooseτ0=andφ∈C∞0(R3,[0,1])such thatφ(x)=1 if|x|≤R,φ(x)=0 if|x|≥2Rand|?φ|≤for allx∈R3,whereis an arbitrary constant independent ofx.Then TakingR=1,(5.4) impliesMoreover which impies (A2) holds,and Theorem 1.2 applies.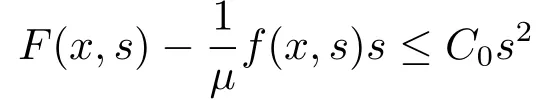

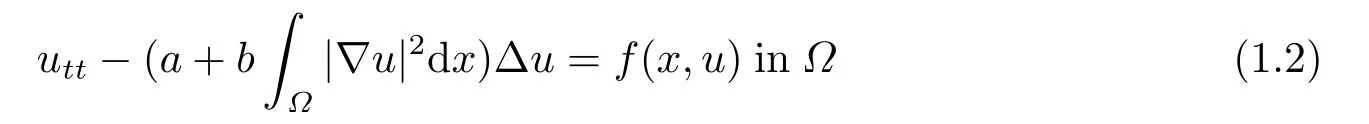
2.Preliminaries
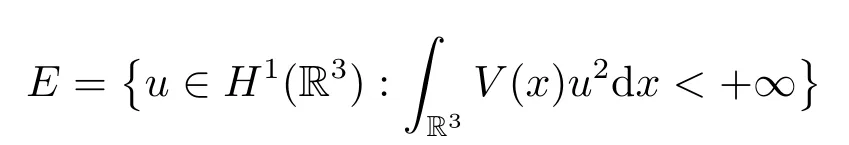
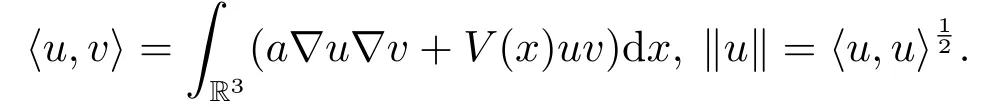
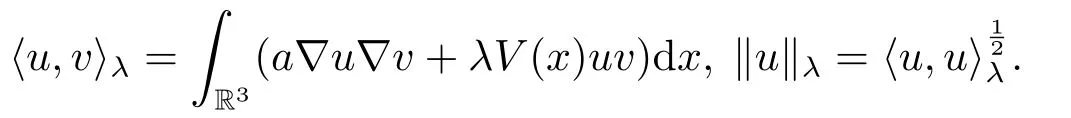
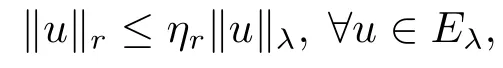
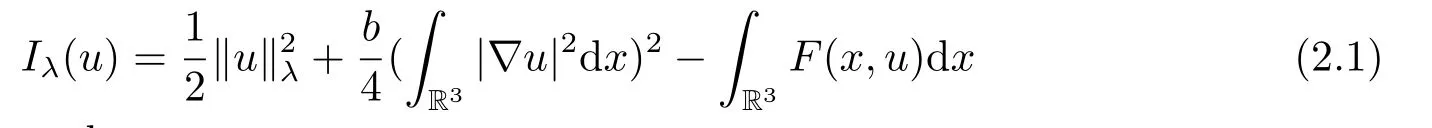
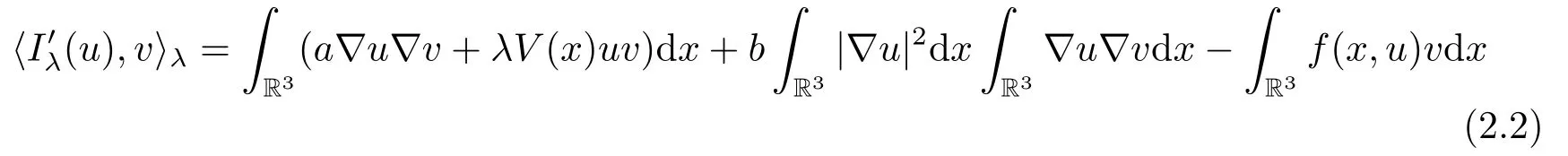
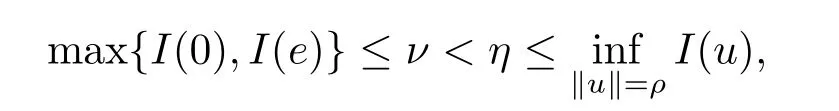

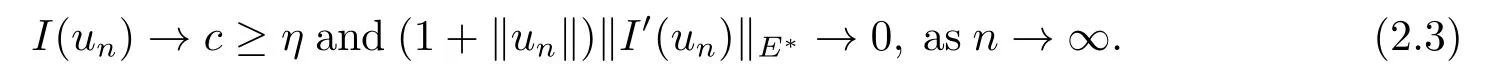
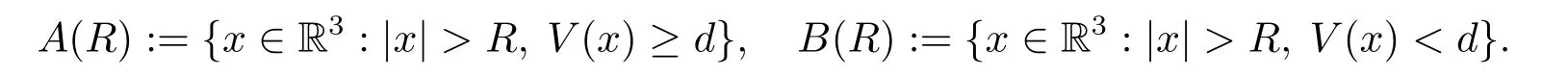
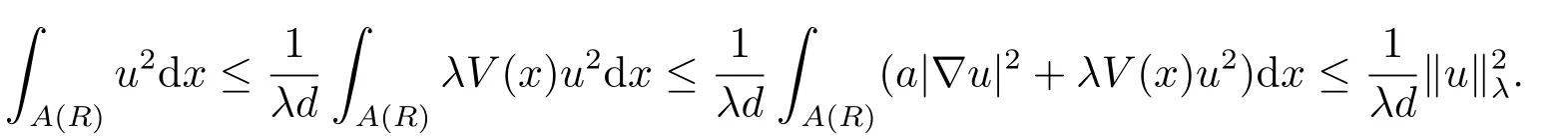
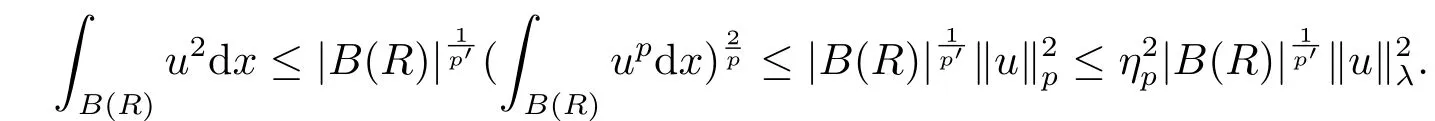
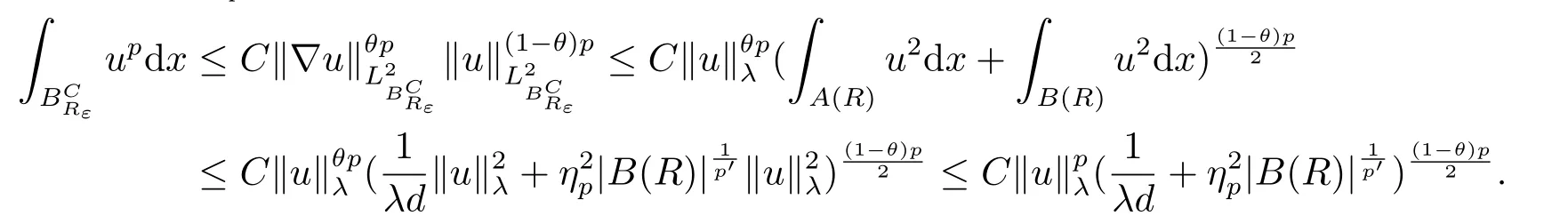
3.The Asymptotically Linear Case




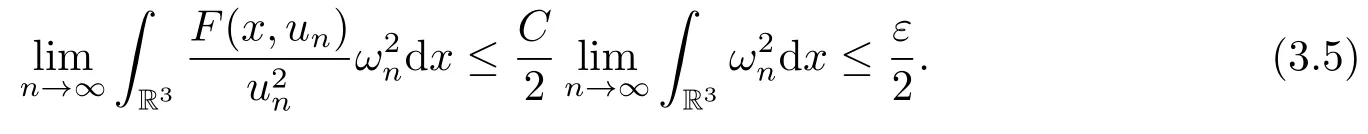
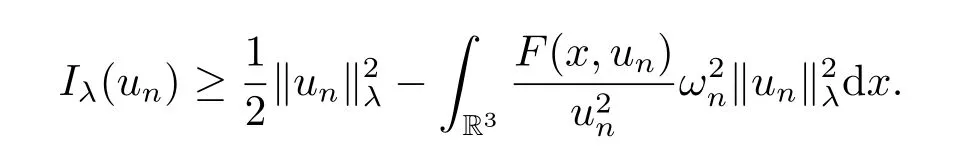
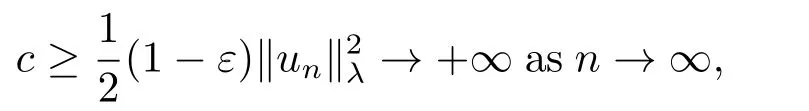



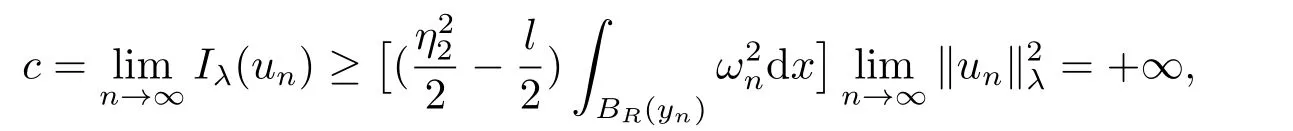
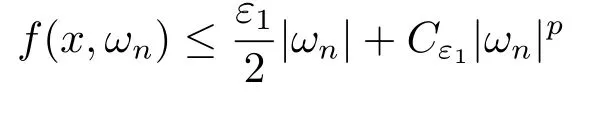
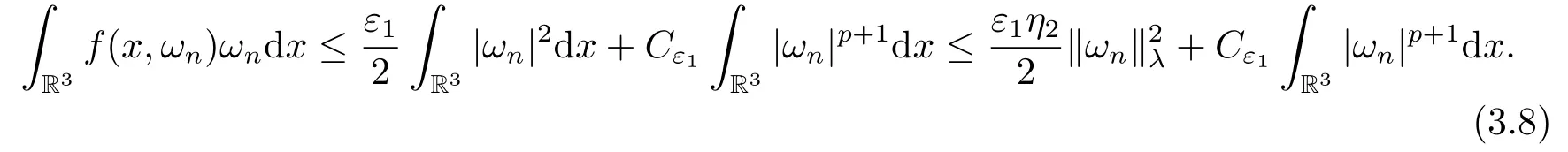
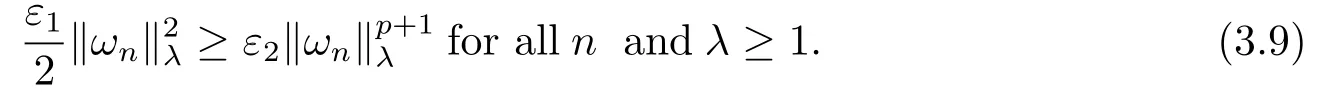
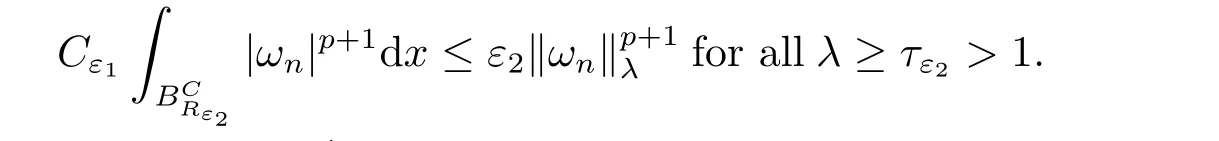

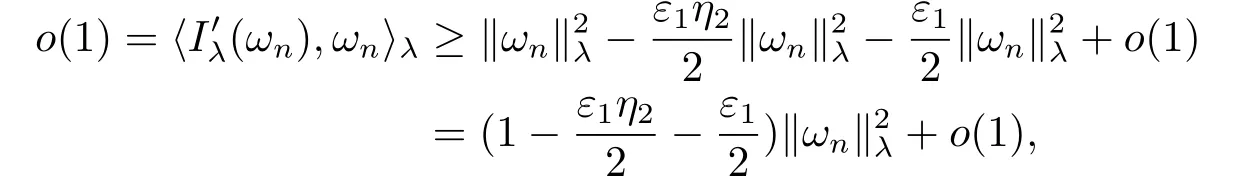

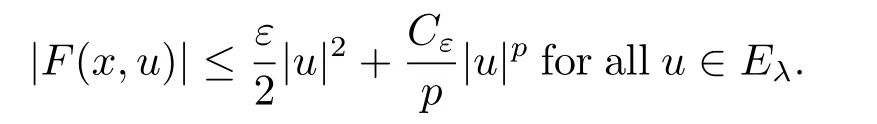
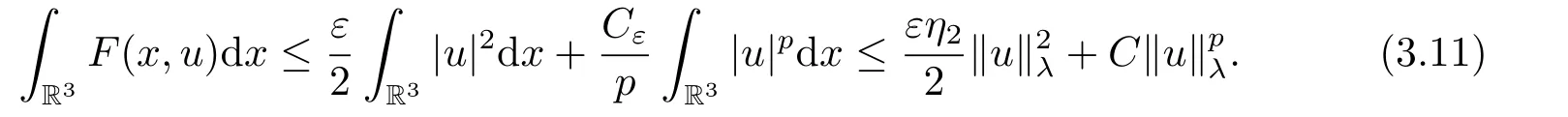
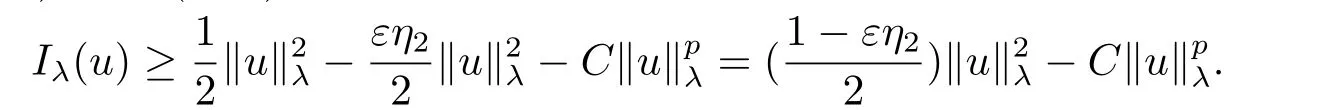
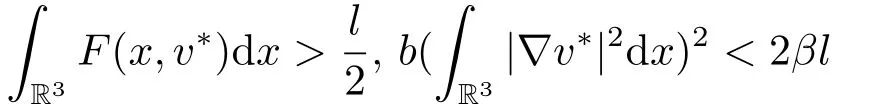
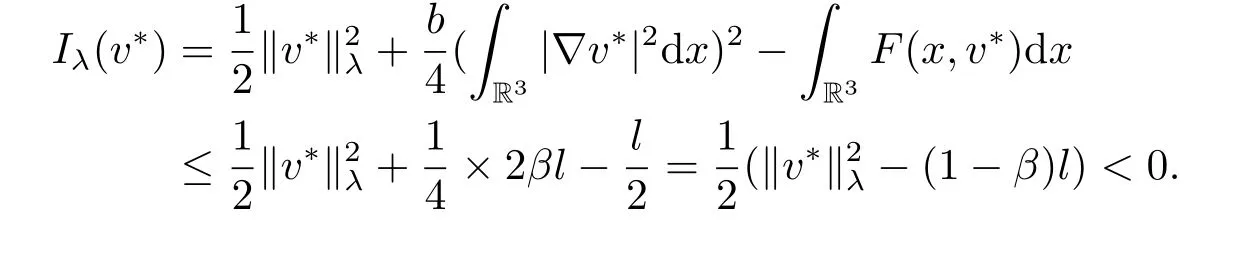
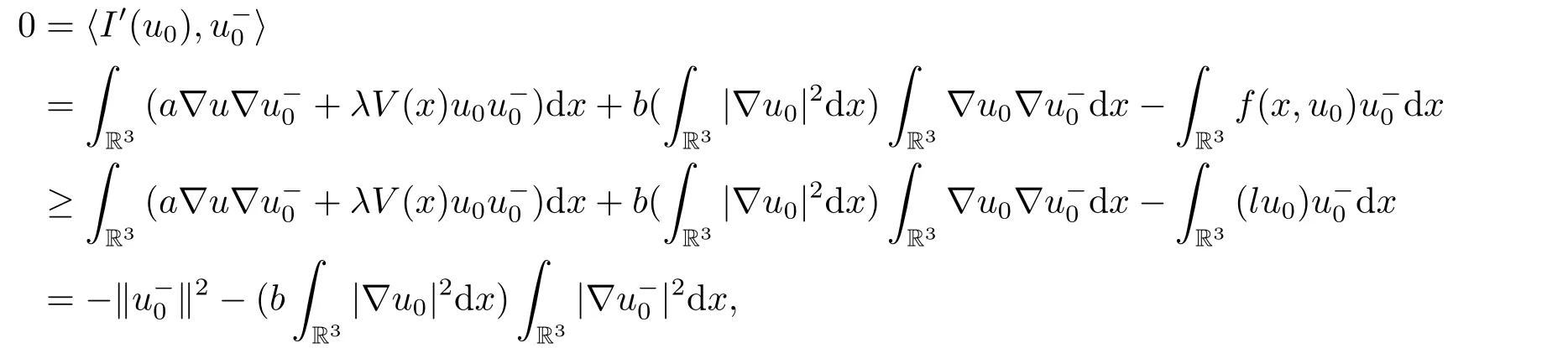
4.The Asymptotically 3-Linear Case
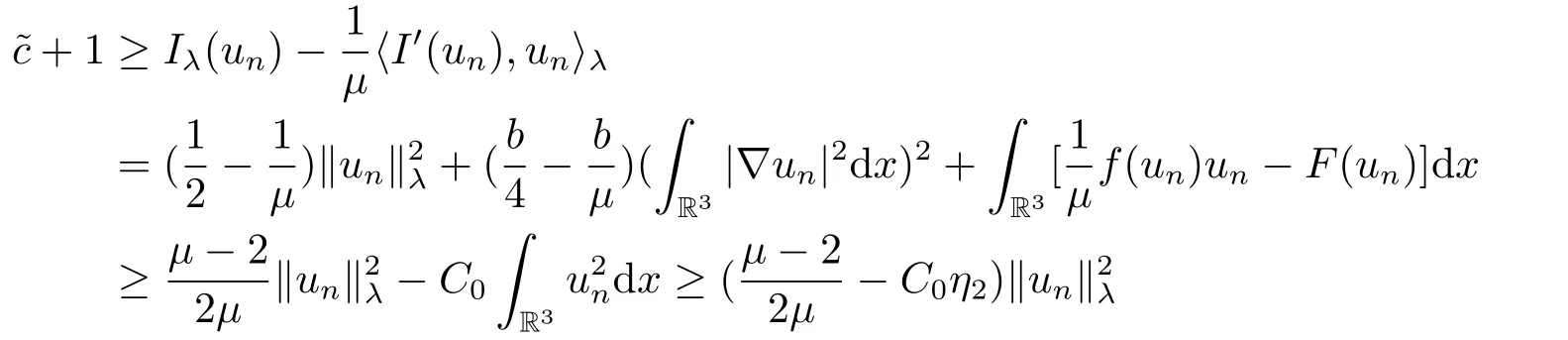
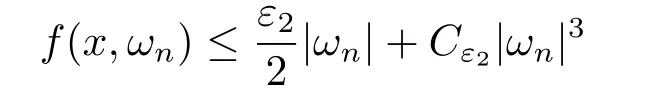
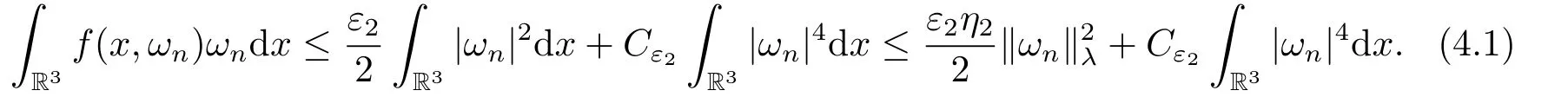
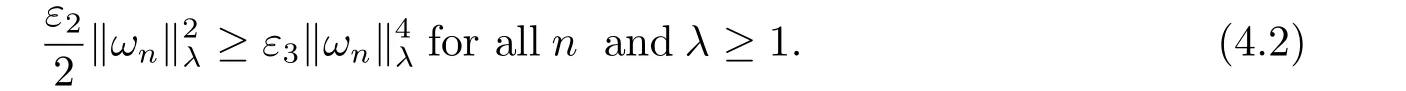
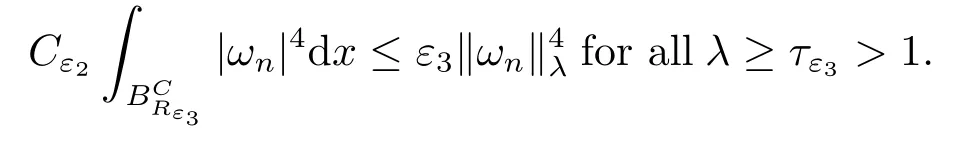
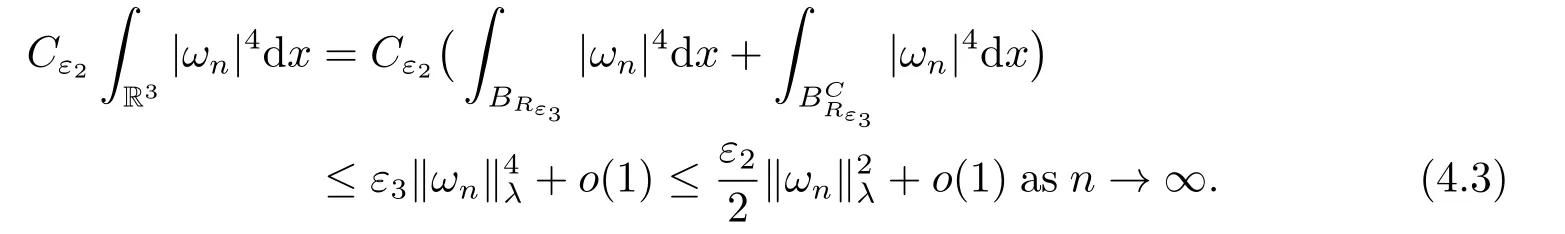
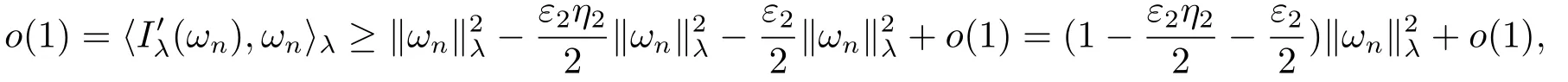
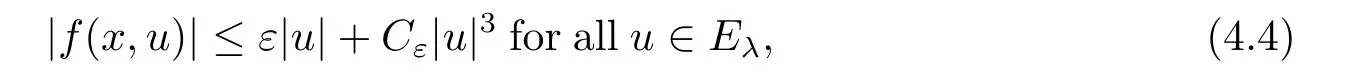

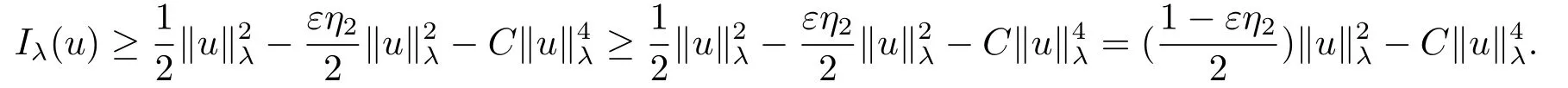
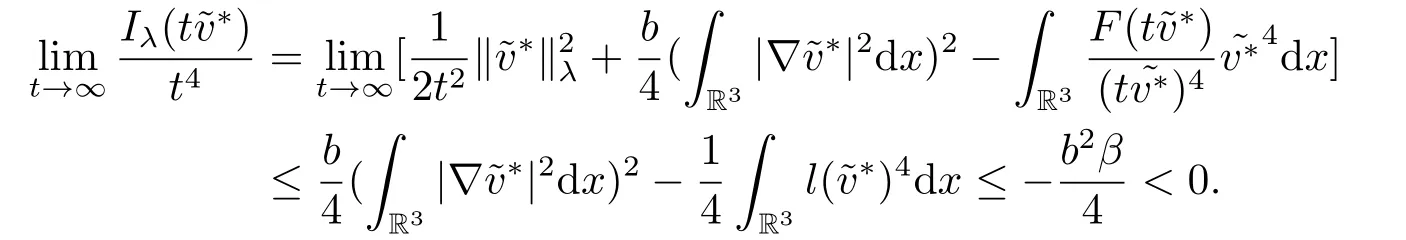
5.Examples