Solution of the Dipoles in Noncommutative Space with Minimal Length?

Meng-Yao Zhang(張夢(mèng)瑤),Zheng-Wen Long(隆正文), and Chao-Yun Long(龍超云)

College of Physics,Guizhou University,Guiyang 550025,China

AbstractThe single neutral spin-half particle with electric dipole moment and magnetic dipole moment moving in an external electromagnetic field is studied.The Aharonov-Casher effect and He-McKellar-Wilkens effect are emphatically discussed in noncommutative(NC)space with minimal length.The energy eigenvalues of the systems are obtained exactly in terms of the Jacobi polynomials.Additionally,a special case is discussed and the related energy spectra are plotted.

Key words:Neutral spin-half particle,noncommutative space,minimal length,Jacobi polynomials

1 Introduction

After the concept of coordinate noncommutativity was first introduced by Snyder.[8]The noncommutative theories are applied to the several areas of physics and have attracted large attention.[9?11]The reason for the emergence of this attention was the discovery in string theory.[12?13]Most results show that the noncommutative effect has influenced some physical phenomena,such as the AB effect,[14?15]the AC effect,[16?19]the HMW effect,[20?21]quantum Hall effect,[22?24]and Landau levels.[25?27]On the other hand,the unification between the general theory of relativity and the quantum mechanics implies the existence of a minimal lengthFurther research shows that the minimal length can be introduced as an additional uncertainty in position measurement.[28?31]So that the usual canonical commutation relation between position and momentum operators can be replaced by[xi,pj]=iδij(1+ αp2),[28?29]where α is a small positive parameter determined from a fundamental theory such as string theory.[32?33]The modification of the uncertainty relation between position and momentum operators is usually termed generalized uncertainty principle(GUP)or the minimal length uncertainty principle.[34]

Most geometrical and topological effects can be realized in physics via studying the charged and neutral particles interact with the electric field and magnetic field.For instance,Aharonov-Bohm(AB)phase,[1]Aharonov-Casher(AC)phase,[2]and He-McKellar-Wilkens(HMW)phase.[3?4]A well known quantum phase is Anandan phase proposed by Anandan,[5]which describes a neutral particle moving in an external electromagnetic field with non-vanishing electric dipole moment and magnetic dipole moment.In 2001,Ericsson and Sjoqvist[6]proposed the neutral particles interact with the non-zero electric field via a magnetic dipole moment can generate an analog of Landau quantization based on the AC interaction.Besides,motivated by the HMW interaction,Ribeiro et al.[7]developed a quantization also similar to Landau quantization for neutral particles with a non-zero electric dipole moment.

Recently,considerable attention has been paid to the study of several physical problems in noncommutative coordinate space with minimal length uncertainty relation.[35?39]In this work,we study a single neutral spinhalf particle moves in an external electromagnetic field in noncommutative space with minimal length.The paper is organized as follows:In Sec.2,we consider the Aharonov-Casher effect.In Sec.3,He-McKellar-Wilkens effect is studied.Section 4 is our conclusions.

2 Aharonov-Casher effect in Noncommutative Space with Minimal Length

In non-relativistic limit,considering the single neutral spin-half particle moving in an external electromagnetic field,and the particle possesses an electric dipole moment and a magnetic dipole moment,the Anandan Hamiltonian[40]can be used to describe the system

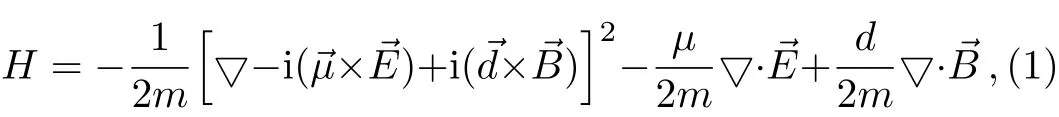
we adopt the system of natural unity were=c=1,and the terms of O(E2)and O(B2)are neglected,μis the magnetic dipole moment,d is the electric dipole moment,E is the electric field,andB is the magnetic field.In fact,the Hamiltonian consists two different physic effects,including Aharonov-Casher effect and He-McKellar-Wilkens effect.In which the particle interacts with electric field and magnetic field through the non-vanishing magnetic dipole moment and electric dipole moment.

Firstly,the Aharonov-Casher effect is considered,in which d andare absent,the electric field configuration can be expressed as,where ρ is the nonvanishing uniform charge density,and the Hamiltonian is given by

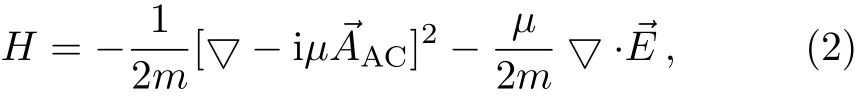
the vector potential is defined asthe unitary vector oriented in the dipole direction,and we choose the magnetic dipole to be parallel to the the zdirection,the associated field strength is=▽×.It is worth noting that the magnetic field must be uniform for Aharonov-Casher system,torque vanishes on the dipole and electric field satisfies the conditions,=0,▽×=0,these conditions satisfy the restrictions of energy quantization.

In non-commutative spacetime the ordinary product is replaced by a star product of the form

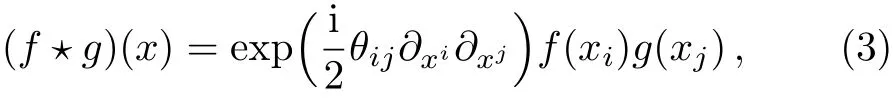
where θij= ?ijθ is the antisymmetric constant matrix,θ is the noncommutativity parameter,representing the antisymmetric tensor of dimension of(length)2.The commutation relations between the spatial and momentum are given by

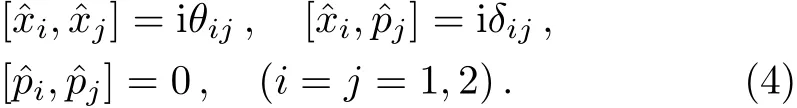
Considering the partical moves in the x-y plane,in this case,the Schr?dinger equation in noncommutative space,which is written by

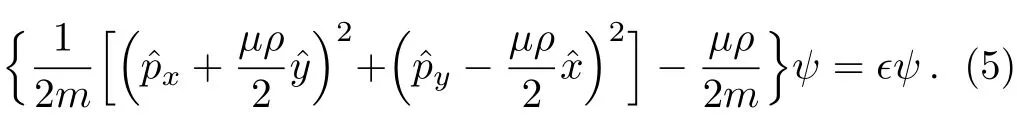
It is possible to go back to the commutative space by replacing the noncommutative operators via Bopp shifts,[41]so the relations between the noncommutative operators and commutative operators are obtained

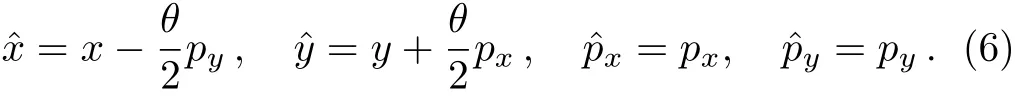
By inserting Eq.(6)into Eq.(5),we rewrite the Schringer equation as

where

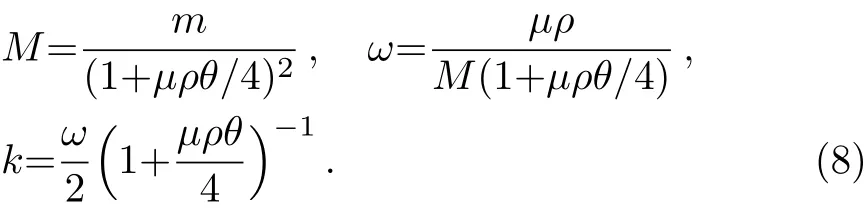
Now we introduce the minimal length formalism,the Heisenberg algebra is given by[28?29]

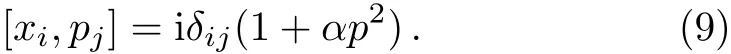
This commutation relation leads to the standard Heisenberg uncertainty relation ?x?p ≥ (1/2)δij(1+α(?p)2+ α ＜p＞2).A representation of xiand pisatisfies Eq.(9),may be taken as

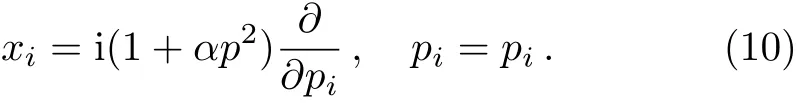
As well as writing the form of polar coordinates

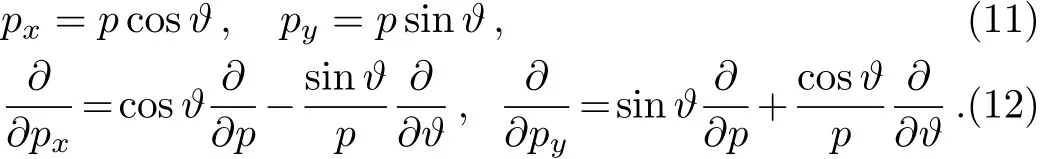
An auxiliary wave function is defined as ψ(p,?) =ei?lφ(p),then Eq.(7)becomes

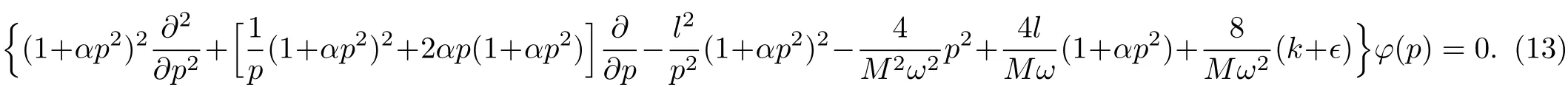
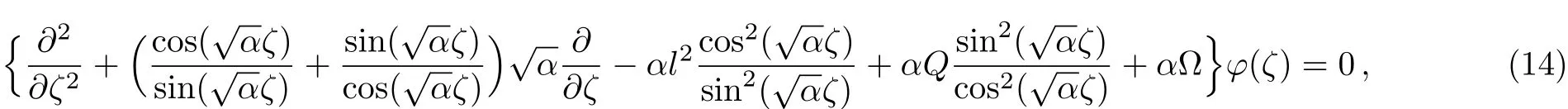
where

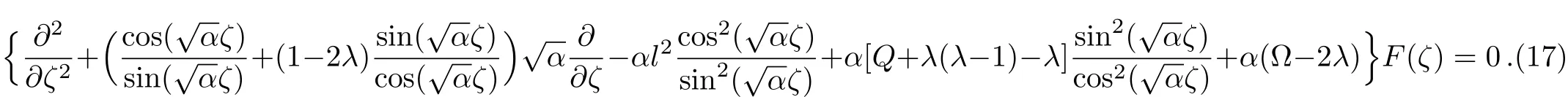
The solution of Eq.(17)can be found by eliminating the term,so we assume that

Then the expression of λ can be solved from above form

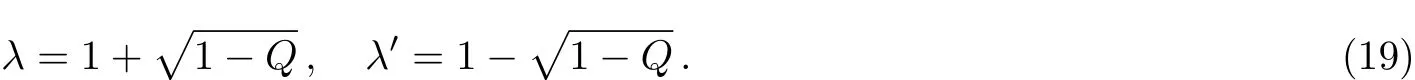
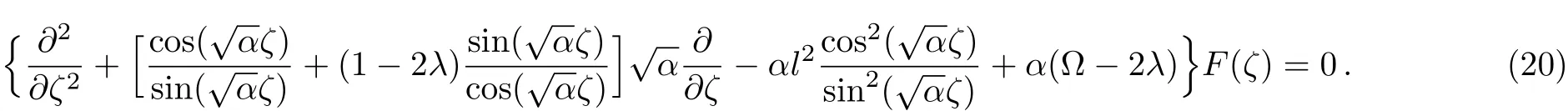
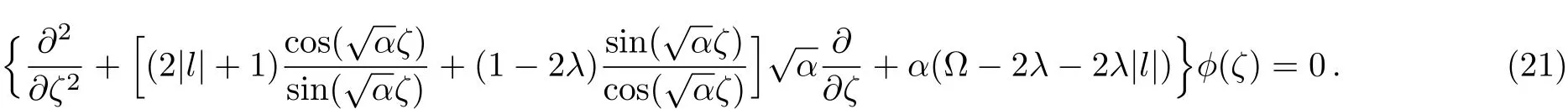
In order to transform Eq.(21)into a class of known differential equations with a polynomial solution,we introduce another variable z=2sin2)?1,where z∈ (?1,1),and impose the following constraint

where n is a non-negative integer.So Eq.(21)becomes the form

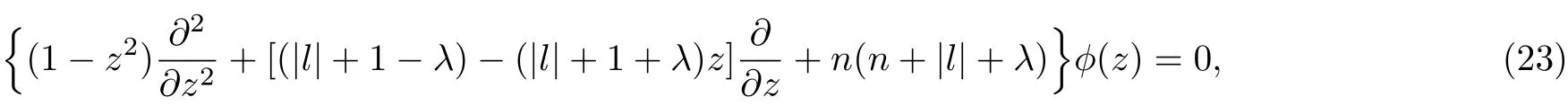
the solution of above equation can be reported by employing Jacobi polynomials as

The eigenvalue equation of the system can be derived from Eq.(22)

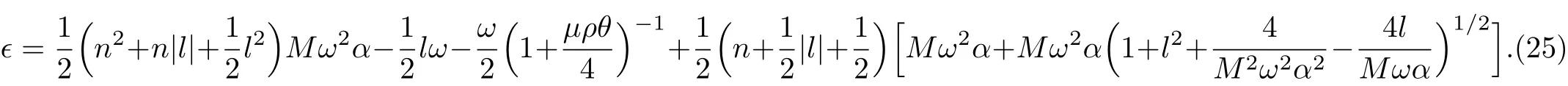
In order to visualize the influence of NC parameter and minimal length parameter on energy spectra,we decided to depict the energy spectra ? versus magnetic dipole moment μ for different values of the azimuthal quantum numbers by means of computer software,and the natural unit n=M=ω =ρ=1 were employed.As shown in Figs.1–3,each curve represents the profile of energy spectra ? versus magnetic dipole moment.

From the results shown in Figs.1–3,we see that the overall energy spectra increases monotonically with the increase of magnetic dipole moment,and the energy ? first rapidly increases then has a slow-growth.From the asymptotic behavior of the curve,it can be seen that the curves have similar linear behavior for the same NC parameter θ.For a fixed value of magnetic dipole moment μ,the energy spectrum increases when the minimal length parameter α grows for the same NC parameter θ,and for the same minimal length parameter α,the energy ? increases with the increase of NC parameter θ.

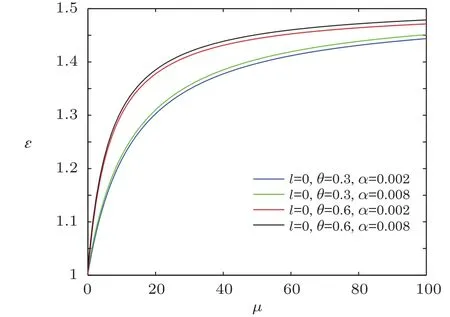
Fig.1 The distribution of the energy spectra ? versus μ(n=M=ω=ρ=1).

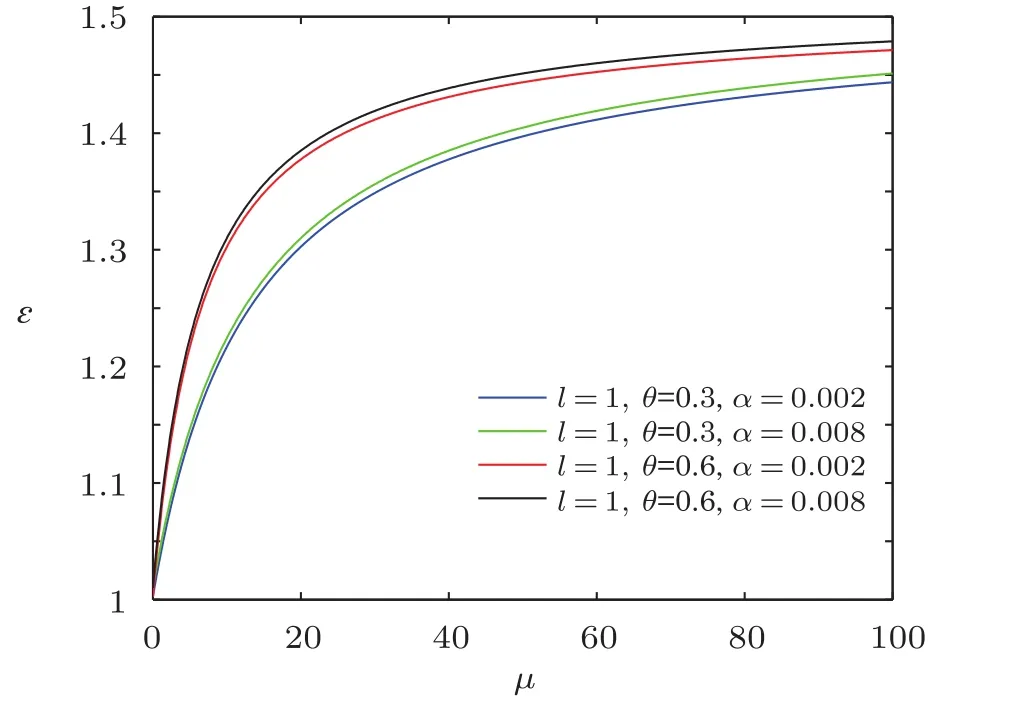
Fig.2 The distribution of the energy spectra ? versus μ(n=M=ω=ρ=1).

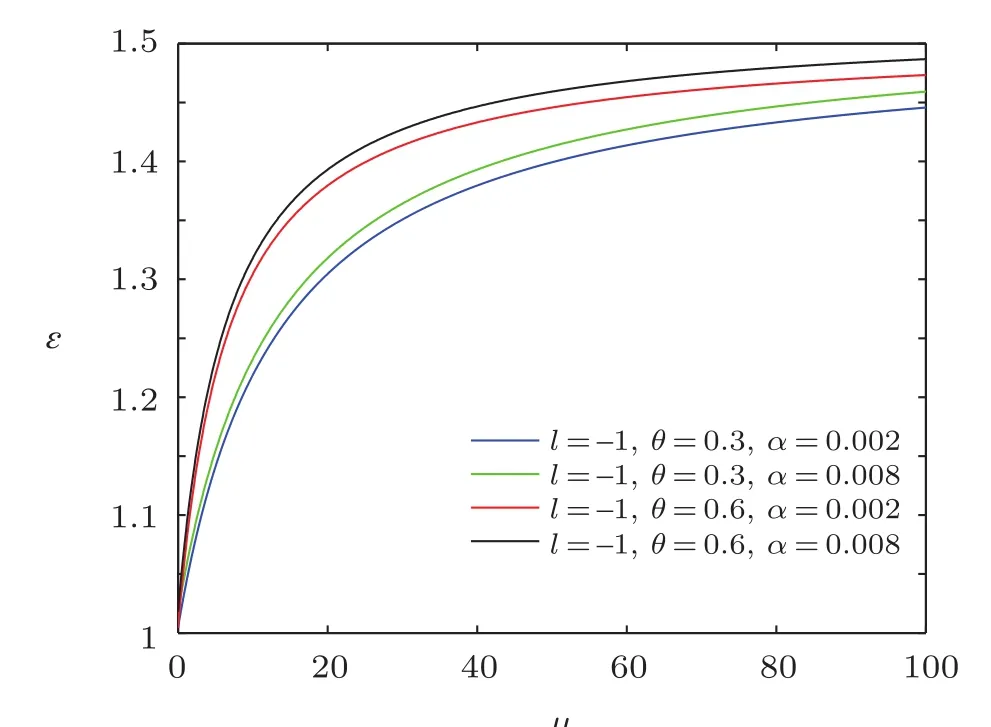
Fig.3 The distribution of the energy spectra ? versus μ(n=M=ω=ρ=1).

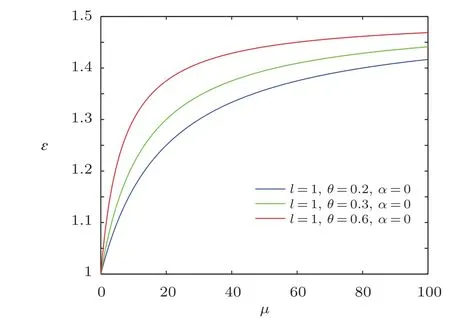
Fig.5 The distribution of the energy spectra ? versus μ(n=M=ω=ρ=1).

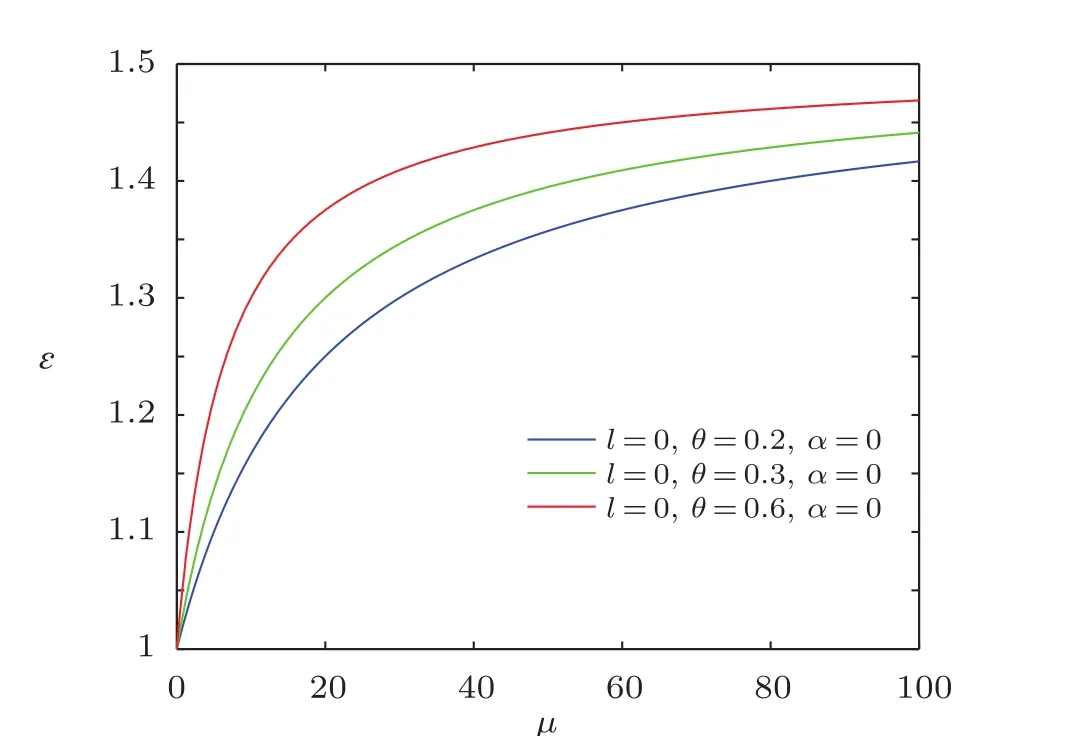
Fig.4 The distribution of the energy spectra ? versus μ(n=M=ω=ρ=1).

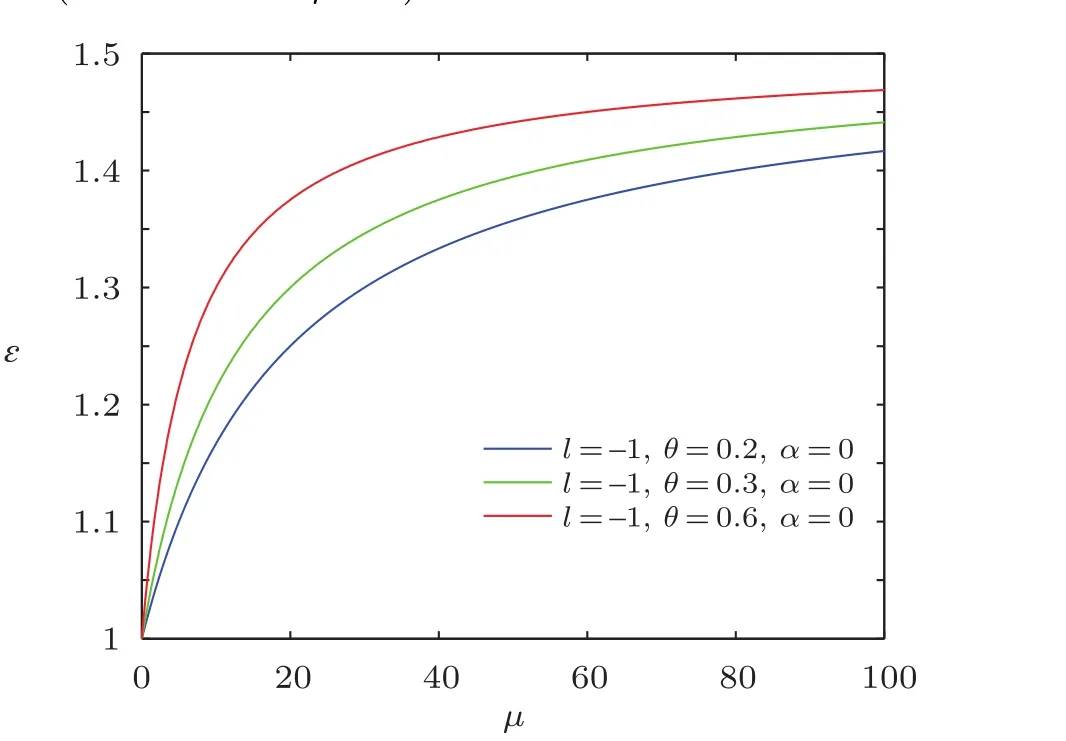
Fig.6 The distribution of the energy spectra ? versus μ(n=M=ω=ρ=1).

Now,we consider the special case of the ninimal length parameter is absent,that is α=0,the eigenvalue equation degrades into

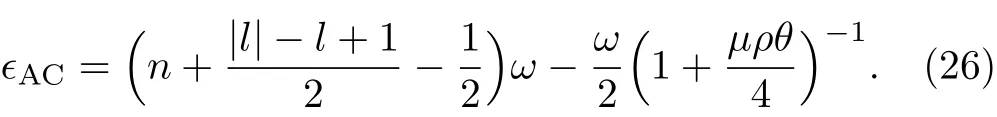
Obviously,it is strictly consistent with the result from Ref.[20].The energy spectra ? versus magnetic dipole momentμ are plotted in Figs.4–6,which show that overall energy spectra increase monotonically with the increases of the magnetic dipole moment.From the asymptotic behavior of the curve,we see that the energy ? rapidly increases at first for increasingμthen slowly grows for largeμ values.The energy ? increases with the increase of NC parameter θ for a fixed value of μ.

3 He-McKellar-Wilkens effect in Noncommutative Space with Minimal Length

In this section,the He-McKellar-Wilkens effect is studied,μandare absent in Eq.(1),the Hamiltonian of neutral particle moves in an external magnetic field can be written as

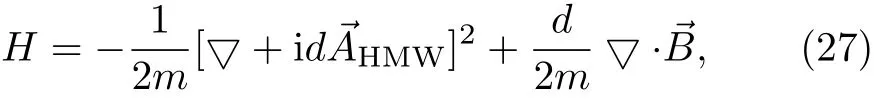
In this case,He-McKellar-Wilkens magnetic field must be uniform,the torque may vanish on the dipole,the magnetic field satisfies the conditions,must be smooth.The Schrodinger equation for the HMW system in NC space appears as

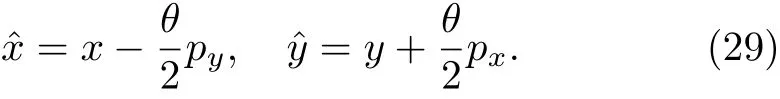
And the Eq.(28)takes the form

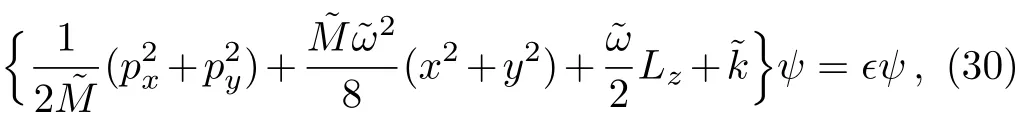
where

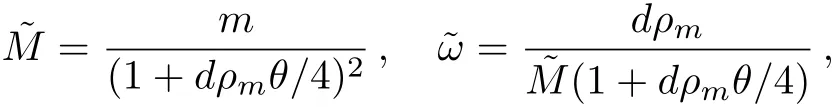
Now,we bring the problem into the momentum space

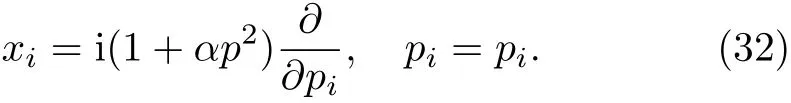
As well as writing the form of polar coordinates

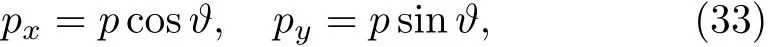
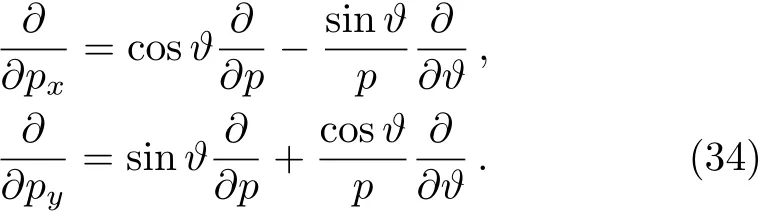
An auxiliary wave function is defined as ψ(p,?) =ei?lφ′(p),then Eq.(30)becomes

By introducing a new variable,which maps the intervalEq.(35)is transformed into

where

In this case,the energy spectra equation can be obtained by employing the same methods

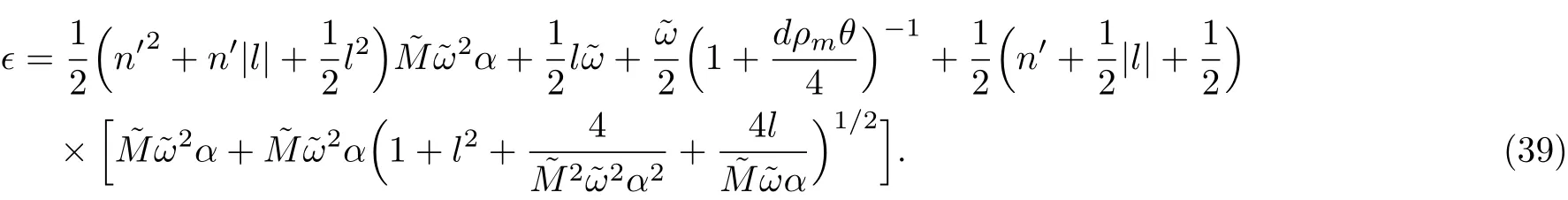
Similarly,it is difficult to analyse how the NC parameter and minimal length parameter a ffect the eigenenergy spectra,so we decide to depict energy spectra ? versus the electric dipole moments d for different values of the azimuthal quantum number,and the natural unit n′==ρm=1 were employed.As shown in Figs.7–9,each curve represents the profile of energy spectra versus electric dipole moment.

From the figures shown in Figs.7–9,we see that the overall energy spectra decreases monotonically with the increase of electric dipole moment,and the energy ? first rapidly decreases then slowly decreases.From the asymptotic behavior of the curve,it can be seen that the curves have similar linear behavior for the same NC parameter.For a fixed value of electric dipole moment,the energy ? increases when the minimal length parameter grows for the same NC parameter θ,and for the same minimal length parameter,the energy ? decreases with the increase of NC parameter θ.

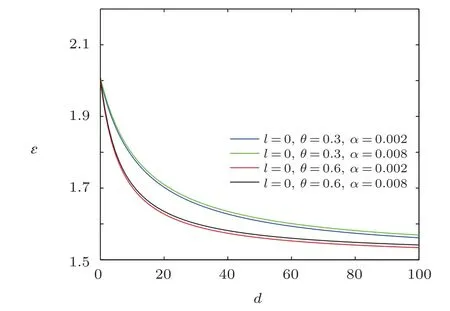
Fig.7 The distribution of the energy spectra ? versus d(n′==ρm=1).

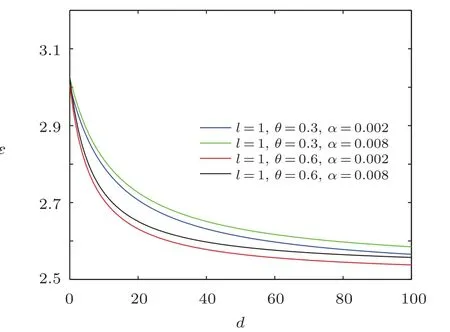
Fig.8 The distribution of the energy spectra ? versus d(n′==ρm=1).

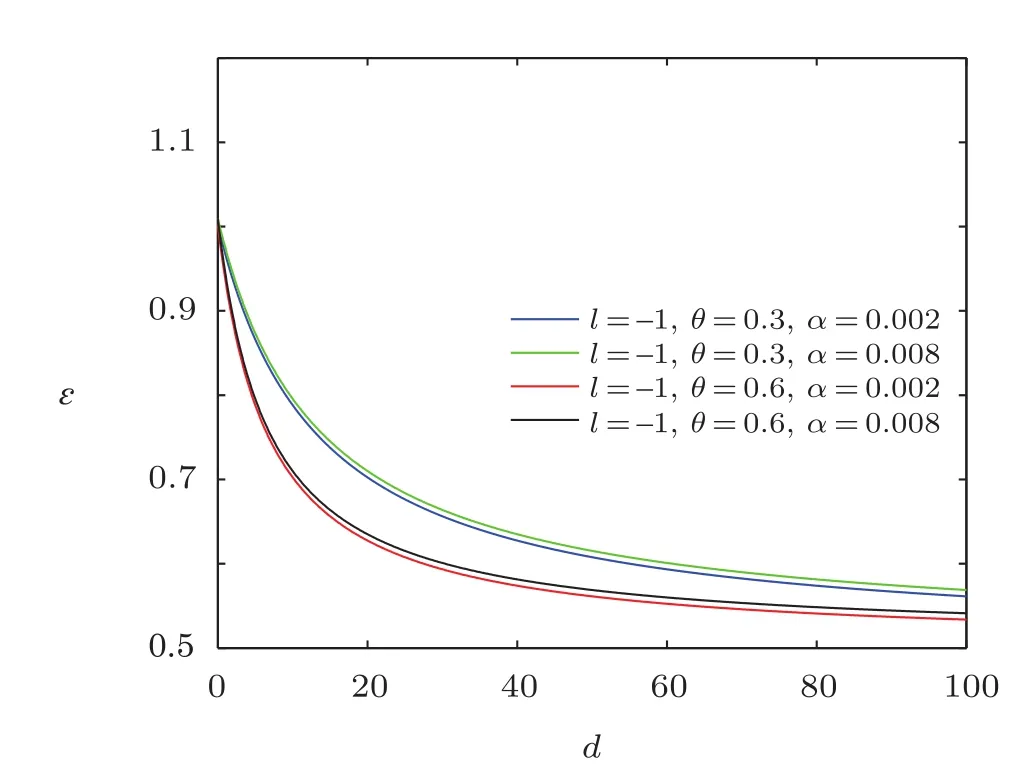
Fig.9 The distribution of the energy spectra ? versus d=ρm=1).

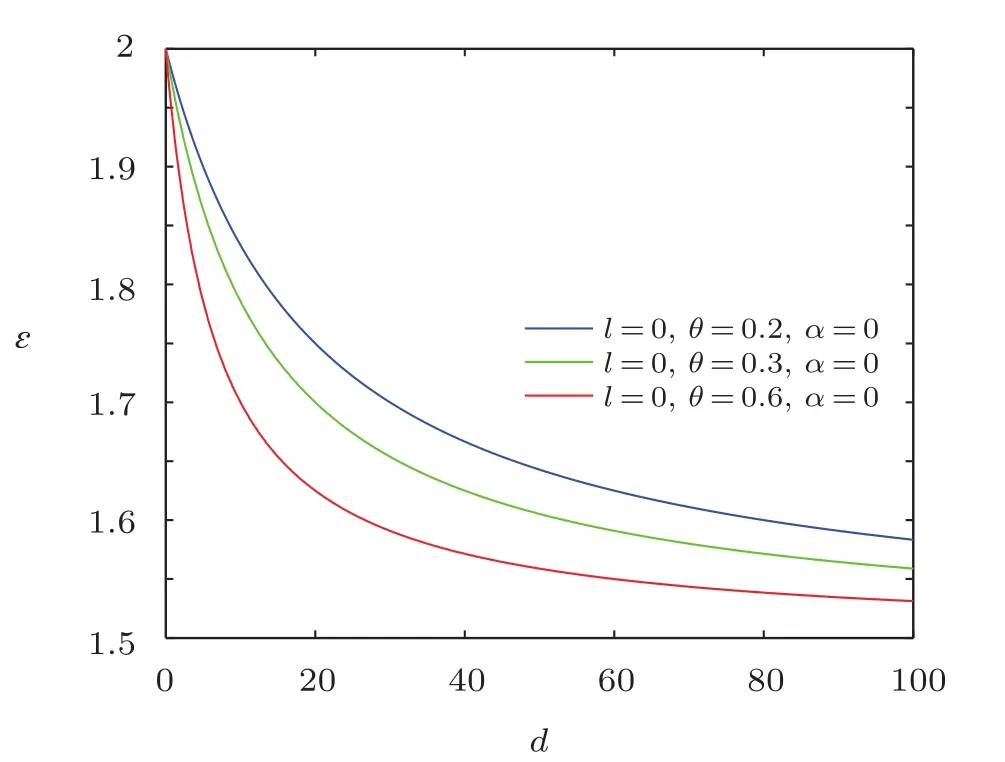
Fig.10 The distribution of the energy spectra ? versus d(n′==ρm=1).

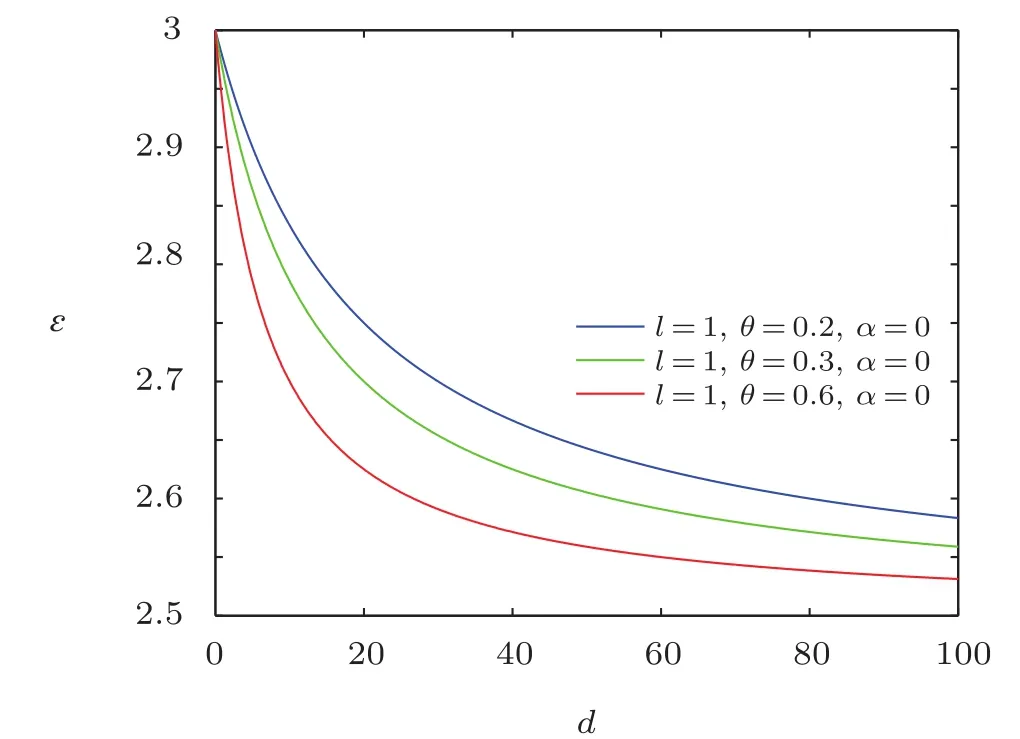
Fig.11 The distribution of the energy spectra ? versus d(n′==ρm=1).

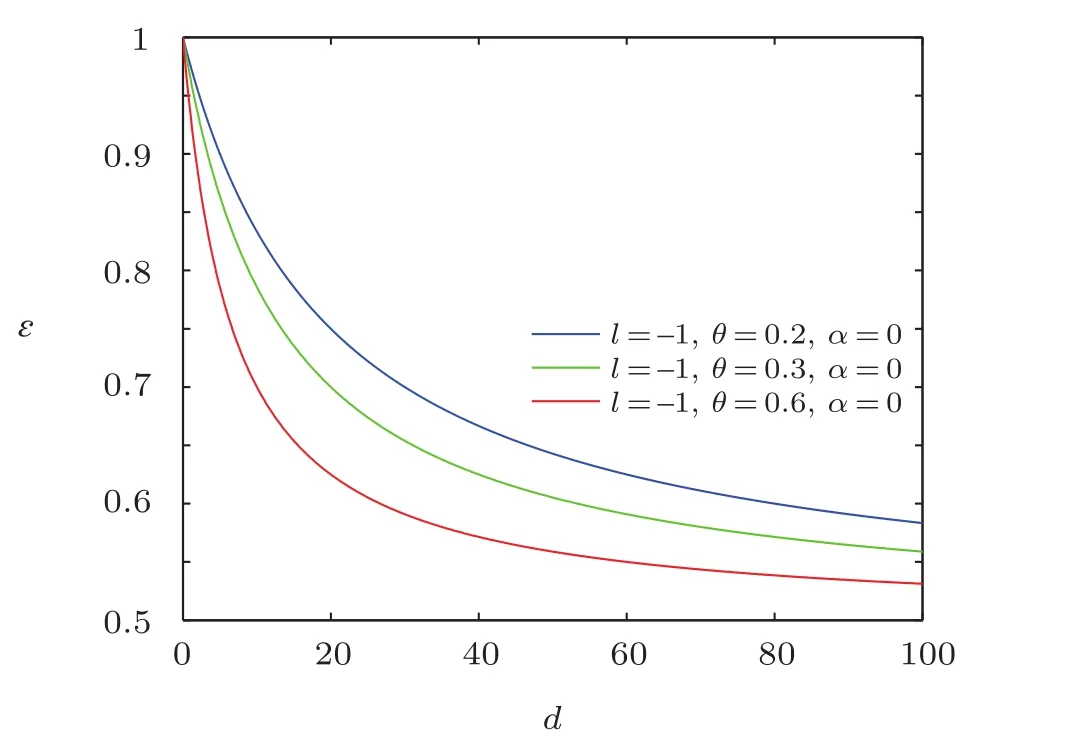
Fig.12 The distribution of the energy spectra ? versus d(n′==ρm=1).

Subsequently,the special case of α=0,that is for vanishing minimal length parameter,the eigenvalue equation degrades into

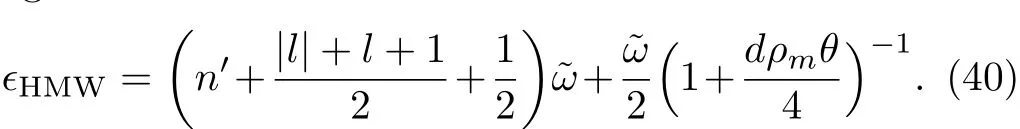
Obviously,it is strictly consistent with the result from Ref.[20].The energy spectra ? versus d are plotted in Figs.10–12,which show that overall energy spectra decreases monotonically with the increase of electric dipole moment.From the asymptotic behavior of the curve,it can be seen that the energy spectra first rapidly decreases then has a slow-decrease.And the energy ? decreases with the increase of NC parameter θ for a fixed value of electric dipole moment.

4 Conclusion

The non-relativistic quantum dynamic with a spin-half neutral particle,which possessing electric dipole moment and magnetic dipole moment in the presence of non-zero homogeneous electric and external magnetic fields was studied.We used the Hamiltonian found by Anandan to describe this system.The AC effect and HMW effect are investigated in the noncommutative coordinates space with minimal length.We transformed the Schrodinger equation into a familiar form,the related energy spectra are obtained in terms of the Jacobi polynomials and we plotted corresponding numerical results.It shows that for AC system,the energy ? increases when the NC parameter and the minimal length parameter increase for the same azimuthal quantum number.The special case of the minimal length parameter α=0 was discussed,and the corresponding numerical result was depicted respectively.It shows that the energy ? increases with the increase of NC parameter.And for HMW system,the energy ? increases with the increase of minimal length parameter but decreases with the growth of NC parameter.Similarly,when the minimal length parameter α=0,the corresponding energy spectrum was depicted respectively.It shows that the energy ? decreases with the increase of NC parameter.Besides,the energy ? increases with the increase of the magnetic dipole moment for AC system but decreases with the increase of the electric dipole moment for HMW system.