Interactions of Lump and Solitons to Generalized(2+1)-Dimensional Ito Systems?

Xuan Du(杜旋)and Sen-Yue Lou(樓森岳)

1Department of Mathematics,Ningbo University,Ningbo 315211,China

2School of Physical Science and Technology,Ningbo University,Ningbo 315211,China

3Shanghai Key Laboratory of Trustworthy Computing,East China Normal University,Shanghai 200062,China

AbstractThe(2+1)-dimensional Ito equation is extended to a general form including some nonintegrable effects via introducing generalized bilinear operators.It is pointed out that the nonintegrable(2+1)-dimensional Ito equation contains lump solutions and interaction solutions between lump and stripe solitons.The result shows that the lump soliton will be swallowed or arisen by a stripe soliton in a fixed time.Furthermore,by the interaction between a lump and a paired resonant stripe soliton,the lump will be transformed to an instanton or a rogue wave.

Key words:generalized bilinear operators,(2+1)-dimensional Ito systems,lump-soliton interactions,instanton and rogue waves

1 Introduction

It is well known that most of integrable systems can be used to describe many important phenomena in physics and other scientific fields.As mathematical models of these phenomena,to seek exact solutions for nonlinear evolution equations(NLEEs)in mathematical physics becomes particularly important.In the last decades,a large number of researchers are interested in the exact solutions including bright[1?2]and dark solitons,[3]breathers,[4]and rogue waves.[5?6]Compared with these solutions,lump solutions localized in all space directions are a special type of rational function solutions.An instanton is soliton,which is localized not only in space directions but also in time.If the amplitude of an instanton is much larger than background waves,then the instanton can be called as a rogue wave.Recently,to study lump solutions,rogue waves and interaction solutions among lumps,rogue waves and solitons become one of the hot topics in many scientific fields such as nonlinear optics,[7]plasmas,[8?9]atmosphere,[10]Bose-Einstein condensations(BECs),[11]and even financial system.[12?13]

To find exact solutions of nonlinear systems,there are many effective methods,for instance,the Lie group method,[14?15]the inverse scattering transformation(IST),[16]the Darboux transformation(DT),[17]the bilinear method,[18]and so on.To research lump solutions of NLEEs,there are a large number of works by using a quite simple and effective Hirota’s bilinear method.[19?22]Usually,lump solutions are defined and found for high dimensional equations,say,the(2+1)-dimensional Boussinesq equation,[23]the(2+1)-dimensional Burgers equation[24]and the(3+1)-dimensional Jimbo-Miwa equation.[25]

However,not any physical system can be changed to appropriate bilinear system by only using Hirota’s bilinear operators.Thus,it is interesting to extend Hirota’s bilinear operators such that more physically important systems can be transformed to suitable bilinear forms.[26]

The(2+1)-dimensional Ito equation

possesses a bilinear form,

under the transformation

with the bilinear operators Dxi,xi=x,y,t being defined by

where u,f,and w are differentiable functions of{x,y,t}and a,b,c,and d are arbitrary constants.

The(2+1)-dimensional Ito equation is interesting equation which was first established by Ito in 1980 s[27]and many researchers have been studied this equation.In Ref.[28],the authors constructed various periodic wave solutions by a multidimensional Riemann theta function to(2+1)-dimensional Ito equation.In Ref.[29],single soliton solution,multiple-soliton solutions,and travelling wave solutions to(2+1)-dimensional Ito equation were derived by using four methods.In Ref.[30],the breather waves,rogue waves and solitary waves were obtained.

In Sec.2 of this paper,we extend the(2+1)-dimensional Ito equation to a new general linear and bilinear forms with some arbitrary constants by using the generalized bilinear operators.In Sec.3,using an appropriate assumption,a lump solution is found for the generalized(2+1)-dimensional Ito equation.Section 4 includes the interaction solution between a lump and a stripe soliton induced by the lump.In Sec.5,the interaction solution between a lump and an induced twin soliton is given.The last section is a short summary and discussion.

2 Generalized Bilinear Operators and Generalized(2+1)-Dimensional Ito Equation

By extending the bilinear operators to more general forms,nonlinear systems can be extended to describe more phenomena in mathematics and physics.The bilinear form of the(2+1)-dimensional Ito equation can be rewritten as

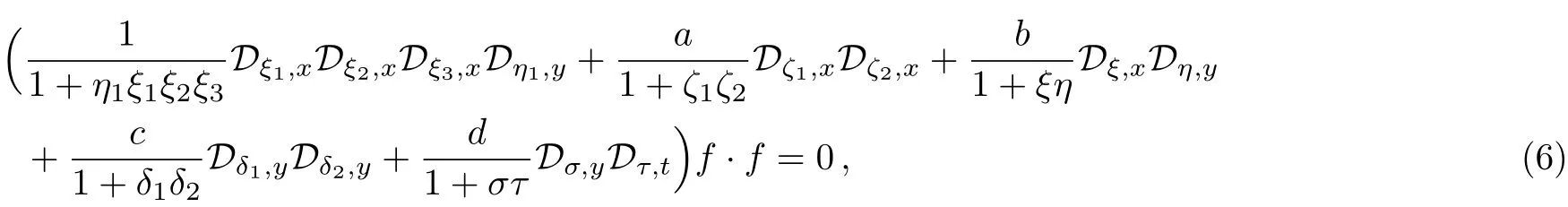
where the generalized bilinear operators Dα,xi,xi=x,y,t are introduced in Ref.[21]and defined by

with arbitrary constant α and seven constant conditions

among twelve parameters ξ1, ξ2, ξ3, η1, ζ1, ζ2, ξ, η, δ1, δ2, σ and τ.When α = ?1,we can find that the Hirota’s bilinear operator Dxiis just the special case of the generalized bilinear operator Dα,xi.

With the definition of the generalized bilinear operators,it is reasonable to extend the bilinear(2+1)-dimensional Ito Eq.(6)to the form

with twelve arbitrary constants{ξ1,ξ2,ξ3,η1,ζ1,ζ2,ξ,η,δ1,δ2,σ,τ}without conditions(8),where

The Hirota’s bilinear(2+1)-dimensional Ito system is equivalent to Eq.(6)under the conditions(8).

The corresponding(2+1)-dimensional generalized Ito system related to the generalized bilinear form(9)possesses the form(a1=1,vx=w)

with

When βi=0,i=0,1,...,6,the generalized(2+1)-dimensional Ito equation(11)is reduced back to the known integrable system(3).

3 Lump Solutions of Generalized(2+1)-Dimensional Ito Equation

In Ref.[21],The authors have pointed out that various bilinear systems possess the polynomial solutions

which are related to lump solutions.

Substituting Eq.(12)into the generalized bilinear form of the(2+1)-dimensional Ito Eq.(9)and vanishing the coefficients of the different powers of{x,y,t},it is easy to find the following two solution parameter constraints,

and four model parameter constraints

where the dot product between two of k,p,a vectors are defined asand

With the above conditions,we can verify the following identities by using the relation(13).

Fig.1(Color online)The exhibition of the lump solution to(2+1)-dimensional Ito equation.(a)shows the lump structure at t=0.(b)is the projective density plot of u at t=0.(c)shows the lump solution is moving along the straight line with a constant speed at different t=?60,t=0,and t=60.(d)shows the wave height in y=0 for t=0 in red,t=?5 in green,and t=5 in the blue.

From the above solution expressions,we can find the lump solution conditions,a6=0,a12=0,p2=0,andIf not,the(2+1)-dimensional Ito equations do not possess lump solution(4)with(12).Figure 1 shows a special evolution of the lump solution with the solution parameters

and the model parameters at t=0.The localized property of the lump is revealed in Fig.1(a).Figure 1(b)is the corresponding density plot of the lump solution. Figure 1(c)is the contour plot showing the location of the lump solution at t=?60,t=0,and t=60.The red line is the straight line of y=(3/32)x+39/148.Figure 1(d)exhibits the lump wave height in y=0 for t=0 in red,t=?5 in green,and t=5 in blue.

4 lumpoff solutions to(2+1)-Dimensional Ito Equation

There are some interaction solutions among lump and stripe solitons for various nonlinear systems no matter it is integrable or not.For the purpose of obtaining the interaction solution between a lump and a line soliton for the generalized Ito equation,we write the function f(x,y,t)in the following form

Substituting Eq.(19)into the generalized bilinear form of the(2+1)-dimensional Ito equation(9),we can find that the constants of{k0,p0,ω0}are completely determined by the lump parameters

Fig.2 (Color online)The evolution plot of the interaction of the lump and a stripe soliton with parameters selections in Eqs.(23)and(24)at times(a)t=?8,(b)t=?1,(c)t=0 and(d)t=5 respectively.

The model parameter conditions are the same as Eq.(15)and propose the existence condition of solutions for the generalized bilinear form of the(2+1)-dimensional Ito equation Eq.(9).The parameter condition(22)states clearly that the constant k0(and then p0and ω0)is completely determined by the lump parameters,the inner products of the vectors k and p and the model parameters.

From Eqs.(20)–(22),we find that the interaction properties of the lumpoff solution is quite interesting.The lump keeps the shape and moves along the same track with a constant speed before the interaction,it only emerges at one side of the stripe soliton.During the interaction,the lump remaining moves on the same track at the same speed.After the interaction,the lump is swallowed by the stripe soliton.And from Eqs.(20)–(22),we know that the parameters of k0,p0,and ω0in soliton part are determined by the lump part,which means the soliton is induced by the lump.In other words,if there is no lump,then there is no stripe soliton.

Figure 2 shows the interaction between lump and one stripe soliton for the field u given by Eq.(4)with Eq.(19)under the parameter selections

and the model parameter selections

Figure 2 is the evolution plot of the interaction solution between the lump and the stripe soliton with the parameter selections in Eqs.(23)and(24)at times(a)t=?8,(b)t=?1,(c)t=0,and(d)t=5 at k0x+p0y+α0<0 area of the stripe soliton and disappears after the collision.

5 Instanton/Rogue Wave Solutions to Generalized(2+1)-Dimensional Ito Equation

The algebraic lump soliton can induce not only one stripe soliton but also a twin stripe soliton for many(2+1)-dimensional integrable and nonintegrable systems.For the generalized bilinear(2+1)-dimensional Ito equation,the algebraic lump soliton can also induce a twin soliton.It is natural to assume the expression of f in the form of

with arbitrary constants a and b while ξ is also defined in Eq.(12).

Substituting Eq.(25)into the generalized bilinear(2+1)-dimensional Ito Eq.(9)and eliminating all the coefficients of{x,y,t,eX0},we can obtain 32 algebraic equations related to all the solution and model parameters.It can be inferred that the solution parameter conditions(13),(20),(21),and(22)and the model parameter condition(15)are satisfied by substituting Eq.(25)into Eq.(9)while the parameter f0should be changed as

Figure 3 exhibits the interaction solution between the lump and the solitons for the field u given by Eq.(4)with Eq.(25)under the same parameters as in Eq.(23)in addition to b=1 and the same model parameters as in Eq.(24).

Figure 3(a)is the two stripe solitons at t=?6 with the instanton hiding behind the soliton at the left side with higher amplitude.In Figs.3(b)–3(e),the instanton appears gradually,passing through the track,reaches its peak at about t=0 and decays gradually at t=2 respectively.At t=8,there is only two stripe solitons shown in Fig.3(e)after the interaction.

It is same as the last section for the lumpoff solution,the instanton solution parameters k0,p0,and ω0are all determined by the lump part,which means the twin solitons are induced by the lump part.In other words,if there is no instanton part,then there is no twin soliton part.

Fig.3 (Color online)The evolution plot of the interaction of the lump and a pair of stripe solitons with parameters selections in Eq.(23)and(24)at times(a)t=?6,(b)t=?2,(c)t=0 and(d)t=2(e)t=8.

6 Summary and Discussion

The(2+1)-dimensional Ito equation is extended to a more general form by extending the Hirota’s bilinear operators to generalized bilinear operators.For the extended(2+1)-dimensional Ito equation,some types of exact solutions such as the lumps,the lumpoffs and instantons(rogue waves)are found by solving the extended bilinear equations.A lump can induce both a single stripe soliton and a twin stripe soliton.Whence a single stripe soliton is induced,the lump becomes a lumpoff,the lump is cut off by the induced stripe soliton before or after the interaction.Whence a twin stripe soliton is induced,the lump becomes an instanton(or a rogue wave if the amplitude of the instanton is much larger than the twin soliton),the lump is cut off by the induced twin soliton before and after the interaction.This kind of lump,lumpoffand instanton solutions can be found in many integrable and nonintegrable systems such as the integrable and nonintegrable KPI equation,the nonintegrable KPII equation and the(2+1)-dimensional Sawada-Kortera equation.