Mathematical Study of A Memory Induced Biochemical System

Mithun Kumar Ghosh,Tridip Sardar,Xianbing Cao,and Priti Kumar Roy

Abstract—In this work,to study the effect of memory on a bi-substrate enzyme kinetic reaction,we have introduced an approach to fractionalize the system,considering it as a threecompartmental model.Solutions of the fractionalized system are compared with the corresponding integer-order model.The equilibrium points of the fractionalized system are derived analytically.Their stability properties are discussed from numerical aspect.We determine the changes of the substances due to the changes of “memory effect”.The effect is discussed critically from the perspective of product formation.We have also analyzed the memory induced system with a control measure in view of optimizing the product.Our numerical result reveals that the solutions of the fractionalized system,when it is free from memory,are in good agreement with the integer-order system.It is noticed that the effect of memory influences the reaction in the forward direction and assists in yielding the product more quickly.However,an extensive use of memory makes the system slower,but introduction of a control input makes the reaction faster.It is possible to overcome the slowness of the reaction due to the undue effect of memory by appropriate use of a control measure.

I.INTRODUCTION

ENZYMES are biological catalysts that are necessary in almost every biochemical reaction[1].These enzymes are proteins synthesized by genes[2].The main function of an enzyme is to catalyze the making and breaking of chemical bonds depending on an accurate sequence of amino acids and its complicated tertiary structure.The catalytic ability of enzymes increases the rate of a reaction.The enzyme is not used up in the reactions and,it does not change the equilibria of the processes[3].This raises a new dimension of thinking towards various fields viz.physics[4],chemistry[5],biology[6],ecology[7],epidemiology[8],pharmacokinetics[9]etc.A lot of research has been done about enzymatic processes of different chemical and biochemical transformations.Enzyme kinetics is the study of rates of these reactions to optimize the velocity of reactions,rate of intermediate complexes and products.

For a better understanding of the reaction kinetics,many authors have implemented different techniques to obtain approximate analytical solutions of the enzymatic systems[10]-[13].Modern day literature related to enzyme activity in enzymatic processes consist of mathematical approaches to study system dynamics for optimization and quantification of product[14].Single substrate or double substrate biochemical reactions make the approaches more interesting,of which the latter is more reasonable and important[15]-[17].

Westerlund stated in[18]that every matter has memory.Although it is debatable,a large number of theoretical physicists considered the memory function as an embedded characteristic of molecular properties,which is discussed in various domains of science and engineering branches[19]-[21].Toledo-Hernandez et al.mentioned in[22]that biochemical reactions involve the participation of living organisms viz.enzymes.The dynamic behavior of living microorganisms not only depends on their current state conditions(e.g.,substrate concentration,medium condition,etc.),but also on their previous states.They have explained this phenomena as the dynamics of the reactions that involve memory effects.Now,it is to be noted that integer-order(IO)derivatives consider only local properties(at time t)while fractional derivatives take into account the history of a process i.e.,their previous states[21].An enzymatic reaction system with IO derivatives is in general memory-less[20],[23]and hence it is unable to reflect the effect of memory.The memory effect can be incorporated in a system by introducing fractional-order(α∈(0,1])derivatives as an index of memory[24]i.e.,α→0 indicates that the system has an ideal memory and α → 1 represents that the system is free from memory.

The conception of fractional calculus is first projected by Leibniz[25]in 1695.A fractional-order differential equation is considered as an alternative model to special nonlinear differential equations[26],[27].In enzyme kinetics,Abdullah[28]employed FDEs in 2011 for modeling the Michaelis-Menten reaction in a 2-d region containing obstacles.In 2013,Alawneh[29]used the multistep generalized differential transform method to solve a time-fractional enzyme kinetics.They investigated dynamical behavior of various complex materials and systems for the benefits of more degrees of freedom and introduction of memory in the model.The drawback of both the studies was the way of introduction of memory.Both of them fractionalized the systems only by changing the orderof the ordinary derivatives on the left-hand side of the ODEs.However,fractionalization of a system of two or more ODEs is not possible without violating mass balance and the system may suffer from unit inconsistencies[21],[30].The problem is not limited to the units.The above difficulty can be removed by considering a common order of all the FDEs of the system,but it is a very particular case and makes its application restricted.Here,we present a more accurate model of a bisubstrate enzymatic reaction,where dynamics are influenced by memory.

In this article,we have introduced fractionalization of a twosubstrate enzymatic reaction to study the effect of memory on it.Nonlinear FDEs cannot,in general,be solved analytically[27],but can be solved by numerical techniques[31].The numerical solutions of the system have been studied here and compared with the integer-order system.We have also observed the dynamics of the different substances of the system by varying the order of the fractional derivatives(which signifies a measure of memory effect in a system[24]).We formulate a control based mathematical model involving the memory effect to conquer the negative effect of the extensive use of memory.

We have organized the rest of the paper as follows.In Section II,we formulate the model of a bi-substrate enzymatic reaction involving the memory effect.Some basic theoretical properties,and the existence and stability of equilibrium points are studied in Section III.In Section IV,a control theoretic approach is introduced towards the fractional-order model.The numerical results are illustrated in Section V.Finally,we have completed our article with a discussion and conclusion of the study in Section VI.

II.THEFRACTIONAL-ORDERMODEL

The schematic diagram of a two-substrate enzyme kinetic reaction,as described by Roy et al.[15],is given by

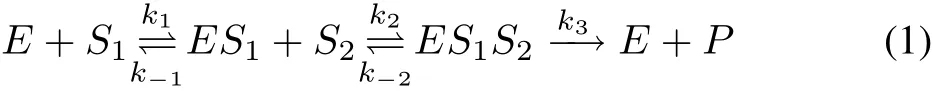
where S1,S2are substrates,E is the enzyme,C1i.e.,ES1and C2i.e.,ES1S2are intermediate complexes and P is the product.k1,k2are the rate constants of formation of the complexes C1and C2respectively,and k3is the rate of product formation.The rates of dissociation of C1and C2are k-1and k-2respectively.

Let us denote the concentrations[S1],[S2],[E],[C1],[C2]and[P]by s1,s2,e,c1,c2and p respectively.From the law of mass action[10],the above enzymatic reaction(1)can be described by the following set of differential equations:

with the initial conditions

From system(2),we have the following relations:

Using the initial conditions(3),from(4),we have

With the help of the relations(5),system(2)can be reduced to the following three dimensional model consisting of substrates s1,s2and complex c2as

with initial conditions,

A.Fractionalization of the System(6)

The schematic diagram(1)can be considered as a threecompartmental model(as shown in Fig.1)[30].The initial stage of the reaction,where substrate S1is reacting with enzyme E to form the complex ES1,is termed as Compartment 1.Compartment 2 describes the intermediate stage where substrate S2is combining with ES1to form ES1S2complex.Compartment 3 consists of the yielding of ES1S2,which may either convert to the product or decompose back to the previous stage of reaction.Here,the mass flux k-2c2is transferred from Compartment 3 to 2(Fig.1)and is common between the second and third equations of(6).We can fractionalize the system(6)as given below[30],[31]:

Fig.1.Three-compartment model corresponding to the schematic diagram(1)of a bi-substrate enzymatic reaction.Rectangular boxes containing E+S1,ES1+S2and ES1S2represent Compartments 1,2 and 3 respectively.E(0),S1(0)and S2(0)are the respective initial values of E,S1and S2.k1,k-1,k2and k-2are the rate at which the mass fluxes are transferred from the source compartment to the targeted one as directed,where k3is the rate of elimination of product P and enzyme E from Compartment 3.

The unit on left-hand side of all the sub-equations of system(8)is Hour-1.Mol/l,the unit of the substances,is nothing but a number.The unit on right-hand side of the first sub-equation of(8)is also Hour-1.Now,the unit ofis Hour-αand that ofi.e.,ofis Hourα-1.Thus,the unit of the termand consequently,the righthand side of both the second and third sub-equations of(8)is Hour-1.Hence,units of all of the sub-equations of(8)remain consistent under the fractionalization process we have considered.

In order to use standard initial conditions,the Riemann-Lioville derivatives must be re-defined as Caputo fractional derivatives[22].The relation between RL and Caputo’s derivatives is given by the following equation:

The system(8)using Caputo derivative can be expressed as follows:

where

Therefore,system(10)becomes

III.THEORETICALSTUDY

In this section,we have determined the equilibrium points of model(11)and discussed their stability from numerical point of view.

A.Existence of Equilibria and Stability

It is not possible to understand the stability of the equilibrium points of the system(11)directly because the fractional derivative does not satisfy Leibniz rule[35].We apply the following transformation:

Using the above transformation(12),system(11)is thus equivalent to the following system:

It is sufficient to study the stability properties of system(13).

System(13)has the equilibrium points(0,0,0,0,s20-s10,0)for δ=s20-s10＞0 and(0,0,0,s?1,0,0)for δ≤0 whereis given by the following equation:

where δ=s20-s10.

Since α is real,it can also be an irrational number.However,there is no existing method for studying such a system with an irrational order of fractional derivatives.Therefore,we assume that α=is rational,where N＞M＞0 and gcd(M,N)=1.

Therefore,the characteristic equation of the matrixis given by,

where “△”and “diag”represent the determinant and the diagonal matrix respectively[36].

Expanding the characteristic equation(16),we have

where

For α=1,from(17),we have

where

Equation(18)is same as the characteristic equation of the integer-order system(6)for the equilibrium point(0,δ,0).

Proceeding as above,we have the characteristic equation ofas follows:

where

Arguments of the roots of the first factor of(19)are of the form,k=0,1,2,...,N-1 and hencefor k=0,1,2,...,N-1.

For α=1,we have,from(19)

which is same as the characteristic equation of the integerorder system(6)for the equilibrium point(,0,0).Hereis defined exactly as in(14).

IV.A CONTROLINDUCEDMODEL

To determine the effect of memory towards the system,we introduce control parameter u(t)into the model(11).Our aim is to get an optimum amount of the product as quick as possible.The control input u(t)is used to reduce the rate of reverse reaction at the second stage satisfying 0≤u(t)≤1.u(t)=1 and 0 represent maximum and minimum use of the control measure respectively.With these assumptions,model(11)becomes:

where s1(0)=s10,s2(0)=s20and c2(0)=0.

Here the control measure basically stands for temperature,pressure,concentrations of the substances[7],[14]etc..We study the effect of the control input on the system(22)from numerical point of view.

V.NUMERICALSIMULATION

In this section,dynamics of reaction kinetics have been analyzed with the help of numerical methods.There are various methods to solve a system of fractional-order differential equations.We have used the numerical scheme given in[31]and solved our system of equations using the Matlab subroutine“l(fā)sqnonlin”and called this method as NS-lsq.Here,we have observed the solutions of the fractional-order system for α =1 i.e.,when the system is free from the “memory effect”and compared them with the integer-order system.The stability region of equilibrium points of the system have also been studied numerically.We have compared the concentration of the substances,particularly the product,for various values of α.Consequently,we determine how the rate of formation of the substances is influenced by the “memory effect”of the system.Here the parameter values are taken from[37]-[39].The units and recommended values of the kinetic parameters used for numerical simulation are as given in Table I.

TABLE I VALUES OFPARAMETERSUSED INNUMERICALCALCULATION

Fig.2.Concentration profiles of the substances for integer-order system(6)(dashed line)and the fractional-order system(13)for α=1(circle).The parameter values are k1=5 M-1h-1,k-1=1 h-1,k2=5 M-1h-1,k-2=1 h-1,k3=5 h-1and the initial values are s10=5 M,s20=5 M,e0=4.5 M where M stands for mol/l.

A.Comparison of the Substance Profiles Obtained From the Fractional System for α=1 and From the Integer-order System

Fig.2 represents the behavioral pattern of the substances for the integer-order(IO)model(6)and the fractional-order(FO)model(13)for α=1 simultaneously.The solutions obtained from both the systems are in good agreement with each other.Concentration of the two substrates(s1and s2)decreases with the progression of the reaction.Consumption of s1is relatively quicker than s2due to faster reaction between enzyme and the primary substrate.Initially,the concentration of the enzyme decreases due to the formation of enzyme-substrate complexes c1and c2.It is recovered as the reaction progresses.Concentration of c1increases gradually from its initial value and it decreases with time,as it binds with s2while forming the second complex.Moreover,the concentration of c2increases as soon as the first complex is formed,and then is decreased as time progresses due to its transformation to the product.Fig.2 displays continuous formation of the product with time until it becomes steady.

B.Stability Region of the Equilibrium Points

The stability regions of the equilibrium points of model system(13)are studied numerically with the help of Theorem 1 of Sardar et al.[31]for reasonable values of the model parameters,where α∈(0,1).We have observed that both equilibrium points are stable for such parameter values,and differentiating only in the time allows it to reach the steady state.Fig.3 represents two stability regions corresponding to the equilibrium pointsandof the system(13).

Fig.3.Stability regions of the equilibrium points(left panel)and (right panel)with respect to α and k-2.Other parameter values corresponding to E?1are taken as k1=5 M-1h-1,k-1=1 h-1,k2=4 M-1h-1,k3=5 h-1,e0=2 M,s10=5 M,s20=6 M and for E?2as k1=5 M-1h-1,k-1=1 h-1,k2=4 M-1h-1,k3=5 h-1,e0=1 M,s10=6 M,s20=5 M.

C.Comparison Among the Concentration Profiles for Different Values of α

We have compared the dynamic profiles of the substances obtained by decreasing α values gradually to 1 and 0.7.It is to be noted that the solutions of(13)for α=1 correspond to the ODE system(6).Fig.4 displays the dynamic profiles of the substances obtained from the IO system(α=1)and the FO system(α=0.7).

As the value of α reduces to 0.7,the concentrations of both the substrates(s1and s2)decrease gradually.It is observed that with and without memory operator has no significant changes in the first substrate.This may be due to the fact that we do not consider memory in the first backward reaction step(see Fig.1).The consumption of the second substrate is faster in comparison to the integer-order system.The profiles of the enzyme concentration show a faster recovery for the lower value of α.Variations in concentration of the first complex(c1)is observed under varying α values.It is found that,the complex concentration c1is lower for α =0.7 than for α =1.It implies that for the lesser value of α,there exists a lower accumulation of c1due to its quicker conversion to the second complex by binding with the second substrate.A relatively faster accumulation of the concentration of second complex(c2)is observed for the smaller value of α.This indicates the possibility of higher conversion of it to the product.Yielding of product is relatively faster for a lower value of α and consequently,its concentration reaches the steady state more quickly.The effect of memory assists in comparatively quickeraccumulation of c2and consequently,a rapid formation of the product.

Fig.4.Concentration profiles of the substances for the fractional-order system(13)for α = 1(solid line)and 0.7(dashed line)where the parameter values are k1=5 M-1h-1,k-1=3 h-1,k2=6 M-1h-1,k-2=3 h-1,k3=5 h-1and the initial values are s10=5 M,s20=5 M,e0=4.5 M.

To study the effect of changes of the time taken for formation of the product due to the changes in α values,we decrease gradually the values of α as 1,0.7 and 0.25.Fig.5 represents the dynamic profiles of the product(p)for the aforesaid α values.Concentrations of the product are observed as 4.771mol/l,4.948mol/l and 4.927mol/l for α=1,0.7 and 0.25 respectively.It is to be noted that as the α values decrease from 1 to 0.7,the formation of product becomes relatively faster than the classic case.However,it is also to be noted that,if the values of α decreased again,the time taken for the formation of product is relatively greater(Fig.5)and consequently,the system slows down.

D.Comparison Among the Concentration Profiles for Different Values of u(t)

Here,we investigate the effect due to the changes of control parameter u(t)to the control induced FO model(22).Fig.6 represents the variation in the substances for u(t)=0,0.4 and 0.9.It is observed that the concentrations of both the substrates(s1and s2)are decreasing more quickly for higher values of the control parameter.Accumulation of the first complex concentration(c1)is lower for upper values of u(t)due to its fast conversion into the second complex.Higher values of the control input corresponds to a more accumulation of c2which ultimately leads to fast formation of the product(p).

We vary the values of the control parameter as 0 and 0.6 to rise above the negative effect of extensive use of memory.Fig.7 represents the concentration profiles of the product for the above values of u(t).The rest of the parameter values are taken exactly as in Fig.5 with α=0.25.Concentration of the product(p)for u(t)=0 is observed as 4.927mol/l,which is decreasing from the value 4.948mol/l for α=0.7(see Fig.5).While,in Fig.7,concentration of the product for u(t)=0.6 is noted as 4.973mol/l.Thus,with proper control measures,it is possible to overcome the above mentioned negative effect.

Fig.5.Concentration profiles of the product p of system(13)for α=1,0.7 and 0.25.Other parameter values are taken as k1=7 M-1h-1,k-1=0.1 h-1,k2=13 M-1h-1,k-2=3 h-1,k3=12 h-1,e0=4.5 M,s10=5 M,s20=5 M.

Fig.6.Concentration profiles of the substances of(22)for u(t)=0,0.4 and 0.9.Other parameter values are taken as k1=5 M-1h-1,k-1=2 h-1,k2=5 M-1h-1,k-2=2 h-1,k3=5 h-1,e0=4.5 M,s10=5 M,s20=5 M and α=0.7.

VI.DISCUSSION ANDCONCLUSION

In this study,we have presented an approach of fractionalizing a bi-substrate enzyme kinetic reaction.The fractionalorder system is solved numerically,as the system is unlikely to have analytical solutions.Our numerical results reveal that the solutions of the fractional-order system for α=1,and the solutions of the corresponding integer-order system are overlapping.Benefits of the fractional-order model are observed from the solutions,mainly in the formation of the product.

Fig.7.Concentration profiles of the product p of system(22)for u(t)=0 and 0.6.Other parameter values are taken as k1=7 M-1h-1,k-1=0.1 h-1,k2=13 M-1h-1,k-2=3 h-1,k3=12 h-1,e0=4.5 M,s10=5 M,s20=5 M and α=0.25.

In Section II,we have calculated the equilibrium points of the FO system and discussed their stability regions.Our study shows that,similar to the integer-order system,equilibrium points remain stable for a fractional-order system with a realistic range of parameters.

We have studied the changes of the concentration profiles of the substances due to the changes in α values(α =1 and 0.7).Lower values of α signifies a faster reaction up to certain threshold values.

We have focused on the changes of concentration of the product due to the change in α values(1,0.7 and 0.25).The system is highly sensitive to the α values.Formation of the product is perceived relatively faster due to “memory effect.”However,extensive effect of memory makes the system slower.The results of our study can predict system dynamics with respect to optimization and quantification of the product.

The dynamical behavior of the substances is observed by varying the control input.Presence of the control parameter corresponds to a quicker reaction.The negative effect of the extensive use of memory can be recovered by proper use of a control measure.

The model can be extended by considering memory in both the backward reaction steps.One can consider the mass k-1c1,which is transferred from Compartment 2 to 1 similar to the way mass k-2c2is transferred from Compartment 3 to 2(see Fig.1).In this context,with the help of relations(5),system(2)can be transformed to a three dimensional model consisting of the substrate s1and the complexes c1,c2.Proceeding as in Section II,one can fractionalize the model.The fractionalized model would consist of termsandof different orders without violating mass balance.Hence in this study,we may summarily conclude that the presence of the mixing parameter may show complex dynamics.