Granular Computing for Data Analytics:A Manifesto of Human-Centric Computing
Witold Pedrycz,Fellow,IEEE
Abstract—In the plethora of conceptual and algorithmic developments supporting data analytics and system modeling,humancentric pursuits assume a particular position owing to ways they emphasize and realize interaction between users and the data.We advocate that the level of abstraction,which can be flexibly adjusted,is conveniently realized through Granular Computing.Granular Computing is concerned with the development and processing information granules–formal entities which facilitate a way of organizing knowledge about the available data and relationships existing there.This study identifies the principles of Granular Computing,shows how information granules are constructed and subsequently used in describing relationships present among the data.
I.INTRODUCTION
THE apparent reliance on data and experimental evidence in system modeling,decision-making,pattern recognition,and control engineering,just to enumerate several representative spheres of interest,entails the centrality of data and emphasizes their paramount role in data science.To capture the essence of data,facilitate building their essential descriptors and reveal key relationships,as well as having all these faculties realized in an efficient manner as well as deliver transparent,comprehensive,and user-oriented results,we advocate a genuine need for transforming data into information granules.In the realized setting,information granules become regarded as conceptually sound knowledge tidbits over which various models could be developed and utilized.
A tendency,which is being witnessed more visibly nowadays,concerns human centricity.Data science and big data revolve around a two-way efficient interaction with users.Users interact with data analytics processes meaning that the terms such as data quality,actionability,transparency are of relevance and are provided in advance.With this regard,information granules emerge as a sound conceptual and algorithmic vehicle owing to their way of delivering a more general view at data,ignoring irrelevant details and supporting a suitable level of abstraction aligned with the nature of the problem at hand.
Our objective is to provide a general overview of Granular Computing,identify the main items on its agenda and associate their usage in the setting of data analytics.To organize our discussion in a coherent way and highlight the main threads as well as deliver a self-contained material,the study is structured in a top-down manner.Some introductory material offering some motivating insights into the existing formalisms is covered in Section II.Section III is devoted to the design of information granules with a delineation of the main directions.The principle of justifiable granularity is presented in depth including both its generic version and a number of essential augmentations.The shift of paradigm implied by the involvement of information granules is covered in Section IV;here a thorough discussion of the main directions building a diversified landscape Granular Modeling and Data Analytics is presented.Passive and active aggregation mechanisms required in the realization of distributed data analysis are included in Section V.
II.INFORMATIONGRANULES ANDINFORMATION GRANULARITY
The framework of Granular Computing along with a diversity of its formal settings offers a critically needed conceptual and algorithmic environment.A suitable perspective built with the aid of information granules is advantageous in realizing a suitable level of abstraction.It also becomes instrumental when forming sound and pragmatic problem-oriented tradeoffs among precision of results,their easiness of interpretation,value,and stability(where all of these aspects contribute vividly to the general notion of actionability).
Information granules are intuitively appealing constructs,which play a pivotal role in human cognitive and decisionmaking activities(Bargiela and Pedrycz[1],[2];Zadeh[3],[4]).We perceive complex phenomena by organizing existing knowledge along with available experimental evidence and structuring them in a form of some meaningful,semantically sound entities,which are central to all ensuing processes of describing the world,reasoning about the environment,and support decision-making activities.
The terms information granules and information granularity themselves have emerged in different contexts and numerous areas of application.Information granule carries various meanings.One can refer to Artificial Intelligence(AI)in which case information granularity is central to a way of problem solving through problem decomposition,where various subtasks could be formed and solved individually.Information granules and the area of intelligent computing revolving around them being termed Granular Computing are quite often presented with a direct association with the pioneering studies by Zadeh[3].He coined an informal,yet highly descriptive and compelling concept of information granules.Generally,by information granules one regards a collection of elements drawn together by their closeness(resemblance,proximity,functionality,etc.)articulated in terms of some useful spatial,temporal,or functional relationships.Subsequently,Granular Computing is about representing,constructing,processing,and communicating information granules.The concept of information granules is omnipresent and this becomes well documented through a series of applications,cf.(Leng et al.[5];Loia et al.[6];Pedrycz and Bargiela[7];Pedrycz and Gacek[8];Zhou et al.[9]).
Granular Computing exhibits a variety of conceptual developments;one may refer here to selected pursuits:
graphs(Wang and Gong[10];Chiaselotti et al.[11];Pal et al.[12])
information tables(Chiaselotti et al.[13])
mappings(Salehi et al.[14])
knowledge representation(Chiaselotti et al.[15])
micro and macro models(Bisi et al.[16])
association discovery and data mining(Honko[17];Wang et al.[18])
clustering(Tang et al.[19])and rule clustering(Wang et al.[20])
classification(Liu et al.[21];Savchenko[22])
There are numerous applications of Granular Computing,which are reported in recent publications:
Forecasting time series(Singh and Dhiman[23];Hryniewicz and Karczmarek[24])
Prediction tasks(Han et al.[25])
Manufacturing(Leng et al.[5])
Concept learning(Li et al.[26])
Perception(Hu et al.[27])
Optimization(Martinez-Frutos et al.[28])
Credit scoring(Saberi et al.[29])
Analysis of microarray data(Ray et al.[30];Tang et al.[31])
It is again worth emphasizing that information granules permeate almost all human endeavors.No matter which problem is taken into consideration,we usually set it up in a certain conceptual framework composed of some generic and conceptually meaningful entities—information granules,which we regard to be of relevance to the problem formulation,further problem solving,and a way in which the findings are communicated to the community.Information granules realize a framework in which we formulate generic concepts by adopting a certain level of generality.
Information granules naturally emerge when dealing with data,including those coming in the form of data streams.The ultimate objective is to describe the underlying phenomenon in an easily understood way and at a certain level of abstraction.This requires that we use a vocabulary of commonly encountered terms(concepts)and discover relationships between them and reveal possible linkages among the underlying concepts.
Information granules are examples of abstractions.As such they naturally give rise to hierarchical structures:the same problem or system can be perceived at different levels of specificity(detail)depending on the complexity of the problem,available computing resources,and particular needs to be addressed.A hierarchy of information granules is inherently visible in processing of information granules.The level of captured details(which is represented in terms of the size of information granules)becomes an essential facet facilitating a way a hierarchical processing of information with different levels of hierarchy indexed by the size of information granules.
Even such commonly encountered and simple examples presented above are convincing enough to lead us to ascertain that(a)information granules are the key components of knowledge representation and processing,(b)the level of granularity of information granules(their size,to be more descriptive)becomes crucial to the problem description and an overall strategy of problem solving,(c)hierarchy of information granules supports an important aspect of perception of phenomena and deliver a tangible way of dealing with complexity by focusing on the most essential facets of the problem,(d)there is no universal level of granularity of information;commonly the size of granules is problem-oriented and user dependent.
Human-centricity comes as an inherent feature of intelligent systems.It is anticipated that a two-way effective humanmachine communication is imperative.Human perceive the world,reason,and communicate at some level of abstraction.Abstraction comes hand in hand with non-numeric constructs,which embrace collections of entities characterized by some notions of closeness,proximity,resemblance,or similarity.These collections are referred to as information granules.Processing of information granules is a fundamental way in which people process such entities.Granular Computing has emerged as a framework in which information granules are represented and manipulated by intelligent systems.The two-way communication of such intelligent systems with the users becomes substantially facilitated because of the usage of information granules.
It brings together the existing plethora of formalisms of set theory(interval analysis)under the same banner by clearly visualizing that in spite of their visibly distinct underpinnings(and ensuing processing),they exhibit some fundamental commonalities.In this sense,Granular Computing establishes a stimulating environment of synergy between the individual approaches.By building upon the commonalities of the existing formal approaches,Granular Computing helps assemble heterogeneous and multifaceted models of processing of information granules by clearly recognizing the orthogonal nature of some of the existing and well established frameworks(say,probability theory coming with its probability density functions and fuzzy sets with their membership functions).Granular Computing fully acknowledges a notion of variable granularity,whose range could cover detailed numeric entities and very abstract and general information granules.It looks at the aspects of compatibility of such information granules and ensuing communication mechanisms of the granular worlds.Granular Computing gives rise to processing that is less time demanding than the one required when dealing with detailed numeric processing.
A.Frameworks of Information Granules
There are numerous formal frameworks of information granules;for illustrative purposes,we recall some selected alternatives.
Sets(intervals)realize a concept of abstraction by introducing a notion of dichotomy:we admit element to belong to a given information granule or to be excluded from it.Along with the set theory comes a well-developed discipline of interval analysis(Alefeld and Herzberger[32];Moore[33];Moore et al.[34]).
Fuzzy sets deliver an important conceptual and algorithmic generalization of sets(Dubois and Prade[35]-[37];Klir and Yuan[38];Nguyen and Walker[39];Pedrycz et al.[40];Pedrycz and Gomide[41];Zadeh[42]-[44]).By admitting partial membership of an element to a given information granule,we bring an important feature which makes the concept to be in rapport with reality.It helps working with the notions,where the principle of dichotomy is neither justified,nor advantageous.
Fuzzy sets come with a spectrum of operations,usually realized in terms of triangular norms(Klement et al.[45];Schweizer and Sklar[46]).
Shadowed sets(Pedrycz[47],[48])offer an interesting description of information granules by distinguishing among three categories of elements.Those are the elements,which(i)fully belong to the concept,(ii)are excluded from it,(iii)their belongingness is completely unknown.
Rough sets(Pawlak[49]-[52],Pawlkak and Skowron[53])are concerned with a roughness phenomenon,which arises when an object(pattern)is described in terms of a limited vocabulary of certain granularity.The description of this nature gives rise to a so-called lower and upper bounds forming the essence of a rough set.
The list of formal frameworks is quite extensive;as interesting examples,one can recall here probabilistic sets(Hirota[54])and axiomatic fuzzy sets(Liu and Pedrycz[55]).
There are two important directions of generalizations of information granules,namely information granules of higher type and information granules of higher order.The essence of information granules of higher type means that the characterization(description)of information granules is described in terms of information granules rather than numeric entities.Well-known examples are fuzzy sets of type-2,granular intervals,imprecise probabilities.For instance,a type-2 fuzzy set is a fuzzy set whose grades of membership are not single numeric values(membership grades in[0,1])but fuzzy sets,intervals or probability density functions truncated to the unit interval.There is a hierarchy of higher type information granules,which are defined in a recursive manner.Therefore we talk about type-0,type-1,type-2 fuzzy sets,etc.In this hierarchy,type-0 information granules are numeric entities,say,numeric measurements.With regard to higher order information granules are granules defined in some space whose elements are information granules themselves.
III.INFORMATIONGRANULES–DESIGNDIRECTION AND MAINCHARACTERIZATION
A.Clustering:From Data to Information Granules
Along with a truly remarkable diversity of detailed algorithms and optimization mechanisms of clustering,the paradigm itself leads to the formation of information granules(associated with the ideas and terminology of fuzzy clustering,rough clustering,and others)and applies both to numeric data and information granules.Information granules built through clustering are predominantly data-driven,viz.clusters(either in the form of fuzzy sets,sets,or rough sets)are a manifestation of a structure encountered(discovered)in the data.
Numeric prototypes are formed through invoking clustering algorithms,which yield a partition matrix and a collection of the prototypes.Clustering realizes a certain process of abstraction producing a small number of the prototypes based on a large number of numeric data.Interestingly,clustering can be also completed in the feature space.In this situation,the algorithm returns a small collection of abstracted features(groups of features)that might be referred to as meta-features.
Two ways of generalization of prototypes treated as key descriptors of data and manageable chunks of knowledge are considered:(i)symbolic and(ii)granular.In the symbolic generalization,one moves away from the numeric values of the prototypes and regards them as sequences of integer indexes(labels).Along this line,developed are concepts of(symbolic)stability and(symbolic)resemblance of data structures.The second generalization motivates the buildup of granular prototypes,which arise as a direct quest for a more comprehensive representation of the data than the one delivered through numeric entities.This entails that information granules(including their associated level of abstraction),have to be prudently formed to achieve the required quality of the granular model.
As a consequence,the performance evaluation embraces the following sound alternatives:(i)evaluation of representation capabilities of numeric prototypes,(ii)evaluation of representation capabilities of granular prototypes,and(iii)evaluation of the quality of the granular model
In the first situation,the representation capabilities of numeric prototypes are assessed with the aid of a so-called granulation-degranulation scheme yielding a certain reconstruction error.The essence of the scheme can be schematically portrayed as x→internal representation→reconstruction.The formation of the internal representation is referred to as granulation(encoding)whereas the process of degranulation(decoding)can be sought as an inverse mechanism to the encoding scheme.In terms of detailed formulas one has the following
1)encoding leading to the degrees of activation of information granules by input x,say A1(x),A2(x),...,Ac(x)with

in case the prototypes are developed with the use of the Fuzzy C-Means(FCM)clustering algorithm,the parameter m(>1)stands for the fuzzification coefficient and‖·‖denotes the Euclidean distance.
2)degranulation producing a reconstruction of x via the following expression
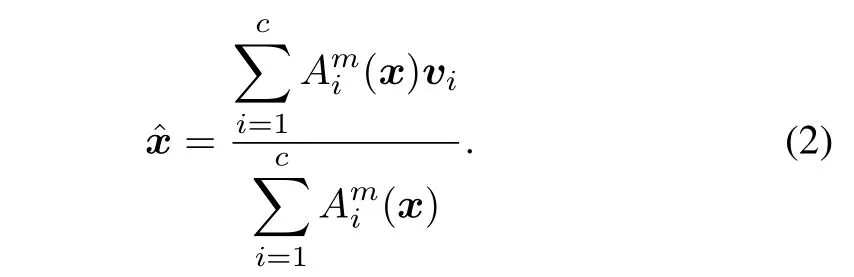
It is worth stressing that the above stated formulas are a consequence of the underlying optimization problems.For any collection of numeric data,the reconstruction error is a sum of squared errors(distances)of the original data and their reconstructed versions.
B.The Principle of Justifiable Granularity
The principle of justifiable granularity guides a construction of an information granule based on available experimental evidence.In a nutshell,a resulting information granule becomes a summarization of data(viz.the available experimental evidence).The underlying rationale behind the principle is to deliver a concise and abstract characterization of the data such that(i)the produced granule is justified in light of the available experimental data,and(ii)the granule comes with a welldefined semantics meaning that it can be easily interpreted and becomes distinguishable from the others.
Formally speaking,these two intuitively appealing criteria are expressed by the criterion of coverage and the criterion of specificity.Coverage states how much data are positioned behind the constructed information granule.Put it differently–coverage quantifies an extent to which information granule is supported by available experimental evidence.Specificity,on the other hand,is concerned with the semantics of information granule stressing the semantics(meaning)of the granule.
The definition of coverage and specificity requires formalization and this depends upon the formal nature of information granule to be formed.As an illustration,consider an interval form of information granule A.In case of intervals built on a basis of one-dimensional numeric data(evidence)x1,x2,...,xN,the coverage measure is associated with a count of the number of data embraced by A,namely

card(·)denotes the cardinality of A,viz.the number(count)of elements xkbelonging to A.The specificity of A,sp(A)is regarded as a decreasing function g of the size(length)of information granule.If the granule is composed of a single element,sp(A)attains the highest value and returns 1.If A is included in some other information granule B,then sp(A)>sp(B).In a limit case if A is an entire space sp(A)returns zero.For an interval-valued information granule A=[a,b],a simple implementation of specificity with g being a linearly decreasing function comes as
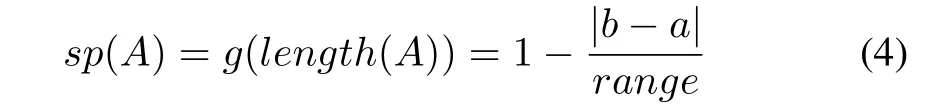
where range stands for an entire space over which intervals are defined.
If we consider a fuzzy set as a formal setting for information granules,the definitions of coverage and specificity are reformulated to take into account the nature of membership functions admitting a notion of partial membership.Here we invoke the fundamental representation theorem stating that any fuzzy set can be represented as a family of its α-cuts,namely
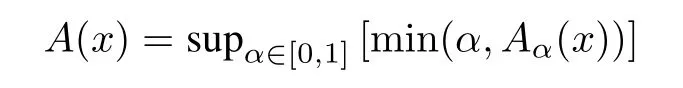
where
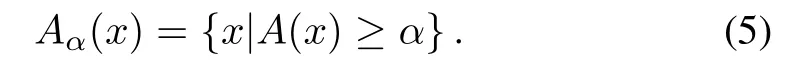
The supremum(sup)is taken over all values of α.In virtue of the theorem we have any fuzzy set represented as a collection of sets.
Having this in mind and considering(3)as a point of departure for constructs of sets(intervals),we have the following relationships
1)coverage
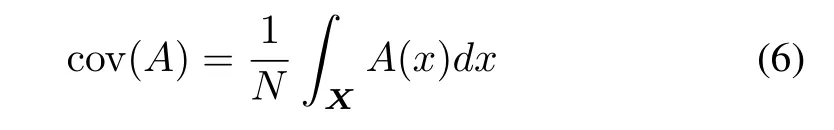
where X is a space over which A is defined;moreover one assumes that A can be integrated.The discrete version of the coverage expression comes in the form of the sum of membership degrees.
2)specificity
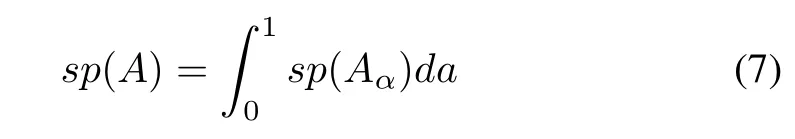
Note that(6)–(7)directly generalize(3).The one-dimensional case can be extended to the multidimensional situation;here the count of data falling within the bounds of the information granule involves some distance function,namely
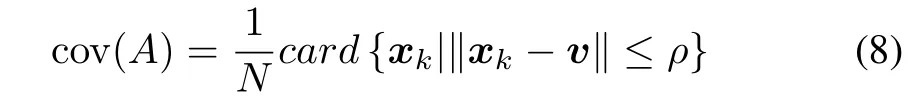
where xkand v are the data and the numeric representative positioned in the space of real numbers Rn.The specificity is expressed as sp(A)=1-ρ(assuming that the data are normalized).
The key objective is to build an information granule so that it achieves the highest value of coverage and specificity.These criteria are in conflict:increasing the coverage reduces specificity and vice versa.A viable alternative is to take the product of these two components and construct information granule so that this product attains its maximal value.In other words,the optimal values of the parameters of information granule,say,wopt,are those for which one has
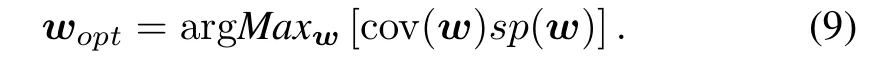
Note that both the coverage and specificity are functions of w.The principle of justifiable granularity highlights an important facet of elevation of the type of information granularity:the result of capturing numeric experimental evidence is a single abstract entity—information granule.As various numeric data can be thought as information granule of type-0,the result becomes a single information granule of type-1.This is a general phenomenon of elevation of the type of information granularity.The increased level of abstraction is a direct consequence of the diversity present in the originally available granules.This elevation effect is of a general nature and can be emphasized by stating that when dealing with experimental evidence composed of information granules of type-n,the result becomes a single information granule of type(n+1).
From the perspective of algorithmic developments,the construction of information granules embraces two phases.First a numeric representative of experimental evidence is formed(usually considering some well known alternatives such as a mean,weighed mean,median,etc.).Second,an information granule is spanned over this initial numeric representative and the development of an interval,fuzzy set,etc.is guided by the maximization of the product of the coverage and specificity.
As a way of constructing information granules,the principle of justifiable granularity exhibits a significant level of generality in two essential ways.First,given the underlying requirements of coverage and specificity,different formalisms of information granules can be engaged.Second,experimental evidence could be expressed as information granules in different formalisms and on this basis certain information granule is being formed.
It is worth stressing that there is a striking difference between clustering and the principle of justifiable granularity.First,clustering leads to the formation at least two information granules(clusters)whereas the principle of justifiable granularity produces a single information granule.Second,when positioning clustering and the principle vis-`a-vis each other,the principle of justifiable granularity can be sought as a follow-up step facilitating an augmentation of the numeric representative of the cluster(such as e.g.,a prototype)and yielding granular prototypes where the facet of information granularity is.
So far,the principle of justifiable granularity presented is concerned with a generic scenario meaning that experimental evidence gives rise to a single information granule.Several conceptual augmentations are considered where several sources of auxiliary information is supplied:
Involvement of auxiliary variable.Typically,these could be some dependent variable one encounters in regression and classification problems.An information granule is built on a basis of experimental evidence gathered for some input variable and now the associated dependent variable is engaged.In the formulation of the principle of justifiable granularity,this additional information impacts a way in which the coverage is determined.In more detail,we discount the coverage;in its calculations,one has to take into account the nature of experimental evidence assessed on a basis of some external source of knowledge.In regression problems(continuous output/dependent variable),in the calculations of specificity,we consider the variability of the dependent variable y falling within the realm of A.More precisely,the value of coverage is discounted by taking this variability into consideration.In more detail,the modified value of coverage is expressed as
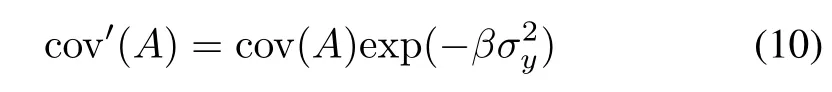
where σ is a standard deviation of the output values associated with the inputs being involved in the calculations of the original coverage cov(A).β is a certain calibration factor controlling an impact of the variability encountered in the output space.Obviously,the discount effect is noticeable,cov′(A)< cov(A).
In case of a classification problem in which p classes are involved ω ={ω1ω2...ωp},the coverage is again modified(discounted)by the diversity of the data embraced by the information granule where this diversity is quantified in the form of the entropy function h(ω)
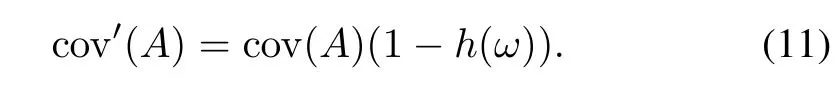
This expression penalizes the diversity of the data contributing to the information granule and not being homogeneous in terms of class membership.The higher the entropy,the lower the coverage cov′(A)reflecting the accumulated diversity of the data falling within the umbrella of A.If all data for which A has been formed belong to the same class,the entropy returns zero and the coverage is not reduced,cov′(A)=cov(A).
C.Symbolic View at Information Granules and Their Symbolic Characterization
Information granules are described through numeric parameters(or eventually granular parameters in case of information granules of higher type).There is an alternative view at a collection of information granules where we tend to move away from numeric details and instead look at the granules as symbols and engage them in further symbolic processing.Interestingly,symbolic processing is vividly manifested in Artificial Intelligence(AI).
Consider a collection of information granules Aidescribed by their numeric prototypes vi.Information granules can be described in different feature spaces F1,F2,...Fi,....In terms of the features,these spaces could overlap.The prototypes are projected on the individual variables and their projections are ordered linearly.At the same time,the distinguishability of the prototypes is evaluated:if two projected prototypes are close to each other they are deemed indistinguishable and collapsed.The merging condition involves the distance between the two close prototypes:If|vi-vi+1|< range/cε then the prototypes are deemed indistinguishable.Here the range is the range of values assumed by the prototypes and ε is a certain threshold value less than 1.
Once this phase has been completed,Ais are represented in a concise manner as sequences of indexes Ai=(i1,i2,...,ini).Note that each Aiis described in its own feature space.Denote by Rija set of features for which Aiand Ajoverlap viz.the features being common to both information granules.The distance between these two granules expressed along the k-th feature is computed as the ratio
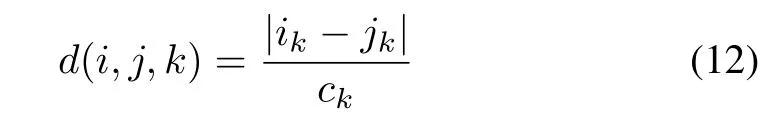
where ckdenotes the number of prototypes(after eventual merging)projected on the k-th feature.Next the similarity between Aiand Ajis determined based on the above indexes determined for the individual features in the form
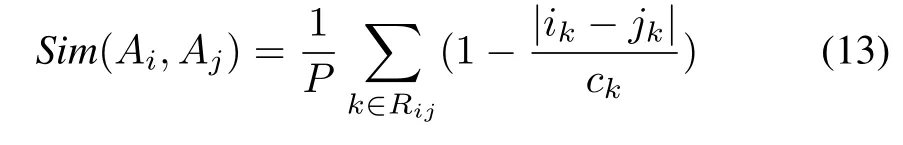
where P is the overall number of features(attributes)present in the problem.
D.Granular Probes of Spatiotemporal Data
When coping with spatiotemporal data,(say time series of temperature recorded over in a given geographic region),a concept of spatiotemporal probes arises as an efficient vehicle to describe the data,capture their local nature,and articulate their local characteristics as well as elaborate on their abilities as modeling artifacts(building blocks).The experimental evidence is expressed as a collection of data zk=z(xk,yk,tk)with the corresponding arguments describing the location(x,y),time(t)and the value of the temporal data zk.
Here an information granule is positioned in a threedimensional space:
(i)space of spatiotemporal variable z
(ii)spatial position defined by the positions(x,y)
(iii)temporal domain described by time coordinate
The information granule to be constructed is spanned over some position of the space of values z0,spatial location(x0,y0)and temporal location t0.With regard to the spatial location and the temporal location,we introduce some predefined level of specificity,which imposes a level of detail considered in advance.The coverage and specificity formed over the special and temporal domain are defined in the form
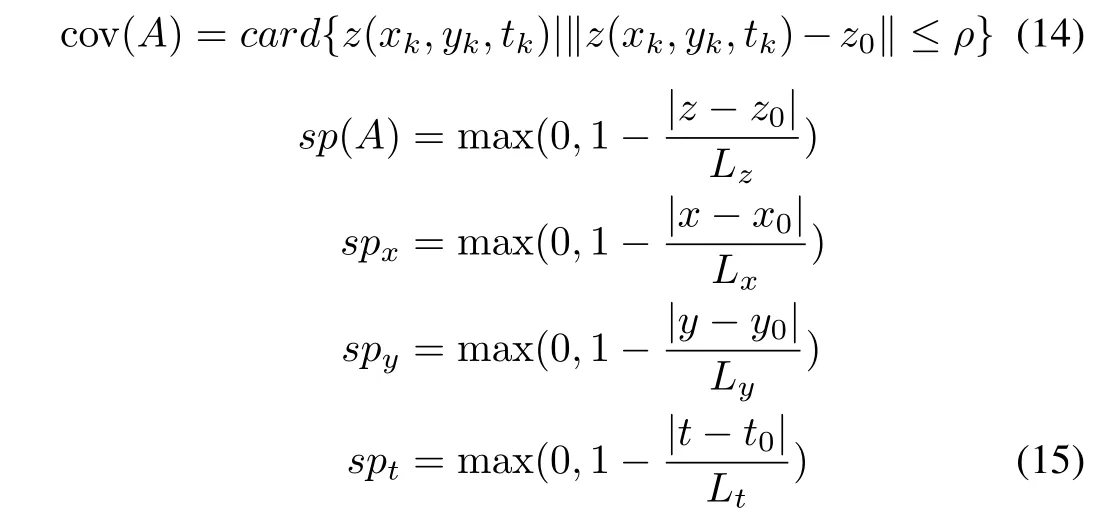
where the above specifity measures are monotonically decreasing functions(linear functions in the case shown above).There are some cutoff ranges(Lx,Ly...),which help impose a certain level of detail used in the construction of the information granule.Information granule A in the space of the spatiotemporal variable is carried out as before by maximizing the product of coverage of the data and the specificity,cov(A)sp(A)however in this situation one considers the specificity that is associated with the two other facets of the problem.In essence,A is produced by maximizing the product cov(A)sp(A)spxspyspt.
E.Building Granular Prototypes
The results of clustering coming in the form of numeric prototypes v1,v2,...,vccan be further augmented by forming information granules giving rise to so-called granular prototypes.This can be regarded as a result of an immediate usage of the principle of justifiable granularity and its algorithmic underpinning as elaborated earlier.Around the numeric prototype vi,one spans an information granule Vi,Vi=(vi,ρi)whose optimal size is obtained as the result of the maximization of the well-known criterion
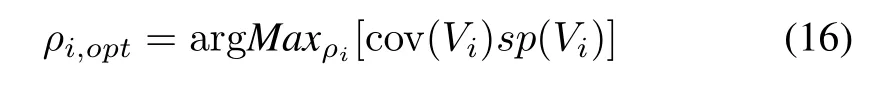
where
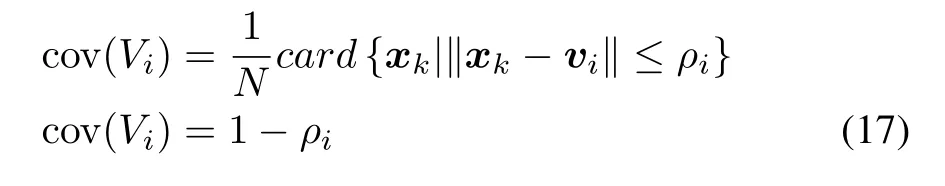
assuming that we are concerned with normalized data.
It is worth noting that having a collection of granular prototypes,one can conveniently assess their abilities to represent the original data(experimental evidence).The reconstruction problem,as outlined before for numeric data,can be formulated as follows:given xk,complete its granulation and degranulation using the granular prototypes Vi,i=1,2,...,c.The detailed computing generalizes the reconstruction process completed for the numeric prototypes and for given x yields a granular resultwhere
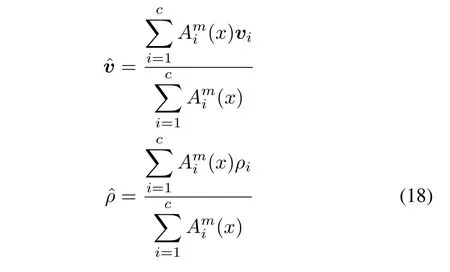
The quality of reconstruction uses the coverage criterion formed with the aid of the Boolean predicate
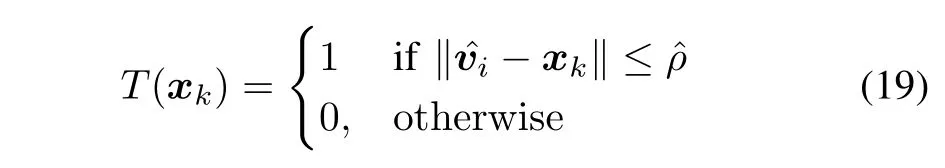
and for all data one takes the sum of(19)over them.It is worth noting that in addition to the global measure of quality of granular prototypes,one can associate with them their individual quality(taken as a product of the coverage and specificity computed in the formation of the corresponding information granule).
IV.THEPARADIGMSHIFT INDATAANALYTICS:FROM NUMERICDATA TOINFORMATIONGRANULES AND MODELINGCONSTRUCTS
The paradigm shift implied by the engagement of information granules becomes manifested in several tangible ways including(i)a stronger dependence on data when building structure-free,user-oriented,and versatile models spanned over selected representatives of experimental data,(ii)emergence of models at various varying levels of abstraction(generality)being delivered by the specificity/generality of information granules,and(iii)building a collection of individual local models and supporting their efficient aggregation.
A functional scheme emerging as a consequence of the above discussion and advocated by the agenda of Granular Computing is succinctly outlined in Fig.1.
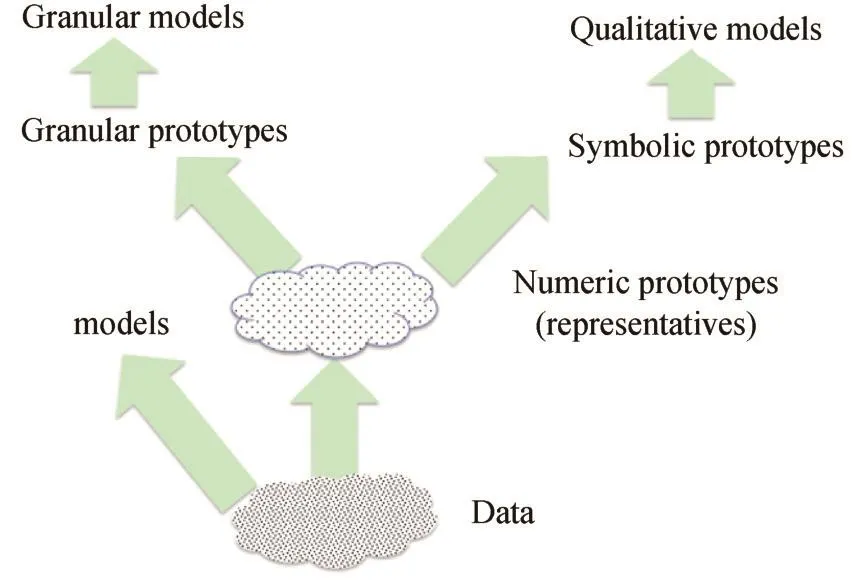
Fig.1.A landscape of Granular Modeling and Data Analytics:main design pursuits.
Here several main conceptually and algorithmically farreaching paths are emphasized.Notably,some of them have been studied to some extent in the past and several open up new directions worth investigating and pursuing.In what follows,we elaborate on them in more detail pointing at the relationships among them.
data→numeric models.This is a traditionally explored path being present in system modeling for decades.The original numeric data are used to build the model.There are a number of models,both linear and nonlinear exploiting various design technologies,estimation techniques and learning mechanisms associated with evaluation criteria where accuracy and interpretability are commonly exploited with the Occam razor principle assuming a central role.The precision of the model is an advantage however the realization of the model is impacted by the dimensionality of the data(making a realization of some models not feasible);questions of memorization and a lack of generalization abilities are also central to the design practices.
data→numeric prototypes.This path associates with the concise representation of data by means of a small number of representatives(prototypes).The tasks falling within this scope are preliminary to data analytics problems.Various clustering algorithms constitute generic development vehicles using which the prototypes are built as a direct product of the grouping method.
data→numeric prototypes→symbolic prototypes.This alternative branches off to symbolic prototypes where on purpose we ignore the numeric details of the prototypes with intent to deliver a qualitative view at the information granules.Along this line,concepts such as symbolic(qualitative)stability and qualitative resemblance of structure in data are established.
data→numeric prototypes→granular prototypes.This path augments the previous one by bringing the next phase in which the numeric prototypes are enriched by their granular counterparts.The granular prototypes are built in such a way so that they deliver a comprehensive description of the data.The principle of justifiable granularity helps quantify the quality of the granules as well as deliver a global view at the granular characterization of the data.
data→numeric prototypes→symbolic prototypes→qualitative modeling.The alternative envisioned here builds upon the one where symbolic prototypes are formed and subsequently used in the formation of qualitative models,viz.the models capturing qualitative dependencies among input and output variables.This coincides with the well-known subarea of AI known as qualitative modeling,see Forbus[56]with a number of applications(Abou-Jaoude et al.[57];Bolloju[58];Guerrin[59];Haider et al.[60];Wong et al.[61];Zabkar et al.[62]).
data→numeric prototypes→granular prototypes→granular models.This path constitutes a direct extension of the previous one when granular prototypes are sought as a collection of high-level abstract data based on which a model is being constructed.In virtue of the granular data,we refer to such models as granular models.
V.DISTRIBUTEDDATAANALYSIS ANDSYSTEM MODELING:PASSIVE ANDACTIVEAGGREGATION MECHANISMS
In distributed data analysis and system modeling,the following formulation of the problem can be outlined.There are some sources of data composed of different data subsets and feature(attribute)subsets.An example is a collection of models built for a complex phenomenon where a lot of data using different features are available locally and used to construct local models.Denote these models as M1,M2,...,Mpwhere p stands for the number of models being considered.As the models provide individual views at the phenomenon,an overall(global)view is obtained by aggregating the results produced by the models,our objective is to develop an aggregation mechanism.Irrespectively of the computing details of the aggregation,one can assume in view of the inherent diversity of numeric results produced by the models,the aggregation outcome becomes an information granule.
Two modes of aggregation architecture are envisioned,namely a passive and an active aggregation mode.
Passive mode of aggregation.The essence of this mode is illustrated in Fig.2.
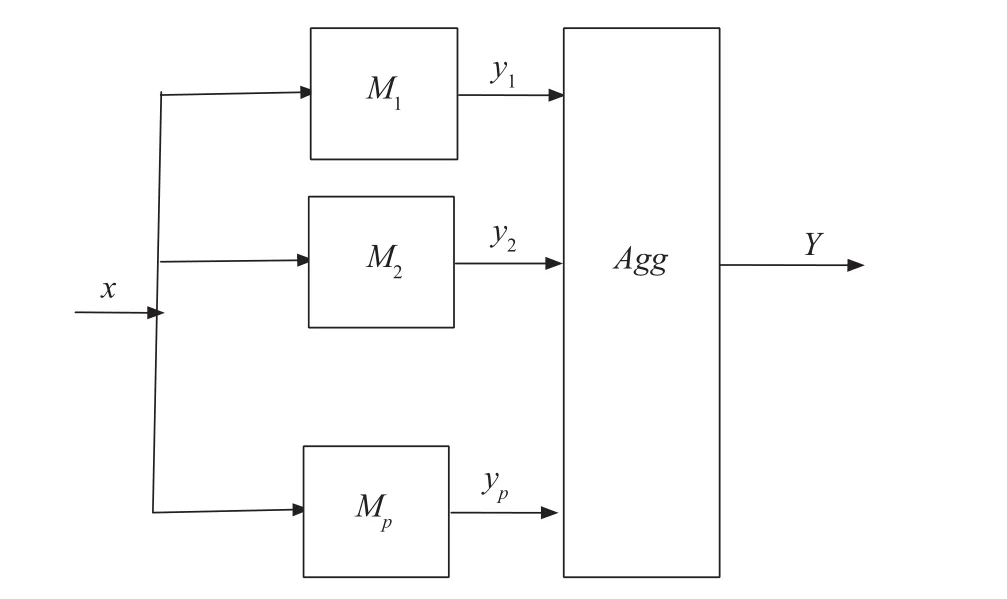
Fig.2. A general scheme of a passive mode of aggregation.
Let us proceed with computing details.The models were constructed using some data.As each model comes with its performance index,we introduce a weight of the corresponding model,say q1,q2,...,qp.The lower the performance(say,an RMSE index obtained for the i-th local model),the higher the corresponding weight qi.
For the realization of the aggregation mechanism and its evaluation,we consider some data set D composed of N data x(k).The inputs are presented to the individual models yielding the corresponding results
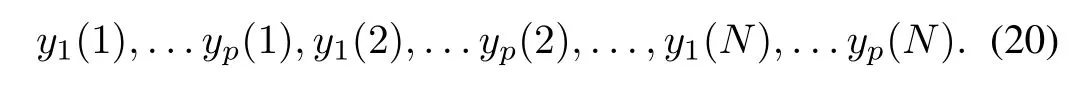
In light of the existing weights,the above data are associated with them forming a set
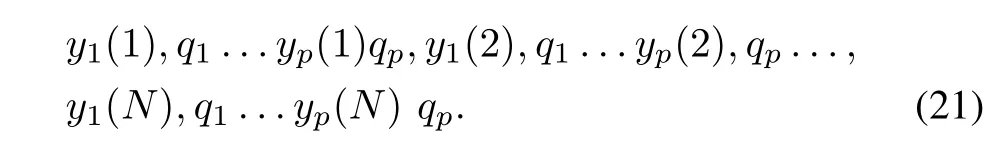
For any x(k),the models produce the results y1(k),y2(k)...yp(k)with the corresponding weights.This means that the principle of justifiable granularity applied to the kth data(outputs of the models)y1(k),y2(k)...yp(k)yields the information granule Y(k).Formally speaking we have Y(k)=arga(k),b(k)[cov(k)sp(k)]where a(k)and b(k)are the bounds of the optimal interval information granule.The principle of justifiable granularity can be also applied to the weighted data coming in the form of the pairs y1(k),q1,y2(k),q2,...yp(k),qp.The aggregation module,Fig.2,produces an information granule by invoking the principle of justifiable granularity where the weighted data are considered.To evaluate the quality of the aggregation based on the data D,we associate with any k,the obtained value of the performance index for which Y(k)has been obtained.For this optimal information granule,the corresponding maximized product of coverage and specificity is denoted as T(k).For all data,we take the averageP.The higher the value of T,the better the quality of the aggregation outcome.
Active mode of aggregation.In contrast to the passive aggregation mechanism used to combine models,active aggregation means that the results produced by the individual models are actively modified(Fig.3).The essence of this active modification is to endow the aggregation process with some highly desired flexibility so that the consensus could be enhanced.While bringing in someflexibility to the results to be aggregated increase overall consensus,at the same time the quality of the local model is reduced(as we strive to improve quality of the aggregated results and are inclined to sacrifice the quality of the model).A sound balance needs to be set up so that the consensus level is increased not significantly affecting the quality of the individual models.
A viable approach is to invoke here a randomization mechanism,refer to Fig.3,see also Li and Wang[63].It makes the numeric output of each model random as we additively include some noise of a certain intensity(standard deviation).The higher the variance,the higher the random flexibility of the model and the higher the ability to achieve higher value of consensus of results produced by the models.In other words,the original outputs of the models y1(k),y2(k)...yp(k)are replaced byi=1,2,...,p where=yi(k)+zi(k)where zi(k)is a certain random variable of standard deviation σ.It is apparent that because of randomness with some probability themay become closer to each other as the original yi(k)s.In other words,we may anticipate higher consensus arising among the models impacted by the noise factor.Obviously,the randomly biased outputs are more distant from the results produced by the already constructed models meaning that the performance of the models produced by the noisy outputs deteriorates and this aspect has to be taken into consideration when quantifying the overall process of reconciling the models.In building information granules Y(k)as already completed in the passive mode of aggregation,we follow the same scheme but now the weighting of the randomized dataare coming with the weightswhose values are discounted because of the difference between yi(k)and the noise-affected versionThe higher the distance between them,the lower the current weight.In this sense,the higher the standard deviation σ,the lower the corresponding weight.An example expression for the weight can be described in the following form
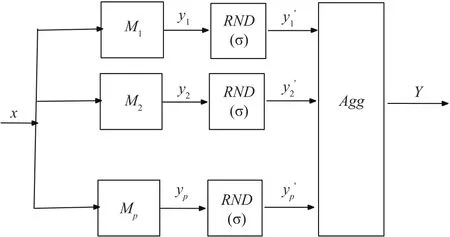
Fig.3. Active mode of aggregation.
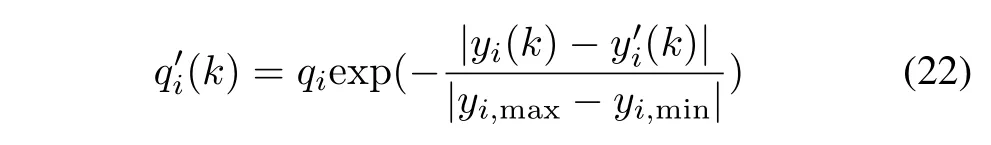
where yi,maxand yi,minare the bounds of the output produced by the i-th model.Note that if the randomized version of the output of the model coincides with the output of the original model,there is no change to the value of the weight,.Progressing with the weighted principle of justi fiable granularity applied to the data in the following format
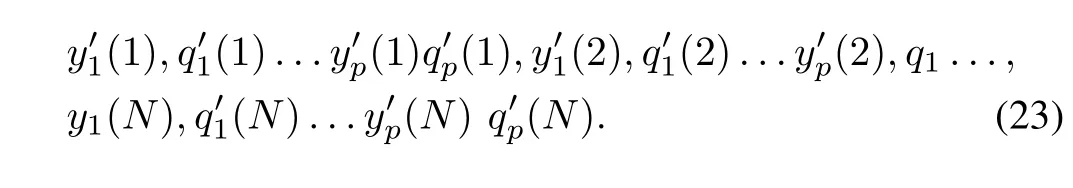
The evaluation of the consensus built for the randomized outputs of the model is more elaborate because of the randomness factor that needs to be taken into consideration.Consider the outputs of the models for some fixed data(k)coming from D,namelyyielding through the use of the principle of justifiable granularity information granule Y(k).In virtue of the random nature of the data used in the principle,the process is repeated many times(with various randomly impacted outputs of the models),the corresponding information granules are determined along with the corresponding values of the product of coverage and specificity.We pick up the information granule Y(k)associated with the highest performance index.In other words,Y(k)can be expressed as
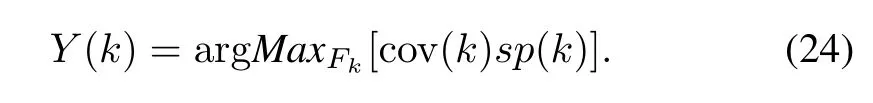
where Fkis a collection of tuples randomly impacted outputs of the models.The overall quality of consensus(aggregation)produced for all,data can be expressed as the following average T
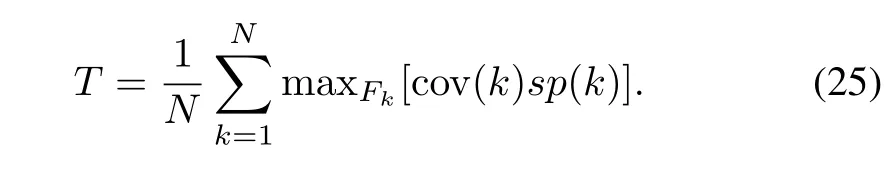
As anticipated,the higher the randomness involved(s),the higher the above average.This implies that the better aggregation outcomes are formed because of higher consistency of the outputs produced by the individual models.As noted earlier,this comes with the deterioration of the quality of the models and this effect can be observed by monitoring the values ofbeing regarded as a function of σ.To gain a general overview,we consider the average
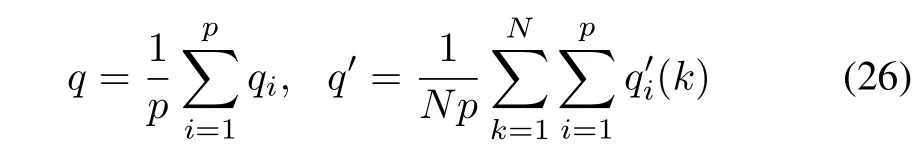
and analyze the ratio q′/q as a function of σ.This ratio is a decreasing function of the increasing intensity of randomness points at the deterioration of the modeling results.The tendency here is opposite to what is seen with respect to the previous performance index T.A mutual analysis of T and q′/q regarded as functions of σ helps establish some sound compromise in terms of the retained quality and the elevated level of consensus.
The above randomization scheme is one among possible alternatives and some other more refined options can be analyzed:
(i)a sound refinement could be to bring the component of randomness of varying intensity(σ1,σ2,...,σp)to different models.Some optimization of allocation of randomness(under the constraint σ = σ1+ σ2+ ···+ σp)could be anticipated as well.
(ii)The modification to the randomized approach could invoke the involvement of the prediction intervals that are quite often associated with the construction of the model.The random modifications of the outputs are confided to the values falling within the scope of the prediction intervals.Obviously,to follow this development path,the prediction intervals have to be provided.This is not an issue in case of some categories of models such as linear regression models(where prediction intervals are developed in a routine basis),however this could be more complicated and computationally demanding in case of models such as neural networks and rule-based models.
The randomization aspect of the output space(outputs of the models)was presented above;another option could be to consider randomization of the parameters of the models and/or a combination of randomization of the output and the parameter spaces.
VI.CONCLUDINGCOMMENTS
The study has offered a focused overview of the fundamentals of Granular Computing positioned in the context of data analytics and advanced system modeling.We identified a multifaceted role of information granules as a meaningful conceptual entities formed at the required level of abstraction.It has been emphasized that information granules are not only reflective of the nature of the data(the principle of justifiable granularity highlights the reliance of granules on available experimental evidence)but can efficiently capture some auxiliary domain knowledge conveyed by the user and in this way reflect the human-centricity aspects of the investigations and enhances the actionability aspects of the results.The interpretation of information granules at the qualitative(linguistic)level and their emerging characteristics such as e.g.,stability enhancement of the interpretability capabilities of the framework of processing information granules is another important aspect of data analytics that directly aligns with the requirements expressed by the user.Several key avenues of system modeling based on the principles of Granular Computing were highlighted;while some of them were subject of intensive studies,some other require further investigations.
By no means,the study is complete;instead it can be regarded as a solid departure point identifying main directions of further far-reaching human-centric data analysis investigations.A number of promising avenues are open that are well aligned with the current challenges of data analytics including the reconciliation of results realized in the presence of various sources of knowledge(models,results of analysis),hierarchies of findings,quantification of tradeoffs between accuracy and interpretability(transparency).
 IEEE/CAA Journal of Automatica Sinica2018年6期
IEEE/CAA Journal of Automatica Sinica2018年6期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Self-Tuning Asynchronous Filter for Linear Gaussian System and Applications
- Necessary and Sufficient Conditions for Consensus in Third Order Multi-Agent Systems
- Optimal Decoupling Control Method and Its Application to a Ball Mill Coal-pulverizing System
- Predictive Tracking Control of Network-Based Agents With Communication Delays
- Mathematical Study of A Memory Induced Biochemical System
- The Cubic Trigonometric Automatic Interpolation Spline
