Self-Similar Solution of Spherical Shock Wave Propagation in a Mixture of a Gas and Small Solid Particles with Increasing Energy under the Influence of Gravitational Field and Monochromatic Radiation

P.K.Sahu

Department of Mathematics,Government Shyama Prasad Mukharjee College,Sitapur-497111,Sarguja University,Ambikapur,Chhattisgarh,India

AbstractSimilarity solution for a spherical shock wave with or without gravitational field in a dusty gas is studied under the action of monochromatic radiation.It is supposed that dusty gas be a mixture of perfect gas and micro solid particles.Equilibrium flow condition is supposed to be maintained and energy is varying which is continuously supplied by inner expanding surface.It is found that similarity solution exists under the constant initial density.The comparison between the solutions obtained in gravitating and non-gravitating medium is done.It is found that the shock strength increases with an increase in gravitational parameter or ratio of the density of solid particles to the initial density of the gas,whereas an increase in the radiation parameter has decaying effect on the shock waves.

Key words:spherical shock wave,dusty gas,similarity solution,gravitational medium,Roche model,monochromatic radiation

1 Introduction

Radiation has an important role in several hydrodynamic processes related to shock waves and explosions.The role of radiation is not only limited to the luminescence of the heated body.It also affects the hydrodynamic movement of matter in form of heat exchange and energy transfer.In gasdynamics,if the effects of radiation are taken into account,the basic non-linear equations are of a very complicated form and therefore it is essential to establish such approximations,which are physically accurate and can afford considerable simplification.The problem of the interaction of radiation with gasdynamics has been studied by many authors by using the method of self-similarity developed by Sedov.[1]Marshak[2]studied the effect of radiation on the shock propagation by introducing the radiation diffusion approximation.He solved both the cases of constant density and constant pressure fields without invoking conditions of self-similarity.Using the same mode of radiation,Elliott[3]discussed the conditions leading to self-similarity with a specified functional form of the mean free-path of radiation and obtained a solution for self-similar explosions.Wang,[4]Helliwell[5]and Nicastro[6]treated the problems of radiating walls,either stationary or moving,generating shock at the head of self-similar flow- fields.Assuming the shock to be isothermal and transparent the self-similar solution of the central explosions in stars has been obtained by Ray and Bhowmick[7]including the effects of radiation.

The self-similar solutions have been used by Khudyakov[8]to discuss the problem of the motion of a gas under the action of monochromatic radiation.Khudyakov[8]has considered that a homogeneous gas at rest occupies a half-space bounded by a fixed plane wall and assumed that a radiation flux moves through the gas in the direction of the wall with a constant intensity j0per unit area.From the instant of the arrival of the radiation at the wall a shock wave is assumed to propagate out from the wall in the direction opposite to the radiation flux.The radiation flux is absorbed in the zone between the shock wave and the wall,and it is not absorbed in the undisturbed medium.It is also assumed that the gas itself does not radiate.Zheltukhin[9]has developed a family of exact solutions of one dimensional motion(plane,cylindrical or spherical symmetry)of a gas taking into account of the absorption of monochromatic radiation.Nath and Takhar,[10?11]Nath,[12]Vishwakarma and Pandey,[13]Nath and Sahu[14])have investigated the motion of a gas under the action of monochromatic radiation when the medium is ideal or non-ideal gas.Singh,[15]Nath and Sahu,[16]Sahu[17]have studied the motion of a gas under the influence of monochromatic radiation when the medium is mixture of gas and small solid particles.

For a long time,study of gas flow containing solid particles has been subject of engineering and scientific research due to its applications to fluidized beds,electrostatic precipitation of dust,centrifugal separation of particular matter from fluids,many chemical processing,solid particle motion in rocket exhaust and dust flow in geophysical and astrophysical problems. The study of shock waves in a mixture of a gas and small solid particles is of great importance due to its applications to nozzle lf ow,lunar ash flow,bomb blast,coal-mine blast,underground,volcanic and cosmic explosions,metalized propellant rocket,supersonic flight in polluted air,collision of coma with a planet,description of star formation,particle acceleration in shocks,shock in supernova explosions,formation of dusty crystals and many other engineering problems(see Refs.[18]–[33]).Recently,applications of dusty-gas flow studies to industrial and environmental issues have drawn attention.Serious studies for developing a system of removing dust particles from semiconductor wafers by using shock waves and nonstationary gasdynamic wave systems are examples of industrial applications(Shibasaki et al.[34]).The flow field,that develops when a moving shock wave hits a two-phase medium of gas and particles,has a close practical relation to industrial applications(solid rocket engine in which aluminum particles are used to reduce the vibration due to instability)as well as industrial accidents such as explosions in coalmines and grain elevators(Park and Baek[35]).

Miura and Glass[26]obtained an analytical solution for a planar dusty gas flow with constant velocities of the shock and the piston moving behind it.As they neglected the volume occupied by the solid particles mixed into the perfect gas,the dust virtually has a mass fraction but no volume fraction.Their results reflect the influence of the additional inertia of the dust upon the shock propagation.Pai et al.[18]generalized the well known solution of a strong explosion due to an instantaneous release of energy in gas(Sedov,[1]Korobeinikov[30])to the case of two-phase flow of a mixture of perfect gas and small solid particles,and brought out the essential effects due to presence of dusty particles on such a strong shock wave.As they considered non-zero volume fraction of solid particles in the mixture,their results reflected the influence of both the decrease of mixture’s compressibility and the increase of mixture’s inertia on the shock propagation(see,Pai,[31]Steiner and Hirschler[32]).

The gravitational forces have considerable effects on several astrophysical problems.A qualitative behaviour of the gaseous mass may be discussed with the help of the equations of motion and equilibrium taking gravitational forces into account.Carrus et al.[36]have obtained the similarity solutions of the propagation of shock waves in a gas under the gravitational attraction of a central body of fixed mass(Roche model).Rogers[37]has discussed a method for obtaining analytical solution of the same problem.

The influence of gravitational field on the medium with monochromatic radiation is not taken into consideration in all of the above mentioned works and the works known to author.The purpose of this study is to obtain similarity solutions for the spherical shock wave propagating in the dusty gas(a mixture of perfect gas and small solid particles)with monochromatic radiation.It is supposed that the medium is under the effect of a gravitational field which is because of the central massat the origin(Roche model).The equilibrium flow conditions are assumed to be maintained(as in Refs.[18–19,32–33]).This work is the extension of the work of Nath and Takhar[10]in spherical geometry under the action of a gravitational field with slightly different transformation.Also,the medium is taken to be dusty gas in place of an ideal gas.Singh[15]has considered same problem in cylindrical geometry with the assumption that medium to be non-gravitating,whereas here medium is under the influence of a gravitational field in spherical geometry with slightly different transformation.

Effects of change in the ratio of the density of solid particles to the initial density of the gas,the gravitational parameter,the mass concentration of solid particles in the mixture and the radiation parameter are work out in details.The viscosity terms are negligible.The cases of without and with gravitational field are compared. It is found that gravitational parameter and radiation parameter have in general opposite behaviour on the shock strength and flow variables.

2 Equations of Motion and Boundary Conditions

In Eulerian coordinates,the system of equations of gas dynamics describing the unsteady,adiabatic and spherically symmetric one-dimensional flow of dusty gas under the action of gravitational field and monochromatic radiation,can be expressed as(c.f.Khudyakov,[8]Nath and Takhar,[10?11]Nath and Sahu,[16]Pai et al.,[18]Vishwakarma and Nath,[33]Zedan,[38]Nath[39])

where r and t are independent space and time coordinates;w is the fluid velocity,ρ is the density,p is the pressure,emis the internal energy per unit mass,is the mass of the heavy nucleus at the center,is the gravitational constant,j be monochromatic radiation at radial distance r and time t,and K is the absorption coefficient.

Equation of state for the mixture of perfect gas and small solid particles may be written as(Nath and Sahu,[16]Pai et al.,[18]Vishwakarma and Nath[33])

where R?is the specific gas constant;T is the temperature of the gas(since equilibrium flow condition is maintained it is also of the solid particles);Z=Vsp/Vmbe volume fraction of solid particles in the mixture(here,Vspis the volumetric extension of solid particles,Vmis total volume of the mixture);and Kp=msp/mmixbe mass fraction of solid particles in the mixture(here,mspis total mass of the solid particles,mmixis the total mass of the mixture).

It is assumed that the specific volume of solid particles are independent from pressure and temperature variations.Hence,in mixture,equation of state of solid particles be

where ρspis the species density of the solid particles.

For the mixture of perfect gas and small solid particles,the internal energy per unit mass emcan be written as(see,Nath and Sahu,[16]Pai et al.,[18]Pai[31])

here Γ is the ratio of the specific heats of the mixture,which is given by(Pai et al.,[18]Pai[31])

We consider the absorption coefficient K to be varying as(Khudyakov,[8]Nath and Takhar,[10?11]Singh,[15]Sahu[17])

where the exponents σ,α,δ,s and l are rational numbers and the coefficient K0is a dimensional constant.

We assume that a spherical shock wave is propagating outwards from the point of symmetry in the undisturbed medium(mixture of perfect gas and small solid particles)with constant density,under the gravitational force.The flow variables immediately ahead of the shock front are

where the subscript “0” denotes the conditions immediately ahead of the shock.

Therefore,from(2),we have

where the undisturbed pressure upon the point of symmetry p0(0)is taken to be zero,since for p0(0)>0 the flow would not be self-similar.Here rsis the shock radius.

The expression for the initial volume fraction of the solid particles Z0is given by,

where μ0= ρsp/ρg0is the ratio of the species density of the solid particles to the initial species density of the gas ρg0in the mixture.

The Rankine-Hugonite jump conditions across the shock front,which is transparent for the radiation flux,are given by the conservation of mass,momentum and energy,(c.f.Nath and Takhar,[10?11]Singh,[15]Nath and Sahu,[16]Zel’dovich and Raizer[40])namely,

where the subscript “1” denotes the conditions immediately behind the shock front,Ws(=drs/dt)denotes the velocity of the shock front.Then from Eq.(14),the conditions across a shock propagating

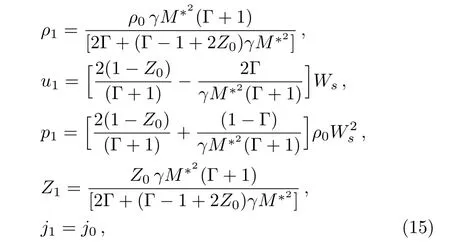
In Eq.(9),the dimensions of the constant coefficient K0are given by(Nath and Takhar,[10?11]Sigh,[15]Nath and Sahu[16])

For the self-similar solution(Sedov[1])the relation between ρ0,j0,p0is given as

Also,for self-similarity the radiation absorption coefficient K0must be dependent on the dimensions of j0,ρ0which is equivalent to s+l=?1.

The speed of sound in the mixture is given by

where the subscript S refers to the process of constant entropy.The effective shock Mach number Mereferred to the speed of soundin the mixture of perfect gas and small solid particles is given by

then the relation between shock Mach number M?and Meis given by

3 Self-Similarity Transformations

The inner boundary of the flow- field behind the shock is assumed to be an expanding piston.In frame work of self-similarity(Sedov[1])the velocity wp=drp/dt of the piston is assumed to obey a power law which results in Refs.[32]and[39].

where rpis the radius of the piston and t0denotes the time at a reference state,W0is the piston velocity at t=t0and n is a constant.The consideration of the ambient pressure p0imposes a restriction on n as n=?1/3(see Eq.(25)).Thus the piston velocity jumps,almost instantaneously,from zero to infinity leading to the formation of a shock of high strength in the initial phase.The piston is then decelerated.To justify the introduction of the form(21)for piston speed it may be observed that,in non-radiative hypersonic flow theory with slender bodies possessing power law profiles,the flow in the shocked layer is given by the solution of analogous unsteady piston problems with the stated piston speed.It is thus natural to take the same form for the corresponding radiative piston problems(following Wang,[4]Helliwell[5]).Concerning the shock boundary conditions,self-similarity requires that the velocity of the shock Wsis proportional to the velocity of the piston,that is

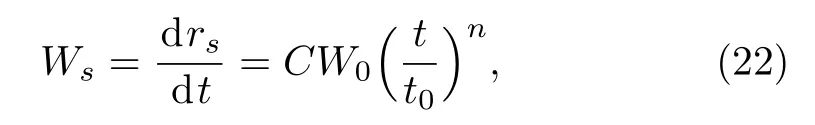
where C is a dimensionless constant.Using Eq.(22),the time and space coordinates can be changed into a dimensionless self-similarity variable η as follows

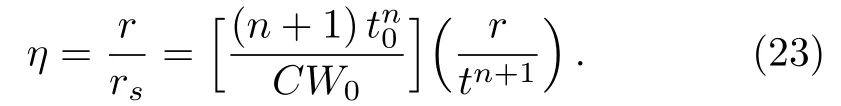
Evidently,η = ηp(=rp/rs)at the piston and η =1 at the shock.To obtain the similarity solutions,we write the unknown variables in the following form[32,39]

here U,P,R,and J are function of η only.

In order to obtain similarity solutions,the shock Mach number M?which occurs in the shock conditions(15)must be a constant parameter.Hence,

Using the similarity transformations(24),the system of governing partial differential Eqs.(1)–(4)transformed to the following system of ordinary differential equations

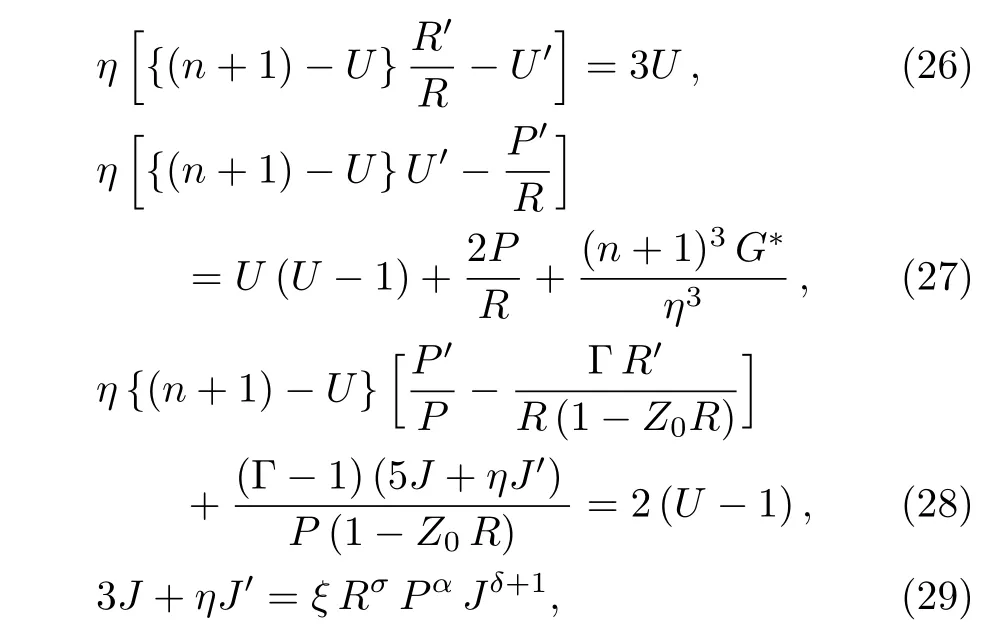
where

Solving the above set of differential equations(26)–(29)for dU/dη,dP/dη,dR/dη and dJ/dη,we have

where

Using the self-similarity transformations(24),the shock conditions(15)are transformed into

The adiabatic compressibility of the mixture of perfect gas and small solid particles may be calculated as(cf.Moelwyn-Hughes[41])

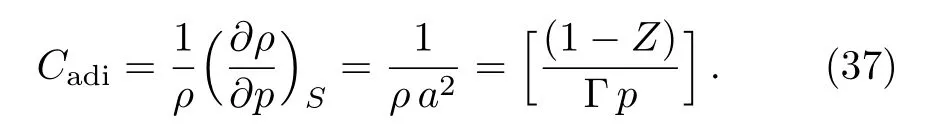
Using Eq.(24)in Eq.(37),we get the expression for the adiabatic compressibility as,

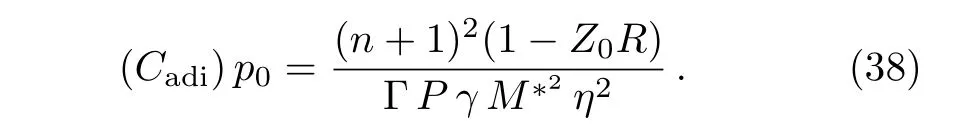
Also,the total energy of the disturbance is given by

Using Eqs.(7)and(24),Eq.(39)becomes

Hence,the total energy of the shock wave is non-constant and varies asThis increase of total energy may be achieved by the pressure exerted on the fluid by inner expanding surface(a contact surface or piston).This surface may be physically,the surface of the stellar corona or the condensed explosives or the diaphragm containing a very high-pressure driver gas.By sudden expansion of the stellar corona or the detonation products or the driver gas into the ambient gas,a shock wave is produced in the ambient gas.The shocked gas is separated from this expanding surface which is a contact discontinuity.This contact surface acts as a “piston” for the shock wave.Thus the flow is headed by a shock front and has an expanding surface as an inner boundary(piston).

The piston path coincides at ηp=rp/rswith a particle path.Using Eq.(21)to Eq.(24)the relation

can be obtained.Along with the shock conditions(36),the kinematic condition(41)at the piston surface needs to be satisfied.

For exhibiting the numerical solutions,it is convenient to write the flow variables in non-dimensional form as

4 Results and Discussion

The variation of flow variables(η =1)and(η = ηp)is obtained from Eqs.(31)–(34)with the boundary conditions(36)and(41)by the Runge-Kutta method of the fourth order.Parameter of the inert mixture(glass or alumina Al2O3)are within the following range:dust particle size is of the order of 1 μm–10 μm(Higashino and Suzuki,[19]Fedrov and Kratova[42]),the mass fraction(concentration)of solid particles in the mixture is varied from Kp=0 to Kp=0.4 and the material density of solid particles ρsp=2.5 g/cm3.This case may be realized in an air flow with a suspension of alumina and glass particles.Here,constant parameters are taken as[8,10?11,15?16,18,32,43]

The values γ =1.4,β′=1 may correspond to the mixture of air and glass particles(Miura and Glass[26]),and Kp=0 correspond to the dust free case.The value M?=5 of the shock Mach-number is appropriate,because we have treated the flow of a pseudo- fluid(small solid particles)and a perfect gas at a velocity and temperature equilibrium.The present work may be considered as the extension of the work of Nath and Takhar[10]in spherical geometry under the influence of a gravitational field with slightly different transformation.Also,the medium is taken to be mixture of a perfect gas and small solid particles in place of an ideal gas.Singh[15]has considered same problem in cylindrical geometry with the assumption that medium to be non-gravitating,whereas we have considered the medium under the influence of a gravitational field in spherical geometry with slightly different transformation.

Table 1 shows the position of the inner boundary surface ηpfor different values of Kp, μ0and G?with σ= ?1/2;α= ?1;s=1;δ=0;ξ=0.1;M?=5;n= ?1/3;γ=1.4;β′=1.Table 2 shows the position of the inner boundary surface ηpfor different values of Kp,μ0and G?with σ = ?1/2;α = ?1;s=1;δ=0;ξ=0.1;M?=5;n= ?1/3;γ=1.4;β′=1.Table 3 shows the position of the inner boundary surface ηpfor different values of Kp,μ0,G?and ξ with σ = ?1/2;α = ?1;s=1;δ=0;M?=5;n=?1/3;γ=1.4;β′=1.

Table 1 The position of the inner boundary surface ηpfor different values of Kp,μ0and G?with σ = ?1/2;α = ?1;s=1;δ=0;ξ=0.1;M?=5;n=?1/3;γ=1.4;β′=1.

Fig.1 Variation of the reduced flow variables in the region behind the shock front(a) fluid velocity w/w1,(b)density ρ/ρ1,(c)pressure p/p1,(d)radiation flux j/j1,(e)adiabatic compressibility(Cadi)p0:(1)Kp=0,G?=2;(2)Kp=0.2,G?=2,μ0=1;(3)Kp=0.2,G?=2,μ0=20;(4)Kp=0.2,G?=2,μ0=100;(5)Kp=0.4,G?=2,μ0=1.0;(6)Kp=0.4,G?=2,μ0=20;(7)Kp=0.4,G?=2,μ0=100.

Table 2 The position of the inner boundary surface ηpfor different values of Kp,μ0and G?with σ=?1/2;α =?1;s=1;δ=0;ξ=0.1;M?=5;n=?1/3;γ=1.4;β′=1.

Figures 1,2,and 3 represent the variation of reduced fluid velocity w/w1,reduced pressure p/p1,reduced density ρ/ρ1,reduced radiation flux j/j1and the adiabatic compressibility(Cadi)p0against the similarity variable η for Kp,μ0(see,Fig.1);for Kp,μ0,G?(see,Fig.2)and for Kp,μ0,G?,ξ(see,Fig.3).

These figures demonstrate that the reduced velocity,the reduced pressure(in gravitating case)and the the adi-abatic compressibility(in non-gravitating case)increases;whereas the reduced density,the reduced radiation flux,the reduced pressure(in non-gravitating case)and the adiabatic compressibility(in gravitating case)decreases as we move from the shock front to the inner boundary surface(see Figs.1,2,and 3).

Fig.3 Variation of the reduced flow variables in the region behind the shock front(a) fluid velocity w/w1,(b)density ρ/ρ1,(c)pressure p/p1,(d)radiation flux j/j1,(e)adiabatic compressibility(Cadi)p0:(1)Kp=0,G?=0,ξ=0.1;(2)Kp=0,G?=0,ξ=20;(3)Kp=0,G?=2.0,ξ=0.1;(4)Kp=0,G?=2.0,ξ=20;(5)Kp=0.2,μ0=20,G?=0,ξ=0.1;(6)Kp=0.2,μ0=20,G?=0,ξ=20;(7)Kp=0.2,μ0=20,G?=2.0,ξ=0.1;(8)Kp=0.2,μ0=20,G?=2.0,ξ=20;(9)Kp=0.2,μ0=100,G?=0,ξ=0.1;(10)Kp=0.2,μ0=100,G?=0,ξ=20;(11)Kp=0.2,μ0=100,G?=2.0,ξ=0.1;(12)Kp=0.2,μ0=100,G?=2.0,ξ=20.

From Tables 1–3 and Figs.1(a)–1(e),2(a)–2(e),3(a)–3(e)it is found that the effects of an increase in the value of Kpare as follows:

(i)To decrease ηpwhen μ0=1 i.e.the shock strength is decreased;whereas reverse behaviour is observed when μ0=20,100(see,Tables 1–3);

(ii)To increase the flow variables w/w1, ρ/ρ1whenμ0=1 but to decrease them for μ0=20,100;whereas the reverse behaviour is obtained for flow variables j/j1at any point in the flow- field behind the shock front(see Figs.1(a),1(b),1(d));

(iii)The flow variables p/p1(forμ0=1),(Cadi)p0(forμ0=20,100)decreases near shock and increases near inner boundary surface;however flow variables p/p1(forμ0= 20,100)increases,(Cadi)p0(forμ0=1)decreases at any point in the flow- field behind the shock front.(see Figs.1(c),1(e));

(iv)The reduced fluid velocity w/w1increases in in nongravitating case;whereas in gravitating case it increases when G?=1(μ0=20)but decreases when G?=1(μ0=100)and G?=2,3 at any point in the flow- field behind the shock front(see Figs.2(a),3(a));

(v)The reduced pressure p/p1decrease for G?=0,1;but it increases when G?=2,3 at any point in the flow- field behind the shock front(see Figs.2(c),3(c));

(vi)The reduced density ρ/ρ1decreases;whereas the reduced radiation flux j/j1increases for all values of G?at any point in the flow- field behind the shock front(see Figs.2(b),2(d),3(b),3(d)).

Physical interpretation of these effects is as follows:

In the case ofμ0=1,small solid particles of density equal to that of the perfect gas in the mixture occupy a significant portion of the volume which lowers the compressibility of the medium remarkably.Then,an increase in Kpfurther reduces the compressibility which causes an increase in the distance between the shock front and the inner expanding surface,a decrease in the shock strength,and the above behaviour of the flow variables.Similar effects may be obtained forμ0=20.

Table 3 The position of the inner boundary surface ηpfor different values of Kp,μ0,G?and ξ with σ = ?1/2;α = ?1;s=1;δ=0;M?=5;n= ?1/3;γ =1.4;β′=1.

In the case ofμ0=100,small solid particles of density equal to hundred times that of the perfect gas in the mixture occupy a very small portion of the volume,and therefore compressibility is not lowered much;but the inertia of the mixture is increased significantly due to the particle load.An increase in Kpfrom 0.2 to 0.4 forμ0=100,means that the perfect gas in the mixture constituting 80%of the total mass and occupying 99.75%of the total volume now constitutes 60%of the total mass and occupies 99.34%of the total volume.Due to this fact,the density of the perfect gas in the mixture is highly decreased which overcomes the effect of incompressibility of the mixture and ultimately causes a small decrease in the distance between the piston and the shock front,an increase in the shock strength,and the above nature of the flow variables.

From Tables 1–3 and Figs.1(a)–1(e),2(a)–2(e),3(a)–3(e)it is shown that the effects of an increase in the ratio of the density of the solid particles to the initial density of the gasμ0are as follows:

(i)The distance of the inner boundary surface from the shock front decreases,i.e.the shock strength increases(see Tables 1–3);

(ii)To decrease the flow variables w/w1,ρ/ρ1;whereas to increase the flow variable(Cadi)p0at any point in the flow- field behind the shock front(see Figs.1(a),1(b),1(e),2(a),2(b),2(e),3(a),3(b),3(e));

(iii)The reduced pressure p/p1decreases for G?=0,1;but it increases when G?=2,3 at any point in the flow- field behind the shock front(see Figs.1(c),2(c),3(c));

(iv)The reduced radiation flux j/j1increase for gravitating case;whereas it increase near the shock and decreases near the piston for non-gravitating case(see Figs.1(d),2(d),3(d)).

The above effects are more impressive at higher values of Kp.These effects may be physically interpreted as follows:By an increase inμ0(at constant Kp),there is high decrease in Z0,i.e.the volume fraction of solid particles in the undisturbed medium becomes,comparatively,very small.This causes comparatively more compression of the mixture in the region between shock and inner boundary surface,which displays the above effects.

From Tables 3 and Figs.3(a)–3(e)it is obtained that the effects of an increase in the value of the radiation parameter ξ are as follows:

(i)To decrease ηpi.e.to decrease the shock strength(see Table 3);

(ii)To decrease the flow variables w/w1,p/p1and j/j1at any point in the flow- field behind the shock front(see Figs.3(a)–3(b),3(d));

(iii)The reduced density ρ/ρ1decreases near shock and increases near inner boundary surface(see Fig.3(c));

(iv)the adiabatic compressibility(Cadi)p0increases for non-gravitating case,but it increases near shock and decreases near inner boundary surface for gravitating case(see Fig.3(e)).

The above effects show that the monochromatic radiation is more absorbed by the gas in the flow- field behind the shock by an increase in the radiation parameter ξ.

From Tables 1–3 and Figs.2(a)–2(e),3(a)–3(e)it is observed that the effects of an increase in the value of the gravitational parameter G?are as follows:

(i)The distance of the inner boundary surface from the shock front decreases,i.e.the flow- field behind the shock become denser.This shows that there is a increase in the shock strength(see Tables 1–3);

(ii)To increase the flow variables w/w1,p/p1and j/j1;whereas to decrease the flow variable(Cadi)p0at any point in the flow- field behind the shock front(see Figs.2(a)–2(b),2(d)–2(e),and 3(a)–3(b),3(d)–3(e));

(iii)The reduced density ρ/ρ1increases near shock and decreases near inner boundary surface(see Figures 2(c)and 3(c)).

The above effects show that an increase in the radiation parameter ξ and the gravitational parameter G?have ingeneral opposite behaviour on the flow variables and the shock strength.

5 Conclusion

In the present work the similarity solution for unsteady adiabatic flow of a mixture of perfect gas and small solid particles behind a spherical shock wave,driven out by a piston,under the influence of monochromatic radiation and a gravitational field due to central mass at the origin(Roche model)is investigated.The constructed diagram of variations in the flow variables and the tables give a clear representation of global variations in the flow- field and the shock strength.It is shown that in the ideal dusty gas under gravitational field,the propagating shock wave is found to be most influenced by the gravitational parameter,as the gravitational parameter is increased the shock strength is increased.On the basis of this study,one may draw the following conclusions:

(i)The effects of gravitational field and monochromatic radiation on the flow variables have been studied in dusty gas(a mixture of perfect gas and small solid particles)which was not done earlier.

(ii)The total energy of the flow field behind the spherical shock wave is not constant but proportional to the shock radius.

(iii)Distance of the inner boundary surface from the shock front is less in gravitating case as compared to the non-gravitating case.

(iv)The consideration of ambient pressure p0sets a value of the inner boundary surface velocity index n as n=?1/3;whereas in the case when p0is neglected n can take any value such that n>?1(see Steiner and Hirschler[32]).

(v)The gravitational parameter G?and the radiation parameter ξ have in general opposite behaviour on the flow variables and the shock strength.

We give examples to make clear the nature of shock waves in dusty medium.However,they serve mainly as illustrations of how the shock waves in dusty medium can be described.In reality,many other processes may be important and a more comprehensive analysis of the shock may be needed for its applications in astrophysics or elsewhere.The presence of gravitational field increases the compressibility of the medium,due to which it is compressed and therefore the distance between the inner contact surface and the shock surface is reduced.The shock waves in gravitating dusty gas can be important for description of shocks in supernova explosions,in the study of central part of star burst galaxies,nuclear explosion,rupture of a pressurized vessel and explosion in the ionosphere.Other potential applications of this study include analysis of data from the measurements carried out by spacecraft in the solar wind and in neighbourhood of the Earth’s surface(Korolev and Pushkar[44]).The present study is related to and our results may be helpful to some questions being investigated in astrophysical plasmas(Popel et al.,[45]Popel and Gisko[21]):

5.1 Star Formation in Shocked Molecular Clouds

One believes that most of new stars are formed in dustmolecular clouds and shock waves initiate this process.They create the increase in density,sufficient for the gravitational selfcompression(Jeans instability).The observations show that the presence of dust is well correlated with star formation in dusty clouds.The problem is to determine which process is more important:condensation due to the dust attraction or the gravitational self-compression in the shock wave.

5.2 Shocks From Supernova Explosions

The layer of dust behind the supernova shock is observed usually.The problem is to verify whether the layer of dust is related to the process of dust condensation behind the shock wave front.

Acknowledgement

The author is grateful to Dr. G.Nath,Associate Professor of Mathematics,MNNIT Allahabad,Allahabad-211004,India for many useful discussions and suggestions.