Existence Results of the Solution to Neutral SFDEs with Infinite Delay
ZHANG Hai-tao, WANG Jun-ping
(1.Hefei Preschool Education College,Hefei 230011,China;2.School of Mathematics,Hefei University of Technology,Hefei 230009,China)
Abstract:This paper is devoted to derive two existence theorems of solutions to a class of neutral stochastic functional differential equations(NSFDEs,in short)with infinite delay at phase space BC((-,0];Rd) which denotes the family of bounded continuous Rd- value functions φ defined on (-,0] with norm ||φ||=sup -<θ0|φ(θ)| under the drift coefficient is increasing,left continuous,satisfying linear growth condition.In doing so,we first obtain a comparison result of the solutions under some Lipschitz conditions on the coefficients by means of truncation and penalization method.
Key words:Neutral stochastic functional differential equation;infinite delay;penalization method
Introduction
For the applications in science and technology,stochastic differential equations(SDEs in short)attracted researchers;great interest.Generally,the state of stochastic systems depend not only on the present state but also on its past history leading to stochastic functional differential equations with delay(SFDEs in short).Mao[8]discussed this kind SFDEs under uniform Lipschitz condition and linear growth condition on the coefficients.An existence theorem of the solutions to SFDEs was obtained under weak condition on the drift coefficient appeared in Halidias and Ren[3].Following this way,Wei and Wang[13]considered one such chlass of the so-called stochastic functional differential equations with infinite delay(ISFDEs inshort)at phase spaceBC((-,0];Rd) to be described below.They proved obtained the existence and uniqueness of the solution to ISFDEs with classical Lipschitz condition and a kind of weakened linear growth condition.Further,the author derived an existence and uniqueness of the solutions to ISFDEs under more generalized conditions[11,12].
Another important kind of SFDEs is the following neutral SFDEs with finite delay which could be used in chemial engineering and aeroelasticity,introduced in Kolmanovskii and Myshkis[5].
d[X(t)-G(xt)]=f(t,Xt)dt+g(t,Xt)dBt.
(1)
Following it,Mao[9]derived the existence,uniqueness and asymptotic properties of the solutions to the following generalized neutral SFDEs with finite delay and the coefficient satisfying the classic Lipschitz condition and linear growth condition.
d[X(t)-G(X(t-τ))]=f(t,Xt,X(t-τ))dt+g(t,Xt,X(t-τ))dBt.
(2)
Motivated by[13]and[9],Zhou and Xue[14]showed the existence and uniqueness theorem of the solution to neutral stochastic functional differential equations with infinite delay(INSFDEs in short)which had the same form as (1)under the conditions raised in[13]on the coefficients.
The classic SDEs:
has a unique solution when the drift and diffusion coefficients,b andσ,satisfy the Lipschitz plusing linear growth condition.Many works have been done to relax the assumptions on b andσ.One can see Barlow[1],Halidias and Kloeden[2],Krylov[6]and Protter[10]for more details.
Motivated by the above works,in this paper we will derive two existence theorems of solutions to INSFDEs under the condition of drift coefficient is increasing,left continuous,satisfying linear growth condition.Such equations arise in the following INSFDEs:
d[X(t)-G(Xt)]=H(Xt)dt+dBt,
whereH:R→Ris the Heaviside function,which is defined by
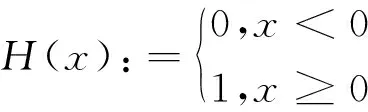
Such equations arise,for example,when one considers the effects of background noise on neutral switching systems with infinite delays or other discontinuous ordinary defferential equations.One can see Heikkil?,and Lakshmikantham[4].In order to obtain the existence of the solutions,we first obtain a comparison result of the solutions under some Lipschitz conditions of the coefficients by means of the truncation and penalization method.
The paper is arranged as follows.In section 2,we show the problem and introduce some notations.In Section 3,we derive an existence result with discontinuous drift coefficient.Another existence result with continuous drift coefficient by means of approximation of Lipschitz functions is given in the last Section.
1 Preliminaries
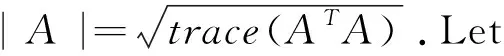
In what follows,we consider the following d-dimensional INSFDEs:
d[X(t)-G(Xt)]=f(t,Xt)dt+g(t,Xt)dB(t),t0tT.
(3)
whereXt={X(t+θ):-<θ0} can be regarded as aBC((-,0];Rd)-value stochastic process,wheref:[t0,T]×BC((-,0];Rd)→Rd,g:[t0,T]×BC((-,0];Rd)→Rd×mandG:BC((-,0];Rd)→Rdbe Borel measurable.
The initial value of(3)is given as follows:
Xt0=ξ={ξ(θ):-<θ0} isFt0- measurable,
BC((-,0];Rd)-value random variable
(4)
Such thatξ∈Μ2((-,T];Rd).
Remark1 Zhou and Xue[14]shows that there exists a unique solution to INSFDEs(3)with initial value(4)under the Lipschitz conditions and linear growth condition.It is obvious that there exists a a unique solutionX(t)∈Μ2((-,T];Rd)for INSFDEs(3)with initial value(4)under Lipschitz condition and the following linear growth condition.Thus,there exist a positive constant C such that for anyφ,ψ∈BC((-,0];Rd)andt∈[t0,T]
|f(t,φ)|∨|g(t,φ)|C(1+||φ||).
(5)
Now,we give a comparison result of the solutions under some Lipschitz conditions on the coefficients by means of the truncation and penalization method.Consider the following problems:
d[X(t)-G(Xt)]=f1(t,Xt)dt+g(t,Xt)dB(t),t0tT,
(6)
d[X(t)-G(Xt)]=f2(t,Xt)dt+g(t,Xt)dB(t),t0tT,
(7)
Suppose thatξ1ξ2a.s.andf1(t,x)f2(t,x)for allt∈[t0,T],x∈BC((-,0];Rd).We wnat to prove the following theorem.
Theorem1 Assume thatf1orf2satisfies the Lipschitz condition,linear growth condition and thatGis monotone decreasing and atisfies the Lipschitz condition.Then,ifX1is a solution of problem(6)andX2of problem(7)theX1X2for all t a.s.
Proof.Suppose thatf2satisfies the Lipschitz condition.We define the truncation and penalization functions as follows
It is easy to see that |p(x,y)-p(x,z)||y-z| and the same holds ofr(·).We consider now the following equation
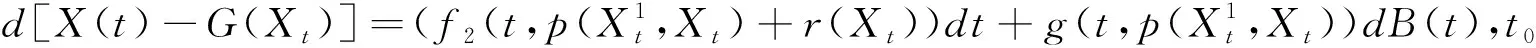
(8)
The coefficients satisfies the above assumptions.So,(8)has a unique solution,denoted asY(t).
We suppose that there exists an interval (t1,t2)?[t0,T] such thatY(t1)=X1(t1) andX1(t1)≥Y(t) for allt∈(t1,t2).Then,it follows that
d[(Y(t)-X1(t))-(G(Y(t))-G(X1(t)))]
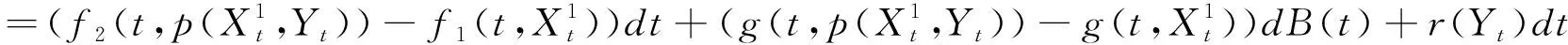
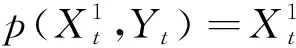
The proof remains in fact the same,with minor modifications,iff1satisfies the Lipschitz condition.
Remark2 Note also,that if we have strict inequalityf1 In this section,we assume thatfis increasing,left continuous and satisfyingf(t,x)≥0 for all (t,x)∈[t0,T]×BC((-,0];Rd) but not discontinuous. In order to obtain the existence of solutions to(3)with initial value(4),fort0tT,wei define following Picard sequence: (9) whereX0=LtwithLtis the unique solution of the following: d[Lt-G(Lt)]=g(t,Lt)dB(t) which has the same initial value as INSFDEs(3). So,X1≥Ltforf≥0 and the Comparison Theorem.Thus,Xnis an increasing sequece and we shall prove thatXnis bounded inS2norm. In the sequel,C>0 is a constant which can change from line to line. |G(φ)-G(ψ)|2K0||φ-ψ||2. (10) Moreover,f,g satisfy the linear growth condition.Then there exists a positive constantC1such that for allt∈(-,T],n≥1 E|Xn(t)|2C1. (11) Proof.Obviously,X0(t)∈Μ2((-,T]:Rd).By induction,Xn(t)∈Μ2((-,T]:Rd).In fact,from(9), E[supt0st|Xn(s)|2] (12) From H?lder inequality,we have E[supt0st|Xn(s)|2] (13) For We obtain 〗E[supt0st|Xn(s)|2]C+8K0E[supt0st|Xn-1(s)|2] (14) Note that maxE|Xn-1(s)|2ds =max {E|ξ(0)|2,E|X1(s)|2,A,E|Xk-1(s)|2} ={E||ξ||2,maxE|Xn(s)|2} (15) So,we have maxE[supt0st|Xn(s)|2] (16) It follows maxE[supt0st|Xn(s)|2] (17) Gronwall inequality shows the desired result. Now,we give the first result of the paper. Theorem2 let f be increasing in the second variable,left continuous,satisfying(5)andf(t,x)≥0 for all (t,x)∈[t0,T]×BC((-,0];Rd),g satisfy Lipschitz condition and(5),G be monotone decreasing and satisfy Lipschitz condition(10).Then,there exists at least one solution for INSFDEs(3)with initial value(4). Proof.From Theorem 1,(Xn)is increasing,and Lemma 1 shows that it is bounded inS2,we deduce from the Dominated Convergence Theorem thatXnconverges inS2.We denote byXthe limit of (Xn).So we get for almost allω, (18) and (19) Thus,for almost allωand uniformly int, (20) From the property ofgand the continuity of the stochastic integral,we get the following convergence in probability: (21) Noting thatXnis an increasing sequence we have also that the above convergence is alsoP- a.s.Finally,it is easy to prove thatXn→Xconverges uniformly int. So,taking limits in(9),we deduce thatXis our desired solution for(3)with initial value(4). In this section we do not suppose thatfis Lipschitz continuous but only continuous.In order to have an existence theory in this case we can approximatefby a monotone sequencefn.For a continuous function with linear growth,we have the following Lemma: Lemma2 (cf.Lepeltier and San Martin[7])Letfbe a continuous function with linear growth(5).Definefn(t,y)=inf{f(t,q)+n|y-q|:q∈Q},then forn>C,fnsatisfies: 1)Linear growth condition:|fn(x)|C(1+|x|); 2)Monotonicity:fn(x)↑f(x); 3)Lipschitz condition:|fn(x)-fn(y)|K|x-y|; 4)Strong convergence:ifxn→x,thenfn(xn)→f(x). Fort0tT,we defineand the following Picard sequence: (22) The under condition offnin Lemma 2,gandGsatisfying the conditions as Lemma 1,then(22)has a unique solution.From the comparison theorem,we have thatXnis an increasing sequence.We want to prove thatXnconverges to someXwhich is a solution to our problem(not unique). Lemma3 Under condition offnshowed in Lemma 2,gandGsatisfying the conditions as Lemma 1,then there exists a positive constantC2such that for allt∈(-,T],n≥1,it holds that E|Xn(t)|2C2. (23) Its main proof follows the same program as Lemma 1.So,we omit it here.Our second existence result of INSFDEs is the following: Theorem3 Letfsatisfy linear growth condition(5),g satisfy(H1)and(5),G be monotone decreasing and satisfy(H2).Then there exists at least one solution to INSFDEs(3)with initial value(4). Its main proof follows the same program as Theorem 2.2 INSFDEs with discontinuous drift coefficient
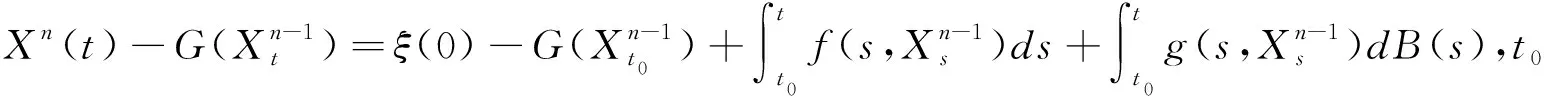
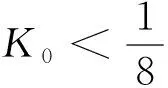
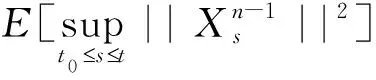

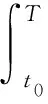
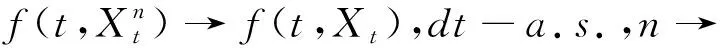

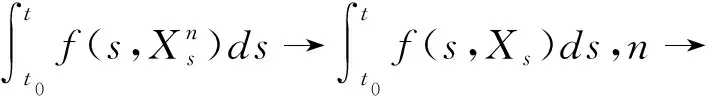
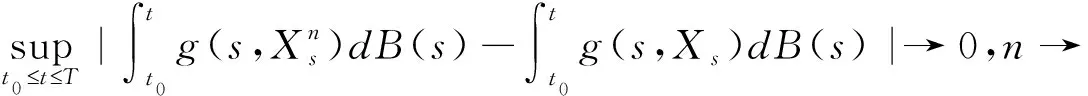
3 INSFDEs with continuous drift coefficient

